Improved Inversion of Scanning Electrical Mobility Spectrometer Data Using a New Multiscale Expectation Maximization Algorithm

Abstract

The accuracy of particle size distributions obtained from scanning electrical mobility spectrometer (SEMS) measurements is strongly dependent on the accurate consideration of the instrument characteristics in the formulation of the SEMS problem and the effective inversion of the resulting SEMS equation. The estimation of size distributions from SEMS measurements requires a solution of the discretized form of the Fredholm integral equation of the first kind. The often ill-conditioned nature of the linear inverse problem coupled with the possible presence of measurement noise complicates these calculations. The use of standard inversion approaches, such as nonnegative least squares (NNLS) or regularization-based algorithms, requires SEMS measurements with significant signal-to-noise ratio or some a priori knowledge of the shape of the sampled size distribution. These severe constraints for SEMS measurements can be relaxed with the new multiscale expectation-maximization SEMS inversion method introduced here. Performance testing with a broad range of sample size distributions and SEMS operating conditions suggests that the multiscale approach is generally more accurate than both the NNLS and regularization approaches.

Copyright 2013 American Association for Aerosol Research

1. INTRODUCTION

The evolution and fate of airborne particles in the atmosphere is dependent on a variety of particle properties, including their size, shape, density, bulk composition, and surface properties. Size is a particularly critical parameter, especially for particles with diameters smaller than 100 nm, that is, ultrafine particles. For example, growth rates or inhalation-based health effects associated with ultrafine particles are more strongly dependent on the size-related surface curvature (Seinfeld and Pandis 2006) or noncontinuum transport characteristics (Brown et al. 2001), respectively, than on other particle properties. Size distribution measurements are, therefore, critical to accurately characterizing aerosol populations, particularly in the sub-100 nm size range.

Size distribution measurements of ultrafine particles are most commonly made using a scanning electrical mobility spectrometer (SEMS; Wang and Flagan 1990). An SEMS system consists of a differential mobility analyzer (DMA) that classifies particles over a narrow range of mobilities, and a downstream particle detector, typically a condensation particle counter (CPC), to count the classified particles. By operating the DMA in a scanning mode, that is, with a time-varying voltage, a broad range of particle mobilities can be continuously classified. The direct inversion of SEMS count data to obtain particle size distributions is possible using the approach of Stolzenburg and McMurry (2008), if the sampled particles are nondiffusive, the SEMS transfer function can be assumed to be the same as that of the fixed-voltage DMA (Knutson and Whitby 1975), and the sampled particle size distribution is much broader than the DMA resolution.

Nonidealities such as particle diffusion (Stolzenburg 1988; Hagwood et al. 1999), concentration smearing between the DMA and the detection region (Russell et al. 1995; Collins et al. 2002), and transfer function distortion resulting from fast-scan DMA operation (Collins et al. 2004; Dubey and Dhaniyala 2008) can, however, complicate the relationship between SEMS count data and the sampled size distribution. Under such conditions, particles of a wide range of sizes will contribute to an SEMS channel count data, and the calculation of size distributions will require the solution of an equation of the form of a Fredholm integral equation of the first kind (Lloyd et al. 1997). The integral equation can be appropriately discretized to obtain a linear algebraic equation that relates the SEMS channel data to the sampled size distribution through a Kernel matrix. Particle size distributions can then be determined from a direct matrix inversion.

A matrix inversion approach to calculate particle size distributions is complicated by the ill-posed and often ill-conditioned nature of the problem. For an ill-conditioned problem, a small error in the measured signal or the problem formulation can result in a huge discrepancy in the estimated size distribution. Errors in the measured signal are primarily associated with CPC counting statistics, which become particularly large as the counts per channel decrease (Owen et al. 2012). Errors in problem formulation may arise from uncertainty associated with the precision and accuracy of DMA voltage and flow measurements, and their associated effect on the instrument transfer function

(Kinney et al. 1991). To overcome the combined effect of data noise and ill-conditioning of the transfer matrix, robust data analysis techniques are required.

Several different algorithms have been proposed to solve inversion problems similar to that associated with the SEMS instrument. These include: linear or nonlinear iterative techniques (Twomey 1963, 1975; Lawson and Hanson 1974), regularization and artificial smoothening estimation techniques (Markowski 1987; Hansen and O’Leary 1993), least-square error approaches (Lawson and Hanson 1974), likelihood estimation (Meyer 1985), and extreme value estimation (Hopke and Paatero 1994). Specifically, for inversion of SEMS data, commonly used approaches include: the Twomey algorithm (Twomey 1975) and the Tikhonov regularization approach (Talukdar and Swihart 2004). Accurate size distribution calculations are often possible with these schemes under typical SEMS operation, that is, with a relatively narrow transfer function and sufficient particle counts per channel.

For fast-scanning operations, accurate calculation of size distributions from SEMS data requires the inverse problem to be formulated considering the diffusional scanning DMA transfer functions and downstream smearing between the DMA and the CPC (Collins et al. 2002, 2004; Dubey and Dhaniyala 2008, 2011). The effectiveness of the existing inversion algorithms in solving the resulting ill-conditioned problem must then be evaluated. Here, a new multiscale inversion technique, based on the approach of Nowak and Kolaczyk (2000), is introduced for the solution of the fast-scanning SEMS problem. The accuracy of this multiscale approach is compared with that of the constrained least-square and regularization approaches for a range of test cases.

2. SEMS PROBLEM FORMULATION

The SEMS data consists of time-varying CPC counts binned into different channels, with the smallest possible bin width being determined by the fastest measurement time of the counter. The SEMS signal, that is, particle counts in the nth channel [y_n ], corresponding to a mean classification voltage, V, and a counting time interval, Δt, is related to the sampled size distribution dN/dlogD_p as

where Q_a is the aerosol flow rate sampled into the DMA, Δt is the counting time interval, η_CPC is the CPC detection efficiency, η_DMA is the DMA penetration efficiency, is the fraction of particles of diameter D_p with n_q number of charges, Ω_SEMS is the SEMS transfer function that determines the fraction of particles of diameter D_p with n_q charges sampled out at a mean classification voltage V over a counting time interval, Δt.

Considering only the singly charged particles in the SEMS data analysis, the problem formulation (Equation (1)) can be simplified to

Calculation of particle size distributions from the measured particle count data using Equation (2) requires consideration of the details of the SEMS operation.

2.1. Ideal Case: High-Resolution SEMS Operation

Often, SEMS measurements are made under high-resolution instrument operation such that only particles of a narrow mobility range, relative to the sampled particle size distribution, contribute to count data in a channel. Such high-resolution SEMS measurements require the DMA to be operated at high sheath-to-aerosol flow ratio and voltage (Flagan 1998), significant voltage scan time (Dubey and Dhaniyala 2008), and minimal transit time for particles between DMA and the downstream counter (Collins et al. 2002). Under ideal SEMS operation, the transfer function can be assumed to be the same as that of the nondiffusive DMA. Under such conditions, the DMA and CPC efficiencies and the fraction of charged particles are largely constant over the size range where the SEMS transfer function is nonzero. The SEMS equation (Equation (2)) can then be simplified to

where D* _p,1 is the mean singly charged particle diameter sampled out at voltage V and is the normalized particle electrical mobility given by the following relation:

where Z_p is the particle electrical mobility and Z* _p is the mean particle electrical mobility extracted from the DMA at a fixed voltage V, Q _sh is the sheath flow in the DMA, r ₂ and r ₁ are the outer and inner radii of the classifier section, respectively, and L is the length of the DMA classifier section. Integrating the transfer function in a mobility space, the SEMS equation becomes

Considering the mobility–diameter relation (Stolzenburg and McMurry 2008),

where a*₁ is the mobility–diameter coefficient, with a value between 1 and 2 corresponding to a mean diameter, D* _p,1, the SEMS problem formulation can be reduced to

The integral term on the right side is the DMA transfer function area, which for a balanced flow case (i.e., identical aerosol and sample flows) is just the aerosol-to-sheath flow ratio, β (Knutson and Whitby 1975). The SEMS equation, thus, reduces to

The particle size distribution can then be obtained directly from the knowledge of the particle count data in the different channels.

2.2. Nonideal Case: Low-Resolution SEMS Operation

Typically, the transfer function of an SEMS system, Ω_SEMS, is different from that of a fixed-voltage DMA, Ω_DMA, as it includes the effects of plumbing delay between DMA and CPC, and particle concentration smearing in the tubing downstream of DMA and within the CPC. The SEMS transfer function, Ω_SEMS can be obtained from Ω_DMA following the procedure shown in Equation (8):

where Ω_ATF,DMA is the DMA arrival time transfer function (ATF), defined as the distribution of arrival times of particles of a selected mobility, for the DMA operated in a scanning mode (Dubey and Dhaniyala 2008). In Equation (8), the first step involves the transformation of the DMA mobility transfer function (Ω_DMA) to an ATF (Ω_ATF,DMA) following the approach described in Dubey and Dhaniyala (2008). In the second step, the time-based SEMS ATF (Ω_ATF,SEMS) is obtained from the time-based DMA ATF (Ω_ATF,DMA) considering the effects of smearing and plumbing delay on the particle arrival times using the approach described in Dubey and Dhaniyala (2011). The SEMS ATF is then transformed to a mobility-based SEMS transfer function (Ω_SEMS) using the approach of Dubey and Dhaniyala (2008).

A low-resolution SEMS transfer function results in particles of a wide range of mobilities contributing to SEMS data in one channel and under such conditions, the simplifications made in Equation (3) are not valid. The size distribution calculations require a solution to the discrete form of the SEMS equation, expressed as

where i is the particle diameter bin number, is the total number of discrete particle diameter bins, is the mean singly charged diameter corresponding to the ith bin, and V_n is the mean voltage over the measurement time period for the nth particle count channel. The discrete SEMS equation can be reduced to a matrix equation

For a total number of discrete particle size bins and total number of particle count channels , the data set, (vector of length ) consists of the CPC counts recorded during an SEMS scan, and x (vector of length ) is the discretized size distribution of the sampled particles, and ( × matrix) is the kernel function of the instrument. The kernel function consists of the size-dependent charge fraction, SEMS transfer function, the CPC counting efficiency, and the DMA penetration efficiency. To calculate the particle size distribution, , the kernel function must be inverted.

Assuming that the measurement noise associated with CPC counts has a Poisson probability density function, the estimated CPC count at any time interval can be expressed as

Consider the special, simple case of monodisperse aerosol (say, bin m₁ ) sampled into the SEMS system. Depending on the nature of the kernel function, these particles might contribute to data in multiple channels. The estimated size distribution () can be obtained from the total count of the monodisperse particles sampled over the entire scan operation (), as

Thus, a Poisson error in the channel count data results in a Poisson error in the estimated size distribution.

3. INVERSION TECHNIQUES

For a polydisperse aerosol, the calculation of particle size distribution from SEMS data requires the solution of a system of linear equation (Talukdar and Swihart 2004). The possible presence of noise in the count data, however, complicates the inverse calculation. The accuracy of the inverted size distribution depends on the signal-to-noise ratio of the data set and the condition number of the kernel function. The condition number of the kernel function can be quantified as the ratio of the maximum to minimum singular value of the matrix and this number determines the propagation of measurement noise to the calculated size distribution. A high condition number can result in a large error in the calculated particle size distribution even if the signal-to-noise ratio is large. For the SEMS system, the condition number of the kernel function increases as the overlap in the transfer functions of neighboring time bins increases, that is, as particles of a selected mobility are sampled in more time bins or channels. The overlap among the neighboring transfer functions increases with decreasing transfer function resolution and increasing number of channels for a fixed range of operating voltages (Talukdar and Swihart 2004). (For more, see online supplemental information.)

Under a fast-scanning operation, the SEMS transfer function is affected in two ways: first, the resolution of the scanning DMA transfer function decreases with faster scanning (Collins et al. 2004; Dubey and Dhaniyala 2008, 2011) and second, the resolution deteriorates because of flow mixing in the tubing between the classifier and the CPC and within the CPC, resulting in a smearing of the particle arrival times at the detection region (Collins et al. 2002). For a given condition number, the SEMS resolution limits the achievable resolution of the measured size distribution (The resolution of the discretized size distribution is its bin width; for more, see online supplemental information.). Thus, for a desired size distribution resolution, the condition number of the kernel function increases with decreasing SEMS resolution. Also, for a fixed number of SEMS channels, as the scan time is decreased, the counting time interval becomes smaller and hence the counts per channel decreases. A fast-scan SEMS operation, therefore, results in increasing the condition number of the kernel matrix and decreasing the measurement signal-to-noise ratio. Both these factors result in complicating the inverse problem of size distribution calculation.

The simplest solution of the linear equation (Equation (10)) is obtained using a least-square estimation or a maximum-likelihood-based approach. A commonly used least-square-based approach for SEMS size distribution calculation is Twomey's (1975) method, which is based on a nonlinear iterative scheme introduced by Chahine (1968). In Twomey's algorithm, the basis functions of the linear inverse problem are obtained using a nonlinear iterative scheme while maintaining the nonnegativity of the calculated size distribution. Another approach to obtain a nonnegative least-square (NNLS) estimation of the linear inverse problem, based on the iterative determination of the basis vector set, was proposed by Lawson and Hanson (1974). All constrained least-square estimation approaches (Lawson and Hanson 1974) and nonlinear iterative approaches that do not consider artificial smoothening or make a prior assumption of the solution form (Twomey 1975) produce comparable results, with the difference primarily in their computational efficiency.

In addition to the least-square-based method, Bayesian approaches have also been used for the solution of the linear inverse problem (Ramachandran and Kandlikar 1996; Lemmetty et al. 2005; Hogan et al. 2009). These approaches use Monte Carlo simulation to determine the maximum-likelihood estimate (MLE) or minimum variance Bayes estimate of the linear inverse problem. In the maximum-likelihood estimation approach (Kaipio and Somersalo 2005), the solution that maximizes the likelihood function is considered to be the optimal solution. In order to obtain the likelihood function, the probability distribution functions of the measurement and the solution are required. For the SEMS operation, the measured particle counts in a time interval can be assumed to represent a random sample from a Poisson probability distribution function (and from Equation (12) it follows that the calculated size distribution would also be Poissonian), thus making it possible to use the MLE approach. To obtain an MLE solution, various optimization schemes such as the Newton–Raphson, conjugate gradient, quasi-Newtonian, expectation-maximization (EM), etc., can be used. Among these schemes, the EM algorithm has the advantage of guaranteeing convergence to the local minima monotonically (Dempster et al. 1977). In the EM approach, the solution is initiated or used from an earlier step to obtain the complete likelihood and the likelihood function is then maximized with respect to the solution. The EM algorithm has a closed form solution for probability distribution functions that are exponential in nature, for example, binomial, Gaussian, Poisson, etc. Thus, for a Poisson assumption of the SEMS channel data, the EM algorithm can be used conveniently.

The solutions obtained from least-square or maximum-likelihood-based estimations are reasonably accurate when the condition number of the kernel function is low or when the signal-to-noise ratio is high. However, under conditions such as fast-scanning, the problem becomes ill-conditioned with a low signal-to-noise ratio. In such a scenario, these approaches (MLE-based approaches and least-square solutions) result in an unreasonably noisy solution even when the actual size distribution has a smooth shape. To overcome this problem, an additional constraint of a smooth solution can be used (Markowski 1987; Winklmayr et al. 1990). Similarly, a maximum-a-posteriori (MAP) approach, where the MLE method is modified by the inclusion of a prior estimation of a solution, acts as a smoothening algorithm and tends to provide a stable solution even if the data are highly noisy or the problem is ill-conditioned. In addition to these approaches, Tikhonov regularization has often been used to provide additional smoothening and obtain a stable solution for an ill-conditioned problem. With Tikhonov regularization, the linear equation is made overestimated (i.e., number of unknowns < number of equations) by including the second derivative of the solution in the problem formulation. Thus, the problem requires minimization of two functions: the Euclidean norms of and (i.e., and ), where , a (n−2,n) matrix, is a discrete approximation of a second-order derivative operator, and for uniformly spaced size intervals, its elements L_i,j can be represented as

With the Tikhonov regularization approach, the function is minimized, where α is a regularization parameter obtained by requiring the norm of one of or to be minimized while maintaining the norm of the other to be less than a predetermined maximum acceptable error.

Accurate solution of the inverse problem requires appropriate determination of the smoothening parameter, α, using approaches such as discrepancy principle (Twomey 1975; Hansen 1997), general cross-validation (Wolfenbarger and Seinfeld 1991), and L-curve regularization (Hansen and O’Leary 1993). Among these approaches, L-curve-based regularization has been shown to have the best accuracy (Hansen 1997) and, thus, only this approach is considered here. In this approach, the logarithm of the norm is plotted against the logarithm of norm for different values of the regularization parameterα. The optimal value of α is then obtained as the point of minimum curvatureκ, which can be expressed as a function of α as

where

The accuracy of the SEMS size distributions calculated using the L-curve-based regularization approach and the constrained least-square-based approach is determined for a range of test cases and their performance is compared against a new multiscale-based approach described below.

4. MULTISCALE APPROACH

A new approach for data inversion relying on multiscale analysis is presented here. The SEMS data, that is, CPC particle count as a function of time, can be analyzed at any desired measurement resolution lower than the highest resolution (determined by the shortest time interval of particle count measurement). For an exactly determined problem (i.e., the number of elements of inverted size distribution channels [] same as the number of CPC count channels []), the measurement resolution can be adjusted by selecting appropriate time intervals of CPC count data. The freedom to obtain size distributions at different resolutions makes multiscale techniques well suited for this kind of problem.

The simplest case of multiscale analysis as applied to SEMS measurement involves calculation of in n size bins by inverting the CPC count data binned into n time intervals. If the SEMS measurement is assumed to cover the entire size distribution, then the total number concentration of particles provides one constraint for the data inversion

where ΔlogD _p,i is the width of ith diameter bin in log-space and N_t is the total particle concentration obtained as . If the diameter bins are of uniform width (i.e., ΔlogD_p is constant), then

If the distribution of CPC counts at each channel is Poissonian, then the probability density function associated with N_t is also Poissonian, as shown in Equation (12). The finer resolution size distribution, , is obtained from the coarsest resolution, , considering a multinomial distribution. Here, , referred to as parent distribution, represents a certain total particle concentration that must be distributed to n children, . This process can be repeated until the size distributions are calculated at the desired resolution.

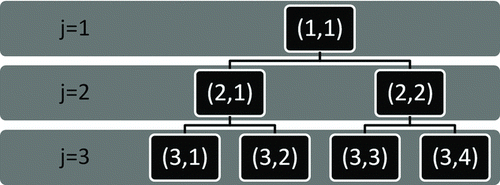
A multiscale inversion approach based on the dyadic tree structure is introduced here. In the dyadic tree structure, the size distribution bin width is varied at different scales, with the bin width doubled at each coarser scale relative to that of the finer bin. The different size bin scales can be represented by the variable j (1, 2, …, J), where 1 refers to the coarsest scale and J the finest scale. A schematic diagram illustrating the different scales of the dyadic tree structure used here is shown in Figure 1. While multiscale analysis with more than two branches from each node is possible, for simplicity of formulation and implementation, only the dyadic structure is considered here. In the dyadic multiscale formulation, the number of elements in the j + 1th scale is twice the number of elements in the jth scale. Every neighboring pair of elements in the j + 1th scale can be related to the elements in the jth scale as shown below:

where refers to the elements degenerated from (or child of) the jth scale of to form the corresponding elements of the next (j + 1th) finer scale. Similarly, the dyadic tree structure can be defined for the actual particle size distribution, .

FIG. 1 A schematic diagram of the dyadic tree structure used for the multiscale analysis. In different scales (j), the SEMS particle count data can be distributed into different numbers of size bins (2j−1).

For a dyadic tree structure, the probability distribution function of conditional on can be expressed as a product of the Poisson distribution function of the root (coarsest bin) and a binomial distribution to the children [ch(x_m (j), :)] at the different levels, j, from the root to leaves (i.e., coarsest to finest bin):

In Equation (18), the variable ω _m (j) determines the proportion of the coarse bin counts allocated among the children, ch(x_m (j), :). For a MAP estimate of x , an appropriate probability distribution function of , P( x ), must be chosen. The gamma distribution is a conjugate to the Poisson distribution and the beta distribution is conjugate to the binomial distribution as shown in Nowak and Kolaczyk (2000). Note that, for a nondyadic tree structure, the binomial distribution of Equation (18) will have to be replaced with the Multinomial distribution and the beta distribution with the Dirichlet distribution for MAP estimate (Ferreira and Lee 2007). With these conjugate functions, a closed form expression for the MAP of the Poisson inverse problem is available using EM algorithm, thereby reducing the computational time. Therefore, for computational purposes, the probability distribution function of x is assumed to be a product of the gamma function () for the root and beta distribution () along the dyadic tree, that is,

Using Bayes rule, the probability of the size distribution conditional on the counts data, , can be expressed as the product of the likelihood function and the prior estimation [P( x )] of the size distribution

or considering the logarithm of the terms on both sides of the above equation:

The log-likelihood function can be expanded for a Poisson distribution (Nowak and Kolaczyk 2000) as

Similarly, the log-likelihood of the prior estimation of the size distribution can be expanded as

where J is the total number of scales used in the multiscale analysis. For a dyadic structure, at any given scale j, there are 2 ^j size bins. The value of that maximizes the MAP function (sum of the log of the likelihood function and the log of the priori estimate of ) is the MAP estimated value. Nowak and Kolaczyk (2000) obtained the closed form solution of the MAP function using an EM algorithm. The resultant solution of the EM algorithm can be shown in two steps—expectation estimation (E) step and maximization (M) step.

E(Step): In the expectation step, the expectation of complete likelihood is obtained using the initial value or the value of the previous step of the size distribution and the particle count data, y . The first term on the right-hand side of the expectation equation distributes the total counts, z , of a selected mobility for the values of x obtained from an earlier iteration (Equation (18)). The second term of the equation is calculated from Equation (21). In order to maximize the expectation, the value of corresponding to the maximum of Q( x , x ^(k)) must be determined. For the finest bin (J), the expression for the corresponding to size bin m (Nowak and Kolaczyk 2000) can be written as

Here, the superscript k represents the iteration step. The value for a coarser bin can be estimated from the finer bin using the dyadic tree relation used for the maximization step.

M(Step): The solution of the maximization step can be obtained from the following steps:.

The solution to the maximization step depends on the parameters of the gamma and beta distributions used for the prior estimation of x . Although the parameter values are a critical factor in obtaining accurate solution, there are no general or optimal values for these parameters. Typically, for an SEMS scan, the integrated particle count will be significant and, correspondingly, the signal-to-noise ratio at the coarsest scale will likely be large. Therefore, the value of the parameters of the gamma distribution can, thus, be chosen such that the size distribution value at the coarsest scale remains unchanged. Here, γ₁ and γ₂ are set as 1 and 0, respectively. Similarly the values of the parameters of the beta distribution are also crucial for the determination of the size distribution from a coarse bin. In this work, for simplicity, the value of β is kept constant for a given scale. For a β value of 1 for all scales, the MAP solution is the same as the MLE solution and no artificial smoothening is added to the solution. This choice of β may, therefore, result in a “noisy” solution for an ill-conditioned problem. Instead, for MAP estimation, a β(j) value of 2 ^j is used, that is, the regularization parameter is increased for finer scales, to counter the increasing ill-conditioning of the problem at the finer scales.

4.1. Summary of the Multiscale Approach

The multiscale approach described in this section determines the nonnegative particle size distribution at the highest resolution of size bin (Equation (22)) based on an initially assumed size distribution. Starting with the obtained size distribution at the finest scale (which can be noisy at low signal-to-noise ratios and when the kernel function is ill-conditioned), the size distributions at coarser scales are determined by following the dyadic tree structure distribution pattern shown in Equation (17). The size distribution at the coarsest scale (where the signal-to-noise ratio is typically high) is then used to modify the finer scales considering the signal strength as well as an assumed extent of smoothness in distribution (Equation (23)). After the new size distribution at the finest scale is determined, this distribution is used as the initial value and the whole procedure is repeated and the iterative calculations are repeated until convergence. The multiscale inversion approach relies on the simultaneous consideration of the measured signal strength at different scales and a smoothening parameter to suppress noise under conditions of low signal-to-noise ratio. The statistical framework of noise distribution at a given scale and the relation between different scales is represented in Equations (19) and (20). This multiscale nature of the SEMS data makes this approach ideal for SEMS size distribution calculations.

5. INVERSION METHODS: INTERCOMPARISON

SEMS size distributions calculated with three different approaches—multiscale, NNLS, and L-curve-based regularization—are compared for a range of test conditions. In general, when the signal-to-noise ratio is high and the condition number is low, the NNLS approach provides the most accurate solution. However, as the problem becomes ill-conditioned, the NNLS approach results in a noisy, unrealistic size distribution. With a regularization-based approach, the noise in the solution because of the ill-conditioned nature of the problem is countered by constraining the solution to be smooth. This artificial smoothening constraint can, however, sometimes result in an oversmooth, unreal solution, especially under conditions where the size distribution elements are narrower than the width of the SEMS size bin. There is, therefore, always a compromise between smoothening and edge determination. The performance of the multiscale approach must be established for a broad regime of smooth and nonsmooth size distributions relative to that of other inversion approaches.

TABLE 1 The SEMS resolution and the corresponding condition number for a DMA operated with a resolution for 10 (sheath flow:aerosol flow of 10:1; Knutson and Whitby 1975) and a CPC smearing constant of 0.83 s (CPC3010; Buzorius 2002)

Scan time	SEMS resolution	Condition number of kernel function
10	4.37	3459
12	4.86	656
15	5.48	144
30	7.27	12.7
60	8.64	4.96
200	9.76	3.03

For a comparative study of the different inversion algorithms, the kernel function is determined considering Gaussian-shaped instrument transfer functions forming the rows of the matrix, with the mean of the distribution populating the diagonal elements of the matrix. The standard deviation of the Gaussian distribution depends on the resolution of the transfer function, and determines the condition number of the kernel function. The condition numbers can be varied by considering different SEMS resolutions, consistent with the operation of the SEMS with different scan times (Table 1). To compare the performance of the three algorithms, a normalized error in the predicted size distributions is determined as a function of the signal-to-noise ratio and the condition number of the kernel function. The normalized error is calculated from the difference between the exact distribution and the one obtained from the inverse calculation, with the area under the exact distribution used as the normalization factor. The signal-to-noise ratio of the measurement is estimated as the area under the exact distribution divided by the L ₂ norm of the error at each bin.

To illustrate the possible difference in the predictions of the different algorithms, an SEMS instrument operated with 32 size bins per decade of voltage range (100–1000 V) is assumed to sample a size distribution with four Gaussian-shaped modes of varying standard deviations. For a low transfer function resolution (resolution of 5), the kernel function has a condition number of 444, making the inversion problem ill-conditioned. Considering the contribution of Poisson noise to count data, the resulting output is inverted using the three algorithms (NNLS, L-curve regularization, and multiscale approach) and the obtained size distributions are shown in Figure 2. It can be observed that the NNLS approach results in a very noisy distribution for the broad (smooth) modes of the distribution, but is able to capture the narrow modes very accurately. The L-curve-based regularization approach accurately predicts the smooth modes of the distribution but oversmoothens the narrow modes of the size distribution. The multiscale approach performs reasonably well for both modes of the size distribution (smooth and narrow).

FIG. 2 SEMS size distributions calculated with three different inversion algorithms (multiscale, nonnegative least square, and L-curve regularization).

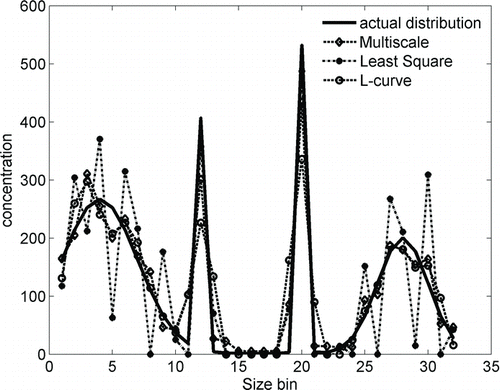
TABLE 2 The mean, standard deviation, and area for the four modes of the assumed multimodal distribution. The mean values correspond to bin numbers and the standard deviation values correspond to number of bins

Type of distribution	Mean	Standard deviation	Area
Smooth	4, 12, 20, 28	2, 3, 2, 3	200, 100, 200, 100
Narrow	4, 12, 20, 28	0.2, 0.3, 0.2, 0.3	40, 20, 40, 20
Mixed	4, 12, 20, 28	2, 0.3, 0.2, 3	200, 20, 40, 100

FIG. 3 Variation of normalized error with signal-to-noise ratio for three different SEMS resolutions: (a) 10, (b) 7, and (c) 5, for a test case of a smooth distribution with four modes of Gaussian distribution.

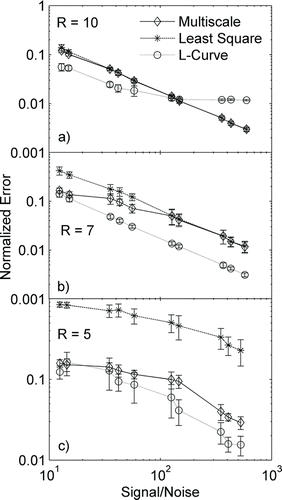
A systematic study of the performance of the three inversion approaches is performed by considering size distributions of different characteristics, as listed in Table 2. Simulations with a smooth distribution and a low condition number (condition number 2.8; resolution 10) were performed for a range of signal-to-noise ratios (corresponding to a range of total number concentration cases). The resultant variation of the normalized error with signal-to-noise ratio for the three algorithms is shown in Figure 3a. The error decreases with increasing signal-to-noise ratio for all three algorithms. Of the three algorithms, the L-curve has the least error while the NNLS has the highest normalized error. The multiscale approach is seen to perform similar to the NNLS approach for this well-conditioned problem. A similar set of simulations was performed for cases with higher condition numbers (resolutions 7 and 5; condition numbers 16.4 and 444, respectively) as shown in Figures 3b and c, respectively. For a given signal-to-noise ratio, the error with a selected inversion algorithm increases with decreasing resolution. The relative performances of the three algorithms, however, remain the same, suggesting that the L-curve regularization scheme is most accurate when the distribution is smooth. Thus, it can be concluded that for ill-conditioned problems, the multiscale-based approach performs reasonably well; better than the NNLS method, but not as good as the L-curve regularization method.

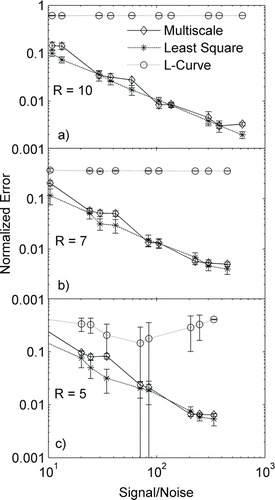
In the second set of simulations the standard deviation of the Gaussian distribution is smaller than the measurement bin width, that is, the size distribution modes span only a narrow size range. The variation of error with signal-to-noise ratio is shown in Figure 4. For this case, with a nonsmooth distribution, the NNLS approach has the least error among the three algorithms. The multiscale-based approach again performs reasonably well, very similar in accuracy to the NNLS approach. As observed for a smooth distribution, the error decreases with increasing signal-to-noise ratio for all

algorithms.

FIG. 4 Variation of normalized error with signal-to-noise ratio for three different SEMS resolutions: (a) 10, (b) 7, and (c) 5, for a test case of a narrow distribution with four modes.

For a third case, a size distribution consisting of narrow and broad features (called a “mixed distribution”) is considered. The relative areas for the different modes are taken in proportion such that the maximum heights for the different modes are very similar. The variation of the error with the signal-to-noise ratio for a well-conditioned problem (resolution 10; condition number 2.8) is shown in Figure 5a. It can be observed that the performance of the multiscale approach is the best among the three approaches. With L-curve regularization, the error increases because of the presence of the narrow mode, while for the NNLS approach the broad mode increases the error. For all algorithms, the error decreases with increasing signal-to-noise ratio. The inversion results with the mixed distribution, as the problem becomes more ill-conditioned (resolutions: 7 and 5; condition numbers: 16.4 and 444, respectively), are shown in Figures 5b and c. The results again show that, for all algorithms, the error decreases with increasing resolution.

FIG. 5 Variation of normalized error with signal-to-noise ratio for three different SEMS resolutions: (a) 10, (b) 7, and (c) 5, for a test case of a mixed distribution with two narrow modes and two smooth, broad modes.

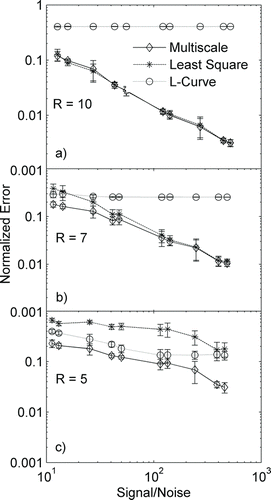
FIG. 6 Variation of normalized error with the standard deviation of an unimodal distribution for an SEMS resolution of (a) 10, (b) 7, and (c) 5. The standard deviation is normalized with the bin width.

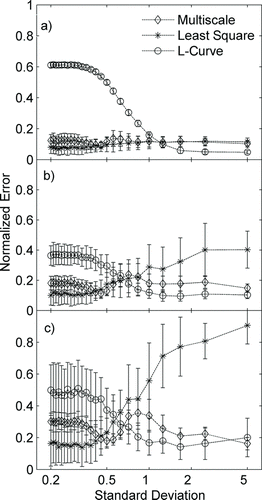
FIG. 7 Comparison of normalized error variation with the standard deviation of distribution for different values of smoothening term.

A further assessment of the relative performance of the different inversion algorithms is made by varying the standard deviation of a sampled unimodal Gaussian-shaped size distribution and determining the resulting error for the three inversion approaches. For this test, an instrument resolution of 7 is assumed. The results of the three approaches under these test conditions are shown in Figure 6a. The NNLS algorithm performs well when the standard deviation of the test distribution is low, but its error increases significantly for larger values of standard deviation. On the other hand, the L-curve regularization algorithm performs well for large values of standard deviations, but oversmoothens the distributions for the low standard deviation test cases and is thus inaccurate for this regime. The multiscale approach performs reasonably well for the entire range of standard deviations. Similar trends were observed for the transfer function resolutions of 10 and 5 (Figures 6b

and c).

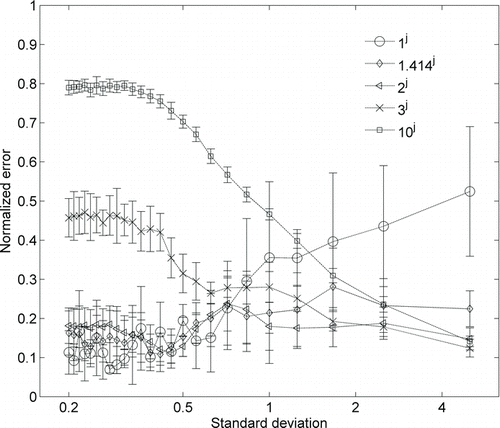
The test results show that the L-curve regularization performs well only if the sampled particle distribution is smooth and the NNLS approach only performs well when the size distribution is narrow. Among the three algorithms studied, the multiscale-based approach is shown to be the most robust for inversion of SEMS data for a broad range of size distribution types. Under conditions of low SEMS signal-to-noise ratio and an unknown nature of smoothness of the sampled size distribution, the multiscale approach is likely to provide the most accurate of the calculated size distributions, and hence, this approach is recommended when the SEMS data are obtained under conditions where particle diffusion, fast-scanning, and low particle number concentration are likely to be encountered. In the multiscale approach, an appropriate choice of β(j) value is critical to obtain accurate solutions. In the current study, for different scales of the dyadic tree, β(j) is selected as 2 ^j . The effect of variation in the normalized error with the choice of β(j) value is shown in Figure 7. It is observed that a β(j) value of ∼1 provides error characteristics similar to MLE, but higher β(j) value results in oversmoothening and may provide erroneous solution for a narrow size distribution. Thus, care must be taken in choosing in an appropriate value of β(j).

6. CONCLUSIONS

Under high-resolution SEMS operation, size distributions of sampled aerosol can be calculated using a simple zeroth-order inversion of the SEMS integral equation (Stolzenburg and McMurry 2008). However, under conditions such as: fast-scan DMA operation, large number of count data bins, or size distribution desired at a resolution higher than the SEMS resolution; a higher order inversion of the SEMS integral equation is required. The inversion of the SEMS equation is, however, complicated by the high condition number of the SEMS kernel function. An accurate solution to an ill-conditioned problem requires an appropriate choice of the inversion algorithm. For SEMS data inversion, a new multiscale EM approach is introduced. An intercomparison of three approaches—constrained least squares, regularization, and multiscale EM—is conducted, considering different condition numbers and signal-to-noise ratios. The test results show that the multiscale-based approach is the most robust of the three. The error in the estimation of size distributions with the multiscale EM approach was largely invariant with the type of the distribution (narrow or smooth), unlike for regularization and the NNLS approaches. Thus, calculation of size distributions from SEMS measurements under nonideal operating conditions is best made using a multiscale EM approach.

NOMENCLATURE

yn	=	SEMS particle count data in nth time bin
V	=	voltage applied across classifier section of DMA
Qa	=	aerosol flow entering the DMA
ηCPC	=	CPC counting efficiency
ηDMA	=	DMA penetration efficiency
	=	particle diameter with nq charges
nq	=	number of elementary charges
	=	normalized electrical mobility
ϕ	=	charging fraction
N	=	particle number concentration
Zp	=	particle electrical mobility
Z* p	=	electrical mobility corresponding to the peak of the DMA transfer function
Q sh	=	DMA sheath flow
r2	=	outer radii of DMA classifier section
r1	=	inner radii of classifier section
L	=	length of classifier section
e	=	charge on an electron
μ	=	dynamic viscosity of air
Cc	=	Cunningham correction
ΩDMA	=	transfer function of DMA
ΩSEMS	=	SEMS transfer function
ΩATF,DMA	=	arrival time transfer function of DMA
ΩATF,SEMS	=	arrival time transfer function of SEMS
	=	mobility–diameter coefficient
V0	=	voltage at the start of upscan
τ	=	scan rate of DMA
Dp	=	particle diameter
Θ	=	kernel function matrix
x	=	vector of particle size distribution
θ n,m	=	elements of the kernel function Θ
xm	=	mth row of the size distribution matrix x
	=	estimated value of xm
	=	estimated value of CPC counts in the nth time bin
	=	the total count of particles corresponding to mobility bin m1 sampled over the entire scan
L	=	smoothening matrix
κ	=	minimum curvature of L-curve
α	=	regularization parameter
ζ	=	error norm of regularization
ξ	=	smoothening norm of regularization
ch	=	children for dyadic tree structure
J	=	total number of scales
P	=	probability distribution function
	=	gamma distribution
	=	beta distribution
β	=	parameter of beta distribution
γ1	=	first parameter of gamma distribution
γ2	=	second parameter of gamma distribution
ω n	=	parameter of binomial distribution
Q(x, xk )	=	expectation of x obtained from complete data (xk ) at previous iteration k
	=	expectation obtained from complete data at previous data at previous iteration (xk )

Acknowledgments

The authors gratefully acknowledge funding support for this research from the National Science Foundation under grant number ATM 0548036. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]