Simulation of Aerosol Coagulation and Deposition Under Multiple Flow Regimes with Arbitrary Computational Precision

Abstract

In computational aerosol coagulation models, a widely used technique is the sectional treatment of the particle size distribution. This approach is used in many first- and second-generation computer codes, where the section boundaries are selected to obey a geometric constraint. While this technique improves computational efficiency, it introduces a number of limitations, including poor representation of the initial size distribution and loss of resolution in the coagulated or final distribution. A robust and versatile computer model, SEROSA, has been developed, which permits an arbitrary number of sections with arbitrary size boundaries to simulate the temporal evolution of coagulation and deposition under multiple flow-regimes and coagulation types. The code permits a large number of parameter combinations and what-if scenarios under user control. Results are benchmarked against an analytical model as well as three coagulation models using coincident section boundaries and coagulation mechanisms. The comparison shows excellent agreement in cases where other computer models are known to perform well. The test cases also included scenarios where previously published computational coagulation models lack capabilities or exhibit numerical difficulties. Computational time varies depending on the number of sections, ageing, and coagulation types from a few seconds to minutes. The software is distributed by the Radiation Safety Information Computational Center of Oak Ridge National Laboratory as Code Package PSR 573.

Copyright 2013 American Association for Aerosol Research

INTRODUCTION

Since its introduction by Gelbard and coworkers in 1980, the sectional treatment in the numerical solution of the Smoluchowski equation (1917) remains one of the best performing methods in computational simulation of simultaneous coagulation and deposition without condensation. Although a number of other models have been introduced (Landgrebe and Pratsinis 1990; Prakash et al. 2003, and summaries in Seigneur et al. 1986; Zhang et al. 1999), the most widely used coagulation model for confined atmospheres is the MAEROS code (Gelbard 1982) or its variants, which have been implemented in other larger computer code systems, for example, MELCOR (Summers et al. 1994). MAEROS has also found numerous applications for open atmospheric modeling (Kreidenweis 1993; Andrews 1996).

Of the significant advances made in coagulation theory, a few have been translated to computational development. For example, models based on the continuous representation of the aerosol size distribution, e.g., COAGUL (Suck and Brock 1979), are potentially the most accurate for large size ranges (Seigneur et al. 1986; Zhang et al. 1999). However, these models may not provide the required resolution in the range where discrete size effects are important (Wu and Flagan 1988) and require large computation times while treating only Brownian coagulation. More recently, an exact discrete method, which is free of some of the numerical artifacts that the sectional method sometimes entails, was introduced by Lehtinen and Kulmala (2003) with applications to condensational growth of freshly nucleated particles. This model provides excellent results in the free molecular condensation regime, but it remains untested for size distributions encompassing many orders of magnitude.

Models based on parameterization, such as the moment method (MOM) (Barrett and Jheeta 1996; Zurita-Gotor and Rosner 2004), do not permit variation in the resolution of the size distribution due to the fixed number of parameters involved. A Taylor-expansion moment method (TEMOM), which is more efficient without losing significant accuracy, was proposed to solve the Brownian coagulation problem by Yu and Lin (2009). The MOM suffers from the shortcoming that a-priori knowledge of the mathematical form of the initial particle size distribution is required, and it performs best when the size distribution is lognormal. Otherwise various kernel approximations are needed. An alternative method is the direct simulation Monte Carlo (DSMC) approach (Kostoglou and Konstandopoulos 2001; Sheng and Shen 2006, 2007). DSMC has the advantage that the information about the history and internal structure of the particles is available during the simulation, which enables improved handling of multidimensional, multicomponent aerosol systems and tracing of the evolution of particle size, composition, morphology, charge level, etc. However, the DSMC computation is very expensive if the number of particles is large. In addition, the continuous decay of the particle number density due to coagulation or agglomeration leads to an unavoidable decrease in the simulation accuracy (Sheng and Shen 2006). Although recent efforts using differentially weighted size intervals while preserving the multivariate property of the Monte Carlo method have shown reduced statistical noise for simple cases of constant coagulation kernels and kernels that have closed-form solutions, under many circumstances they still exhibit relatively large discrepancies (factor of ∼10 and greater) compared to analytical results (Zhao et al. 2009).

The most widely used technique for many applications, ranging from atmospheric science to nuclear safety, is the sectional treatment of the aerosol size distribution, especially when condensation is not pronounced, which is the focus of the present work. In this method, the particle size spectrum is divided into a finite number of sections, within which the aerosol property (e.g., number or volume concentration) is integrated to obtain a series of coagulation coefficients. In this way the continuous equations may be written in terms of discrete summations (Gelbard et al. 1980). Because the sectional representation does not accurately describe processes occurring among molecular clusters, there have been several attempts to formulate a hybrid method in which this limitation is resolved: Discrete-sectional methods treat molecular clusters as discrete particles, falling into a discrete regime, while larger particles are treated in a sectional regime (Wu and Flagan 1988; Landgrebe and Pratsinis 1990; Biswas and Wu 1997; Kim et al. 2003).

The sectional method is used in the MAEROS code, developed at Sandia National Laboratory (Gelbard 1982). This code has been incorporated in many thermal hydraulic applications to assess the accidental nuclear source term (Summers et al. 1994; Powers et al. 1996), and in other applications where changes in particle size distribution are of interest, such as vapor scavenging of atmospheric aerosols (Andrews 1996) and gas-to-particle conversion models (Kreidenweis 1993). In MAEROS, the particle size boundaries are selected to obey a geometric constraint limiting the size of each section to double that of the lower section, v_k ≥ 2 v_k-1 . This technique significantly reduces the computational cost of the problem, and has been widely used. Because in many applications decreasing the section spacing does not result in substantial increase in accuracy, the increased computational requirement is not always justified. For example, using geometric constraint, Prakash et al. (2003) developed a simple numerical algorithm for solution of nucleation, surface growth, and coagulation. Their method is based on the sectional representation but employs Lehtinen and Zachariah's nodal solution technique (2001) with a node-splitting algorithm to simplify the computations. This is a clever technique, which results in substantial reduction of computational requirements. Although the original method of Lehtinen and Zachariah (2001) is not restricted to logarithmic section spacing, the implementation by Prakash et al. (2003) still suffers from the limitations imposed by the geometric constraint, and it does not permit the fine resolution of the coagulated spectrum. This tendency gains increasing significance in case of multimodal distributions when at least one of the modes has a geometric standard deviation near one, which is characteristic of certain man-made aerosols, bio-aerosols, and threat agents, introduced in an urban atmosphere. Landgrebe and Pratsinis (1990) developed a method, which partially alleviates the geometric constraint, but it nevertheless imposes a restriction in which the section width must increase with increasing particle size. Following Gelbard, Landgrebe, and Pratsinis’ work, current versions of the sectional method invariably share the numerical simplification that the section boundaries are selected to obey a constraint in that each section size equals a multiple of the lower section, v_k ≥ f v_k-1 , where the multiplier, a.k.a. spacing factor f, is ≳1. Thus, applications in which a mode with large geometric standard deviation at a small particle size is simultaneously present with a mode having a small standard deviation at a larger particle size do not benefit from this method (Wallace et al. 2009).

This article reports the development of a new computer code, SEAROSA, which is based on the sectional method permitting an arbitrary number of sections with arbitrary size boundaries. The computer model employs an efficient numerical algorithm without any approximations or simplifications other than what the constraint-free sectional method inherently entails. This results in a more robust treatment of aerosol dynamics in general, and in a more accurate resolution of the temporal evolution of coagulation in particular. The code partially relies on multiprecision (a.k.a. arbitrary precision) arithmetic (Smith 2003), and it uses an adaptively called variable-order Gaussian integration scheme to find the sectional coagulation coefficients, and a fifth- and sixth-order Runge–Kutta–Verner method (Burden and Faires 1993) to solve the set of stiff differential equations describing the time rate of change in the particle spectrum. Among its many features, it uses a variety of user-selectable coagulation kernels and their combinations, permits user-defined initial conditions, carrier fluid properties, and computes surface deposition from boundary layer theory. The coagulation kernels used in the code are for particles in the continuum, transition, and free molecular flow regimes undergoing a variety of commonly occurring mechanisms, including Brownian and gravitational coagulation, turbulent coagulation, electrostatic effects, surface deposition, and gravitational settling simultaneously, separately or in any physically meaningful combinations selectable by the user. Results were benchmarked against an analytical model and three computer models, MAEROS (Gelbard 1982), COAGUL (Suck and Brock 1979), and NGDE (Prakash et al. 2003), using coincident section boundaries and coagulation mechanisms.

MATERIALS AND METHODS

Aerosol Characterization

The aerosol property of interest, which is numerically conserved by the coagulation models cited in the Introduction, may be the particle number density or any related quantity. Following notation by Gelbard et al. (1980), the differential aerosol property may be defined as

Here, v is the particle volume, is the spatial location, and is the scalar aerosol number density per unit volume of carrier fluid, function of particle size via v, at time t. The parameters α and γ can be chosen such that could represent number density distribution (α = 1, γ = 0), volume distribution (α = 1, γ = 1), or other properties of interest. The numerical scheme in SAEROSA tracks the volume density of the particles.

The integral aerosol property can be obtained for the entire size distribution as

or for a volume interval, or section, ranging from v_{k- 1} to v_k as

It is readily seen that Equation (2) is related to the moments of the size distribution.

Coagulation Dynamics

The basis of our coagulation model is Smoluchowski's equation (1917):

which describes the time rate of change in the number of particles having size v assuming binary collisions. The first term in the right hand side is the production of particles of size v via collision between particles with size u and v–u. The second term on the right hand side is the loss due to collisions between particles with size v and u. Here, the function K(u,v) is known as the coagulation kernel, and it is defined such that K(u,v)n(u)n(v) is the rate at which particles having volume v collide and adhere to other particles whose volume is u. The form of the kernel depends on the coagulation mechanism, and it is often an analytical function based on theory.

Generally, aerosol particles are divided into three regimes according to their sizes. For particles ranging from 10⁻³ μm to 100 μm in equivalent radius, the Knudsen number (Kn), which relates the particle size to the mean distance traveled by an air molecule between collisions, or mean free path λ, varies between 65 and essentially zero. At high Knudsen numbers (Kn > 1), the aerosol particles are in the free molecular flow (FM) regime and experience forces that depend on the Maxwell–Boltzmann molecular speed distribution, while at low Knudsen numbers (Kn < 0.1), the particle is many mean free paths in size, and the gas acts as a continuous fluid (CF) regime. When the Knudsen number is neither high nor low, the particles are considered in the transition regime. In this regime, the particle transport exhibit characteristics of both FM and CF regimes. Note that the limits of the transition regime vary in the literature; e.g., Williams and Loyalka (1991) use 0.1 < Kn < 1.0 while Hidy and Brock (1971–1973) use 0.25 < Kn < 10.

The rate of coagulation is a function of both particle size and the flow regime. Therefore, when the particle size spectrum spans many orders of magnitude, giving rise to multiple flow regimes within the same aerosol field, or when more than one physical process contribute to the particle collisions, a single kernel in Equation (4) does not adequately describe the true coagulation mechanism. Many attempts were made to unify the coagulation theory and find a form of the kernel, which is valid throughout some, possibly all flow regimes. For example, Simons and coworkers (1986) derived a kernel for combined Brownian and gravitational coagulation, Williams (1988) presented a unified theory of coagulation, and Sajo (2008, 2010) extended the numerical evaluation of Simons’ results for gravitational settling dominated regimes.

TABLE 1 Coagulation kernels implemented in SAEROSA. In the input the user can select a single kernel or any physically meaningful combination

Coagulation type	Coagulation kernels
Brownian
Diffusion regime^1
Slip flow regime^1
Free molecular regime^1
Fuchs’ method^1
Da and Db are the Cunningham-corrected diffusion coefficients for particle radii a and b. v ab is the average thermal velocity and δ ab is the jump distance.
Turbulent
Inertial^2
Diffusion^1
Diffusion + Inertial
Gravitational^1
Electrostatic^1
Coulomb interactions in continuum regime only
Brownian + Gravitational^3	KBG =γ BG (KB +KG )
The value of γBG is tabulated in Sajo (2008) up to β = 2E4 and a least-squares fit is given in Sajo (2010).
Brownian + Turbulent^1
Gravitational + Turbulent
Brownian + Turbulent + Gravitational
Other combinations	Root mean square of kernels
^1From Williams and Loyalka (1991).
^2Powers et al. (1996).
^3Simons et al. (1986), Sajo (2008, 2010).
The explanations of these kernels are given in the cited references.

There are many combinations of flow regimes, however, for which no exact coagulation kernel has been derived. Under such cases simultaneous processes are invariably handled by the addition of the kernels, referred to as sum kernel. A more sophisticated method is the computation of the root-mean-square of kernels (Powers et al. 1996). In this way, the combined kernel of, e.g., three simultaneous collision mechanisms is

In SAEROSA, all flow regimes and a number of different coagulation types, including Brownian, gravitational, turbulent, and electrostatic are considered, and particles may undergo a single process or a combination of simultaneous processes. In the latter case, a simple addition of the kernels (sum kernel) may underestimate the true kernel by up to 30% if two processes are superimposed (Williams 1988), or more if many simultaneous processes are present (Powers et al. 1996). SAEROSA rigorously computes the kernels for simultaneous processes following the theoretical development by Williams (1988) and the computational algorithm by Sajo (2008, 2010). In the case when exact kernels are not available, the root-mean-square summation is used.

The user can either select the desired kernel in the input, or let the code use the most appropriate kernel for the coagulation problem. When the kernel is selected by the code, it will evaluate in each integration step that which kernel is needed based on the coagulating particle sizes and the flow regime. This in turn is superimposed onto other kernels that do not explicitly depend on the flow regime, if needed. The kernels used in SAEROSA are summarized in Table 1.

Aerosol Size Discretization

In the sectional approximation of the Smoluchowski equation (4), the continuous particle size spectrum is divided into a finite number of size intervals or sections. When more sections are placed in the size distribution, the resolution becomes finer, and the approximation of the continuous equation improves. In this way, the rate of change in the integral aerosol property in a particular section can be written as (Gelbard et al., 1980):

Here, Q _k (t) is the integral aerosol property in size section k, (which may be volume or mass concentration). The β^(m) factors in this formula are the sectional coagulation coefficients, which represent integral values of the coagulation kernels between the appropriate section boundaries (Gelbard et al. 1980). Table 2 summarizes the β^(m) coefficients for arbitrary sectionalization for the case when the aerosol property is the particle volume density. SAEROSA uses an adaptively called variable-order Gaussian integration scheme to find the sectional coagulation coefficients for each desired size interval. The first term on the right hand side in Equation (6) represents particle flux into section k due to collision of particles in two sections, i and j, both smaller than k. The second term is the flux out from section k due to collision between section k and a section i smaller than k. The third term gives the flux out from section k due to collisions within the same section. The fourth term is the flux out from section k due to collisions between section k and a section i higher than k.

TABLE 2 Inter- and intrasectional coagulation coefficients for arbitrary sections. Here, the aerosol property is volume density. θ = 1 when the conditions are met, and θ = 0 when the conditions are not met

β^(1) i,j,k	2 ≤ k ≤ m
	1 ≤ i < k
	1 ≤ j < k
	β^(1) i,j,k =β^(1) j,i,k
β^(2) i,k	2 ≤ k ≤ m
	i < k
	β^(2) i,k =β^(2) k,i
β^(3) k,k	1 ≤ k ≤ m
β^(4) i,k	1 ≤ k < m
	i > k
	β^(4) i,k =β^(4) k,i

Equation (6) represents a nonlinear system of simultaneous differential equations with k = 1,2, …, G. The nonlinearity is provided by the last term, which prevents its reduction to a triangular form. Various numerical methods, particularly higher order Runge–Kutta rules, can be successfully applied. SAEROSA uses a 5th–6th order Runge–Kutta–Verner method with adaptive time steps and error control that can be specified by the user (Jackson 1985; Burden and Faires 1993). The optimal time step and error tolerance depend on the stiffness of Equation (6), which in turn is function of the minimum and maximum particle size and the number of sections.

The number of coefficients necessary to calculate the discrete coagulation equation is (G ³ + 6G ² − G)/6 for an arbitrary discretization of G sections. It is possible to reduce the number of coefficients by careful selection of group boundaries. When the lower (v_{k− 1}) and upper boundaries (v_k ) of sections meet the condition v_k ≥ 2v_{k -1}, the first term on the right side of Equation (6) reduces to a single summation, as β⁽¹⁾ _i,j,k =0 for i, j < k−1. This is known as the geometric constraint, which allows particle flux into section k only by collision between section k–1 and lower sections. Because one of the sections participating in the collision is now fixed, this reduces the number of coefficients to 2G(G+2), and Equation (6) simplifies (Gelbard et al. 1980):

Although Equation (7) is not used by SAEROSA directly, it can reproduce it by the appropriate selection of section boundaries in the input file. Also, this formula is presented here to permit a comparison and explanation of computational methods.

Limitation of the Geometric Constraint

The advantage of the geometric constraint is its numerical efficiency. Its disadvantage is the progressively deteriorating particle size resolution and that it is not possible to resolve large gradient spectra. The situation is not much better when the particle size distribution is lognormal. Since the geometric constraint uses logarithmic section boundaries, v_{i+ 1} /v_i = 2, if the size spectrum ranges from v ₀ to v_max , the maximum number of sections G_max = ln(v_max )/ln(2). This means that for each order of magnitude in the particle diameter G _max = 9.96, i.e., there is a maximum of nine sections in each order of magnitude of the size range.

This puts a considerable limitation on the computation of transport and coagulation of aerosols that have a relatively small geometric standard deviation. Such aerosols are often bio-aerosols, including threat agents, and nanoparticles whose geometric standard deviation is close to one. To illustrate this, consider Figure 1, which shows an aerosol size distribution with a median diameter of 1.0 μm and geometric standard deviation of 1.05. The upper tail of the lognormal distribution cannot be accommodated into a single bin centered at 1.0 μm. A minimum of two sections is needed to capture most of the particles. Hence, the geometric constraint shows inefficient sectionalization and poor resolution, introducing an error into the computations at the outset by incorrectly reproducing the initial size distribution.

FIG. 1 A particle size distribution using sections with geometric constraint versus arbitrary size boundaries, σ_g = 1.05, d _m = 1.0 μm. (Color figure available online.)

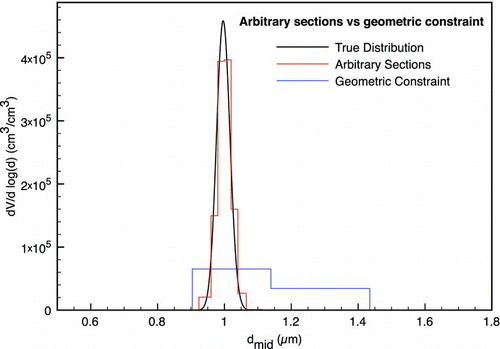
Using the geometric constraint, the maximum number of sections within N standard deviations about the geometric mean diameter, [d_max/Nσ_g, d_maxNσ_g ], is G_max = 6 ln(Nσ_g ). Consequently, if the standard deviation is smaller than exp(1/6) = 1.18, the spectrum cannot be resolved. In the example illustrated by Figure 1, using one standard deviation (N = 1) leads to G _max = 0.29. Hence, no section boundary can be added within one standard deviation range. If the section boundary around the geometric mean diameter is larger than one standard deviation, the geometric constraint cannot reproduce the actual distribution, as seen in the figure. Therefore, for a small geometric standard deviation a finer separation of sections sizes is needed. Because of this limitation, the geometric constraint is not always sufficient.

The discrete sectional model (Landgrebe and Pratsinis 1990) alleviates this problem but does not solve it. In this model a generalized constraint v_k ⩾f v _k−1 is used, with the spacing factor f ≳ 1. In practice, this factor ranges from 1.08 to 3.0, making the maximum number of sections per decade of particle diameter G_max = 89. However, because the section spacing must monotonically increase with particle size, particle distributions exhibiting large gradients or where a narrow mode is present at the higher end of the initial size spectrum will either require very small section spacing in the lower end of the size spectrum where they are not needed, leading to unnecessarily large computation time, or will result in the introduction of a nontrivial error due to the insufficient resolution of this mode.

Arbitrary section spacing, which is implemented in SAEROSA, resolves this limitation. The section boundaries and the total number of sections may be chosen at will, reducing or increasing the size resolution where needed, to achieve the desired resolution at both the initial and final spectra.

Surface Deposition

Deposition in SAEROSA is treated as a removal mechanism. Without the presence of extraneous and hydrodynamic forces, such as impaction, deposition is via diffusion and gravitational settling. Therefore, it is a function of the gravitational acceleration, the material and temperature of the wall, the temperature and composition of the carrier fluid, and of particle size. In SAEROSA deposition is currently computed by assuming that the wall is composed of flat surfaces, and it is a perfect sink without resuspension. The rate of change in aerosol property due to deposition can be written as:

Here, R_k is the particle removal fraction per unit time in section k. It equals the sum of the removal fractions via gravitational deposition, , and diffusional deposition, :

where V_s(v) is the gravitational settling velocity and V_d(v) is the diffusional deposition velocity of a particle with volume v. Further, V is the volume of the aerosol compartment (computational domain), A _⊥ is that area of the aerosol compartment, which is perpendicular to the gravitational acceleration vector, and A_wall is the total area of the wall in contact with the aerosol. In order to accommodate the description of the deposition via different input parameters, including those based on measurements, SAEROSA allows the user to select one of two ways for computing the diffusional deposition via explicit boundary layer theory and via the computation of particle current using dimensional analysis.

In the explicit treatment, boundary layer theory is applied to determine the diffusional deposition velocity, a.k.a. particle transfer coefficient:

Here, D(v) is the diffusion coefficient and δ_d (v) is the diffusion boundary layer at the wall for particles with volume v. In practical implementation, for a flat plate immersed into a fluid flow parallel to the plate, the integral-averaged boundary layer thickness over length L is used (Arpaci and Larsen 1984):

Here, Pe is the Peclet number, which relates the bulk mass transfer to the diffusive mass transfer, Pe = LU/D(v), U is the free stream velocity of the carrier fluid over the surface, and C is the diffusion boundary layer constant. C may be obtained from the relation of the diffusive boundary layer to the momentum boundary layer, δ_d (v)/δ_m (v) ∝ C(Pe/Re) ^p , where the exponent p varies by author, but tends to be −1/3. The momentum boundary layer may be obtained from Blasius’ and von Karman's theory, detailed elsewhere, e.g., by Arpaci and Larsen (1984).

In the dimensional analysis, the mean particle current toward the boundary, ⟨J⟩, is computed and the particle transfer coefficient, ⟨J⟩/Q, becomes (Williams and Loyalka 1991):

Here Sc is the Schmidt number, Sc = ν/D(ν), Re is the Reynolds number, Re = LU/ν, and ν is the kinematic viscosity of the carrier fluid. The coefficient f is the Fanning friction factor. For flat plates, f = 0.072 Re ^−0.2 (Arpaci and Larsen 1984). In this way, Equation (11) becomes

TABLE 3 Tri-modal lognormal aerosol size distributions used for sensitivity analysis and benchmarking against MAEROS and COAGUL

		Mode 1			Mode 2			Mode 3
Case ID	dmin	⟨d⟩	σ g	V n	⟨d⟩	σ g	V n	⟨d⟩	σ g	V n
1^§	0.01	0.038	1.8	0.63E-12	0.32	2.16	38.4E-12	5.7	2.21	30.8E-12
2	0.01	0.038	1.8	0.63E-11	0.32	2.16	38.4E-11	5.7	2.21	30.8E-11
3	0.1	0.038	1.8	0.63E-12	0.32	2.16	38.4E-12	5.7	2.21	30.8E-12
4	0.1	0.38	1.8	0.63E-12	3.2	2.16	38.4E-12	57.0	2.21	30.8E-12
5	0.1	0.038	1.8	0.63E-12	0.32	2.16	38.4E-12	5.7	2.21	30.8E-12
6	0.5	0.038	1.8	0.63E-12	0.32	2.16	38.4E-12	5.7	2.21	30.8E-12
dmin = Minimum particle diameter in simulation, ⟨d⟩ = median diameter (μm), σg = geometric standard deviation, and Vn = volume density (cm^3/cm^3).
Cases 5 and 6 were used for Brownian coagulation only.
^§Urban atmospheric aerosol distribution (Seigneur et al. 1986).

It can be shown that in the case of laminar flow, when the parameters p = −1/3 and C = 3/(2·0.678) = 2.212, ⟨J⟩/Q = D/δ.

In addition to computing the diffusional boundary layer, SAEROSA also allows the user to specify it as direct input. This serves as a tool for using measured values or performing what-if analyses, and permits comparison with other computational aerosol dynamics programs, such as MAEROS, where the diffusion boundary layer is hard-coded, having a value of 1.0E−5 m for all particles sizes, independent of carrier fluid properties and free-stream velocities.

The above formalism can be readily incorporated into the sectional coagulation Equation (6), and the time rate of change in aerosol property Q_k due to simultaneous coagulation and deposition can be written as

Benchmark and Comparison to Previous Work

Benchmarking of SAEROSA was performed against MAEROS (Gelbard 1982) and NGDE (Prakash et al. 2003). An indirect benchmarking against COAGUL (Suck and Brock 1979) by way of Zhang et al. (1999) was also completed. In all cases, an attempt was made to use identical conditions. Unique capabilities of SAEROSA were tested against theory and analytical models, where possible. Metrics used for comparison included section-wise relative discrepancies, total or spectrum-wide discrepancies, and volume conservation. Discrepancies are presented in terms of percentage deviation from the model to which SAEROSA is compared, as follows:

FIG. 1 Benchmark against MAEROS. Simultaneous gravitational and Brownian coagulation (Case 1). (Color figure available online.)

Comparison with MAEROS

In order to benchmark against MAEROS, input options in SAEROSA were selected such as to reproduce conditions and methods used in MAEROS. In all cases, twenty sections were used (the maximum allowed by MAEROS) with boundaries selected to match the geometric constraint. Simulation results for various types of coagulation mechanism alone followed by simultaneous coagulation and deposition at different aerosol ageing times and with different total initial aerosol properties were quantitatively compared. In these cases MAEROS is known to perform well. Results showed excellent agreement between the two computer codes. In nearly all cases, the section-wise discrepancy remained within 1% in those sections where the aerosol number density is greater than one particle per cm³. To test the code for both small and large size distributions, and within the capabilities of MAEROS, various tri-modal aerosols were simulated based on data for atmospheric aerosols (Seigneur et al. 1986). In each of the modes therein, the particles follow a lognormal distribution. The parameters of some of the tested distributions, including those that resulted in the worse agreement between the two codes are listed in Table 3, and the corresponding discrepancies between the two codes are summarized in Table 4.

The worse agreements are seen for simultaneous Brownian and gravitational coagulation and for Brownian deposition. Figure 2 shows the results for distribution Case 1 undergoing Brownian and gravitational coagulation over 24 h. The agreement between the two codes in simulating this particular scenario is generally good. The section-wise average discrepancy in those sections where there is more than one particle left after aerosol ageing is 8%. The highest discrepancies are observed in the lowest sections. In the largest sections, the discrepancy virtually disappears even if the number of particles in the section is less than one. The small section-wide differences observed in these test cases are due to the different numerical algorithms employed by the two models. The fractional discrepancy for the total conserved volume is 2.18E−5. Here as well as in all other cases, SAEROSA tends to conserve the aerosol property better than MAEROS.

TABLE 4 Absolute average discrepancies between SAEROSA and MAEROS in sections with particle number density greater than 1.0 cm⁻³. Decimals are rounded

Coagulation or
Deposition scenario	Case 1	Case 2	Case 3	Case 4	Case 5	Case 6
Brownian and gravitational coagulation	7%	8%	0%	0%	—	—
Brownian coagulation	7%	5%	0%	0%	1%	0%
Gravitational coagulation	0%	0%	0%	0%	—	—
Turbulent coagulation	0%	0%	0%	0%	—	—
Brownian (diffusional) deposition	21%	24%	27%	<1	—	—
Gravitational deposition	0%	1%	5%	—	—	—
<1 indicates that all sections were depleted to a number density below 1 particle per cm^3.

Figure 3 shows results for diffusional deposition over 24 hours using aerosol distribution Case 3. In this scenario, there is a nontrivial discrepancy ranging from 20% to 30%, which is worse at small sizes (<0.5 μm) where diffusion is more pronounced, and it rapidly improves with section size. This is the largest disagreement we have seen during the extensive testing of this code. The underlying reason appears to be the different numerical methods and error tolerance used in MAEROS versus SAEROSA. The fractional discrepancy in the total conserved volume between the two models, however, remains very good: 2.5E−2.

Comparison with COAGUL

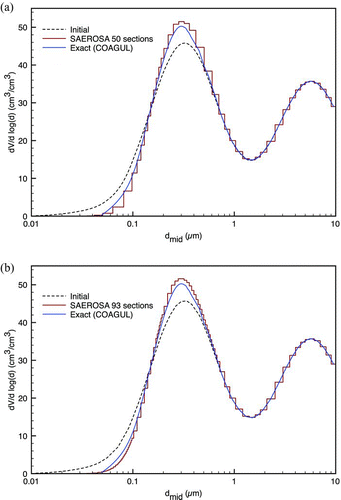
An accurate numerical solution of Smoluchowski's equation was developed by Suck and Brock (1979), which provides point-wise results with respect to particle diameter but it treats only Brownian coagulation. Seigneur et al. (1986) evaluated the performance of various models and compared them to COAGUL. Because this computer model was not available for us, data given by Seigneur et al. (1986) and Zhang et al. (1999) were used to reconstruct COAGUL's results for a tri-modal urban aerosol size distribution equivalent to Case 1 in Table 3. This particular distribution is thought to be the most stringent test of coagulation models (Zhang et al. 1999).

FIG. 1 Benchmark against MAEROS. Diffusional surface deposition (Case 3). (Color figure available online.)

Figure 4 shows the initial particle size distribution along with the results of COAGUL and SAEROSA after 12 h of ageing. Figure 4a displays SAEROSA results for 50 sections while Figure 4b is for 93 sections. The agreement between the two models is excellent. The discrepancies between SAEROSA and COAGUL are marginally different for the two different sectionalizations. The main difference between the two simulations is how smoothly SAEROSA follows COAGUL. At the peak of the accumulation mode (at 0.3 μm diameter), the discrepancy is 2.4% and it remains below 4% at all diameters above 0.1 μm. Between 0.1 and 2.5 μm diameters, the average relative difference between the models is 2.9%, and above 2.5 μm there is no discrepancy.

FIG. 1 Comparison with COAGUL—12 h Brownian coagulation using Case 1: (a) SAEROSA simulation results with 50 sections; (b) SAEROSA simulation results with additional 43 sections between 0.05 μm and 0.7 μm. (Color figure available online.)

Comparison with the NGDE Model

Comparisons are also made between our work and Prakash et al. (2003), who developed a numerical algorithm for solution of nucleation, surface growth, and coagulation for initially monodisperse particles using the geometric constraint (NGDE model). Because the NGDE model uses additional numerical simplifications, we do not anticipate very good quantitative agreement. However, trends are likely represented well, and a comparison therefore is warranted. Because NGDE uses a nodal model, an initially monodisperse aerosol is represented by a single diameter or volume. In contrast, SAEROSA uses the sectional method, in which particles within a range of diameters may occur in a single volume section. Therefore in order to compare the two models, in SAEROSA, a very narrow section was defined to hold the initial particles, and further section boundaries were set up such that the NGDE nodes would coincide with the section midpoints. In this way, 40 sections whose boundaries matched the geometric constraint of NGDE were used.

Since at this time SAEROSA does not simulate nucleation and condensation, the comparisons were made only for Brownian coagulation without removal. NGDE uses a modified version of Fuchs’ method for the free-molecular and transient regimes, which was matched in SAEROSA for the purpose of this benchmark. The comparison considered two cases: 0.01 μm diameter initially monodisperse particles with a number density of 10¹⁵ particles/m³ (Case A), and 0.1 μm diameter initially monodisperse particles with a number density of 10¹² particles/m³ (Case B), both with 24 h ageing time. The respective results are presented in Figures 5 and 6.

FIG. 1 Comparison with NGDE using 0.01 μm initially monodisperse particles. Case A. (Color figure available online.)

The figures indicate that SAEROSA reproduces the qualitative features of the coagulated spectrum computed by NGDE. However, when the relative discrepancies are examined, there is a nontrivial disagreement between the two models, primarily due to the nodal size splitting in NGDE. For Case A, the average discrepancy in sections containing more than one particle is 52%. NGDE exhibits a 1.4% volume loss, whereas SAEROSA conserves the volume. In Case B, the average section-wise discrepancy in sections with more than one particle is 37%. The volume loss by NGDE in this case is less than 1%, whereas SAEROSA conserves the volume.

FIG. 1 Comparison with NGDE using 0.1 μm initially monodisperse particles. Case B. (Color figure available online.)

Note, however, that these results are acceptable only from the perspective of model comparison. In this benchmark, SAEROSA input was designed with the explicit intention to determine if SAEROSA could reproduce the results of the NGDE model. The result of the NGDE simulation, however, is inaccurate. An initially monodisperse system undergoing pure binary coagulation is a discrete process. In that, particles of volume v₀ collide and form particles of volume 2v₀ , which in turn undergo further coagulation to form a series of larger particles having volumes 3v₀, 4v₀ … m·v₀ . In time, this gives rise to a multimodal size distribution, with each mode having a unique volume. For example, in Case B of this comparison, discrete particle volumes at 5.24E−4, 1.04E−3, 1.57E−3, … μm³, corresponding to diameters of 0.1, 0.126, 0.158, … μm (if equivalent spherical particles are assumed) should be seen instead of the quasi-continuous distribution shown in Figure 6. This behavior is due to the geometric constraint used in NGDE. The latter does not allow particles to appear at other size intervals than 2 ^m−1·v₀ (m = 1, 2, 3,…), and does not allow particle concentration to become zero in between size intervals. This shortcoming is also present in MAEROS. SAEROSA, on the other hand does not suffer from this limitation, as will be shown in the next section.

Comparison with Analytical Model for Monodisperse Aerosols

Narrow particle size distributions are often observed in the case of nanoparticle manufacturing, threat agents and bio-aerosols. Hence, this benchmark serves dual purpose: to test SAEROSA's ability to accurately predict such scenario and to benchmark its performance against an analytical model.

An elegant analytical solution of the coagulation equation can be obtained for the case when the coagulation kernel is not a strong function of particle size, as was proposed by Smoluchowski (1917) for Brownian coagulation of nearly equally sized particles in the continuum regime. In this case, for 1 ≤ u/v ≤ 2 the kernel is nearly constant at K = 8kT/3μ, where k is Boltzmann's constant and μ is the dynamic viscosity of the carrier fluid. Integration with respect to time using the initial condition of N(t = 0) = N₀ gives the solution for the total particle concentration (or integral particle number density) as a function of time during the coagulation process:

For an initially monodisperse aerosol, N ₁(t = 0) = N ₀, and for a coagulation kernel independent of particle size, the particle density in each of the subsequent modes, m = 1, 2, …, evolves as (Friedlander 2000):

Here, t/τ is a characteristic dimensionless time, where τ is defined as τ = 2/KN ₀. The latter is also known as the half-value time; the time it takes for the particle number concentration to reduce to one half of its original value. Equation (18) is generally valid for small values of t/τ.

The analytical solution is compared to the numerical simulation of an initially nearly monodisperse aerosol using SAEROSA. The initial particle size was 1.0 μm cast in an initial section ranging from 0.99 to 1.01 μm, having a number density of 1.9E4 cm⁻³. The aerosol ageing time was 7.2E4 seconds, which gives rise to a characteristic time of t/τ = 0.45, therefore Equation (18) is valid. 47 sections with a constant section width (i.e., d_{i +1} –d_i ≈ 0.025 μm), up to 2.1 μm were used. In terms of particle volume, this diameter range spans from 0.52 to 4.51 μm³, which provides sufficiently fine spacing to resolve the anticipated modes (m = 1…8) of the coagulated size spectrum. The results of this simulation are shown in Figure 7a and Table 5.

FIG. 1 SAEROSA models of monodisperse aerosol coagulation (a) using arbitrary but sub-optimal sectionalization and (b) using arbitrary sections with a-priori knowledge of modal boundaries. (Color figure available online.)

TABLE 5 Comparison of SAEROSA results to analytical computation of coagulation of a monodisperse initial aerosol distribution, d = 1 μm, using 47 linear sections. N_m = Total number concentration (cm⁻³) in the m^th mode (integral aerosol property)

Mode, m	Nm Analytic	Nm SAEROSA	Discrepancy
1	9.11E + 03	8.75E + 03	−3.9%
2	2.82E + 03	2.83E + 03	0.6%
3	8.71E + 02	9.14E + 02	4.9%
4	2.70E + 02	2.94E + 02	9.0%
5	8.34E + 01	9.45E + 01	13.4%
6	2.58E + 01	3.04E + 01	18.1%
7	7.98E + 00	9.79E + 00	22.8%
8	2.47E + 00	3.15E + 00	27.7%
Total	1.32E + 04	1.29E + 04	−1.9%

The agreement in the lower modes of the coagulated spectrum (m < 4) is very good. At higher modes, there is an apparent discrepancy, up to 28% at m = 8, which arises mainly due to the fact that the analytical solution uses K = K(a,a) = constant. This is correct in the case when the coagulation is computed within the same section, but it breaks down when the sections are far apart. Specifically, in the first mode, m = 1, the aerosol property appears to be under-predicted by SAEROSA by about 4% compared to the analytical solution. This is because in addition to within-mode coagulation, particles in this mode collide with higher modes as well, and K(a,b>a) > K(a,a) resulting in higher removal rate than permitted by the analytical solution. Therefore SAEROSA provides a better estimate than the analytical solution. The best agreement between the analytical results and SAEROSA is predictably in the second mode, m = 2, because the source obeys K(a,a) while removal is much weaker than the source. From the third mode up, the numerical solution appears to overestimate the analytical one. This is because all K(a,a>b) > K(a,a), resulting in higher rate of production into these sections from lower sections that have higher population. The removal is also higher, but the population is smaller. None of these are considered by the analytical solution. Therefore, in summary, the discrepancy shown in Table 5 is due to the fact that the analytical model assumes a constant rate of coagulation across the particle size spectrum, which is clearly not the case when the coagulation time is nontrivial.

Note that the section spacing used in this simulation is sub-optimal. The computation does not take advantage of a-priori knowledge of the volumes of the coagulated modes. Therefore at successively higher modes, there is a gradual spreading of the aerosol property into adjacent sections centered on the theoretical volumes m·v₀ (m = 1, 2, 3…). In reality, initially this is not a true monodisperse aerosol, and particles in the range 0.99–1.01 μm³ will not have discrete coagulated modes. Notwithstanding, the results correctly reproduce the expected multimodal distribution with nearly discrete modes. A well-designed sectionalization, in which the initial aerosol property is placed into a section v₀ ± ϵ, where ϵ is a sufficiently small incremental volume to capture the monodisperse particles, and each subsequent mode has lower and upper section boundaries equaling and , respectively, results in a perfect discrete multimodal coagulated distribution, as shown in Figure 6b. Here, the total number of sections up to 2 μm is only 15 as opposed to 47 in the previous simulation.

FIG. 1 SAEROSA model of a narrow particle distribution undergoing simultaneous Brownian, gravitational, and turbulent coagulation with and without gravitational settling (deposition): (a) test particles in an otherwise clean environment (39 sections); (b) test particles are superimposed on a background aerosol (64 sections). (Color figure available online.)

Capabilities of SAEROSA

SAEROSA has numerous features that cannot be tested either by simple benchmarking or comparison to analytical computations owing to either the lack of comparable computational models or the complexity of the simulation, respectively. Furthermore, existing models lack the capacity to include simultaneous coagulation phenomena, and they often exhibit numerical instabilities for high gradients, including exponential and narrow initial size distributions. For example, all of the tested computational models break down for a surprisingly simple scenario. Consider a relatively narrow initial particle distribution undergoing simultaneous Brownian, gravitational, and turbulent coagulation with or without gravitational settling. Practical importance of this scenario may be provided by, e.g., nanomanufacturing, where the size distribution is tightly controlled. Figure 8 shows the simulation results using SAEROSA for test particles with lognormal initial distribution (median = 0.1 μm, σ_g = 1.02) undergoing the processes listed above for 24 h. Figure 8a shows a situation when the particles are released into a clean well-stirred atmosphere, while Figure 8b shows a scenario when the test particles are superimposed on a background aerosol characterized by Case 1 (Table 3). The figures clearly show the aerosol conditioning effect of the background aerosol by shifting the low-end of the coagulated spectrum to larger sizes and removing a significant fraction of the test particles.

In addition to the capabilities discussed above, SAEROSA allows the user to specify a number of simulation parameters that control how the computations will be performed. This includes description of carrier fluid properties, surface and boundary layer properties, particle density and shape factor, and other related aspects, and to enable or disable defined processes. Fundamental properties, such as viscosity or mean free path may be computed by the code or specified by the user. In aggregate, the code permits the what-if-analysis of a variety of situations and the isolation of certain processes to examine their effects alone or in combinations.

CONCLUSIONS

Coagulation models based on the sectional method are used in numerous computational tools in many disciplines, ranging from atmospheric sciences to nuclear engineering. Seigneur and co-workers (1986) showed that this simulation method has the best performance across various metrics. Using the geometric constraint, however, leads to coarse resolution and it may result in incorrect simulation due to its inability to properly represent the initial size distribution in cases when one or more modes of the initial spectrum are narrow, or in cases when the distribution exhibits large gradients with respect to particle size at any time during its time evolution.

SEAROSA is a versatile tool that implements arbitrary precision at multiple levels. It permits an arbitrary number of sections with arbitrary size boundaries, which results in a more accurate resolution of the temporal evolution of coagulation. The code employs exact formulations based on multiprecision arithmetic for the description of some of the frequently occurring simultaneous coagulation kernels. Surface deposition is included based on boundary layer theory. Different coagulation and deposition (either single process or combined processes), covering particle sizes from 0.01 μm to 700 μm, have been tested with different ageing times and particle load. Benchmarking was performed by direct comparison to two computer models, MAEROS and NGDE, by an indirect comparison to the COAGUL model, and to an analytical model. Results show excellent agreement, with the exception of a few identified cases where discrepancies were expected due to the different numerical methods and handling of the underlying physics. SAEROSA permits a number of parameter combinations and what-if scenarios under user control. Running time is comparable to those of MAEROS and NGDE, ranging from a few seconds to a few minutes on a laptop computer, depending on the number of sections used and the type of coagulation and deposition scenario simulated.

SAEROSA is distributed by the Radiation Safety Information Computational Center of Oak Ridge National Laboratory as RSICC Code Package PSR 573 (Sajo et al. 2012). The package contains precompiled executables for Linux, MacOS, and Windows systems, source code, sample problems, and referenced documentation. SAEROSA has also been implemented in the three-dimensional aerosol transport model CAEROT.

Additional information

Notes on contributors

J. Geng

Funding for this study has been provided in part by the US Department of Defense DTRA, Project CA08PRO002, and the US Department of Energy Health Physics Faculty Research Award Program Administered by Oak Ridge Associated Universities under Management and Operating Contract DE-AC05-76OR0003.

Notes

Funding for this study has been provided in part by the US Department of Defense DTRA, Project CA08PRO002, and the US Department of Energy Health Physics Faculty Research Award Program Administered by Oak Ridge Associated Universities under Management and Operating Contract DE-AC05-76OR0003.