Development of a Transfer Function for a Personal, Thermophoretic Nanoparticle Sampler

Abstract

Effective assessment of nanoparticle exposures requires accurate characterization of the aerosol. Of increasing concern is personal exposure to engineered nanoparticles that are specifically designed for use in the nanotechnology sector. This manuscript describes the operation and use of a personal sampler that utilizes thermophoretic force to collect nanoparticles onto a standard TEM (transmission electron microscope) grid. After collection, nanoparticles on the TEM grid are analyzed with an electron microscope, and the resultant data used to determine the characteristics of the nanoparticle aerosol sampled. Laboratory experiments were conducted to determine the inlet losses and collection efficiency of the thermophoretic sampler for particles between 20 and 600 nm in diameter. These results are used together with theory for thermophoretic velocity to form a transfer function that relates the properties of the collected particles to the properties of the sampled aerosol. The transfer function utilizes a normalization factor, F(d), which is larger than unity for very small particles but approaches unity for particles larger than about 70 nm.

Copyright 2014 American Association for Aerosol Research

INTRODUCTION

Human exposure to airborne nanoparticles is of growing interest and stems from growth of the nanotechnology industry, where contact with engineered nanomaterials has increased substantially (Roco 2005). Individuals who work in the nanotechnology sector are at greatest risk (Maynard et al. 2006), although consumers of nanomaterial-containing products may be at risk as well. Interest is also growing to characterize nanoparticle exposures among the general population (HEI 2010). Here, we refer to engineered nanoparticles as those specifically designed for use in the nanotechnology sector and incidental nanoparticles as being anthropogenic (e.g., welding fumes, vehicle exhaust, and other combustion-related particles) but not intended for nanotechnology-specific use. Biogenic nanoparticles have natural origins, such as from sea spray, wildfire, or other terrestrial sources.

Inhaled aerosol may contain particles of engineered, incidental, and biogenic origin; the latter two are ubiquitous. Identifying such particles and quantifying their contributions to human exposure are important from the standpoints of source attribution and risk assessment. Biogenic and incidental nanoparticles typically outnumber engineered nanoparticles, even in locations where engineered nanoparticles are produced (Tsai et al. 2011). An exposure assessment method that cannot distinguish engineered from biogenic and incidental nanoparticles lacks specificity, especially if the goal is to evaluate exposure to a specific nanoparticle type. Lack of specificity is a crucial drawback to nearly all nanoparticle measurement methods.

Filter sampling is often used to assess aerosol exposure, and although filters capture nanoparticles they also capture larger particles whose mass often overshadows that of the nanoparticles of primary interest. Consequently, analyses conducted on filter samples rarely detect mass signatures from nanoparticles, especially if the nanomaterials are embedded or agglomerated onto larger particles. Near major freeways where nanoparticle number concentration approaches 10¹²/m³ (Zhu et al. 2002), the corresponding nanoparticle mass concentration would be less than 2 μg/m³, assuming a lognormal size distribution (CMD = 60 nm, GSD = 1.7). Issues also arise with the filter substrate itself, as the filter matrix and its contaminants can interfere with spectroscopic analyses or mask the signature of the collected sample. Recent research has demonstrated that most nanoparticles penetrate deeply into the filter matrix before being collected, so that some spectroscopic methods may not detect nanoparticles quantitatively (Cyrs et al. 2010).

Electrostatic precipitators (ESPs) have also been employed to collect airborne nanoparticles (Miller et al. 2010). The advantages of ESP technology include high collection efficiency, low pressure drop, and a flat collection substrate. However, ESP technology also has drawbacks. First, collection efficiency varies with particle size (Cardello et al. 2002; Miller et al. 2010) and tends to drop off precipitously below 20 nm (Cardello et al. 2002). Second, the corona discharge creates reactive ions such as O⁺ ₂ and H₃O⁺ (Dzidic et al. 1976) that charge the aerosol, but also creates oxidizing agents such as O₃ and NO_x (Nashimoto 1988) that can alter particles’ surface chemistry and cause a chemical artifact on the sample (Kaupp and Umlauf 1992; Volckens and Leith 2002a,b).

Many direct-reading techniques have been applied to nanoparticle measurement, for example: condensation particle counters, diffusion chargers, and scanning mobility particle sizers (Lee et al. 2010; Mills et al. 2013); however, none provides particle composition. Thus, these techniques have limited ability to quantify engineered nanoparticle concentrations, as incidental and biogenic aerosol often confound a measurement. Many of these devices are too large for use as personal samplers.

Aerosol mass spectrometry is capable of particle counting, sizing, and chemical analysis (Voisin et al. 2003; DeCarlo et al. 2006). Unlike the methods discussed above, this technique shows promise for nanoparticle identification; however, these instruments are expensive, too large for personal exposure assessment, and currently limited to the evaluation of organic species (Tolocka 2007).

Another promising alternative for nanoparticle exposure assessment is thermal precipitation. A thermal precipitator collects airborne particles by applying a relatively large temperature gradient to a narrow flow channel. Because of the temperature gradient, gas molecules on the hotter side of the particle have greater kinetic energy than those on the colder side. Thus, the hotter molecules transfer more net momentum per collision to the particle than do molecules on the colder side, causing a thermophoretic force. The movement of a particle in the direction of decreasing temperature, its thermophoretic velocity, causes the particle to deposit onto the colder side of the flow channel. For a temperature gradient of 100°C across a 1-mm gap (10⁵ C/m), particle thermophoretic velocities can be several millimeters per second, sufficient for particle capture under well-defined flow geometries (Hinds 1999). Thermal precipitation avoids the artifact problems associated with electrostatic precipitation, but must operate at substantially lower flows than ESPs for a given collection efficiency.

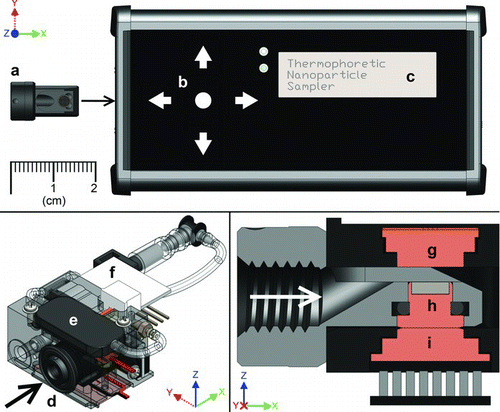
FIG. 1 Thermal precipitation sampler (TPS). Top panel: overall TPS device including removable sample cartridge (a), interface panel (b), and status screen (c); bottom left: oblique view of TPS sampling core containing inlet (d), pump (e), mass flow sensor (f), and associated connections; bottom right: normal section view of thermal precipitation region containing hot plate (g), TEM grid holder (h) located within the sample insertion cartridge (gray), and cold plate (i). Arrows in bottom drawings indicate direction of air flow.

The concept of thermophoretic force is over a century old (Aitken 1884). Thermophoretic aerosol samplers were first employed to assess exposures within the dusty trades, such as mining; these early designs were used primarily as area monitors with sample focused onto a glass slide for analysis by optical microscopy (Watson 1936; Oldham and Roach 1952; Roach 1959). More contemporary designs tend to employ cylindrical (Rogak et al. 1993; Wang et al. 2012) or plate-to-plate geometries (Tsai and Lu 1995; Wang et al. 2012) with sample analysis by electron microscopy (Rogak et al. 1993; Maynard 1995; Bang et al. 2003; Lorenzo et al. 2007). Size distribution measurements made with thermal precipitators tend to agree well with measurements from scanning mobility particle sizers (Boskovic and Agranovski 2012; Miller et al. 2012). Recently, thermal precipitators have been miniaturized so that the sampler is wearable within the breathing zone (Azong-Wara et al. 2009, 2013; Thayer et al. 2011).

We have previously described a proof-of-concept device for personal sampling that employs thermal precipitation to capture nanoparticles onto electron microscopy grids for subsequent analysis of particle size, concentration, and chemical composition (Thayer et al. 2011). In the present article we describe a second-generation thermal precipitator along with the development of a transfer function that relates the number, size, and composition of the collected particles to the concentration, size distribution, and composition of the sampled aerosol.

Description of the Thermal Precipitator Sampler (TPS)

Figure 1 is a drawing of the thermal precipitator sampler (TPS) used in this work. The device measures approximately 150 × 60 × 35 mm in size and weighs about 300 g. The TPS is entirely stand-alone, containing a micro sample pump and battery that allows up to 8 h of continuous sampling. The top of the TPS has a three-line digital display and buttons used to view and adjust setpoints for temperature and sample air flow. A thin-film resistive heater and a thermoelectric cooler maintain the hot and cold plate temperatures, respectively. The TPS samples air at a programmable setpoint between 1 and 10 cm³/min, then integrates and tracks the total volume of air sampled.

The TPS utilizes a removable sample cartridge that holds a transmission electron microscopy (TEM) grid and slides into the TPS body for sampling (Figure 1). The cartridge is shown removed from the body of the TPS in the top panel of Figure 1. When inserted (Figure 1, bottom right panel), the cartridge sits immediately below the hot plate while maintaining thermal contact with cold plate to establish the thermophoresis zone. In that zone, particles deposit onto a hole-free carbon film supported by a 200 mesh, nickel TEM grid (Electron Microscopy Sciences, Hatfield, PA, USA). Because nickel is ferromagnetic, the grid is held in place by a small magnet located between the cold plate and the grid itself. After use, the cartridge with exposed TEM grid can be removed easily from the TPS body and exchanged with a fresh sample cartridge. Since the cartridge contains most of the path through which incoming aerosol flows, switching to a new cartridge minimizes inadvertent contamination from previous samples. The exposed grid is then analyzed by electron microscopy to determine the number and sizes of the particles collected. When appropriate, single particle composition can be obtained using energy-dispersive X-ray spectroscopy (EDS).

Transfer Function

A TPS transfer function expresses the relationship between the number concentration and size distribution of the aerosol sampled and the number and size distribution of the particles found on the TEM collection grid. From examination with an electron microscope, the number of particles with size “d” on the collection substrate, X(d), can be estimated as

where x(d) is the number of particles with size “d” counted in a microscope field with area “S” and the total area of the substrate is “A.” F(d) is a normalization factor that adjusts for known and unknown factors including, for example, any differences in the particle deposit between the field examined and the entire collection substrate.

From a balance for particles entering and leaving the sampler, the number of particles with size “d” on the sampler substrate will be

where N(d) is the number concentration of particles with size “d” that enters the sampler, Pt(d) is the fractional penetration of these particles through the sampler inlet, η(d) is the fractional collection efficiency for these particles onto the sampler substrate, Q is flow through the sampler, and t is sampling time.

Combining Equations (1) and (2), then solving for the number concentration of the sampled particles, yields

Equation (3), the transfer function, shows how the number concentration of particles with any size “d” can be determined. The first bracketed term in Equation (3) corresponds to the number concentration that would be found if the sampler behaved ideally, whereas the second bracketed term contains factors that adjust for nonideal behavior. If all sampled particles penetrate through the inlet passage without loss, and if these particles all collect uniformly over the sampler substrate and nowhere else, then Pt(d) = η(d) = F(d) = 1. In this case the second bracketed term is unity. The theory and experiments reported below investigate the factors in the second bracketed term and establish their dependence on particle size.

Theoretical Collection Efficiency, η (d)

For particles smaller than the mean free path, λ, thermophoretic deposition velocity, U_T , is constant (Waldmann and Schmitt 1966) but gradually decreases as particle size increases (Brock 1962). Talbot et al. (1980) present a unifying equation for particles both smaller and larger than λ,

Here, C_s , C_t , and C_m are dimensionless constants with values of 1.17, 2.18, and 1.14, respectively; ν is the gas kinematic viscosity; C is slip correction factor; k_g and k_p are the thermal conductivities of the gas and particle, respectively; R is particle radius; (∇T) _x is the thermal gradient in the X direction; and T ₀ is gas temperature.

Flow through the TPS collection channel is laminar so that no turbulent particle mixing occurs there. Equation (5) can then be used to calculate collection efficiency for particles of any size, η(d), along any gas flow path through the channel from

where V_g is the gas velocity through the channel, H is the channel height, and L is collection length, that is, the length of the flow path through the thermophoresis zone where particles can collect. Mercer (1973) provides values for thermal conductivity for use in Equation (4) for thermophoretic velocity, U_T . To determine the efficiency of the collector as a whole, efficiencies from Equation (5) are integrated over all parallel gas flow paths across the TPS collection channel. Because the collection channel is wider than the round collection substrate, the corresponding values of L, the length of the thermophoresis zone, are zero for flow paths at the sides of the substrate, and are a succession of chords with varying lengths for flow paths that cross the round substrate.

Relatively low thermophoretic velocity, and the low collection efficiency that results, are advantageous in a thermal precipitator. If collection efficiency were too high, all particles would deposit near the leading edge of the collection substrate, although smaller particles with somewhat higher thermophoretic deposition velocities would deposit closer to the edge than larger particles. Representative analysis of the substrate would be complicated because the particle deposit would be nonuniform. Reduced TPS efficiency assures that particles of all sizes deposit uniformly along the length of the collection substrate so that representative analysis is simpler.

Particles can collect in TPS air passages due to diffusion; however, calculations (Hinds 1999) suggest that fewer than 10% of incoming particles larger than about 20 nm should collect in this way. Because the air passages upstream and downstream of the collection region make several sharp turns, larger particles may be subject to collection by inertial impaction at these locations.

METHODS

Experiments were conducted to characterize each term in the second bracket of the transfer function, Equation (3).

Evaluation of Pt(d) and η (d)

The TPS contains two components in series: the sampling core and the flow controller. In the sampling core (Figure 1, bottom right panel) aerosol flows through an inlet passage and into a flow channel that includes the thermophoresis zone, then through an outlet passage that leads to the flow controller. The flow controller contains a filter, pump, and mass flow controller in series. Equation (3) shows that penetration through the inlet passage, Pt(d), and thermophoretic deposition onto the substrate, η(d), are of primary interest. To assess these terms and their dependence on particle size, the sampling core and the flow controller were physically separated.

Particles can collect in air flow passages within the sampling core due, primarily, to diffusion. Penetration through these passages was measured using tests in which the sampling core was alternately added and then removed from the experimental setup described below, when the TPS operated without a thermal gradient,

Here C(d)_core and C(d)_{no core} represent the count of particles with size “d” when the sampling core was present and absent, respectively. Particles may collect in both the inlet passage to the thermophoresis zone and in the outlet passage from the thermophoresis zone; however, only collection in the inlet passage is of interest. Because measurements made here include penetration through the outlet as well as the inlet passages, they underestimate penetration through the inlet passage alone.

FIG. 2 Experimental setup used to measure TPS performance.

Particle collection by the sampler due to the thermal gradient, η(d), was evaluated through tests in which the number of particles that passed through the sampling core was measured when the thermal gradient was alternately turned on, C(d)_on and then off, C(d)_off. The reduction in particles counted with the gradient turned on is caused by the gradient, so that

In this study, thermophoresis was considered to be driven by a thermal gradient between only the hot and cold plate surfaces. In reality, “thermal bleed”—conduction between these plates and the surrounding chassis—creates complex, three-dimensional thermal gradients that cause particles to collect at lesser, but unknown rates on surfaces other than the collection substrate. As a result, sampler efficiency measured through experiments will tend to overestimate the collection efficiency of primary concern here, which is collection onto the substrate surface alone.

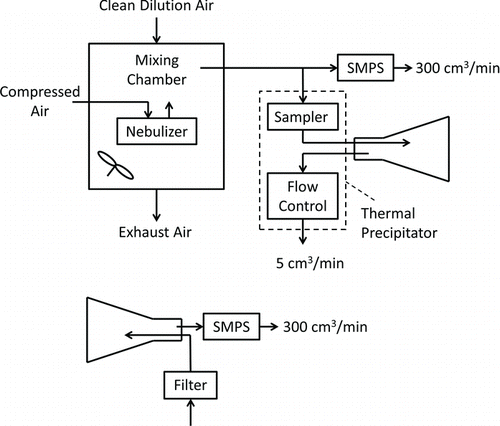
Measurement of nanoparticle concentrations was complicated by the need to operate the sampler at its mid-range flow of 5 cm³/min, whereas the flow into the reference instrument, a sequential mobility particle sizer (SMPS, Grimm Aerosol Technik GmbH & Co., Ainring D, Germany), was 300 cm³/min. This complication was addressed through the experimental setup shown in Figure 2. Previous TPS designs have operated at a variety of flow rates, ranging from 2 cm³/min (Azong-Wara et al. 2013) up to several liters per minute (Tsai and Lu 1995). We selected a target of 5 cm³/min so that a reasonably dense particle deposit could be achieved across a relatively small collection surface (i.e., a 3-mm diameter TEM grid).

An aerosol of phosphate-buffered saline particles was generated in a 0.76 m³ chamber using a six-jet Collison nebulizer (BGI, Waltham, MA, USA) operated with air at gauge pressure of 1/3 atm and a timing cycle of 1 s on, 15 s off. Filtered, dilution air flowed continuously through the chamber at 70 L/min to produce an aerosol between 20 and 600 nm in diameter that had a steady number concentration of about 5 × 10¹⁰/m³. Because RH in the chamber was always below 20%, particle size was stable.

The diagram at the top of Figure 2 depicts the arrangement used to conduct a test. Aerosol was drawn from the chamber to the SMPS, which continuously measured and recorded aerosol number concentration and size distribution. Simultaneously, test aerosol passed through the sampling core and into a 1-L flask that initially contained particle-free air. Flow through the sampling core and flask was controlled by the precipitator's flow controller. After 1 h the flask was removed from the sampling core; the flask inlet was connected to a HEPA filter and its outlet was connected to the SMPS as shown in the diagram at the bottom of Figure 2. The SMPS then drew aerosol from the flask for 15 min, and the total number of particles counted in each SMPS size bin was recorded. Flushing the flask with clean air in this way provided about 4.5 flask air changes, and by that point essentially all particles had been removed and counted.

Penetration through the sampling core was then determined using Equation (8),

where C_f (d) is the number of particles with size “d” counted in the flask from the 15 min measurement, and is the average concentration of particles of that size measured during the 60-min-test as determined by the SMPS. The right-most term in Equation (8) adjusts for any difference in the concentration of the aerosol for tests with and without the sampling core, and was always close to unity. Values of η(d) were determined in an analogous way using Equation (7).

The need to collect particles for analysis in a flask over 60 min arose from the need to analyze aerosol that had passed through the core at its design flow (5 cm³/min), but had not passed through the flow controller, because the controller contained a pump, filter, and mass flow measurement device that would also collect particles. The particle collection flask was placed between the core and the flow controller to prevent this problem. Although use of the flask led to other concerns, they could be addressed. Some aerosol was displaced from the flask during the sampling period; however, the resultant reduction in counts would be proportional to particle concentration in the flask as long as the inlet aerosol had constant concentration and size distribution. When taking a ratio of particle counts (e.g., core vs. no core as in Equation (8)) this proportional reduction in concentration cancels, so that no bias to Pt(d) or η(d) occurs. Further, some sampled particles were undoubtedly lost to the flask walls by diffusion and settling during the sampling period, but because the resultant reduction in counts is again proportional to concentration in the flask, no bias occurs when count ratios are taken. Thus the use of this method, although cumbersome, should not introduce bias to the accuracy of the penetration or efficiency values obtained.

Experiments to determine Pt(d) were conducted as follows. Each experiment employed four tests: with-without, and then without-with the core. These four tests allowed calculation of two independent measurements of penetration as a function of particle size for each sampling core. Experiments were conducted in this way with sampling cores from four different TPS units for a total of eight penetration tests.

Experiments to characterize η(d) were conducted in a similar way. These experiments utilized samplers with thermal gradients of 55°C/mm or 85°C/mm, corresponding to hot side temperature set to 80°C or 110°C, and cold side temperature set to 25°C, respectively. Again, each efficiency experiment employed four tests: gradient off-gradient on, and then gradient on-gradient off. These four tests allowed calculation of two independent measurements of efficiency as a function of particle size. Experiments were conducted in this way for two different TPS units with hot side temperatures of 80°C providing four efficiency measurements at 80°C, and for five different TPS units with hot side temperatures of 110°C providing ten efficiency measurements at 110°C. Variations in the number of different TPS units tested in this work reflect variations in the number of units available at the time the experiments were run.

Evaluation of F(d)

Additional experiments were conducted to evaluate F(d). These experiments investigated the relationship between the numbers and sizes of particles the sampler collected, and the number concentration and size distribution of the particles sampled. For these experiments, aerosol was generated in the mixing chamber as before to produce an aerosol with steady properties. A TPS sampled the aerosol inside the chamber while the SMPS simultaneously sampled the same aerosol from a point adjacent to the TPS inlet. Sampling took place for 90 min. Each SMPS scan took a little over 2 min, so that 44 scans were taken during the sampling period. The TPS operated with a thermal gradient of 55°C/mm obtained using a high-temperature setpoint of 80°C and a low-temperature setpoint of 25°C.

Particles that were collected on the TEM grids were analyzed (RJLee Group, Monroeville, PA, USA) using a Hitachi S-5500 high resolution field emission scanning electron microscope (HR-FESEM) with scanning transmission electron microscopy (STEM) capabilities. STEM images were acquired at a magnification of 25,000× using a resolution of 2 nm/pixel for particles measuring between 20 and 100 nm, and secondary electron images were used to measure particles between 100 and 600 nm at a magnification of 5,000× with a resolution of 10 nm/pixel. All images were acquired at an accelerating voltage of 30 kV. Images were compiled and analyzed using ImageJ (Rasband 2009) to determine the number and sizes of particles on each substrate. For each TEM grid analyzed, data from both magnifications were adjusted for differences in the areas analyzed at the two magnifications, then combined to give the size distribution of nanoparticles between 20 and 600 nm in projected area diameter. The particle counts obtained, x(d), were then binned into the same size intervals used by the SMPS.

For size binning, each projected area diameter, d _pa, measured using ImageJ was converted to an equivalent volume diameter, d _ev, using

where the volume shape factor, S_v , was assumed to be 1.11, the value for a cube, for all particles. Mobility diameters, d _mo, from the SMPS were converted into equivalent volume diameters through

where C _ev and C _mo are slip correction factors for the equivalent volume and mobility diameters, respectively, and the dynamic shape factor, S_d , was assumed to be 1.02, again the value for a cube. Using values of S_v and S_d for a cube is reasonable because the phosphate-buffered saline solution used to generate the test particles was primarily sodium chloride.

Values of F(d) were then developed by rearranging Equation (3),

Particle count data, x(d), obtained from the STEM analyses, were used with data for sampler air flow, Q; sampling time, t; substrate area, A; and field area, S; to calculate the bracketed term in Equation (11). These data were paired with measurements of number concentration, N(d), from the SMPS; η(d) values from theoretical calculations as discussed above and shown in Figure 4; and Pt(d) values from the experimental measurements; to determine F(d) as a function of particle size.

Separate analyses for F(d) were conducted at locations that were about 10%, 50%, and 90% of the distance along the diameter of each TEM grid as measured from the inlet side. For each of these three analysis, between 1300 and 2000 particles were counted and sized. Data for each grid location were analyzed separately to establish location-specific values of F(d) for the TPS. This experimental program was conducted twice, to assess the reproducibility of methods and results.

FIG. 3 STEM images of particles collected by the TPS in these tests. Note higher magnification for the image in the inset.

RESULTS AND DISCUSSION

The aerosol size distribution used in these experiments, as measured by the SMPS, was approximately log-normal with a count median diameter of 74 nm and a geometric standard deviation of 2.1. Figure 3 contains images of particles collected by the TPS in these tests. The particles were roughly cubic as expected, as they were primarily NaCl.

Figure 4 contains data for particle penetration through the sampler air passages, Pt(d), on the right vertical axis. Air passage penetration ranged from about 0.7 to about 0.85, with the highest values observed for particles around 100 nm in diameter. Diffusion to channel walls may have reduced penetration for the smallest particles, whereas impaction in passage bends may have reduced penetration for the largest particles. In addition to diffusion and impaction, some particles may have collected in the passages due to residual electrical charge on the particles, although previous experiments with and without an aerosol neutralizer gave negligible differences in penetration measurements. The penetration values reported here are consistent with previous TPS designs (Thayer et al. 2011; Boskovic and Agranovski 2012).

FIG. 4 Fractional efficiency, η(d), versus equivalent volume diameter, d _ev, for sampler with thermal gradients of 85°C/mm and 55°C/mm and for sampler from theory with thermal gradient of 55°C/mm (left axis), and fractional penetration, Pt(d), for sampler inlet and outlet passages without thermal gradient (right axis). Error bars represent one standard deviation. Dotted lines are regression equations; see text.

The left vertical axis in Figure 4 shows results of the tests to measure particle collection in the sampler, η(d), when operated with thermal gradients of 85 and 55°C/mm. Fractional efficiency was above 0.85 for particles of all sizes when the sampler operated with the thermal gradient of 85°C/mm, and was lower with the lower gradient. For both thermal gradients, collection efficiency decreased with increasing particle diameter, in keeping with the trend predicted from theory. The collection efficiency pattern in Figure 4 is consistent with that in other plate-to-plate TPS designs (Lorenzo et al. 2007; Miller et al. 2012). Theoretical efficiencies calculated in this way for a thermal gradient of 55°C/mm are shown in Figure 4. Theoretical efficiency, η(d), decreases from 0.25 to 0.20 as particle size increases from 20 to 500 nm.

Regression equations for Pt(d) and for η(d) with a thermal gradients of 55°C/mm and 85°C/mm are

and

The relationships for Pt(d) and η(d) from Equations (12)–(14) are shown as dashed lines in Figure 4.

As seen in Figure 4, the measured efficiency for the TPS is considerably higher than that predicted from theory. This difference could be caused by deficiencies in either the theory or the experiments, but may be driven largely by thermal bleed in the TPS sampling core, which would increase the thermophoretic zone and cause particles to collect across a wider area than the collection substrate alone. The substantial difference between measured and theoretical efficiencies suggests that thermal bleed in the TPS is important.

Figure 5 is a plot of F(d) against d _ev for analyses at each of the three TEM grid openings. Results for the three openings are similar, and an analysis of variance found no significant difference in F(d) for the three locations along the grid where analyses were done, p = 0.48. This finding is consistent with the idea that low collection efficiency onto the collection substrate, as predicted by theory, leads to a uniform particle deposit. An analysis at any, single point along the grid diameter in the direction of gas flow should provide representative results.

FIG. 5 Normalization factor, F(d), versus equivalent volume diameter, d _ev, for analyses at locations 10%, 50%, and 90% along the centerline of the TEM grid as measured in the direction of gas flow; see inset. For each particle diameter, the average F(d) for all three locations is calculated and these averages are connected by the solid line. Error bars represent one standard deviation.

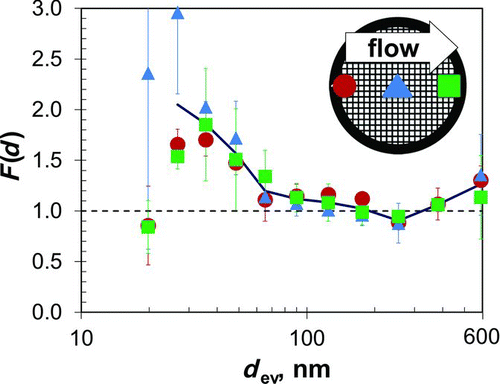
Values of F(d) vary significantly with particle size, p < 0.001. F(d) is close to unity for particles larger than about 70 nm but greater than unity for smaller particles. F(d) values close to unity tend to support the validity of both the collection efficiency theory and the measurement methods used. The F(d) values greater than unity for particles smaller than about 70 nm suggest nonideal behavior and could arise from difficulty in measuring all of the smallest particles by STEM, from overly high concentrations of these particles reported by the SMPS, from overestimates of theoretical collection efficiency for these particles, or from a combination of all these and other reasons. Regardless, the finding that F(d) is greater than unity for particles smaller than about 70 nm underscores the importance of knowing F(d) when measuring particles smaller than that size.

The thermal precipitation sampler (TPS) investigated here shows promise for determining exposure to nanoparticles. To our knowledge, this is the first thermophoretic sampling device that is fully self-contained (e.g., precipitator, battery, pump, flow control, etc.) and is sufficiently compact and light weight for use as a personal sampler; these features should help foster worker acceptance when used to assess personal exposures. The ability to vary operating conditions via user-defined input (flow rate, plate temperatures) allows for a range of operating conditions that can be tailored to specific environments and sampling needs.

CONCLUSIONS

Nanoparticle concentration and size distribution can be measured with the TPS using Equation (3), the transfer function presented here, which is specific to the flow (5 cm³/min) and temperature gradient (55°C/mm) applied. In practice, Equation (3) is used to determine the concentration of particles with any size, “d,” from data that include sampler flow, sampling time, and from counts of particles with that size in one or more electron microscope fields along the diameter of the TEM grid aligned with the direction of gas flow. Corrections for nonideal sampler behavior are made using F(d) from Figure 5 for particles smaller than about 70 nm.

For nanoparticle concentrations of about 5 × 10¹⁰/m³, a sample of about 90 min provides ample particles for analysis. For higher or lower concentrations, sample time can be decreased or increased in an inversely proportional way. Alternatively, the temperature gradient and/or instrument flow, and hence collection efficiency, may be modulated to allow further optimization of sampling duration as a function of particle concentration. This optimization algorithm will be the subject of future work.

Although the results presented here are encouraging, work in several areas remains. The TPS analyzes nanoparticles using electron microscopy. Thus, engineered nanoparticles of particular concern should be distinguishable from nanoparticles from natural or incidental sources by their morphology or by their elemental makeup as identified through energy-dispersive X-ray spectroscopy. This ability remains to be demonstrated. Further, the work reported here has been conducted in the laboratory. Field studies should be undertaken to investigate TPS performance under less ideal conditions, and to compare TPS results with measurements made using other field instruments. Finally, microscopic examination of the TPS sample grids indicated collection of PBS particles up to 5000 nm in diameter; however, particles above 600 nm were neither sized nor counted given the limitations of the SMPS. Future work should focus on extending the transfer function into this size range.

NOMENCLATURE

A	=	total area of substrate where particles collect
C	=	slip correction factor
Cm , Cs , Ct	=	constants; see Equation (4)
d ev	=	equivalent volume diameter of particle
F(d)	=	normalization factor that accounts for nonuniformity of particle deposition
H	=	height of the collection channel
kg	=	thermal conductivity of gas
kp	=	thermal conductivity of particle
L	=	length of the thermophoresis zone in the direction of gas flow
N(d)	=	number concentration of particles with size “d” in the aerosol sampled
Pt(d)	=	fractional penetration of particles with size “d” through sampler inlet passages
Q	=	flow through sampler, normally 5 cm3/min
R	=	particle radius
S	=	area of a microscope field where particles are counted
t	=	sampling time
T	=	temperature
T 0	=	gas temperature near the particle
U T	=	thermophoretic velocity
Vg	=	gas velocity through the collection channel
x(d)	=	number of particles with size “d” counted in microscope field with area “S”
X(d)	=	number of particles with size “d” on the sampler substrate with area “A”
ν	=	gas kinematic viscosity
η(d)	=	fractional collection efficiency onto the sampler substrate for particles with size “d”

Acknowledgments

^©David Leith, Dan Miller-Lionberg, Gary Casuccio, Traci Lersch, Hank Lentz, Anthony Marchese, and John Volckens Received 3 June 2013; accepted 22 October 2013. This work was made possible by support from the National Institute for Occupational Safety and Health (OH009381), Pennsylvania NanoMaterials Commercialization Center (Nano-2011-0048), and the U.S. Environmental Protection Agency (EP-13-H-000188).