Development of High Fidelity Soot Aerosol Dynamics Models using Method of Moments with Interpolative Closure

Abstract

The method of moments with interpolative closure (MOMIC) for soot formation and growth provides a detailed modeling framework maintaining a good balance in generality, accuracy, robustness, and computational efficiency. This study presents several computational issues in the development and implementation of the MOMIC-based soot modeling for direct numerical simulations (DNS). The issues of concern include a wide dynamic range of numbers, choice of normalization, high effective Schmidt number of soot particles, and realizability of the soot particle size distribution function (PSDF). These problems are not unique to DNS, but they are often exacerbated by the high-order numerical schemes used in DNS. Four specific issues are discussed in this article: the treatment of soot diffusion, choice of interpolation scheme for MOMIC, an approach to deal with strongly oxidizing environments, and realizability of the PSDF. General, robust, and stable approaches are sought to address these issues, minimizing the use of ad hoc treatments such as clipping. The solutions proposed and demonstrated here are being applied to generate new physical insight into complex turbulence-chemistry-soot-radiation interactions in turbulent reacting flows using DNS.

Copyright 2014 American Association for Aerosol Research

1. INTRODUCTION

Combustion-generated particulate formation arises from incomplete fuel oxidation and poses serious environmental and health concerns (Lahaye and Prado 1983; U.S. EPA 2009; Bond et al. 2013). Stringent regulations on pollutant emissions from combustion systems across all energy sectors demand new technologies to reduce soot emissions. To achieve this goal, it is important to understand the fundamental dynamics of soot formation, the underlying physical and chemical processes, and their interactions with turbulence and radiation.

Direct numerical simulation (DNS) of turbulent combustion is increasingly being used as a tool for physics discovery and model development. The term “DNS” in the context of turbulent combustion refers to a simulation where all relevant continuum gas-phase length and time scales are fully resolved, and the chemical processes are modeled with varying degrees of approximation. Advances in high-performance computing have allowed DNS of some laboratory-scale flames with detailed chemistry. However, DNS studies incorporating detailed high-fidelity soot models are still very limited. One of the main difficulties in modeling soot formation and transport is the multiscale nature of soot dynamic processes. Soot formation, growth, and oxidation take place primarily at molecular scales while the transport of soot particles takes place at much larger scales that can be on the order of millimeters to meters (Frenklach and Wang 1990; Bockhorn 1994; Dryer and Sawyer 1997). Fully resolved description of physical and chemical processes that span such a large spectrum of scales is cost-prohibitive even with the state-of-the-art computing power. Therefore, some modeling approximations and simplifications are inevitable.

Earlier DNS studies of luminous turbulent flames employed semi-empirical soot models (Lignell et al. 2007; Yoo and Im 2007b; Narayanan and Trouvé 2009), which require only a small number (usually two) of additional transport equations. Such models are computationally efficient and robust, but require problem-dependent modifications of the physical parameters in order to match experimental data, and hence have limited predictive capability and generality. Another drawback is their limited level of the statistical representation of the soot particle size distribution function (PSDF), which is typically assumed to be a mono-disperse distribution (Kennedy 1997).

Detailed soot models, on the other hand, attempt to model soot dynamics from first principles with minimal empiricism and thereby explicitly represent each of the key physical processes involved in soot formation, growth, and oxidation (to the extent that those are known). Such models are usually based on aerosol dynamics frameworks without a priori assumptions concerning the shape of the PSDF, and consider interactions between soot and key gas-phase species including (but not limited to) C₂H₂ and polycyclic aromatic hydrocarbons (PAHs). The aerosol dynamics models have enabled steady advancement in understanding of soot physics and chemistry over the past several decades (Haynes and Wagner 1981; Kennedy 1997; Wang 2011; Karataş and Gülder 2012) leading to evolution of several detailed soot models.

High-fidelity soot aerosol models can be classified into three categories. A Monte Carlo (stochastic) approach (Balthasar and Kraft 2003; Zhao et al. 2003; Singh et al. 2005) tracks a statistically significant number of soot particles individually, and has the potential to provide a very detailed representation of the PSDF. Due to high computational cost, however, the stochastic approach has often been limited to postprocessing of the data rather than being fully integrated with the flow solver. The second approach is the discrete sectional method (DSM), where the PSDF is represented as a finite number of particle size bins (Gelbard et al. 1980; Gelbard and Seinfeld 1980; Colket and Hall 1991; Hall et al. 1997; Pope and Howard 1997). DSM models have successfully been used in a number of laminar flame simulations (Smooke et al. 1999, 2004; Zhang et al. 2009a,b; Dworkin et al. 2011; Eaves et al. 2012). However, to provide a realistic representation of the PSDF, this approach requires a large number of bins (on the order of 20–100), each of which requires an additional governing equation to be solved, and the computational effort scales approximately exponentially with the number of size bins. As such, the DSM approach remains prohibitively expensive for turbulent combustion simulation. Finally, as a reasonable compromise between fidelity and computational efficiency, the method of moments (Dobbins and Mulholland 1984; Frenklach 1985; Frenklach and Harris 1987; McGraw 1997; Wright et al. 2001; Frenklach 2002; Moody and Collins 2003; Lignell et al. 2008; Mueller et al. 2009a,b) describes the key soot variables and the size distribution information by solving for a subset of moments of the PSDF, which are transported along with the gas-phase species.

Although these high-fidelity soot models have been available for some time, their implementation in combustion DNS applications is still new. A method of moments has been utilized in DNS for various nanoparticle-related simulations over the last decade (Moody and Collins 2003; Settumba and Garrick 2003, 2004), but its use in sooting flames has been limited. Lignell and coworkers (Lignell et al. 2008, 2009) conducted DNS of turbulent nonpremixed sooting flames using the method of moments with logarithmic interpolative closure, employing a semi-empirical soot chemistry description. More recently, a method based on bivariate moment variables (Blanquart and Pitsch 2009; Mueller et al. 2009a) has been developed and implemented in DNS (Bisetti et al. 2009, 2012). We have adopted a higher-order method of moments with interpolative closure (MOMIC) in DNS of ethylene-air nonpremixed flames based on detailed gas-phase chemistry to consider more complex soot precursor species, such as PAHs (Arias et al. 2011b). During the model development stage, however, a number of computational issues were encountered. These issues are relevant to moment methods in general, particularly in the DNS context, because many strategies to suppress spurious numerical behavior arising from the lack of resolution cannot be applied to DNS where all continuum scales are fully resolved. The present article provides discussion on a number of subtle issues associated with developing a robust, consistent, and stable numerical implementation of MOMIC-based soot aerosol models in DNS.

In the following section, the MOMIC modeling framework is described. Subsequently, the issues specific to DNS applications are addressed and the proposed remedies are explained. In particular, important issues such as monotonicity and realizability, often neglected in engineering simulations, are carefully examined. Some examples on DNS results are then presented and the performance of the improved model is evaluated.

2. METHOD OF MOMENTS WITH INTERPOLATIVE CLOSURE (MOMIC)

The formation and growth of soot particles involve both physical and chemical processes. A key process for soot growth involves collision of soot particles, or coagulation. The transient evolution of particles due to coagulation because of Brownian motions are represented by the Smoluchowski equation (Friedlander 1976; Frenklach 2002):

where N_i is the number density of particles of size class i and β _i,j is the collision frequency factor between particles of size classes i and j. The first term on the RHS of Equation (1b) corresponds to the number of particles added to the ith size class due to collisions among particles of smaller sizes, whereas the second term represents the loss of particles from the ith size class due to collisions between particles of the ith class with those of other size classes.

For accurate description of the PSDF using the Smoluchowski equation, a large number of size class is required, resulting in high computational cost. The method of moments allows a significant benefit in computational efficiency by only solving for a finite number of lower-order moments of the PSDF. Assuming that soot consists entirely of carbon, the rth moment of the particle number density N_i is defined as:

where N_i is the number of carbon atoms in a particle of size class i. The two lowest-order integer moments have clear physical interpretations: M ₀ is the total particle number density and M ₁, when multiplied with the mass of one carbon atom, represents the total mass of soot per unit volume. The knowledge of the moments of all orders is mathematically equivalent to the exact knowledge of the PSDF (Frenklach 2002). However, the underlying idea of MOMIC is that most of the statistical properties of interest can be deduced from a small number of the lowest-order moments.

If we consider only the coagulation process for now, the evolution equation of the moment variables can be derived from the Smoluchowski equation (1) by multiplying by n^r _i and summing over all size classes, yielding (Frenklach 1985; Frenklach and Harris 1987):

where G_r involves moments of all orders. For the problem to be tractable, it is necessary to retain only a small subset of the lowest-order moments in computing G_r . This requires either some a priori assumptions regarding the PSDF or a suitable closure scheme. One closure scheme for the moment equations involves quadrature-based methods (McGraw 1997; Wright et al. 2001; Marchisio and Fox 2005). Another type of closure is interpolative, as proposed by Frenklach and Harris (1987), hence the name MOMIC (Frenklach 2002). The MOMIC approach has been applied to several modeling studies in both laminar (Kazakov et al. 1995; Kazakov and Frenklach 1998; Appel et al. 2000; Mehta et al. 2009a; Mueller et al. 2009a) and turbulent (Lindstedt and Louloudi 2005; Mehta et al. 2009b, 2010a,b) sooting flames.

One of the main difficulties in evaluating G_r is the nonadditive character of the collision coefficients β _i,j . As proposed by Frenklach (2002), this problem can be addressed by expressing β _i,j in terms of integer- and fractional-ordered “grid functions.” This requires double interpolation/extrapolation. The first interpolation is required to obtain the value of the fractional-ordered grid functions from integer-ordered grid functions. This operation is referred to as the “grid interpolation.” The integer-ordered grid functions are functions of both integer- and fractional-ordered moments, but only integer-ordered moments are carried and transported in the numerical simulation. Hence, a second interpolation/extrapolation is required to evaluate the fractional-ordered moments from the integer-ordered moments. This operation is referred to as the “moment interpolation/extrapolation.” Frenklach proposed using Lagrange polynomials for both operations (Frenklach 2002). Note that the grid interpolation and moment interpolation/extrapolation are independent of each other, and are used at different levels of the interpolative closure. The grid interpolation is only used in the evaluation of G_r , whereas the moment interpolation/extrapolation is used whenever a fractional-ordered moment is required in the calculation.

As mentioned earlier, Equation (3) only accounts for the aerosol-dynamics-based collision or coagulation processes among soot particles. The moments of the PSDF also change as a result of particle inception, nucleation, and heterogeneous reactions with gas-phase species. A more general form of the moment equation is thus written as:

where R_r , G_r , and W_r are, respectively, the nucleation, collision/coagulation, and heterogeneous surface interaction terms. Details of the mathematical description of each term are separate research subjects, and can be found in the literature (Frenklach and Harris 1987; Frenklach and Wang 1994; Brown et al. 1998; Kazakov and Frenklach 1998; Appel et al. 2000; Mehta 2008). A summary of the submodels that have been adopted for these source terms is provided in the online supplementary information (SI). A discussion of the effects of a dissipative filter on solution stability and soot diffusion for the particular class of numerical schemes (time-explicit, high-order finite differences) used in the current simulations is also provided there.

3. DNS CONSIDERATIONS USING MOMIC

In Section 2, a homogeneous system was considered for simplicity. In more general cases of turbulent combustion, convective and diffusive transport must be accounted for. A general equation governing the transport of soot moments (in Cartesian coordinates) can be written as:

where the subscript l=1, 2, 3 denotes the Cartesian coordinates, U_l is the convection velocity, U _T,l is the thermophoretic velocity, and D_i is the diffusion coefficient for particles of size class i. The first term on the RHS of Equation (5) is the diffusive term, and is discussed in Section 3.1.

In the current study, six moments (r=0, 1, …, 5) are retained. A gas-phase chemical mechanism with 62 species including pyrene (C₁₆H₁₀ or A4) has been used. This mechanism was reduced from a detailed mechanism (Appel et al. 2000) using a directed relation graph (DRG) technique (Lu and Law 2005; Lu et al. 2009). Pyrene is treated as the only PAH that participates in soot dynamics. For the surface reactions, the hydrogen-abstraction-C₂H₂-addition (HACA) pathway is considered for the main surface growth and oxidation, along with additional soot oxidation via OH (Wang et al. 1996; Appel et al. 2000). The oxidation by OH does not require the presence of soot surface radicals, and the reaction efficiency is taken to be 0.13 following the suggestions in the literature (Neoh et al. 1981; Appel et al. 2000). For the surface growth via C₂H₂ and surface oxidation via O₂, a temperature- and size-dependent “steric factor” is used as proposed in a previous study (Appel et al. 2000).

The soot model has been implemented into S3D, a compressible DNS code (Sankaran et al. 2007; Arias et al. 2011a) which employs an explicit 4th-order Runge-Kutta time integration (Kennedy et al. 2000), coupled with an 8th-order central finite-differencing scheme (Kennedy and Carpenter 1994) to integrate the compressible form of the Navier-Stokes equations. Boundary conditions are treated using the Navier-Stokes characteristic boundary conditions (NSCBC) (Yoo et al. 2005; Yoo and Im 2007a).

In addition to capturing the correct physics, critical issues in the development of DNS include the stability and robustness of the numerical integration. The high-order spatial and temporal methods that have been developed for DNS have been extensively analyzed and tested for detailed gas-phase chemistry and transport. Additional considerations are needed for implementation of MOMIC soot models to be compatible with the rest of the numerical schemes for DNS.

One of the first numerical issues encountered was a result of the wide dynamic range of values taken on by soot moments, which could exceed the range available for double precision floating point arithmetic. In the original formulation (Frenklach 2002) used M ₀ for normalization (). The current flame simulation, this definition created problems in the nonreactive region where M ₀ vanishes. As a remedy, in the present study all moment variables were normalized as , where is Avogadro’s number (a constant). Additional issues related to the implementation in DNS are described in the following subsections.

3.1. Transport Properties of the Moment Variables

The diffusivity of soot can be orders of magnitude lower than that of gas-phase species and molecular diffusion of soot is usually not significant in turbulent reacting flows. Nevertheless, a careful treatment of the molecular diffusivity is desirable in DNS to minimize departures from the correct physics. The diffusion coefficient of a particle of size class i, D_i , is given by the Stokes-Einstein expression (Friedlander 1976):

where f is the friction coefficient and D_i is the diameter of the particle of size class i. Assuming a free-molecular regime, the friction coefficient is expressed as (Friedlander 1976):

where α_acc is the accommodation coefficient, is the average molar mass of the mixture, ρ _s is density of a soot particle, k_B is the Boltzmann constant, and T is the local temperature.

Integration of the moment transport equation (5), requires the knowledge of D_i . This requires careful physical consideration. Two alternative approaches are considered here. First, recognizing that diffusion is a surface phenomenon, it is expected that particles of different size classes will have different diffusivity (D_i ). If it is assumed that the soot particles are purely spherical (which is appropriate for low-to-moderate sooting flames with average primary soot particle diameter less than 25 nm [Kazakov and Frenklach 1998; Lindstedt and Louloudi 2005]) and consist of only carbon atoms, one can express the diameter of a soot particle of size class i in terms of its mass as:

The diffusion coefficient then can be expressed as:

where

The size dependence of the diffusion coefficient comes from the presence of N_i , the number of carbon atoms in the particle. With this, the moment transport equation (5) can be written as:

In the above, is a fractional moment for which a transport equation is not being solved; it is determined from integer-ordered moments by interpolation/extrapolation. As such, is subject to interpolation errors, which can lead to numerical instabilities in the simulation process. Furthermore, problems also can arise in satisfying the realizability conditions (discussed in Section 3.4).

As an alternative, we followed an approach similar to the one proposed in (Garrick and Khakpour 2004; Settumba and Garrick 2003, 2004)—a size-averaged diffusion coefficient for soot particles, , is defined as:

where is the number of carbon atoms in a notional particle size class g, which corresponds to the local geometric average of the soot population. In this approach, all soot particles at a given location and time diffuse at the same rate. Equation (5) is then written as:

such that the appearance of a fractional moment in the diffusive flux term is eliminated. It has been reported that the local geometric mean diameter-based diffusion formulation (Equation (12)) yields similar mean particle size with slightly larger values of higher order moments as compared to the size-dependent formulation (Equation (9)) (Settumba and Garrick 2004b). Based on these discussions (Garrick and Khakpour 2004; Settumba and Garrick 2004a,b) and considering the slow diffusion of soot particles, it is expected that the final results from the two alternative transport models will not be significantly different. Therefore, the size-averaged diffusion model is anticipated to serve as a numerically stable option without sacrificing the fidelity of the simulation.

FIG. 1 Profiles of first three integer-ordered moments and soot volume fraction for the transport test case with size-averaged diffusion (no artificial diffusion) in quiescent air at 1 atm. Moments are plotted using a log scale. (a) t = 0.0 ms; (b) t = 0.075 ms; (c) t = 0.225 ms.

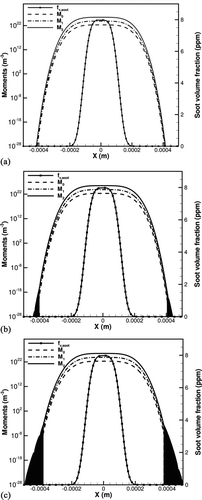
To test the stability of the proposed transport model, one-dimensional simulations of a purely diffusive transport process are conducted. In quiescent air at atmospheric pressure, a Gaussian temperature distribution with temperature ranging from 300 to 1600 K was imposed as the initial condition. The domain size was 1.5 cm, with a resolution of 5 μm. The initial soot profile is given by and M_r =(32+2 ^r )M _r−1, where r=1, 2, … ,5, and x represents the spatial coordinate. The pre-exponential factor for the initial condition was chosen to conform to the realizability conditions described in Section 3.4. Starting from the initial field, the system evolves in time by soot diffusion and thermophoresis.

FIG. 2 Profiles of first three integer-ordered moments and soot volume fraction for the transport test case with size-averaged diffusion and high-signal-pass filter (ω) in quiescent air at 1 atm. The initial profile is the same as Figure 1a. (a) t = 0.55 ms; (b) t = 1.725 ms.

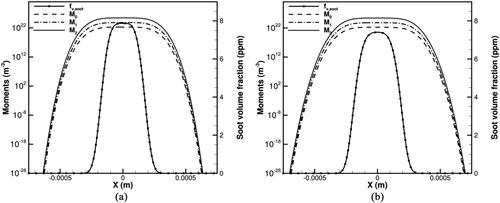
Figure 1 presents the first three moments at different times. High-frequency oscillations start from the regions near the domain boundaries where the moment variables are at extremely low values (Figure 1b), and the oscillations subsequently propagate toward the center (x=0) with time until the simulation eventually fails (Figure 1c). To mitigate the oscillations, a high-signal-pass filter is implemented such that the soot diffusivity is artificially increased when the moment variables have extremely small values that correspond to negligible levels of soot. This is implemented by adding an extra term in Equation (13):

where ν is the mixture kinematic viscosity. Here, the filter function, ω(M ₀), is developed based on the following criteria:

•	All moments diffuse at the same rate for sufficiently small values of M 0 (M 0<106m−3, that is, one soot particle per cm3, a value that is negligible for any practical purpose);
•	The weighting function depends only on the local value of M 0;
•	The magnitude of the mass diffusion coefficient for soot approaches that of the momentum diffusion coefficient of the mixture in the limit.

The adopted form for ω(M ₀) in the current study is:

where M ₀ is represented in m⁻³. Therefore, ω is close to unity for very small M ₀, and decreases to zero as M ₀⩾10⁶m⁻³.

This filter is only active at low values of local soot concentration to avoid contaminating the solution at locations with higher soot. The artificial diffusion due to the high-signal-pass filter makes the moment profiles slightly wider. The application of this filter allows nonoscillatory soot moment profiles even for long integration times. This is seen in Figure 2, which presents the results of the purely diffusive test with size-averaged diffusion described earlier in this section (Figure 1) after including the high-signal-pass filter (ω). The profiles of moments at t=0.225 ms in Figure 2a show a drastic reduction in numerical noise. Even after a long integration time, no oscillation is observed in this case (Figure 2b).Therefore, it is concluded that the size-averaged diffusivity model along with the filter (ω) yields stable and high-fidelity solutions for the soot moment transport.

3.2. Interpolation Schemes

As discussed in Section 2, MOMIC requires two levels of interpolation: grid interpolation and moment interpolation/extrapolation. The grid interpolation is required to interpolate the grid functions for evaluating the source term due to coagulation of soot particles (G_r in Equation (4)), while moment interpolation/extrapolation is required to obtain fractional-ordered moments from integer-ordered moments. Fractional-ordered moments are needed to evaluate the surface interaction (W_r in Equation (4)) and coagulation (for evaluation of grid functions) source terms, as well as for size-dependent diffusion terms (Equation (11)). In the original MOMIC formulation proposed by Frenklach, Lagrange polynomials were used for moment interpolation/extrapolation (Frenklach 2002). Unfortunately, it is well known that Lagrange interpolation is susceptible to the Runge phenomenon when the order of interpolation is increased (Jeffrey 2001). This may result in oscillations and unphysical solutions, especially when coupled with high-order discretization schemes. To resolve this numerical issue, possible remedies are: (a) to reduce the order of the Lagrange interpolation and/or carry fewer moments in the solution, or (b) to switch to a different interpolation scheme.

As for option (a), the main reason for retaining the higher-order moments is to increase the accuracy of the required moment interpolation/extrapolation. As the number of retained moments decreases, more extrapolation (versus interpolation) is required. Moreover, the second- and higher-order moments carry important information about the PSDF and particle morphology, and it has been reported that third and sixth moments can be experimentally evaluated from laser light scattering (LLS) measurements (D’Alessio 1981; Zhao et al. 2003). For these reasons, and based on findings from initial numerical tests, a reduction in the order of the Lagrange interpolation was not pursued and six moments were retained. Therefore, the alternative option to explore a different interpolation scheme is pursued. To this end, considering its nonoscillatory behavior, Stineman interpolation (Perillo and Piccolo 1991) was adopted for the moment interpolation/extrapolation scheme. Another key advantage of this choice is that unlike Lagrange interpolation, Stineman interpolation rigorously conserves the monotonicity of the set of the interpolated moments. The grid function and grid interpolation scheme remain the same as in the original formulation. It is noted here that the moment interpolation/extrapolation is performed in the logarithmic scale as discussed in (Frenklach 2002).

FIG. 3 Comparison between Lagrange and Stineman interpolation schemes for moment interpolation/extrapolation. DSM refers to moments extracted from a DSM simulation. The moments of orders between 0 and 1 are presented in the inset.

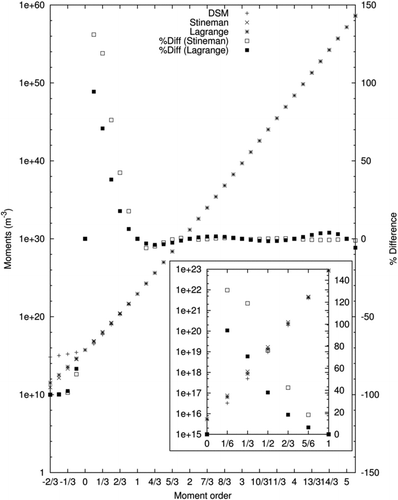
FIG. 4 Comparison of results for a steady one-dimensional laminar premixed atmospheric-pressure flame (Kazakov et al. 1995) using MOMIC with two different moment interpolation/extrapolation schemes. (a) Soot volume fractions; (b) natural logarithms of first four moments.

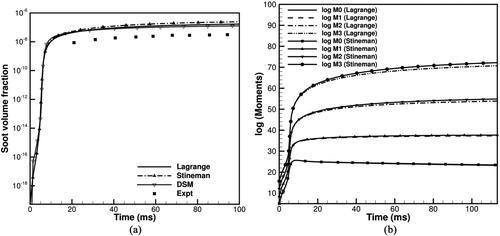
The fractional moments obtained using the Stineman interpolation scheme are compared with those obtained using Lagrange interpolation in Figure 3. As a reference, the moments obtained using a DSM model (Colket and Hall 1991, 1994) for a steady one-dimensional laminar premixed flame are plotted for comparison. The DSM results are not necessarily the “correct” results, but they provide a way for deducing fractional-order moments that does not involve interpolation from integer-order moments. The integer-ordered moments reconstructed from a DSM solution are used as input for the moment interpolation/extrapolation schemes under consideration. The percent errors of the two moment interpolation/extrapolation schemes with respect to DSM are also shown. The current formulation with six integer-ordered moments requires evaluation of fractional moments M_r , where r=−2/3, −1/2, −1/3, …, 31/6. The fractional moments M_r , where r∈(0, 5) are obtained via interpolation, while the rest of the fractional moments are obtained via extrapolation. It can be seen that the two moment interpolation/extrapolation schemes give very similar results. While the errors for both schemes relative to DSM are large for fractional-ordered moments between −1 and +1, both schemes yield fractional-ordered moments that are of the same order of magnitude. The deviations seen in the profiles of the negative order moments may be partly due to the linear extrapolation scheme. Use of an interpolation scheme involving an additional moment M _−∞≡N ₁, where N ₁ is the number density of the smallest particles, as proposed in (Frenklach and Harris 1987; Frenklach 2002), would probably reduce the discrepancy, but would increase computational cost due to an additional transport equation for N ₁. Another way to eliminate this discrepancy would be to increase the order of extrapolation (Frenklach 2002), but that was found to be numerically unstable for the current configurations. The high relative errors for fractional moments M_r , where r=1/6, …, 5/6, could be partially due to limited resolution (25 sections) of the DSM. The important point is that both interpolation schemes provide similar values both in terms of the magnitudes of the fractional moments and the relative errors. These errors are not inherent of the MOMIC formulation, but are an outcome of numerical implementation limitations. The comparison of interpolation schemes suggests that using Stineman interpolation instead of Lagrange interpolation should not significantly affect the accuracy of the MOMIC solution.

To further explore this, both interpolation schemes were used to simulate the steady one-dimensional atmospheric-pressure laminar premixed flame previously studied by Kazakov and coworkers (Kazakov et al. 1995). This flame has C₂H₄ as fuel and air as oxidizer, and the peak soot volume fraction is 0.05 ppm. The results from the simulations using the PREMIX code (Kee et al. 1985) are presented in Figure 4. While small differences between the two interpolation schemes can be seen, the results are similar and it is not possible to determine which is “better.”

3.3. Monotonicity of Moments in Strongly Oxidizing Environments

Monotonicity of moments refers to the requirement that , which arises from the physical consideration that each soot particle must consist of one or more carbon atoms. In a mildly oxidizing situation, soot particles lose carbon atoms without any reduction in the total number of soot particles. There is no surface source term accounting for the oxidation process in the equation for M ₀ (SI). In a strongly oxidizing environment, however, it is physically possible for all the carbon atoms of a soot particle to be completely oxidized, thereby acting as a surface sink term for M ₀. The standard MOMIC formulation does not account for this situation (Frenklach 2002). In the case of strong oxidation in a flame, this can lead to a situation where (for example) M ₁ would drop below M ₀, and the requirement of monotonicity of the moments breaks down. Figure 5 shows such an example from a one-dimensional DNS simulation. The physical configuration of the test is similar to a fuel core (i.e., centrally placed infinitely long strip of fuel) surrounded by air on either side. Details of the configuration can be found in (Arias et al. 2011b; Lecoustre et al. 2013). A steady-state solution for an opposed-flow steady laminar diffusion flame (Lutz et al. 1996) with scalar dissipation rate of χ_st=7s⁻¹ was mapped to the DNS domain based on the mixture fraction Z using the following relationship:

where x represents the spatial location, the parameter δ controls the width of the fuel strip, and the slope parameter σ₁ controls the peak value and the slope of the profile (the higher the slope parameter, the flatter the profile). The values of these parameters were taken as δ=3.5 and σ₁=1.8. The DNS domain size is 2.4 cm (x∈[−1.2 cm, 1.2 cm]) with a grid resolution of 3.75 μm.

FIG. 5 Profiles of first three integer-ordered moments and soot volume fraction for a one-dimensional fuel-core diffusion flame in a strongly oxidizing environment. (a) Without oxidation cutoff at t = 0.37 ms; (b) with oxidation cutoff at t = 0.37 ms; (c) with oxidation cutoff at t = 1.0 ms.

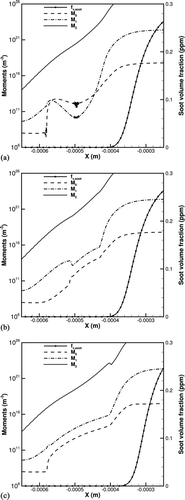
For transport, the size-averaged soot diffusion along with the ω filter (Section 3.1) was used, and no convective flux was specified. Boundary conditions were assumed to be periodic. Although the initial moment profiles satisfy the monotonicity criteria, because of the continued oxidation at very low soot concentrations, the value of M ₁ begins to approach, and ultimately falls below the value of M ₀. At t=0.37 ms, the profiles of M ₀ and M ₁ cross over, leading to an instability that ultimately results in a simulation failure (Figure 5a). Frenklach (2002) suggested carrying an equation for number density of the smallest particles (N ₁) to address this. A more physical solution to this problem would be to introduce a source (sink) term in the equation for M ₀. However, that would require tracking of an additional scalar, N ₁, as well as an appropriate strategy to determine the chemical transformation of the soot particles into gas-phase species to account for gas-phase mass conservation. In the current study, we employed a straightforward and less computationally costly approach. Since these issues occur at very low values of moments, a numerical fix to implement the oxidation cutoff mechanism was employed. The oxidation source term for all moments is set to zero as oxidation reduces the value of M ₁ to a prescribed threshold; here the threshold is taken to be M ₁/M ₀=32. Although somewhat arbitrary, this condition corresponds to a situation where the average particle has been oxidized to the size of the incipient soot particle which has 32 carbon atoms; this is consistent with the nucleation based on collision of two pyrene molecules. It should be noted that this scheme does not capture the actual phenomenon of complete depletion of soot particles due to oxidation. Instead, it treats the smallest soot particles as being inert to oxidation, thereby potentially overpredicting the number of smallest soot particles without significantly affecting the soot volume fraction. A more rigorous, physical model for complete soot oxidation is left for future work.

Figure 5b shows the results at 0.37 ms with the oxidation cutoff included, demonstrating that the monotonicity of the soot moments is preserved. In this case, the simulation can continue for arbitrarily longer times without violating the monotonicity requirement (Figure 5c).

3.4. Realizability of the Soot PSDF

For moment-based methods, an often overlooked yet important physical condition is realizability, which is a metric to determine whether the solutions correspond to a physically realizable PSDF. A truncated finite subset of moments, as used in the MOMIC approach, is not sufficient to uniquely reconstruct the PSDF without further assumptions. By checking the realizability conditions, however, one can determine whether there exists at least one “physically plausible, positive semidefinite, distribution function” for the given set of moments (Groth and McDonald 2009).

If one represents the PSDF at any instant and spatial location as P(m), where the particle size variable is represented by the soot mass m, for a given particle size m_i the PSDF can be written as:

The moments of the distribution P are then obtained by taking an appropriate mass-dependent weight, , over the entire mass space. In MOMIC, the set of moments M ^(r)=[M ₀, M ₁, M ₂, …, M _r−1] are obtained considering the set of weights , or

For a given set of moments M ^(r) and a weight function , one can show that for P to be a positive-valued distribution, the matrix , which is a real symmetric matrix, must be positive definite; hence all its eigenvalues must be positive. The matrix H is a symmetric matrix; more specifically, it is a Hankel matrix:

In our simulation, we carry six moments. From the above definition, to prove the realizability of the entire set of moments carried in the simulation (M ⁽⁶⁾), one needs to evaluate moments up to M ₁₀. Therefore, one cannot verify the realizability of M ⁽⁶⁾. The realizability of the first three moments (M ⁽³⁾), on the other hand, requires only knowledge of moments upto M ₄, and can be tested. The Hankel matrix associated with M ⁽³⁾ is:

According to Sylvester’s criterion, H ⁽³⁾ is positive definite, if and only if, all the principal minors are positive (Gilbert 1991; Horn and Johnson 2013). From this, one can deduce the following three criteria for moment realizability:

Equations (21) express the constraints exerted on the even standardized moments of the distribution. Physically, the first constraint states that the number of particles must be positive, whereas the second and third state that the variance and kurtosis of the PSDF must be positive, respectively.

Realizability can be a useful criterion for monitoring accuracy and physical plausibility of DNS results. To our knowledge, the issue of realizability has not been addressed in the context of MOMIC-based soot modeling, although it has been discussed in other contexts (Desjardins et al. 2008; Vikas et al. 2011). According to these studies, standard second- and higher-order finite-volume schemes as well as standard Runge-Kutta schemes cannot always guarantee realizability of the solution. Vikas et al. proposed a framework of developing a finite-volume scheme for maintaining the realizability criteria in the context of a quadrature-based method of moments (Vikas et al. 2011). Instead of developing a new numerical scheme, here we use realizability as an a posteriori evaluation of the fidelity and consistency of the numerical solution. Starting with a set of moments that correspond to a realizable PSDF everywhere, a consistent and convergent numerical scheme (i.e., one whose solutions converge to the solution of the PDEs in appropriate limits) should maintain a realizable PSDF as the solution is advanced in time.

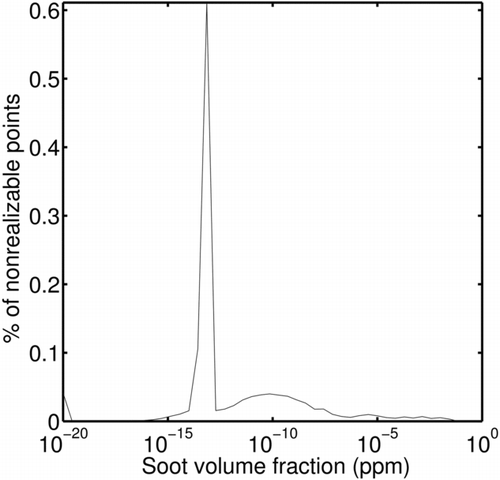
To explore this, an atmospheric-pressure two-dimensional DNS simulation was conducted using the approaches described in the earlier sections that were found to be successful (i.e., size-averaged transport with ω filter, Stineman interpolation, and the modified oxidation model). The domain was taken as 1.4 cm by 2.5 cm with 8 μm grid spacing and 7 ns timestep. Details of the test configuration has been reported in (Arias et al. 2011b; Lecoustre et al. 2013). The initial flame profile is that of a fuel core in an initially isotropic, homogeneous, two-dimensional turbulent flow field generated with a Passot-Pouquet energy spectrum (Passot and Pouquet 1987). The mean flow field is set to zero and the root mean square of the velocity is set to U′=8m/s. The length of the most energetic scale is set to 1 mm, while the Kolmogorov length scale is set to 14 μm. The simulation was initialized with a flamelet obtained from a converged OPPDIF (Lutz et al. 1996) solution with no nonrealizable points and a peak soot volume fraction of 0.27 ppm. Figure 6 shows the number of points where the solution is nonrealizable at t=1ms. The maximum number of nonrealizable point is less than 1% of the total number of grid points, and the realizability violations are limited almost exclusively to locations where the amount of soot is negligible for all practical purposes. The amount of soot mass in locations with nonrealizable PSDF is 0.003% of the total soot mass in the domain. The nonrealizability at low soot concentrations may be a result of the interpolation scheme as well as the numerical strategies (e.g., artificial diffusion filter, oxidation cutoff) employed at low soot concentrations. It must be emphasized here that the realizability criteria has been used as an a posteriori verification of the numerical integrity of the solution. Even at locations where realizability is violated, one can still compute quantities such as local soot volume fraction and local soot particle average diameter, but a realizability violation suggests that one should be careful about extracting quantitatively accurate data at these locations. Additional supporting results can be found in the SI.

FIG. 6 Histogram of percentage of grid points where realizability (Equation (21)) is violated at t=1.0 ms plotted as a function of the local soot volume fraction. The peak soot volume fraction is 0.27 ppm.

4. CONCLUSION AND FUTURE WORK

The present study addressed several issues related to the implementation of a MOMIC in the context of high-fidelity DNS. The findings, though made in the context of DNS, are generally relevant to any numerical implementation of a MOMIC-based soot model. In the current study, canonical one- and two-dimensional configurations were chosen for the numerical testing in the spirit of adopting the simplest configuration that suffices to make the point of interest.

Size-dependent soot diffusion (Equation (11)) can lead to numerical instabilities in the solution. A size-averaged diffusion formulation (Equation (13)) mitigates the issue, but is still unable to eliminate numerical oscillations at very low levels of soot. A combination of a high-signal-pass filter for artificial diffusion along with a size-averaged diffusivity formulation (Equation (14)) allows solutions to remain stable even for long integration times.

The high-order Lagrange-polynomial-based moment interpolation/extrapolation scheme has been identified as another potential source of numerical problems. A more stable Stineman scheme can be used to avoid this problem without sacrificing solution accuracy.

The current MOMIC formulation cannot handle strongly oxidizing cases robustly. A cut-off scheme that enforces moment monotonicity in strongly oxidizing situations at very low soot concentrations was proposed and demonstrated to address this. However, this approach will not be appropriate where complete oxidation of fine soot particles must be captured accurately. A more rigorous approach would require a source (sink) term for M ₀. This has been left for the future.

Finally, an a posteriori evaluation of realizability of the PSDF obtained from MOMIC has been presented and discussed. These criteria can be used to evaluate the fidelity of a soot simulation. It is expected that implementation of a physically sound model of soot formation and growth along with appropriate diffusion model using a consistent and convergent numerical scheme should satisfy the realizability criteria at locations with nonnegligible soot concentration.

A two-dimensional DNS study is currently underway with the approaches discussed in this article to better understand the fundamental process of soot formation and its interaction with chemistry, turbulence, and radiation.

SUPPLEMENTAL MATERIAL

Supplemental data for this article can be accessed on the publisher's website.

ACKNOWLEDGMENTS

This work has been supported by the National Science Foundation’s PetaApps Program under awards made to multiple institutions: grants OCI-0904660, 0904484, and 0904649. The authors thank Drs. Ramanan Sankaran, Tianfeng Lu, and Kwan-Liu Ma for useful discussion and contributions in the code development.