Moderated, Water-Based, Condensational Particle Growth in a Laminar Flow

Abstract

Presented is a new approach for laminar-flow water condensation that produces saturations above 1.5 while maintaining temperatures of less than 30°C in the majority of the flow and providing an exiting dew point below 15°C. With the original laminar flow water condensation method, the particle activation and growth occurs in a region with warm, wetted walls throughout, which has the side-effect of heating the flow. The “moderated” approach presented here replaces this warm region with two sections—a short, warm, wet-walled “initiator,” followed by a cool-walled “moderator.” The initiator provides the water vapor that creates the supersaturation, while the moderator provides the time for particle growth. The combined length of the initiator and moderator sections is the same as that of the original, warm-walled growth section. Model results show that this new approach reduces the added heat and water vapor while achieving the same peak supersaturation and similar droplet growth. Experimental measurements confirm the trends predicted by the modeling.

Copyright 2014 American Association for Aerosol Research

INTRODUCTION

For more than a century, condensational enlargement has been employed to enable particle number concentration measurements for particles too small to be detected optically (McMurry 2000). Over the last few decades, water-based condensation systems have been used to capture particles for online chemical speciation instruments (Khlystov et al. 1995; Simon and Dasgupta 1995; Orsini et al. 2003), or for air-to-air particle concentration (Gupta et al. 2004; Geller et al. 2005). Each of these methods relies on condensational growth to enable the detection, capture or focusing of particles which are otherwise too small.

The obvious advantages afforded by the condensational growth are accompanied by certain disadvantages, including temperature extremes and vapor-laden flows. Water condensational growth, which has advantages for chemical analyses and high-flow applications, is especially challenging in this regard. Mixing-type water condensation systems, such as the particle-into-liquid sampler (Orsini et al. 2003), and the steam-jet aerosol collector (Khlystov et al. 1995), combine the sample flow with steam. While creating the supersaturation necessary to activate particle growth, this creates a warm and humid output flow. Similarly, when using the condensationally-enhanced particle concentrators in exposure studies, it is necessary to dry the concentrated aerosol flow, a process that sometimes requires dilution of the concentrated sample (Geller et al. 2005; Ning et al. 2006).

An alternative to the mixing methods for water-based condensational growth is the laminar-flow approach introduced by Hering and Stolzenburg (2005). Taking explicit account of the high diffusivity of water vapor, these systems use a warm, wet-walled growth region to create the supersaturation for particle activation and growth. This laminar flow provides well-defined saturation profiles. It is capable of activating particles as small as 3 nm, and has served as the basis of a line of water-based condensation particle counters (WCPCs, TSI Inc, Shoreview, MN, USA; Hering et al. 2005; Liu et al. 2006; Petäjä et al. 2006; Iida et al. 2008; Kupc et al. 2013).

While providing defined, calculable saturation profiles and small particle activation, the temperature and the water content in the WCPC output flow are elevated. The typical operating temperature for the walls of the growth region of the general-purpose WCPC is 60°C. With the preceding conditioner set at 20°C, this activates particles as small as 5 nm, but the centerline temperature approaches 50°C, and the exiting dew point is close to 60°C. These warm temperatures are not so problematic for particle counting, as even if the particle shrinks somewhat due to loss of volatile species, it will still be counted under most circumstances. However, when using the growth tube to collect particles for chemical assays, any volatilization loss of the target analyte degrades the accuracy of the measurement. While it is possible to achieve the same supersaturation with less heating by lowering the temperature of both the conditioner and of the growth region, the output temperature and dew point remain elevated, approaching 40°C.

Motivated by the need to enlarge ultrafine particles without producing elevated temperatures or humid output flows, we have developed a new “moderated” laminar-flow water-condensation approach. This new approach starts with the same cool-walled “conditioner” of the original laminar flow WCPC, but replaces the warm, wet-walled growth region with two sections—an “initiator” that provides the supersaturation for particle activation, and a “moderator” that cools the flow while maintaining the supersaturation. This approach decreases the temperature of the output flow, allowing the operator to control its dew point. At the same time, this approach reduces the peak temperature seen by the majority of the flow. As shown below, the saturation profiles are similar to the original WCPC approach, providing equivalent particle activation and growth. This article presents numeric modeling and experimental validation of this new approach.

MODERATED WATER CONDENSATIONAL GROWTH CONCEPT

Figure 1a illustrates the original, warm-walled laminar flow water condensation method described by Hering and Stolzenburg (2005), and used in the first WCPCs. It consists of a cool-walled “conditioner” followed by a warm-walled “growth region.” Both have wetted walls. As the cooler laminar flow passes from the cooler conditioner into the warm-, wet-walled growth region, both water vapor and heat diffuse into the flow from the walls. Due to its higher diffusivity, the water transport is more rapid, creating a region of vapor supersaturation with its maximum along the centerline.

FIG. 1 Original and new, moderated approaches for laminar flow water condensation, with flow from left to right. With the original approach (top), flow from the conditioner enters a growth region with warm, wetted walls over its entire length. With the new, moderated approach (bottom) the flow from the conditioner enters a short, “initiator” section with warm wetted walls, followed by a cooler-walled “moderator” section. The overall length required is the same for both approaches.

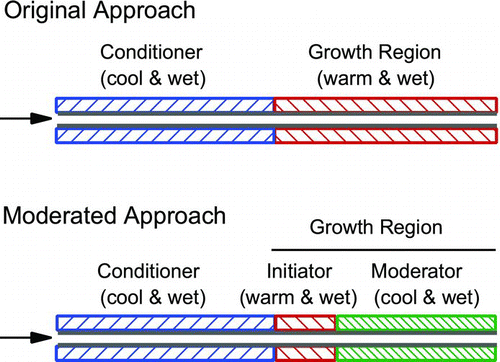
Figure 1b illustrates our new, moderated aerosol condensation approach. The original, single-temperature growth region is replaced by a two-stage growth region consisting of a short warm “initiator” section followed by a longer colder “moderator” section. The conditioner section that precedes this is unchanged. Walls are wetted throughout. The combined length required for the initiator and moderator is approximately the same as that required for the original WCPC configuration, or a length to air-flow ratio of 0.7 s/cm². With this new moderated approach, the water vapor from the short warm “initiator” section provides the water vapor for particle activation, while the moderator provides distance (hence time) for particle growth.

EVALUATION METHODS

Numeric Modeling

Temperature and humidity profiles were calculated using COMSOL Multiphysics®, finite element modeling software. Both the cylindrical and parallel-plate geometries were modeled in two dimensions, using approximately 15,000 rectangular mesh elements. Parabolic flow was assumed. The tube wall was treated as a temperature (Dirichlet) boundary. The vapor concentration at the wall was set to the saturation concentration for that temperature, in other words 100% RH. Axial temperature transitions were modeled as short ramps with length/flow = 0.03 s/cm², corresponding to a few millimeters at 1 L/min flow. The incoming air was assumed to be 95% RH at the temperature of the conditioner. The convection-diffusion equation was solved numerically to calculate the temperature and the water vapor concentration profiles. The calculations assume a thermal diffusivity of 0.215 cm²/s, and a water vapor mass diffusivity of D = 0.251 cm²/s.

Additionally, particle growth, as well as the temperature and relative humidity were calculated using a numerical model developed by our research group (Lewis and Hering 2013). This model, written in the Igor programming environment (Wavemetrics, Beaverton, OR), solves the 2-D axial symmetric diffusion equations for heat and mass transfer assuming fully developed laminar flow. Fluid properties evaluated at a mean temperature are treated as constants over the domain. Upon activation, the condensational growth is calculated along each step of the trajectory by solving the coupled, quasistatic mass and energy balance relations presented by Chang and Davis (1974) and Barrett and Clement (1988), among others. Our calculations include the Kelvin effect, but not solute effects; i.e., we assume wettable, insoluble particles. Neither heterogeneous activation nor the kinetics of particle activation were not considered. The effects of high number concentrations are handled in an iterative fashion. After the droplet growth has been calculated, the depletion of the vapor and the condensational heat are added into the convection-diffusion calculation, and the growth and diffusion calculations are repeated until reaching a self-consistent result. In the low concentration limit the model was validated against the analytical solution of Stolzenburg and McMurry (1991). Further details are provided by Lewis and Hering (2013).

Experimental Evaluation

A three-stage system following the new design was constructed using components from an existing low-flow growth tube system. The final configuration consists of a 4.6-mm ID tube extending through a 154-mm-long conditioner, a 76-mm initiator, and a 100-mm moderator, with a design flow rate of 1.5 L/min. The system was operated vertically, with the flow downwards. Because of its construction from existing components, this system employed two wicks in series. A single wick spanned the conditioner and initiator sections, and was wetted by means of a small water reservoir at the bottom (downstream side) of the initiator. A second wick spanned the moderator section, also with its own overflow reservoir at the end of the moderator. A parasitic flow removed the accumulated water from the overflow reservoir.

The output droplet size distributions were examined using an aerodynamic particle sizer (APS, TSI Model 3321). This was done by sampling directly into the 1 L/min APS aerosol sample flow tube. As shown by Lewis and Hering (2013) the droplet sizes from the APS compare well to that indicated by a series of measurements of the droplet penetration through a single-stage impactor whose cutpoint was varied through changing the jet diameter. Tests were done with varying moderator temperatures and flow rates. For comparison to the original configuration the moderator and temperature was set to the same value as the initiator.

RESULTS

Model Calculations of Saturation and Temperature Profiles

Figure 2 compares calculations for the new, moderated approach to that of the original warm-walled growth region. Shown are the centerline saturation ratios obtained when a 5°C, 95% RH flow is introduced into a uniformly heated 35°C growth region, or into a 35°C initiator followed by a moderator with wall temperatures of either 5°, 10°, or 20°C. This is for the growth region only; the conditioner is not shown. The saturation ratio S is plotted as a function of the nondimensional parameter z/z _o where z is the axial distance downstream from the entrance of the initiator, and z _o is the characteristic length, defined as ratio of the volumetric flow rate Q to the water vapor diffusion constant D:

FIG. 2 Saturation ratio calculated at the centerline of a laminar flow at 5°C and 95% RH entering a tube with wetted walls and various wall temperature profiles. In all cases the wall temperature ramps quickly from 5°C to 35°C. For the original configuration the walls stay at 35°C throughout the remaining length. For the new, moderated configuration the wall temperature is lowered after about 25% of the length to either 5°, 10°, or 20°. Plotted as a function of the axial distance from the entrance of the initiator, z, normalized by the characteristic length z ₀ = Q/D (Equation (1)).

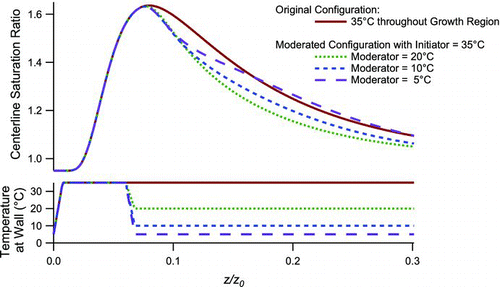
For water vapor diffusing into air under ambient conditions, z _o = 100 cm calculations are for a cylindrical geometry in the limit of low particle concentrations, wherein condensational heating and vapor depletion are ignored. The length of the initiator section was selected to be just long enough to provide the same maximum saturation ratio as obtained with the original approach with warm walls throughout the growth region.

As shown in Figure 2, the saturation ratio along the centerline is relatively insensitive to the wall temperature of the downstream, moderator section. All trajectories exhibit the same value for the maximum saturation ratio. Moreover, along the centerline this maximum occurs just downstream of the initiator exit, at an axial position of 0.08z _o. The delay is due to the time required for the water vapor to be transported from the walls of the initiator to the centerline of the flow, during which time convection carries the water vapor downstream. Further downstream the flow cools, and water vapor is removed by the cold wall. The relative rate of these two processes is such that the removal of water vapor is offset by the reduction of equilibrium vapor pressure due to cooling with the result that the saturation ratio profile is nearly the same for all selected operating temperatures within the moderator. As shown, the downstream value of S for the initiator-moderator design is within 9% of that for the original design.

Figure 3 provides further detail for the specific case with a 95% RH flow at 5°C entering a 35°C initiator section followed by a 10°C moderator. Comparison is given to the original approach with wetted 35°C walls throughout the condensation region. As in Figure 2, these calculations are for a low concentration limit, wherein condensational heating and vapor depletion are ignored. Shown are the saturation ratio, temperature, and water vapor content along three trajectories, from the centerline (r/R_o = 0) to near the edge of the tube (r/R_o = 0.75, where R_o is the tube radius). For fully developed laminar flow, 44% of the flow volume is contained between the trajectory at r/R_o = 0.5 and the centerline.

FIG. 3 Axial profiles of the (a) saturation ratio, (b) temperature, and (c) water vapor content in for a laminar flow in a tube at 5°C and 95% RH entering a growth region with 35°C wetted walls throughout (dashed lines, original approach) and for a growth region with a short “initiator” section at 35°C followed by a “moderator” section at 10°C. Profiles are shown along three trajectories at radial positions r = 0 (centerline), r = 0.50R _o, and r = 0.75R _o, where R _o is the tube radius. The axial coordinate z is normalized with respect to the characteristic length z ₀ = Q/D.

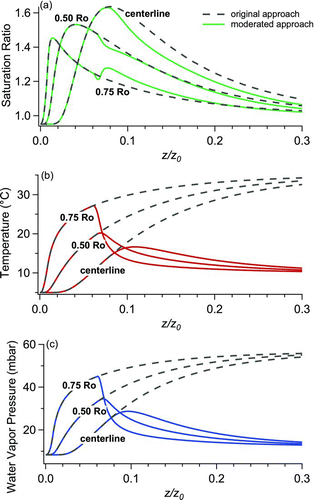
As seen in Figure 3a, the peak supersaturation is the same at all radial positions for the initiator-moderator as for the single-stage growth region. Indeed, both the temperature and the saturation ratio track exactly until reaching the point of maximum supersaturation. This implies that the activation of particle condensational growth, including material dependencies, will be the same as for the single-stage growth region. Particles activate within, or just past the exit of the initiator, and then continue to grow in the moderator. Within the moderator, the saturation ratio is within 6% of that for the original design (i.e., with 35°C walls throughout). Because the saturation ratio is similar for either approach, and because to first order the droplet growth depends on the saturation ratio (Lewis and Hering 2013) one expects similar droplet growth.

While the saturation ratio is similar to the original design, Figures 3b and c show that the temperature and water content within the cooled moderator section are much lower. With the original design, the temperature along each trajectory approaches the temperature of the warmed growth tube wall (equal to 35°C in the example shown). In contrast, with the new moderated design, the centerline temperature increases by an increment of 35–40% of the initiator–conditioner temperature difference, and then slowly cools. In our example, where a 5°C flow enters a short 35°C initiator followed by a longer 10°C moderator, the maximum centerline temperature is 16°C. The midpoint temperature (along the r/R _o = 0.5 trajectory) never climbs above 22°C. Thus most of the flow is not significantly heated by the initiator, an important aspect when handling semivolatile materials. In contrast, with the single-stage growth region the flow continues to warm after reaching its peak supersaturation, with exiting temperatures between 29°C and 34°C.

As shown in Figure 3c, the use of the initiator-moderator in place of the single-stage growth region reduces the water vapor content by a factor of about 3. This can be reduced further by selecting a yet colder wall temperature for the moderator. With the single-stage growth region water vapor is continually added to the flow throughout the growth region. In contrast, with the initiator-moderator, water is added to the flow only when passing through the initiator. Additionally, some of the water vapor is removed within the moderator. With the reduced water vapor content it is possible to collect, or focus or detect the droplets that are formed without complication from condensation. Specifically, for the example given, the exiting dew point is between 11°C and 16°C (depending on radial position), and thus it is possible to avoid condensation by operating the downstream components at a moderate 20°C instead of the 35°C that would be required of the single-stage growth region.

Modeled Droplet Diameters

The peak supersaturation governs the minimum Kelvin diameter, which describes the minimum size of a water droplet that would be more likely to grow than to shrink, and characterizes much of the vapor properties important to activation. Similarly, the mass transport of condensate to the droplet is driven primarily by the saturation ratio, a result that is seen by combining the mass and heat balance relations for droplet growth, and applying the Clausius Clapeyron relation for vapor pressure (Barrett and Clement 1988; Stratmann et al. 2010). Because the moderated condensational growth approach provides the same peak supersaturation, and similar supersaturation profiles as in the original approach, one expects that both the particle activation and subsequent droplet growth will be similar.

Figure 4 compares the droplet growth in the moderated system to that from the original, warm-walled growth approach. These calculations are for a cylindrical geometry for the case of an airflow at 5°C entering an initiator with wetted walls at 35°C followed by a moderator with wetted walls at 20°C. Comparison is made to the same 5°C flow entering a single-stage growth region with wetted walls at 35°C throughout. The length of the initiator and moderator are 0.07z ₀ and 0.15z ₀, respectively, and the length of the single-stage growth region is the sum of these two, or 0.22z ₀. At an airflow rate of 1.5 L/min these lengths correspond to 6 cm for the initiator and 14 cm for the moderator.

FIG. 4 Evolution of droplet diameter calculated for original approach with 5°C, 95% RH flow entering a wet walled tube at 35°C, and for the moderated approach of this article where the flow enters a 35°C inititiator followed by a 20°C moderator.

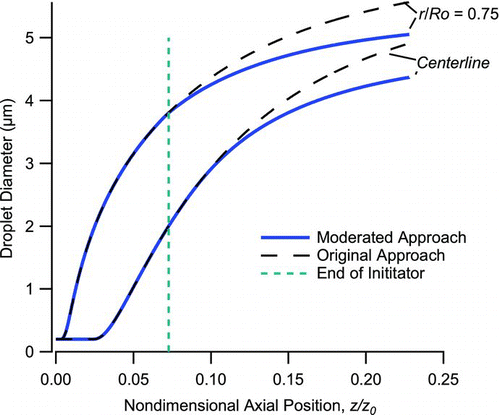
The droplet size that exits at the end of the initiator-moderator configuration, with its short warm section followed by a longer cold section, is nearly the same as for the single-stage growth region, with warm walls throughout. Much of the droplet growth occurs in the moderator section. The initiator by itself is too short to serve the function of the single-stage growth region. The moderator section provides the time for transport of water vapor from the warmed walls of the initiator into the center core of the flow. It is the combined initiator-moderator that provides both the activation of condensation and the time for the droplet growth.

The calculations of Figure 4 apply to the low concentration limit, when condensational heating and vapor depletion are ignored. Using the model of Lewis and Hering (2013) we examined concentration effects with this new, initiator-moderator geometry. With the original configuration Lewis and Hering show that as particle concentrations increase, the minimum activated Kelvin equivalent diameter also increases, while the droplet size decreases. This is primarily due to the warming of the flow from condensational heat release, which lowers the saturation ratio. Similar concentration effects are found for the initiator-moderator approach. As with the original design, these effects may be minimized by employing narrower tubes.

Although not shown, these calculations were also done for a parallel plate geometry, with similar results. The saturation profiles and droplet growth are largely unaffected when the uniformly warm growth region of the original design are replaced by a short initiator section with walls at the same growth region temperature followed by a cooler moderator. As in the original design, use of more closely spaced plates decreases the size of the droplets formed at low concentration and minimizes the concentration effects.

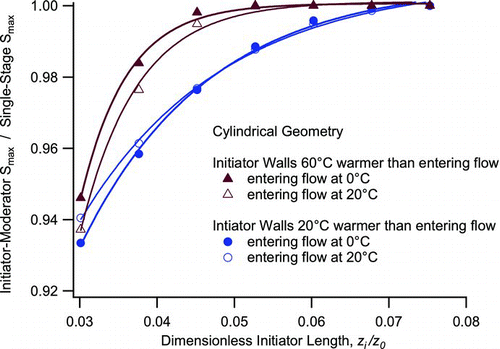
FIG. 5 Ratio of the peak supersaturation achieved with the initiator-moderator configuration to that from the original configuration, as a function of the initiator length z_i , where z ₀ = Q/D. Calculations are presented for cylindrical geometry at four sets of operating temperatures, where the entering temperature refers the entrance of the initiator or growth region (i.e., to that exiting the conditioner).

Effect of the Initiator Length

The numerical model was used to examine how the length of the initiator affects the peak supersaturation. As can be seen in Figure 2, if the initiator is sufficiently long, the peak supersaturation is independent of the temperature of the moderator downstream. However, if the initiator is too short, this peak supersaturation will be lower because insufficient water vapor has reached the centerline before being removed by the colder moderator walls. We used our model to quantify this effect. In the first two cases presented, the conditioner is at either 0°C or 20°, the initiator wall temperature is 20°C warmer than the conditioner, and the moderator wall temperature is 20°C cooler than the initiator walls. In the third and fourth cases, the conditioner temperature is either 0°C or 20°, as before, but now the initiator is 60°C warmer than the conditioner, and the moderator is 35°C cooler than the initiator.

Figure 5 shows these results for a cylindrical geometry. We plot the ratio of the maximum supersaturation achieved divided by the maximum supersaturation produced by an infinitely long initiator operated at the same input flow and wall temperatures. When the walls of the initiator are 60°C warmer than the entering flow, an initiator length of about 0.04z _o is sufficient to achieve 99% of the saturation ratio produced by an infinitely long wet-walled tube. When the walls of the initiator are just 20°C warmer than the entering flow, a somewhat longer initiator length to flow-rate ratio of about 0.06z ₀ is needed to achieve 99% of the maximum supersaturation for these operating temperatures. This difference in the required initiator length has its origins in the nonlinear dependence of the saturation vapor pressure on temperature, which delays the point of peak supersaturation further downstream for smaller temperature differences even for long initiators (for example, for the original configuration with a uniformly warm growth region the centerline maximum supersaturation occurs at 0.06z ₀ for 60°C temperature difference, and 0.08z ₀ for a 20°C difference). Although not shown, we find that these results are consistent over a range of moderator temperatures.

Figure 6 shows the analogous calculation for a parallel plate geometry, where the characteristic length is now

FIG. 6 Ratio of the peak supersaturation achieved with the initiator-moderator configuration to that from the original configuration, as a function of the initiator length z _i , where z _{p 0} = qδ/D. Calculations are presented for parallel geometry, where the entering temperature refers the entrance of the initiator or growth region (i.e., that exiting the conditioner).

where q is volumetric flow per unit width of the plates and δ is the plate separation. For plates separated by a 5-mm gap operated at a flow rate per unit plate width of 1 Lmin⁻¹cm⁻¹, z _{p 0} = 33 cm. The results are quite similar. When the wall temperature of the initiator is 60°C above the temperature of the entering flow, and initiator length of 0.05 z _{p 0} is sufficient to achieve 99% of the saturation ratio possible with a single-stage growth region. As with the cylindrical geometry, somewhat longer initiator lengths are required when operating with a smaller temperature difference between the walls of the initiator and the conditioner.

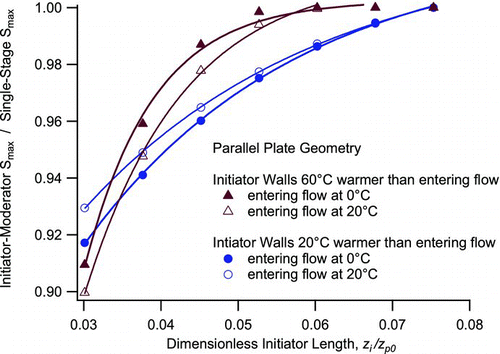
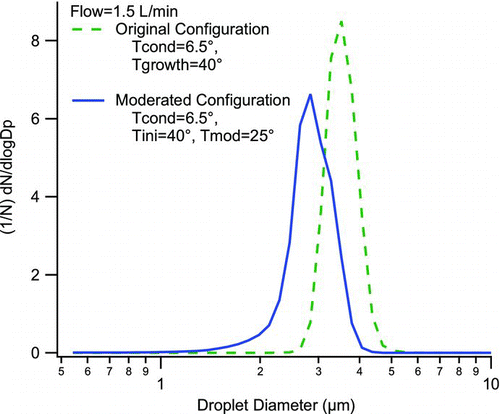
FIG. 7 Output droplet size distributions measured by an aerodynamic particle sizer for the original, warm-walled growth region and for the moderated approach of this article. Input is diluted ambient laboratory air.

For both cylindrical and parallel plate geometries, the modeling shows that it is possible to achieve the same particle activation diameters, and nearly the same droplet growth, using a short, wet-walled warm “initiator” followed by a longer colder-walled “moderator,” as when using a uniformly heated, wet-walled growth region of the same overall length. This equivalency requires the initiator length span 80% of the distance to the point that provided the maximum supersaturation in the original, uniformly heated growth region. For typical operating temperatures (with the initiator ∼30°C warmer than the conditioner), this corresponds to 0.06z ₀ in a cylindrical geometry, or about 0.25Q s cm⁻². This is of order of 35% of the overall length of the growth region used in the commercial WCPCs (TSI Models 3785-3788). If the initiator is shorter, the peak supersaturation will be somewhat lower than would be obtained with a longer one operated at the same temperature. If the initiator is longer, the peak supersaturation will be the same and the droplet size will be somewhat larger. However, the peak temperature along the centerline and the amount of added water vapor will be higher. With a relatively short initiator, one can provide all of the water vapor necessary to create the same peak supersaturation as the longer single-stage growth region.

Experimental Measurements

Figure 7 shows measurements of the size distribution of droplets exiting the growth tube for the moderated design, and compares this to measurements for the same system when operating the moderator at the same temperature as the initiator. The flow rate is 1.5 L/min, the conditioner was operated at 6°C, the input is diluted ambient aerosol. The droplet size distributions are from an APS. With the initiator and moderator sections both set to 40°C, the system mimics the original configuration, with uniformly warmed walls throughout the length of the growth region. With the same initiator temperature of 40°C, but with the moderator operated at 25°C, i.e., the moderated condensational growth approach, the resulting droplets are shifted to slightly smaller particle sizes, from 3.5 μm to 3.0 μm number median diameter. The respective number concentrations are within 2% (606 and 616 /cm³), indicating equivalent activation. This is in qualitative agreement with the modeling.

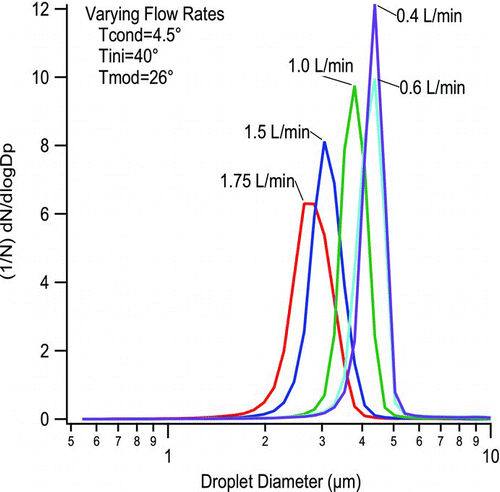
Figure 8 compares the droplet size over a range of flow rates at fixed operating temperatures of 5°C, 40°C, and 25°C for the conditioner, initiator, and moderator, respectively. A lower flow rate corresponds to effectively lengthening the growth tube. This promotes larger droplet growth, both through increasing the nondimensional conditioner length, providing lower flow temperature at the inlet of the initiator, and by increasing the nondimensional length of the initiator, which brings the system closer to the original approach. The data show similar behavior for flow rates varying by a factor of 3, with exiting droplet diameters changing by less than 40%.

FIG. 8 Output droplet size distributions for the moderated approach at varying flow rates, with wall temperatures of 4.5°C, 40°C, and 26°C for the conditioner, initiator, and moderator, respectively. Input is diluted ambient laboratory air.

The insensitivity of the droplet size to the temperature of the downstream wetted walls, as indicated by the model calculations, also helps explain why it is possible to measure droplet size with the APS. Naively, one would assume that a water droplet is too volatile to be retained once it exits the growth tube. However, by operating the final stage of the growth tube at above-ambient temperature, the transport line to the APS inlet become slightly moist, and hinders evaporation of the droplet.

These experiments confirmed that this technique produced nearly the same droplet size as a single-stage warm walled growth region of the same diameter and length. Moreover, this size varies only somewhat with the air sample flow rate, with a the droplet diameter decreasing by 30% (4.4 μm to 3.1 μm) when the flow was lowered by a factor of 4 (from 1.5 to 0.4 Lmin⁻¹). The maximum flow rate that produced a consistent droplet sizes corresponds to an initiator length to flow rate ratio of about 0.3 s/cm² similar to that predicted by the modeling above. At lower flow rates the initiator was long compared to the position of maximum supersaturation, and the droplet growth was similar to that for a single-stage growth region. The subsequent moderator simply served to provide a bit more time and distance for droplet growth while dropping the temperature and dew point.

SUMMARY

A new, three-stage laminar flow water-based condensational growth system has been introduced that replaces the warm, wet-walled growth region of the original WCPCs with a short, warm, wet-walled initiator section followed by a cool, wet-walled moderator section. The initiator spans approximately one-third of the length of the growth region of the original design. For the same operating temperatures, the modeled peak supersaturation is the same as with the original design with warm, wet walls throughout the growth region. Additionally, the downstream supersaturation profiles are similar, while both the temperature and the dew point are significantly reduced. Particle activation occurs either in the inititator or near the entrance of the moderator. Neither the peak supersaturation nor the extent of droplet growth is sensitive to the temperature of the moderator stage. By operating with a cool moderator stage, it is possible to produce peak supersaturations in excess of 1.5 while limiting the extent to which the flow is warmed. Moreover, the moderator temperature can be selected by the operator to provide the dew point conditions desired at the outlet. Essentially this three-stage approach decouples the temperature and water content of the output flow from conditions required for particle activation. The moderated approach provides similar particle activation and growth, while significantly reducing water vapor and temperature in the output flow. The lower output temperature and dew point has many practical advantages when coupling the water condensation growth tube to detectors, focusing orifices or collectors.

FUNDING

This research was funded by the NIH grants RC3ES019081 and R44ES014997.

ACKNOWLEDGMENTS

U.S. and foreign patents on the concept in this article are pending.