Analytical Approximation Schemes for Mean Nucleation Rate in Turbulent Flows

Abstract

Nucleation rate is a very sensitive function of the temperature and vapor mole fraction. Analytical approximation schemes for the mean nucleation rate in turbulent flows are derived using Laplace’s approximation method. The schemes only require the derivative of the nucleation rate function and the probability density function (pdf) of the vapor mole fraction and/or temperature at the point of maximum nucleation rate. Based on the relation between the mole fraction and temperature, i.e., linearly correlated or not, different approximation schemes are developed. Numerical examples are constructed to investigate the accuracy of these approximation. In the examples, the pdfs of mole fraction and/or temperature in various turbulent flows are assumed to come from the beta distribution with five distinct forms. The mean nucleation rate of dibutyl phthalate (DBP) aerosol in these turbulent flows are calculated from the approximation schemes, and compared with exact numerical integration. The relative errors are less than 1% for cases when nucleation rate diminishes at the bounds of temperature fluctuations, and no more than 50% for all studied examples. Furthermore, the approximation schemes are not sensitive to the precise form of the pdfs. Hence, these developed approximation schemes can be used to estimate the mean nucleation rate in a broad range of turbulent flows conveniently.

Copyright 2014 American Association for Aerosol Research

1.  INTRODUCTION

Aerosol nucleation is ubiquitous in both natural and industrial processes. Nucleation takes place under supersaturation condition, which can arise from chemical or physical processes. Physical processes producing supersaturation include adiabatic expansion or mixing with cool air or radiative or conductive cooling (Friedlander 2000). Turbulence is characterized by strong mixing, hence nucleation in turbulence is important and has received much attention (Lesniewski and Friedlander 1995; Chan et al. 2010a,b; Zhou and Chan 2011; Fager et al. 2012). Due to the complexity of turbulence, a practical approach is to estimate the mean nucleation rate efficiently based on the fundamentals of turbulence, that is, easily obtainable information.

Nucleation rate is a sensitive function of temperature T and vapor mole fraction c, that is, . The mean nucleation rate can be computed as

when the joint probability density function pdf(T, c) is known. In many different types of flows, such as jets (Lesniewski and Friedlander 1998; Zhou and Chan 2011) and mixing layers (Zhou et al. 2012), the temperature and vapor mole fraction are linearly related to each other, under the assumption Le=1 (where Le is the Lewis number, that is, the ratio of thermal diffusivity to mass diffusivity of the gas). Then, the mean nucleation rate can be simplified as

where the mixture fraction

is introduced for convenience. T _min, T _max, c _min, and c _max are the minimum and maximum temperature and vapor mole fraction, respectively, which are specified according to the boundary conditions. Sources or sinks of temperature or vapor mole fraction are not considered here. It is observed that the nucleation rate function contains an exponential term (Equation (4a)), Shaw (2004) used an asymptotic analysis to obtain an approximation for Equation (2). Independently, Zhou and Chan (2011) also developed an approximation for Equation (2) from geometric intuition. Their obtained results (Shaw 2004; Zhou and Chan 2011) only differ by a constant factor, versus 2, which can be seen as trivial after taking into account the substantial uncertainties in turbulence and the kinetic theory of nucleation.

However, there are two limitations in both of the approximations (Shaw 2004; Zhou and Chan 2011). One is that the integration domain in Equation (2) is assumed to be large enough (termed as infinite bounds) that the nucleation rate is then intrinsically to be zero at the integration bounds. Usually, this assumption is satisfied. But if the temperature or vapor mole fraction fluctuates in a range (termed as finite bounds) that the nucleation rate does not vanish at the bounds of the studied range, then the approximations of Shaw (2004) and Zhou and Chan (2011) will introduce big errors. The other limitation is the assumption of Le=1, which is generally not true in practice.

In this study, new approximations are developed and introduced, which relieve the two limitations mentioned above, and are applicable to the cases of Le=1 and Le≠1, and of the infinite bounds and the finite bounds.

2. NUCLEATION RATE

From the classical nucleation theory, the nucleation rate satisfies (Friedlander 2000)

where h and g are shorthands for the corresponding terms. They are not distinguished for the two cases Le=1 and Le≠1, since they are discussed separately in Sections 3 and 4, respectively. A simple but very useful transformation is

which converts the nucleation rate function to an exponential form completely. In the nucleation rate function (Equation (4a)), P_v is the vapor pressure, m is the molecular mass, ρ _p is the particle density, is the vapor saturation ratio where is the saturation vapor pressure, k is the Boltzmann constant, and σ is the surface tension. For a specific vapor, all properties can be expressed as functions of temperature and vapor mole fraction through the empirical equations.

3. APPROXIMATIONS OF MEAN NUCLEATION RATE FOR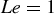

3.1. Infinite Bounds

From Equations (2)–(5), it is clear that the mean nucleation rate can be computed as

where f(T) is a shorthand for . The pdf is assumed to be known beforehand. The precise form of the pdf is not crucial, but it is expected to be a “mild” function when compared to the exponential function.

Long ago, Laplace (1986) made the observation that the major contribution to the integral type of Equation (6) should come from the neighborhoods of the point where the integrand obtains its greatest value. More precisely, assume f(T) obtains its minimum at T*, and T _min<T*<T _max, then (Wong 2001)

This is known as the Laplace’s approximation. The following gives a simple proof of the Laplace’s approximation, which helps to understand the basic idea of the approximation and provide the clues for the generalization of the approximation. Since f′(T*)=0 and f″(T*)<0 (because f(T*) is the minimum), then f(x) may be approximated to quadratic order (by Taylor expansion, see Figure 1)

Hence

FIGURE 1 Quadratic approximation of the nucleation rate function

for DBP. A and B denote the maximum and inflection points, respectively.

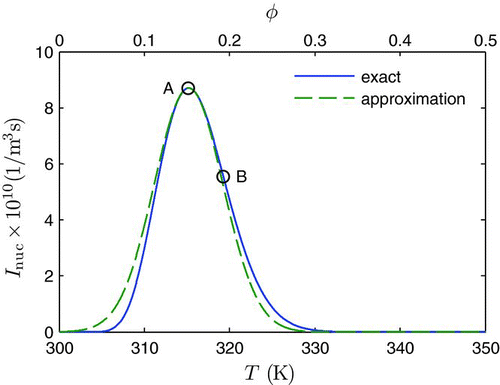
The first approximation is obtained by replacing h(x) with its quadratic expansion. The second approximation is based on the assumption that T _min and T _max are far away from T* and the exponential function nearly decays to zero beyond T _min and T _max. Therefore, it is permissible to extend the integral domain to infinity. The last step uses the Gaussian integral.

The applicability of the Laplace’s approximation (Equation (8)) relies on two prerequisites: (i) f(T) has a minimum inside the domain, and (ii) the integrand almost vanishes beyond the integration bounds. Fortunately, the prerequisites are usually satisfied when evaluating the mean nucleation rate in turbulence. The approximation of Equation (8) is slightly different from that of Shaw (2004) (There is a typo of missing the absolute sign therein.)

In fact, f″=h″−ln [g(T)pdf(T)]″≈h″, because h″ greatly dominates over ln [g(T)pdf(T)]″ (which is clearly demonstrated in the numerical examples below). The Laplace’s approximation of Equation (8) here is slightly more “exact” than Equation (10), while Equation (10) is more convenient for some cases, since h does not contain the and h″ only needs to be computed once, which is irrespective of the changes of throughout the flow field. Usually, the two approximations Equations (8) and (10) can be considered equivalent, and chosen for the sake of convenience.

3.2. Finite Bounds

If the nucleation rate function is far from zero at either bound of the domain, neither Equation (8) nor (10) is a good approximation any longer (Figure 1). First, the nucleation rate is assumed to be much larger than zero at the lower bound of temperature fluctuation T _lower, which is not necessarily equal to T _min (but T _lower⩾T _min) as discussed in the Introduction section. For this case, it is still possible to use the same quadratic expansion of Equation (8), and to follow the derivation of Equations (9a) and (9b), but only to extend the upper bound to infinity and keep the lower bound intact. It is then straightforward to obtain

where the error function erf(x) approaches to 1 as x→∞, and −1 as x→−∞. If T _lower=T*, then the error function is zero, and Equation (11) will be half of Equation (8), as expected (Figure 1). If T _lower=T _min, Equation (11) becomes the same as Equation (8).

If the nucleation rate is much larger than zero at the upper bound of temperature fluctuation T _upper (T _upper⩽T _max), the approximation can be obtained by replacing (T _lower−T*) with (T*−T _upper) in Equation (11) due to the symmetry

The case for nonvanishing nucleation rate at both T _lower and T _upper can be obtained by the simple integration relation

where the integrations on the right hand side can be computed from the approximation Equations (8), (11), and (12), respectively.

The approximations of Equations (11) and (12) are based on the quadratic order Taylor expansion of f(T) at T*. If T _lower or T _upper is far way from T*, it is better to expand f(T) at T _lower or T _upper. Since T _lower and T _upper are not local minimum points, f′(T _lower)≠0 and f′(T _upper)≠0, then f(T) can be expanded to the linear order

or

Analogous to the derivation of Equation (11), it renders

and

For the case of evaluating the mean nucleation in the range from T _lower to T _upper, the integral relation of Equation (13) can be used, with corresponding terms substituted by Equations (16) and (17).

3.3. Numerical Examples

Here, the nucleation of dibutyl phthalate (DBP) is investigated as numerical examples. DBP as condensate has been used in various experimental investigations (Higuchi and O’Konski 1960; Brock et al. 1986; Okuyama et al. 1987; Lesniewski and Friedlander 1998; Pyykönen et al. 2007), because it is a stable compound and does not need any cooling to observe nucleation. There are also numerical simulations (Garmory and Mastorakos 2008; Zhou and Chan 2011; Zhou et al. 2012) on DBP aerosol dynamics. Empirical equations for ρ _p , , and σ are taken from Okuyama et al. (1987), which are given in Table 1.

Physical properties of DBP, from Okuyama et al. (1987)

Molecular mass (kg)	m=0.27835/6.02×10^23
Density (kg/m^3)	ρ p =1063−0.826(T−273.16)
Surface tension (N/m)	σ=3.53×10^−2−8.63×10^−5(T−273.16)
Saturation pressure (Pa)

The temperature and vapor mole fraction are set as T _min=300 K, T _max=400 K, c _min=0 ppm, and c _max=500 ppm, which correspond to the boundary conditions for a turbulent jet studied in the experiment (Lesniewski and Friedlander 1998) and the numerical simulations (Garmory and Mastorakos 2008; Zhou and Chan 2011).

FIGURE 2 Beta distribution with various parameters.

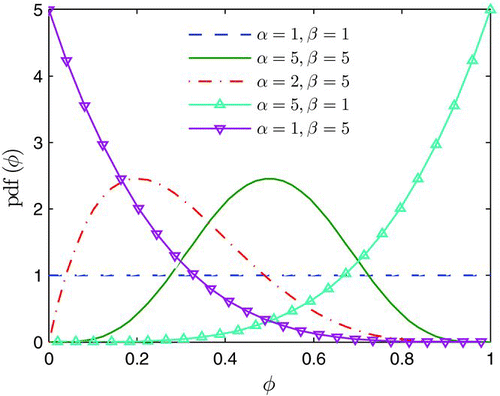
To compute the mean nucleation rate in turbulence, it requires the pdf of the mixture fraction (a representative of temperature and vapor mole fraction). A popular model for the pdf is the beta distribution (Girimaji 1991)

where Γ denotes the gamma function, α and β are two parameters to determine the shape of the pdf. Figure 2 shows the beta distribution for five sets of parameters, which mimic various possible pdfs of scalars in turbulence. When α=β=1, the beta distribution is uniform. When α=β≫1, it resembles the normal distribution. It can also approximate the pdf typically found in scalar diffusion from a source point (e.g., α=5, β=1 and α=1, β=5). The shape corresponding to α=2 and β=5 is usually found for scalars in turbulent mixing layer (Attili and Bisetti 2012).

Relative errors of the quadratic and linear approximations to the mean nucleation rate, with a linear correlation between T and c

	T range		%Err	%Err
case	(K)	beta pdf	(quadratic)	(linear)
1	300–400	α=1, β=1	0.7	N.A.
2	(I-B)	α=5, β=5	1.4	N.A.
3		α=2, β=5	0.6	N.A.
4		α=5, β=1	1.6	N.A.
5		α=1, β=5	0.7	N.A.
6	315–400	α=1, β=1	10.1	≫100
7	(F-B)	α=5, β=5	14.5	≫100
8		α=2, β=5	10.5	≫100
9		α=5, β=1	16.1	≫100
10		α=1, β=5	7.9	≫100
11	330–400	α=1, β=1	159.6	8.8
12	(F-B)	α=5, β=5	64.5	12.3
13		α=2, β=5	171.8	8.5
14		α=5, β=1	41.9	14.6
15		α=1, β=5	250.2	7.6
I-B denotes infinite bounds and F-B denotes finite bounds. N.A. means the data are not applicable.

It is useful to briefly discuss how to evaluate the derivatives in the Laplace’s approximations. Although the function f(x) is complex, its derivative can be obtained by symbolic computation software, or by finite difference approach. When using finite difference, attention should be paid to the choice of the spacing. For example, in the central difference scheme f′(x)=[f(x+l)−f(x−l)]/(2l), in order to optimize the truncation and roundoff errors, it is optimal (Press et al. 1992) to set l=ε^1/3 x_c , where ε is the machine precision, and x_c is a “characteristic scale” of the function f(x), which is usually assumed x_c =x (except near x=0).

Table 2 gives the relative errors of the quadratic/linear approximations to the mean nucleation rate for various cases. Three temperature ranges are investigated, the infinite bounds case (300–400 K) and two finite bounds cases (315–400 K and 330–400 K). For each temperature range, the five beta pdfs shown in Figure 2 are used to evaluate the mean nucleation rate. The relative error is defined as , where the Exact value is obtained by direct numerical integration of Equation (6). The relative errors using the quadratic and the linear approximations are compared. For the infinite bounds cases (300–400 K), the relative errors using the quadratic approximation of Equation (9c) are from 0.6 to 1.6% for all the pdfs considered here. The linear approximation is not applicable for the infinite bounds case, since the linear term in the Taylor expansion (8) vanishes. In the cases with temperature range 315–400 K, the relative errors using the quadratic approximation are from 7.9 to 16.1%. The relative errors using the linear approximation are much more than hundred percent. For the temperature range 330–400 K, the relative errors using the quadratic approximation are from 41.9 to 250.2%, which are around one order of magnitude higher than the linear approximation. A thumb of rule for choosing between the quadratic or the linear approximation is to compare the temperature bound with the inflection point (B in Figure 1). If the temperature bound exceeds the inflection point, the linear approximation performs much better. If the temperature bound is close to the maximum point (A in Figure 1), the quadratic approximation should be used. It is worth pointing out that the case for temperature range of 330–400 K is not very important in practice, because the value is not very high at the tail of the nucleation rate function. Hence, the quadrature approximation can generally be used.

FIGURE 3 The pdfs of a passive scalar (mixture fraction φ) in a turbulent mixing layer at three crosswise locations, corresponding to mean values of

,

and

. The DNS data are taken from Zhou et al. (2012). The beta distribution has the same mean and variance as the pdf from the DNS.

The pdf shape affects the approximation to some extent, but without clear trend. A general conclusion is that the precision of the approximation is not very sensitive to the pdf. In the Laplace’s approximation, the whole pdf over the domain is not required, but only the probability density at the point where the nucleation rate obtains its maximum. The maximum point can be determined from the given boundary conditions for a specific turbulent flow. Therefore, it is possible to approximate the mean nucleation rate in turbulence by estimating the probability density at the maximum nucleation point, which is very convenient and efficient. The error in the approximation is nearly proportional to the accuracy for estimating the probability density at the maximum point. This fact has also been observed by Shaw (2004) in the analysis for the infinite bounds case.

To further clarify the application of the Laplace approximation scheme, a practical example is given to estimate the mean nucleation rate at a turbulent mixing layer. In the recent work of Zhou et al. (2012), the pdf of a passive scalar (mixture fraction φ) is obtained by means of direct numerical simulation (DNS). Here, the mean nucleation rate evaluated from the pdf and the corresponding approximation using beta distribution is compared. Besides, the error in evaluating the mean nucleation rate by the Laplace approximation is also investigated. In Figure 3, from the DNS at three crosswise locations with the corresponding beta distribution are shown. The beta distribution is determined from the mean (μ) and variance (σ²) of the pdf, as

Assume the temperature and vapor concentration are linearly correlated, and T=T _min+(T _max−T _min)φ and c=c _min+(c _max−c _min)φ, then the mean nucleation rate can be directly evaluated from Equation (6). The relative errors of the mean nucleation rate from the beta distribution to the DNS are 62%, 18%, and 13%, respectively, for three different beta distributions (φ) cases (a), (b), and (c) as shown in Figure 3. On the other hand, the quadrature Laplace approximation Equation (9c) can be used to approximate the mean nucleation rate with these three selected beta distributions, and their relative errors are 0.9%, 0.6%, and 1.5%, respectively. Hence, using the Laplace approximation scheme in this practical problem shows that the numerical error mostly comes from how well to model the real pdf, while the error introduced by the Laplace approximation is negligible. However, it is worth pointing out that in general there are many difficulties to approximate the pdf with the assumed distribution (Givi 1989; Baurle et al. 1994). On another aspect, the Laplace approximation scheme also helps to understand the difference in evaluating the mean nucleation rate from the beta distribution and the real pdf. The difference does not depend on how good the beta distribution approximates the overall real pdf, but only depends on whether the beta distribution can capture the probability distribution at around φ=0.13 (corresponding to the maximum nucleation rate here).

4. APPROXIMATIONS OF MEAN NUCLEATION FOR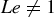

4.1. Infinite Bounds

Quite similar to the single integral of an exponential function, Laplace’s approximation is also developed for double integral (Hsu 1948)

where , and (ξ, η) is the point where f(x, y) obtains its minimum.

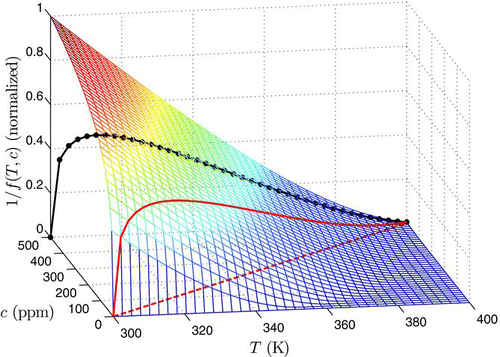
However, Equation (20) is generally not applicable to the approximation of the mean nucleation rate. Because the nucleation rate of Equation (4a) is a monotonically decreasing function of T, and is a monotonically increasing function of c. In other words, nucleation prefers high vapor mole fraction and low vapor temperature. It is impossible to find a point (T_c , c_c ) inside the domain (Rectangular domain is assumed, and irregular domain is not considered here) at which f(T, c) obtains the minimum. To demonstrate this point more clearly, Figure 4 plots a surrogate function 1/f(T, c), which has the same monotonicity as the nucleation rate function e^−f(T,c). The reason to use the surrogate function other than the original one is that e^−f(T,c) variates so dramatically, hence it is difficult to show the characteristics clearly in the plot. Obviously, the nucleation rate obtains its maximum at the corner of the domain, (T, c)=(300, 500), when T and c are independent to each other. However, if T and c are linearly related to each other (the dashed line in the T–c plane), the nucleation rate function has a peak inside the domain, as shown in the continuous curve (the curve with dots is the projection onto a plane ). That is the case of Le=1 discussed in Section 3. Of course, the nucleation rate function may also have a peak or peaks if T and c are related in a more involved way than the linear relation discussed here, which should be studied on a case-by-case basis.

FIGURE 4 The surrogate function 1/f(T, c) for the nucleation rate, normalized by its maximum in the domain. If T and c are linearly correlated (dashed line in the T–c plane), f(T, c) is then the continuous curve shown. For clarity, the curve is projected to a plane of

(curve with dots), which has a peak at around T=313 K, corresponding to the maximum nucleation rate.

4.2. Finite Bounds

Although the simple quadratic order approximation of Equation (20) is not applicable for nucleation, it is possible to obtain simple approximation from a linear order. Following the developed method of López and Pagola (2008), the function f(T, c) can be approximated to first order

where , , and (T_c , c_c ) is the corner point of the integration domain with T_c ⩽T and c_c ⩾c. Then

The first approximation is obtained by replacing f(T, c) with its linear approximation of Equation (21). The second approximation is obtained through two steps: first step, by changing the variables (T−T_c )→T and (c−c_c )→−c, and then extending the upper integral bound to infinity. The second step is carried out straightforwardly.

The approximation of Equation (22) is applicable to a rectangular domain of integration (T_c , T _max)×(c _min, c_c ), with the assumption that nucleation rate vanishes at the bounds T=T _max or c=c _min. If the nucleation rate is far from zero at the upper temperature or lower vapor mole fraction bounds, then it only requires to represent the domain of integration (T_c , T _max)×(c _min, c_c ) as the subtraction of (T _max, T _∞)×(0, c _min) from (T_c , T _max)×(0, c_c ), and apply the approximation of Equation (22) to the last two domains. Here, T _∞ denotes a high temperature at which the nucleation rate is zero.

4.3. Numerical Examples

The numerical examples shown in this section have similar setting with those in Section 3.3, except that the integral domain is two-dimensional instead of one-dimensional. Since it has shown that the Laplace approximation is not sensitive to the pdf in Section 3, here only the uniform pdf is considered for convenience.

Table 3 shows the relative errors for three temperature and three vapor mole fraction ranges (total nine cases). Only linear approximation is constructed. Generally, the smaller the temperature range (or vapor mole fraction range) is, the smaller the relative error will be. The maximum error is less than 40% for T=300–400 K and c=0–500 ppm cases. Taking into account the substantial uncertainties in turbulence and the kinetic theory of nucleation, the approximation of the mean nucleation rate is quite satisfactory.

Relative errors of the linear approximation of the mean nucleation rate, with independent T and c

case	T range (K)	c range (ppm)	%Err (linear)
1	300–400	0–500	38.7
2	(I-B)	0–300	34.9
3		0–100	26.9
4	330–400	0–500	23.4
5	(F-B)	0–300	19.3
6		0–100	11.4
7	360–400	0–500	9.4
8	(F-B)	0–300	6.8
9		0–100	4.6
I-B denotes infinite bounds and F-B denotes finite bounds.

4.4. Discussion

The analytical approximation method derived here has advantage over numerical scheme on certain aspects. It is much easier to investigate the functional dependence of the mean nucleation rate on the pdf of temperature and vapor concentration. The analytical approximation method here may be used to solve some specific aerosol evolution problems, combined with asymptotic methods.

On the numerical aspect, the analytical approximation scheme is numerically far more efficient than direct numerical double integration in evaluating the mean nucleation rate, while sacrificing the numerical precision to certain extent. Although the computational resource becomes much cheaper, the numerical efficiency is still critical for some complex problems. One example is the DNS of aerosol evolution in turbulent flows. In a DNS, the grid size is required to resolve the Kolmogorov scale, which renders the number of grid cells proportional to Re ^9/4 (where Re is the Reynolds number) (Pope 2000). However, due to the sensitivity of nucleation rate to the temperature, the nucleation layer might be still under-resolved at some fast mixing regions (Zhou et al. 2014). It is extremely expensive to reduce to the grid size in order to resolve the nucleation layer. A good workaround is to reconstruct the temperature T and vapor concentration c in a grid cell through an interpolation from neighbor grid cell values, and to evaluate the mean nucleation rate in the grid cell from the reconstructed field of T and c. The mean nucleation rate is evaluated as the nucleation rate function is convoluted with the distribution of T and c, which has exactly the same form as Equation (20). Although numerical schemes can be used to carry out the double integration, it is very expensive to do so at every grid cell (usually tens of millions to even billions). The Laplace approximation scheme here (Equation (22)) is far more efficient to evaluate the mean nucleation rate than the numerical double integration (of course, with mild sacrifice of its numerical precision).

5. CONCLUSION

Nucleation rate is a very sensitive function of temperature and vapor mole fraction. The mean nucleation rate in turbulence is the convolution integral of the nucleation rate function with the joint pdf of temperature and vapor mole fraction. If the temperature is linearly related to the vapor mole fraction (Le=1), the evaluation of mean nucleation rate is simplified to one-dimensional integration over the temperature fluctuation range in a turbulent flow. Depending on where the nucleation rate obtains its maximum, that is, inside the temperature range or at one end of the temperature range, two approximation equations are developed to evaluate the mean nucleation rate using Laplace’s method. These equations only require the derivative (either first or second order) of the nucleation rate function and the probability density at the point of maximum nucleation rate. Five pdfs from the beta distribution are used to model the pdfs of temperature in various turbulent flows, then the approximation equations are used to compute the mean nucleation rate of DBP aerosol for the five pdfs. The numerical examples show that the relative errors are around 1% when the nucleation rate approaches zero at both ends of the temperature range. For other cases, the relative errors are larger, but no more than 20% with the best adequate analytical approximation scheme (linear or quadratic). Taking into account the substantial uncertainties of the nucleation kinetic theory and turbulence, these approximation schemes are well acceptable.

If the temperature and vapor mole fraction are independent to each other (Le≠1), it is found that the nucleation rate function cannot obtain a local maximum inside the domain, but it can only obtain its maximum at the bound of the domain, corresponding to the minimum temperature and maximum vapor mole fraction. An approximation equation for the mean nucleation rate is also derived, and the numerical examples show that the approximation scheme is also accurate and efficient.

Hence, these developed approximation schemes can be used to estimate the mean nucleation rate in a broad range of turbulent flows conveniently.

FUNDING

This work was supported by the grants from the Mechanical Engineering Department and the Central Research Grant of The Hong Kong Polytechnic University (Project Nos. G-U918 and G-YK66).