Crossover from Ballistic to Epstein Diffusion in the Free-Molecular Regime

Abstract

We investigate, through simulation, a system of aggregating particles in the free molecular regime that undergoes a crossover from ballistic to diffusive motion. As the aggregates grow, the aggregate mean free path becomes smaller and the motion between collisions becomes more diffusive. From growth kinetics, we find that when the ratio of the aggregate mean path to the mean aggregate nearest neighbor separation reaches of the order of unity, a crossover to diffusive motion occurs. This ratio, called the nearest neighbor Knudsen number, becomes an important parameter in understanding aerosol aggregation in the free molecular regime.

Copyright 2014 American Association for Aerosol Research

1. INTRODUCTION

From understanding climate change to nanomaterial synthesis, aggregation of aerosol particles is of great importance in both natural phenomena and our technology (Friedlander 1977; Dahneke 1983; Family and Landau 1984; Oh and Sorensen 1997). Aggregation of dispersed aerosol particles can occur under a host of different conditions. In the simplest case, aggregates are formed of approximately the same sized monomers (roughly spherical in shape) that come together under stochastic thermal forces (interactions with the medium) and bind permanently on contact via van der Waals forces. Even within such constraints, a number of particle/medium properties can be varied that highly affect the growth rate, particle morphologies, and resulting cluster size distributions of aggregating systems. In a gaseous medium the pressure, temperature, and molecular mass of the gas are determining factors. The initial particle volume fraction can also be adjusted over a large range, from the very dilute to very dense. The variation of these and other parameters leads to the limiting cases of either ballistic or diffusive type motion of particles between collisions with each other.

All particles dispersed into a medium experience drag forces. If the particles are dispersed in a dense medium, the paths of the medium molecules impinging on the surface of the dispersed particle will be severely affected by those leaving the surface. This produces a “stick” boundary condition at the particle surface in what is known as the continuum regime with a continuum, Stokes drag. Stokes drag is inversely proportional to the particle effective mobility radius, which is the geometric radius a if the particle is spherical, and the shear viscosity, which is a continuum property of the medium. If the particles are dispersed in a rarefied medium, the paths of the impinging medium molecules are essentially unaffected by those leaving the particle surface. This produces a “slip” boundary condition at the particle surface in what is known as the free molecular regime with an Epstein drag. Epstein drag is inversely proportional to the effective cross sectional area of the particle with a mobility radius squared functionality. The parameter that quantifies the continuum to free molecular regime change is the Knudsen number, Kn = mfp/a, where mfp is the mean free path of the medium molecules. When Kn → 0, the continuum regime holds, when Kn → ∞, the free molecular regime holds.

Another important parameter in classifying aggregate motion in a medium is the diffusional Knudsen number Kn_D, which is the ratio of the suspended particle's persistence length, l_a to some other characteristic length (the persistence is the stopping distance used to calculate the Stokes number (Kulkarni et al. 2011) when the velocity has the equipartion value). An aggregate's (we shall henceforth consider the suspended particles as aggregates) motion is taken to be on a straight line over a distance equal to its persistence length. When Kn_D → ∞ the persistence length dominates all other length scales and the motion is considered ballistic. When Kn_D → 0 the persistence length is small compared to the system's other length scales and the motion is considered diffusive. The crossover between these two limits occurs when . When the system is cluster dilute, the only characteristic length scale is the linear size of the aggregate (Pierce et al. 2006). Here, we use a definition of Kn_D similar to that used by Rogak and Flagan (1991) and Gopalakrishnan and Hogan (2011), in the dilute limit [1] where k_B is the Boltzmann constant, T is temperature, μ_ij is the reduced mass between an aggregate and its collision partner, R_g,i is the radius of gyration of the ith cluster and Γ_ij is the reduced drag coefficient between these two aggregates defined as were Γ_i is the drag coefficient of the ith cluster. The collision partner for a given cluster is assumed to be its nearest neighbor. This definition of Kn_D is equivalent to the ratio of the collision partners’ reduced persistence length to their combined size.

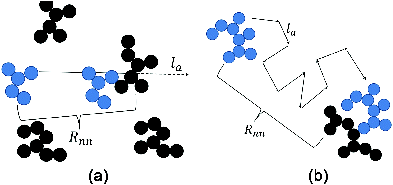
As the system becomes more crowded, the nearest neighbor separation R_nn becomes another important length scale (Pierce et al. 2006). If the persistence length of the aggregate l_a is large compared to the nearest neighbor separation then the movement of aggregates between collisions would be on a straight line, that is, ballistic motion. But if l_a is small compared to R_nn, the aggregate will have to travel many such l_a s, which follow each other randomly, before it collides with another aggregate; then the movement is diffusive. This is illustrated in the Figure 1 where in part (a), the light shaded cluster moves ballistically whereas in part (b) it moves diffusively. With this physical picture in mind, we introduce a new diffusional Knudsen number based on the nearest neighbor separation as a characteristic length scale: [2]

FIG. 1. (a) Illustration of a ballistic collision where the light shaded cluster does not make one full persistence length before colliding with its neighbor. (b) Illustration of a diffusive collision where the light shaded cluster makes several persistence lengths before colliding.

To distinguish it from the traditional diffusional Knudsen number, we will refer this new one as the nearest neighbor Knudsen number from here on. (Pierce et al. 2006) We anticipate that the nearest neighbor Knudsen number would be a better descriptor of the crossover from the ballistic to Epstein diffusion as the system becomes cluster dense or when the mean persistence length an aggregate travels becomes close to the nearest neighbor distance.

In this article, we present a simulation study of the aggregation of dispersed solid particles in the free molecular regime to demonstrate the effect of crossover between ballistic and Epstein diffusive type motion, a crossover that occurs due to cluster growth. Due to the evolving size of the aggregates or clusters, systems that initially aggregate in a ballistic fashion can cross over to Epstein diffusive as aggregation proceeds. The kinetics of aggregation, resulting cluster size distributions, and aggregate morphologies can all be affected by this crossover, and it is the results of these processes that this article addresses. We use two simulation methods to study this crossover: a direct integration of the Langevin equation (Mountain et al. 1986; Gopalakrishnan and Hogan 2011; Thajudeen et al. 2012) along with a simple and fast Monte Carlo aggregation algorithm that captures the essential physical characteristics of the crossover. The physical realization of this ballistic to diffusive crossover lies, for example, in highly sooting flames.

The rest of the article is organized as follows. In Section 2, we discuss both of our simulation algorithms. In Section 3, we describe the aggregation kinetics and how they are governed by the Smoluchowski equation. Next, Section 4 deals with the scaling of the aggregation kernel and the scaling of the aggregate mass distribution is discussed in Section 5. Results from our simulation studies are given in Section 6 and finally we give our concluding remarks in Section 7.

2. SIMULATION METHODS

Two simulation models, Langevin dynamics and Monte Carlo cluster-cluster aggregation, are used in this article. While Langevin dynamics simulations have been used in the past to describe aggregation in the free molecular regime (Nowakowski and Sitarski 1981; Mountain et al. 1986; Mulholland et al. 1988; Ranganathan and Hogan 2011), they are computationally expensive. We have developed a Monte-Carlo (MC) method for the crossover study similar to ones used in the past for continuum regimes (Pierce et al. 2006; Heinson et al. 2010). This MC method has the advantage of being computationally very efficient. Both simulations are constructed so that the crossover from ballistic to Epstein diffusive motion occurs as aggregation proceeded and the aggregate size increased. While the simulations differ in the mechanisms of aggregate movement, they share similar starting points. All simulations start with 100,000 monomers of radius a, diameter σ = 2a and mass m_o that are placed at random in a 3D simulation box to obtain the desired volume fraction by adjusting the box size. If a monomer placed overlaps with another, it is given new set of random coordinates. Work presented here was done at volume fraction of . Periodic boundary conditions are in place to negate edge effects.

2.1. Langevin Dynamics

In this part, we integrate the Langevin equation for an aggregate: [3] where m_a is the aggregate mass, Γ is the drag coefficient, R(t) the stochastic thermal force and r the position of a given aggregate center of mass. Aggregate mass can also be written as m_a = Nm_o where N is the number of monomers in an aggregate. The system is set to a constant temperature initially through the assignment of monomer velocities via the Maxwell-Boltzmann distribution. Solving Equation (3)[3] one finds: (Gunsteren and Berendsen 1982) [4] Here, the initial aggregate velocity is v(0) and the characteristic time, is a measure of how long an aggregate will move along a ballistic trajectory before it feels the influence from the medium.

Integration of Equation (4)[4] is done at time steps of Δt = 0.1 in reduced units of . Reduced units of monomer mass m_o = 1, monomer radius a = 0.5 and k_BT = 1 are used to simplify the integration. When two aggregates collide they irreversibly stick, the total number of aggregates N_c is decremented by 1 and the new aggregate moves with a thermal velocity determined by equipartition.

Simulations presented here set out to model aerosol systems at low background gas densities often induced by high temperature and therefore are firmly in the free molecular drag regime. The free molecular drag coefficient is given as [5] In Equation (5)[5] , δ is the accommodation coefficient, P is pressure, m_g is the mass of a gas medium molecule and R_m is mobility radius of the aggregate. Experiments and previous simulations have shown that the mobility radius for fractal aggregates is [6] where the mobility-mass exponent x = 0.46 (Wang and Sorensen 1999; Sorensen 2011). Now the drag coefficient becomes [7] The ballistic motion persists over a distance given by the product of the characteristic time, t_c and thermal velocity . Thus, the persistence length is written as [8] Notice that both the drag coefficient and persistence length have a power law dependence on N. Setting N = 1 yields the monomer persistence length [9] Rescaling Equations (7)[7] and (8)[8] by l₀ provide a more compact from of Γ and l_a [10] [11] From Equation (10)[10] it is clear that l₀ and N define the drag coefficient and therefore are necessary to solve the Langevin equation. Thus, l₀ along with f_v and number of monomers, become a primary input in the simulation. All l₀ values are given are in units of monomer diameter σ. Values of l₀ = 1, 10, 50, 200, 10,000 were used in this work. We will show that when l₀ = 1 the system acts as Epstein diffusion while l₀ = 10,000 leads to purely ballistic motion.

2.2. Monte Carlo Cluster-Cluster Aggregation

Instead of solving the Langevin equation to move the aggregates, the Monte Carlo CCA method picks an aggregate at random, calculates a probability of movement P_m to determine if the aggregate moves, and then increments time by 1/N_c where N_c is the number of aggregates in the system including lone monomers. When the aggregate moves, it travels a distance of one monomer diameter σ. This model is standard for aerosol Monte-Carlo simulations in the continuum regime, where we differ is how P_m is calculated. In ballistic (BLCA) systems P_m is

proportional to the aggregate velocity and is set as (Pierce et al. 2006) [12] For Epstein diffusion the probability of movement is proportional to the aggregate's drag coefficient Γ and is set as (Pierce et al. 2006) [13] Our proposed crossover P_m must let an aggregate move ballistic on the scale of its persistence length l_a and diffusively on length scales larger than l_a. Also as an aggregate grows, its persistence length will decrease until l_a = 1 via Equation (11)[11] . Since in our simulation the minimum step size is one, at the l_a = 1 point, P_m must also crossover from ballistic to diffusive. Our proposed P_m is a linear combination of inverse of P_m,B and inverse P_m,D, that is, a harmonic sum of two probabilities. [14]

Normalizing so monomers have P_m = 1 and crossover happens at l_a = 1 Equation (14)[14] becomes [15] where 1 ≤ l_o ≤ ∞.

We must note that the procedure for selecting P_m represented in Equation (15)[15] is purely ad hoc. However, it captures the physics of the aggregate motion. We will test it by comparing to the Langevin result. Equation (15)[15] determines if an aggregate will move but does not say anything about the direction of movement. Since an aggregate must move on average a distance of l_a before it randomly changes direction due to the influence of the medium molecules, we calculate a probability of random direction change, P_r, that is checked every time an aggregate is moved. We chose to use the inverse of l_a for the probability of direction change: [16] As in Equation (15)[15] , P_r is purely ad hoc but still captures the physics of the system.

Care must be taken how time is incremented in this hybrid system where a cluster can move either ballistically or diffusively. The time, τ_D for an aggregate to move one monomer diameter by diffusion is given by the mean square displacement equation which yields [17] Comparing the time to move ballistically one monomer diameter [18] to τ_D and setting N = 1 and l₀ = 1, the ratio of Equation (17)[17] to Equation (18)[18] is [19] In Monte Carlo simulations a cluster moves a distances of σ and time is incremented by 1/N_c but when the movement is diffusive the time scale needs to be normalized by Equation (19)[19] .

3. AGGREGATION KINETICS

The kinetics of aerosol aggregation are governed by the Smoluchowski equation, which describes how the number concentration of clusters of size N monomers, n_N(t), changes with time (Friedlander 1977). [20]

The aggregation kernel K(i,j) is the collision rate between aggregates made up of i monomers with aggregates of j monomers. K(i,j) is assumed to be a time-independent homogeneous function of particle size. To simplify the scaling we work under the assumption that the aggregation is between like-sized clusters, then the Smoluchowski equation becomes [21]

Since K is homogeneous, one can write Equation (21)[21] as [22] where λ is the degree of homogeneity, and K(1,1) is the kernel for a monomer–monomer collision. The aggregate size N changes with time and the concentration can be written as, [23] Then Equation (22)[22] becomes [24] Finally, integration yields [25] or [26] with a kinetic exponent, z as first seen by van Dongen and Ernst [27] and [28] Expanding Equation (26)[26] for small time t < t₀ one finds that N(t) ∝ t. After this, small transient time, there is a transition when , and then ultimately at large time when t > t₀, the cluster size increases with power law N(t) ∝ t^z. If the crossover happens during the linear transient regime, then information about the homogeneity will be absent. To avoid this below we simply graph average aggregate size versus t₀ = t; a process that by Equation (26)[26] linearizes a double logarithmic graph.

4. SCALING ANALYSIS OF THE AGGREGATION KERNEL

The previous section discussed how aggregation governed by the Smoluchowski equation yielded an average cluster size that increased with time via a power law with the kinetic exponent. Here, we present a simple scaling analysis that describes how the collision kernel and its homogeneity determine the kinetics for different regimes of motion. Beginning with the general statement that K is proportional to the colliding particles relative collision cross-sectional area, A and relative velocity, v, we write [29]

4.1. Ballistic Regime

In the ballistic regime velocity is due to equipartition of energy and since one finds from Equation (29)[29] : [30] Using the accepted value of fractal dimension, , in the ballistic limit (Fry 2003), the homogeneity is found to be and via Equation (30)[30] , hence the kinetic exponent is .

4.2. Epstein Diffusion Regime

In the diffusion regime, the characteristic velocity is , where is a characteristic diffusional length scale. In the dilute limit, the only length scale is and from Equation (29)[29] one finds the homogeneity as [31] Aggregates in the Epstein diffusion regime have a fractal dimension of which yields and . As the system becomes more crowded the relevant length scale becomes. The nearest-neighbor separation is where is the number of clusters in the system. The total number of monomers, is constant and equals , thus and the homogeneity is [32] In the Epstein limit, as the system becomes crowded, then, by Equation (32)[32] homogeneity is and the kinetic exponent is .

5. SCALING ANALYSIS OF THE CLUSTER SIZE DISTRIBUTION

As aggregation proceeds in the system, the aggregate size distribution develops a scaling form given by where n(N) is the number concentration of aggregates of size N, M₁ is the 1st moment of the size distribution and s is the average size (van Dongen and Ernst 1985). The scaling variable is x = N/S and the scaled distribution function, ϕ(x) has the form for large sizes (x > 1) (Oh and Sorensen 1997). Thus, [33]

6. RESULTS

The aggregation kinetics for both Brownian dynamics and Monte Carlo simulations are shown in Figures 2a–f. The graphs shown the inverse number of clusters versus t + t₀ for various l₀'s. Since the number monomers remains constant, is directly proportional to average cluster size. The constant t₀ was calculated by Equation (28)[28] . The monomer aggregation kernel K(1,1) and z used in Equation (28)[28] were decided based on the initial Kn_D and Kn_n. Diffusive and nearest neighbor Knudsen numbers were found for each aggregate by Equations (1)[1] and (2)[2] , respectively, then averaged to obtain Kn_D and Kn_n for the system. For runs with l₀ = 1 both Kn_D and Kn_n were less than unity and firmly in the diffusive regime, so values of diffusive K(1,1) and z were used. All other runs started with larger Kn_D and Kn_b and therefore ballistic values of K(1,1) and z were used to find t₀. When l₀ =1, the system is entirely diffusive due to both Kn_D and Kn_n being less than unity and yields a kinetic exponent of z = 0.8 for f_v = 10⁻³ and 10⁻⁴ and z = 0.88 for the dense f_v = 10⁻². Both these values are consistent with predicted values of z = 0.73 for dilute Epstein diffusion and z = 0.88 for dense Epstein diffusion, respectively (Pierce et al. 2006).

FIG. 2. Inverse cluster count versus t + t₀. t₀ was found from Equation (28)[28] . The lower dashed guide line has a kinetic exponent z = 0.80 − 0.88 and the upper guide line has z = 2.2. The points where Kn_n = 1 are marked and noted in the legend. The points where Kn_d = 1 are noted as stars in their respective runs. (a) Monte Carlo simulation at f_v = 10⁻⁴; (b) Brownian Dynamics simulation at f_v = 10⁻⁴; (c) Monte Carlo simulation at f_v = 10⁻³; (d) Brownian Dynamics simulation at f_v = 10⁻³; (e) Monte Carlo simulation at f_v = 10⁻²; (f) Brownian Dynamics simulation at f_v = 10⁻². Notice that in (e) and (f) the Epstein diffusion exponent is z = 0.88 as expected when in the cluster dense regime. Also of note in (e) and (f) the trend has upward curvature do to the onset of gelation.

At large l₀, Figure 2's parts all show for both types of simulation a kinetic exponent of z = 2.2 as expected for ballistic motion at all f_v (Pierce et al. 2006). The intermediate values of l₀ initially follow the ballistic track then evolve to the diffusive z exponents. For all intermediate l₀ runs, the places where Kn_D = 1 are marked by a star and places where Kn_n = 1 are marked by symbols. While both Knudsen numbers fall within the crossover Kn_n does a better job of marking the beginning of the transition.

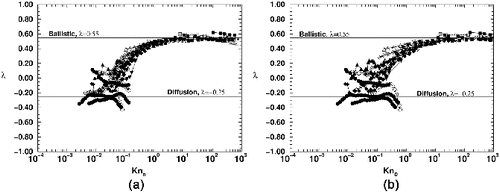
Figure 3 plots the aggregation kernel homogeneity λ versus either diffusional Knudsen number. By numerically finding z from the data in Figure 2 and using Equation (27)[27] to find λ, we compare Kn_n to λ in Figure 3a and Kn_D to λ in Figure 3b. Closed symbols represent data from Monte Carlo simulations and open symbols are data from Brownian dynamics. All runs follow the same trend with a ballistic like upper limit of λ = 0.55 and an Epstein diffusional lower limit between λ = −0.36 for cluster dilute systems with f_v = 10⁻⁴, 10⁻³ and λ = −0.14 for cluster dense systems with f_v = 10⁻². A crossover present when either Knudsen number is in the 0.1 to 10 range.

FIG. 3. (a) Aggregation kernel homogeneity λ versus nearest neighbor Knudsen number Kn_n for all Monte Carlo and Brownian Dynamic simulations. (b) The diffusive Knudsen number Kn_D versus homogeneity λ for all Monte Carlo and Brownian Dynamic simulations. Both measurements show similar behavior and provide a means of detecting the crossover.

In Figures 4a and b the size distributions at different times for the system at l₀ = 50 and f_v = 10⁻³ are shown for Brownian Dynamics and Monte Carlo simulations, respectively. The homogeneity is found from fitting Equation (33)[33] . At early times when Kn_n > 1, the homogeneity is λ = 0.55 ± 0.1 consistent with ballistic motion, and at late time when Kn_n < 1, the system moves to λ = −0.4 ± 0.2 for the Brownian Dynamics runs and to λ = −0.3 ± 0.2 for the Monte Carlo runs, both of which are in the range of previous reported values of λ = −0.36 to −0.14 for Epstein diffusion (Pierce et al. 2006). The transition of λ can be seen more clearly by scaling Equation (33)[33] by . Figures 4c and d show the rescaled mass distributions at different Kn_n values for runs of l₀ = 50. Again as in Figures 4a and b, λ moves from a ballistic value to diffusive with changing Kn_n.

FIG. 4. Aggregate size distribution from Brownian Dynamics with l₀ = 50 and f_v = 10⁻³. Lines represent fits from Equation (33)[33] . The system starts off with ballistic λ then enters an intermediate regime during the crossover and finally at late time and small Kn_n reaches a diffusive λ. (a) Size distribution from Monte Carlo simulations; (b) size distribution from Brownian Dynamics simulations; (c) rescaled data from (a), here the homogeneity λ transition from ballistic to diffusive can be clearly seen. The system starts with ballistic homogeneity of λ = 0.55 ± 0.1 then changes to λ = −0.3 ± 0.2, consistent to other values of λ reported for Epstein diffusion. (d) Rescaled data from (b), the system starts with ballistic homogeneity of λ = 0.55 ± 0.1 then changes to λ = −0.40 ± 0.2, consistent with Epstein diffusion.

7. CONCLUDING REMARKS

We have performed simulations of the common yet previously unexplored aerosol situation in which the motion of the aggregates transforms from ballistic to Epstein diffusive while in the Free Molecular regime. Two algorithms were used. First, a slow but rigorous Brownian Dynamics method that solved for aggregate motion through the integration of the Langevin equation. Second, a less exact but faster Monte Carlo method that decides aggregate movement through use of an ad hoc probability of movement and probability of random walk. The probability of movement is a combination of the well-established probability of movements from ballistic and diffusive simulations and a probability of random walk insures aggregates on average move in a ballistic a distance of l_a. All simulations over all produced fractal aggregates of dimension 1.8 except for the very large l₀ = 10,000 that yielded fractal dimension of 1.9. Both systems were in good agreement with regard to the time evolution of the nearest-neighbor and diffusion Knudsen number.

Volume fractions used went from the light to a dense to highlight the importance of as the dominant length scale in dense systems. To our surprise we found that at all volume fractions studied both nearest-neighbor separation and aggregate size were equally adequate at describing the crossover. In the future, simulations must be done with both denser and lighter systems to determine if both length scales do indeed remain markers of aggregation kinetics.

One physical situation in which the results of this article would apply is dense high temperature aerosols. Consider, for example, air at STP with a mean free path of 66 nm which means monomers of radius a = 10 nm would experience Epstein drag. Using an accommodation coefficient of δ = 1.36 for N₂ gas yields by Equation (9)[9] l₀ = 30 nm. If these monomers had a volume fraction of f_v = 10⁻⁶ then one finds Kn_n = 0.03, placing the system in the Epstein diffusion regime. As the aggregates grow from these initial conditions, the system would move to the continuum regime which is not accounted for in our simulations. Raising the temperature to that of typical flame experiments, T = 2100 K, the persistence length of the monomers grows to l₀ = 210 nm yielding a Kn_n = 0.21, placing the system in the crossover regime between ballistic and diffusive motion, see Figure 3. Raising the volume fraction in the flame to f_v = 10⁻⁴ lowers the nearest neighbor separation which in turn gives a Kn_n = 1.00, in the middle of the ballistic to diffusive crossover. These latter conditions have been studied experimentally in the past 15 years (Sorensen et al. 1998, 2003; Kim et al. 2004, 2006; Chakrabarty et al. 2012). Finally, we remark that the reverse crossover from diffusive to ballistic aggregation can occur in dense systems near the gel point (Sorensen and Chakrabarti 2011).

FUNDING

This material is based upon work supported by the National Science Foundation under grant no. AGS 1261651.