Extension of the Smoluchowski Theory to Transitions from Dilute to Dense Regime of Brownian Coagulation: Triple Collisions

Abstract

In order to study the transition from dilute (controlled by binary collisions) to dense (controlled by multiple collisions) regime of coagulation of colloidal or aerosol suspensions, the Smoluchowski equation is generalized by consideration of triple collisions in the kinetic approach, recently proposed by the authors for coagulation of comparable size particles. A good agreement of the new model predictions with more general results of the direct numerical simulations by Langevin dynamics (from the literature) is attained in a relatively wide range of the fractional volume, corresponding to the transition from dilute to dense regime of coagulation dynamics, in which multiple collisions among more than three particles can be neglected.

Copyright 2014 American Association for Aerosol Research

1. INTRODUCTION

The evolution of the size distribution for a system of coagulating Brownian particles over time is described using a kinetic model based on the Smoluchowski equation (Smoluchowski 1917). For particles, homogeneously distributed in space and characterized by a continuous size distribution function n(R)dR, the number of particles of radius R to R + dR per unit volume, under an assumption that collided particles of radii R₁ and R₂ instantly coalesce to form a new particle of radius R₁₂ = (R³₁ + R³₂)^1/3, the Smoluchowski coagulation equation takes the form [1] where β(R_i, R_j) is the collision frequency between two particles i and j randomly located in unit volume. The first term on the right-hand side (rhs) of Equation (1)[1] represents the formation of new particles from collisions between two smaller particles and the second term accounts for the loss of particles of radius R by collision with any other particle in the system.

The model assumes binary collisions, whereby the rate of change is second order in particle concentration n. For this reason, the Smoluchowski equation cannot describe the coagulation of highly concentrated colloidal or aerosol suspensions (particle volume fraction above ≈ 1%). Such highly concentrated suspensions are well known in emulsions, where the droplet volume fraction may vary from zero to almost one (Bibette et al. 1999) but can also be observed in aerosols. For example, a transition from dilute to dense (or concentrated) particle dynamics may take place during flame aerosol synthesis of nanostructured, fractal-like carbon black, fumed silica (Heine and Pratsinis 2006) or titania (Heine and Pratsinis 2007a) particles at industrially relevant conditions. Even though in such processes the particle volume fraction, f, is only 0.001–0.01%, depending on the process temperature, fractal-like silica agglomerates form and grow to occupy more than 10% of the gas volume during typical reactor residence times in the absence of restructuring or fragmentation (Heine and Pratsinis 2007a).

Under these conditions, in order to calculate the coagulation rate of concentrated particulate suspensions, further development of the coagulation theory in the next orders in particle concentration n, taking into consideration multiple collisions of Brownian particles, is needed. Direct numerical simulation of particle trajectories by Langevin dynamics (LD) has been used to compute particle motion regardless of concentration. Gutsch et al. (1995) investigated the detailed structure evolution of aerosol particles formed by monomer-cluster aggregation by LD simulations. Trzeciak et al. (2004) used LD to study the collision frequency function of monodisperse aerosol particles in the Brownian free molecular and continuum regimes and found faster coagulation rates for particles larger than the free mean path of the fluid at f > 1%. Similarly, Sorensen et al. (1998) showed experimentally that soot clusters at high concentrations close to aerogelation grow faster than predicted by classic coagulation theory.

Heine and Pratsinis (2007b) investigated the growth of spherical (complete coalescence upon collision) and fractal-like particles by Brownian coagulation in the continuum regime by solving the Langevin dynamics equations for each particle trajectory of polydisperse suspensions. By monitoring the LD attainment of the self-preserving size distribution, it was shown that the classic Smoluchowski collision frequency function is accurate for dilute particle volume fractions, f, below 0.1%. At higher f, coagulation was about 4 and 10 times faster than for the classic theory at f = 10 and 20%, respectively. At high particle concentration, an overall coagulation rate was proposed that reduced to the classic one at low concentration. The Langevin dynamics approach was later extended to the investigation of the coagulation rate of highly concentrated, polydisperse aerosols from the free molecule to the continuum regime by Buesser et al. (2009).

High concentration significantly increases the coagulation rate of fractal-like particles (agglomerates), consistent with experimental observations. For agglomerates, even initially low particle volume fractions can become effectively large because growing agglomerates occupy far more volume than their equivalent solid mass. As a result, agglomerates may experience a transition from dilute to highly concentrated coagulation dynamics that can lead to gelation. Results showed that the kinetics became more rapid as the system evolves into the cluster dense regime as quantified by an increase in the aggregation rate (Heine and Pratsinis 2007b). A similar approach to investigation of the effect of high concentrations on the aggregation kinetics of colloidal nanoparticles by Langevin dynamics in a broad range of particle volume fractions in the continuum regime was recently presented in (Lattuada 2012) and (Kelkar et al. 2014).

Enhanced aggregation rates in dense systems have also been observed with Monte Carlo diffusion-limited cluster–cluster simulations, both on- and off-lattice, in particulate systems as they evolve from the cluster dilute limit to the cluster dense regime and ultimately the gel point (Sorensen and Chakrabarti 2011). For instance, Fry et al. (2002), Gimel et al. (1995, 1999) simulated 3D systems with a broad range of monomer volume fractions from 0.0005 to 0.3 and found a crossover in the scaling of mass versus the linear size form fractal dimensions of 1.8 at small size to 2.5 at large.

In order to study the transition from dilute (controlled by binary collisions) to dense (controlled by multiple collisions) regime of coagulation, the Smoluchowski equation should be generalized by consideration of triple collisions. As will be shown below, this transition regime corresponds to a relatively wide interval of the particle volume fraction f, from ≈ 0.1% to ≈ 10%. Above the upper limit of ≈ 10%, multiple collisions among more than three particles should be taken into consideration, which is beyond the scope of the current article. However, in the regime of triple collisions, solution of the modified Smoluchowski equation is in a rather sound agreement with the results of direct numerical simulation by Langevin dynamics in (Heine and Pratsinis 2007b); this confirms the validity of the new approach to consideration of the transition from dilute to dense regime for spherical particles.

2 MODEL FORMULATION

In the traditional, “diffusion,” approach to the analysis of Smoluchowski equation, Equation (1)[1] , in the continuum mode, Fick's laws are employed to calculation of particle collision frequency β(R_i, R_j) by consideration of a quasi-steady-state concentration profile around colliding particles (Smoluchowski 1917; Chandrasekhar 1943).

In a previous paper (Veshchunov 2010), it was shown that the traditional diffusion approach is applicable only to the special case of coalescence between large and small particles, (where is the mean inter-particle distance), and becomes inappropriate to calculation of the coalescence rate for particles of comparable sizes, . In the latter, more general case of comparable size particles, R₁ ≈ R₂ ≈ R, coalescences occur mainly in the kinetic regime (rather than in the diffusion one) characterized by random (homogeneous) spatial distribution of particles. This kinetic regime is realized under the mixing condition, τ_d ≪ τ_c (where is the characteristic time of the particles diffusion redistribution (mixing) on the length scale of the mean inter-particle distance n^{− 1/3} after each collision, and τ^{− 1}_c is the collision frequency), which has a clear physical sense in terms of the mean free path λ of a particle between its two subsequent collisions, and is valid under the basic “dilution” condition of the theory, .

In the kinetic regime, the phenomenological form of the pair-wise kernel β(R_i, R_j) in the Smoluchowski kinetic equation, Equation (1)[1] , derived for spatially homogeneous systems, is justified, and the original multi-particle problem is rigorously reduced to consideration of two-particle collisions, by calculation of the collision rate between two particles (of radii R_i and R_j) randomly migrating (with the diffusivities D_i and D_j) in a sample of unit volume.

In its turn, the latter value can be equally calculated as the rate of volume sweeping by the effective particle of radius R_i + R_j migrating with the diffusivity D_i + D_j, which for spherical particles in the continuum regime takes the form [2] and fortuitously coincides with the traditional formula derived in the diffusion approximation (as the diffusion flux of particles j into particle i), which is valid only for collisions between large and small particles (Veshchunov 2010). The swept volume dV_ij is calculated during a time step dt that is small enough in comparison with the characteristic time of the particle concentration variation τ_c, in order to ignore variation in dt of the mean particle concentration n, and large enough in comparison with the diffusion relaxation (or mixing) time τ_d, in order to sustain the main assumption of the kinetic regime on random (homogeneous) distribution of coalescing particles. Besides, this time step dt should be large enough in comparison with the characteristic time , during which the steady state value of the sweeping rate d < V_ij > /dt is attained, .

For fractal-like particle agglomeration in the continuum regime this expression takes the form (similar to the expression derived by Mountain et al. (1986) in the traditional diffusion approach, valid for collisions of small and large particles) [2a] where d_f ⩽ 3 is the fractal dimension of aggregates, V_i is the volume of aggregate i, whereas the volume of the newly formed particle “i + j“ of radius is . To account more accurately for the influence of nonspherical particle geometry, a modified kernel can be used [2b] with the Smoluchowski radius for a single particle, R_{S, i}, and the combined Smoluchowski radius for the collision of two particles, R_{S, ij}, which were recently calculated using Brownian Dynamics approach (Thajudeen et al. 2012). For simplicity and for direct comparison with the Langevin dynamics simulations (Heine and Pratsinis 2007b), Equation (2a) will be further used in calculations (Section 4).

As above explained, the Smoluchowski equation, Equation (1)[1] , assumes binary collisions and is derived in the second order of approximation nR³ ≪ 1. In the next, third-order, triple collisions of comparable-size particles during their Brownian migration should be taken into consideration. In this approximation collisions which occur among any combination consisting of more than three particles, can be ignored, and the probability dP₁₂₃ of collisions in the above specified dt among three particles randomly migrating in a sample of unit volume is calculated as [3] where dP_ik is the probability of a pair collision between particles i and j (of radii R_i and R_j, respectively) in dt calculated, in accordance with Equation (2)[2] or (2a), as the volume swept in dt by the effective particle of radius R_i + R_j, migrating with the diffusivity D_i + D_j, [4] and P_{i + j, k} is the probability of a collision between the newly (instantly) formed particle “i + j’’ of radius R_ij and the particle k of radius R_k during the considered time step dt.

Evaluating the probability P_{i + j, k}, one should keep in mind that there are two possibilities of a collision between the particles k and i + j: (1) an instantaneous collision (with the probability P_{i + j, k}(0)) of the particle k with the particle i + j at the moment of the two particles i and j coalescence, and (2) a collision (with the probability dP_{i + j, k}) of the two migrating particles i + j and k in dτ, where dτ ⩽ dt is the remainder of the time step dt after the collision of the particles i and j.

The probability of the second event is calculated as the volume swept by the effective particle of radius R_ij + R_k in dτ, i.e., dP_{i + j, k} = β(R_ij, R_k)dτ ⩽ β(R_ij, R_k)dt, and thus, should be dropped after substitution in the rhs of Equation (3)[3] as a term of the higher order, dP_ijdP_{i + j, k} = O(dt²), in the first (linear) approximation with respect to the small (on the scale of the particle concentration variation time τ_c) value dt → 0.

The probability of the first event, P_{i + j, k}(0), is equal to the probability that the particle k at the moment of the particles i and j collision is located at the position, where its perimeter overlaps with the perimeter of one of the coalesced particles i and j, or, under the above-presented assumption of instantaneous coalescence of colliding particles, with the perimeter of the formed particle i + j (Figure 1). This probability is of the zero's order with respect to the time step, and thus should be kept in Equation (3)[3] in the limit dt → 0, since P_{i + j, k}(0)dP_ij = O(dt) (Appendix A).

FIG. 1. To the derivation of Equation (6)[6] : the perimeter of the calculated volume is represented by a thick solid line.

Therefore, the probability P_{i + j, k} is calculated as [5] where V(R_i, R_j; R_k) is equal to the sum of two volumes: V_{ij, k} of two overlapping spheres of radii R_i + R_k and R_j + R_k, surrounding centers of particles i and j in the moment of their contact (a light gray “dumbbell” in Figure 1), and ΔV_{ij, k} (dark gray area), additionally (instantaneously) swept by the particles i and j in the moment of their coalescence, [6] where [7] is the intersection volume of two spheres of radii x and y, and z is the inter-center separation, see Appendix A. In particular, for equisize spherical particles of volume V [8] where q₀ ≈ 15 is the numerical factor.

Therefore, the mean number of triple collisions in dt per unit volume among randomly migrating particles, is [9] and the coagulation rate equation takes the form [10] where [11] [12] and V(R_i, R_j; R_k) is defined in Equation (6)[6] .

In terms of the discrete variable i, the number of monomers in a particle (i = 1 corresponds to monomers), the coagulation rate equation for the concentration of particles containing i monomers, c_i(t), takes the form [13] where β_ij ≡ β(R_i, R_j), β⁽³⁾_jkl = β⁽³⁾(R_i, R_j, R_k) and δ_ij is the Kronecker symbol.

3 QUALITATIVE ANALYSIS

The triple terms in Equation (13)[13] change the particle growth kinetics. Considering the indexes in Equation (13)[13] as continuous variables and integrating the both sides over i, one obtains [14] where c(t) = ∫^∞₀c(i, t)di is the total number of particles per unit volume, and are the kernels averaged over the particle size distribution. It is straightforward to demonstrate (Appendix B) that for homogeneous kernels [15] a self-preserving mass spectrum [16] where is asymptotically attained. Here, is the mean number of monomers in the particles, which asymptotically depends on time as [17] where z = 1/(1 − λ).

However, in contrast to the standard Smoluchowski theory, these conclusions are generally valid only for non-fractal particles (d_f = 3). In particular, Equation (17)[17] is not anymore valid, if d_f ≠ 3 (however, it can be formally used considering z as a time-dependent value). For this reason, following Heine and Pratsinis (2007b), it is convenient to characterize the enhancement of the coagulation rate by another dimensionless factor [18] where is the kernel averaged in the dilute limit; for the kernel Equation (2)[2] β_dilute ≈ 1.073β₀ (Friedlander 2000).

It is useful to consider the above formulas in the framework of monodisperse approximation, . Then Equation (14)[14] reduces to [19] where is the radius of particle containing monomers, is the volume fraction, q₀ is defined in Equation (8)[8] . The first term in the rhs of Equation (19)[19] represents the well-known approximation for binary collisions (Friedlander 2000), whereas the second term (enhancing the concentration change) accounts for the effect of triple collisions. Neglecting this second term and taking into account mass conservation, , one easily derives Equation (17)[17] . This formula is valid also with triple collisions taken into account but only for the spherical particles (d_f = 3), in agreement with the general consideration (Appendix B).

From Equation (18)[18] one derives in the dilute limit for spherical particles (d_f = 3) [20] where parameter q ≈ 15 is close to q₀ (the difference is due a finite width of the distribution in the dilute limit). As seen dependence of parameter γ is linear at small values of f and almost entirely is due to triple collisions (the second term in the rhs). Additional linear contribution is due to dependence of on f due to widening of the distribution (which is an indirect effect of the triple collisions); however this contribution is small in comparison with the second term. As for nonlinear terms, they are mainly due to tetrad and higher order collisions and become essential at higher values of f.

4 QUANTITATIVE ANALYSIS

In numerical analysis of Equation (13)[13] , the discretization similar to that of the sectional method (Gelbard and Seinfeld 1980) was used according to which the particle groups (below numerated by the capital letters) are introduced, each group I containing particles with the number of monomers within interval (a_I, b_I) defined as [21] where a₁ = 1 and s > 1 is the progression factor, […] denoting truncation operation. Within each group, the particle concentrations are approximated as [22] where Δ_I = a_{I + 1} − a_I and c_I is the total particle concentration in group I. Then, Equation (13)[13] is approximated by the group equations [23] where , and the group transfer coefficients are defined as [24] for details see Appendix C.

Results of calculations are compared with the results of direct numerical simulations of particle trajectories by Langevin dynamics (Heine and Pratsinis 2007b) for the typical conditions for Brownian coagulation in the continuum regime in air at T = 293 K of spherical particles (d_f = 3), initially monodisperse with 2R₀ = 1 μm in diameter and with a density of 1 g cm⁻³. For these conditions the overall collision frequency is evaluated as β_dilute = 6.4 × 10^{− 16} m³/s, which determines the characteristic time scale, (e.g., τ_sp ≈ 0.2 s for f = 1 %, however in practice the actual time lag to attain the self-preservation is greater by an order of magnitude, (Heine and Pratsinis 2007b)).

The normalized self-preserving size distribution function ϕ(x), Equation (16)[16] , calculated for f = 0.3%, 1%, and 3% with and without triple collisions taken into consideration, is presented in Figure 2 (for convenience, the relative particle size, , is chosen as the ordinate instead of ).

FIG. 2. Self-preserving size distribution function calculated with consideration of pair collisions (dashed curves) and pair and triple collisions (solid curves).

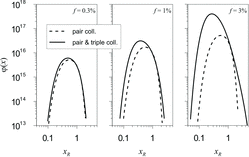
From Figure 2 it is seen that the particle size distribution function broadens quickly during growth and attains the self-preserving form for spherical agglomerates, d_f = 3, in accordance with the analysis in Appendix B. The width of the attained self-preserving size distribution function somewhat increases with the increase of the fractional volume f in the transition range, in accordance with LD simulations of Heine and Pratsinis (2007b), but rather moderately. In particular, it is seen that the majority of particles are concentrated in a relatively narrow size-band (within one order of magnitude, ) around the mean size , where the particle concentration decreases by ≈ 2–3 orders of magnitude. This allows excluding from consideration, with a sufficient accuracy, the particle sizes outside this narrow band. On the other hand, the remaining sizes (located within this band), being distributed within one order of magnitude, can be considered as comparable. Therefore, only collisions among comparable size particles (distributed around the mean size) can be taken into consideration (despite formally integration over the particle sizes will be extended from − ∞ to + ∞). This justifies consideration of a homogeneous spatial distribution of particles, which rapidly reinstates in-between particle collisions owing to their diffusion mixing, in accordance with the general assumption of the kinetic approach.

The γ values calculated at different fractional volumes are plotted in Figure 3, in comparison with the results of Langevin dynamics simulations performed by Heine and Pratsinis (2007a). A good agreement for the transition from dilute to dense regime at f ≤ 10% reasonably confirms the validity of the new approach. At f higher than ≈ 10%, well in the dense regime, the deviation of the current results from LD simulations becomes notable, manifesting the influence of multiple (more than three-particle) collisions.

FIG. 3. Enhanced collision frequency in simulations of Brownian coagulation of spherical agglomerates, d_f = 3, with β_dilute = 6.4 × 10^{− 16} m³/s and the initial size 2R₀ = 1 μm.

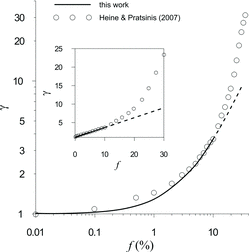
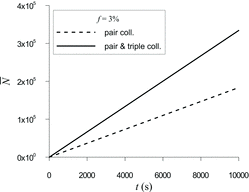
As shown in the (linear scale) inset of Figure 3, in the transition range (f ≤ 10%) the enhanced collision frequency almost linearly depends on f, in a good agreement with the mean field approximation result, Equation (22)[22] . Moreover, this equation provides a good prediction of the slope of the curve; for instance, at f = 3% the calculated enhancement factor of 1.9 well corresponds to the mean field value of 1.82. These results are additionally illustrated in Figure 4, from which the almost twice acceleration of the kinetics due to triple collisions at f = 3% is clearly seen.

FIG. 4. Temporal dependence of the mean number of monomers in spherical agglomerates for f = 3%.

FIG. 5. Temporal dependence of the geometric standard deviation, σ, the enhanced collision frequency, γ, and the volume fraction, f, in simulation of the fractal particles (d_f = 1.8) growth kinetics.

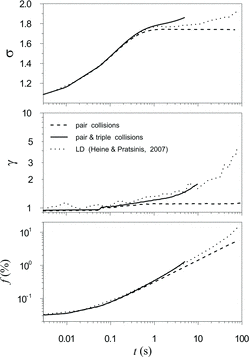
It should be noted that, in accordance with the analysis presented in Section 3 (and in Appendix B), for fractal agglomerates with d_f < 3 the self-preserving size distribution is not attained (asymptotically). Simultaneously the particle volume fraction, f, grows and the size distribution function significantly broadens at large times (the width of distribution grows faster than the mean value). In particular, these peculiarities were illustrated by LD analysis (Heine and Pratsinis 2007b) of the growth kinetics of agglomerates with d_f = 1.8. In these calculations the population was assumed to be initially monodisperse with the monomer radius of 0.11 μm and concentration of 5.4 × 10¹⁶ m⁻³, so that the initial volume fraction f was 0.03% corresponding to the characteristic timescale of ≈ 0.06 s.

Results of calculations for this regime, using the rate equation, Equation (13)[13] , with the kernel for non-spherical, fractal particles, Equation (2a), are presented in Figure 5, where the temporal dependencies are plotted of the volume fraction, f, the enhanced collision frequency, γ, and the geometric standard deviation, σ, defined as [25]

The geometric standard deviation characterizes the relative width of distribution so that it stabilizes with time if the self-preserving limit is attained (see the standard Smoluchowski curve in Figure 5). In the case of the dilute fractal agglomerates the distribution first tends to the self-preserving form but then is distorted by the triple collisions resulting in eventual growth of σ value at large f. For this reason, the kinetic approach, developed for comparable size particles basing on the assumption of a narrow size distribution function, is well justified only in the initial stage of coalescence (i.e., at relatively small f), and thus numerical calculations for fractal particles were not attempted at f ≥ 5%. Nevertheless, in the initial range of the transition from dilute to dense particle volume fractions, 0.1% < f < 5%, the results of calculations are in a reasonable agreement with LD simulations.

Further modification of the theory for consideration of a broad particle size distribution is foreseen in the near future.

5 CONCLUSIONS

The Smoluchowski theory of Brownian coagulation assumes binary collisions, described in the second order in particle concentration n, and for this reason cannot describe the coagulation of highly dense (or concentrated) colloidal or aerosol suspensions. In order to study the transition from dilute (controlled by binary collisions) to dense (controlled by multiple collisions) regime of coagulation, the Smoluchowski equation is generalized by consideration of triple collisions. This modification of the classical theory is realized in the kinetic approach, recently proposed by the authors for coagulation of comparable size particles, which cannot be treated within the traditional approach.

After attainment of the self-preserving size distribution function in the system of coagulating spherical particles (d_f = 3), the majority of particles are concentrated in a relatively narrow size-band (within one order of magnitude) around the mean size , where the particle concentration decreases by ≈ 2–3 orders of magnitude. This allows, with a sufficient accuracy, excluding from consideration the particle sizes outside this narrow band and considering the remaining sizes as comparable. This justifies the validity of the new kinetic approach (applied to comparable size particles) and allows comparing the new model predictions with more general results of the direct numerical simulations by Langevin dynamics (Heine and Pratsinis 2007b). A good agreement is attained in a relatively wide range of the fractional volume of spherical particles (up to ≈ 10%), corresponding to the transition from dilute to dense regime of coagulation dynamics, in which multiple collisions among more than three particles can be neglected.

For fractal particles (d_f < 3) the particle size distribution function first tends to the self-preserving form but then is distorted by the triple collisions and broadens with time. For this reason, numerical calculations for fractal particles were not attempted at large f with a broad size distribution function. Nevertheless, in the initial stage of transition from dilute to dense particle volume fractions, 0.1% < f < 5%, the results of calculations are also in a reasonable agreement with LD simulations.

ACKNOWLEDGMENTS

The authors thank Dr. Y. Drossinos (JRC EC) and Dr. C. J. Hogan (University of Minnesota) for valuable discussion and critical comments.

APPENDIX A

The probability dP₁₂₃ of a collision in the time step dt ≪ τ_c among three particles randomly migrating in unit volume can be calculated as follows. The full set of events among three particles consists of three options: (a) there are no collisions; (b) there are pair collisions, but no triple collisions; (c) there is a triple collision (instantaneous). As explained in the text, collisions of one of the three particles with a newly formed particle after a moment of the two other particles collision (during the remaining part of the time step dt) can be neglected in the first order of approximation , required for derivation of the collision rate equation, and thus only instantaneous triple collisions should be considered. For this reason, for the probabilities of the three events (a), (b) and (c) one obtains [A.1]

Since the pair collisions 12, 23, and 31 are incompatible events, the total probability of the event (a) is calculated as [A.2] where the probability of a pair collision is determined by Equation (4)[4] , dP_ij = β(R_i, R_j)dt.

The probability of a pair collision between particles i and j, given no triple collision with a particle k takes place, is equal to the probability dP_ij multiplied by the probability that the particle k is outside the volume V(R_i, R_j; R_k), defined in Equation (6)[6] . Similarly to the event (a), three various options are incompatible events so that the total probability of the event (b) is calculated as [A.3]

Substituting Equations (A2) and (A3) into Equation (A1), one obtains [A.4] where V(R_i, R_j; R_k), presented in Figure 1, can be calculated as the volume V_ABC of a figure consisting of three arbitrary intersecting spheres A, B and C, [A.5] where V_A is the volume of sphere A, V_A∩B is the volume of intersection of spheres A and B, V_A∩B∩C is the volume of intersection of all three spheres. In the considered particular case the spheres A, B and C have radii R_A = R_i + R_k,  R_B = R_j + R_k and R_C = R_ij + R_k, respectively. Taking into account that R_C > R_A,  R_B and that the center of particle C is located between the centers of spheres A and B one derives from a simple geometrical consideration that the intersection of the spheres A and B is located entirely within the sphere C. This means that V_A∩B∩C = V_A∩B so that Equation (A2) reduces to [A.6] which coincides with Equation (6)[6] , the intersection volume of two spheres being given by Equation (7)[7] , e.g., see Chkhartishvili 2006.

APPENDIX B

Considering asymptotic behavior of the distribution function in the case of homogeneous kernel one represents the distribution function in form (van Dongen and Ernst 1985) [A.7] where is the mean number of particles in the cluster. Substituting Equation (A7) in the continuous form of Equation (13)[13] , one derives [A.8] where

If only two-particle collisions are taken into consideration (f₃ = 0), the variables x and t in Equation (A8) separate [A.9] resulting in the self-preserving solution for the particle size spectrum.

If triple collisions are taken into account, the variables in Equation (A8) separate only if d_f = 3. In this case, the self-preserving spectrum is attained; however its form (satisfying f₂(x) + f₃(x) = const) differs from that for the case of pair collisions, Equation (A9). Note that this conclusion is valid also for multiple collisions of higher order, since each new term introduces an additional term in Equation (A8), which is asymptotically proportional to , similarly to the triple term. However, in the case of fractal particles (d_f ≠ 3) no self-preserving solution is generally attained.

APPENDIX C

The group transfer coefficients are calculated as

where

and

The coefficients satisfy the symmetry condition

and the completeness condition the latter providing the particle mass conservation