Asymptotic Solution of Moment Approximation of the Particle Population Balance Equation for Brownian Agglomeration

Abstract

In the present study, the asymptotic solutions for particle moment approximation of population balance equation for Brownian agglomeration have been obtained analytically. At long time, the dimensionless particle moment (M_C) is an explicit monotonic decreasing function of fractal dimension in the free molecule regime, while it is a constant in the continuum regime. The asymptotic agglomerate growth rate is consistent with previous qualitative analysis and numerical solution, but the present asymptotic solution is more concise and straightforward.

Copyright 2015 American Association for Aerosol Research

INTRODUCTION

Equations of population balance (PBE) are general mathematical framework for modeling of particulate systems (Friedlander 2000). The behavior of these systems is largely governed by the collision rate, i.e., the number of collisions per unit time per unit volume of aerosol. For dilute aerosol systems particle collision can be modeled as two-body interactions wherein thermal/Brownian motion drives collisions. In the framework of monovariants internal coordinate and time for each particle, the PBE is characterized as Smoluchowski equation, which takes the form: [1] in which n(υ,t)dυ is the number of particles per unit spatial volume with particle volume from υ to υ + dυ at time t, and β is the collision kernel/collision rate coefficient of coagulation. Accurate calculation of particles size evolution requires accurate collision kernel coefficient. In free molecule regime, the collision frequency function for power law agglomerates is given by (Friedlander 2000): [2] where B₁ is a function of fractal dimension D_f as [3] with k_B is the Boltzmann's constant; T is the temperature; and ρ_p is the particle density; a_p0 is the radius of a primary particle. In the continuum regime, the corresponding collision frequency function is (Friedlander 2000): [4] where the constant B₂ = 3k_BT/2μ, and μ is the gas viscosity.

In the transition regime, the Cunningham correction factor is used to account for the noncontinuum effects when calculating the drag on small particles with Knudsennumber between the continuum regime and freemolecularflow (Cunningham 1910). The slip correction factor C_c is given by [5] with A₁ = 1.257, A₂ = 0.400, and A₃ = 1.100 (Davis 1982), or A₁ = 1.165, A₂ = 0.483, and A₃ = 0.997 obtained in experiments (Kim et al. 2005), The Knudsen number (Kn) is a dimensionlessnumber defined as the ratio of the molecular meanfreepath length (λ) to a representative physical length scale (the particle radius a in the present study), i.e., Kn = λ/a. Recently, Gopalakrishnan and Hogan (2011) use the mean first passage time calculations to find a dimensionless form (H) of the collision kernel across the entire diffusive Knudsen number (Kn_D) that applies in the limit where the ratio of the masses of colliding entities to gas molecule mass approaches infinity. It can be obtained by the limiting expressions for H: in the continuum regime, H = 4πKn_D², and in the free molecule regime, H = (8π)^1/2Kn_D. The diffusive Knudsen number Kn_D in particulate systems is a dimensionless number defined as the ratio of the mean persistence distance of the colliding entities to the collision radius. For collision processes with one moving entities, Kn_D = (k_BTm_i)^1/2/f_ia_i, where m_i is the masses of entities i, f_i is the friction factors, with f_j = k_BT/D_i, and D_i is the diffusion coefficient defined appropriately for the entity i, in the transition regime, the friction factors can be obtained as f_i = 6πμa_i/C_c. It should be pointed out that the calculation formula could be easily extended to the collision processes with two moving entities. In the mean first passage time's calculations, the motion of collision entities is monitored with Langevin equations of motion of a set of interacting monomers in the continuum regime (Isella and Drossinos 2010), Monomers interact via a radial rapidly decaying intermonomer potential. The morphology of generated clusters is analyzed through their fractal dimension (D_f) and the cluster coordination number. The time evolution of the cluster fractal dimension is linked to the dynamics of two populations (small and large clusters). The collision kernel is inferred from the time required for collision. Following Vshchunov (2010), Gopalakrishnan and Hogan (2011) proposed a four parameter fit function of diffusive Knudsen number Kn_D, [6] in which the tuning constants are C₁ = 25.836, C₂ = 11.211, C₃ = 3.502, and C₄ = 7.211. Through comparison of mean first passage time calculations to existing collision kernel expressions (Fuchs 1964; Fuchs and Sutugin 1970; Loyalka 1973; Dahneke 1983; Veshchunov 2010), the examined expressions are within several percent of mean first passage derived values across the entire diffusive Knudsen number range. The excellent agreement suggests that a single collision kernel expression can be used to describe collision processes at all ratio of the masses of colliding entities to gas molecule mass across the entire particle size regime with reasonable accuracy. It should be noted that the mean first passage requires only prior knowledge of dimensional analysis as well as an understanding of force balance, and hence is suitable for beginning practitioners in aerosol science.

Then the collision frequency function in the transition regime is given by [7] The researchers have found similarity solutions of the PBE characterized by shape preservation of particle size distribution during the evolution of particle coagulation and agglomerate many years ago (Friedlander 2000). Vemury and Pratsinis (1995) and Yu and Lin (2009) have validated the self-preserving distribution theory numerically with sectional method and moment method, respectively. In our recent work (Xie and Wang 2013; Xie 2014), we have combined the observation of shape preservation and the moment equations derived from the Taylor series expansion method of moments, to demonstrate that an asymptotic solution of particle coagulation can be derived analytically. In the present work, the asymptotic analysis will be extended to the Brownian agglomeration.

THE MOMENT MODEL

Due to the nonlinear integro-differential structure of the Smoluchowski equation, only a limited number of known analytical solutions exist for simple coagulation kernel. The analytical solution of PBE, especially in terms of a particle size dependent coagulation kernel, still remains a challenging issue. Because of the relative simplicity of implementation and low computational costs, the moment method has become a powerful tool, for investigating aerosol microphysical processes for many applications (Pratsinis 1988). In the conversion from PBE to the moment equation, the k-th order moment M_k is defined as: [8] By multiplying both sides of the PBE, Equation (1), with υ^k and integrating over all particle sizes, a system of transport equations for M_k are obtained. In a spatially homogeneous system, the particle moments evolving with time due to the Brownian coagulation can be expressed as: [9]

The minimum set of moments required to close the particle moment equation is the first three, M₀, M₁, and M₂. The zeroth moment represents the particle number concentration, the first moment represents the particle volume concentration, and the second moment is a polydispersity variable. It should be pointed out that M₁ remains constant due to the mass conservation requirement, and its initial conditions for the particle moment evolution equation can be noted as M₀₀, M₁, and M₂₀, respectively.

Recently, Yu et al. (2008) have proposed a moment-based approach termed as Taylor-series expansion method of moment (TEMOM) to approximate the Smoluchowski equation due to Brownian aggregation. This approach makes no prior assumption on the shape of particle size distribution; therefore, the limitation inherent in the lognormal distribution theory automatically disappears. Several studies have demonstrated that TEMOM is a promising method to approximate the particle PBE with high computational efficiency and acceptable physical accuracy (Yu et al. 2008; Xie et al. 2012). Based on the detailed derivations of Taylor series expansion method of moment (Yu et al. 2008; Yu and Lin 2009), the resulting closed-form equations for the first three moments equations for the collision frequency function in free molecule regime can be rearranged explicitly as: [10] and the coefficients a₀, a₁, a₂ and b₀, b₁, b₂ are [11] The corresponding moment equations in the continuum regime are [12] where the dimensionless moment M_C is defined as [13] The geometric standard deviation σ of particle size distribution is the function of dimensionless particle moment can be noted as ln²σ = ln(M_C)/9 (Pratsinis 1988). The ordinary differential Equations (10) and (12) can be solved numerically with fourth order Runge-Kutta method and its initial conditions (Yu et al. 2008; Yu and Lin 2009; Xie et al. 2012).

Asymptotic Solution in the Free Molecule Regime

This shape preservation (Friedlander 2000) implies that the standard deviation or dimensionless moment tends to a constant as time advances, thus [14] then there is a relationship between fractal dimension D_f and dimensionless particle moment M_C [15] which is a third-order algebraic equation with the coefficients c₀, c₁, c₂, and c₃ are [16] and its solution can be obtained as [17] where the parameters d₁, d₂, d₃, and d₄ are [18]

There are three asymptotic values for dimensionless particle moment, but only one value is effective according to the mathematical and physical constraints, e.g., for aerosol particles, the zeroth moment must decrease while the second moment must increase with the time when its dynamical process is solely dominated by Brownian motion (Xie and He 2013; Xie 2014; Yu et al. 2015), then [19]

Table 1 shows the calculated asymptotic solution of dimensionless particle moment as a function of fractal dimension. It can be found that the asymptotic value for M_C decreases gradually with the increasing of D_f value. When D_f = 3, M_C = 2.2, which is consistent with our previous results (Xie and He 2013; Xie and Wang 2013).

TABLE 1 The asymptotic solution of dimensionless particle moment (M_C), the prefactor of agglomerate growth rate and exponent of particle primary size as function of D_f

Df	MC	|(4Df − 12)/(4 − 3Df)|	|2Df /(4 − 3Df)|
2.0	3.07	2.00	2.00
2.1	2.94	1.57	1.83
2.2	2.81	1.23	1.69
2.3	2.70	0.97	1.59
2.4	2.60	0.75	1.50
2.5	2.51	0.57	1.43
2.6	2.43	0.42	1.37
2.7	2.36	0.29	1.32
2.8	2.30	0.18	1.27
2.9	2.25	0.09	1.23
3.0	2.20	0.00	1.20

The asymptotic solution of M_C is independent with time, and is only determined by the value of D_f. So the particle moment equation at long time can be simplified as [20] where the prefactors g₁ and g₂ are defined as a function of D_f [21] the simplified moment Equations (17) for particle evolution can be solved directly as [22] which is consistent with previous qualitative analysis (Friedlander 2000), and the effect of primary particle size (a_p0) on moment evolution at long time can be expressed as [23] when D_f = 3, the exponent is zero, and the agglomerate size is independent of the primary particle size. The effect of primary particle size becomes more important with decreasing D_f because the magnitude of exponent increases, which is shown in Table 1. And the primary particle size has a major influence on the growth of agglomerates when D_f = 2.

Based on the asymptotic solution of particle moment, the relative agglomerate growth rate can be obtained as [24] Table 1 also shows that the agglomerate growth rate is larger than the coagulation rate for compact spheres.

ASYMPTOTIC SOLUTION IN THE CONTINUUM REGIME

The moment model for Brownian agglomeration in the continuum regime is simple enough, so that its asymptotic solution for dimensionless particle moment (M_C) can be solved directly as [25] The dimensionless particle moment is independent of the fractal dimension (D_f). And the first three particle moment equations at long time are reduced to [26] then the asymptotic solution for particle moment evolution are solved directly as [27] And the corresponding agglomerate growth rate is [28]

It should point out that the asymptotic agglomerate growth rate in the continuum regime does not depend on the primary particle size (a_p0) and fractal dimension (D_f) (Friedlander 2000).

ASYMPTOTIC SOLUTION IN THE TRANSITION REGIME

Following the previous analysis (Xie 2014), it can be found that the particle mean volume u at long time [29] then [30] and the corresponding collision kernel is reduced to [31] then the particle moment evolution equation and its asymptotic solution in the transition regime is reduced to the same as that in the continuum regime. The results reveal the physical processes clearly, i.e., the size of the particles may be initially small in the free molecule regime, however the particle volume will grow due to Brownian aggregation, and the mean volume of particles will change from the free molecular regime via the transition regime to the continuum regime. Correspondingly, the asymptotic behavior of the PBE solution will gradually tend to that in the continuum regime.

FIG. 1. The decay of particle number density with time in a logarithmic plot. (a) In the free molecule regime, the asymptotic slope are −2 and −6/5 for D_f = 2 and 3, respectively, and the dimensionless time is τ = g₁(D_f)M₀^(1−λ)t. (b) In the continuum regime, the asymptotic slope remains a constant −1 for different D_f, and the dimensionless time is τ = B₂t.

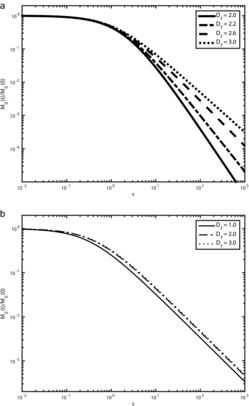
THE EFFECT OF D_f ON AGGLOMERATE GROWTH

The decay of particle number density can be obtained by integrating simplified particle moment Equations (20) in the free molecule regime as [32] where λ = 2/D_f-1/2. Thus a logarithmic plot of M₀ versus t approaches a slope of 1/(1 − λ), this corresponds to asymptotic values of −2 and −6/5 for D_f = 2 and 3, which is consistent with Friedlander's (2000) analysis. In the continuum regime, the corresponding relationship can be found as [33] But the slope is a constant −1 in a logarithmic plot for different fractal dimension D_f. the effect of D_f on agglomerate growth is shown in Figure 1. The maximum asymptotic growth rate in the free molecule regime with a slope of −6/5 is smaller than that in the continuum regime with a slope of −1 in the log–log coordinates. More importantly, the results reveal that for different fractal dimension D_f, whether in the free molecule regime or in the continuum regime, the particle moments evolve smoothly from the initial condition to the asymptotic solution at dimensionless time about τ = 10.

CONCLUSION

In the present study, an asymptotic analysis of particle moment for Brownian agglomeration is proposed. To derive the asymptotic solution, the moment model proposed by Yu and Lin (2009) has to be rewritten as a function of dimensionless particle moment (M_C) and fractal dimension (D_f) explicitly. The results show that the asymptotic value of M_C is an explicit monotonic decreasing function of fractal dimension (D_f) in the free molecule regime, while it is a constant and independent of D_f in the continuum regime. The result is consistent with the Friedlander's qualitative analysis (Friedlander 2000), such as the asymptotic solution of agglomerate growth rate and zeroth particle moment, but the present quantitative asymptotic solution is more concise and straightforward.

FUNDING

This work was supported by the National Natural Science Foundation of China through Grant No. 50806023, and the National Natural Science Foundation of China with Grant No. 50721005, the Fundamental Research Funds for the Central Universities (Project No. 2013TS078), the Foundation of State Key Laboratory of Coal Combustion (Project No. FSKLCCB1401), and the Programme of Introducing Talents of Discipline to Universities (“111” Project No. B06019), China.