Divine Proportion Shape Invariance of Diffusion Limited Cluster–Cluster Aggregates

Abstract

Aggregation is a non-equilibrium process of fundamental importance for all dispersed particulate systems, and the aggregates so produced are common in nature and technology. The resulting aggregates show fractal morphology with a universal, quantifiable fractal dimension. Current quantitative explanations for the fractal aggregate structure are based on simulation models that successfully describe experimental findings and have the key feature that as aggregates form, they continue to move and eventually connect with other aggregates. If the motion between meetings is diffusive, which is very typical, the process is called diffusion limited cluster aggregation (DLCA). We have shown previously that a three-parameter description, including the fractal dimension, the scaling prefactor, and the shape of these aggregates, is both necessary and sufficient to completely describe their morphology. Here we define a new shape description and find geometric relations between the dimensions of the aggregates. Moreover, we show that with this new shape description the aggregate shape is described by the Divine Proportion and its generalization to any dimension. Finally, we recall a simple, analytical theory for DLCA aggregate structure, the Restricted Hierarchical Model, to find that it accurately predicts shape, fractal dimension, and scaling prefactor to yield a necessary and sufficient three-parameter description of aggregate structure.

Copyright 2015 American Association for Aerosol Research

1. INTRODUCTION

Aggregation is a process of fundamental importance to all dispersed particulate systems such as aerosols and colloids, and the aggregates so produced are common in nature and our technical world (Family and Landau 1984; Jullien and Botet 1987). The process is universal (Lin et al. 1989) for all types of materials and across all scales as are the resulting aggregates that, in their pristine form before possible subsequent modification, show fractal morphology. This fractal description (Mandelbrot 1977, 1982) with a quantifiable and universal fractal dimension opened a renaissance for understanding the physical properties of aggregates in terms of their structure (Sorensen 2001, 2011). Current quantitative explanations for the fractal aggregate structure are based on simulation models (Kolb et al. 1983; Meakin 1983) that have the key feature that as cluster aggregates form, they continue to move and eventually find other clusters to connect with. If the motion between meetings is diffusive, the process is called diffusion limited cluster aggregation or DLCA for short. However, there is more to aggregate morphology than the fractal dimension and missing from this field is a complete analytic theory that can accurately predict the morphology of the aggregates.

The defining scaling relation connecting the aggregate's linear dimension, as described by its radius of gyration R_g, and its mass, as described by the number of monomers N in the aggregate, is (Sorensen and Roberts 1997; Lattuada et al. 2003)[1]

Equation (1)[1] introduces the fractal dimension D and the prefactor k₀ (a is the monomer radius). In three-dimensional space (d = 3) DLCA leads to fractal aggregates with D = 1.78 ± 0.1 and k₀ = 1.3 ± 0.2. These numbers are supported by a wealth of studies, both experiment and simulation. However, aggregate morphology is described not only by the fractal dimension and prefactor, but also by shape (Heinson et al. 2010, 2012)—a three-parameter description that is both necessary and sufficient for a complete description (Heinson et al. 2012). The shape describes aggregate anisotropy and is quantified by the ratios of the lengths of the aggregate in d perpendicular directions, where d is the spatial dimension. Since an aggregate has by its nature random boundaries, the definition of “length” is ambiguous. In past work we have used the inertia tensor of the aggregate that can be diagonalized to yield the d principal radii of gyration, which serve the purpose of lengths (Fry et al. 2004; Heinson et al. 2012). However, a troubling aspect of the principal radii magnitudes is that for d = 3 aggregates the intermediate radius is not the geometric mean of the largest and smallest. Given the random nature of the aggregates, why would two of the lengths be similar and much different than the other? This led us to seek a possibly better description of aggregate shape.

In this article, we revisit the DLCA simulation model with a new perspective for describing aggregate shape based on circumscribing rectangular solids. We show that this yields shape descriptors that are geometrically related and that the empirical shapes are described by the Fibonacci series, the Divine Proportion, and their generalizations to arbitrary spatial dimensions. We then recall a simple analytical model, the Restricted Hierarchical Model (RHM), that predicts these shapes and can also correctly calculate the fractal dimension of DLCA aggregates (Sorensen and Oh 1998). Here we add to that previous theoretical work and show that the RHM also yields the correct prefactor. Thus, in summary, we find a new and effective shape description for DLCA aggregates and revive a simple theory that provides an accurate and complete three-parameter description of the aggregates.

2. SIMULATIONS

DLCA aggregation was simulated using the well-known off-lattice method (Meakin 1999). Initially monomers with radius of were randomly placed in the simulation box. The box size was determined so that the desired monomer volume fraction in three dimension or area fraction in two dimension was attained. The three-dimensional DLCA work presented here was done at volume fraction of and the two-dimensional DLCA work was run at area fraction of . At the beginning of each time step, the number of cluster aggregates was counted (note the number of lone monomers was included in ). A random aggregate was chosen and time was incremented by . Next the probability that the selected aggregate moved was calculated. The probability of movement was inversely proportional to the frictional drag. Since the simulations assumed the Stokes–Einstein regime, the probability of movement went as the inverse of the aggregate's radius of gyration, , and was normalized so that monomers had . Aggregates moved a random direction a distance of one monomer diameter. When two aggregates collided, they irreversibly stuck together and was decremented by 1.

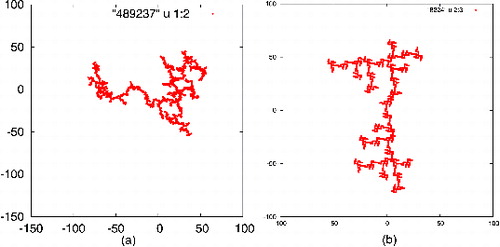
The RHM builds monodisperse clusters in a hierarchical fashion as first proposed by Botet et al. (1984). We introduced a “restriction” to the model by only allowing side-to-end connections, as described below, between clusters (Sorensen and Oh 1998). In the simulation a dimer was made of two circular (spherical) monomers. This dimer was circumscribed with a rectangle. One of the dimer's rectangle two longest sides, the sides, and two shortest sides, the ends, were chosen at random. The aggregate was cloned and the chosen end was linked with the clone's chosen side. Then the cloned aggregate was moved down the side of the original aggregate until a monomer–monomer connection was made, thus forming a new aggregate. This process was repeated to make larger aggregates. At later stages, the aggregates were open (not compact) and the algorithm often needed to try all combinations of ends and sides before a connection could be found. This process continued until a target mass was achieved. Sometimes a connection could not be found and the aggregate was set aside before it reached a target mass. Randomly selecting the sides to be joined insured that the clusters had some variety in their structure. Examples of both d = 2 DLCA and RHM aggregates are shown in Figure 1.

FIG. 1. Examples of d = 2 aggregates simulated with: (a) DLCA model, N = 1148; (b) RHM, N = 1024.

3. RESULTS

Figure 2 shows N versus R_g /a for both the DLCA simulation (closed circle symbols) and the RHM (open squares), hence tests the scaling relation Equation (1)[1] for both. Values for the prefactor and fractal dimension from fits to the data for both two- and three dimensions are given in the figure and Table 1 and agree well with previous work (Kolb et al. 1983; Meakin 1983; Sorensen and Roberts 1997; Meakin 1999; Lattuada et al. 2003; Heinson et al. 2010, 2012). The RHM simulation creates an ensemble of aggregates that are monodisperse in N, but for a given N are polydisperse in R_g. Despite this, the predictions of the model are essentially identical graphically to the DLCA simulation for both spatial dimensions. This is seen numerically for D and k₀ in Table 1 and displayed in the figures. Note that all clusters made under DLCA and RHM have the same values for D but the k₀ values in Table 1 are system averages.

FIG. 2. Number of monomers N versus the reduced radius of gyration, R_g /a, for DLCA (closed circles) and Restricted Hierarchical Model (RHM, open squares) aggregates for two and three spatial dimensions, (a) and (b) respectively.

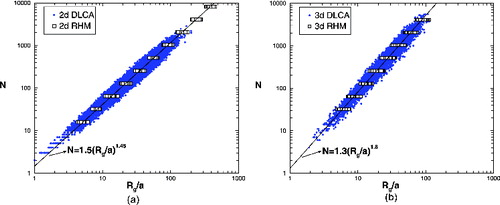
TABLE 1 Numerical values for the prefactor k₀ and the fractal dimension D from fits of Equation (1)[1] to the simulations or from the analytic calculation for the Restricted Hierarchical Model (RHM). Simulation values for given system have the same D for all clusters while values for k₀ are system averaged

	2d DLCA Simulation	2d RHM Simulation	3d DLCA Simulation	3d RHM Simulation	2d RHM Analytic	3d RHM Analytic
k0	1.50 ± 0.20	1.50 ± 0.10	1.30 ± 0.10	1.20 ± 0.10	—	—
D	1.45 ± 0.03	1.45 ± 0.03	1.80 ± 0.05	1.80 ± 0.05	1.440	1.815

Aggregate shape was explored by first diagonalizing the inertia tensor T and finding the aggregate principle axes, which are the eigenvectors of T (Fry et al. 2004; Heinson et al. 2012). For a three-dimensional body of distinct masses, the inertia tensor is[2]

For d = 2, set z_i = 0 in T. The ratios of the principal radii of gyrations R_i were found to be R₁/R₂ = 2.25 for d = 2 and R₁/R₂ = 1.03, R₂/R₃ = 1.53, and R₁/R₃ = 1.63 for d = 3. Note that for d = 3, the ratios of consecutive R_i are not equal and imply a surprising lack of symmetry for the shape. To investigate the source of this asymmetry, we calculated the principal radii for a d = 3 rectangular solid box with dimensions 1 × 2 × 4, a geometric progression. The resulting ratios of the principal radii are R₁/R₂ = 1.085, R₂/R₃ = 1.84, and R₁/R₃ = 2.00, which is not a geometric progression. This result is crucial to the realization that the magnitudes of the principal radii are in general poor descriptors of shape, but circumscribing rectangles are excellent descriptors of shape.

The rectangular solid box example suggests that aggregate shape could be well described by constructing a circumscribing rectangular solid with sides parallel to the principal radii, but with magnitudes determined by the condition that the circumscribing rectangle is the smallest one that contains every monomer of the aggregate. This certainly works for a rectangle. This circumscribing rectangle shape analysis was applied to the DLCA clusters to yield side lengths L_i. This analysis draws the smallest circumscribing box.

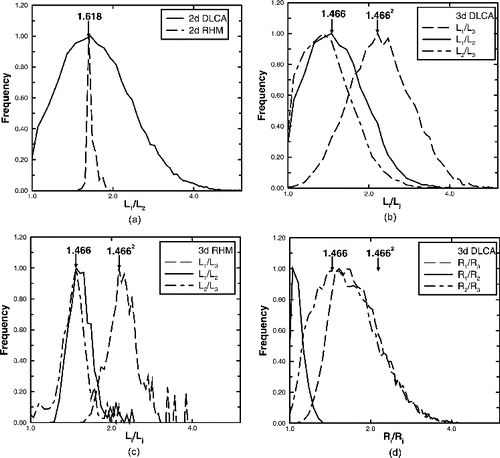
Figure 3a shows that the side ratio for d = 2 DLCA aggregates peaks at 1.63 ± 0.34 (widths determined via log-normal fits). This value is very close to the classical Divine Proportion (the Golden Mean; Coxeter 1969; Huntley 1970) as indicated by the arrow. Figure 3b shows that for d = 3 DLCA the ratios of circumscribing rectangle consecutive sides are peaked at L₁/L₂ = 1.46 ± 0.27 and L₂/L₃ = 1.35 ± 0.24 and the ratio of the longest to shortest side has a peak at L₁/L₃ = 2.14 ± 0.27. The near equality of the consecutive size ratios, within the uncertainty of distribution breadth, and the fact that implies that the intermediate side length is the geometric mean of the longest and shortest sides. In contrast, Figure 3d shows frequency distributions of the principle radii of gyration ratios, R_i/R_j, for three-dimensional DLCA aggregates and no geometric relation is seen.

FIG. 3. Distributions of side length ratios L_i/L_j for: (a) circumscribing rectangles around two-dimensional DLCA and Restricted Hierarchical Model (RHM, introduced below) aggregates. Arrow indicates the Divine Proportion ϕ₂ = 1.618. (b) Circumscribing rectangles around three-dimensional DLCA aggregates. Arrows indicate the three-dimensional Divine Proportion ϕ₃ = 1.466 and its square. (c) Circumscribing rectangles around three-dimensional RHM aggregates. Arrows indicate the three-dimensional Divine Proportion ϕ₃ = 1.466 and its square. (d) Distribution of principle radii of gyration ratios, R_i/R_j, for three-dimensional DLCA aggregates. Arrows indicate the three-dimensional Divine Proportion ϕ₃ = 1.466 and its square.

The results above give a complete description of DLCA aggregates by quantifying the three necessary and sufficient parameters, D, k₀, and shape (Heinson et al. 2012).

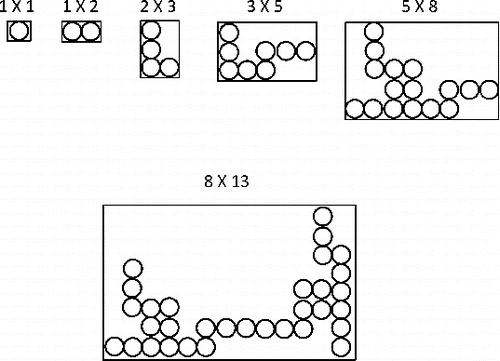
Now we show that these results are predicted analytically by the RHM by giving a brief review following Sorensen and Oh (1998). As described above, the RHM assumes an on-lattice hierarchical growth in which aggregates of equal size come together to form larger aggregates. Thus the number of monomers in an aggregate after the nth iteration is 2ⁿ. Monomers can have any shape and the lattice can have any symmetry. Here the concepts are illustrated with circular or spherical monomers on a square lattice. Confined to a square lattice, the clusters can be circumscribed by a rectangular solid; the longest edge of this rectangle is defined as the side, the shortest as the end. End-to-end aggregations lead to straight chains with a fractal dimension of 1. Side-to-side aggregations lead to dense aggregates with a fractal dimension of d. But restriction to side-to-end aggregations leads to aggregates as drawn in Figure 4 for d = 2. This side-to-end restriction is essentially the same as the T model restriction that Warren and Ball (1989) applied to the hierarchical model. The dimensions of the circumscribing rectangles for these aggregates follow the Fibonacci series (Coxeter 1969; Huntley 1970) with increasing size as illustrated in Figure 4:

FIG. 4. Two-dimensional aggregates created by the Restricted Hierarchical Model.

[3]

In each RHM aggregation step, the linear dimensions of the aggregates increase by the ratio of consecutive Fibonacci numbers, which in the large size limit is the Divine Proportion ϕ,[4]

The number of monomers increases by a factor of two with each step. Thus the fractal dimension of these aggregates formed in two spatial dimensions D₂ is[5]

For d spatial dimensions Sorensen and Oh (1998) generalize the Fibonacci series to[6]

The simplest case starts with d ones and then follows Equation (6)[6] . For example: d = 1, f_n,1 = 1, 2, 4, 8, 16, … , the geometric series; d = 3, f_n,3 = 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, … . These d-dimensional Fibonacci series are also known mathematically as Narayana's cow sequences (see The On-Line Encyclopedia of Integer Sequences®, OEIS®). An example of the geometric realization of this generalization in three dimensions is to start with a sphere with a circumscribing cube, one by one by one. As the aggregates grow, the shortest side of the circumscribing rectangular solid is the end, the longest is the side. Then side-to-end aggregation yields the series.

Sorensen and Oh (1998) defined the ratio of consecutive d-dimensional Fibonacci numbers as the d-dimensional Divine Proportion[7]

For d = 3 ϕ₃ = 1.46557…. Then Equation (5)[5] generalizes to[8]

Equation (8)[8] successfully calculates the fractal dimensions for DLCA aggregates for d ≤ 6 including D₃ = 1.815.

Another RHM rule is that no part of the circumscribing rectangles of two joining aggregates extends within or beyond the limits of the other. With this the RHM predicts the shape of the circumscribing d-dimensional rectangles to have consecutive side length ratios equal to the generalized Divine Proportion ϕ_d. Thus for d = 2, the side ratio is predicted to be L₁/L₂ = ϕ₂ = 1.618 (now the two-dimensional Divine Proportion) and for d = 3, L₁/L₂ = L₂/L₃ = ϕ₃ = 1.466 (the three-dimensional Divine Proportion). These predicted ratios are in excellent agreement with the peak values for both two- and three-dimensional DLCA aggregates shown in Figure 3.

Figure 3a and c show the frequency distributions of circumscribing rectangle side length ratios for the RHM simulation. The peaks are consistent with the analytical values of the generalized Divine Proportions. The distributions are narrower than those for DLCA, as expected. Nevertheless, the predictions of the RHM for the shape of the DLCA aggregates are very accurate, and we conclude that the RHM successfully describes the complete structure on DLCA aggregates.

4. CONCLUSIONS

We find that the shape of fractal aggregates formed by diffusion limited cluster–cluster aggregation is best described by the smallest circumscribing rectangular solid. We claim that this is the best method because the circumscribing rectangular solid side ratios are related in a geometric manner. Moreover, the side ratio distributions peak at the Divine Proportion for DLCA aggregates formed in two spatial dimensions and its generalization in three.

We also find that the RHM for DLCA aggregate morphology not only predicts these shapes but also the fractal dimension and the scaling prefactor. This three-parameter description is both necessary and sufficient for a complete description of fractal aggregate morphology. Note that any given cluster made from either DLCA or RHM will have D = 1.8 but it will have a unique and shape. Thus any two clusters from either DLCA or RHM that share these parameters will have the same morphology. The RHM model length ratios have a narrower distribution than those from DLCA but the system average agree.

It is useful to ask why such a simple model is so successful. No doubt the statistical nature of aggregation helps the simple model. In reality two aggregates of different sizes come together from any direction. However, at any point during the aggregation of an ensemble of particles, collision of mean-sized aggregates is the most common. Regarding the direction of approach, note that in two dimensions solely end-to-end collisions lead to D = 1 and solely side-to-side collisions lead to D = 2. The geometric mean of these is 1.41, very close to D₂ (See also Meakin 1985). To continue, if during aggregation one makes the reasonable assumption that end-to-end and side-to-side occurred at ¼ probability and side-to-end at ½ probability, then the predicted fractal dimension would again be very close to D₂ for this simple extension of the present RHM. Similar arguments can be used for higher dimensions but are not really worthwhile. We have not made detailed comparison of the RHM to other forms of aggregation such as reaction limited and ballistic aggregation. These have fractal dimensions 5–10% larger than DLCA so the agreement is qualitative but not exact.

Finally, we digress to point out that it is interesting to observe that many living organisms, which, like aggregates, are non-equilibrium phenomena, create structures, such as the phyllotactic arrangement of leaves or the parastichies of flowers, in which the Fibonacci series and the Divine Proportion can be found (Thompson 1945; Huntley 1970; Douady and Couder 1996). Moreover, the growth of many organisms follows the simple law expressed by Thompson (1945): “it shall widen and lengthen in the same unvarying proportion” because it grows “by accretion of accumulated material” and “the parts, once formed, remain in being, and are thenceforth incapable of change.” Here we find, again empirically, that these properties of growing with unvarying proportions due to accretion without affecting the previous structure are those of DLCA aggregates as well. This is the essence of DLCA alluded to above. And, remarkably, the Fibonacci series and the Divine Proportion appear again in a quantitative description of DLCA aggregate morphology with the addition of a generalization to any dimension. Thus we close with a speculation that it matters not what is growing, soot or sunflowers, but how it grows. And if it grows as Thompson described, the mathematics of Fibonacci and its generalization describe the structure.

ACKNOWLEDGMENTS

We thank N. Rozhkovskaya for useful conversations regarding the Fibonacci series.

Funding

This work was supported by NSF grant AGM 1261651.