Eulerian Model for Prediction of Particle Transport and Deposition in Turbulent Duct Flows with Thermophoresis

Abstract

The Reynolds-averaged equations for turbulent particle population/transport in an Eulerian framework must be closed by specifying models for several terms: a turbophoretic force; a turbulent thermophoretic force; and a turbulent particle-diffusion term. In this article, new models are proposed for the turbophoretic term, as a particle-size dependent extrapolation of the corresponding turbulent fluid-velocity correlation, and for the turbulent thermophoretic term as an eddy-viscosity-scaled multiple of the corresponding mean thermophoretic term, appropriate for small low-inertia particles with τ⁺_p < 10. When the turbophoresis model is incorporated in a system of equations that describes particle motion within the surrounding fluid, it predicts particle deposition velocities that are in good agreement with experimental data over a range of particle sizes. When this equation system is included in a computational model to predict particle transport in turbulent pipe flows, the efficiency of particle deposition in pipes with upstream heating and downstream cooling is found to be in fair agreement with experimental measurements at two different Reynolds numbers, and over a range of particle sizes and temperature differences.

Copyright 2015 American Association for Aerosol Research

1. INTRODUCTION

The transport of airborne particles is of both scientific and engineering interest in many flows and is important in a wide range of practical problems, from the deposition of particles and fine droplets in gas and steam turbines to particulate fouling of heat transfer equipment, soot deposition from combustion processes, transport of chemical aerosols, and the motion of particles inhaled in mammalian lungs. When temperature gradients exceed about 10 K per cm, in applications such as engine exhaust systems, exhaust gas recirculation coolers, and turbines, thermophoretic forces on particles ranging from nanometers to tens of microns in size are especially significant and tend to drive them towards colder regions of the flow. This thermophoretic drift of particles becomes much more complicated when the Reynolds number of the gas-phase flow is sufficiently high that it is turbulent. The long-standing problem of making accurate engineering predictions of particle transport and deposition in such flows using efficient Eulerian models to describe particle population has proved to be a challenging one, and the most widely used predictive models are currently of the Lagrangian particle-tracking kind, within flowfields computed in an Eulerian reference frame by solving Reynolds-averaged equations (Tian and Ahmadi 2007).

The most successful Lagrangian particle tracking methods to date incorporate Langevin-based models to describe the turbulent fluctuations in velocity experienced by individual particles, using local turbulence intensities deduced from concurrent Eulerian computations of the turbulent stress field. This particle transport modeling approach has been shown to yield accurate descriptions of turbulent particle dispersion in isothermal turbulent flows (Mito and Hanratty 2002, 2004; Debhi 2008) when appropriate drift velocity corrections are included in the Langevin equations. Debhi (2009) extended this approach to turbulent thermophoretic flows, by adding a thermophoretic force driven by the mean local temperature to the particle force-balance equation, and approximating the viscosity in the particle drag force and turbulent velocity statistics as if at a constant value. Predictions of experimentally measured deposition efficiencies were accurate in some flows but significant underestimates in others. These methods do not ordinarily account for particle concentration or diffusion effects or the coupling of these effects with local variations in velocity and temperature, which are represented as modeled turbulent correlations in Reynolds-averaged closures. They are also not well suited to modeling the motion of low-inertia particles, for which diffusion is an important transport mechanism that can be difficult and expensive to resolve numerically.

Eulerian-Eulerian or two-fluid treatments of particle-laden flow introduce a degree of approximation in describing particle velocity fields. When compared with more fundamental approaches based on probability-density functions of particle-fluid and particle-particle velocity/positional behavior, such two-fluid descriptions have been shown to be typically valid only in Gaussian particle velocity fields when particle inertia is small, and when spatial variations in the mean velocity and turbulent intensity of the carrier gas flow are small over lengthscales of the order of the particle mean free path. They have been shown to be seriously in error when describing particle transport when particle inertia is high, in which case the particle velocity field will not be Gaussian and particle diffusion depends on both local concentration gradients and their higher-order derivatives (Reeks 1992, 2005). However, heuristically derived two-fluid models of particle deposition in turbulent boundary layers have been shown to reproduce measured particle deposition rates and efficiencies reasonably well (Young and Leeming 1997), which suggests that some of the approximations in this approach may not be too flawed for engineering application, especially for flows laden with low-inertia particles.

The most cost-effective approach for approximate calculation of particle-laden flow is the two-fluid one, in which the governing equations for the behavior of the bulk fluid flow and the population/transport of particles are both cast in an Eulerian reference frame. This calculation efficiency is achieved at the cost of using equations of particle motion that, in some circumstances, are of lower fidelity. The conventional approach to solving these coupled equations in turbulent flow is to attempt to model unclosed terms in the Reynolds-averaged Navier-Stokes and particle population/transport equations and solve them numerically. However, the gradient-transport hypotheses that yield acceptably accurate closures for fluid turbulence have not been as successful in modeling turbulent particle transport, especially close to the wall. In this region of particle-laden flows, turbulent particle motion loses correlation with turbulent fluid motion (Brooke et al. 1994), and particles are driven towards the wall by turbophoresis—a forcing of particles from more turbulent to less turbulent regions—for which it has proved difficult to develop reliable models, especially in the immediate vicinity of the wall.

In one of the first studies targeted at modeling deposition in turbulent flow, Friedlander and Johnstone (1957) developed a “free flight” deposition model based on the idea that particles that reached a given “stopping distance” from the wall would then deposit on it, though the assumptions on which the model was based appeared to be difficult to justify. Cleaver and Yates (1975) later proposed a phenomenological model for particle deposition in turbulent flow, based on the sweep motion in the ejection-sweep bursting cycle observed close to the wall in turbulent flows. Young and Leeming (1997) devised a non-local turbophoresis model that equated the deposition velocity at the wall to the maximum value of the turbophoretic component of mean particle velocity, found at y⁺ ≃ 20. While Guha (1997) proposed a local model for the turbophoretic component of mean particle velocity, in which correlations of particle fluctuating velocities were modeled as the corresponding fluid-turbulence correlations multiplied by a function of the local fluid-turbulence and particle-turbulence timescales, the timescales were not defined uniquely and were undetermined at the wall.

The experimental studies of Liu and Agarwal (1974) have often been used as a benchmark against which the results of models and simulations have been compared. In these pipe-flow experiments, in which the wall deposition rate of olive-oil droplets of different sizes were measured, it was shown that when the dimensionless deposition velocity V⁺_dep was plotted against the dimensionless particle response time τ⁺_p, data at Reynolds numbers of 10,000 and 50,000 appeared to collapse over three decades of τ⁺_p. McCoy and Hanratty (1977) reviewed available data on droplet deposition rates in annular flows and observed a similar collapse of data, from which they obtained the fit V⁺_dep = 0.000325 τ_p⁺² for τ⁺_p < 1. In the turbulent pipe-flow experiments of Romay et al. (1998), measurements of deposition efficiencies of particles of different sizes over a fixed length of a cooled pipe with a heated upstream section demonstrated the effects of both Reynolds number (via eddy impaction/turbophoresis) and thermophoresis on deposition efficiency.

The challenges of developing engineering models for predicting deposition and the need to better understand the mechanisms of deposition in turbulent flow have also motivated numerical simulations of wall-bounded particle-laden flow, such as the direct numerical simulations of Ounis et al. (1993), Brooke et al. (1994), and Picciotto et al. (2005), and the large eddy simulations of Wang and Squires (1996). Although limited to low Reynolds numbers, direct numerical simulations resolve quantities for which no experimental measurements have been reported, such as profiles of particle fluctuating-velocity correlations, and are invaluable as reference data for modeling.

In this article, Eulerian closures for turbophoresis and thermophoresis in turbulent particle-laden flow are reexamined and new models developed for these effects. The models are tested against experimental data for deposition velocity for particles of different size/response time (Liu and Agarwal 1974), and then incorporated in a code for the computation of pipe flows in order to calculate particle deposition efficiencies. The adequacies of these models are assessed by comparing predicted deposition efficiencies with the experimental measurements of Romay et al. (1998), for turbulent pipe flows with and without thermophoresis.

2. MODELING OF PARTICLE DEPOSITION IN TURBULENT FLOW

Before discussing particular approaches to modeling, a brief summary is given of definitions and terminology used to describe particle transport and deposition (see Appendix). The principal measure of particle scale is the particle relaxation time τ_p. It is proportional to the square of particle radius and is defined as[1] and represents the timescale over which particles adjust to differences between particle and bulk fluid velocities. In this expression, which is just the particle slip velocity divided by the Stokes drag force per unit mass on a sphere, ρ°_p is the density of the particle material, r is the particle radius, and μ is the absolute viscosity of the surrounding fluid. It is often expressed as the dimensionless relaxation timescale, τ⁺_p,[2] where u_τ is the fluid friction velocity, and ρ and ν are the fluid density and kinematic viscosity. Ranges in values of the dimensionless particle timescale τ⁺_p have been identified with particular physical effects that influence particle motion and deposition.

The particle deposition velocity V_dep is usually defined as the particle mass flux onto the surface J₀ divided by the bulk or inflow particle concentration ρ_p0. It can also be expressed as the dimensionless deposition velocity V⁺_dep after normalization by the fluid friction velocity so that[3] Dimensionless deposition velocities V⁺_dep from experiments and simulations of particle-laden flows over a wide range of particle sizes and flow conditions have been observed to collapse quite well onto a single curve when plotted against τ⁺_p. This observed dependence of V⁺_dep on τ⁺_p therefore serves as a benchmark against which the fidelity of particle deposition models can be tested. Velocity components and correlations of products of velocity may be made dimensionless by division by u_τ and u²_τ, respectively, and the surface-normal distance y may be expressed in the dimensionless form of wall units, as y⁺ = yu_τ/ν.

2.1. Continuum Model for Particles in Fluid Flow

Ramshaw (1979) proposed a continuum model for particle motion in fluid flow, in which particles are modeled as if they had the field properties of an independent ideal gas mixed within the fluid, with partial particle pressure p_p and particle concentration or density ρ_p. In this dilute mixture model, particles are assumed to be in local thermal equilibrium with the surrounding fluid and so at the local fluid temperature. The motion of this particle continuum is then governed by the continuity and linear momentum equations of fluid mechanics, as if a fluid within a dissimilar fluid, as[4] where v_p is the particle velocity vector, f is the net force per unit particle mass vector exerted by the fluid (drag, thermophoretic, diffusive, buoyancy, added mass, Basset-Boussinesq, lift), and g is the net external body force per unit particle mass vector (gravitational, electromagnetic). In this two-fluid model, diffusion is represented in the particle linear momentum equation as one contributor to f, as the Brownian force on particles that arises through particle concentration gradients. The particle velocity is the value of v_p that satisfies Equation (4[4] ). It is used as an improvement on the sum of the Brownian diffusive component of particle velocity determined from Fick’s law (without regard for other forces on particles) and the bulk velocity of the fluid, which approximates the particle velocity in more simplistic models of particle-laden flow. In typical applications, the force terms in Equation (4[4] ) are simplified to represent those relevant to the particle size and the flow of interest and these equations, coupled with the equations of motion and thermal energy of the bulk fluid, are solved numerically for ρ_p and v_p.

2.2. Modeling of Turbulent Particle-Laden Flows

Guha (1997) and Young and Leeming (1997) applied Ramshaw’s model to turbulent particle flows by decomposing each flow variable in Equation (4[4] ) and the corresponding bulk-flow equations into the sum of a mean and a fluctuating component and time-averaging each equation to yield its Reynolds-averaged form, with averaged components denoted by capitalized Roman letters (e.g., V_p) or bars above lowercase Greek letters (e.g., ) and fluctuating components by primes (e.g., ρ′_p). After making a boundary-layer approximation that wall-normal gradients of turbulent correlations were much greater than streamwise ones, the averaged particle continuity equation is simplified to[5] from which it follows that the mean particle mass flux in the y direction is .

The mean particle y-momentum equation has many more terms and the choice of which to retain, neglect, approximate, and model is a matter of conjecture (Cerbelli et al. 2001). Guha (1997) has proposed that it takes the simplified form[6] where the first four terms on the right-hand side describe the mean particle drag force, diffusive force, thermophoretic force, and the dominant contribution to the mean turbophoretic force, respectively. F_y and G_y represent the mean y-direction surface and body force in Equation (4[4] ); τ_p is the local particle relaxation timescale and V is the y-component of the mean velocity of the fluid. It is noteworthy that no effect of turbulence on thermophoresis was retained in this equation.

The role of the mean turbophoretic term in Equation (6[6] ) has been considered by Young and Leeming (1997), who proposed equating the deposition velocity at the wall to the maximum value of the turbophoretic component of mean particle velocity, found at y⁺ ≃ 20, and by Guha (1997) who proposed modeling assuming that the local fluid Reynolds stress could be determined independently, and that could be scaled on the local value of as[7] and τ_t is a local turbulent fluid timescale. This turbophoretic term accounts for deposition through turbulent eddy impaction of particles at the wall. It is well known from the theory of fluid turbulence that in the vicinity of a solid surface (see, for example, Warsi 2006) and so and at the wall. The model of Equation (7[7] ) therefore implies that and at the wall. Thus, there is no effect of turbophoresis on V_p and on deposition at the wall unless the V_p∂V_p/∂y acceleration term in the y-momentum equation at the wall is non-zero. And since turbophoresis has been observed to enhance deposition for small particles (τ⁺_p ≃ 1) at small deposition velocities (V⁺_dep ≃ 0.001) in experiments (Romay et al. 1998), when effects of particle acceleration might be expected to be small, the modeling of this turbophoresis term is worth reconsidering.

2.3. Improved Model for

The turbophoresis model proposed in this article is based on the modeling assumption that, in the limit of very small particle size, particles follow the turbulent flow and . It is also based on the presumption that the profile of the wall-normal component of the fluid Reynolds stress is known, either through an empirical fit to data such as the model of Grass (1971), or through a Reynolds-averaged turbulence model calculation such as the k-ε- closure (Durbin 1993). The data used to develop this improved model are the direct numerical simulations of a turbulent channel flow of air within which particles with relaxation timescales τ⁺_p = 0.2, 1, 5, and 25 are tracked in Lagrangian frames (Picciotto et al. 2005). Results from their simulations are plotted in Figure 1 and indicate that, for dilute particle-air mixtures, profiles of the fluid Reynolds stress were indistinguishable from those of the particle Reynolds stress when τ⁺_p = 0.2. For data closer to the wall than y⁺ = 5, it was not possible to distinguish between turbulence levels at different particle response times. Similar profiles have been obtained in the simulations of Brooke et al. (1994).

FIG. 1. Profiles of in fully developed turbulent flow for particle response times τ⁺_p = 0.2, 1, 5, and 25, from the turbulent channel-flow simulations of Picciotto et al. (2005) at Re_τ = 150.

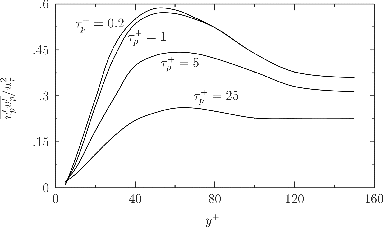
For particles for which τ⁺_p = 1, the profile was indistinguishable from that of in the outer flow beyond y⁺ = 60, but lower by a few percent between y⁺ = 60 and the wall. However, for particles still larger in size (τ⁺_p = 5 and 25), the maximum values of were 78% and 43% of the peak values of , respectively. This reduction in particle turbulent velocity, relative to turbulent fluid velocity, was attributed to:

1. the tendency for larger particles with greater inertia to be more concentrated in regions of momentarily low streamwise velocity and low fluid-turbulence intensity; and

2. the effect of increasing particle size and inertia in progressively attenuating the high-wavenumber region of the particle turbulence spectrum and thereby reducing the particle turbulence intensity and .

While it is logical to attempt to model the profile in terms of the profile and τ⁺_p, it is important to do so precisely and unambiguously, especially in the very-near-wall region (y⁺ < 5) where the profile assumes a complex shape, the subtleties of which are critical to the accurate modeling of , turbophoresis, and particle deposition.

To model as a function of y⁺ and τ⁺_p, the asymptotic cases of infinitely small and large particles are considered. For infinitely small particles τ⁺_p = 0 and while, for large particles and large values of τ⁺_p, is expected to approach a uniformly small value over y. Such a dependence can be modeled by a differential diffusion equation for over y as a function of particle response time τ_p as[8] The smoothing of in the vicinity of the wall is assumed to be predominantly a viscous fluid effect and it is for this reason that the diffusion coefficient is chosen to be the fluid viscosity ν. The initial condition is that when τ⁺_p = 0, with the boundary conditions that at y⁺ = 0 and at y⁺ = h⁺ as a far-field symmetry condition at the center of a channel of half-width h.

Equation (8[8] ) can be solved numerically or analytically, by separation of variables and the method of eigenfunction expansions. It has no physical basis and so its solution is no more than a modeling tool to extrapolate profiles of and of its wall-normal gradient at arbitrary values of τ⁺_p, from a profile prescribed for the case of τ⁺_p = 0. An algebraic equation is used to describe the profile—a rescaling of that of Grass (1971) to match the data of Picciotto et al. (2005)—and takes the form[9] Solutions to Equation (8[8] ) are plotted in the form of profiles of in the region close to the wall in Figure 2, for different values of the particle response time τ⁺_p. From this figure, it can be seen that the profile at τ⁺_p = 0 is flat at the wall and so there is no turbophoretic force there. At larger particle sizes and greater response times, a positive gradient in develops at the wall as the model diffusion equation smooths out the profile, yielding a turbophoretic deposition force. It is important to note that the gradient in predicted by this model changes continuously with y⁺ in the near-wall region. It would require a very fine grid to achieve adequate resolution in such a computation if a suitable turbulence model were to be solved with the Reynolds-averaged Navier-Stokes equations. The utility of this improved model for in predicting deposition velocities is assessed in Section 3.

FIG. 2. Profiles of in the near-wall region of fully developed turbulent flow for particle response times τ⁺_p = 0, 2.5, 5, and 10, calculated as solutions to Equation (8[8] ), with Equation (9[9] ) as the initial condition.

The proposed use of diffusion-equation solutions as a tool to extract, at the wall, wall-normal gradients in can also be extended to turbulent wall-bounded flows with larger particles. However, van Dijk and Swailes (2012) have shown in their PDF simulations of particle dispersion in a turbulent boundary layer that, for particles with τ⁺_p > 10, the wall value of can no longer be approximated as zero but is a monotonically increasing function of τ⁺_p. Therefore, the “small-particle” wall boundary condition given above of must be replaced with the corresponding simulation value for at the wall; the method can otherwise be used as described.

2.4. Model for the Mean Thermophoretic Force in Turbulent Flow

In particle-laden gas flow, the thermophoretic force is derived from kinetic theory and specifically the thermal creep condition applied at the spherical particle surface, which leads to its dependence on the momentary temperature as ∇T/T. In this expression, ∇T is the spatial temperature gradient in the gas, at the particle surface, while T is the gas temperature at the particle surface, in Kelvin. In particle-laden turbulent flows of engineering interest, the Kolmogorov microscale of length is usually significantly larger than the particle diameter, so the velocity field around a particle can be considered as if locally viscous. In gas flows with Prandtl numbers near unity, the corresponding temperature microscale of length is of the same order as the Kolmogorov microscale—typically significantly larger than the particle diameter—and so the local effect of the temperature field on thermal creep and so on the thermophoretic force is not expected to be changed by turbulence.

Following Ramshaw (1979), the particle y-momentum equation, which balances the momentary particle acceleration with the instantaneous particle pressure gradient, drag force, and thermophoretic force, is written as:[10] where m is the particle mass, the particle relaxation timescale τ_p is defined as m/(6πμr), the Brownian diffusion coefficient is (kT/m)τ_p (multiplied by 1 + 2.7 Kn to correct for Knudsen-number effects), and k is the Boltzmann constant. Were it not for the ∂ρ_p/∂y term, the particle concentration ρ_p in each term would cancel. The mean particle y-momentum equation can be determined by: (i) a Reynolds decomposition of the particle density and velocity, and the local gas temperature, into mean and fluctuating components; (ii) their substitution into Equation (10[10] ); and (iii) ensemble averaging of the resulting equation. Note that temperatures that appear in the denominators of terms in Equation (10[10] ) are absolute temperatures—usually several hundred Kelvin. Since turbulent fluctuations in these temperatures are typically much smaller than their means, they are neglected for the purposes of Reynolds decomposition.

After neglecting turbulent velocity-concentration correlations, dividing by , and neglecting other minor terms, the mean particle y-momentum equation can be written as[11] where the thermophoretic diffusion coefficient is defined as and the thermophoretic force coefficient η_th is determined according to the “fitting” equation of Talbot et al. (1980). Thus, the effect of turbulence on the mean particle y-momentum equation is to add a mean turbulent thermophoresis term, driven by the correlation between turbulent fluctuations in concentration and temperature gradient, and a turbophoresis term.

As a first step towards modeling the mean turbulent thermophoretic term in Equation (11[11] ), it is noted that transverse eddy-driven mixing processes may be described by gradient-transport hypotheses for correlations of v′_p with ρ′_p and such as[12] where both coefficients are positive. From the similarity between the two expressions in Equation (12[12] ) and the expectation that and share the same sign, it can be inferred that ρ′_p and T′ are positively correlated. Moreover, in the region close to the wall where particle transport is most important, and so ρ′_p and should also be positively correlated. Therefore, when the two thermophoretic terms are combined as[13] the mean turbulent term is expected to augment the mean thermophoresis.

The mean and fluctuating components of particle concentration are assumed to be of comparable order and so . The size of the augmentation term then depends upon the degree of positive correlation and the size of relative to . A model for in the near-wall region can be deduced from Reynolds-averaged closures for , which are typically in proportion to , where α_T is the turbulent thermal diffusivity, modeled as the eddy viscosity ν_T divided by the turbulent Prandtl number Pr_T, and τ is the appropriate turbulent timescale (Launder 1975). If the eddy viscosity is expressed as ν_T = c_μk²/ε, where k and ε are the turbulent kinetic energy and its rate of dissipation, as in k-ε models, then[14] Close to the wall—the only part of the flowfield in which is likely to be significant—it is again assumed that , and that k ∼ u⁴_τy⁴/ν² and ε ∼ u⁴_τ/ν, in which case[15] where c_th is a constant and the multiplication by τ⁺_p reflects the expectation that this augmentation term should approach zero for infinitely small particles. When τ is chosen as the near-wall viscous timescale y²/ν, so that the augmentation term is , and c_th is set to 1.6, good agreement is found with experimental data for thermophoretic deposition (Section 4.4). There do not appear to be other models for this turbulent thermophoresis term in the literature, though the outer boundary-layer fit of Kröger and Drossinos (2000) for might be useful for extending this near-wall model over the entire boundary layer. It is also worth pointing out that observations have been made in particle tracking computations that the effect of including turbulent fluctuations when describing thermophoresis in particle force balances has little effect on deposition (Kröger and Drossinos, Thakurta et al. 1998). However, these computations typically do not include effects of particle concentration or diffusion and so do not address the question of how the correlation between turbulent particle concentration and temperature fluctuations affects deposition.

3. PREDICTIONS OF TURBOPHORETIC DEPOSITION VELOCITY

The improved model for described in Section 2.3 is tested by comparing its predictions of the deposition velocity V⁺_dep in fully developed turbulent isothermal pipe flow with the experimental data of Liu and Agarwal (1974). In fully developed pipe flow V = 0, and if the particles are sufficiently small that the advective acceleration terms in Equation (6[6] ) may be neglected, and if turbophoresis is the only significant force, the mean particle y-momentum equation may be simplified to[16] or its radial equivalent. If effects of particle diffusion are not considered, V⁺_dep = −V⁺_p and may be evaluated as a function of τ⁺_p by substituting the solution to Equation (8[8] ) into Equation (16[16] ). This deposition velocity is plotted as function of particle relaxation time in Figure 3 together with the experimental data of Liu and Agarwal (1974), for the test case of olive-oil droplets of density ρ°_p = 920 kg/m³ in air. The predicted deposition velocity is in very good agreement with experimental data for τ⁺_p < 20—the approximate range over which the advective acceleration terms in Equation (6[6] ) are assumed to be small. The agreement is all the more remarkable as the model equation for has no adjustable coefficients.

FIG. 3. Turbophoretic particle deposition velocity V⁺_dep in turbulent channel flow, as a function of the particle relaxation timescale τ⁺_p, for the model predictions of Equation (16[16] ) and the experimental data of Liu and Agarwal (1974): × at Re = 10, 000 and + at Re = 50, 000.

It is emphasized that the predicted deposition velocity in Figure 3 is only the contribution to the deposition velocity from turbophoresis. In the limiting case of very small particles, the deposition velocity would be determined primarily by diffusion and would scale on Sc^−2/3, where Sc is the particle Schmidt number (Beal 1970). The data of Figure 3 do not extend below τ⁺_p ≃ 0.1 into the diffusion-dominated regime and it is for this reason that these data do not reproduce an “S”-shaped deposition-velocity curve.

In the absence of modeling errors, which fortuitously compensate for one another, this agreement implies that the term is a satisfactory representation of turbophoresis in the mean particle y-momentum equation. The predictions of this model are also in quite good agreement with the empirical fit to these data: V⁺_dep = 0.0006 τ_p⁺² (Liu and Agarwal 1974). For particles of τ⁺_p < 10, the predicted deposition velocity scales on the particle relaxation timescale to a power of approximately 1.8, which is slightly smaller than the quadratic dependence reported in experimental studies by Liu and Agarwal and by McCoy and Hanratty (1977), who proposed V⁺_dep = 0.000325 τ_p⁺², and significantly less than the dependence on τ⁺_p to the power of 2.72 determined from large-eddy simulations by Wang and Squires (1996). For τ⁺_p > 20, effects of particle acceleration are believed to be significant, in which case Equation (16[16] ) is not valid and discrepancies between the model and experimental data are to be expected.

4. PREDICTION OF PARTICLE DEPOSITION IN TURBULENT PIPE FLOWS

The turbophoresis and turbulent thermophoresis models described in the preceding sections were tested by incorporating them in a computer program to predict particle deposition in turbulent duct flows. The computational model for predicting bulk and particle flow is described briefly, together with its predictions of particle deposition in the pipe-flow experiments of Romay et al. (1998), in which deposition efficiency was measured in a turbulent pipe flow with a heated development section and a cold-walled test section.

4.1. Computational Model for Turbulent Pipe Flow

The Reynolds-averaged Navier Stokes and thermal energy equations describing the average velocity and temperature of the bulk gas flow in a pipe were written in the boundary-layer approximation in a cylindical coordinate system as[17] where the eddy viscosity ν_T was prescribed as an algebraic mixing-length model with Van Driest damping and the turbulent thermal diffusivity was expressed as α_T = ν_T / Pr_T, with Reynolds-number dependent models for the turbulent Prandtl and Schmidt numbers[18] In the ν_T model, described in detail in Kays et al. (2005), the Van Driest damping coefficient is not constant but adapts to the prevailing pressure gradient according to the fit of Kays and Moffat (1975). With wall boundary conditions of no slip/no penetration for velocity and a prescribed surface temperature or heat flux, the x-momentum and thermal energy equations were solved in finite-difference form using a variation on the Crank-Nicolson space-marching scheme (Worsøe-Schmidt and Leppert 1965), with the V component of velocity computed explicitly from the continuity equation in Equation (17[17] ).

In this article, in which the capabilities of the improved model and the turbulent thermophoresis model are illustrated, attention is restricted to particles with response times τ⁺_p less than about 20 so that particle-acceleration terms in the particle linear momentum equations may be neglected. At each step in the axial direction, the particle r-momentum equation (Equation (6[6] )) is solved as an explicit equation for V_p as[19] or, after substitution of the turbulent thermophoretic model,[20] with the model of Section 2.3 used in place of the turbophoretic term.

The averaged particle continuity equation (Equation (5[5] )) is simplified by assuming that particle slip in the flow direction is negligible so that U_p = U, and that the turbulent particle concentration to transverse velocity correlation can be described by a gradient-transport hypothesis as[21] or its radial equivalent, where c_d is a constant and multiplication of the modeled term by τ⁺_p reflects the expectation that this term should approach zero for infinitely small particles. The averaged particle continuity equation (Equation (5[5] )) written in a cylindrical coordinate system is then[22] and setting c_d to 10 appears to yield good agreement with the data on deposition by turbophoresis presented in Section 4.3. This advection-diffusion equation is solved using a Crank-Nicolson scheme to determine the numerical solution for at each step in the streamwise direction.

A final point is made concerning the boundary condition for in Equation (22[22] ) at the pipe wall. Particle-laden flows have a diffusion sublayer—a very thin layer at the wall characterized by Brownian diffusion, within which large changes in particle concentration are accommodated to match the concentration at the wall, which, for a perfectly absorbing surface, is zero. The thickness of this sublayer δ_D appears to scale on Sc⁻¹, where Sc is the Schmidt number of particles in the flow (Walker et al. 1979). The Schmidt numbers encountered in particle-laden gas flows typically range from 1 for nanometer particles to 10⁶ for micron particles (Brereton 2014), and consequently diffusion sublayers in flows with micron particles are much too thin to be resolved with affordable computer grids. It follows that it is unrealistic to perform computations for micron-scale particles with a wall boundary condition of , from which a particle deposition flux of would ordinarily be deduced.

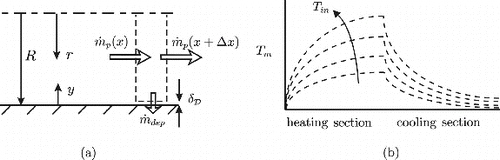
Instead, a boundary condition is applied just above the wall, at the edge of the diffusion sublayer at y = δ_D, which enforces local conservation of particle mass in a cylindrical control volume of radius R and length Δx, by equating the particle flow rate to the pipe wall over distance Δx, at y = δ_D, to the difference between the streamwise particle mass inflow rate at x and the outflow rate at x + Δx, as[23] and is shown in schematic form in Figure 4a. This boundary condition is applied while solving Equation (22[22] ) to determine the value of at y = δ_D, at each streamwise step in the computation. It effectively determines the value of which, when multiplied by the boundary value of V_p in Equation (20[20] ), yields the boundary value of the flux that conserves particle mass. This flux should be equal to the true flux at the wall, even though the true flux can only realistically be resolved for nanoparticles. The overall scheme is then, at each streamwise step, to first solve Equation (17[17] ) for U, V, and , then solve Equation (20[20] ) for V_p, after which Equation (22[22] ) is solved with the boundary condition of Equation (23[23] ) for . Computations were typically carried out with 150 evenly spaced points across the pipe radius and streamwise steps of Δx = 20Δy. The streamwise stepsize Δx was chosen to satisfy the Courant-Friedrichs-Lewy stability criterion, approximated from Equation (22[22] ), that V_p Δx/(U Δr) < 1. For the flow and geometry of the experiments of Romay et al. (1998), each calculation was completed in less than 5 min on a personal computer with a 3 GHz processor.

FIG. 4. (a) The particle mass flux boundary condition applied at the pipe surface. (b) The mixed-mean temperature as a function of cooling-section inlet temperature T_in in the heated pipe-flow experiments of Romay et al. (1998).

4.2. Deposition in Heated Laminar Pipe Flow

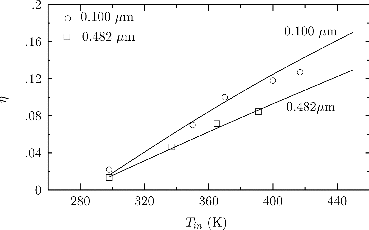
Romay et al. (1998) carried out a series of experiments in which the efficiency of deposition of sodium chloride particles of different controlled sizes was determined from particle concentration measurements, from samples of a particle-laden air flow taken upstream of and downstream of a 1.905 m length of straight 0.49 cm diameter pipe. Laminar-flow experiments were carried out at Re = 1379, with NaCl particles of 0.1 and 0.482 μm in diameter, and provide target data against which the thermophoresis model and the treatment of the wall boundary condition can be assessed in a laminar-flow computational model. The corresponding particle relaxation times τ⁺_p at 298 K, at inflow to the pipe, were 0.0004 and 0.01, respectively.

The deposition efficiency measurements of Romay et al. are plotted in Figure 5, together with the predictions of the computational model when its turbulent terms were set to zero, and when the particle concentration at inflow to the pipe was assumed to be uniform. The use of other inflow concentration profiles resulted in only very minor changes in computed deposition efficiencies. The predictions appear to be in good general agreement with the experimental data, for which uncertainty levels of roughly ±1% in η were reported, and illustrate the effect of increased particle size in reducing the deposition efficiency in laminar flow at any given value of inlet temperature. This effect of particle size is primarily through the inverse proportionality of the Brownian diffusion coefficient to the particle radius and so is a consequence of reduced diffusion for larger particles. For micron-scale particles, the thermophoretic diffusion coefficient is practically independent of particle size and so thermophoresis plays no role in the reduced deposition efficiency with increased particle size in laminar flow. The good agreement between prediction and experiment implies that the diffusive and thermophoretic properties of NaCl particles are specified accurately and that the laminar-flow aspects of the computational method and its boundary conditions describe the experimental flow correctly.

FIG. 5. Deposition efficiency η of NaCl particles as a function of cooling-section inlet temperature T_in in laminar pipe flow at Re = 1397. Solid lines describe model predictions and symbols denote the experimental data of Romay et al. (1998).

4.3. Deposition in Unheated Turbulent Pipe Flow

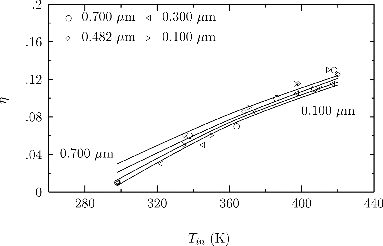
In the turbulent flow experiments of Romay et al., one series was conducted so that flow was almost isothermal at 298 K, in which case particle deposition would arise primarily through diffusion and turbophoresis. These experiments were carried out at Reynolds numbers of 5517 and 9656, with particles of 0.1, 0.3, 0.482, and 0.7 μm in diameter and provide target data for models for turbophoresis and turbulent diffusion without the effect of thermophoresis. For reference, the particle relaxation times τ⁺_p at 298 K at inflow to the pipe in these two series of experiments are: 0.0053; 0.0479; 0.124; 0.261; and 0.0178; 0.160; 0.409; 0.873 at Re = 5517 and 9656, respectively.

The deposition efficiency measurements of Romay et al. for unheated pipe flow at Re = 5517 are plotted in Figure 6, as the four discrete data points at T_in = 298 K, which are almost coincident at η ≃ 1%. The predictions of the computational model varied from η = 1% for the smallest particles (0.1 μm, τ⁺_p = 0.005) to η = 3% for the largest (0.7 μm, τ⁺_p = 0.26), when the particle concentration at inflow to the pipe was assumed to be uniform. Slightly different deposition efficiencies were found when other inflow concentrations were assumed. The uncertainty levels in η reported for these measurements were roughly ±0.01 and so the model predictions appear to be in reasonably good agreement with the experimental data, although they clearly exhibit a dependence on particle size that is not discernible in the scatter in the experimental data. The deposition efficiencies reflect the combined actions of turbophoresis in driving particles towards the wall and turbulent diffusion in smoothing the particle concentration profile, both of which are modeled to scale linearly on τ⁺_p. The relatively small values of τ⁺_p for these particles at this flow Reynolds number appear to explain the low observed deposition efficiencies.

FIG. 6. Deposition efficiency η of NaCl particles as a function of cooling-section inlet temperature T_in in pipe flow at Re = 5517. Solid lines describe model predictions and symbols denote the experimental data of Romay et al. (1998).

The corresponding unheated deposition-efficiency data at Re = 9656 are plotted in Figure 7, as the four discrete data points at T_in = 298 K. The effect of the higher Reynolds number is to increase both the turbulence levels and the particle relaxation times, with the consequence that deposition efficiency increases monotonically with particle size. The model predictions are in excellent agreement with the experimental data for all sizes of NaCl particle for which data are available. This observation implies that the turbulent particle diffusion model used in the mean particle continuity equation (Equation (22[22] )) and the turbophoresis model (Equation (8[8] )) provide, in combination, reasonable representations of experimental data, and use appropriate values for the model coefficients.

FIG. 7. Deposition efficiency η of NaCl particles as a function of cooling-section inlet temperature T_in in pipe flow at Re = 9656. Solid lines describe model predictions and symbols denote the experimental data of Romay et al. (1998).

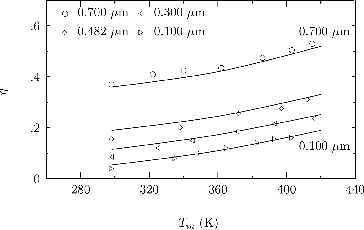
4.4. Deposition in Heated Turbulent Pipe Flow

In a second series of experiments carried out by Romay et al., the particle-laden air flow was heated from ambient inlet conditions in a development section of 0.94 m, before flowing into a 0.965 m cooling section with its wall maintained at 293 K. The lengths of both sections were less than their thermal entry length. These experiments were conducted at the same Reynolds numbers, and with particles of the same sizes as the isothermal ones, only the heating was controlled so that the air temperature at inlet to the cooling section could be varied between 298 K and 420 K. The axial dependence of the mixed-mean temperature in this flow is depicted in Figure 4b. The effect of wall heating in the development section was that thermophoresis drove particles towards the pipe center, as far along the development section as significant temperature gradients persisted. This effect was countered by diffusion, which tended to smooth out the particle concentration profile, and turbophoresis, which, for y⁺ < 50, drove particles towards the wall and, for y⁺ > 50, drove them towards the pipe center. In the cooling section, turbophoresis and diffusion played the same roles as in the heating section, whereas thermophoresis drove particles towards the pipe wall as far along the cooling section as temperature gradients persisted. The net effect of these particle transport phenomena in the two pipe sections was measured as a particle deposition efficiency, as a function of cooling-section inlet temperature. This efficiency is the cumulative result of these three combined effects in a temperature field that changes along the pipe and so is a challenging test for predictive models of turbophoresis, turbulent thermophoresis, and turbulent particle diffusion.

The deposition efficiency measurements for heated pipe flow at Re = 5517 are shown in Figure 6, as the discrete data points plotted between T_in = 325 K and T_in = 420 K. The effect of increasing the temperature in the development section is to increase the deposition efficiency almost linearly, with no apparent dependence on particle size. The scatter in experimental data appears to be of about the same size for all cases with thermophoresis (T_in > 298 K). The predictions cover an envelope of similar size and suggest a small but systematic effect of increased η at larger particle sizes/response times, though it is difficult to discern if the experimental data support this trend. Although there is no apparent dependence of η on particle size, it should not be inferred that the transport processes are unaffected by particle size—rather, the effect of particle size on thermophoresis driving particles away from the wall in the heating section and towards the wall in the cooling section, while tempered by turbulent diffusion, is size dependent but appears to cancel in the overall deposition of particles under these experimental conditions.

The corresponding deposition efficiency measurements at Re = 9656 are shown in Figure 7, as the discrete data points plotted between T_in = 325 K and T_in = 420 K. As was observed for the lower Reynolds-number data, the deposition efficiency appears to increase almost linearly with increased inlet gas temperature. The features of the computational model that produce this effect are the mean and turbulent thermophoretic terms acting on the concentration profile created by turbo and thermophoresis in the upstream heating section. When the coefficient in Equation (15[15] ) was chosen as 1.6, the model predictions were in good agreement with the experimental data for all particle sizes for which NaCl deposition data were available. The predictions appear to exhibit a slight upward curvature that is not clearly discernible in the experimental data. The general agreement between predictions and experimental data implies that the turbulent diffusion, turbophoresis, and thermophoresis models are all reasonable representations of the underlying physical effects for the range of particle sizes/relaxation times considered.

5. CONCLUDING REMARKS

In this article, Reynolds-averaged treatments of Ramshaw’s Eulerian description of particle population/transport have been extended to provide practical closures for turbulent particle transport correlations, in a model that was used to make quite accurate calculations of particle deposition in turbulent pipe flows with thermophoresis. Gradient transport hypotheses and extrapolation were used to model the unclosed turbulent correlations in the governing equations, which resulted in a computational scheme that potentially has significant advantages of speed and efficiency over the more widely used Lagrangian particle tracking methods in straight-walled duct flows.

Turbophoresis, which describes surface-normal transport of particles by turbulent eddies and their impaction on the wall, was modeled with a novel scheme for extrapolating from either an a priori algebraic model or a computed profile of as a function of τ⁺_p, as the solution to a diffusion equation. When the algebraic model for was used, the scheme yielded remarkably good predictions of the deposition velocity V⁺_dep in turbulent pipe flow and did not require the additional timescales, non-local modeling, or stopping distances used in other turbophoresis models. While the primary purpose of the extrapolation scheme is to provide accurate values of the wall-normal gradient of near the pipe surface, it could be extended, if desired, to model the entire profile of by adding a dissipation term or a y-dependent diffusion coefficient to the diffusion equation. In flows with more complex surface shapes, a turbulence closure such as Durbin’s k-ε- might have to be solved on a fine grid to provide the local profile from which the gradient in is extrapolated. Turbulent particle diffusion was modeled using the gradient transport hypothesis, the validity of which is difficult to assess without reference data on particle concentration/population profiles.

From a modeling perspective, the data of Romay et al. pose some interesting challenges. In laminar flows, in which thermophoresis and Brownian diffusion are the driving forces for deposition, the deposition efficiency decreases with increasing particle size, as demonstrated by experiment and theory in Figure 5, as a consequence of the inverse proportionality to particle diameter of the Brownian diffusion coefficient. However, in turbulent flows, the deposition efficiency increases with increasing particle size and flow Reynolds number for several reasons. First, Brownian diffusion tends to be overwhelmed by turbulent particle diffusion, which also promotes particle motion towards the wall and is modeled to scale on τ⁺_p—thus, it is proportional to the square of particle diameter. Second, turbophoresis drives deposition to higher efficiencies at higher Reynolds numbers, and its contribution to the mean particle velocity in the y-momentum equation scales on τ⁺_p. Third, the laminar thermophoretic force is augmented by a turbulent thermophoresis term attributed to the correlation between turbulent particle concentration and turbulent temperature gradient correlation, for which a provisional near-wall model was proposed, which is also modeled in proportion to τ⁺_p. In the experiments of Romay et al., the upstream heating followed by downstream cooling generates a flow with unidirectional turbophoresis and bidirectional thermophoresis, coupled with the smoothing effect of diffusion, for which the only guide to model performance is the overall deposition efficiency. Therefore, it seems remarkable that so complex a flow appears to be modeled quite accurately with the somewhat simplistic approach of gradient-transport models multiplied by the particle relaxation timescale. On the other hand, there have been no assessments of the size of the turbulent thermophoresis term in other studies, and it is possible that the model used in this article inadvertently compensates for some other shortcoming of the closure. While these models were developed for low-inertia particles, and tested against experimental data only for τ⁺_p < 1, direct numerical simulation data with larger particles or experimental studies similar to those of Romay et al., over a wider range of turbulent flow Reynolds numbers with larger particles, would be very helpful for evaluating the fidelity of these kinds of models more thoroughly.

These closures and simplifications appropriate to small particles were incorporated in a computer code written to model turbulent particle-laden flow through heated/cooled pipes, with a concentration boundary condition applied not at the wall but at the edge of the diffusion sublayer. The particular mean particle y- or r-momentum equation used (Equation (19[19] )) was a simplified version appropriate for particles for which τ⁺_p < 10, in which the advective acceleration terms were neglected, while the mean particle velocity in the x-direction was assumed to be that of the fluid. For particles with longer relaxation times, the mean particle x- and y-momentum equations would have to be solved together with the mean particle continuity equation to resolve U_p, V_p, and . In this model, the Reynolds stress and turbulent heat flux in the mean x-momentum and thermal energy equations were prescribed with an algebraic eddy viscosity model for reasons of simplicity, though very similar results would be expected if a two-equation closure like a k-ε model—which is widely used in commercial codes—had been used since both schemes are effectively calibrated against data from steady turbulent wall-bounded flow. The apparent success of these closures in modeling turbulent deposition of low-inertia particles in steady pipe flow suggests that it would be worthwhile to develop general three-dimensional models for turbulent particle diffusion, turbophoresis, and thermophoresis, for use in complex flows such as sinuous cooling passages with internal fins, where there is a great need for reliable methods of prediction of soot and water droplet deposition.

NOMENCLATURE

cd, cth	=	model coefficients for turbulent diffusion and thermophoresis
d	=	particle diameter
	=	Brownian diffusion coefficient
	=	thermophoretic diffusion coefficient
J	=	particle flux (kg/m2s)
Kn	=	particle Knudsen number—ratio of mean free path to particle radius
k	=	Boltzmann constant
m	=	mass of a particle
p	=	pressure, or particle value, as a subscript
Pr, PrT	=	laminar and turbulent fluid Prandtl number
r	=	particle radius, radial direction
R	=	pipe inner radius
Sc, ScT	=	laminar and turbulent particle diffusion Schmidt number (=, )
T	=	temperature (K unless otherwise stated), or, as a subscript, turbulent component
u, up	=	streamwise fluid velocity and particle velocity
uτ	=	fluid friction velocity
U, Up	=	mean streamwise fluid velocity and particle velocity
v, vp	=	surface-normal or radial fluid velocity and particle velocity
V, Vp	=	mean surface-normal or radial fluid velocity and particle velocity
v, vp	=	fluid and particle vector velocity
x	=	streamwise direction
y	=	surface-normal direction
0	=	surface value, as a subscript
	=	wall-unit value, as a superscript
	=	turbulent or fluctuating component, as a superscript

Greek Symbols

δD	=	diffusion sublayer thickness
Δx, Δy, Δr	=	grid spacing
η, ηth	=	deposition efficiency, thermophoretic force coefficient
μ	=	fluid absolute viscosity
ν, νT	=	fluid laminar and turbulent kinematic viscosity
φ	=	dimensionless concentration
ρ, ρp	=	fluid and particle density/concentration (kg/m3)
τp	=	particle relaxation timescale

APPENDIX

A Summary of the Pipe-Flow Particle Transport Model

The particle transport model for pipe flow is summarized briefly below. It is solved together with the continuity, momentum, and energy equations for the carrier gas, for which sets of differential equations with well-tested eddy-viscosity-based turbulence closures have long been available (Kays et al. 2005).

The differential equation that describes conservation of particle mass is[A1] as the gradient-transport model for with c_d = 10. It is solved for the mean particle concentration . The particle r-momentum equation, in the simplified form appropriate for fully developed flow with low-inertia particles (τ⁺_p < 10), is solved for the mean particle radial velocity V_p and is written as[A2] with the turbulent thermophoretic model[A3] where c_th = 1.6 and the model of Section 2.3 is used for the turbophoretic term . The mean particle streamwise velocity U_p is assumed to be equal to the mean carrier-gas velocity U. The eddy viscosity ν_T is provided by the turbulence closure for the carrier gas flow and the turbulent Prandtl and Schmidt numbers are modeled as[A4]