Methodology to quantify the ratio of multiple-to single-charged fractions acquired in aerosol neutralizers

ABSTRACT

A methodology for the quantification of the ratio of multiple- to single-charged fractions acquired in aerosol neutralizers is presented. These quantities are necessary for an accurate monodisperse calibration of aerosol instrumentation. A tandem Differential Mobility Analyzer (DMA) setup is required, with the second DMA scanning the electrical mobility spectra classified in the first DMA. In contrast to previous studies on the quantification of bipolar charge distribution utilizing tandem DMA schemes, the methodology targets at the direct determination of the multiple- to single-charge fractions and does so through the analysis of the raw signal instead of the inverted size distributions, thus circumventing errors associated with the assumptions in the DMA data inversion. The proposed methodology is employed for the characterization of different types of aerosols commonly employed for instrument calibration. Spherical liquid particles (emery oil and dioctyl sebacate) were found to acquire lower multiple charge fractions than those suggested by the commonly employed regression fits of Wiedensohler, which was published in the year 1988 in the Journal of Aerosol Science (vol. 19, pp. 387–389), but still within the range of values reported in the literature. Diffusion flame soot and spark generated graphite particles, produced by a miniCAST 6203C burner and a PALAS DNP 3000, respectively, exhibited higher fraction of multiple charges, in good agreement with previous work on agglomerates. The use of a soft X-ray bipolar charger (TSI 3088) yielded systematically higher multiple fractions of positive charges compared to a ⁸⁵Kr neutralizer (TSI 3077A), confirming the importance of direct photoionization charging on the former.

Copyright © 2016 American Association for Aerosol Research

EDITOR:

• Matti Maricq

Introduction

Differential Mobility Analyzers (DMAs) (Knutson and Whitby 1975) are widely employed for the calibration of aerosol instrumentation. Their superior size resolution compared to other techniques (i.e., diffusion screens), and the flexibility they offer in controlling it, constituted them the reference size classification technique. The operating principle of the DMA is well documented in the scientific literature (Knutson and Whitby 1975). In brief, the sample first passes through a charger to condition the charge state of the particles. The charged aerosol then enters the classification region where it flows adjacent to a particle-free sheath air in the presence of an external electric field. The electrical force, acting on the charged particles, causes them to migrate through the sheath air path towards the walls of the classification region. The actual particle trajectories depend on the operating flowrates and electrical field strength but also on the electrical mobility (being a function of particle size and number of attached charges). Particles within a narrow electrical mobility range reach an exit slit and are thus classified. The transmitted aerosol, therefore, consists of single charged particles of the desired size, but also larger particles with the same electrical mobility carrying multiple charges.

The presence of multiple charged particles complicates the data inversion in size distribution measurements (Collins et al. 2002), but also introduces uncertainties in the application of DMA for instrument calibration, where their contribution to the measured signal needs to be precisely quantified (ISO 15900). In both cases, accurate measurements require an accurate knowledge of the multiple charge fractions acquired in the charger. Different types of chargers can be employed. Unipolar chargers produce significantly larger fractions of multiple charges than their bipolar counterparts and, therefore, their use is generally limited in the ultrafine particle size range (ISO 27891). In bipolar chargers (also referred to as neutralizers), the test aerosol is exposed to bipolar ion mixtures where particle-ion collisions bring the aerosol in a steady state charge distribution, provided that the product of ion pairs concentration times residence time is large enough (Liu and Pui 1974). The most widespread method of producing such bipolar ion atmosphere is through the use of a weak radioactive source (typically ⁸⁵Kr, ²⁴¹Am or ²¹⁰Po, with the first one emitting β radiation while the last two α radiation). However, limitations posed by handling radioactive materials triggered a substantial amount of research work on alternative bipolar charging methods, including bipolar corona neutralizers (Romay et al. 1994; Stommel & Riebel 2004; Han et al. 2009; Kallinger et al. 2012), dielectric barrier discharging (Kwon et al. 2006) and soft X-rays (Shimada et al. 2002; Yun et al. 2009; Kallinger, et al. 2012; Jiang et al. 2014).

In principle the calculation of the bipolar charge distribution requires that the collision rate coefficients between particles and ions are known (Marlow and Brock 1975). These coefficients generally depend on the properties of both particles (size, shape, material) and ions (electrical mobility, mass). The approximate charging model developed by Fuchs (1963), to circumvent the complexities arising from the description of ion-particle interactions in the transition regime, was found to describe reasonably well experimentally determined charging efficiencies for radioactive neutralizers (Reischl et al. 1996). An attractive feature of the Fuchs model is that the sole parameters required for the calculation of the charging probabilities are the mass and mobility of the negative and positive ions. Yet it is difficult to predict these ion properties, since in reality, the ions evolve inside the charger from fresh primary ions (such as N₂⁺, O₂⁺, and e⁻) to larger composite ions (such as H₃O⁺(H₂O)_n or more complex structures), with the exact spectrum depending on the amount of impurities in the air (Reischl et al. 1996) and even the tubing material (Steiner and Reischl 2012). Therefore, there actually exists a spectrum of ions whose properties can differ depending on the installation, location, time but also type of neutralizer (Kallinger et al. 2012). To a certain extent this is reflected in the different set of ion masses and mobilities that were found to best fit published experimental charging probabilities for radioactive neutralizers (Hussin et al. 1983; Porstendörfer et al. 1983; Adachi et al. 1985; Hopel and Frick 1986; Wiedensohler et al. 1986; Wiedensohler 1988; Hoppel and Frick 1990; Wiedensohler and Fissan 1991; Reischl et al. 1996). For example, Figure 1 Illustrates the ratio of double to single charged fractions calculated from the Fuchs model for the aforementioned studies.

Figure 1. Ratio of doubly to singly charged fractions as a function of mobility diameter calculated from the Fuchs charging model for ion properties suggested in different studies: [1] Reischl et al. (1996), [2] & [3] Adachi et al. (1985), [4] Porstendörfer et al. (1983) & Hussin et al. (1983), [5] Hoppel and Frick (1986), [6] Wiedensohler et al. (1986), [7] Hoppel and Frick (1990), [8] Wiedensohler and Fissan (1991), [9] Wiedensohler (1988) & ISO 15900 recommendation.

The actual design of neutralizers can also affect their performance due to spatial inhomogeneities of ion concentrations and carrier gas velocity (Hoppel and Frick 1990; de La Verpilliere et al. 2015). Nonequilibrium effects have also been reported (Maricq 2006) especially in the case of ultrafine particles at high concentrations (de La Verpilliere et al. 2015) or when highly charged (Liu and Deshler 2003). Limited information is available on the performance of neutralizers that do not rely on radioactive sources (Kallinger et al. 2012; Jiang et al. 2014). Direct photoionization charging (Jiang et al. 2007) was reported to affect the charging probabilities acquired in a recently commercialized soft X-ray neutralizer (3088 model by TSI inc.) owing to the high energies of X-rays employed (Jiang et al., 2014). Furthermore, the importance of particle shape has long been recognized (Laframboise and Chang 1977; Rogak and Flagan 1992), though it is still generally neglected (Giechaskiel et al. 2009).

When DMA is employed for size distribution measurements, the individual fractions of singly and multiply charged particles are required for the data inversion. Inaccuracies in the assumed charged fractions is one of the main contributors of the measurement uncertainties of such spectrometers (Liu and Deshler 2003) and can have a strong effect on the recovered number concentrations (Xiao et al. 2012). Any progress in the understanding of charging mechanisms can help improve the quality of DMA size distribution measurements (Gopalakrishnan et al. 2015), especially since experimental quantification of charging probabilities would be impractical in such applications.

Another important application of DMAs is in calibration of aerosol instrumentation (ISO 15900). In this setup, particles classified in a DMA are sampled in parallel by the instrument under calibration and a reference instrument. Since the instrumentation responses generally depend on particle size and charge, a precise knowledge of the contribution of multiple charged particles is important for an accurate calibration. The most accurate approach of quantifying the contribution of larger multiple charged particles relies on the measurement of the instrument responses at the DMA setting corresponding to their mobility when carrying a single charge, and adjusting them by the ratio of the multiple- to single-charged fraction at this size (ISO 15900).

The ISO 15900 standard recommends the use of the regression fit formulas suggested by Wiedensohler, 1988 (curve [9] in Figure 1) for the calculation of these ratios. By setting limits in the maximum acceptable multiple charge correction (e.g., 10% in ISO 27891), the uncertainties introduced by the use of such default charging probability values are somehow controlled. This approach is effectively equivalent to introducing a lower threshold on the classification size for a given aerosol size distribution, which might not be possible in some cases. Furthermore, the proposed approximate formulas in ISO 15900 are strictly based on the assumption of spherical particles, as explicitly stated in the standard. Particles of more complex shapes, for example, agglomerates (Rogak and Flagan 1992) and ellipsoids (Laframboise and Chang 1977) are known to exhibit different charging probabilities. A methodology to experimentally quantify the ratio of multiple to single charged fractions would allow for more accurate calibrations.

Up to now, the research on this topic was focusing on the quantification of the individual charge fractions. The most common experimental technique for these measurements is based on the use of a tandem DMA setup (Hussin et al. 1983). Sequential measurements are performed in which the electrical mobilities of particles classified in the first DMA are scanned with the second DMA, after first passing through a neutralizer and subsequently through an identical blank stage of the same geometry. A comparison of the two spectrums yields information on the probabilities of acquiring different charges on the neutralizer employed between the two DMAs.

In this study, it is shown that the procedure can be simplified if the ratio of differently charged fractions is the desired quantity, as in this case the blank test is not necessary. This approach further reduces the potential for errors associated with aerosol source fluctuations between sequential tests (Maricq 2008). The methodology is first described, and it is shown that the limited information required besides the scanned spectrum has a smaller than 5% effect on the accuracy of the determined ratios of multiple to single charge fractions. The proposed methodology is then employed for the characterization of the ratio of multiple to single charged fractions for different type of aerosols that are commonly employed in aerosol instrumentation calibrations. These include, spherical oil (Dioctyl sebacate and Poly-alpha-olefin) particles produced by the evaporation condensation technique, diffusion flame soot produced in a miniCAST burner and spark-generated graphite particles from a PALAS DNP 3000. Experiments are also performed to evaluate the relative performance of commercial ⁸⁵Kr (TSI 3077A) and soft X-ray (TSI 3088) neutralizers.

Methodology

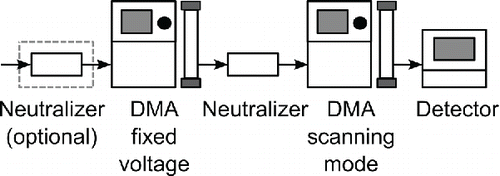
Figure 2 illustrates a schematic for the setup required for the proposed methodology. The polydisperse calibration aerosol is first conditioned in a neutralizer to acquire a steady state charge distribution. As it will be shown later, the actual charge distribution at this stage is not of much importance as long as it is steady. In fact, this step is practically necessary for uncharged aerosol (e.g., produced through the evaporation-condensation technique), or aerosol containing excessive amount of multiple charges (as for example in the case of spark discharge). The aerosol subsequently enters a first DMA that operates at a fixed voltage corresponding to the targeted mobility diameter. For the most commonly employed cylindrical DMA , the mobility diameter (d_B) of classified particles depends on the applied voltage (V) through:

Figure 2. Schematic of the setup required for the application of the proposed methodology.

[1] where, Z_p is the electrical mobility, Q_sh is the flowrate of sheath air, L, r₁, and r₂ are the dimensions of the DMA (namely length, inner radius, and outer radius of the annulus constituting the classification region), C_C is the Cunningham correction factor (Hinds 1999), e is the elemental charge, n is the number of charges on the classified particles and µ is the carrier gas viscosity. In the case of negligible diffusion and recirculating sheath flow, the transfer function (transmission efficiency as a function of electrical mobility) is triangularly shaped with a bandwidth of: [2] where Q_a is the flowrate of the sampled aerosol.

It is evident through Equation (1[1] ) that in addition to the desired particle size, larger multiple-charged particles having the same electrical mobility are also classified in the DMA. All particles classified in the first DMA, which carry charges of the same polarity (positive if the inner rod of the DMA is maintained at lower voltage than the grounded cylinder wall), are once more conditioned in a second bipolar charger. The redistribution of charges results in a relocation of different sized particles on the electrical mobility axis. By scanning the operating voltage of the second DMA and measuring in real time the number concentration of transmitted particles with a Condensation Particle Counter (CPC), a spectrum of electrical mobilities is obtained containing quantitative information (in the form of distinct peaks) for the contribution of particles of different sizes classified in the first DMA and for the contribution of different charges acquired in the second neutralizer.

For example Figure 3, shows the simulated Tandem DMA response for a lognormal input distribution peaking at 80 nm with a geometric standard deviation of 1.8, when the first DMA is set to classify particles at 150 nm. The calculations were performed for the geometric characteristics of TSI's 3081 DMA, assuming that both DMAs operated at sheath over sample flowrates of 3 over 0.3 lpm and that the voltage of the second DMA was exponentially scanned to cover the full operating size range of the specific DMA (13 nm to 750 nm for the specific sheath flowrate) over the maximum allowed scan time of 300 s. The input lognormal distribution was first multiplied with the charging probabilities calculated from the regression fit of Wiedensohler (1988), to calculate the number-weighted size distribution of single-, double-, triple-, and quadruple-charged particles exiting the first neutralizer. Each of these four distributions was convoluted with the transfer function of the DMA, calculated using the semianalytical solution of Stolzenburg (1988), which accounts for the effect of particle diffusion in the classification region. The resulting four monodisperse distributions were once more multiplied by the second charger efficiencies for +1, +2, +3, and +4 charges. Each of the 16 resulting distributions was convoluted with the transfer function of the second DMA corresponding to the instantaneous voltage, at time steps of 0.1 s. The time scale (t_m) can be translated to particle electrical mobility through:

Figure 3. Simulated Tandem DMA response for a lognormal distribution with mean diameter of 80 nm and geometric standard deviation of 1.8, with the first DMA set to classify particles of 150 nm. The areas in different colors illustrate the contribution of different sized particles at each recorded peak. The dashed lines illustrate the integration limits defined in Equations 5a[5a] and 5b[5b] . Calculations were performed for the geometry of TSI 3081 DMA at sheath and sample flowrates of 3 and 0.3 lpm, respectively, and a total scan time of 300 s.

[3a] where, Q_s is the extracted flow through the DMA, t_f is the mean residence time inside the DMA and α and τ are parameters of the exponential voltage ramp (Wang and Flagan 1990): [3b] [3c] where V_min and V_max are the selected minimum and maximum voltages of the scan, t_scan is the duration of the scan and t_d is the delay time between particle extraction from the DMA and their actual detection on the CPC.

The different colored areas in Figure 3 illustrate the distribution of different sized particles on the Tandem DMA response, which for the sake of clarity is plotted in logarithmic scale. The four black-shaded areas, when replotted in linear scale, are directly proportional to the probabilities of acquiring 1–4 charges in the second neutralizer. This is because all these signals originate from the single charged particles exiting the first DMA, and besides their different charges, their transmission efficiencies through the tubing (losses), the second DMA (transfer function) as well as their detection efficiency in the CPC are equivalent (Stolzenburg and McMurry 2008). Accordingly, the ratio of these areas equals to the ratio of the corresponding charging probabilities. However, since the CPC cannot differentiate between different sized particles, the contribution of larger particles on the CPC signal needs to be estimated. Noting that the vertical axis in Figure 3 is in logarithmic scale, the contribution of such larger particles on the measured peaks is small and to a first approximation can be neglected, in which case: [4a] [4b] where is the CPC response at time instance t, and is the fraction of particles of diameter d_i carrying j positive charges, where d_i stands for the mobility diameter corresponding to the set electrical mobility for particles carrying i number of charges. The integral limits correspond to the instances that the extremes of the band of mobilities transmitted by the second (scanning) DMA reaches the extremes of the band of mobilities transmitted from the first DMA. For the case that the diffusion broadening of the transfer functions can be neglected, and assuming that the two DMAs operate on the same sheath flowrates, these limits can be calculated through: [5a] [5b] where is the electrical mobility of particles with mobility diameter () carrying i charges (Equation (1[1] )).

While several types of larger multiple charged particles contribute to the integrals in Equations (4a[4a] ) and (4b[4b] ), the largest contribution by far is that from the population of doubly charged particles having the same electrical mobility with the targeted size. The contribution of these particles can be estimated as the product of the integral on their single charge peak ( to , Equations (5a[5a] ) and (5b[5b] ), respectively) and the ratio of their doubly to singly charged fraction: [6a] [6b]

By repeating these measurements at progressively larger sizes, doubling at each step the voltage of the first DMA (i.e., doubling the electrical mobility) until the second integral in the denominator of Equations (6a[6a] ) and (6b[6b] ) becomes negligible, all information required for this correction becomes available.

The accuracy of the proposed methodology will depend on the size distribution of the calibration aerosol and the selected particle size. In order to estimate the errors associated with Equations (4[4a] ) and (6[6a] ), the tandem DMA responses were simulated for a range of lognormal distributions with geometric mean diameters and geometric standard deviations in the range of 40–80 nm and 1.4–2.0, respectively. Calculations were performed for the case of the TSI 3081 DMA operating at 3 lpm sheath flow and 0.3 lpm sample flow, with the second DMA scanning the entire size range covered at this sheath flow over a period of 300 s. The charging probabilities resulting from the regression fit of Wiedensohler (1988) and the semianalytical expression of Stolzenburg (1988) for the diffusion broadened transfer function were employed in the simulations.

The results of the simulations are summarized in Figure 4, which shows the percentage difference of the results obtained by applying Equations (4[4a] ) and (6[6a] ) from those resulting from the charging probabilities employed in the simulations. The maximum error increases with increasing the peak of the distribution as larger particles have more multiple charges. Similarly, broadening the distribution results in an increase of the maximum error, as the relative concentration of larger multiple charged particles increases. In absolute terms, however, the error remains lower than 6.5% even if no correction is applied (i.e., using Equations (4[4a] )). The calculated results are lower than the true ratios of multiple to single charged fractions because the population of single charged particles is overestimated. Consideration of the correction term in Equations (6[6a] ), effectively eliminates the error. A small overestimation of a maximum 2% occurs at very large classification sizes (>200 nm) and is related to the quadruple charged population in the double charge peak ( to ).

Figure 4. Error associated with the calculation of the ratio of double to single (black likes) and triple to single (grey lines) charge fractions through the integrals in Equations 4[4a] (solid lines) and 6 (dashed lines).

It should be stressed that the results presented in Figure 4 are valid for all DMA geometries and configurations. The use of high enough sheath over sample flow ratios is advisable as it would facilitate the discrimination of the individual peaks in the Tandem DMA signal. To improve the signal over noise ratio, the size range can also be confined to cover the regime of interest ( to ). It is also important to note that the performance of the first neutralizer is not much critical. An inefficient neutralization at this first stage (due to high number concentration and/or particle charges, or simply decay of the activity levels of the radioactive source) can only affect the relative portion of peaks above . The performance of the second neutralizer is much more important, but with this approach the burden is much lower due to the lower particle concentrations and the more conditioned charge state (i.e., compared to the extremely large fractions of multiple charges in spark-generated soot). The results of the methodology are also practically unaffected by the amount of particle losses as the relevant peaks correspond to particles of the same size, and as such are experiencing the same amount of losses (provided that the DMA is properly designed to avoid electrostatic losses – Jiang et al. 2011). The only point at which the particle losses could theoretically play a role is in the correction term in the denominator of Equation (6[6a] ), which corresponds to larger sizes. However, this would only result in an adjustment of the correction factor that eventually translates to a small fraction of the maximum 6.5% effect.

Experimental

The methodology was tested using a tandem DMA setup that consisted of two TSI 3081 DMAs and a TSI 3775 Condensation Particle Counter (CPC) for detection (nominal cut off size at 4 nm). The aerosol was first conditioned in a TSI 3077A neutralizer containing a 10 mCi ⁸⁵Kr source before entering the first DMA. In the majority of the experiments, a TSI 3077A neutralizer was also employed for the conditioning of the particles entering the second DMA. However, in selected tests the latter was replaced by a TSI 3088 neutralizer utilizing soft X-rays. Tests were conducted with the CPC operating at both high (1.5 lpm of which 1.2 lpm are bypassing the detector) and low (0.3 lpm) flow modes. The sheath over sample flow ratio was always set to 10 over 1, and the scan time to 300 s in order to increase the signal to noise ratio. For the same reason, the size range was adjusted at each diameter setting to only cover the spectrum of the electrical mobility that gave a distinct signal (concentrations greater than 10 #/cm³). With the specific experimental setup, a concentration input (at the inlet of the first DMA) of 10⁵ #/cm³ and 10⁶ #/cm³ was sufficient for an accurate quantification of the ratios of double to single and triple to single fractions, respectively. Tests were performed with inlet concentrations spanning from 10⁵ to 5 × 10⁷ #/cm³. Following each adjustment of the voltage setting in the first DMA, the system was left running for sufficient time to purge the lines. Measurements were conducted at progressively larger sizes, doubling each time the operating voltage of the first DMA, thus allowing for a correction for double charges (Equation (6[6a] )). Both DMAs operated on negative center rod voltage and, therefore, the study only assessed the ratios of positively charged fractions acquired in the bipolar chargers.

Experiments were performed with Dioctyl-Sebacate (DOS), Poly-(alpha) Olefin (PAO), diffusion flame soot, and graphite particles. DOS and PAO particles were produced in an in-house generator operating on the evaporation-condensation technique. Pure nitrogen was employed for the production of these oil particles to avoid a potential oxidation of the vapors at the evaporator (∼170°C). Diffusion flame soot was produced in a miniCAST (combustion aerosol standard) 6.203C burner and a modified version employed in the AVL Particle Generator (APG). Graphite particles were produced in a PALAS DNP3000 spark-discharge generator. The aerosol produced by the different generators was diluted with dehumidified, particle-free air. The operating conditions tested with the different particle generators and the properties of the produced size distributions are summarized in Table 1.

Table 1. Operating conditions and properties of the aerosols produced in the different particle generators employed in the study.

Aerosol	dg [nm]	σg [−]	Operating conditions
PAO	45	1.55	Vapours of PAO at 155°C carried by 1 lpm N2 and mixed with 10 lpm of N2 at ambient temperature.
DOS	70	1.40	Vapours of PAO at 155°C carried by 1 lpm N2 and mixed with 10 lpm of N2 at ambient temperature.
Soot #1 (miniCAST)	80	1.7	0.018 lpm C3H8, 0.8 lpm oxidation air, 1.5 lpm quench N2, and 2 lpm dilution air
Soot #2 (APG)	75	1.7	0.018 lpm C3H8, 0.53 lpm oxidation air, 2 lpm quench N2, and 5 lpm dilution air
Soot #3 (APG)	45	1.7	0.018 lpm C3H8, 0.84 lpm oxidation air, 2 lpm quench N2, and 5 lpm dilution air
Graphite #1	40	1.8	3 lpm N2, 3 lpm dilution air, 2 mA
Graphite #2	70	1.8	3 lpm N2, 3 lpm dilution air, 7 mA

Results

Figure 5 summarizes the calculated ratios of double (upper panel) and triple (lower panel) to single charged fractions determined from all experiments conducted with the ⁸⁵Kr source. Results collected over a period of a year generally agreed within ∼5% (relative difference), but it should be stressed that the environmental conditions (ambient pressure of 970 mbar and temperature of 25°C) were controlled and were thus similar in all tests. Interestingly, graphite and soot particles exhibited very similar charging probabilities (with the results agreeing within 5–10%), at least at the operating conditions of the miniCAST and the DNP3000, examined here.

Figure 5. Calculated ratios of double (upper panel) and triple (bottom panel) to single charged fractions from all experimental data collected using the ⁸⁵Kr sources. Each symbol corresponds to the average result from 2 to 6 scans. Different colors indicate results determined from tests conducted on different dates. The line corresponds to the regression fit by Wiedensohler (1988).

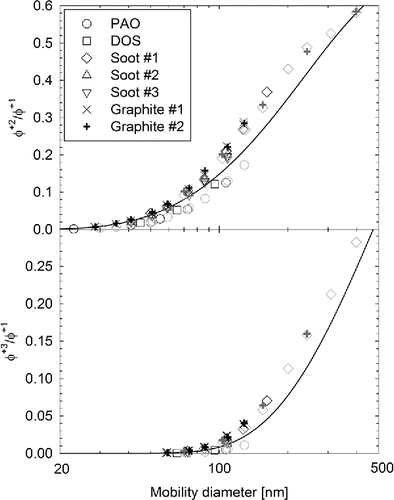
The ratios were determined to be systematically higher for soot and graphite particles compared to the PAO and DOS ones. The ratios of double to single charge fractions were approximately two times higher for soot and graphite at 50 nm and ∼60% higher at 120 nm. The relative differences were even higher for the ratios of triple to single charge fractions, with the results for soot and graphite particles being 3–5 times higher than those for PAO in the 70–130 nm range.

The multiple-charged fractions determined for PAO and DOS spherical particles lie within the range of values determined from earlier studies on charge probabilities of particles of simple geometries (spherical and crystalline), although on the lower end (Figure 1). The determined ratios of double to single charge fractions differ from those calculated by the regression fit of Wiedensohler (1988) by 10–20% at 120 nm to 40–60% at 40 nm. The corresponding differences for the ratios of triple to single charge fractions ranged from 40–60% at 70 nm to 30–50% at 120 nm. Some recent studies have also suggested an overestimation of the ratios of the multiple to single positively charged fractions for oil particles by the fit of Wiedensohler (1988). The fits reported by Maricq (2008) on his experimental results for PAO particles are in quantitative agreement with the results of this study, suggesting a 20% and 65% overestimation of the ratios of double to single charge fractions at 120 and 40 nm, and 40% and 55% overestimation of the ratios of triple to single charge fractions at 70 and 120 nm. Jiang et al. (2014) also reported a systematic overestimation of the ratio of double to single charged fractions for 70 nm DOS particles by 20–30%, for different types of radioactive source (⁸⁵Kr, ²¹⁰Po, ²⁴¹Am). Xiao et al. (2012), however, found his experimental results for DOS and ammonium sulfate particles to agree very well with the regression fit of Wiedensohler (1988).

In the case of graphite and miniCAST soot particles, the recommended charging probabilities of the ISO 15900 standard were found to reproduce the ratios of double to single charge fractions within ±10% for mobility diameters below 50 nm (Figure 5). At larger sizes the experimentally determined ratios of double to single charge fractions were systematically higher by ∼15–35%. The experimental data from Maricq (2008) suggested that the regression fit by Wiedensohler (1988) reproduce the ratios of the positively double to single charged particles within ±12% for neutralized soot particles produced in a premixed ethylene flame. On the other hand, the experimental results of Xiao et al. (2012) for neutralized diesel soot particles, suggested that the ratios of double to single positively charged particles are underestimated by approximately 20% by the regression fit of Wiedensohler (1988).

Table 2 compares the results determined for particles produced by the miniCAST (Soot #1 condition) when employing ⁸⁵Kr and X-ray sources in the second neutralizer. A systematic difference was observed with the X-ray source producing relatively higher ratios of multiple to single charged fractions compared to the ⁸⁵Kr source. The ratios of double to single charge fractions were up to ∼25% higher while the ratios of triple to single charge fractions up to ˜55% higher over the 70–300 nm range. The limited information available on the performance of the X-ray charger, also supports these findings. The charging efficiencies reported by Jiang et al. (2014) for 70 nm DOS particles suggest an 11–20% higher ratio of double to single positively charged fractions in the same X-ray charger (TSI 3088) compared to neutralizers of different radioactive sources, which was attributed to the direct photoionization charging.

Table 2. Comparison of ratios of double- and triple to single charge fractions for Soot #1 after neutralization in a 85Kr (TSI 3077A) and a Soft X-ray (TSI 3088) bipolar charger.

	^85Kr		Soft X-ray		Difference
dB [nm]	φ^+2/φ^+1	φ^+3/φ^+1	φ^+2/φ^+1	φ^+3/φ^+1	φ^+2/φ^+1	φ^+3/φ^+1
70	0.092	0.002	0.113	0.003	23.0%	53.4%
103	0.190	0.015	0.228	0.022	19.9%	45.0%
125	0.269	0.032	0.292	0.037	8.8%	14.0%
155	0.326	0.058	0.398	0.088	21.9%	50.7%
309	0.526	0.213	0.664	0.328	26.4%	54.2%

Discussion and conclusions

A methodology is proposed for the experimental quantification of the ratio of multiple to single charge fractions acquired in aerosol neutralizers. Precise knowledge of these quantities is important for accurate calibration of aerosol instrumentation against particles classified in DMAs, especially considering the growing evidence of the uncertainties associated with the charge distribution acquired in bipolar chargers. An important advantage of the proposed methodology is that it allows for a direct calculation of these fractions from the raw signal of a single measurement, therefore reducing the uncertainties originating from propagation of errors (i.e., due to the need for repeated tests or inherent assumptions in the number weighted size distributions reported by commercial DMA software).

Application of the methodology revealed that the commonly employed fit by Wiedensohler (1988) can introduce errors even for spherical oil particles. Neutralized spark-generated graphite and diffusion flame soot particles were also found to exhibit ratios of multiple to single charge fractions that exceed those derived from the aforementioned fit. The experimental results also showed that the recently introduced soft X-ray neutralizer results in systematically higher ratios of multiple to single charged fractions compared to conventional radioactive neutralizers. The simplification introduced by the use of a default charging probability can, therefore, have detrimental effects on the calibration of aerosol instrumentation.

To understand the effect that uncertainties in the ratios of multiple to single charge fractions would have on the calibration accuracy it is useful to examine the typical correction approach, as for example described in the ISO 27891 standard. The instrument response, R, is measured at the DMA voltage setting, V₁, corresponding to the size of interest, d₁, but also at multiples of V₁, nV₁, corresponding to larger particles, d_n, which when multiply charged are also transmitted at V₁. Then, assuming that the responses at larger voltages are not themselves affected by the presence of multiply charges, the contribution of particles of size d₁ on the response at V₁ can be determined as follows (ISO 27891): [7] where, accounts for the potential dependence of the instrument response on the number of charges carried by particles (i.e., in the case of an electrometer which detects number of charges).

Examination of Equation (7[4b] ) reveals that the magnitude of the correction will depend on the magnitude of the ratio of multiple to single charged fraction, the magnitude of the instrument responses at nV₁ settings and also on the nature of the instrument response dependence on multiple charges, . The larger the calibration size, and the larger the dependence of instrument response on size and charge, the larger the correction would be. Since typically the calibration of an instrument reduces to comparing its response to that of a reference instrument, the magnitude of the calibration error will depend on the relative dependence of the two responses on particle size and charge. It will be minimal for instruments exhibiting similar dependence on size and charge (i.e., calibration of a CPC against a CPC) but will increase in magnitude when the responses on size and/or charge differ (i.e., calibration of a light scattering sensor against a CPC).

For example, in the case of a CPC calibration against an electrometer, the errors in the ratio of multiple to single charge fractions will introduce a moderate effect owing to the dependence of the electrometer response on particle charge. To simplify the analysis it can be assumed that the multiply charge interference is confined to doubly charged particles, and that doubling the DMA voltage (2V₁) results in a nine-fold reduction in the CPC responses (R (V₁) = 9R(2V₁)) as required by the ISO 27891 standard. If then the regression fit of Wiedensohler (1988) is assumed while employing soot particles neutralized in a soft X-ray charger ( Table 2), the error in the measured efficiency of the CPC will range from −0.3% at 50 nm to −1.5% at 100 nm, and −2% at 200 nm. If the contribution of multiple charges cannot be confined to 10% of the sum of all responses (), for example, because it is of interest to calibrate an instrument over a wide range of sizes using the same settings of the burner (and, therefore, similar particle properties, i.e., Mamakos et al. 2013), the error will increase proportionally to the increased contribution of multiple charges.

Notes

¹ For the sake of conciseness, all equations presented in the manuscript assume the use of cylindrical DMAs.