Characterization of filter performance under low-pressure operation

ABSTRACT

Particulate gas filters are a critical element in the purification systems used to ensure defect-free manufacturing in semiconductor industry. In atomic layer deposition (ALD) processes, these filters are typically operated under sub-atmospheric pressure conditions, but their filtration characteristics are, often, only known at atmospheric pressure. In this study, performance of a metal filter that is typically used in low-pressure ALD precursor delivery systems is studied experimentally and theoretically down to 4.5 kPa. The experimental procedure was designed to minimize the presence of multiply charged particles in the test aerosol for different operating pressures and flowrates. The experimental results suggest that most penetrating particle size only slightly varies with pressure, but the shape of the penetration curve and the maximum value of the penetration changes significantly with pressure. The experimental data are used to test predictions of filter performance at low pressures made using classical theory. The comparison results suggest that the combination of classical theory and manufacturer-specified parameters results in large errors in calculated penetration values at low pressures. Accurate predictions are seen to be possible for particle Stokes numbers less than 0.1, when an inhomogenous filtration model is used in combination with effective filter parameters that are obtained from experimental measurements of filter efficiency and pressure drop at atmospheric pressures.

Copyright © 2016 American Association for Aerosol Research

EDITOR:

• Takafumi Seto

1. Introduction

In the semiconductor industry, particle contamination is a critical concern. For the vast majority of semiconductor processes, gaseous reactants are delivered to the processing chamber at super-atmospheric pressures. However, for most atomic layer deposition (ALD) processes, the precursor is delivered to the reactor at pressures typically in the range of 5 Torr to 100 Torr. ALD precursors can readily form particles in the precursor delivery system through both nucleation and reaction with residual oxygen-containing species. With solid precursor sources, there is an added risk that source material particulate can be entrained by the carrier gas. To remove these particles from the low-pressure gas lines, metal filters originally designed for high-pressure application are typically used. The choice of these filters is primarily driven by their compatibility with the gases and process conditions used in the semiconductor process equipment (Vereecke et al. 1997), the expected filtration performance, and pressure drop. The ability to predict or test filter performance under low-pressure conditions will help optimize the selection or development of appropriate filters for low-pressure operation.

To determine particle penetration through fibrous filters, Friedlander (1957) and Fuchs and Stechkina (1963) developed a simple model, with the filter represented by layers of circular-shaped fibers placed along the flow direction. The different layers were uniformly spaced, and staggered with respect to each other. With appropriate flow and particle boundary conditions, it was shown that the filter layers could be reduced by a single cell with one fiber in it. Ignoring the inertial terms in the Navier–Stokes equations, the continuum flow field around a cylindrical fiber within the cell was independently derived by Kuwabara (1959) and Happel (1959). Fibrous filter collection efficiency was determined considering three main mechanisms: convective diffusion, direct interception, and inertial impaction. Based on the Kuwabara flow, the fibrous filter collection efficiency was determined for pure convective diffusion deposition (Stechkina and Fuchs 1966; Kirsch and Fuchs 1968; Lee and Liu 1982), direct interception (Lee and Liu 1982), and inertial impaction under the condition of small Stokes number (Stechkina et al. 1969; Yeh and Liu 1974). In addition to the collection efficiency associated with the above individual mechanisms, researchers also studied the interaction effects between diffusion and interception (Kirsch and Fuchs 1968), inertial impaction and interception (Davies 1952), and the interaction effect due to the three mechanisms (Davies 1952).

The particle collection efficiencies derived based on the Kuwabara–Happel flow field are valid in the continuum flow regime and are not applicable for low pressure filter operation. According to the definition of Devienne (1958), the traditional Kuwabara flow can only be used to describe the case when fiber Knudsen number () is less than 0.001. For , the flow field can be described using a method similar to that of Kuwabara (1959) but with slip boundary condition applied (Pich 1966a), and this flow is usually named as aerodynamic slip flow. The fiber collection efficiency due to diffusion was obtained based on the flow with slip boundary condition by Pich (1966b). In a Knudsen number range of 0.25 to 10, the flow is in a transition regime. If the Knudsen number is even larger, the flow is considered to be in the free molecular regime. In both these regimes, there are no analytical solutions to describe the flow field, and numerical simulations are required (e.g., Zhao and Povitsky 2013).

All the above theoretical efforts to characterize fibrous filter performance are based on the assumption of uniform spatial distribution of fibers. In real filters, the inhomogeneity of fiber distribution must be considered for accurate theoretical predictions of filter performance. One of the earliest efforts to consider the fiber inhomogeneity was by Yeh and Liu (1974) who introduced the concept of effective fiber length. Besides the fiber distribution inhomogeneity, fiber polydispersity was also considered by Kirsh et al. (1975). The most commonly used approach to consider filter inhomogeneity is to use a constant inhomogeneity factor introduced by Lee and Liu (1982) to scale diffusion and interception filter efficiencies. The same idea was extended to aerodynamic slip flow regime (Liu and Rubow 1990; Payet et al. 1992). A more robust method to consider fiber inhomogeneity was proposed by Dhaniyala and Liu (2001) where a distribution of fiber packing densities was considered in each layer and the effect of this distribution on local flow velocities and single fiber efficiencies was determined. This approach was seen to result in better agreement with experimental results than when a constant inhomogeneity factor was used.

The above theoretical developments have been tested successfully with experimental data for a range of filter media under atmospheric pressure conditions. The accuracy of the theoretical approach to predict low-pressure filter performance is, however, largely untested. There is minimal penetration data for fibrous filters operating under sub-atmospheric pressure conditions (Stern et al. 1960; Zhang and Liu 1992; Hubbard et al. 2012), complicating theoretical validation. In this study, we validate the filtration theory for aerodynamic slip and transition flow regimes with experimental results of filter performance made at a range of pressures and face velocities. The tests are conducted with metal filters commonly used in semiconductor industry.

2. Experimental setup and method

Using filter parameters listed in Table 1, an estimate of penetration characteristics can be obtained using classical filtration theory (Supplemental Information (SI); Equation (S16)). He et al. (2015) showed that the shape of the filter penetration curve can be represented by a lognormal function, with the penetration curve characteristics represented by two factors—the mode of the curve representing the most penetrating particle size (MPPS) and the geometric standard deviation () of the lognormal function representing the width of the penetration distribution curve. For a flowrate of 1.0 l min⁻¹ through the filter (face velocity 2.71 cm s⁻¹), the filter penetration characteristics, determined from classical filtration theory calculations, are shown as a function of pressure in Figure 1. With decreasing operating pressure, is seen to decrease while the MPPS increases. These trends are likely because, at lower pressures particle diffusion coefficient is higher, and hence diffusional capture of particles is enhanced. This particularly enhances the capture of smaller particles, shifting the MPPS to a larger size. Also, with decreasing pressures, particle Stokes numbers increase, resulting in increased capture of particles by impaction on the fiber. The enhanced collection of particles by impaction primarily affects particles larger than the MPPS. The combination of these two effects results in narrowing the penetration distribution curve (i.e., become smaller) with decreasing pressure. For filters with narrow penetration curves (small ), He et al. (2015) showed that conventional differential mobility analyzer (DMA)-based filter testing approach can result in measurement errors because of the presence of multiply charged particles in the test aerosol. This is because particles classified by a DMA can be of several different sizes, with the proportion of particles of different sizes being governed by their charge distribution. Typically, multiply charged particles are low in concentration and hence their presence can be ignored, and the test aerosol from the DMA can be assumed to be near-monodisperse. But He et al. (2015) showed that the presence of even a small concentration of multiply charged particles can result in significant errors in filter efficiency measurements when their penetration curves are narrow. Following the recommendation of He et al. (2015), for accurate low-pressure filter testing the particle size distributions upstream of the DMA were carefully tailored to eliminate the presence of multiply charged particles in the test aerosol. The details of the experimental test setup used in our low-pressure filter tests are given below.

Figure 1. The geometric standard deviation and maximum penetration particle size (MPPS) under different pressures using the filter parameters in Table 1.

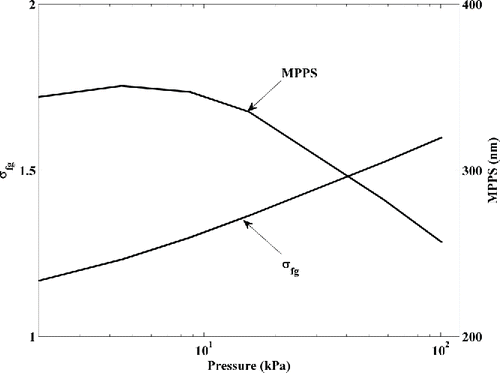
Table 1. Filter parameters from optimization using the Lee and Liu (1982) correlation.

Packing density α	Fiber diameter Df (µm)	Filtration area A (cm^2)	Media thickness L (mm)
0.0793	1.24	3.94	0.33

2.1. Setup

The experimental setup used for the low-pressure filter testing is shown in Figure 2. The experiments were conducted by varying the test conditions of filter face velocities, operating pressures, and particle sizes. To test filter performance as a function of particle size, a high concentration of monodisperse test particles were generated using an electrospray (TSI 3480) with sucrose solution and a downstream differential mobility analyzer (DMA). The mode sizes of the generated particles were adjusted by varying the volume fraction of sucrose in a buffer solution (ammonium acetate in deionized water) and the size distributions of the generated particles were measured using a Wide-Range Particle Spectrometer (WPS; MSP 1000XP). By varying the volume fractions of sucrose, particles with mode sizes of 12 nm, 19 nm, 25.6 nm, 54 nm, and 78 nm were generated, and these mode sizes were seen to be consistent with the predictions in the electrospray manual for the selected volume fractions. The generated particles were of sufficiently high concentration and narrow size distribution with a long tail in the smaller sizes. The details of the different generated test particles are presented in Table 2. The electrospray-generated particles were sent through a DMA (TSI 3071) to remove particles in the tail of the distribution and generate a narrow size distribution for the metal filter tests.

Figure 2. Schematic diagram of the experimental setup used for the low-pressure filter tests. For particles smaller than 300 nm, the DMA sheath and aerosol flows were set to 10 and 1.0 l min⁻¹, respectively. For larger particles, the DMA sheath and aerosol flows were set as 3.75, 0.375, l min⁻¹, respectively.

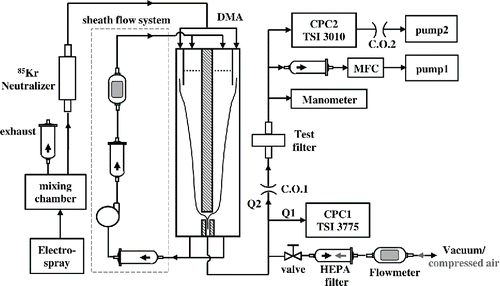
Table 2. The parameters of the sucrose particles generated from the electrospray for the different filter tests.

Size from DMA (nm)	30	40–50	60–70	80–140	>140
Solution mode size (nm)	12	19	25.5	54	78
Geometric standard deviation	1.069	1.075	1.149	1.096	1.097
Concentration (cm^−3)	4.3E6	1.2E7	1.3E7	5.5E6	5.0E6

To reduce the possibility of multiply charged larger particles being present in the DMA-classified flow, the electrospray is operated such that the generated particles have a mode size smaller than the expected size. This ensures that the concentration of multiply charged particles, with sizes in the tail of the distribution, is minimal. For example, consider the case where a 54 nm sucrose solution is used with a DMA to classify singly charged particles of one of two sizes: 37 nm or 80 nm. Along with the singly charged 37 nm particles, the doubly charged particles classified from the DMA will be from the diameter at the peak of the generated distribution (54 nm). Even though the doubly charged fraction of 54 nm particles is small, the absolute concentration of these particles in the DMA-classified flow will be similar to that of singly charged particles, and thus, the presence of these particles could significantly affect the filter efficiency measurements. The influence of multiply charged particles on filter testing is detailed in He et al. (2015). With 80 nm singly charged particles, the doubly charged particles classified from the DMA will correspond to ∼120 nm diameter. The concentration of these doubly charged particles from the 54 nm sucrose solution will be less than 1% of the singly charged particles. Thus, the DMA-classified particles from the large-particle tail of the distribution will be largely monodisperse in size. The choice of the electro-sprayed solution (characterized by the mode of the generated particles) for the different sizes of the classified test particles are shown in Table 2. Also shown in Table 2 are the distribution characteristics of the particles generated from the electrospray.

The experimental setup used for the filter tests is shown in Figure 2. The electrospray-generated particles were sent to a mixing chamber to ensure stable particle concentrations over the duration of the test. A 10 mCi ⁸⁵Kr neutralizer (TSI 3077A) with an insert (TSI 3007022) was used upstream of the DMA to ensure steady-state charging fraction of the particles (He and Dhaniyala 2014). At ambient pressure (∼1.0 atm), the DMA was operated with 10.0 l min⁻¹ sheath flow and 1.0 l min⁻¹ aerosol flow to classify particles smaller than 300 nm, and 3.75 l min⁻¹ sheath flow and 0.375 l min⁻¹ aerosol flow to classify particles larger than 300 nm. Therefore, particles were classified with a constant DMA resolution, irrespective of the face velocity used in the tests, and the DMA operation is consistent for all tests.

The particle number concentration upstream of the test filter (N₀) was measured using a condensation particle counter (CPC1, TSI 3775) operated with a flowrate Q₁ of 0.3 l min⁻¹. The TSI 3775 model CPC can only be operated at atmospheric pressure, but it allows for the measurement of particles at high concentrations (up to 10⁷ particles cm⁻³). The test pressures and face velocities were established by using critical orifices of different diameters (O'Keefe Controls Co., Monroe, CT, USA). The critical orifice is labeled in Figure 2 as C.O.1, and the mass flowrate through the critical orifice is labeled as Q₂. When the sum of the upstream CPC flowrate (Q₁) and the flowrate through the test filter (Q₂) was greater than the DMA sample flowrate, a makeup flow was provided immediately downstream of the DMA. The flow was passed through a mixing tube containing a turbulence-generating curled coil to ensure that the particle flow and the clean flow were well mixed. When the sum of the flowrates Q₁ and Q₂ was less than the DMA sample flowrate, a vacuum line was connected to provide a bypass flow.

Downstream of the test filter, another CPC (CPC2; TSI 3010) was used to measure the concentration of particles penetrating the filter. A vacuum pump (ACP 40; pump2 in Figure 2) was used downstream of the critical orifice (C.O.2 in Figure 2) to operate CPC2 at close to the default flowrate (∼1.0 l min⁻¹) at different test conditions. A bypass flow system was used downstream of the test filter for experiments at higher face velocities and/or lower pressures. The particle concentration downstream of the critical orifice C.O.1 (N₁) is corrected from the upstream CPC (CPC1) concentration measurements as: , where and are the pressures upstream and downstream of the critical orifice, respectively.

In the setup, conductive tubing was used for particle transportation, and Vacuum Coupling Radiation (VCR) fittings (Swagelok) were used for the setup connections under low pressure operation. All the flow meters including the mass flow controller (MFC) were well calibrated with a standard flowrate gauge (Gilibrator, Sensidyne, St. Petersburg, FL, USA). At different face velocities and operating pressures, the pressure drop across the filter was measured using a pressure transducer (MKS 223B). For each test condition, three repeated measurements were made to determine variability in the data. For each measurement, the counting error was controlled by setting the minimum number of particles detected by the CPC2 as 300 counts.

2.2. CPC calibration

At different test operating pressures, the two CPCs (CPC1 and CPC2 in Figure 2) were co-calibrated as a function of particle size. In these tests, CPC1 was always operated at ambient pressure in the filter test setup, while CPC2 was operated at different desired pressures. The experimental setup for these calibrations was same as the one in Figure 2 with the test filter replaced by an empty filter holder. These calibration tests account for differences in the counting efficiencies of the two CPCs, effect of wall loss at low pressures, losses due to turbulent flow downstream of the critical orifice (C.O.1), change in the CPC2 detection efficiency as a function of its operating pressure, and the effect of operating the CPC2 at low mass flowrates at low pressures.

The counting efficiencies of the CPC2 (TSI 3010, TSI Inc., Shoreview, MN, USA) at different low pressures are shown in Figure 3. The efficiency is normalized by the CPC counting efficiency of 50 nm particles at 1.0 atm. With decreasing pressure, particle counting efficiency decreases because of increased particle diffusional loss and reduced particle growth rates. Our results of CPC (TSI 3010) counting efficiencies are compared against similar measurements made with an older generation CPC (TSI 3760) by Zhang and Liu (1991) and a newer model CPC (TSI 3771) by Takegawa and Sakurai (2011) in Figure 3. For four different sizes (10, 20, 30, 50 nm), the counting efficiencies of the three model CPCs are similar at varying low pressures, except for the TSI 3771 efficiency at 10 nm. Consistent with the findings of Zhang and Liu (1991), the counting efficiency is seen to drop sharply when the CPC operating pressure is reduced to below 20 kPa.

Figure 3. The counting efficiency of CPC2 (TSI 3010) as a function of pressure and particle size for varying temperature difference (17 and 25°C) between the CPC condenser and saturator. Also, shown are the data from Zhang and Liu (1991, labeled ZL; for CPC model TSI 3760) and from Takegawa and Sakurai (2011, labeled TS; for CPC model TSI 3771).

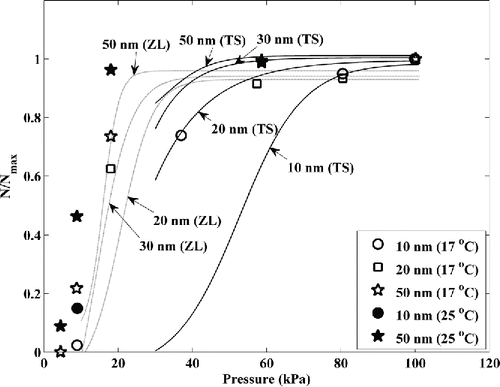
The particle counting efficiency at lower pressures can be increased by increasing the temperature difference between the CPC condenser and saturator (Mertes et al. 1995). Increasing the TSI 3010 CPC temperature difference from the default value of 17°C to 25°C was seen to improve the counting efficiency of 10 and 50 nm particles at pressures <20 kPa. With the increased temperature difference (ΔT = 25°C), CPC2 counting efficiencies were determined to be reasonable for filter tests down to pressures of 4.5 kPa. As the increased temperature difference did not affect measurements at higher pressures, the modified temperature difference was maintained for all filter tests.

3. Experimental results

3.1. Filter penetration

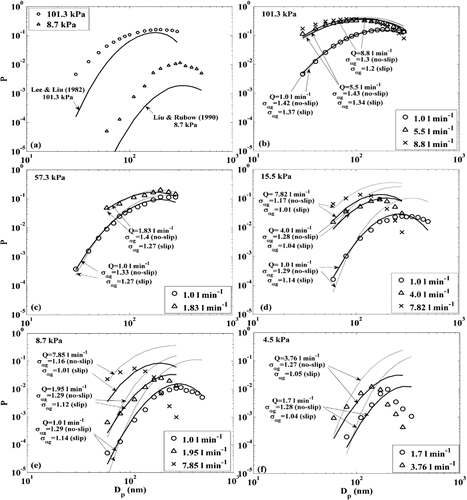
In this study, test results of the metal filter (Pall, Model 4HD4886) are reported. The experimental results of the filter penetration tests are shown in Figure 4. The filter penetrations as a function of particle size and flow rate through the test filter (1.0 l min⁻¹, 5.5 l min⁻¹, and 8.8 l min⁻¹) for 101.3 kPa operating pressure are shown in Figure 4a. With the increasing filter face velocity, the penetration increases and the MPPS decreases. At low pressures, the particle penetration characteristics are similar to those seen at atmospheric pressure, i.e., higher penetration and smaller MPPS with increasing face velocities, as shown in Figure 4b–e. This suggests that, at low pressures, for the flowrates studied, the MPPS and the peak penetration are primarily determined by the balance of particle diffusion and interception, with inertial impaction being largely unimportant, consistent with past findings (Dhaniyala and Liu 1999). Comparing the penetrations at four different pressures (101.3 kPa, 57.3 kPa, 15 kPa, and 8.7 kPa) for similar face velocities (Figure 4f), the results show that lower filter operating pressures result in decreased penetrations and increased MPPS. These trends are opposite to that observed with increasing flowrates and suggest that at lower pressures, the MPPS and maximum penetrations are determined by the balance of diffusion and inertial impaction capture mechanisms.

Figure 4. The filter penetration data at different operating conditions (a) 101.3 kPa with flow rates of 1.0, 5.5, and 8.8 l min⁻¹; (b) 57.3 kPa with flow rates of 1.0 and 1.83 l min⁻¹; (c) 15.5 kPa with flow rates of 1.0, 4.0, and 7.82 l min⁻¹; (d) 8.7 kPa with 1.0, 1.95, and 7.85 l min⁻¹; (e) 4.5 kPa with 1.7 and 3.76 l min⁻¹; (f) constant flow rate (1.0 l min⁻¹) under different pressures, 101.3, 57.3, 15.5, and 8.7 kPa. The error bars represent the standard deviation of three repeated experiments. The lines represent the log-scale lognormal distribution (He et al. 2015) fit to the experimental data.

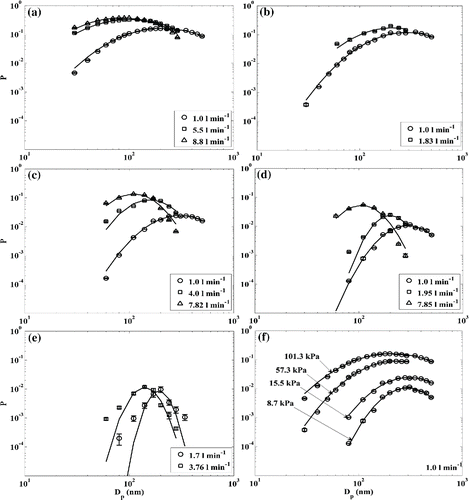
The filter penetration curve in a logarithmic penetration scale was shown by He et al. (2015) to have the shape of log-normal distribution curve. For the current experimental data, the log-normal fit was seen to fit well for all cases, except for the lowest pressure (Figure 4). The MPPS, the geometric standard deviation (), and the most penetration (P_max) obtained from the fit distribution for the different operating conditions are summarized in Table 3. To characterize the pressure and flowrate (or face velocity) dependence of MPPS, , and P_max, a multivariable linear regression analysis of the data in logarithmic scale was conducted. The analysis yielded the coefficients of the penetration curve properties (y = MPPS or or P_max), which are expressed as a function of pressure (Pr) and flowrate (Q) as

Table 3. Filter penetration curve parameters and pressure drop across the metal filter under different operating pressures.

P (kPa)	101.3			57.3		15.5			8.7			4.5
Fiber Knudsen number	0.11			0.19		0.70			1.25			2.41
Q (l min^−1)	1.0	5.5	8.8	1.0	1.83	1.0	4.0	7.82	1.0	1.95	7.85	1.7	3.76
Face velocity (cm s^−1)	2.71	14.91	23.85	2.71	4.96	2.71	10.84	21.19	2.71	5.28	21.27	4.61	10.19
MPPS (nm)	209	102	85	287	207	304	156	109	294	199	105	192	139
	2.137	2.137	2.058	1.981	1.960	1.723	1.543	1.523	1.539	1.350	1.450	1.212	1.277
Pmax	0.163	0.328	0.375	0.120	0.173	0.024	0.086	0.139	0.011	0.024	0.056	0.009	0.012
Pressure drop (kPa)	0.27	1.3	2.14	0.16	0.33	0.12	0.47	0.86	0.09	0.18	0.65	0.11	0.23

[1] where Pr₀ is a reference pressure (101.3 kPa) and Q₀ is a reference flowrate (1.0 l min⁻¹). The coefficients (α, β₁, and β₂) corresponding to the different penetration curve properties are summarized in Table 4.

Table 4. Multivariable regression parameters for MPPS, σ_fg, and P_max.

y	α	β1	β2	R^2
MPPS (nm)	250.47	−0.0466	−0.4851	0.920
σfg	2.1923	0.1655	−0.0239	0.968
Pmax	0.1621	0.9779	0.5863	0.648

From Table 4, it can be seen that the MPPS increases with decreasing pressure and flowrate, with a much greater sensitivity to flowrate (face velocity) than pressure. The goodness of the correlation to the observed MPPS data is represented by a high R-square value (0.92). The values are seen to decrease with decreasing pressure and increasing flowrate, with the pressure being the dominating factor. The general trends of MPPS and with pressure are consistent with the predictions from classical theory (Figure 1). The maximum penetration (P_max) is found to vary with both the operating pressure and flowrate, with P_max increasing with increasing pressures and flowrates. A comparatively low R-square value (0.648) is seen for the P_max correlation. This is because the P_max values range over several orders of magnitude, and the correlation fits are largely determined by the two largest P_max values that correspond to the highest flowrate and pressure combinations. Ignoring these two values, the regression results in coefficients with an R-square value of 0.902.

3.2. Penetration versus particle shape

The results shown in Figure 4 were obtained with spherical particles. Often, in semiconductor process equipment, where these metal filters are typically used under low-pressures, particles maybe non-spherical in shape and it is important to understand if the tests with the spherical particles are an underestimate or overestimate of filter performance. For non-spherical particle tests, the PALAS (GmbH GFG-1000) spark generator was used to generate carbon particles. Downstream of the generator, the small carbon particles combine to quickly form larger aggregates. The polydispersed particles from PALAS were then classified by the DMA to obtain monodispersed test particles. The method proposed in He et al. (2015) was applied to minimize multiple charging effect.

In Figure 5, the filter penetration results obtained with the aggregated carbon particles are shown along with those obtained using spherical particles. The penetrations obtained with non-spherical particles were seen to be lower than those obtained with spherical particles. For the same operating conditions, the difference in the filter penetration for the two types of test particles increases with increasing particle size. At the smallest measured sizes, the penetrations with spherical and aggregate particles were seen to be sufficiently close. A similar phenomenon was also observed by Boskovic et al. (2005) under ambient pressure (1.0 atm). The difference between the penetrations of the two particle types was seen to increase with decreasing pressure (Figure 5). The parameters (MPPS and ) from the curve fitting with lognormal shaped function for each dataset are also shown in Figure 5.

Figure 5. Filter penetration measurements made with non-spherical particles from a spark generator and near-spherical electro-sprayed particles under the same operating conditions.

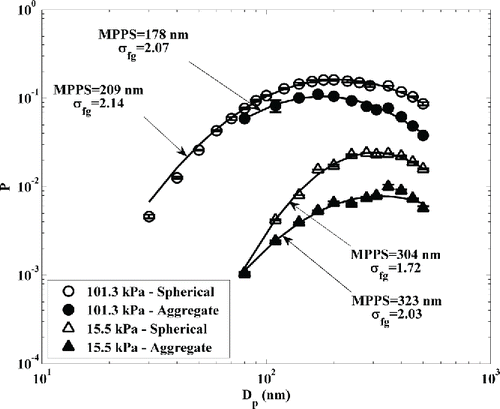
The difference in the filter response to the two types of particles was mainly ascribed by Boskovic et al. (2005) to their differences in motion along the fiber surface: sliding or rolling for spherical particles versus sliding or tumbling for non-spherical particles. In our filter tests, the test particles were sized using a DMA and hence these sizes are mobility-equivalent. These particles will have similar diffusional behavior and hence their diffusional capture efficiencies are expected to be similar and that is the observed at the smallest sizes. With increasing particle size, the aggregate chain becomes longer, and the physical sizes of spherical and non-spherical particles become increasingly different. The increasing different physical sizes results in their differing interception capture efficiencies, as observed in the experimental data at larger sizes.

3.3. Pressure drop

The pressure drop across the test filter is an important filter characteristic. The pressure drops under different pressures and flow rates are summarized in Table 3. As expected, the pressure drop is seen to be linearly proportional to face velocity for a selected pressure. At a constant face velocity, the pressure drop across the metal filter decreases with decreasing pressure, as predicted by Pich (1966b).

4. Model predictions

4.1. Effective filter parameters

Using the experimental data of filter pressure drop as a function of face velocity and penetration as a function of particle size and operating conditions, effective filter parameters that ensure a match between theoretical predictions and experimental filter performance data can be calculated. In this study, effective filter parameters were obtained by matching experimental results with filtration theory predictions at ambient pressure.

Using the approach of Lee and Liu (1982), the experimental data at atmospheric pressures and different flowrates can be compared to classical theory predictions using the two parameters: and , where is filter packing density, is Kuwabara hydrodynamic parameter, is the Peclet number, is the interception parameter, and is the single fiber collection efficiency. The detailed definitions of these parameters are included as SI. The two parameters consider the effect of diffusion and interception on particle capture in filters. In the current study, the filter parameters were varied until the experimental penetration data obtained at atmospheric pressures have minimum deviation from the theoretical correlation between the parameters and these parameters were recorded as the effective filter parameters. The procedure for optimization is:

1. Calculate the values of the above two parameters and for the experimental data obtained at three different flow rates at ambient pressure.

2. The experimentally calculated single fiber efficiency is then compared against a theoretical expectation (, where and are the parameters listed in step 1; Lee and Liu 1982). The R-square value of the deviation of the data from the theoretical prediction in the log-log scale is then determined.

3. The different filter parameters—packing density, , filtration area, , fiber diameter, , and media thickness, L—are varied and the parameter combination that results in the highest R-square value is determined.

4. With the obtained parameters in step (3), the filter pressure drops are predicted for the three different test flowrates. From the comparison of predicted and measured pressure drops, a chi-square value is obtained.

5. Further tune the values of , , , and L from step 3 to minimize chi-square values and note the optimized filter parameters.

The optimized filter parameters are listed in Table 1. Using the effective filter parameters, the predicted pressure drop is seen to agree well with the measured pressure drop (R² > 0.99). To analyze the accuracy of the filter efficiency prediction considering the optimized filter media values, the correlation between the parameters and is shown in Figure 6. With the optimized parameters, the correlation over-predicts collection efficiency of particles at the smaller size range and slightly under-predicts collection efficiency in the larger size range.

Figure 6. Comparison of filtration efficiency data at 101.3 kPa, obtained from the current study, and theoretical predictions, using the correlation of Lee and Liu (1982). The filter parameters are optimized to ensure minimal error in the calculated filter efficiencies over the entire range of correlation parameter values.

With the effective filter parameters listed in Table 1, filter penetrations at pressures of 101.3 and 8.7 kPa and a flowrate of 1.0 l min⁻¹ are predicted according to the filtration theory of Lee and Liu (1982) and the modified form for low pressures (Liu and Rubow 1990), respectively, shown in Figure 7a. The classical filtration theory is seen to mostly over-predict filter efficiency, i.e., under-predict filter penetration. This over-prediction was also observed by others and attributed to the challenges of accurately accounting for filter inhomogeneity. In the predictions of Figure 7a, a constant inhomogeneity factor of 1.6 is used to scale diffusion and interception particle capture efficiencies (Lee and Liu 1982). Using a constant inhomogeneity factor, however, results in significant error in penetration prediction at lower pressures (Figure 7a).

Figure 7. Filter penetration predictions based on the filtration theory of (a) Lee and Liu (1982) and the modified version (Liu and Rubow 1990); (b–f) Dhaniyala and Liu (2001). Theoretical filter penetrations are calculated considering no-slip and slip boundary conditions for the pressure conditions of (b) 101.3 kPa; (c) 57.3 kPa; (d) 15.5 kPa; (e) 8.7 kPa; (f) 4.5 kPa. The darker lines are predictions based on no-slip boundary condition, and the lighter ones are prediction based on slip boundary condition.

Another approach to account for the effect of inhomogeneity on filter performance was introduced by Dhaniyala and Liu (2001). In their approach, the filter was modeled as being composed of parallel sub-units of varying packing densities. The particle capture efficiency of the entire filter was then calculated from the particle capture efficiencies of the individual units. For the individual units, particle penetration predictions were made based on the optimized filter parameters (Table 1) considering the particle capture mechanisms of: diffusion, direct interception, interaction between diffusion and interception, and inertial impaction, summarized in Table 5 and detailed in the SI. As the Knudsen numbers based on our test conditions and fiber diameter ranged from 0.11 to 2.41, the effect of flow slip could be important (Devienne 1958). Particle capture calculations were, thus, made based on both continuum (no-slip flow; Kuwabara 1959) and non-continuum flow (slip flow; Pich 1966b). Note that, for fiber Knudsen numbers >0.25 (at pressures of 15.5, 8.7, and 4.5 kPa), the flow is considered to be in the transition regime. In the transition and free molecular regimes, filtration theory is not well established, and hence, only slip and no-slip flows are considered here.

Table 5. Theoretical expressions used for calculation of single fiber efficiency based on different capture mechanisms.

Capture mechanism	Equation	Reference
Convective diffusion ()		Lee and Liu (1982)
Direct interception ()		Lee and Liu (1982)
Interaction between diffusion and interception ()		Stechkina and Fuchs (1966)
Inertial impaction ()		Stechkina et al. (1969)

* Where Stk is particle Stokes number, and , R is the interception parameter (Lee and Liu 1982), Pe is particle Peclet number, and Ku is the Kuwabara factor (Kuwabara 1959).

4.2. Application of filtration theory

The prediction of filter penetration using the theory of Dhaniyala and Liu (2001) requires knowledge of the packing density distribution characteristics. As in Dhaniyala and Liu (2001), a log-normal distribution was considered here. The packing density value calculated along with the other effective filter parameters (Table 1) was considered as the mean value of the distribution. To determine the effective geometric standard deviation () of the distribution, a parametric study was conducted. In the study, values were varied, and an optimal value was calculated corresponding to the minimal error between theoretical predictions of particle penetration and experimental data. The optimal values and the corresponding penetration curves are shown in Figure 7b–f for the different test cases studied.

A comparison of the filter penetration predictions with experimental data suggests that the theoretical predictions with no-slip boundary condition match better with experimental data than the predictions with slip boundary conditions. Another observation from the results is that the calculated values are pressure- and flowrate-dependent. Using multivariable regression analysis, the dependence of on filter operating conditions (pressure, flowrate) can be expressed as[2] where Q₀ is reference flowrate (1.0 l min⁻¹), Pr₀ is reference pressure (101.3 kPa), and the coefficients a and b_1–4 are determined from the regression analysis to be: 1.2382, −0.0046, 0.0255, 0.0199, and 0.1632, respectively.

The accuracy of theoretical predictions can be established based on first-norm error, normalized relative to the experimental data, for all particle sizes, flowrates, and pressures studied. Using the pressure- and flowrate-dependent values (Equation (2)[2] ), the first-norm error for theoretical predictions as a function of particle Stokes number, calculated assuming a particle density of 1.59 g cm⁻³, is shown in Figure 8. For Stokes numbers larger than ∼0.1, the predictions have large errors. The increased error at larger Stokes numbers is not unexpected, as the inertial impaction model used here (Stechkina et al. 1969) is only valid for particle Stokes numbers <<1 and when the particle velocity equals the gas velocity. There has been some effort to model particle collection in filters at Stokes numbers >0.1 (e.g., Landahl and Herrmann 1949; Davies and Peetz 1956; Suneja and Lee 1974; Hubbard et al. 2012), but most of these studies have focused on flows with Reynolds number >1. In our tests, the highest Reynolds numbers reached were less than 0.03. The results obtained here suggest that a new inertial collection efficiency theory is required for the case of particles with large Stokes numbers and flows with low Reynolds number.

Figure 8. The relative first-norm error in theoretical prediction of particle penetration using no-slip boundary condition as a function of particle Stokes number. The filled markers are the prediction errors using the according to Equation (2)[2] , while the open circles are the prediction errors using the according to Equation (3)[3] .

To determine the coefficients of the , expression in Equation (2)[2] required data from low-pressure filter tests at varying flowrates. Considering the challenges of low-pressure filter tests, we wanted to determine if the dependence on pressure could be ignored. Ignoring pressure-dependence, the flow-rate dependent can be expressed as[3] where the coefficients c and d_1–2 are determined from regression analysis considering atmospheric pressure data to be: 1.3884, −0.0053, and 0.0369, respectively. Using the expression of Equation (3)[3] for all pressures, the first norm error in predictions is shown in Figure 8. These results suggest that ignoring pressure-dependence in increases prediction errors at all Stokes numbers.

The need to consider pressure-dependence of the effective filter packing density distribution parameter complicates theoretical prediction of low-pressure filter performance with existing models. Using the semi-empirical relations obtained here (Equations (1) and (2)), some initial guidance about the behavior of media under low-pressure conditions is available for researchers and engineers. As these relations were obtained from experiments with just one filter type, care must be taken in extending these results to other filter media types.

5. Conclusion

There is limited understanding of filter behavior as a function of operating pressure and existing filtration theories are largely untested under sub-atmospheric pressure conditions. In this study, performance of a metal fibrous filter, commonly used in industry for low-pressure applications, was conducted at a range of ambient and sub-ambient pressures and different flowrates. From measurement of size-dependent particle collection efficiencies over pressures ranging from 4.5 to 101.3 kPa, it was observed that the broadness of the penetration curve was primarily dependent on the operating pressure, while the particle size corresponding to maximum penetration varied largely with flowrate through the filter and minimally with operating pressure. The maximum penetration decreased with decreasing pressure and flowrate.

Using a combination of classical single fiber theory and an inhomogeneity model along with experimental filter penetrations, a set of effective filter parameters were determined. Accurate prediction of low-pressure filter performance was seen to critically depend on the effective distribution of filter packing densities. Using a pressure-dependent effective packing density distribution, accurate prediction of filter behavior over the entire pressure range studied was possible if particles Stokes numbers are smaller than 0.1. The current study exposes the need for theoretical advances in modeling particle behavior around fibers at Stokes numbers larger than 0.1 and for considering the effect of inhomogeneity as a function of pressure.

Funding

This work was supported with funding from Pall Corp. and Center for Advanced Materials Processing (CAMP) at Clarkson University.