Brownian diffusion of fibers

ABSTRACT

Motion of nanoparticles suspended in fluids are dominated by Brownian diffusion—a physical property well understood following the work by Einstein in 1905. While theoretical derivation and experimental measurement of the diffusion coefficients for spherical particles are well developed, such information is lacking for non-spherical particles as the coupled rotational and translational motion hinders a clear description of the overall diffusive outcome. In this study, the Brownian diffusion of elongated nano-fibers is investigated numerically. Motion of the nano-fiber is resolved by solving the system of equations governing its coupled translational and rotational motion. To isolate the Brownian diffusion from other diffusive forces, test fibers are immersed in an unbounded quiescent fluid where only the hydrodynamic drag and Brownian forces are present. The study allows a close look at the Brownian diffusion of nano-fibers with respect to the translation, rotation, coupling, and how the rotation affects the particle's macroscopic diffusion properties. In this study, the Brownian diffusion of ellipsoidal particles are studied. The translational and the rotational Brownian motions and their coupling are included in the analysis. Particular attention was given to the rotational relaxation time in determining the non-spherical particle's isotropic and anisotropic diffusive properties. Theoretical and semi-empirical equations are developed to quantify the diffusion coefficients of nano-fibers. The predications are compared with available experimental data. The comparison to the analytic solution in the limiting case of a sphere is with excellent accuracy. The study opens up new approaches for studying fundamental diffusive processes of non-spherical elongated particles that are abundant in natural environment.

Copyright © 2016 American Association for Aerosol Research

EDITOR:

• Peter H. McMurry

Introduction

Brownian motion of small particles suspended in a fluid was first scientifically reported by Robert Brown in 1828 (Brown 1928). Not until 1905, following the pioneering work of Einstein (1905), the Brownian diffusion theory was developed and the Brownian displacement was quantified. The applications of Brownian motion in nature are abundant in life science, environmental science, and engineering applications where random fluctuation and drifting of extremely small particles are of concern. While the theories of diffusion for spherical particles are well developed, the diffusion process of non-spherical particles is not fully understood. In fact, very few papers in the literatures could be found on diffusion of non-spherical particles. Brenner (1967) theoretically derived the coupling between the translational and rotational Brownian motions of rigid particles of arbitrary shape. Based on this study, it was found out that, due to the sensitivity to particle orientation, the non-spherical particles exhibit anisotropic macroscopic transport properties. Gallily and Cohen (1976) studied the dynamic interaction between the translation and Brownian rotation of non-spherical particles, and a close coupling between the translational and rotational motions was illustrated for particles of long aspect ratios. Gentry et al. (1991) measured the diffusion coefficients of chrysotile fibers by relating the fractional penetration and size distribution of the test fibers before and after a diffusion battery. Asgharian et al. (1988) calculated the translational diffusion coefficients and the equivalent diffusion diameter of fibers by using an ellipsoidal particle model. Chen and Yu (1992) used a Monte Carlo method to determine the fiber orientation and translational mobility in a shear flow. More recently, Gopalakrishnan et al. (2015a) investigated the mobility of modest-to-high aspect ratio particles in transitional and free molecular regimes by direct measurement and theories using the “adjusted sphere approach.” Due to the complexity of the coupled translational and rotational motions, the role of Brownian rotation on the non-spherical particle transport is still poorly understood.

Except for Gentry et al. (1991) and Gopalakrishnan et al. (2015a), very few experimental measurements were performed on non-spherical particles in the diffusion regime. Most of the reported experiments were in the continuum regime where particles are in micrometer or larger scales. Focus of these experiments was on measuring the terminal velocities of the irregularly shaped particles in a quiescent fluid to derive a corrected drag coefficient (dynamic shape factor) corresponding to an equivalent aerodynamic sphere. Examples of such study include Lasso and Weidmann (1986), Haider and Levenspiel (1989), Chhabra et al. (1995), Cichocki and Hinsen (1995), and Tran-Cong et al. (2004). Nature of these experiments excludes the direct observation of the effect of rotation; therefore, only the translational motion is correlated. Rarely the orientation of the non-spherical particle is factored in, so the derived empirical models are largely isotropic. Measurements of non-spherical submicron asbestos deposition in rats and human lungs have been reported in the work of Stanton et al. (1977, 1981), Lippmann et al. (1988, 1990), and Berman et al. (1995); however, in these studies the contribution from Brownian diffusion alone is not quantified. Similar theoretical and computational studies have been reported by Fan and Ahmadi (2000), Tian and Ahmadi (2012, 2013, 2016), and Harris and Fraser (1976), where the dispersion of ellipsoidal fibers in a turbulent flow field, a low Reynolds number flow, and the deposition of ellipsoidal and cylindrical fibers in the human respiratory system were studied, respectively.

To fill the knowledge gap, current study numerically investigated the Brownian diffusion of non-spherical particles, specifically the elongated fibers, in an unbounded quiescent fluid. The fibers' random motion was reproduced by a fiber transport model accounting for both the translational and rotational motions. Coupling between the translation and rotation was resolved through the interactions between the fiber's translational and rotational dyadic tensors. Brownian diffusion was isolated by eliminating other diffusive processes such as flow convection, turbulence diffusion, and electromagnetic diffusion. The fiber transport model was implemented with in-house C++ code, and the Brownian dynamics (BD) computer simulation technique, developed by Ounis and Ahmadi (1990), was used in this study. The Brownian diffusion of nano and micron fibers with respect to the translation, rotation, and their coupling was analyzed. Particular attention was given to the effect of rotational Brownian motion on the particle macroscopic diffusion properties. The rotational relaxation time, in determining the non-spherical particle isotropic and anisotropic diffusive properties, is described. The fiber Brownian diffusion coefficients were quantified with respect to the fiber geometry and fluid property. In addition, theoretical and semi-empirical equations for mobility assessment of nano-fiber were developed. The predications were compared with the experimental data. The comparison to the analytic solution in the limiting case of spheres and the comparison to the measured mobility diameters of nanorods show great accuracy. The study provides an opportunity for exploring the diffusive processes of non-spherical particles in different applications.

Fiber equation of motion

The nano-fiber is modeled as a slender elongated ellipsoid characterized by its diameter d, the semi-minor axis a (a = d/2), the length l, and the aspect ratio beta β (the ratio of the length to its diameter). Kinematics of the fiber is described in a fixed global coordinate (x, y, z), a co-moving coordinate () attached to the centroid of the fiber and parallel to the global frame, and an attached fiber coordinate () with the three axes aligned with the fiber's principle axes. Details of the fiber kinematics could be found in the work of Tian and Ahmadi (2013). Accordingly, for the ellipsoid of revolution immersed in a quiescent fluid, the translational motion is governed by[1] and the rotational motion is governed by the following equations in the fiber coordinate:[2] [3] [4]

In the above equations, V is the fiber centroidal translational velocity, and () is the angular velocity. Here m^p is the mass of the fiber, g is the gravitational acceleration, f ^h is the hydrodynamic drag, and f ^B is the Brownian diffusion force. In Equations (2)–(4), () is the moment of inertia about the principle axes in the fiber frame, and () and () are, respectively, the hydrodynamic and the Brownian torques acting on the fiber. Based on the work of Brenner (1964), the hydrodynamic drag f ^h acting on an ellipsoid is given by[5]

Here μ is the fluid viscosity, U is the fluid velocity at the fiber centroid, and is the translational dyadic in the co-moving frame given by[6]

Here A is the transformation matrix between the fiber and the co-moving coordinates (Tian and Ahmadi 2013). The translational dyadic in the fiber frame is a diagonal matrix. For an ellipsoid of revolution along the - axis, the diagonal elements are given as (Jeffery 1922; Oseen 1927)[7] [8]

Here 's are the translational slip-correction factors (Fan and Ahmadi 2000).

The Brownian diffusion force f ^B in Equation (1)[1] can be evaluated as[9]

Here = [] is the Brownian force expressed in the fiber coordinate. The component of Brownian forces can be modeled as independent zero-mean Gaussian white-noise processes in the following form:[10]

Here τ is the time lag, δ() is the Dirac Delta Function, a pair of angular brackets < > stands for the ensemble average, and correlations are obtained by averaging the time-shifted dyadic products . In the above equations, S^t is the spectral intensity tensors for the translational Brownian motion, which is a diagonal matrix in the fiber frame, and is given as[11] where κ is the Boltzmann constant, and is the absolute temperature. is the resistant coefficient for an ellipsoidal translating along its principle axes in a quiescent fluid, that is,[12]

The hydrodynamic torque acted on an ellipsoidal fiber suspended in a linear shear flow is given by Jeffery (1922). Accordingly, for an ellipsoid of revolution with its major axis along the - axis, the hydrodynamic torques are given as[13] [14] [15]

Here and are, respectively, the strain and spin tensors (Tian and Ahmadi 2013). Equations (13)–(15) assume that the flow near a small particle may locally be approximated as a linear shear flow. 's in Equations (13)–(15) are the rotational slip-correction factors (Fan and Ahmadi 2000). The dimensionless parameters in Equations (13)–(15) are given by Gallily and Cohen (1979):[16] [17]

The Brownian torque in the fiber frame can be modeled as independent zero-mean Gaussian white-noise processes with the following statistics:[18] where t' is the time lag, is the dyadic products, and S^r is the spectral intensity tensors for the rotational Brownian motion, which is a diagonal matrix in the fiber frame, given as[19]

In the above expression, is the resistance coefficients for an ellipsoid rotating about its principle axis in a quiescent fluid, that is,[20] where[21]

Fokker-Planck equation

An alternative approach to describe the Brownian motion of a small particle is to use the Fokker-Planck equation associated with the Langevin equations, where the time evolution of the probability density (PDF) of a Brownian particle is described. Given Itô's equation (Itô 1944),[22]

The joint probability density function f(X, t) is given by the Fokker-Planck equation as[23]

The Langevin equations governing the translational and rotational motions of ellipsoidal fibers are given by Equations (1)–(4), where X_i represents the translational and rotational velocity vectors, ξ_i represents the Brownian force and torque, and h_i and G_ij refer to the drifting and diffusion terms. Equation (23)[23] then governs the corresponding probability density function with D_ij = πS_ij/2, where S_ij is the spectral intensity tensors for the Brownian translational and rotational motions given by Equations (10) and (18).

For stationary condition, due to the linearity of the Langevin equation given by (1)[1] , Equation (23)[23] leads to the probability distribution of the fiber translational velocity as[24]

Here is the standard deviation or the root-mean square velocity. Similarly, using , it follows that[25]

Here σ(t) is the time-dependent standard deviation or the root-mean square displacement of x_i.

For the fiber's rotational motion, a similar Gaussian probability distribution could be obtained if the cross-drifting terms involving vanishes in the Fokker-Planck equation. Expanding Equation (23)[23] for the fiber's rotational motion gives[26]

Here[27]

For stationary process, then,[28] and[29]

The solution for Equations (28) and (29) is Gaussian, if[30]

For ellipsoidal fiber, Equation (30)[30] is satisfied as = , = , and vanishes. Therefore, the probability distributions for the fiber angular velocity are independent normal random processes, given as[31]

Similarly, using , it follows that[32]

Here is the time-dependent standard deviation or the root-mean square of . Given the probability distributions of Equations (25) and (32), the translational and rotational diffusion coefficients for the Brownian particle can be derived from[33]

Computational domain

An unbounded space containing quiescent air is considered in this study. Motion and trajectories of test fibers immersed in the quiescent air are analyzed. Due to the absence of convection and flow shear, test fibers undergo diffusion governed by the pure balance between the Brownian forces and the hydrodynamic drag. Test fibers are free to travel in all directions and rotate. As the test domain is unbounded, a lab coordinate system is conveniently chosen such that, at initial time t = 0 s, the fiber's principle axis is aligned with the y-axis.

Results and discussion

The air properties used in the simulation are temperature T = 293 K, dynamic viscosity μ = 1.84 × 10⁻⁵ Ns/m², and air density ρ = 1.23 kg/m³. Carbon fibers with density of 2560.5 kg/m³, diameters of 1 to 1000 nm, and aspect ratios of 3 to 1000 are considered. Test fibers are originally located at (0.2, 0.2, 0.0) m in the lab coordinate. Test fibers are dispersed under the effect of Brownian excitation with time. Parameters measuring the coupled translation and rotation are recorded and analyzed.

Fiber motion

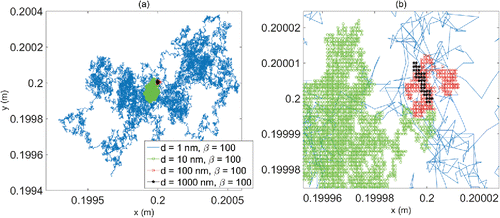
Figure 1 displays the dispersion of four fibers, originally located at (0.2, 0.2, 0.0) m and aligned with the y-axis, after 5 s. The diffusion paths in the projection of the x–y plane are shown. The fiber diameters are 1, 10, 100, and 1000 nm (blue, green, red, and yellow in Figure 1), and the fiber aspect ratios are 100 for all cases studied; therefore, the fibers in Figure 1 are needle-like slender bodies varied by diameter sizes. The overall diffusion pattern is given in Figure 1a, while the magnified local diffusion region, highlighting the low dispersion fibers, is shown in Figure 1b. Figure 1 clearly shows the random nature of the Brownian diffusion for fibers of all sizes. It also clearly shows that the level of Brownian fluctuation strongly depends on the inverse of fiber diameter. The displacement of the 1 nm fiber covers the largest span of 1 mm while the 1000 nm fiber travels the minimum distance of about 0.005 mm. Anisotropy of the fiber dispersion is revealed by examining the variation of the dispersion in different directions. The maximum degree of anisotropy is observed with the 1000 nm fiber measured by a 68% difference in the axial and radial dispersion distances (0.11 and 3.5 µm). Also, 1 and 10 nm fibers exhibit the lowest degree of anisotropy measured by a maximum of 30% difference in the dispersion distances in all directions (0.901 and 1.3 mm for 1 nm fiber, 0.1 and 0.129 mm for 10 nm fiber).

Figure 1. Dispersion of nano-fibers originally located at (0.2, 0.2, 0.0) m after 5 s.

Figure S1 in the online supplemental information (SI) shows the same simulation results as in Figure 1, however, with a magnified view to illustrate the details of fiber three-dimensional (3D) motions as they diffuse. That is, while Figure 1 described the macroscopic translational property of the nano-fibers, Figure S1 (in the online SI) provides a window to observe the fiber orientations along its flight path that is shown by the red line. It should be noted that the diffusion data shown in Figure S1 (in the online SI) are sampled such that a representative view could be displayed while the key features of the fiber diffusion characteristics are kept. It should also be noted that the fiber geometries in this figure are scaled for proper visualization. Similar to what was observed in Figure 1, Figure S1 (in the online SI) shows that the level of the Brownian rotational fluctuation varies strongly with the inverse of fiber diameter. Along the diffusion paths, frequent rotation occurred for the 1 and 10 nm fibers, and the fibers are randomly oriented along the paths in all directions (Figures S1a and b in the online SI). On the other hand, the 1000 nm fiber maintained its alignment with the y-axis throughout the dispersion time considered. The random rotational oscillation for the 1000 nm fiber is too weak to be seen (Figure S1d in the online SI). In between the two extremes, Brownian rotation is observed for the 100 nm fiber though with lower level when compared to those of 1 and 10 nm fibers (Figure S1c in the online SI). The rotation of the 100 nm fiber appears to be less random and a clear preferred alignment with the initial orientation could be seen. In connection to Figure 1, a clear link exists between the fiber macroscopic translational property and its microscopic rotational characteristics. For the 1000 nm fiber, the high anisotropy in the radial and axial displacements, with 68% differences observed in Figure 1b, could be explained with trend seen in Figure S1d (in the online SI), where a consistent alignment of the fiber in the y-axis (axial direction) implies a maximum hydrodynamic resistance variation in the axial and radial directions. Similarly, the low anisotropy of the translational dispersion of the 1 and 10 nm fibers in Figure 1a could be explained with the trends seen in Figures S1a and b (in the online SI) that the rather random orientation of the fiber along its flight path implies a more uniform hydrodynamic resistance in all directions. Figures 1 and S1 (in the online SI) clearly show a strong coupling between the nano-fiber translational and rotational motions along their diffusion paths, which has subsequent implications to the fiber macroscopic transport properties.

Fiber diffusion

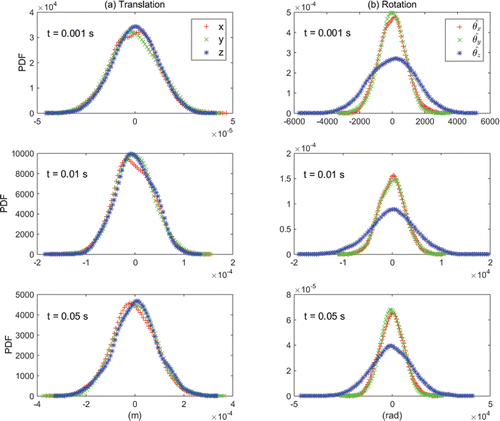
The temporal evolution of the probability density (PDF) of a small Brownian particle in the neighborhood of its initial position/orientation is given by the Fokker-Planck equation (Equation (23)[23] ). For non-spherical particles, no analytical solution is available due to the variation of the particle orientation and the coupling of its diffusion coefficients in the 3D space. However, the time evolving PDFs of the nano-fibers could be recovered with the current modeling approach, as the coupling between the fiber translational and rotational motions is resolved numerically. Figure S2 (in the online SI) shows the sample PDFs of fiber Brownian displacements in the 3D space at times 0.001, 0.01, and 0.05 s, for fibers of 1 nm diameter and 100 aspect ratio, resembling that of Figure S1a (in the online SI). In Figure S2 (in the online SI), the recovered PDFs are plotted with the “+, x, *” signs, and the different colors represent the evolution of the PDFs in the time domain. Along with the simulation data, Gaussian fit based on the simulation are plotted as well. A close match between the simulated PDFs and the Gaussian fit indicates that the Brownian motion of the fiber follows the Fokker-Planck prediction, and at each instance in the temporal space, the PDFs are described by Equations (25) and (32). It is shown from Figure S2 (in the online SI) that, for both the translational and rotational Brownian displacements, nano-fiber spreads over time. The translation covers a wider space while the rotation implies more spinning around over the time.

Figure 2 shows the same simulated PDFs as in Figure S2 (in the online SI), however, with the emphasis on assessing the orientational dependency of the fiber's Brownian motion in the observation domain. For 1 nm diameter fibers with an aspect ratio of 100, Figure 2a shows clear, consistent isotropic translational displacements with minor statistical variations. Though the corresponding Brownian rotation varies for different orientations, the rotation about the principle axis is notably faster than others (Figure 2b); however, this does not seem to affect the overall translational outcome. The rotational displacements shown in Figure 2b reveal that the fibers have completed roughly 300 to 3000 full rotations in all orientations in the observation domain.

Figure 2. PDFs of fiber translational and rotational Brownian displacements at times 0.001, 0.01, and 0.05 s in three-dimensional space (fiber diameter = 1 nm, β = 100).

To evaluate the orientational dependency of larger-sized fibers, sample PDFs of the Brownian displacements for fibers of 1000 nm diameter and 100 aspect ratio are shown in Figure S3 (in the online SI). It should be noted that, in real physical situations, fibers of this dimension is greatly affected by the gravitational sedimentation; however, gravity is neglected here so that the study can focus on the pure Brownian diffusion. Contrary to the 1 nm fiber, 1000 nm fiber shows distinct anisotropic translational motion. The translational dispersion in direction of the fiber's principal axis, denoted by the green “x” sign in Figure S3a (in the online SI), spreads much faster than that in the transverse directions (as indicated by a larger variance). The rotational dispersion (Figure S3b in the online SI) in the fiber frame also shows significant anisotropy in the principal and lateral directions. So, what causes this macroscopic anisotropy in translation? A closer look at the rotational displacements in Figure S3b (in the online SI) reveals a very small magnitude of rotation, less than one-tenth of the principle and one-thousandth in the transverse direction, of a full rotation. This implies that the 1000 nm elongated fiber maintain its initial orientation, with the principal axis in alignment with the y-axis, during the entire course of the observation time domain. This confirms that the faster spread of the fiber along its principal axial direction (y-axis in Figure S3a in the online SI) is due to the geometric anisotropy.

Figures 2 and S3 (in the online SI) show a clear link between the fiber macroscopic translational property and the corresponding rotational frequency. It appears that a high rotational frequency implies translational isotropy, while a low rotational frequency means anisotropy. If we define the particle rotational relaxation time τ_r to be the time it takes for the particle to complete one full rotation, then τ_r is given as 2π²/D_r. For fibers of 100 aspect ratio, the rotational relaxation time τ_r is in the order of 10⁻⁸ s for a 1 nm diameter fiber; whereas, for a 1000 nm diameter fiber, τ_r is in the order of 10¹ s. With the finding of this relationship, it is safe to state that the translational isotropy/anisotropy of a fiber is a relative term in context of the time scale in the observation domain. For prior simulations with an observation time scale of 10⁴ s⁻¹, significantly lower than the rotation frequency of the 1 nm fiber, a translational isotropy is observed. It is estimated that, by reducing the observation time scale of the simulation to a value much lower than the rotation frequency of the 1000 nm fiber, translational isotropy should be exhibited. This is verified with Figure S4 (in the online SI), where an isotropic translational motion is observed for the 1000 nm fiber with an observation time scale of 10⁻⁴ s⁻¹. Similarly, fibers will always exhibit isotropic translational Brownian motion after a sufficient long time. The observed small anisotropy in Figure S4a (in the online SI) might be related to the statistical fluctuations in the initial development of the Brownian process.

Fiber diffusion coefficients

A series of simulations is performed on carbon fibers with a density of 2560.0 kg/m³, diameters from 1 to 1000 nm, and aspect ratios from 3 to 1000, originally located at (0, 0, 0) m in the lab frame. The principal axis of the test fibers is initially aligned with the y-axis. For each geometric configuration, an ensemble of 1000 fibers is evaluated and the corresponding fiber diffusion coefficients are calculated and analyzed. In addition, theoretical and semi-empirical equations to characterize the fiber diffusion are derived.

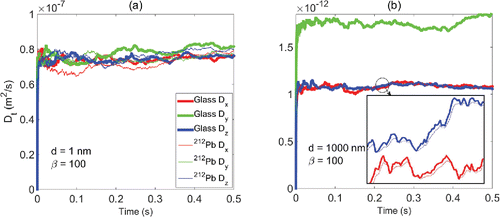
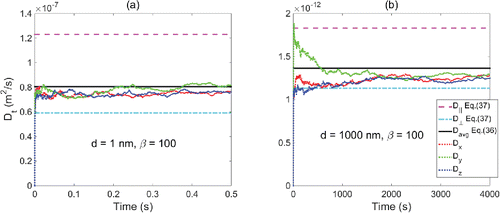
Figure 3 displays the simulated time evolving diffusion coefficients in the 3D space for fibers of aspect ratio 100, and diameters of 1 and 1000 nm. For comparison, the maximum diffusion coefficients in direction of the fiber's principal axis (D_||), the minimum diffusion coefficients in direction perpendicular to the fiber's principal axis (D_┴), and the orientation averaged diffusion coefficients (D_avg) are shown. Figure 3a shows that the 1 nm fiber instantaneously reaches the isotropic diffusion phase with a terminal diffusion coefficient close to the orientation averaged D_avg (given by Equation (36)[36] ). On the other hand, it takes about 2000 s for fibers of 1000 nm diameter, in the evaluated ensemble, to exhibit isotropic macroscopic diffusion behavior (Figure 3b). Prior to this time, the diffusion of elongated 1000 nm diameter fiber is anisotropic, clearly orientation dependent, and bounded by D_┴ and D_||. An estimate 100 rotations have occurred for the 1000 nm diameter fiber during the transition period. It should be noted that the final translational isotropy applies to the ensemble after the initial transition period or to the individual fiber with an observation time scale comparable to the reciprocal of this transition period. For the individual fiber at a much smaller time scale, the diffusion is still highly anisotropic.

Figure 3. Time evolving fiber diffusion coefficients: (a) diameter = 1 nm, β = 100; (b) diameter = 1000 nm, β = 100.

One benchmark to characterize the fiber's macroscopic diffusional isotropy is the rotational relaxation time τ_r, defined as the time it takes for the particle to complete one full rotation. The simulation suggested a minimum τ_r, in all orientations, which is relevant in the 3D domain. This might be attributed to the coupling of the rotation in all directions. Based on the analysis, the expression for the fiber rotational relaxation time τ_r is given as[34]

An estimated time scale for a fiber to exhibit an isotropic macroscopic translational diffusion is nτ_r, where n is a coefficient >>1. Based on the simulation result, n = 100 is a good estimate with satisfactory statistical consistency. It should be pointed out that this time scale also defines the time it takes for an ensemble of fibers, with the same initial orientation, to exhibit random orientations or isotropic macroscopic translational diffusion property. Therefore, it is convenient to define a time scale, τ_ri, as the relaxation to isotropy time for an ensemble of fibers. That is,[35]

The isotropic translational diffusion coefficient at this stationary phase is given as[36]

Here D_|| and D_┴ are given by[37]

Before the individual or the ensemble of the fibers reaches the isotropic diffusion phase, or the observation time scale is significantly lower than the fiber rotational relaxation time, an anisotropic diffusion characteristics bounded by D_|| and D_┴ will be displayed.

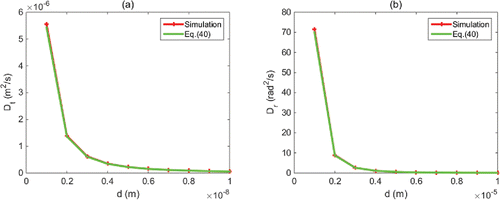
Figure 4 displays the predicted fiber rotational relaxation time τ_r and the translational diffusion coefficient D_t as given by Equations (34) and (36). Figure 4a shows that the fiber rotational relaxation time is directly related to its diameter and the aspect ratio. For the 1 nm diameter fiber, τ_r is in the range from 10⁻¹⁰ to 10⁻⁷ s, and for the 1000 nm diameter fiber, τ_r is from 10⁻¹ to 10² s. In general, when the fiber's aspect ratio grows from 3 to 1000, τ_r is increased by three orders of magnitude. It is safe to state that, under typical conditions, the diffusion of 1 nm fibers is isotropic for all lengths; however, for fibers of 10 nm diameter and above, it is important to consider the fiber length in determining its diffusion characteristics. Diffusion of the 1000 nm fiber most likely is anisotropic under typical conditions. The diffusion coefficient of the nano-fiber is inversely related to its diameter and the aspect ratios (Figure 4b). Figure 4 shows that, for both τ_r and D_t, the rate of change with respect to the aspect ratio is rapid for shorter fibers (β < 100). As the aspect ratio grows (β > 100), a slight but steady trend of variation continues.

Figure 4. Prediction of (a) fiber rotational relaxation time τ_r (Equation (34)[34] ); (b) fiber macroscopic translational diffusion coefficient D_t (Equation (36)[36] ).

Fiber diffusion—equivalent spheres

Based on Equations (36) and (37), an equivalent diameter sphere, describing the isotropic diffusion characteristics of the nano-fiber, is defined as[38]

Here C_c is the Cunningham correction for the equivalent diameter sphere. Without prior knowledge of d_eq, C_c is taken as the average of or the Cunningham correction for the equivalent volume diameter sphere. A simplified formula, without the need of prior knowledge of C_c, and , is given as[39]

in Equation (39)[39] is given by Equations (7) and (8), however, without accounting for the slip-correction . Equation (39)[39] is shown to be very accurate. For the extreme case of an elongated nano-fiber of 1 nm diameter and 10,000 aspect ratio, the difference between Equations (38) and (39) is below 5.0% if C_c is chosen to be the average of .

A comparison of the predicted d_eq to the measured mobility diameter of nanorods (Gopalakrishnan et al. 2015b) is given in Table 1. Agreeable results are observed. It is shown that Equations (38) and (39) have higher accuracy for long aspect ratio nanorods than shorter ones. It is also noted that though Equation (38)[38] with C_c (equivalent volume) produces the highest accuracy for long aspect ratio nanorods, the theoretical ground needs to be further evaluated. Equation (39)[39] is shown to be convenient and reliable to calculate d_eq for isotropic Brownian diffusion of fibers.

Table 1. Equivalent diffusion diameter of nanorods—comparison with the experiment.

			deq(nm)
d (nm)	Length (nm)	β	Experiment	Equation (38)[38] , Cc^1	Equation (38)[38] , Cc^2	Equation (39)[39]
17.3	257.0	14.9	68.1	72.5	69.5	75.8
20.9	232.0	11.3	70.9	72.4	70.1	75.5
11.2	47.4	4.3	30.9	21.2	20.8	21.9
43.3	94.9	2.2	64.6	58.8	58.1	59.5

C_c¹: average of ; C_c²: Cunningham correction for the equivalent volume diameter sphere.

Effect of density

The effect of material density on fiber Brownian mobility is investigated by an additional set of simulations on heavy ²¹²Pb fibers of density 11,340 kg/m³. Figure 5 displays the comparison of the time-evolving diffusion coefficients (D_t) for the carbon and ²¹²Pb fibers. Two fiber configurations of 1 and 1000 nm diameter, and 100 aspect ratio are considered. D_t's of the carbon and ²¹²Pb fibers do not show noticeable difference. For the 1 nm diameter fiber, all D_t's fluctuate about the averaged value of Equation (36)[36] (Figure 5a). For the 1000 nm diameter fiber, D_t's of the ²¹²Pb is consistently lower than that of the carbon fiber, though with a magnitude almost unnoticeable (Figure 5b). This subtle difference implies that for the extremely thin fibers, such as the 1 nm diameter, inertia of density is insignificant compared to the Brownian forces. As the Brownian forces decreases, effect of the density might be more consistently reflected (Figure 5b), though still insignificant to that of the Brownian force. In summary, the effect of particle density on Brownian diffusion can be neglected.

Figure 5. Density effect on fiber diffusion coefficients: (a) diameter = 1 nm, β = 100; (b) diameter = 1000 nm, β = 100.

Comparison to experimental data

Experimental data of fiber diffusion coefficient is scarce. The only systematic measurement of the fiber diffusion coefficient was performed by Gentry et al. (1991), where the diffusion coefficients of chrysotile fibers were investigated by measuring the fractional penetration and size distribution of the test fibers before and after a diffusion battery consisting of a tubular bundle of straight cylindrical tubes. The measured diffusion coefficients were then related to the fiber diameter and length (aspect ratio). Figure S5 (in the online SI) compares the predicted fiber diffusion coefficients by simulation and the experiment. For fiber diameters of 30, 50, 77, 97, and 120 nm, the fiber diffusion coefficients are plotted against the aspect ratios. As the preparation of the test fibers in the experiment involved multistage and lasted more than hours, a randomized fiber orientation is assumed; therefore, an averaged D_t by Equation (36)[36] is used. It is shown in Figure S5 (in the online SI) that the simulated fiber diffusion coefficients are in the same order of magnitude of the experiment data, though a consistent lower value is estimated. A second observation is that while the simulated diffusion coefficients are inversely related to the aspect ratios for fibers of all diameters, the experimental data are scattered, especially for fibers of diameters 77 and 120 nm (Figures S5c and e in the online SI). For fibers of diameters 30, 50, and 97 nm, the variations of the measured diffusion coefficients with respect to the aspect ratios are similar to the simulation prediction that they are inversely related (except for Exp. # 2) (Figures S5a, b, and d in the online SI).

Figure 6 compares the variation of the fiber diffusion coefficients versus the fiber diameter between the simulation and the experimental measurements. Here, in Figure 6, the averaged diffusion coefficients over the four runs of the experiments are displayed. A consistent trend is observed with the simulation data in Figure 6a that as the fiber diameter increases, the fiber diffusion coefficients decreases. The same trend is observed in the experimental data for fibers with thin diameters from 30 to 77 nm (Figure 6b). As the fiber diameter increases from 77 to 120 nm, the fiber diffusion coefficients increase with the fiber diameter. Another observation from the experimental data is that, for thicker fibers of diameter larger than 77 nm or for all fibers at very large aspect ratio, the measured diffusion coefficients increases with the aspect ratios.

Figure 6. Comparison of predicted fiber diffusion coefficients with experiments: (a) simulation; (b) experiment (averaged over four experiments).

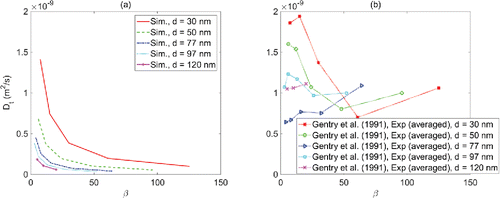
Analyzing the experimental data of Gentry et al. (1991), a couple of controversies are noted: (1) the measured fiber diffusion coefficients are flow-rate dependent in that higher flow rate indicated higher diffusion coefficients. The four runs of the experiments were performed at flow rates of 0.3, 0.14, 0.48, and 0.48 L/min, respectively. This contradicts with the physical description of the fiber diffusion coefficient that it is a property that depends only on the flow viscosity and the size of the particle (except for the universal constants and the absolute temperature) (Einstein 1905); (2) since the Brownian diffusion is a statistical manifestation of the free molecular collision, therefore, it should be inversely related to the size of the diameter and the aspect ratio. As noted in Figure 6b, both inverse relationships are violated for fibers thicker than 77 nm and for all fibers with very large aspect ratios.

The experimental discrepancies might arise from the presence of diffusive forces other than the Brownian diffusion. One possibility is that the high shear (estimated 50 to 150 s⁻¹) in the long channels of the diffusion battery might have coupled with the convective forces, generating minor turbulence, and contributing to the dispersion of the nano-fibers. This could explain why in experiment #2 (Figure S5 in the online SI) and in certain sections of the experiment (Figure 6b), fiber diffusion coefficients increase with the fiber inertia. It was also mentioned in the work of Gentry et al. (1991) that large experimental scattering and the challenge of enforcing a consistent fiber shape were encountered in the measurements under similar test conditions.

In the limiting case of a sphere

In the limiting case, the current fiber model converges to that of a spherical particle. For spherical particles, the diffusion coefficients are given by the Stokes-Einstein formula. Accounting for the free molecular slip correction, the modified translational and rotational diffusion coefficients are given as[40]

In Equation (40)[40] , d_s is the diameter of the sphere, C_c is the Cunningham correction, and C_r is the slip correction for the rotation (Cunningham 1910; Tian and Ahmadi 2007). Figure 7 compares the simulated translational and rotational diffusion coefficients with the theoretical prediction by Equation (40)[40] , and excellent agreement is observed.

Figure 7. Fiber diffusion coefficients in the limiting case of a sphere: (a) translational diffusion coefficient; (b) rotation diffusion coefficient.

Conclusions

In this study, the Brownian motion of nano and micron fibers in a quiescent fluid was investigated. The coupled translational–rotational Brownian diffusion of ellipsoidal fibers were analyzed and the associated diffusive characteristics were discussed. The effect of the rotational relaxation time in determining the non-spherical particle isotropic and anisotropic diffusive properties is described. Analytical and semi-empirical equations for the fiber rotational relaxation time and translational diffusion coefficients were developed. Based on the presented results, the following conclusions are drawn:

• The Brownian diffusion of nano and micron fiber is a function of the absolute temperature, fluid viscosity, particle size and shape, and the coupling between its translational and rotational motions. The Brownian diffusion is not affected by particle density.

• Whether the diffusion of a fiber is isotropic or anisotropic depends on the observation time scale and the fiber rotational relaxation time τ_r. For 1 nm diameter fiber with extremely small τ_r, anisotropy of the diffusion tensor is negligibly small. For 1000 nm diameter fiber with large τ_r, the diffusion is most likely anisotropic and orientation of the fiber is needed to study its diffusion. For other size fibers, the ratio of the observation time scale and the fiber rotational relaxation time need to be evaluated.

• Theoretical and semi-empirical equations are developed to quantify the fiber rotational relaxation time τ_r, the diffusion coefficient D_t, and the relaxation to isotropy time, τ_ri, for an ensemble of fibers. While the rotational relaxation time τ_r is directly related to the fiber diameter and aspect ratio, the diffusion coefficient D_t is inversely related to both parameters. For both τ_r and D_t, the rate of change with respect to the aspect ratio is rapid for shorter fibers (β < 100), and slow for longer ones (β > 100).

• Current study quantified the pure Brownian diffusion of nano and micron fibers in a quiescent fluid. It is anticipated that in presence of other diffusive mechanisms and/or shear forces (such as convection, turbulence diffusion, and external fields), and in case of a complex geometry, an accurate prediction of the fiber diffusion outcome requires a comprehensive analysis of the coupling by all the contributing dynamics. Should any of the coupling enforces or disrupts a preferential alignment of the fiber, or alter the fiber rotational relaxation time, the fiber diffusion need to be modified. These points are left for a future study.

Funding

The financial supports provided by the National Basic Research Program (973) of China (Grant No. 2012CB720100), the Natural Science Foundation of China (Grant No. 21277080), and an earlier financial support from NIOSH are gratefully acknowledged.