Real-time effective density monitor (DENSMO) for aerosol nanoparticle production

ABSTRACT

A new instrument, density monitor (DENSMO), for aerosol particle size distribution characterization and monitoring has been developed. DENSMO is operationally simple and capable of measuring the effective density as well as the aerodynamic and the mobility median diameters with a time resolution of 1 s, from unimodal particle size distributions. The characterization is performed with a zeroth order mobility analyzer in series with a low pressure impactor and a filter stage. The operation of DENSMO was investigated with sensitivity analysis and, based on the results, optimal operation parameters were determined. DENSMO was also compared, in lab test measurements, against a reference method with several particle materials with bulk densities from 0.92 to 10.5 g/cm³. The results show that the deviation from the reference method was less than 25% for suitable materials.

Copyright © 2016 American Association for Aerosol Research

EDITOR:

• Peter H. McMurry

1. Introduction

The use of aerosol nanoparticles in functional materials and commercially available products has increased as production routes, especially those employing the gas phase, have become more viable and more improved properties have been discovered (Aitken et al. 2006). The production of nanoparticles requires some form of quality control as well as analysis methods. This ensures the produced materials are up to standard. Control and analysis can be achieved with both offline and online methods. From these two, the online methods give access to immediate information on desired aspects of the process. When aerosol routes are being utilized, one suitable property to be monitored is the effective density. In situations where the value of the effective density changes, the monitored aerosol particles have undergone morphological or chemical changes. For example, the change in the effective density has been recently used to determine the coating thickness of core–shell particles (Weis et al. 2015). These kinds of shifts in the produced material do not necessarily exhibit changes in the mass or diameter of the individual particles. For a more in-depth theoretical overview on the subject of the effective density, see DeCarlo et al. (2004). Typically, in order to determine the effective density, a set of two properties from the aerosol is required, such as the mobility and the aerodynamic median diameters.

One of the first approaches to measure the effective density was presented by Kelly and McMurry (1992), which consisted of impacting mobility selected particles. This paved the way for using multiple instruments in series in order to measure the effective density. The introduction of instruments capable of measuring mobility diameter, aerodynamic diameter, surface area, and mass have further advanced the measurement routes for the effective density. Good examples of these kinds of instruments are a Scanning Mobility Particle Sizer (SMPS; Wang and Flagan 1990), an Electrical Low Pressure Impactor (ELPI; Keskinen et al. 1992), a Nanoparticle Surface Area Monitor (NSAM; TSI Inc., Shoreview, MN, USA), an Aerosol Particle Mass Analyzer (APM; Ehara et al. 1996), and a Single Particle Laser Ablation Time-of-Flight Mass Spectrometer (SPLAT I; Zelenyuk and Imre 2005). The measurement accuracy and performance of these instruments have been improved since their introduction, for example, by an ELPI+ (Järvinen et al. 2014), a SPLAT II (Zelenyuk et al. 2009), and a Couette Centrifugal Particle Mass Analyzer (CPMA; Olfert and Collings 2005). Various combinations of these devices and methods implementing them have been introduced. The background for this work originates from the SMPS+ELPI method presented by Ristimäki et al. (2002). There are various other methods, some of which are basing their operation on measuring the mobility size and mass, for example, Tandem Differential Mobility Analyzer (TDMA)+APM (McMurry et al. 2002), on the mobility size and surface area, for example, Condensation Particle Counter (CPC)+DMA+NSAM (Universal NanoParticle Analyzer; UNPA) (Wang et al. 2010), on the mobility selection with a supersonic impaction (e.g., Hering and Stolzenburg 1995), and on a mobility selection followed by an aerodynamic characterization, for example, DMA+SPLAT (Zelenyuk et al. 2005).

These complex and often expensive methods (as you need several standalone instruments) are not ideal for use in production facilities where it would be preferable to have monitoring on each individual production line. Some simplified versions of the previously mentioned methods have been introduced. For example, the SMPS+ELPI method has been a starting point for several simplifications, such as a modified ELPI, where several impactor stages were replaced with a mobility analyzer (Rostedt et al. 2009) and a commercially available Dekati Mass Monitor (DMM, Dekati Ltd., Kangasala, Finland), which focuses on the mass measurement rather than the effective density. The DMM employs a similar construction as the modified ELPI, with the difference of having one impactor stage fewer and no filter stage. The main difference arises in the information given by these instruments: the DMM provides the user with a mass and a number concentration, whereas the modified ELPI provides a mobility median and an aerodynamic current size distribution from the measured aerosol.

Here we present DENSMO (DENSity MOnitor). It was developed to be even simpler in construction and operational principle than the earlier SMPS+ELPI method variations and thus to be cheaper to manufacture and more suitable for widespread use. The aim was to reduce the amount of functional parts without losing much of the information acquirable and without compromising the reliability of the information. After introducing the operational principle and the construction of DENSMO, detailed calibration and sensitivity analysis results are presented. Fully characterized and calibrated DENSMO is then compared against the SMPS+ELPI method. Lastly, an example case of a real-time measurement of silver nanoparticle sintering is presented.

2. Principle of operation

In order to quantify the effective density (), indirect measurements are needed. One route becomes apparent from the definition of the effective density, which relates aerodynamic (d_a) and mobility (d_b) diameters with the following equation:[1] where ρ₀ is the unit density (1 g/cm³) and C_c is the Cunningham slip correction factor of the denoted characteristic diameter (Kelly and McMurry 1992; Ristimäki et al. 2002). The mobility and aerodynamic diameters can be determined by utilizing a zeroth order mobility analyzer, a low pressure impactor, and a filter stage. Utilization of these methods requires the aerosol to be unipolarly charged prior to the characterization and measurement of the three obtainable currents I₁₋₃, which is achieved here by utilizing a corona charger. 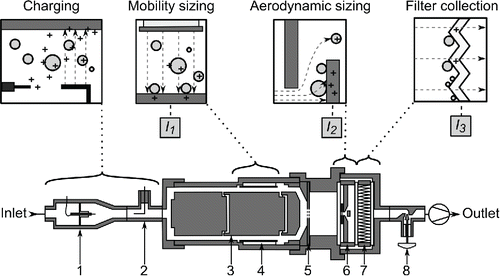The operation of the charger is quantified with its charging efficiency[2] where I(d_b) is the produced current distribution, e is the elementary charge, Q is the volumetric flow of the aerosol, and N(d_b) is the number size distribution. This process is presented in a schematic view of DENSMO, which is shown in Figure 1.

Figure 1. The upper part of the figure shows schematically how DENSMO operates from charging to mobility sizing and aerodynamic sizing and finally residual collection by the filter stage. Each of the measured currents has been depicted with the associated part of the process. The lower part of the figure illustrates a cross-section of DENSMO with eight labeled operational sections: 1. Mini corona charger, 2. ion trap, 3. mobility analyzer collection cylinder, 4. mobility analyzer voltage cylinder, 5. critical orifice plate, 6. low pressure impactor, 7. filter, and 8. needle valve.

Based on the previously presented approach and the schematic view in Figure 1, the measured aerosol, and the characterization of it, can be seen to follow the steps described below, where step 5 summarizes the rest of this section.

1. Unipolar charging of the aerosol

2. Mobility sizing with a constant electric field (current I₁)

3. Aerodynamic sizing with a low pressure impactor (current I₂)

4. Collecting the remaining particles with a filter stage (current I₃)

5. Calculation of the collection efficiencies from I₁₋₃, followed by a conversion to d_b, d_a, and

In order to retrieve the diameter information from the mobility analyzer and the low pressure impactor, the collection efficiencies (η) are needed, as a function of their respective characteristic diameters. The collection efficiency of the mobility analyzer (η_ma) can be theoretically formulated using its dimensions (length L, inner radius , and outer radius ; for values see Table 1), the voltage (U) being applied across the electrodes, the volumetric flow of the aerosol (Q), and the electrical mobility of the aerosol particles (Z) (Fuchs 1964):[3] The included electrical mobility is[4] where is the average number of elementary charges on the aerosol particle with a diameter d_b and μ is the gas viscosity (Hinds 1999). A commonly used fit function (Dzubay and Hasan 1990) has been taken to characterize the collection efficiency of the low pressure impactor (). The function is modified to include an offset factor to take into account the collection of sub-cut particles, enhanced by flow penetration into a porous collection surface:[5] where d₅₀ is the cutpoint diameter of the collection efficiency curve, s is its steepness, and λ is the offset factor (numerical value from 0 to 1) that sets the minimum collection efficiency value for the fit function (Rao and Whitby 1978a, 1978b; Dzubay and Hasan 1990).

DENSMO measures number median diameters from aerosol particle distributions, which are integral quantities, therefore no information is gained from the finer structure of the distribution. This poses the following limitations to the measured aerosol particle distribution: unimodal log-normality and beforehand known or assumed geometric standard deviation (GSD). The determined characteristic diameters are thus the mobility equivalent median diameter and the aerodynamic median diameter.

The first of the three used integral values that can be obtained is the total current[6] where I₁, I₂, and I₃ are the currents measured from the mobility analyzer, the low pressure impactor, and the filter, respectively. The current fractions collected from the total available current distribution by the characterization zones can be calculated by utilizing the collection efficiencies of the mobility analyzer and the low pressure impactor. The current fraction collected by the mobility analyzer is the second integral value and can be written as follows:[7] which links the median mobility size to the measured current fraction. A similar equation can be written for the third integral value, the current fraction of the low pressure impactor, and is as follows:[8] which in turn links the median aerodynamic diameter to the corresponding current fraction. For the data processing, these relations are simulated to produce unique solutions for a certain parameter set of a geometric standard deviation, a low pressure impactor pressure, and a mobility analyzer collection voltage.

By measuring the effective density with the method described above, utilizing three electrometers to measure the presented currents, one is able to retrieve median diameters from the measured currents in real-time. Section 3 contains a detailed description of the construction of DENSMO, including the mobility analyzer and the low pressure impactor, which are used for the main characterization.

3. Construction of DENSMO

DENSMO has been constructed so that the measured aerosol is conducted through one flow channel, where its charge state is first conditioned and then particle size characterized. A cross-sectional view of DENSMO is presented in Figure 1. After the inlet of DENSMO, the measured aerosol is charged with a small form factor unipolar corona charger, which has been designed to charge effectively in the nanometer scale. The charger is driven with a constant 1 µA current with a positive voltage around 2.5 kV. This charging approach is similar to the one implemented by Arffman et al. (2014). The excess ions are scavenged with the subsequent ion trap operating at 20 V, which creates a radial electric field from the electrode positioned on the centerline of the flow channel.

The characterization of the aerosol starts with the mobility analyzer, which collects aerosol particles based on their electrical mobility. The mobility analyzer has a radial electric field, which is produced by applying a positive voltage in the outer electrode. This electric field guides the charged aerosol particles to an electrically floating collection cylinder from which the first current signal (I₁) is measured. After the mobility analyzer, the aerosol flow is choked with a plate with three critical 0.3 mm in diameter orifices, so that the volumetric flow rate stays at constant 1.65 lpm, even when the pressure of the low pressure impactor is altered. The next portion of the aerosol particles is collected with the low pressure impactor, which collects the aerosol particles based on their aerodynamic diameter. The aerosol particles are accelerated toward a sintered collection surface with 12 nozzles, each 0.3 mm in diameter. The collection stage is also in a floating potential to accommodate the measurement of the second current signal (I₂). The critical dimensions of the low pressure impactor have been designed specifically for this use, as the collection efficiency is desired to rise slowly over a wide particle size range. This has been achieved by a high jet-to-plate distance (S) to the nozzle diameter (W) ratio and with the utilization of sintered collection surface (Arffman et al. 2011). These critical dimensions, as well as those of the mobility analyzer, are presented in Table 1.

Table 1. Critical dimensions and operational parameter ranges of the mobility analyzer (MA) and the low pressure impactor (LPI). From the MA, the collection volume length (L), inner diameter (r), outer diameter (r), and the range of collection voltage are listed. From the LPI, the jet-to-plate distance (S), nozzle throat length (T), individual nozzle diameter (W), and the range of upstream pressure are listed.

MA			LPI
L	3.13	cm	S	3	mm
r	4.27	cm	W	0.3	mm
r	5.31	cm	T	0.1	mm
U	10–150	V	P	200–300	mbar

The residual of the aerosol particles after the two characterization sections and the charge carried by the particles is collected on a high efficiency metal filter (Marjamäki et al. 2002). The third and last current signal (I₃) is measured from the filter, which is also electrically floating in its housing. The last operational section of DENSMO is a needle valve positioned after the filter, which is used to control the absolute pressure above and below the low pressure impactor. The control over the pressure is achieved by introducing another pressure drop in the valve, similar to the ones produced by the critical orifice plate and the low pressure impactor. These operational sections create a stepwise drop in the pressure from the atmospheric pressure to the applied low pressure in the outlet.

4. Calibration

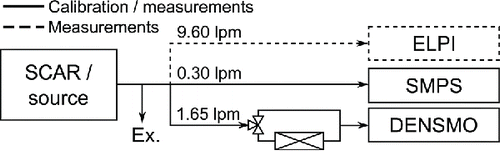
The device functions of DENSMO were calibrated using SCAR (Single Charged Aerosol Reference; Yli-Ojanperä et al. 2010), which produces monodisperse singly charged reference aerosol distributions from dioctyl sebacate (DOS). The calibration setup is depicted in Figure 2.

Figure 2. Calibration and measurement setups. The calibration setup includes, along with DENSMO, particle production by SCAR and a reference measurement with a SMPS. During laboratory measurements, an ELPI is also used.

The calibration was only performed against an SMPS as the density of liquid DOS is known to be 0.92 g/cm³ (CRC 2009), and thus the aerodynamic diameter can be calculated from Equation (1[1] ). The charging efficiency (Pn) of the corona charger was calibrated as described by Marjamäki et al. (2000). It is the product of the particle penetration and charge state of the aerosol after the charger and is used here to simulate current distributions from number size distributions. The calibration results can be seen in Figure 3.

Figure 3. Charging efficiency of the mini corona charger and the average number of charges on a charged aerosol particle as a function of the mobility diameter.

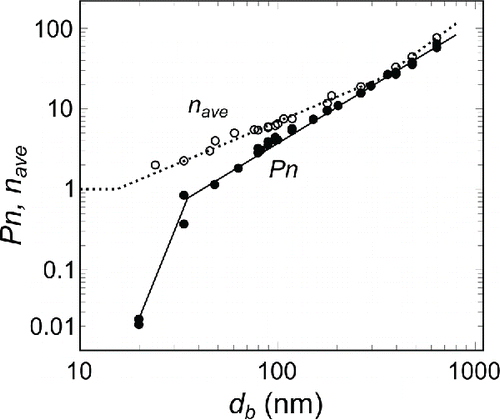
The value of Pn can be seen dropping rapidly for particle sizes smaller than 35 nm. Because of this significantly weaker charging efficiency in this particle size range, these particles have only a small impact on the total collected current. When singly charged monodisperse aerosol is charged using the corona charger and measured by the mobility analyzer, is the only unknown parameter in Equation (3[3] ). These calibration results are also shown in Figure 3. A set of power functions was fitted to these calibration results and are as follows:[9] and[10] The average number of charges is always greater in value than the Pn for a certain diameter, as the particle penetration of a charger cannot exceed unity without it producing particles. The average number of charges is also limited to values higher than one as only charged particles are detected.

The calibration results of the mobility analyzer and the low pressure impactor are depicted in Figure 4.

Figure 4. Collection efficiency measurement points for the mobility analyzer and the low pressure impactor. Solid and dashed lines show the theoretical collection efficiency curves of the mobility analyzer for 50 V and 150 V collection voltages, respectively. The curves fitted to the mobility analyzer measurements are from the theory and only have one scaling parameter: the collection voltage. The solid and dashed curves fitted to the low pressure impactor measurements are from the fit function with pressure as the scaling parameter, 200 mbar and 300 mbar, respectively, and three fitting parameters: slope, baseline offset, and cutoff diameter.

The mobility analyzer was calibrated using two different collection voltage (U) values: 50 and 150 V. Equation (3[3] ) was plotted alongside these calibration measurements, with the value of set to one. With these measurements, the functioning and scalability of the mobility analyzer, as predicted by theory, was verified with different collection voltages. The low pressure impactor was likewise calibrated for two different values, namely, upstream pressure (P) values at 200 and 300 mbar. Equation (5[5] ) was fitted to these calibration measurements and the parameter values are shown in Table 2.

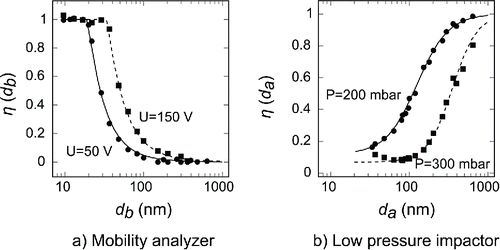
Table 2. Fitting parameters of the collection efficiency curves of the low pressure impactor, where P is the used upstream pressure, s is the steepness, d₅₀ is the cutpoint diameter, and λ is the baseline offset factor.

P (mbar)	s	d50(nm)	λ
200	1.1	120.2	0.12
300	1.4	353.4	0.07

As hinted above, the collection efficiency of the low pressure impactor does not reach zero as the particle size decreases. This is due to the secondary collection mechanisms, enhanced by flow penetration into the porous collection surface (see, e.g., Rao and Whitby 1978a, 1978b; Marjamäki and Keskinen 2004). The secondary collection is expected to be increased for the smallest particles. In practice, however, they do not reach the impactor but are collected by the mobility analyzer. Therefore, the offset of Equation (5[5] ) was found to be sufficient to give good correlation with the measured data.

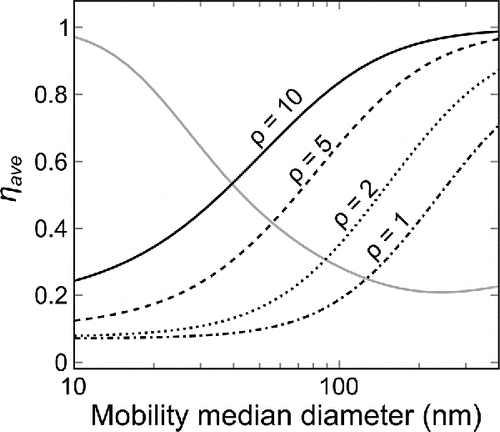
Unique sets of solutions can be calculated based on these calibrations and using Equations (7[7] ) and (8[8] ). One set of unique solutions as a function of the mobility median diameter for different effective densities is shown in Figure 5. The current measurements, and especially the collection efficiencies based on them, can now be linked explicitly to the mobility and aerodynamic median diameters. The aerodynamic median diameter can be determined from the line corresponding to the unit density; alternatively, the effective density can be determined by identifying the line that crosses the collection efficiency value of the low pressure impactor at the measured mobility median diameter. For example, at a mobility median diameter of 90 nm, 60% collection efficiency results from the effective density value of 5 g/cm³.

Figure 5. Current ratios of the mobility analyzer (gray line) and the low pressure impactor (black lines) as a function of the mobility median diameter for different effective densities. The figure presents a unique set of solutions for a number size distribution with a GSD of 1.6 and operational parameter values of 50 V and 300 mbar.

5. Results

5.1. Sensitivity analysis

The data inversion of the DENSMO currents to the characteristic diameters and the effective density relies on the robustness of the collection efficiency curves of the mobility analyzer and the low pressure impactor. If the geometric standard deviation of the log-normal number size distribution is as assumed and the signals of the electrometers have no or negligible noise levels, the correlation between measured currents and the characteristic diameters is unambiguous. In some scenarios, though, this is not the case. For example, the noise of the electrometers can overpower the signal measured from distributions with small total number concentrations. The sensitivity analysis was conducted to study the effects these unwanted deviations have on the data inversion.

The method to resolve characteristic diameters from the measured current fractions described before was used inversely to simulate the current signals from the initial number size distribution with a certain effective density. The effective density of the particles was kept at 2.0 g/cm³, the GSD of the initial distribution was kept at 1.6, while the CMD was varied from 20 to 300 nm (30 different values). For each CMD value, random noise was added to the simulated current values and 100 noise-affected current sets were generated. The noise level was ±5 fA and ±10% for absolute and relative noise, respectively. These noise levels are expected to cover the overall uncertainty within the current, flow, and pressure measurements, as well as the thermal noise and drift of the electrometers. These uncertainty sources were not investigated separately and only a combined effect on the measurements was estimated based on various measurement data acquired from DENSMO.

The noise-affected simulated current sets were used to calculate the effective density. The effect of wrongly assumed distribution GSD was studied by the same simulated dataset by calculating the density using both the correct initial GMD value of 1.6 and also values of 1.4 and 1.8. Figure 6 shows the results of the sensitivity analysis. The calculated effective density values are plotted, for the three GSD values, as a function of the initial CMD. The solid lines show the mean value of the calculated effective density for the set of 100 noise-affected current values. The darker and lighter gray areas indicate the standard deviation of the calculated density values for the correctly and wrongly assumed GSD values, respectively.

Figure 6. Sensitivity of the measured effective density with different assumed geometric standard deviations (GSD). The simulated GSD was kept at 1.6 and the assumed GSD was varied from 1.4 to 1.8. The effective density was kept at 2.0 g/cm³, collection voltage at 50 V, pressure at 200 mbar, and total number concentration at 10⁸ #/cm³ in all of these simulations. The solid line and the darker gray area denote the mean and standard deviation from the simulation with both assumed and simulated GSD values of 1.6. Additionally, the dashed lines denote the mean of the simulations where the assumed GSD was ±0.2 from the simulated one and the lighter gray area is its combined standard deviation.

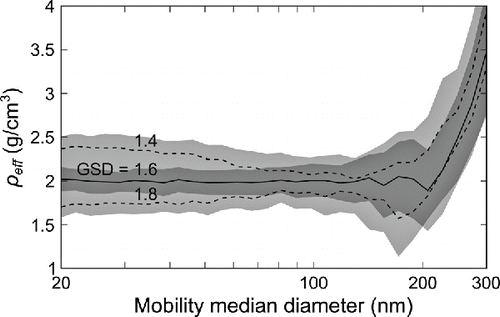
When the assumed GSD was set as 1.4 and 1.8, the calculation deviates from the initial effective density value and even averaging over a longer sample does not improve the result. The uncertainty of the effective density resolved from these simulations is ±7.5% due to aforementioned uncertainty sources and 12% per 0.2 change in assumed GSD. Comparably, with similar simulation Ristimäki et al. (2002) simulated an uncertainty of 4% for the SMPS+ELPI method.

The optimized operation of DENSMO was determined to be achieved when both current ratios and minimum current per electrometer are limited. Current ratios of the mobility analyzer and the low pressure impactor should be in the range of 30–90%. If, however, this is not the case, some adjustments can be done to remedy this by altering the collection voltage (U) and the pressure of the low pressure impactor (P). This is of use only if the measured aerosol complies with the other requirements set by DENSMO. The used charger and the mobility analyzer also limit the measurable mobility median diameter range from around 20 nm to 240 nm. The lower limit comes from the charging efficiency of the corona charger used and its inability to charge particle distributions that fall well below 35 nm, which can be seen from Figure 3. The upper limit comes from the fact that the collection efficiency of the mobility analyzer has a minimum at 240 nm, which can be seen in Figure 5. If this upper limit was not set, the current ratio of the mobility analyzer could not be unambiguously resolved to a single mobility equivalent median diameter.

Similar behavior can be observed with other mobility-based instruments, like a Fast Mobility Particle Sizer Spectrometer (FMPS; Levin et al. 2015). Exceeding the point of minimum collection efficiency leads to an underestimation of the mobility diameter and an overestimation of the effective density. In some applications, this situation can therefore be detected as unphysically high effective density values, such as those exceeding the bulk material density of the particles. To be on the safe side, low collection efficiency values of the mobility analyzer are to be avoided. The operation was determined to be optimal within collection efficiency values of 30–90%.

5.2. Measurements

DENSMO was tested with test aerosols in laboratory conditions with the following materials: dioctyl sebacate (0.92 g/cm³), sulfuric acid (1.80 g/cm³), sodium chloride (2.17 g/cm³), titanium dioxide (rutile, 4.23 g/cm³), and silver (10.49 g/cm³) (CRC 2009). These materials were synthesized in the size range of 23 to 151 nm in the mobility median diameter with mostly spherical morphologies. DOS and H₂SO₄ having their melting temperatures below room temperature were, by default, spherical and assumed to have their effective densities equal to their bulk densities. NaCl is known to exhibit particle bouncing and charge transfer by contact charging in the low pressure impactor based on previous studies (e.g., Kuuluvainen et al. 2013). It was selected as one of the materials to give insight on how particle bounce affects the measured median diameters. Titanium dioxide and silver were measured in their agglomerated state as well as in spherical form in order to see if these two states could be distinguished from each other.

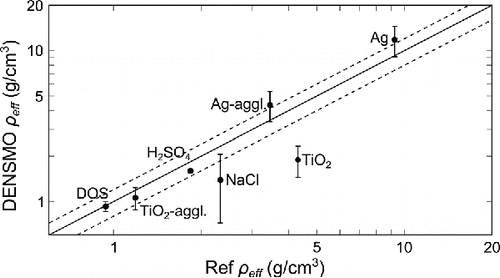
The results from the measurements are shown in Figure 7. The reference effective density values were obtained by a method utilizing SMPS and ELPI distributions, where the effective density functions as a fitting parameter between these distributions (Ristimäki et al. 2002). The measurements of the liquid aerosol particles were found to correlate well with the bulk densities of the materials, just as the agglomerates did with the reference method. Note that the shape factor of the particles is incorporated into the effective density values and should affect both DENSMO and the reference method alike. Measurements from both sintered and agglomerated silver particles and TiO₂ agglomerates yielded results comparable to the reliability of the reference method across the whole range of measured effective densities. The results from the NaCl particles were off as anticipated, most probably due to unwanted particle bounce from the collection plate of the low pressure impactor. This effect also caused the deviation between the measurements of sintered TiO₂ particles and the respective reference measurements, as also reported by Harra et al. (2015). Although the reference method also utilizes low pressure impactor stages, the bounce probability is lower because of the limited size ranges of the individual impactor stages.

Figure 7. Effective density measurements with the SMPS+ELPI density method as a reference. Aerosol particles were synthesized from multiple materials and with a wide range of diameters. The ±20% uncertainty of the reference method has been denoted with the dashed lines on both sides of the unity line (Ristimäki et al. 2002).

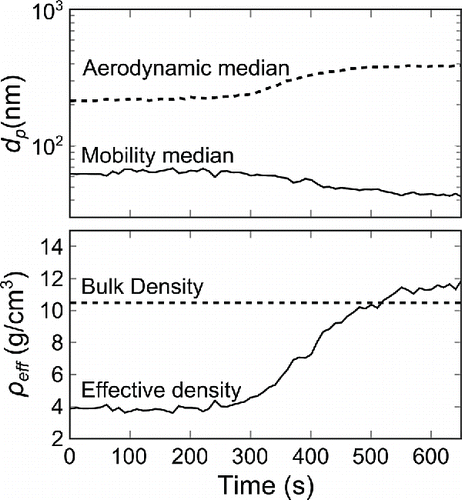
The measurement capabilities of DENSMO were also tested in transient conditions. A transient measurement of silver agglomerate sintering is presented in Figure 8. The silver agglomerates were sintered using a tubular furnace and the measurements made while the temperature increased from 20°C to 300°C. As the temperature rises, both the aerodynamic and mobility equivalent median diameters deviate from their initial values. The effective density of the silver particles increases from around 4 g/cm³, where the particles are clearly agglomerated, to around 11.5 g/cm³, which is within 10% from the bulk density and can be presumed to be fully sintered.

Figure 8. Transient measurement of silver agglomerate sintering with a temperature change from 20°C to 300°C.

6. Conclusions

We introduced DENSMO, a real-time instrument with a simple construction and the ability to measure effective density as well as aerodynamic and mobility median diameters from unimodal aerosol distributions. A sensitivity analysis was conducted in order to determine the operational ranges of the device in terms of total number concentration and characteristic diameters. The effect of wrongly assuming the GSD of the measured distribution was also investigated, as the need for the assumption is inbuilt into the method described, and was determined to be 12% per 0.2 absolute change in the assumed GSD. Overall, the uncertainty of DENSMO was assessed to be ∼ 25%. This entails that if the desired value is, for example, coating thickness on spherical 100 nm silica nanoparticles (2.2 g/cm³), DENSMO can detect, for example, titania (4.2 g/cm³), silver (10.5 g/cm³), and platinum (21.5 g/cm³) coatings with 18, 3.5, and 1.5 nm resolutions, respectively.

The functionality of DENSMO was investigated with laboratory measurements and it was shown to give good correlation with the chosen reference method. Based on these test measurements, the accuracy of DENSMO is reasonable for quantitative measurements, when the criteria for optimal operation are met. Comparing the results given by DENSMO to the previously available methods, the further simplifications have not reduced the accuracy significantly and the results were in good agreement.

The most suitable application for DENSMO and similar methods, which are restricted to unimodal aerosol distributions, is to be used in production monitoring, where the stability of the produced material is essential. In these kind of production environments, DENSMO could also be used as a reference while process parameters are being changed, to determine when the desired values are met and the production is again stabilized.

Acknowledgment

This publication reflects only the authors’ views, and the Community is not liable for any use made of the information contained therein.

Funding

This research was funded by the European Union’s Seventh Framework Programme (FP7/2007-2013) under the Grant Agreement no. 280765 (BUONAPART-E).