Fractal scaling of coated soot aggregates

ABSTRACT

Recent field observations have shown soot aggregates (SAs) to contain significant amounts of surface coatings of organic compounds which obfuscate their native fractal morphology and make them visually appear as “near-spherical.” Morphologies of these aggregates are currently parameterized using fractal dimension (D_f) values greater than the universal 1.8. This is done to account for the supposedly morphological restructuring of an aggregate to a more compact form upon condensation of organic materials. Using multiple-angle light scattering analysis, it has been experimentally shown that restructuring of SA morphology only takes place during the evaporation process, not condensation. Based on this seminal finding, here we formulate the correct parameterizations to describe the morphology of surface coated aggregates. We perform detailed three-dimensional morphological characterization of computer simulated coated aggregates that mimic atmospheric SAs and show that their D_f remains invariant at 1.8 with increasing coating mass by as much as 18 fold. We find coating to affect only the fractal prefactor k₀, an understudied parameter which controls the aggregate shape anisotropy and local packing fraction of monomers. Specifically, k₀ was observed to scale with the ratio of aggregate's total (coating + bare) mass M_total to bare mass M_bare as k₀ = 1.34*(M_total/M_bare)^0.56.

Copyright © 2017 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

Introduction

Soot aggregates (SAs) in the atmosphere significantly influence the Earth's radiation balance and climate (Haywood and Ramaswamy 1998; Panel on Aerosol Radiative Forcing and Climate Change 1996), visibility (Kaufman et al. 2002; Mishchenko et al. 2004), and public health (Grahame et al. 2014; Janssen et al. 2012). These particles are formed from high-temperature, incomplete combustion of fossil, and biomass fuels via diffusion-limited aggregation of spherical monomers (repeating units) that consist of many layers of graphitic carbon bound by short-range forces. The monomers attach to each other in point-contact, thereby resulting in an overall fractal-like morphology for the aggregate. The scaling of the number of monomers (N) with aggregate size (radius of gyration R_g) follows a power-law:[1] where a is the monomer radius, D_f is the fractal dimension and k₀ is a scaling prefactor. For an aggregate, D_f describes its space-filling characteristic, while k₀ is strongly influenced by shape anisotropy (stringiness) and monomer packing density (Sorensen and Roberts 1997; Lapuerta et al. 2010; Heinson et al. 2010, 2012; Liu and Chakrabarty 2016).

It has been extensively shown via laboratory experiments and computer-simulations that point-contacting SAs have a universal D_f ≈ 1.8 (Dhaubhadel et al. 2006; Sorensen 2001). However, recent field studies suggest that this “point-contacting” morphology of SAs is rarely observed in the atmosphere (Adachi et al. 2010; Cappa et al. 2012; China et al. 2013; Liu et al. 2015; Moffet and Prather 2009; Shiraiwa et al. 2007). Real-world combustion sources, for example, wildfires, co-emit large amounts of gas-phase organic compounds along with SAs (China et al. 2013; Spracklen et al. 2007). These compounds, upon undergoing phase transformation, condense on the aggregate surfaces as layers of external coating. This process of coating starts with filling in of the crevices between monomers which blurs its contact points. Ultimately, if prolonged, this process could completely engulf the bare structure of the aggregate leaving only its thickened silhouette intact (China et al. 2013).

Organic-coated SAs with obfuscated monomer–monomer contact points have been observed to comprise greater than 75% of total soot population in the atmosphere (China et al. 2013; Liu et al. 2015). Further, it has been suggested that coating leads to compaction of the open-structured bare aggregate morphology resulting in an increase of D_f to values greater than 1.8 (Adachi et al. 2010; China et al. 2013). This alteration in morphology has been held responsible for enhanced absorption of incoming solar radiation—up to a factor of three—by SAs in the atmosphere (Adachi et al. 2010; Cappa et al. 2012; Liu et al. 2015; Moffet and Prather 2009; Peng et al. 2016). For quite some time, the community was yet to reach a consensus on the mechanism and parameterization of the structure evolution of aggregates with coating. Some studies argued that the surface tension of coating materials resulted in collapse of the bare aggregate network, thereby increasing the D_f of the coated aggregate to values greater than 2 (Miljevic et al. 2012; Schnitzler et al. 2014). This debate was ultimately settled by Ma et al. (2013) who experimentally showed that it is the capillary effect during the evaporation process following condensation that caused the morphological restructuring of water-coated SAs. Note that water has a much higher surface tension than most organic compounds found occurring in the atmosphere. They used multiple-angle light scattering analysis to measure the D_f of coated aggregates in the range 1.45–1.94, implying that surface tension of the condensed liquid did not play a role in morphological restructuring.

However, there is currently a lack of understanding on how the fractal parameters in Equation (1[1] ) for a bare SA evolve with increasing coating. Almost all previous studies have analyzed the fractal properties of coated SAs from their two-dimensional projections obtained from electron microscopy images (China et al. 2013; Dzepina et al. 2015; Liu et al. 2015). This process requires a priori information on the aggregate structure such as average a, coating thickness, and whether the expected D_f is less than 2 (Chakrabarty et al. 2012; Loh et al. 2012). Image analysis of electron micrographs of aggregates may also lead to overestimation of their aggregate morphological parameters (Chakrabarty et al. 2011a,b, 2012). This lack of understanding manifests itself in incorrect parameterization of coated SAs during radiative forcing calculations (Adachi et al. 2010; Cappa et al. 2012; Dzepina et al. 2015; S. Liu et al. 2015).

In this study, we comprehensively analyze the structure of computer-generated SAs with varying coating thickness using the q-space structure factor technique (Sorensen 2001; Loh et al. 2012) and an analytical “bottom up” formalism that relates aggregate D_f, k₀, shape and monomer packing (Heinson et al. 2012; Nicolai et al. 1994). We show that D_f remains invariant for coated SAs, and identify those morphological parameters that get affected upon coating. Finally, we suggest new power-law expressions for scaling the fractal morphology of SAs as a function of coating thickness.

Methods

Aggregates were simulated using an off-lattice diffusion limited cluster–cluster aggregation (DLCA) algorithm (Meakin 1985, 1999). Numerous experimental studies have shown that DLCA accurately predicts the formation of real-world combustion generated aggregates (Cai et al. 1993; Jullien and Botet 1987; Sorensen et al. 1992; Sorensen and Feke 1996). Our simulation started with 10⁷ spherical monomers of radius a = 25 nm randomly placed in a three-dimensional box of a given length. The monomer volume fraction was 0.001. At the beginning of each iteration, the number of aggregates N_c were counted. Note that the number of lone monomers was included in N_c. A random aggregate was chosen and the simulation time was incremented by 1/N_c. Next, the probability that the selected aggregate would move was calculated by assuming that its drag force was in the Stokes–Einstein regime; hence, the probability of movement was inversely proportional to the R_g of the aggregate. If the aggregate moved, it would be a distance of one monomer diameter in a random direction. When two aggregates collided, they irreversibly stuck together and N_c was decremented by 1.

After a population of aggregates was generated, the process of coating was initiated. The coating algorithm first discretized the simulation space into high-resolution cubic lattices of equal sub-volumes. A bare DLCA aggregate was placed in the simulation space, which resulted in the sub-volumes being either filled with portions of the aggregate or left empty. Empty sub-volumes that were on or bordering the aggregate surface were identified and filled with the coating material. Next, the algorithm checked if the desired coating thickness was reached. If not reached, the process of identifying and filling empty sub-volumes on the aggregate surface was repeated.

Results and discussion

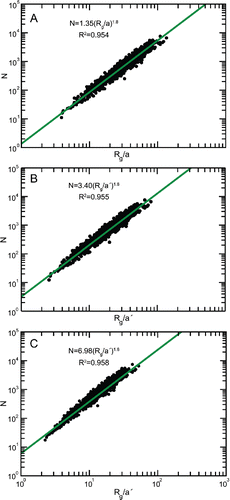
Figure 1 visually depicts the morphological evolution of our computer-generated SAs with increasing coating thickness as observed by China et al. (2013). Based on thousands of electron microscopy images analyzed, China et al. (2013) categorized SA morphology into three types–“bare” with point-contacting monomers (Figure 1a), “partly coated” (Figure 1c) with monomer crevices filled with coating material but the aggregate not completely engulfed, and “embedded” (Figure 1e) with the aggregate heavily coated and only the contours of the monomers evident. As evident from Figures 1b, d, and f, our simulated aggregates closely mimic these three morphological categories. The ratio of aggregate's total (coating + bare) mass to bare mass varied between 1 for bare, 5 for partially coated, and 18 for embedded.

Figure 1. Aggregate morphology evolution with increasing coating thickness. Simulated aggregates are shown in (b), (d), and (f). These aggregates closely mimic real-world soot aggregates (a), (c), and (e) from China et al. (2013). (a) and (b) are bare soot aggregate with point contacting monomers and an open morphology (D_f = 1.8). Partially coated aggregates are shown in (c) and (d). Thickly coated or embedded aggregates are displayed in (e) and (f). Although the aggregates in (c) through (f) have had voids filled with coating and thus appear to be compact, their mass continues to scale with D_f = 1.8 as shown in Figure 2.

For Figures 1d and f, describing the aggregate morphologies using Equation (1[1] ) is not possible because coating obfuscates the structure of individual monomers. Equation (1[1] ) was originally formulated for bare aggregates with point-contacting monomers. In order for Equation (1[1] ) to be applicable for describing coated aggregates, an effective monomer radius a’, which takes into account of the coating, needed to be introduced. By assuming the coated mass to be uniformly distributed over a bare aggregate, a’ could be expressed as:[2] where M_total and M_bare are aggregate's total (coating + bare) and bare mass, respectively. Since these new monomers of radius a’ incorporate the coating material, they can no longer be thought of as having point contacts, but instead can have substantial overlap as the coating becomes thicker. A consequence of defining a’ as per Equation (2[2] ) is the conservation of N between a bare and coated aggregate in Equation (1[1] ) when replacing a with a’. It is, however, important to note that the material densities of SA monomers and the coating are assumed to be equal in this study. In the case of unequal material densities, replacing M_total/M_bare in Equation (2[2] ) with V_total/V_bare, the ratio of aggregate's total (coating + bare) to bare volume, would yield equivalent results.

We now explore the scaling relationship for bare, partly coated, and embedded aggregates using Equation (1[1] ) with the appropriate substitution of a’ for a. For bare aggregates (Figure 2b), we get a D_f = 1.8 and k₀ = 1.35 consistent with past experimental and theoretical investigations (Heinson et al. 2012; Sorensen and Roberts 1997; Jullien and Botet 1987; Cai et al. 1995; Meakin 1988; Heinson et al. 2015). Contrary to intuition, the plots for partially coated and embedded aggregates reveal that the value of D_f remains invariant; instead the prefactor k₀ increases with increasing coating thickness: k₀ = 3.40 for partially coated and k₀ = 6.98 for embedded aggregates. One would have expected the aggregate D_f to have increased with coating thickness to a value of 3 (Adachi et al. 2010; China et al. 2013). But this is clearly not the case–coating affects only the k₀ of an aggregate.

Figure 2. Scaling of coated aggregate mass with size. (a) Bare simulated aggregates exhibit D_f = 1.8 and k₀ = 1.35. The partially coated (b) and embedded (c) aggregates both exhibit D_f = 1.8 with k₀ = 3.40 and k₀ = 6.98, respectively. These plots show that D_f is invariant with increasing coating mass. Coating affects k₀, which controls the shape anisotropy and monomer packing density of an aggregate.

To explain this unique dependency of k₀ on coating thickness, we investigate the fundamental relationship between the aggregate structure factor S(q) (Heinson et al. 2012; Loh et al. 2012; Sorensen 2001) and morphological parameters D_f, k₀, and a’. Our goal here is to provide an analytical model for describing the effects of coating on the aggregate morphological parameters. We start with rearranging Equation (1[1] ) and writing the prefactor k₀ as:[3]

The terms, N and R_g, on the right-hand side of Equation (3[3] ) are the zeroth and second moments of the monomer pair correlation function g(r), which is defined as the probability that another monomer will be found at distance from a given monomer center:[4a] and[4b] where N(r) in Equation (4a[4a] ) is the number of monomers in a sub-volume of an aggregate with radius r. As r→∞ Equation (4a[4a] ) must converge to N. For aggregates, N(r) is a function of the local monomer packing fraction ϕ and a’ as:[5]

Using Equation (5[5] ) in Equation (4a[4a] ) gives the expression for g(r) as:[6]

The limitation of Equation (6[6] ) is that it does not provide the necessary cut-off size for aggregates as r→∞. We overcome this limitation by modulating Equation (6[6] ) with an appropriate cut-off function:[7]

A stretched exponential form of the cutoff function was adopted as per past recommendations (Heinson et al. 2012; Nicolai et al. 1994; Sorensen 2001). γ is the shape descriptor and ξ is the characteristic length of the aggregate. Combining Equations (4a[4a] ), (4b[4b] ), and (7[7] ) with (3[3] ) leads to an analytical expression for k₀ based on the morphological parameters—D_f, γ, ϕ:[8] where Γ is the gamma function. Our simulation results for DLCA aggregates show that the application of coating does not change the aspect ratio of an aggregate. Thus, in our analytical model of Equation (8[8] ), we could substitute γ = 2.0 and D_f = 1.8, which are typical values for bare aggregates (Heinson et al. 2012); this further simplifies the k₀ for coated aggregates as:[9]

This simple analytical form of k₀ clearly shows that coating effects only the packing of local monomers.

We now connect Equation (9[9] ) to the aggregate structure factor S(q)—the reciprocal space structure of an aggregate via the Fourier transform of g(r).[10]

Inserting the analytical expressions of g(r) and k₀ from Equations (7[7] ) and (8[8] ), respectively, into Equation (10[10] ), we get,[11]

Equation (11[11] ) is an analytical expression connecting S(q) with the aggregate morphological parameters. Note that Equation (11[11] ) is only valid for a’< q⁻¹<R_g. The Fourier variable q or more specifically q⁻¹ represents a probe length scale. When q⁻¹ > R_g, an aggregate is seen as a point scatter and S(q) is constant. For a’< q⁻¹ < R_g, S(q) proceeds as Equation (11[11] ). When q⁻¹ > a’, S(q) scales with a power-law exponent of −4 corresponding to the spherical monomeric units constituting an aggregate. We simplify Equation (11[11] ) by replacing D_f and γ with 1.8 and 2.0, respectively, to obtain a simple working form of S(q) as:[12]

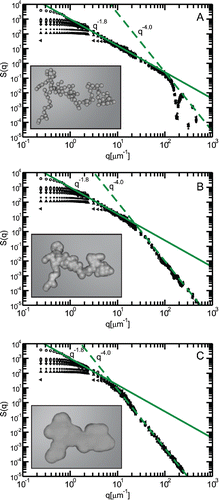
Figure 3 shows the plots of S(q) for bare, partially coated, and embedded aggregates with N ranging from 30 to 4000 monomers. Since the aggregates were already discretized into small equally sized sub-volumes prior to simulating the process of coating, the S(q) for aggregates is calculated by squaring the Fourier transform of the sub-volumes' coordinates. It is important to note that the S(q) is not presented to be a measure of the optical properties but is used to probe the inner structure of the aggregates. Equation (12[12] ) is plotted as a solid line in Figure 3 and agrees well with the S(q) of aggregates. The S(q) of bare aggregates show a characteristic D_f = 1.8 slope till the crossover length q⁻¹ = a is reached. At this point, S(q) starts seeing the constituting monomers of the aggregates denoted by a −4 slope. The crossover to −4 exponent starts to shift to smaller q values with increase in coating thickness, thereby implying a continual increase in a’. At the thickest coating scenario, the S(q) plot shows a very early inflection from −1.8 to −4 power-law exponent. The point to note here is that the global structure of an embedded structure still shows a −1.8 scaling, which is contrary to the commonly held consensus (Adachi et al. 2010; Saathoff et al. 2003; Shiraiwa et al. 2007).

Figure 3. Structure factor S(q) of bare and coated aggregates. Aggregates were simulated in the range N = 30–4000. In (a), the S(q) of bare simulated aggregates show a D_f = 1.8 for q⁻¹ < a; beyond this size, S(q) exhibits a power-law exponent of −4 which is characteristic of a spherical three-dimensional monomer. For the partially coated (b) and embedded (c) aggregates, the crossover from −1.8 to −4 moves to smaller q values due to the increase in effective monomer size with coating. The key point to note in these plots is the existence of the −1.8 slope for even the extremely coated (embedded) aggregates.

Figure 4 shows the scaling relation for k₀ with a’ and M_total/M_bare and results in the following analytical expressions:[13a] [13b]

Figure 4. Scaling relationships for fractal prefactor k₀ with coating mass and a’. (a) The ratio of total aggregate to bare aggregate mass M_total/M_bare scales with prefactor k₀ and follows the relationship k₀ = 1.34(M_total/M_bare)^0.56. (b) The effective monomer radius a’ scales with prefactor k₀ and follows the relationship k₀ = 1.34(a’/a)^1.70.

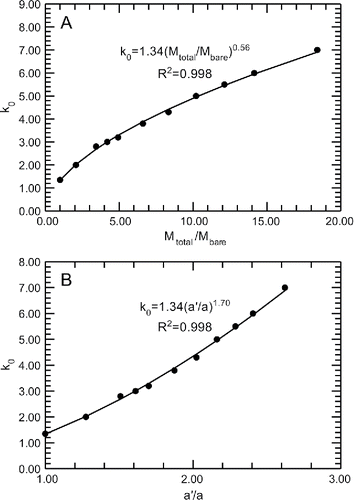
These simple relationships provide a simple way to model coated aggregates from the knowledge of total particle and coating masses, quantities measurable using contemporary instruments (Adachi and Buseck 2008; China et al. 2013). By fixing D_f at 1.8 and scaling k₀ as a function of coating mass using Equations (13a[13a] ) and (13b[13b] ), coated SAs could be modeled and calculated for their optical properties in climate models and related studies.

Conclusions

We have generated using computational methods aggregates that mimic the three types of widely prevalent atmospheric soot: bare, partly coated, and embedded. The goal of this study was to investigate the morphological scaling relations of these aggregates; more specifically, determining how the parameters D_f, k₀ evolve with increasing coating thickness. We show that with increasing coating thickness, the aggregate D_f remains at a constant value of 1.8. The effect of coating thickness is clearly shown to affect only the prefactor k₀. Bare SAs exhibit a k₀ = 1.35 that scales with increasing coating thickness in power-law exponents given by Equations (13a[13a] ) and (13b[13b] ). k₀ has been shown to be a descriptor of the aggregate anisotropy and shape (Heinson et al. 2012). Our results further extend the importance of k₀ as being a descriptor of monomer packing fraction in aggregates. Overall, this work highlights the importance of accounting for the correct k₀, which is a fundamental yet understudied parameter, in describing SA morphology. One important caveat to note is that these results are only applicable to aggregates, such as soot, which are grown via the DLCA mechanism. The effects of coating on aggregates grown via other mechanisms, for, e.g., reaction limited cluster aggregation and ballistic particle-cluster aggregation, will be the subject of future work.

The reciprocal space structure factor S(q) for coated aggregates was studied, and these power-law plots revealed insight into the inner structure of the coated aggregates. S(q) of coated aggregates for q⁻¹ < R_g ≤ a’ followed a power law exponent = −1.8 highlighting the retention of their inherent overall D_f = 1.8 fractal morphologies. Our parameterization of coated SA morphology has implications on accurate estimation the effects of carbonaceous particles on earth energy balance and climate change. Speculating the impact of fixed D_f ≈1.8 and increasing k₀ of coated SAs on their radiative forcing efficiency is beyond the scope of this study and is a subject matter for future research.

Funding

This work was partially supported by the US National Science Foundation awards AGS-1455215, CBET-1511964) and NASA Radiation Sciences Program NNX15AI66G.