Modeling Critical Air Exchange Rates (CAERs) for aerosol number concentrations from nano-particle sources using an “effective coagulation coefficient” approach

ABSTRACT

An important issue in the context of air pollution by indoor combustion sources pertains to the joint effect of source strength, coagulation, and ventilation rate on the ultrafine particle exposure metrics. It was recently predicted by detailed numerical analysis of the Smoluchowski coagulation equation with continuous source and sink terms that the ultrafine particle number, mass, and surface area concentrations do not monotonically decrease with increasing air exchange rate, but display peak concentrations at certain Critical Air Exchange Rates (CAERs). As these results are of considerable significance for exposure assessment as well as for implementing particle control technologies, it is necessary to assess the CAER for different aerosol characteristics. Given the fact that the numerical method of solving coagulation equation with realistic Fuchs kernel is computationally intensive, simpler semi-analytical approaches are desired for providing reasonable estimates of CAER and clearer insight into the counter-intuitive, peaking behavior. In this article, we present such an approach by replacing the Fuchs kernel by a spectrum-averaged effective coagulation coefficient, within the framework of the steady-state model. The effective coagulation coefficient is size independent but depends implicitly on the aerosol concentration thus capturing the combined effect of coagulation and removal processes. The number concentrations obtained from this method have been compared and validated against the numerical solutions. The model predicts more pronounced effects on the peaking behavior as well as larger CAER values for fractal particles as compared to compact particles. The results are further discussed.

Copyright © 2017 American Association for Aerosol Research

EDITOR:

• Nicole Riemer

Introduction

The combustion of biomass, candles, incense sticks, tobacco, mosquito coils as well as particle formation from indoor chemicals are among the major sources of indoor aerosol pollution. The Ultra-Fine Particle (UFP) component of this aerosol is being increasingly imputed as the causal factor for the observed deleterious health effects among exposed populations. To take this into account, the overall risk is generally represented by the UFP number and surface area concentrations in addition to the more conventional PM2.5 mass concentration metric (Oberdorster et al. 2005; Pedata et al. 2015). In a recent study, Anand et al. (2016a) demonstrated that unlike the PM2.5 mass concentration, the UFP metrics have complex dependencies on ventilation rate and source strength. Improved understanding of these dependencies is crucial for several mitigation strategies such as source control, ventilation removal, exposure duration control, and air cleaning technologies by filtration. Although source control is the most effective solution for the indoor air quality problem, natural and mechanical ventilation are also suggested as an alternative strategy to improve air quality.

Using a steady-state analysis, Anand et al. (2016a) showed that in the case of strong aerosol emission sources, the number concentration increases with ventilation rate, reaches a peak value, and then decreases at a slower rate due to the competition between coagulation and ventilation removal. The value of the ventilation rate at which the number concentration peaks is termed as the Critical Air Exchange Rate (CAER). This is a counter-intuitive result which indicates that having ventilation rates below CAER is a counterproductive exercise from the point of view of reducing number concentrations. Hence, it is important to know the values of CAER for obtaining a proper perspective of UFP mitigation and control strategies in the context of exposure scenarios involving widely varying source strengths and ventilation rates. Additionally, these results are of specific relevance for the assessment of long-term exposures originating from daily exposure scenarios to indoor aerosols (particularly from biomass cooking), where high particle number concentration is encountered (Hussein et al. 2015; Dhaniyala et al. 2011).

The concentration peaking effect and the occurrence of CAERs is a unique consequence of the competition between removal process and size-dependent hetero-coagulation process occurring in the aerosol system sustained by strong and steady emission sources. This effect cannot be captured by using a simplistic constant coagulation kernel in the Smoluchowski coagulation equation, but requires the use of explicit size-dependent kernels. Anand et al. (2016a) employed a computationally intensive numerical scheme to obtain CAERs for various aerosol metrics by integrating the coagulation equation using the realistic Fuchs kernel (Fuchs, 1964), combined with source and sinks terms. Although based on interpolation, the Fuchs kernel is widely employed for treating coagulation problems in the entire particle size range. It must be remarked that the general equation for the steady-state coagulating system with sources and sinks, either individually or together, were examined by Klett (1975), White (1982), and Crump and Seinfeld (1982) for seeking the existence of solutions. These authors obtained exact analytical solutions under certain conditions for system with coagulation kernels of multiplicative type. It was also shown that for source enhanced coagulation in the presence of removal, steady-state solutions (for number concentrations) exist for both free-molecular and continuum kernels. As Fuchs kernel is essentially a transition regime interpolation between these two kernels, its large size behavior will be similar to that of the continuum kernel and accordingly, it will possess a bounded steady-state solution. Davies et al. (1999) solved the coagulation model with monodisperse sources and sinks for gelation system using analytical, numerical, and asymptotic methods. Simons (1998) obtained solution of the coagulation equation with time-dependent source but with constant coagulation kernel. However, there is no analytical solution available for the Brownian coagulation problem with Fuchs kernel due to its nonhomogeneous nature and complicated size dependency. It requires considerable investment of time to handle numerical computations with Fuchs kernel, especially for varying exposure scenarios and system parameters. A simpler approach is highly desirable that would not only retain the essential features of the Fuchs kernel, but also will save considerable computational time. Apart from this, there is also a fundamental need to look for alternative formulations to provide newer perspectives for the counter-intuitive ventilation related concentration peaking result. With these in view, in the present study, we propose a simpler effective coagulation coefficient approach and demonstrate its usefulness for predicting steady-state number concentrations for aerosol systems with widely varying structural characteristics (i.e., fractal versus compact), source strengths, and ventilation rates. This approach may be used as an alternative solution for the numerical model to provide aerosol number concentration in steady-state problems involving sources and sinks.

The effective coagulation kernel presented here reduces the problem to a semi-analytical constant kernel equivalent system, yet retains the relevant features of the size-dependent Fuchs kernel. Interestingly, it turns out that the effective kernel captures the effect of two independent parameters, viz., the emission rate and removal rate, through a single parameter (β, see the“Effective coagulation coefficient model” section) which combines these two variables. The β parameter implicitly introduces concentration and ventilation dependence for the effective kernel, which explains how the effective coagulation rate undergoes a shift with changing ventilation rate. Being an approach rather than an approximation, it cannot be justified a priori and its usefulness and reliability stem from its validation vis-a-vis the numerical solutions (Anand et al. 2016a) for different fractal dimensions, wide range of emission, and air exchange rates. In the foregoing sections, we describe the approach, validate it against numerical solutions, and apply it for predicting CAERs for fractal and compact particles under varying source emission conditions. Additionally, we also examine the implications of including Hamaker–van der Waals and viscous forces between particles, on their concentration profiles and CAER.

Theory

Let us consider a scenario in which ultrafine particles are injected continuously into a large volume, and the aerosol system evolves by coagulation, particle removal due to wall deposition and ventilation. It is assumed that the aerosol is mixed rapidly in the air space either by buoyancy effects or due to air currents induced by local temperature gradients, or due to the presence of mixing elements such as fans, natural or forced ventilation, or by a combination of all these factors. Then, to a first approximation, one may treat the aerosol concentration as spatially homogeneous at all times. Accordingly, the rate of change of aerosol concentration in the chamber is given by[1] where K(u, u’) is the coagulation kernel (m³ s⁻¹) between particles of volumes u and u’, n(u, t) is the number concentration distribution (m⁻³ μm⁻³) for particles of volume u, λ_v is the ventilation rate (s⁻¹), λ_d(u) is the size-dependent removal rate (s⁻¹) due to wall/surface deposition processes, is the particle number injection rate of the source (m⁻³ s⁻¹), and u₀ is the primary particle volume emitted at the source (μm³). The initial number concentration in the chamber is assumed to be zero (n(u, 0) = 0). The first term in the right-hand side of Equation (1[1] ) represent continuous source injection, the second and third terms represent coagulation, and the fourth for ventilation and size-dependent removal processes.

Constant kernel case

For the sake of illustrating the effect of ventilation on concentration for an analytically solvable case, let us assume that the coagulation coefficient may essentially be approximated by a constant, i.e., K (u, v) = K, which does not depend on size, particle concentration, or ventilation rate. Let us further assume that the total removal rate in this system is represented as the sum of ventilation and size-independent (spectrum averaged) wall deposition rates, i.e., . Then, upon integrating over all sizes, one obtains the following nonlinear equation from Equation (1[1] ):[2] where the total number concentration is defined as . Regardless of the initial concentration, Equation (2[2] ) asymptotically attains a steady-state having a solution[3] Equation (3[3] ) shows that the steady-state number concentration decreases monotonically with increase in removal rate (ventilation rate, or air exchange rate) regardless of the values of K and S. However, as shown by Anand et al. (2016b), this is not true for strong emission sources; instead, the opposite turns out to be true (i.e., the concentration increases with increasing ventilation rates) below certain Critical Air Exchange Rates (CAER). The great advantage of the simplicity of the results of constant kernel approximation, so often used in the context of one time injection problems, is marred by its inability to predict this conceptually and qualitatively important result for continuous emission scenarios. This is where the concept of “effective coagulation coefficient” comes into picture as a means of retaining the simplicity of the constant kernel approach without sacrificing the intricacies associated with the interplay of coagulation and ventilation for continuous emission scenario.

Effective coagulation coefficient model

As shown by Anand et al. (2016b), the main difference between constant and effective coagulation kernel is that the former is a constant throughout the history of evolution of particle-size spectrum, whereas the latter captures the transformation of the particle-size characteristics from the source region to the exposure environment. The effective coagulation coefficient (K_eff) is then introduced into the constant kernel model, and the steady-state form of Equation (2) is written as[4] where K_eff turns out to be a function of a single parameter , the ratio between prescribed total removal rate () and steady-state total number concentration (N₀). Here, constant kernel (K) in the steady-state solution (Equation (2[2] )) is replaced by an effective coagulation coefficient (K_eff). The K_eff is obtained by integrating the Fuchs coagulation kernel (K_Fuchs) for the entire particle size range above the initial particle diameter emitted at the source. The steady-state number spectrum () used for integration is obtained self-consistently from the solution of the steady-state model, as described in detail in the Appendix of Anand et al. (2016b). The effective coagulation coefficient is then given by[5] where is a function of and K_eff itself as shown below:[6] Equations (5[5] ) and (6[6] ) are nonlinearly coupled implicit equations which are solved for K_eff in an iterative manner, through an initial guess for the value of . The essential input comes from the Fuchs coagulation kernel (K_Fuchs(u, u’)) which describes the rate at which particles of size u coagulate with particles of size u' due to kinetic+diffusion mechanisms and intermolecular forces. When interparticle forces are not considered, it is given by[7] where r_u and r_u’ are the radii of the particles with volume u and u’, respectively, K_co(u, u’) is the Brownian coagulation kernel in the continuum regime, K_fm(u, u’) is the Brownian coagulation kernel in the free-molecular regime, and δ_uu' is the distance between the collision surface and the regime dividing surface. Fuchs (1964) proposed, for a single particle,[8] where d_u is the particle diameter and λ_u is the mean free path of the particle, and for a pair of particles,

The Fuchs kernel (Equation (7[7] )) is used in Equations (5[5] ) and (1[1] ) for all the analytical and numerical calculations, respectively. To evaluate the effective coagulation coefficient for fractals, the Fuchs kernel is modified by replacing the volume-equivalent particle diameter with fractal diameter,[9] where d_uf is the fractal diameter, d_u is the volume-equivalent diameter, d_u0 is the diameter of the individual spherule that forms the fractal, and D_f is the fractal dimension. The fractal shapes enhances the coagulation rate compared to that of compact spherical particles. We have not considered D_f < 2, since this case requires modification for the effective cross-section area for kinetic fluxes within the “Fuchs limiting sphere” and hence requires additional thought. This will be carried out in the future and for the present we restrict to cases of D_f ≥ 2. Equation (7[7] ) is substituted in Equation (5[5] ) and the integral is evaluated using Mathematica (Wolfram Inc. 2005) for various fractal dimensions and initial particle diameter.

It must be emphasized that the effective coagulation coefficient method is more of a simplified procedure (rather than a systematic approximation), which cannot be rigorously justified a priori by theoretical analysis. However, the usefulness of this method is justified a posteriori by validating it against numerical results in the following section.

Results and discussion

Validation of the effective coagulation coefficient model

The steady-state results predicted by the effective coagulation coefficient model (Equation (4[4] )) are validated against numerical solution of the coagulation equation with the Fuchs kernel for various emission rates and fractal dimensions. The numerical model solves the coagulation equation with source and sinks as described in Equation (1[1] ) using the semi-implicit nodal method (Prakash et al. 2003; Anand et al. 2012). The size distribution of emitted particles from the continuous source is lognormal with a count median diameter of 10 nm and geometric standard deviation of 1.3. The size-dependent wall deposition rate is considered for the numerical simulations. However, in all the analytical simulations, an equivalent effective wall deposition rate (λ_w) of 0.45 h⁻¹ (obtained by averaging the size-dependent rates over the size spectrum) is added to the ventilation removal rate (Anand et al. 2016a). The predicted number concentrations by the “effective coagulation coefficient” model are plotted as a function of ventilation rates (Figure 1) along with those obtained from numerical simulation with Fuchs kernel. The numerical simulations show that the steady-state condition for the total number concentration reaches after ∼2 h for the minimal removal rate of 0.45 h⁻¹.

Figure 1. Total number concentration vs. ventilation rate for (a) high and (b) medium source emission rates—comparison of models.

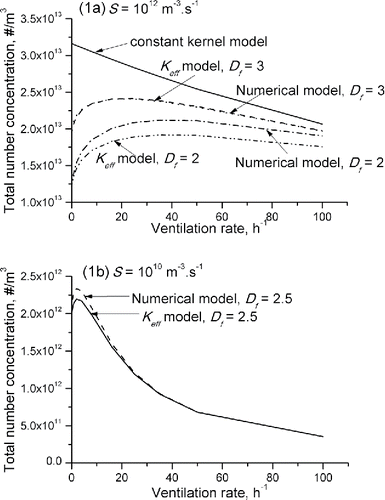
Figure 1a shows a case study for high emission rate (10¹² m⁻³ s⁻¹) and for D_f = 2, 3 along with results for the constant kernel model (Equation (3[3] ) with K = 2 × 10⁻¹⁵ m³ s⁻¹). The constant kernel model result shows the expected monotonic fall of concentration with ventilation rate. On the other hand, both effective coagulation coefficient and numerical models clearly show the peaking behavior (at CAERs ∼ 22 h⁻¹ and 40 h⁻¹ for D_f = 3 and 2, respectively). The peak positions are closely reproduced by both the models for both the D_f cases thereby validating the applicability of the K_eff model. Besides, the concentration plot predicted by K_eff model almost merges indistinguishably with numerical plot for D_f = 3 and differs (underestimates) by not more than 9% for D_f = 2. The reasons for this difference could be due to the fact that the coagulation coefficient for fractal particles possesses a much larger variation across the entire size range as compared to compact particles. Hence, the error introduced by using a single, size averaged representative value (K_eff) for describing poly-disperse coagulation shows up more prominently for fractals as compared to compact particles. Another case study carried out with medium emission rate (10¹⁰ m⁻³ s⁻¹) and for D_f = 2.5 (Figure 1b) also confirms close agreement for CAER and a deviance of less than 6% for concentration. These studies clearly demonstrate that the effective coagulation coefficient model captures the steady-state concentration variations reasonably well over a wide range of ventilation rates, source strengths and fractal dimensions.

Effect of Hamaker–van der Waals and viscous forces on the coagulation process

Apart from Brownian diffusion (Equation (7[7] )), other important processes that contribute to the coagulation kernel are gravitational collection, turbulent inertial motion, turbulent shear, and van der Waals forces; however, their contribution to the coagulation kernel depends on the particle size and ambient conditions. The gravitational collection, turbulence shear, and inertia effects are very important only for large-sized particles (∼10 μm) and at atmospheric conditions with higher turbulent kinetic energy (TKE) dissipation rate (Jacobson 2005). In contrast, the present case of ultrafine particle emission in the ambient indoor atmosphere deals with far smaller particles and much lower TKE dissipation rate ∼ (1–5) cm² s⁻³. For these situations, only van der Waals and viscosity forces are more likely to enhance the coagulation kernel (Wallace et al. 2008).

An interpolation formula for the van der Waals/viscous collision kernel between free-molecular and continuum regimes (Alam 1987; Jacobson 2005) is given by[10] where are diffusion coefficients, are mean velocities of interacting particles of volumes u and u’, respectively. and are individual correction factors for the continuum and free-molecular regimes. is given by[11] where is a viscous-force correction factor to the diffusion coefficient in the continuum regime, is the sum of the individual diffusion coefficients of particles ( ), is a relative diffusion coefficient between particles u and u’. The ratio is given by[12]

is the van der Waals interaction potential given by[13] where A_H is the Hamaker constant, which depends on van der Waals properties of each substance, whose values generally range from 20 to 200.

, the individual correction factor in the free-molecular regimes, is then given by[14]

The derivatives in the above expression are obtained using Mathematica (Wolfram Inc. 2005),[15] [16]

The integral in W_c and W_k are evaluated using Gauss–Legendre quadrature formula numerically after transforming the variable r using the relation so that limits becomes , and then the coagulation kernel is calculated using the interpolation formula (Equation (10[10] )). This formulation is applicable only for compact spherical particles and there appears to be no simple prescription to extend this for the fractal particles.

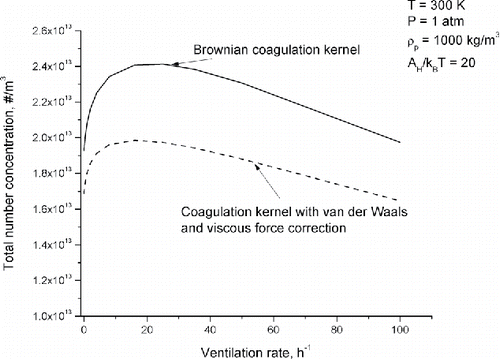
In view of the extremely complicated steps involved in evaluating this kernel, we could not implement it for evaluating “Hamaker–van der Waals and viscous corrected effective coagulation coefficient” (K_eff). Instead, we make an assessment of the effect of inclusion of Hamaker–van der Waals and viscous forces by using the numerical model. Figure 2 shows the variation (with respect to ventilation rate) of the steady-state total number concentration obtained with and without the inclusion of Hamaker–van der Waals and viscous forces. The source emission rate of 10¹² m⁻³ s⁻¹ and A_H/kT = 20 (for water) are assumed in the calculations. From Figure 2, it is seen that the steady-state number concentration is reduced after inclusion of Hamaker–van der Waals and viscous forces in the coagulation kernel, as compared to the pure Brownian kernel results. This is due to the enhancement of the coagulation coefficient of the ultrafine particles (i.e., maximum enhancement factor of ∼2.75 for the coagulation rate of particles with particle Knudsen number >10). In the case of pure Brownian kernel, CAER value is around 16 h⁻¹ with a steady-state number concentration of ∼2.4 × 10¹³ m⁻³. After the inclusion of the effect of Hamaker–van der Waals and viscous forces, CAER remains at the same value of ∼16 h⁻¹ but the number concentration reduces to ∼1.9 × 10¹³ m⁻³. It thus appears that while the inclusion of Hamaker–van der Waals forces lowers the peak concentrations by about 20%, it does not affect the CAER values at which this peak occurs. One will not be too much off the mark in assuming that this would be the situation in general, regardless of whether the particles are compact or fractals. In view of these observations, we have not included these forces in the foregoing analyses.

Figure 2. Effect of Hamaker–van der Waals and viscous forces on the steady-state number concentration—numerical model results.

Estimation of effective coagulation coefficient (K_eff) for various fractal dimensions

Using Equations (5[5] ), (6[6] ), and (9[9] ), K_eff for three different fractal dimensions (D_f −2, 2.5, 3) are estimated and plotted in Figure 3 as a function of β. The K_eff values are obtained for an initial particle diameter of 10 nm. From Figure 3, it is seen that K_eff for large β values are the lowest, and it increases with decreasing values of β. This is due to the fact that for large β, the aerosol evolution is controlled by ventilation rather than coagulation and K_eff will essentially be K_Fuchs(u_0, u₀), i.e., that corresponding to the primary particles emitted by the source. Coagulation process dominates in the region of low β and accordingly K_eff increases to its maximum value. While the ratio between the maximum and minimum values of K_eff is about 3.7 for compact particles (D_f = 3), it is higher for fractal particles, increasing up to 12 for D_f = 2. These results are consistent with the well-known fact that the coagulation effects are more pronounced for fractal particles as compared to compact particles. Representation of K_eff variations in terms of empirical formulae may be more useful for the purposes of computations using Equation (4[4] ). The curves in Figure 3 are best fitted with the logistic function,[17] and the fitting parameters (A₁, A₂, B, C) are tabulated in Table 1 for different values of D_f. A₁ represents the large β limit, A₁+A₂ is the limit at low β (∼0.005) and C represents the steepness of the transition of K_eff between these values. Although the values of C are similar for all the three cases, it is highest for compact particles, thereby implying a steeper fall of K_eff with β for this case. Equation (17[17] ) along with Equation (4[4] ) may be easily implemented in a program for estimating source emission rates, if the number concentrations are available from experimental measurements. If on the other hand, source strength is given, one may solve for number concentrations by root finding methods through built-in programs in Mathematica or by employing bisection or Newton–Raphson methods.

Figure 3. Effective coagulation coefficient vs. for an initial particle diameter (d_u0 = 10 nm) at the source.

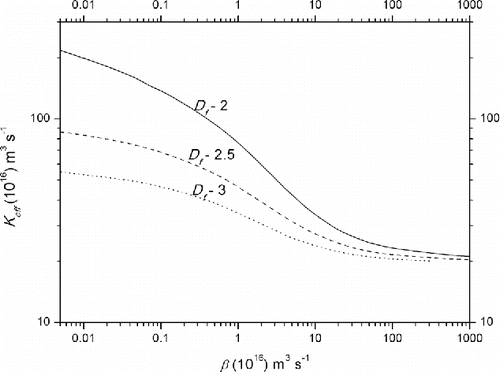
Table 1. Parameters to estimate K_eff (Equation (17[17] )) for various D_f.

Df	A1	A2	B	C
2	18.638	226.242	8.026	0.555
2.5	18.914	70.389	2.228	0.616
3	19.255	36.540	1.719	0.657

CAERs for aerosol systems with different D_f

The steady-state number concentrations (N₀) are evaluated for three source emission rates (low – 10⁸ m⁻³ s⁻¹, medium – 10¹⁰ m⁻³ s⁻¹, high – 10¹² m⁻³ s⁻¹) using Equation (4[4] ) along with appropriate fitted formula for K_eff, for different fractal dimensions (Equation (17[17] ) and Table 1). A uniform value of surface deposition rate (λ_w) of 0.45 h⁻¹ is assumed. This helps to establish a steady-state concentration even when there is no air exchange rate. Values of normalized concentration, i.e., N₀(λ)/N₀(λ = 0) are plotted against ventilation rate (λ) in Figure 4 for fractal dimensions, D_f = 2, 2.5, and 3 and for different emission rates, classified above. For high emission rates, the steady-state values increase between the low λ regime and medium λ regime, reach a peak and then decrease with ventilation rate in the high λ regime. The increase in the steady-state value between the low λ regime and medium λ regime is due to the removal of large size particles in the system by the small ventilation thereby reducing the effective coagulation rate. For low emission rates, there is no peak and the concentration tends to decrease monotonically as the ventilation rate increases, for all D_f values.

Figure 4. Steady-state number concentration ratio (N₀(λ)/N₀(λ = 0)) vs. ventilation rate for different fractal dimensions (D_f) and source strengths (S). N₀(λ = 0) is different for each of the emission scenario.

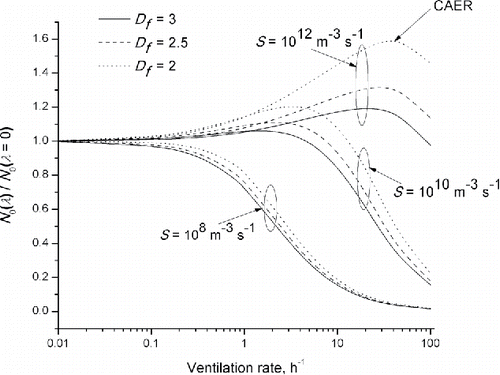
While the occurrence of the peaking behavior is similar between fractals and compact particles (Anand et al. 2016a), fractal particles exhibit more pronounced peaks in the normalized concentrations as compared to the latter. This is primarily due to the higher sensitivity of the dependence of hetero-coagulation coefficient with respect to size for fractals as compared to compact particles. It must be pointed out that although the normalized concentrations are higher for fractals than for compact particles, actual steady-state number concentrations are lower for fractals (Figure 5) because their coagulation rates are larger.

Figure 5. Steady-state number concentration vs. ventilation rate for fractal dimensions (2, 2.5, 3); S = 10¹² m⁻³ s⁻¹.

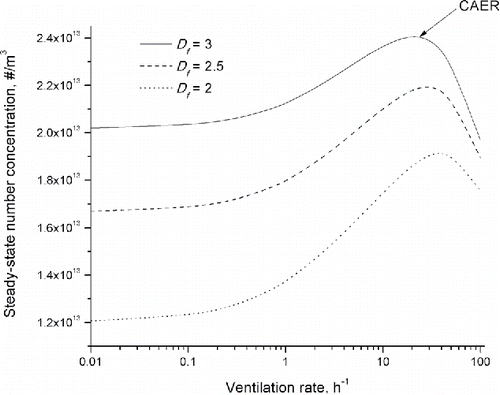
The values of CAER, the practically relevant quantity, are tabulated in Table 2 for different source strengths and fractal dimensions. The CAER values are markedly higher for fractals because of the greater dominance of coagulation as compared to that for compact particles. For strong sources, the critical air-exchange rates required to break-even the concentration peaking effect are 24 h⁻¹ for D_f = 3 and 39 h⁻¹ for D_f = 2. As discussed previously (Anand et al. 2016a), for visible reduction of concentrations, one requires far higher ventilation rates, and the concept of Half-Value Air-Exchange Rates (HaVAER) was postulated. Since such strong sources are not uncommon in indoor cooking situations (Dhaniyala et al. 2011) across several parts of the world, this study indicates the near impossibility of controlling UFP number concentrations using ventilation technique. On the other hand, if the source emission rates are brought down to medium levels by improved stove technologies, then CAER values (∼3 h⁻¹) and the corresponding HaVAER values will be within practically achievable range (Anand et al. 2016a).

Table 2. CAER values for different S and D_f.

	CAER (h^−1)
	Df – 2	Df – 2.5	Df – 3
Low S (10^8 m^−3 s^−1)	—	—	—
Medium S (10^10 m^−3 s^−1)	3.5	2.4	1.6
High S (10^12 m^−3 s^−1)	39	30	24

Thus, the number concentration of particles exhibits great persistence especially for strong UFP emission sources. Apart from providing a simpler computational tool, the effective coagulation coefficient approach also serves to explain this persistence and the counter-intuitive, ventilation-dependent peaking effect. The argument is as follows. The steady-state concentration exists as a balance between UFP emission, evolution by coagulation and loss by removal process (λ_w + λ) at all sizes and the UFPs contribute overwhelmingly to the total number concentration (N₀). Let us consider the situation of a small ventilation rate well below CAER, yet much larger than a specified small value of λ_w. Then for UFPs, loss due to hetero-coagulation with large particles dominates over loss due to ventilation removal whereas for large particles ventilation removal remains the only relevant loss mechanism. As the ventilation rate is increased slightly, it will affect (enhances) the removal rate of large particles more predominantly (than that of UFPs) thereby lowering their concentration. This in turn lowers the overall removal rate of UFPs by lowering their hetero-coagulation rate (small–large particles interaction), which is reflected in a systematic reduction in the value of K_eff (Figure 3) of the system with increase in for all values of D_f. Thus, a small increase in ventilation rate will cause a decrease in the over-all removal rate of UFPs which will then result in their concentration increase (since UFP's being constantly injected all the time). This process will continue to operate until the peak value at CAER is reached and beyond this point, the ventilation rate will virtually dominate over coagulation loss rate for both large and small particles, there-by giving rise to a monotonic fall in the number concentrations. Essentially, the larger the K_eff values in the low β regime, the higher will be the CAER values as well as the sharpness of the concentration peaks. This analysis provides a new perspective that the effective coagulation coefficient carries the signature of the behavior of number concentration with ventilation rate.

Conclusions

In this study, we have successfully validated and demonstrated the utility of the concept of an effective coagulation coefficient (K_eff) approach for addressing the combined effect of coagulation, source strength, and removal mechanism on the steady-state behavior of ultra-fine particles produced from strong emission sources. The approach not only provides a simple alternative to the computationally intensive numerical methods for problems involving steady-state coagulation with Fuchs kernel, but also provides greater insight into the counter-intuitive concentration-peaking effect with respect to ventilation and the associated concept of Critical Air-Exchange Rate (CAER). It also predicts more pronounced concentration peaking effects for fractal particles (D_f < 3) as compared to compact particles (D_f = 3), in agreement with the corresponding numerical solutions. The method of constructing the K_eff essentially transforms the size-dependent Fuchs kernel into a concentration-dependent effective kernel, thereby capturing the hetero-coagulation effects in a self-consistent manner. The method is attractive for practical applications such as (1[1] ) assessment of long-term exposures to ultra-fine particles from indoor cooking sources, (2[2] ) predicting the long-term effectiveness of ventilation-based UFP control strategies for strong emission sources, and (3[3] ) for applying coagulation corrections to number emission rate estimations for combustion and other sources.

Notwithstanding the above-mentioned simplicity and advantages, the K_eff method, as it stands, is inadequate for addressing the transient behavior of the total number concentration. This is partly because, K_eff will then be time dependent and the nonlinear algorithm for evaluating it at every timestep becomes formidable almost as much as the original time-dependent coagulation equation itself. This is an aspect that requires further investigation. On the whole, it may be concluded that, seen from a toxicological perspective, the K_eff approach possesses considerable practical utility for long-term assessment of nano-particle exposures from strong emission sources.