Analytical expression for the friction coefficient of DLCA aggregates based on extended Kirkwood–Riseman theory

ABSTRACT

We use a self-consistent field method, which we have previously validated, to calculate the translational friction coefficient of fractal aerosol particles formed by diffusion-limited cluster aggregation (DLCA). Our method involves solving the Bhatnagar–Gross–Krook model for the velocity around a sphere in the transition flow regime. The velocity and drag results are then used in an extension of Kirkwood–Riseman theory to obtain the drag on the aggregate. Our results span a range of primary sphere Knudsen numbers from 0.01 to 100 for clusters with up to N = 2000 primary spheres. Calculated friction coefficients are in good agreement with experimental data and approach the correct continuum and free molecule limits for small and large Knudsen numbers, respectively. Results show that particles exhibit more continuum-like behavior as the number of primary spheres increase, even when the primary particle is in the free molecule regime; as an illustrative example, the friction coefficient for aggregates with primary sphere Kn = 1 is approximately equal to the continuum friction coefficient for N > 500. We estimate that our calculations are within 10% of the true values of the friction coefficients for the range of Kn and N presented here. Finally, we use our results to develop an analytical expression (Equation (38[38] )) for the friction coefficient over a wide range of aggregate and primary particle sizes.

Copyright © 2017 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction

Aerosol particles formed at high temperature are often fractal aggregates described under the assumption of equally sized spherical primary particles as[1] where N is the number of primary spheres, R_g is the radius of gyration of the agglomerate, a is the primary sphere radius, and d_f  and k₀ are the fractal dimension and prefactor.

The transport properties of these particles (e.g., the diffusion coefficient, settling velocity, and electrical mobility) can be related to the particle scalar friction coefficient , which is defined by the relationship between the drag force and the relative velocity between the particle and the fluid,[2] where and are the velocities of the fluid and the particle, respectively. Knowledge of the friction coefficient is crucial to predicting particle diffusional, phoretic, and electrostatic behavior in real-world applications.

For the simple case of a sphere with radius a, the friction coefficient is given by Stokes' law,[3] where is the gas viscosity, Kn = λ/a is the Knudsen number, λ is the gas mean free path, and C_c is the Cunningham slip correction factor,¹ [4]

Spheres that are very large compared to the mean free path () are in the continuum regime. In this case, the slip correction is unity, and the continuum friction factor is simply[5]

Spheres that are very small compared to the mean free path are in the free molecule regime, where the friction coefficient is given by Epstein's equation[6]

The momentum accommodation coefficient α is equal to unity for purely diffuse reflection and zero for purely specular reflection at the surface of the particle. Epstein (1924) determined that most collisions are diffuse.

Determination of the friction coefficient is much more complicated for fractal aggregates. In the continuum regime, the friction coefficient is given by[7] where R_H is the particle hydrodynamic radius, which may be obtained by applying either the Kirkwood–Riseman (Chen et al. 1984; Meakin et al. 1985; Meakin and Deutch 1987; Lattuada et al. 2003) or Hubbard–Douglas (Hubbard and Douglas 1993; Zhou et al. 1994) method. For the free molecule regime, one can obtain the friction coefficient using a ballistic approach (Chan and Dahneke 1981; Meakin et al. 1989; Mackowski 2006), such that the friction coefficient is related to the orientation-averaged projected area of the particle.

Both computational and experimental results seem to support power-law-type relationships between the number of primary spheres in the aggregate and the friction coefficient:[8]

Sorensen (2011) reviewed available experimental data for particles formed by diffusion-limited cluster aggregation (DLCA) and proposed exponents of 0.46 for N < 100 and 0.56 for N > 100 in the continuum regime and 0.92 for all N in the free molecule regime.

In many practical applications, the primary sphere radius is smaller than the gas mean free path, such that the primary spheres may be in the free molecule flow regime. For situations in which the primary sphere Knudsen number is in the free molecular regime, many researchers (Chan and Dahneke 1981; Meakin et al. 1989; Mackowski 2006) have used free molecular techniques to compute the scalar friction coefficient for fractal aerosol particles. However, the agglomerate size characterized by the radius of gyration may be comparable to or larger than the mean free path, which leads to some ambiguity about the appropriate flow regime. Therefore, an alternate approach is needed to determine the friction coefficient for particles whose geometric measures (primary sphere radius and radius of gyration) lie in the transition flow regime.

To date, most of the approaches for transition regime drag are based on extrapolation of free molecule or continuum methods to the transition regime or power-law fits to experimental data. One exception is the adjusted sphere method (ASM) developed by Dahneke (1973) and Zhang et al. (2012), which applies a slip correction to the continuum drag based on an aggregate Knudsen number,[9] [10] where the hydrodynamic radius and the projected area PA are continuum and free molecular measures of particle size, respectively. Zhang et al. (2012) found good agreement between the friction coefficient computed using the adjusted sphere method and direct simulation Monte Carlo (DSMC) results for a dimer and for open (, ) and dense (, ) 20-particle aggregates for a range of aggregate Knudsen numbers. For this approach, one must obtain the hydrodynamic radius and projected area, either through transmission electron microscopy (TEM) analysis or through moderately expensive computational models mentioned previously.

Recently, we developed a self-consistent field method to compute the friction coefficient for a fractal aggregate across the entire Knudsen range (Corson et al. 2017). This method is based on Kirkwood–Riseman theory for the drag on a particle or macromolecule in continuum flow. Initial applications of the self-consistent method show good agreement with DSMC results (Zhang et al. 2012) and with the adjusted sphere method.

In this work, we apply our self-consistent field method to compute the scalar friction coefficient for a wide range of primary sphere radii and aggregate sizes. We compare our results to experimental data in the literature (Shin et al. 2009, 2010) and to the predictions of other models that have been developed for the transition regime, including the adjusted sphere method and the correlations developed by Rogak et al. (1993), Lall and Friedlander (2006), and Eggersdorfer et al. (2012).

2. Theoretical methods

2.1. Kirkwood–Riseman theory

Consider an aggregate consisting of N identically sized spherical particles of radius a. Kirkwood and Riseman (1948) demonstrated that the force on the ith spherical element can be obtained by considering the effects of all the other elements on the fluid flow pattern, as described by[11]

Here, is the friction coefficient on the primary spheres as given by Stokes' law, is the unperturbed (or free stream) velocity of the fluid at particle i,² and is the hydrodynamic interaction tensor. The original version of the theory uses the Oseen tensor for .

Later researchers extended this approach to fractal aerosol particles (Chen et al. 1984; Meakin et al. 1985; Meakin and Deutch 1987) and colloids (Lattuada et al. 2003). These later studies used the modified form of the Oseen tensor derived independently by Rotne and Prager (1969) and Yamakawa (1970):[12]

Here, is the vector from the ith particle to the jth particle.

These applications of Kirkwood–Riseman theory involve objects in continuum flow. We now wish to extend this approach to the transition flow regime, using appropriate expressions for the friction coefficient and the hydrodynamic interaction tensor .

We start by dividing Equation (11[11] ) by the friction coefficient to give the fluid velocity at a point [13]

In other words, the fluid velocity at a point is the sum of the free stream velocity and the velocity perturbations caused by each primary sphere in the particle.

For uniform Stokes flow around an isolated sphere, the velocity obtained by solving the Navier–Stokes equation can be written in the form[14] where[15] is the velocity perturbation tensor at the point and r is the distance of that point from the origin (i.e., the center of the sphere). We can also write the velocity as[16] where[17] and is the drag force on the sphere.

The tensor is the same as the Rotne and Prager hydrodynamic interaction tensor (Equation (12[12] )), with the exception of the factor of 2 in the term. Since we are primarily concerned with the velocity perturbation at distances greater than 2a from the sphere, we can ignore the factor of 2 with minimal error and replace in Equation (11[11] ) with . Now, the drag force on the ith sphere of a fractal particle is[18] where is the velocity perturbation at the ith sphere caused by the jth sphere.

Of course, there is no reason to make the approximation for continuum flow. However, this approximation allows us to extend Kirkwood–Riseman theory to the transition regime because solving for the velocity profile around an isolated sphere in the transition regime is considerably easier than explicitly considering the hydrodynamic interaction between two spheres in the transition regime. Numerous solutions of the former problem are available in the literature (Sone and Aoki 1977; Lea and Loyalka 1982; Law and Loyalka 1986; Takata et al. 1993), whereas we have not been able to find any reference to the latter problem.

Before we proceed further with our derivation of the force on a fractal aggregate in the transition regime, we will first consider the solution of the kinetic equation for the velocity around a sphere.

2.2. Flow around a sphere

Consider steady flow around a sphere in the transition regime. The gas density, velocity, and temperature far from the sphere are , , and , respectively. In the absence of external forces, the Boltzmann equation can be written as[19] where is the velocity distribution function and is the gas molecular velocity. The right-hand side of Equation (19[19] ) is the collision operator, which describes the evolution of the distribution function as a result of collisions between gas molecules. The full collision operator is exceedingly complicated, so we will consider the simplified collision operator proposed by Bhatnagar et al. (1954):[20]

Here, is the collision frequency and is the Maxwellian velocity distribution at point [21] where m is the mass of a gas molecule, k_B is the Boltzmann constant, and n, , and T are the local gas number density, bulk velocity, and temperature. Essentially, the BGK model assumes that the non-equilibrium distribution f relaxes to the equilibrium distribution after one collision, with the collision frequency given by , where is the gas pressure.

If the velocity of the gas around the sphere is small relative to the thermal speed of the gas molecules and the perturbation caused by the sphere is relatively small, then the distribution function can be linearized, giving[22]

The Maxwellian distribution represents a gas with zero velocity at the far-away gas density and temperature. The first two terms of the linearization represent the distribution far from the sphere, while the function h represents the perturbation to the distribution caused by the sphere. Likewise, the linearized local Maxwellian distribution can be written as[23] where , , and are perturbations to the density, velocity, and temperature of the gas defined below as moments of the distribution function h.

Now define the following non-dimensional variables:[24]

The final expression for the non-dimensional radius makes use of the previously defined expressions for the collision frequency and the viscosity of a hard sphere gas. With these definitions, the linearized, non-dimensional BGK equation is[25] with the moments related to the gas number density, velocity, and temperature by[26]

The integrals in the moment equations represent triple integrals over the entire molecular velocity space. The boundary conditions for flow around a sphere are diffuse reflection at the sphere surface and vanishing h far from the sphere.

Lea and Loyalka (1982) solved the above problem numerically for the number density and velocity perturbations around the sphere assuming isothermal conditions (). Their solution procedure involved solving for the perturbations using a Gaussian quadrature out to a radius of , or about 8.9 mean free paths from the surface, then matching the numerical solution at to a trial function based on the continuum (Stokes flow) solution. They adjusted the numerical coefficients of the trial function until the inner and outer solutions converged. Law and Loyalka (1986) applied this approach for non-isothermal conditions.

We follow the general approach of Loyalka and colleagues, but using the asymptotic solution to the BGK equation for large r (Takata et al. 1993) as the trial function for . Like in continuum flow, the velocity in the transition regime can be written as separable radial and angular components[27] where and are functions describing the radial dependence of the r- and θ-components of the velocity perturbation obtained by solving the BGK equation. These functions depend on the primary sphere radius, so that the solution procedure applies to a specific Knudsen number. We can also obtain the friction coefficient from the solution of the BGK equation. In general, our velocity results compare well with the velocities reported by Takata et al. (1993) based on their solution of the linearized Boltzmann equation, and our drag results compare well with Millikan's data (Millikan 1923). Note, however, that our calculated friction coefficients for the near continuum regime (Kn < 0.1) are less accurate, likely due to numerical error that is more prominent for lower Knudsen numbers.³ We will discuss this point further in Section 3.2.

2.3. Application of BGK results to Kirkwood–Riseman theory

We now apply Kirkwood–Riseman theory to particles in the transition regime by explicitly writing the friction coefficient and velocity tensor in Equation (18[18] ) as functions of the primary sphere Knudsen number[18] where the velocity perturbation tensor is[28]

For primary spheres separated by distances , and are tables of data; for spheres separated by greater distances, and are the asymptotic solutions to the BGK equation for large r with coefficients chosen to match the inner solution for that Knudsen number.

Equation (18[18] ) gives the force on each primary sphere for a given flow velocity. (Dividing Equation (18[18] ) by the friction coefficient gives the velocity at each primary sphere.) The total force on the particle is the vector sum of the force on each primary sphere. We obtain the friction tensor by solving Equation (18[18] ) for the velocity in three mutually orthogonal directions. The force on the particle for arbitrary fluid velocity is then[29]

In the slow rotation limit, the scalar friction factor is the harmonic mean of the three eigenvalues of the friction tensor (Happel and Brenner 1965). In the fast rotation limit, the scalar friction factor is the arithmetic mean of the eigenvalues (Li et al. 2014).

3. Results and discussion

We have calculated the scalar friction coefficient for a large range of primary sphere sizes and number of primary spheres. All calculations involve particles with d_f = 1.78 and k₀ = 1.3, which are representative of aggregates formed by DLCA. The particles have been generated with an algorithm that imitates cluster–cluster aggregation. Due to limitations with our fractal generator, aggregate size is capped at 2000 primary spheres. In this article, we are reporting the friction coefficient for the slow rotation limit, meaning we are taking the harmonic average of the friction tensor eigenvalues.

3.1. Comparison to experimental data and power-law models

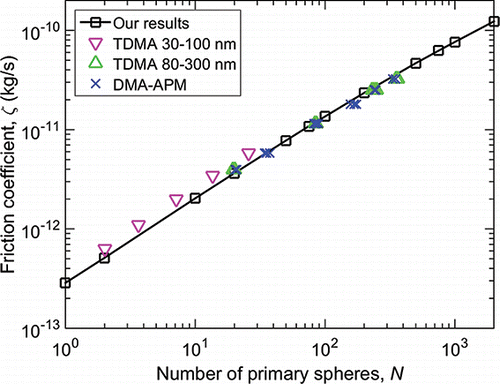
Figure 1 compares the results of our friction coefficient calculations for a primary sphere Knudsen number of 7 to tandem differential mobility analyzer (TDMA) and combined DMA and aerosol particle mass analyzer (DMA-APM) results (Shin et al. 2009, 2010). The primary sphere size for the TDMA 80–300 nm and DMA-APM curves was experimentally determined to be 19.5 nm with a standard deviation of 6.1 nm, while the primary sphere size is assumed to be 19.5 nm for the TDMA 30–100 nm curve (Shin et al. 2010). Our self-consistent field results compare very well to the experimental data. Furthermore, the self-consistent results support the observation of Shin et al. (2009) that deviations from a power-law relationship at high N may be due to hydrodynamic interactions among the primary spheres in the aggregate.

Figure 1. Friction factor results for fractal aggregates with primary sphere diameter 19.5 nm in ambient air (Kn = 7). TDMA and DMA-APM results (Shin et al. 2009, 2010) are shown for comparison.

Next, we compare our friction coefficient results to the results from three models for DLCA particle drag in the transition regime.

Lall and Friedlander's (2006) model,[30] is based on Chan and Dahneke's (1981) calculations for the drag on straight chain aggregates in the free molecular regime. Here, c* = 9.17 is a dimensionless drag force that assumes 93% diffuse reflection and 7% specular reflection. Chan and Dahneke (1981) argued that Equation (30[30] ) should be valid for aggregates with N > 12 that have occasional kinks and branches. Implicit in Lall and Friedlander's model is that the aggregate behaves as if it is in the free molecule regime as long as the primary spheres are in the free molecule regime. Eggersdorfer et al.'s (2012) model relates the mobility radius—or the radius of a sphere that has the same drag as the particle—to the number of particles through the relationship[31] where and are based on DLCA simulations. The friction coefficient is obtained by substituting the mobility radius into Stokes' law[32]

Finally, Rogak et al. (1993) noted that the mobility radius is approximately equal to the orientation-averaged projected area radius for particles with mobility radii less than 200 nm. Thus, we compare our results to the friction coefficient calculated using the particle projected area:[33]

We also compare our results to friction coefficients calculated using the adjusted sphere method, Equation (9[9] ). We computed the particle hydrodynamic radius using the Zeno code (Mansfield et al. 2001), which uses the Hubbard–Douglas approximation, and we computed the projected area using our own algorithm.

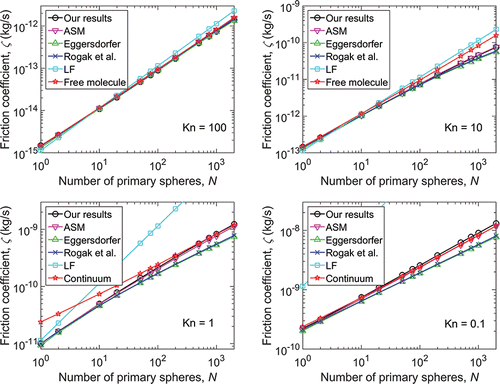
Figure 2 shows the comparison between our results and the aforementioned models for primary sphere Knudsen numbers of 100, 10, 1, and 0.1, corresponding to sphere radii of 0.68 nm, 6.8 nm, 68 nm, and 680 nm, respectively. We also include free molecule results obtained with our own free molecule code and continuum results obtained with Zeno on select figures. All of the models give results for Kn = 100 for all N that are very similar to the free molecular limit, which is not surprising given the very small primary sphere size. However, for large N all of the models—with the exception of the Lall and Friedlander model—begin to diverge from the free molecular limit for Kn = 10 primaries, suggesting that hydrodynamic interactions among the primaries are important even at this primary Knudsen number. Interestingly, our results and the ASM results approach the Zeno continuum results as N increases for Kn = 1. Finally, our Kn = 0.1 results compare favorably to the continuum results and to the ASM.

Figure 2. Comparison of self-consistent field results to other models for the scalar friction factor for (a) Kn = 100, (b) Kn = 10, (c) Kn = 1, and (d) Kn = 0.1. Results are for particles in ambient air. Where appropriate, free molecular results from a ballistic algorithm and continuum results from the Zeno code are displayed for reference.

Figure 3 shows the ratio between the predictions of the aforementioned models and our friction coefficient results for N = 2000. Values of unity represent perfect agreement between our results and other models. Once again, we see very good agreement with the adjusted sphere method across the entire Knudsen range. The Eggersdorfer and Rogak friction coefficients are notably lower than our results at low to moderate primary sphere Knudsen numbers, though it is important to reiterate that this comparison is for large aggregates (N = 2000). The agreement between the models is better for smaller aggregates at lower primary sphere Knudsen numbers, as indicated in Figure 2.

Figure 3. Ratio of friction coefficients from other models to our results for N = 2000. Free molecule and continuum results are calculated using our own Monte Carlo algorithm and the Zeno algorithm, respectively. For the upper plot, our friction coefficient results are obtained using the calculated drag from the BGK model. For the lower plot, our friction coefficient results use the Cunningham slip formula for the monomer friction coefficient ( in Equation (18[18] )). Free molecule results for Kn < 15, LF results for Kn < 35, and continuum results for Kn > 15 are more than twice our self-consistent field results and thus do not appear in the plots above.

Additionally, Figure 3 illustrates how the aggregate approaches the continuum limit for decreasing Knudsen number: the ratio of the continuum result calculated using the Zeno code to our Kirkwood–Riseman results is near unity for a primary sphere Knudsen number as high as 2. This figure explicitly shows the difference between using the monomer friction coefficient from the BGK model solution and using the monomer friction coefficient from the Cunningham slip correction factor. Differences are largest for small Knudsen numbers, though results are in good agreement with the continuum results at low Knudsen number whether we use the BGK friction coefficient or the Cunningham slip coefficient for in Equation (18[18] ).

Figure 4 clearly illustrates how the friction coefficient diverges from the free molecular limit and exhibits more continuum-like behavior as the particle size (both in terms of N and a) increases. Here, calculated friction coefficients are normalized to the monomer friction coefficient for several primary sphere Knudsen numbers in the transition regime. The power-law exponent (i.e., η from Equation (8[8] )) decreases from a value of approximately 0.9—corresponding to the free molecule regime—as both the number of primary spheres and the primary sphere size increases, until it reaches a limit of approximately 0.54 for the continuum regime. The free molecule and continuum values are in agreement with previous observations (Sorensen 2011). The change in the power-law exponent reinforces the importance of accounting for hydrodynamic interactions among primary spheres, even for fairly open aggregates with primary spheres in the near-free molecular regime.

Figure 4. Normalized friction coefficient results for a range of aggregate sizes.

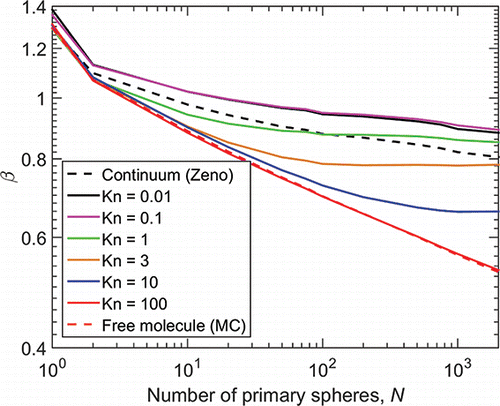
Previously researchers have looked at the evolution of the ratio between the mobility radius and the radius of gyration as the number of primary spheres increases. Figure 5 compares our self-consistent field results for this ratio () to the same calculation in the continuum (where the mobility radius and the hydrodynamic radius are equivalent) and free molecule regimes. Our results agree with previous observations (Meakin et al. 1985; Meakin and Deutch 1987; Lattuada et al. 2003) that β approaches an asymptotic value in the continuum regime. Our results also agree qualitatively with the general observations of Sorensen (2011), specifically Figure 2 of that work. However, our asymptotic results for Kn = 0.01 and Kn = 0.1 are approximately 0.85, which is significantly different (i.e., outside of numerical uncertainty) from the value of 0.75 recommended by Sorensen for the continuum regime. (Note that the Zeno results for the hydrodynamic radius suggest an asymptotic value of for large N.) Figure 5 also notably shows that the Kn = 1, Kn = 3, and Kn = 10 curves also reach asymptotic limits, again suggesting that aggregates approach the continuum regime behavior as the number of primary spheres increases, even when the primary spheres are in the near-free molecule or transition regime.

Figure 5. Relationship between the mobility radius and the radius of gyration for several Knudsen numbers.

3.2. Uncertainty in the calculated friction coefficients

We have demonstrated in this article and in our earlier paper (Corson et al. 2017) that the friction coefficient for DLCA aggregates computed using our extended Kirkwood–Riseman method is in good agreement with experimental data, the continuum and free molecule limits, the adjusted sphere method (Dahneke 1973; Zhang et al. 2012), and direct simulation Monte Carlo results (Zhang et al. 2012). But the question becomes, how accurate is our extended Kirkwood–Riseman method? To answer this question, we provide a very rough estimate of the error in our results.

There are two primary sources of error in our calculations: the BGK results for the velocity around and drag on a sphere in the transition flow regime, and the Kirkwood–Riseman method itself. There is ample discussion in the literature about the accuracy of the Kirkwood–Riseman method for continuum flow; see de la Torre and Rodes (1983), Hubbard and Douglas (1993), Sorensen 2011, and Swanson et al. (1980) for a small sample. We refer the reader to the literature for a thorough discussion. We simply note that in our experience, the Kirkwood–Riseman results (using either the Stokes flow velocity perturbation or the Rotne–Prager tensor) is within 3% of the Zeno results for DLCA aggregates with 10–2000 primary spheres. For N = 10, the Kirkwood–Riseman method underpredicts the friction factor by less than 3%. At N = 2000, the Kirkwood–Riseman result is approximately 2% greater than the Zeno result. Thus, we estimate the error in our calculated transition regime friction coefficients due to the Kirkwood–Riseman method itself is on the order of a few percent.

The second source of error is related to the solution of the BGK equation. From this solution, we obtain the velocity around a sphere and the ratio of the drag on the sphere to the free molecule drag. We can easily estimate the error in the drag on a sphere by comparing our results from the BGK equation to the drag from Stokes' law with the Cunningham slip correction factor. If we apply Davies' coefficients in the slip correction formula, then the calculated error in the BGK drag results is less than 3% for Kn > 0.2. The error is greater at lower Knudsen numbers, as we have noted in Section 2.2; for Kn = 0.01, the BGK drag is approximately 7% greater than the drag from Stokes' law. For most of the Knudsen range, the error in our calculated drag force is comparable to the error in Stokes' law for the slip regime (either due to the model parameters used in the slip correction factor or to experimental uncertainties); the BGK results are only in significant error near the continuum regime.

We can compare our velocity results to the linearized Boltzmann equation results of Takata et al. (1993). The linearized Boltzmann model is more rigorous than the BGK model, but its associated computational cost is much higher than that required to solve the BGK model. Takata et al. present the velocities as a function of the parameter . Our velocity results are generally within 1%–2% of the linearized Boltzmann results for Kn = 0.11, 1.1, and 11 (k_∞ = 0.1, 1, and 10). From these comparisons of our BGK velocity and drag results to the linearized Boltzmann results and to Stokes' law, we estimate that the error in our aggregate friction coefficient results due to the use of the BGK model is less than 5% for Kn > 0.2 and up to 10% for 0.01 < Kn < 0.2.

Combining the two sources of error, we would estimate the overall error in our results to be less than 10% for most of the Knudsen range. This estimate is supported by comparing our friction coefficient results to the ASM results for N = 2000 (Figure 3): the difference is less than 10% for 0.01 < Kn < 100. Also, our calculated friction coefficient results for a primary sphere Knudsen number greater than 5 are within 10% of the direct simulation Monte Carlo results of Zhang et al. (2012) for a 20-particle aggregate with a fractal dimension of 1.78 and a prefactor of 1.3 (Corson et al. 2017).

3.3. Analytical expression for friction coefficients of aggregates

While the Kirkwood–Riseman method is capable of providing the friction coefficient of an aggregate quickly—within seconds for N ∼ 100 and within minutes for N ∼ 1000—it is still not fast enough for use in an aerosol dynamics code. Thus, it would be beneficial to use our friction coefficient results to develop a simple model that provides the friction coefficient given only the number of primary spheres, the primary sphere size, and the gas properties.

Sorensen and Wang (2000) proposed computing the friction coefficient in the transition regime as the harmonic sum of the continuum and free molecule expressions,[34]

For a sphere, the continuum and free molecule friction coefficients are given by Stokes' law (Equation (5[5] )) and Epstein's equation (Equation (6[6] )), respectively. We adopt this approach for our model of the friction coefficient of DLCA aggregates with fractal dimension and prefactor of 1.78 and 1.3.

We start by writing the continuum and free molecule aggregate friction coefficients as power laws[35] where is the continuum (m = c) or free molecule (m = FM) monomer friction coefficient from Equation (5[5] ) or Equation (6[6] ), and and are model parameters obtained from fits to the continuum (Zeno) or free molecule (Monte Carlo) results for N = 1 to 2000. We include the term in the power-law fits to give the correct friction coefficient for a monomer. The free molecule coefficients and are in excellent agreement with Mackowski's correlation for the free molecule friction coefficient ( and for and ; Mackowski 2006). The continuum coefficients and from our Zeno results are also in good agreement with previous studies, as reported in Sorensen's review article (Sorensen 2011).

Taking the harmonic sum of the continuum and free molecule power-law fits, we obtain the following expression for the aggregate friction coefficient as a function of the number of primary spheres, the primary sphere radius, and the gas properties:[36]

Here, B = 1.612 for a hard-sphere gas with a momentum accommodation coefficient of unity (i.e., pure diffuse reflection), consistent with our assumptions throughout this article. For a monomer in the transition regime, the above relation reduces to[37]

Sorensen and Wang (2000) point out that the monomer friction coefficient given by the harmonic sum is up to 10% less than the friction coefficient given by Stokes' law with the slip correction factor. Thus, we apply a correction factor to our model to give the same monomer drag as Stokes' law. The final result is Equation (38[38] ), which provides an easily deployed analytic result to compute the friction coefficient over a wide range of aggregate and primary particle sizes[38]

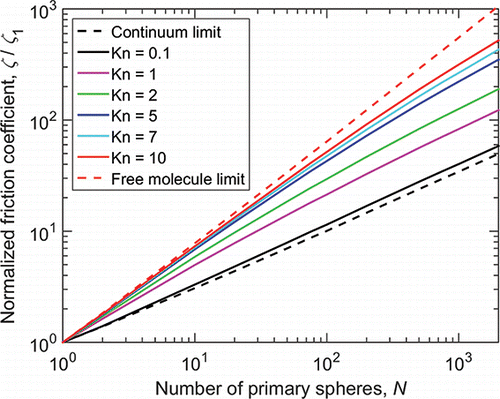
Figure 6 plots the friction coefficient calculated from Equation (38[38] ) as a function of primary sphere Knudsen number and the number of primary spheres. Results are normalized using Stokes' law evaluated for a = λ/Kn. The figure shows a clear transition between continuum behavior, where the friction coefficient is proportional to 1/a for a given number of primary spheres, and free molecule behavior characterized by a 1/a² dependence. (The normalized coefficients have no dependence on a in the continuum and a 1/a dependence in the free molecule regime.) This figure shows that the transition from the continuum regime to the free molecule regime occurs at larger Knudsen numbers as the number of primary spheres increases, demonstrating once again that particles exhibit more continuum-like behavior as both the Knudsen number and the number of primary spheres increase.

Figure 6. Normalized friction coefficient as a function of the primary sphere Knudsen number and the number of primary spheres, N, calculated using Equation (38[38] ). Friction coefficients are normalized by Stokes' law evaluated at the specified Knudsen number.

Figure 7 shows the error in our fit relative to our self-consistent field results,[39] with given by Equation (38[38] ). The figure presents the error for a range of aggregate sizes and primary sphere Knudsen numbers. Overall, Equation (38[38] ) provides a good fit to our self-consistent field results for all values of N and Kn that we have evaluated. Note that we compare our fit to our self-consistent field results using the semi-empirical slip correction for the monomer drag coefficient, instead of the drag coefficient we obtain by solving the BGK model. As we have stated, this distinction is only significant for monomers near the continuum limit.

Figure 7. Error of our harmonic sum model for the friction coefficient, Equation (38[38] ), relative to our Kirkwood–Riseman friction coefficient results for a range of Knudsen numbers. Error is calculated with Equation (39[39] ); the Kirkwood–Riseman results in this equation use the monomer friction coefficient from Stokes' law instead of the friction coefficient computed from the BGK model.

4. Conclusions

We have presented our self-consistent field results for the translational scalar friction coefficient of DLCA aggregates of 10 to 2000 primary spheres with primary sphere Knudsen numbers between 0.01 and 100. Our results compare well to the experimental data of Shin et al. (Shin et al. 2009, 2010) and to the friction coefficient from the adjusted sphere method (Dahneke 1973; Zhang et al. 2012). We estimate that our results are within approximately 10% of the true friction coefficient for DLCA aggregates up to 2000 primary spheres for 0.01 < Kn < 100, though we would need to compare our results to experimental data over a wide range of primary sphere Knudsen numbers and aggregate sizes to verify this estimate. These results have been obtained by taking the harmonic mean of the eigenvalues of the translational friction tensor. The difference between the harmonic and arithmetic averages of the eigenvalues is generally less than 1%, which is consistent with previous calculations for low-aspect-ratio particles in the free molecule regime (Li et al. 2014). This difference is minor compared to the estimated uncertainty in our results.

One significant finding of this study is that aggregate drag becomes more continuum-like as the number of primary spheres increases, even for primary sphere Knudsen numbers near the free molecule regime. Thus, one should not use free molecule techniques to compute the drag on an aggregate unless the aggregate size is very small with respect to the gas mean free path. This finding supports the theory behind the adjusted sphere method that one can calculate the drag on an aggregate using an aggregate Knudsen number instead of the primary sphere Knudsen number.

Our method is fast, but not fast enough to implement in an aerosol dynamics code. The same is true of the adjusted sphere method, unless one already knows the hydrodynamic radius and projected area of an aggregate. For this reason, we have compared our results to the harmonic sum of power laws for the friction coefficient in the continuum and free molecule regimes. The result presented in Equation (38[38] ) provides an analytical expression for the drag over a range of aggregate and primary particle size. The simple model is within 8% of our self-consistent field results for the entire range of aggregate sizes and primary sphere Knudsen numbers that we have studied. This analysis is for fractal clusters generated using a cluster–cluster aggregation method for a fractal dimension of 1.78 and a prefactor of 1.3.

Notes

¹ In this article, we define the viscosity by the relation , where is the gas density and is the mean thermal speed. This expression describes a hard sphere gas. Furthermore, we use Davies' coefficients (A = 1.257, B = 0.4, and C = 1.1) in the slip correction factor.

² If the flow is uniform, then , where is the uniform velocity.

³ This is because the friction coefficient obtained from our solution of the BGK equation is non-dimensionalized by the free molecule friction coefficient (Epstein's equation). As a result, the friction coefficient decays to zero for decreasing Knudsen number, meaning numerical errors are more prominent for the near-continuum regime.