Improved prediction of intersubject variability in extrathoracic aerosol deposition using algebraic correlations

EDITOR:

• Yannis Drossinos

1. Introduction

For inhaled pharmaceutical aerosols, large in vivo intersubject variability in respiratory tract deposition (Heyder et al. 1982; Rudolf et al. 1994) can confound a priori prediction of device performance in patient populations. Given the costs and ethical concerns associated with clinical trials, alternative approaches for predicting deposition, including in vitro and in silico methodologies, provide useful benchmarks for the evaluation of inhaled aerosol products in the early stages of their development. In vitro models of the human upper airways—both realistic and idealized—have proven useful in estimating extrathoracic deposition and total lung doses of pharmaceutical aerosols (Stapleton et al. 2000; Olsson et al. 2010; Delvadia et al. 2012). At the same time, in silico methods can provide insight into deposition mechanisms that are difficult to examine experimentally (Finlay and Martin 2008). In either case, a typical desired outcome from these nonclinical methodologies is an accurate prediction of average deposition in a target population.

While average deposition in a patient population is indeed useful information, of equal importance is the variation in deposition that can occur between individuals. The notion of using “small,” “medium,” and “large” airway models along with physiologically realistic breathing patterns to quantify deposition variability in vitro has been explored in a number of studies (Olsson et al. 2010; Delvadia et al. 2012). While helpful, these methods require extensive numbers of experimental measurements and are limited by the fact that not every patient group can be captured using the same three given adult geometries. As an alternative, deposition equations like those proposed in the widely adopted International Commission on Radiological Protection (ICRP) Publication 66 (1994) can be used to estimate intersubject variability in deposition. Subsequent to the creation of the ICRP model, additional predictive correlations have been presented in the literature, with some incorporating subject-specific measures of airway geometry that can be obtained with relative ease using modern imaging techniques (Grgic et al. 2004; Golshahi et al. 2013; Cheng et al. 2015).

However, the ability of existing methods to accurately predict intersubject variability in deposition has been called into question by Clark and Hartman (2012), who concluded, using extensive Monte Carlo simulations, that targeted delivery on an individual basis was not a realistic endeavor given the wide variations in central and peripheral doses for aerosols with identical physical properties in different individuals. Indeed, comparisons of extrathoracic deposition correlation predictions versus in vivo data (Yang et al. 2017) support this conclusion, wherein no correlation was able to reliably predict deposition on an individual basis for subjects inhaling nebulized radiolabeled aerosols.

The availability of new in vivo deposition data of nebulized aerosols obtained with modern SPECT imaging that includes measurements of each subject's extrathoracic airway dimensions (Yang et al. 2017) has allowed us to examine specifically whether deposition models, including that proposed by the ICRP (1994), provide accurate predictions of the intersubject variation in extrathoracic deposition. More importantly, we present an empirically derived methodology for estimating population variance in deposition of nebulized aerosols using the predictive correlation of Golshahi et al. (2013). This new method for estimating deposition variance allows for more straightforward and accurate predictions of intersubject variability than are available through existing methods.

2. In vivo study summary

As described by Yang et al. (2017), participants recruited for the in vivo study at the Royal Prince Alfred Hospital and the University of Sydney in Sydney, Australia were healthy non-smokers 18 to 45 years old with BMIs less than 30 kg/m³. Eleven males and eight females of primarily Caucasian or Asian ethnicities were included in the study, with all subjects displaying normal spirometry results. Subjects ranged in height from 156 to 192 cm, with an average of 174 ± 10 cm, and in weight from 50 to 108 kg, with an average of 72 ± 15 kg. Extrathoracic airway measurements were obtained using acoustic pharyngometry, inhalation flow rates during testing were measured using an ultrasonic flowmeter, and particle sizes were measured a posteriori using a Spraytec laser diffraction system across a range of relevant in vivo inhalation flowrates. Subjects inhaled ^99mTc-DTPA-radiolabeled 0.9% saline for a duration of 90 s delivered via a PARI LC Sprint nebulizer driven by a PARI Boy SX compressor. Humidified dilution air was used to ensure the absence of hygroscopic droplet size changes. Immediately after administration, subjects were imaged using SPECT, allowing for quantification of extrathoracic deposition in terms of total deposition. Total deposition was itself defined as the sum of deposition measured in the subject and the exhaled dose captured on a filter. A summary of the relevant parameters obtained during the in vivo study is presented in Table 1, with additional details available in Yang et al. (2017).

Table 1. Summary of relevant parameters from the in vivo study of Yang et al. (2017). MMAD = mass median aerodynamic diameter; GSD = geometric standard deviation.

Parameter	Average ± Standard deviation
Inhalation flowrate, Q (L/min)	19.1 ± 5.6
Inhalation volume, VT (L)	0.90 ± 0.33
Characteristic throat diameter^*, dc (cm)	1.88 ± 0.27
Aerosol MMAD (µm); GSD (−) at Qave	3.71 ± 0.23; 1.96 ± 0.06
Extrathoracic deposition fraction, η (−)	0.193 ± 0.103

* Defined as the square root of the average cross-sectional area of the oropharyngeal region (Golshahi et al. 2013).

3. Intersubject variability with the ICRP deposition model

The extrathoracic deposition correlation advocated by the ICRP (1994) is a sigmoidal function of the particle aerodynamic diameter d_a, the inhalation flowrate Q, the tidal volume V_T, and a scale factor SF accounting for gender—SF is 1 in adult males and 1.08 in adult females:

As specified in the model, upper and lower 95% confidence bounds (two-sided, see Rudolf et al. 1994) can be obtained by multiplying or dividing, respectively, the factor by the constant . The most general use of this formula involves estimating deposition in a group of subjects with known or estimated average inhalation flowrates, tidal volumes, and particle size distributions. Integrating across a particle size distribution with a defined mass median aerodynamic diameter and geometric standard deviation— performed here by parsing the size distribution into 0.1 µm wide bins between particle sizes of 0.05 and 30.05 µm (and subsequently applying the ICRP 1994 model across each bin using the half-width as the particle diameter)—accounts for the nonlinear relation between deposition and particle size as occurs with polydisperse aerosols. Using the average inhalation flowrates and inhalation volumes as defined in Table 1, an averaged scale factor of 1.04, and the particle size distributions measured in the in vivo study of Yang et al. (2017), the ICRP (1994) model predicts an average deposition of 0.170, an upper 95% limit of 0.313, and a lower 95% limit of 0.080.

These upper and lower limits must be converted to a measure of variance (i.e., standard deviation) for comparisons to the observed in vivo deposition presented in Table 1, which requires the assumption of a form of distribution. An Anderson–Darling test of normality suggests that the in vivo deposition data do not differ significantly from a normal distribution (p > 0.05, calculated using the adtest function in MATLAB R2016a); the distribution of deposition data is therefore assumed to be normal in the present work. Given that the central 95% of data lies within a range of approximately plus or minus two times the standard deviation in a normal distribution, the upper and lower 95% bounds calculated above can be used to estimate the standard deviation (s_ICRP) of the distribution of deposition predictions obtained with the ICRP (1994) model, i.e., . This yields a standard deviation of 0.058, which is approximately half the in vivo value of 0.103 (Table 1). The difference between the standard deviations of the measured in vivo data (0.103) and the corresponding ICRP predictions (0.058) is significant (F-statistic = 3.154 > F-critical = 2.217, α = 0.05, with 18 degrees of freedom in both sets), indicating that the ICRP model fails to capture the full range of deposition observed in vivo.

There are a number of potential causes for this discrepancy. For example, the basis for the scaling factor of 3.3 for predicting the upper and lower 95% confidence bounds in the ICRP model is unclear, and the lower 95% bound appears to predict higher deposition than was noted in a number of the studies used to develop the model (particularly the studies of Lippmann 1977 and Chan and Lippmann 1980; see Figure D.7 in ICRP 1994). In addition, it is possible that the 133 subjects upon whom the ICRP (1994) variance is based (pooled from seven studies) may differ significantly from those included in the work of Yang et al. (2017). However, as the 19 subjects included in the Yang et al. (2017) study represent a typical cross-section of the healthy adult population, this latter explanation is unlikely. Ultimately, and regardless of the cause, the ICRP (1994) model used with population-based breathing parameters does not appear to capture adequately the range of deposition observed in a typical subset of the healthy adult population inhaling from nebulizers such as the PARI LC Sprint.

4. Improving predictions of deposition variability using the Golshahi et al. (2013) correlation

In the study of Yang et al. (2017), the Golshahi et al. (2013) correlation applied on a subject-specific basis provided an accurate estimate of average in vivo deposition and better captured the range of values observed in vivo than did other examined models. The Golshahi et al. (2013) correlation was developed from in vitro measurements in extrathoracic airway casts of nine subjects (eight males, one female) 17 to 41 years old, with characteristics similar to those of the subjects included in the study of Yang et al. (2017): heights ranging from 163 to 195 cm with an average of 182 ± 9 cm, weights ranging from 56 to 146 kg with an average of 92 ± 27 kg, and characteristic diameters ranging from 1.35 to 2.25 cm, with an average of 1.82 ± 0.33 cm. Given the apparent difficulty in capturing deposition variability using the ICRP (1994) model, the question arises as to whether the Golshahi et al. (2013) correlation could provide a more accurate estimate of both the mean and variation in deposition through the selection of appropriate model parameters based on aerosol properties and population distributions of inhalation flowrates and characteristic diameters. The Golshahi et al. (2013) correlation, corrected as noted in the Yang et al. (2017) study, is expressed as a function of the Stokes (Stk) and Reynolds (Re) numbers using the square root of the average cross-sectional area of the oropharyngeal region as a characteristic diameter d_c:

Other relevant parameters include the reference density ρ_ref of 1000 kg/m³, the particle aerodynamic diameter, , average flowrate of a tidal inhalation, , the dynamic viscosity and density of the carrier gas— and , respectively—and the Cunningham correction factor, , itself dependent on the gas phase mean free path, . An estimation of average deposition in a population with known distributions of inhalation flowrates and characteristic diameters can be obtained using the average values of Q and d_c in the above definitions of the Reynolds and Stokes numbers in the Golshahi et al. (2013) correlation. This calculation yields a predicted average deposition of 0.172 for the parameters summarized in Table 1—essentially the same value as obtained with the ICRP (1994) model (0.170) considering the variability observed here.

Of more interest in the present work is the establishment of a method for predicting not just the average but also the variation in deposition. A simple method for predicting deposition variation in different populations using existing correlations can be developed by drawing from the concept of propagation of uncertainty, where the overall variation in a value of concern can be estimated using a sum-of-squares method based on the variation caused by all relevant constitutive parameters, a result of the central limit theorem (International Organization for Standardization 2008; Castrup and Castrup 2010). Noting that in uncertainty analysis, as uncertainty and standard deviation are equivalent (both being equal to the square root of the distribution variance [Castrup and Castrup 2010]), the total uncertainty (standard deviation) of a parameter is thus estimated from the uncertainty (standard deviation) of constituent variables. For deposition in the extrathoracic region, these constituent mechanisms may generally be summarized as variations due to flowrate (denoted ), variations caused by differences in geometry captured by the characteristic diameter (denoted ), and variations caused by geometrical differences not captured in d_c (denoted geometric dissimilarity, or ). Although particle size also plays a predominant role in determining deposition, effects of varying particle size are not of interest here since they are readily captured by the particle size dependence already present in existing correlations, namely, through the integration scheme mentioned earlier in the discussion of the ICRP 1994 model. This scheme was again used, now in conjunction with the Golshahi et al. (2013) correlation, to account for the nonlinear relation between particle size and deposition.

A first-order estimate of the total uncertainty in deposition, , can thus be predicted from the three aforementioned mechanisms through calculation of the l²-norm:

This calculation assumes negligible covariance among parameters—a reasonable assumption given the lack of any logical reason for such covariance. Indeed, others have noted the lack of correlation between the size of the extrathoracic region and the size of the airways within the lungs, the latter presumably a factor in the determination of inhalation flowrates and volumes (Lippmann and Albert 1969; Clark and Hartman 2012).

can be determined by first assuming that all variation in deposition due to this factor arises from variation in the average inhalation flowrate Q among different subjects, with the characteristic diameter treated as a constant equal to the average characteristic diameter measured in the population under consideration. For a given group of subjects, inhalation flowrates will follow a distribution of values with an average, , and standard deviation, . As shown in Table 2, deposition, , is calculated first using a flowrate of , yielding a value of , then with a flowrate of , yielding . Note here that the Golshahi et al. (2013) correlation was developed in vitro using sinusoidal inhalation profiles, which can vary somewhat in form from those observed during real human breathing through nebulizers. However, Roth et al. (2003) demonstrated that the average inspiratory flow is the breathing parameter of most interest when characterizing nebulizer output and further showed, using simulations, that a sinusoidal inhalation and a realistic breathing pattern with the same average flowrate result in the same regional deposition. Furthermore, a Fourier analysis of the individual breathing patterns of subjects involved in the study of Yang et al. (2017) revealed that deviations from a perfect sinusoid were unlikely to be a source of major errors in predicting deposition, given that no correlation was observed between the fraction of spectral power contained in the fundamental frequency of breathing for each subject and the absolute error of the Golshahi et al. (2013) prediction of in vivo extrathoracic deposition (Pearson correlation coefficient = −0.255, p = 0.292, calculated using the corr function in MATLAB R2016a). Thus, the relatively minor deviations of realistic inhalations from perfect sinusoids observed in the data of Yang et al. (2017) are unlikely to be a significant source of error in the application of the Golshahi et al. (2013) correlation.

Table 2. Values used in the calculation of deposition for the in vivo data of Yang et al. (2017).

Deposition	Flowrate (L/min)	Characteristic diameter (cm)	Deposition (−)
Average
Uncertainty due to flowrate
Uncertainty due to characteristic diameter

To estimate , a similar process can be performed treating the characteristic diameter as the primary source of intersubject deposition variation, with the inhalation flowrate treated as a constant equal to the average measured in the population under consideration, leading to the calculation of and . Numerical values of these parameters for the in vivo study of Yang et al. (2017) are summarized in Table 2.

The calculation of and then follows from a similar vein of reasoning as we performed with the ICRP (1994) predictions; i.e., approximately 68% of data lie in a range defined by two times the standard deviation ( and ) leading to uncertainties in deposition due to varying flowrates () of 0.0407 and varying characteristic diameters () of 0.0774.

The third major source of uncertainty in the estimation of deposition arises from variations in the shape of the extrathoracic region that are not captured by the characteristic diameter, termed . While the characteristic diameter of the Golshahi et al. (2013) model provides a global measure of extrathoracic airway dimension, it does not allow consideration of differences in localized shape within the oropharyngeal region between and among subjects. Because such localized inter- and intra-subject variations in geometry are known to significantly influence deposition (Heenan et al. 2004; Sandeau et al. 2010; Katz et al. 2013), it is perhaps unsurprising that the prediction of deposition on a subject-specific basis given knowledge of only one characteristic diameter is relatively inaccurate, a conclusion noted by Yang et al. (2017). The question then arises as to how best to estimate the effects of these unaccounted-for intersubject dissimilarities in geometric shape of the extrathoracic airways, given that no existing correlations have an explicit parameter incorporating this information.

A plausible approach in this regard follows from a deeper examination of the in vitro data used to develop the Golshahi et al. (2013) correlation. In particular, when the Golshahi et al. (2013) correlation is used to predict deposition in the in vitro casts on which it was developed (based on archived data of particle sizes, flowrates, and characteristic diameters from the original study), a measure of variability in deposition due to geometric dissimilarity can be estimated by observing the distribution of model predictions versus in vitro measurements as in Figure 1, where the line of identity corresponds to the case of perfect predictions of deposition. As variations in flowrate and characteristic diameters are incorporated into the equation for predicting extrathoracic deposition—and given that Golshahi et al. (2013) performed experiments under controlled conditions with known, fixed particle sizes, inhalation flowrates, and characteristic diameters—deviations of model predictions from in vitro measurements must arise from another source of uncertainty. As excellent repeatability in in vitro measurements was noted by Golshahi et al. (2013), presumably the only remaining variable that could account for such wide variations as observed in Figure 1 must relate to intersubject differences in the shape of the extrathoracic region that are not captured in the average cross-sectional area d_c of the oropharyngeal region.

Figure 1. Predicted versus measured deposition using the Golshahi et al. (2013) correlation for in vitro data used in its development. The solid line indicates the line of identity, while the dashed lines correspond to the approximate 95% bound on in vitro deposition data.

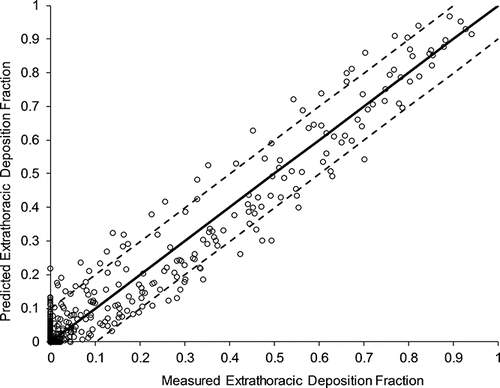
Under the assumption that deviations in Figure 1 from the line-of-identity with the Golshahi et al. (2013) data are solely due to geometric dissimilarity, an estimate of can be obtained by noting that the distribution of data about the line-of-identity appears reasonably symmetric across the full range of measured deposition. Linear bands indicating the bounds of approximately 95% of the data are obtained by adding and subtracting 0.10 from the line-of-identity. The symmetrical and linear behavior across the full range of deposition allows for the estimation of the variation due to geometric dissimilarity in the same manner as was performed with the ICRP (1994) model predictions, i.e., , yielding an uncertainty due to geometric dissimilarity, , of 0.05.

With measures of uncertainty of the three major parameters of concern in hand (, , ), application of the above equation defining the l²-norm yields a total predicted uncertainty (standard deviation) in deposition of 0.101, which is not significantly different than the observed in vivo standard deviation of 0.103: F-statistic = 1.040 < F-critical = 2.217, α = 0.05, with 18 degrees of freedom in both sets. The above method thus appears to offer a relatively straightforward method that provides a more accurate estimate of variation in deposition in healthy adults inhaling nebulized aerosols than is given by existing correlations, at least under controlled conditions in a clinical setting.

5. Relative importance of parameters affecting deposition

The variation in deposition in the study of Yang et al. (2017) due to variations in flowrates (), characteristic diameters (), and geometric dissimilarities () are similar in magnitude, indicating that all three parameters contribute non-negligibly to intersubject variations in extrathoracic deposition in vivo. The dependence of deposition on flowrate and the dimension of the extrathoracic region is certainly to be expected, but the similarly large magnitude of uncertainty caused by geometric dissimilarities between subjects is somewhat surprising, given that current correlations do not explicitly account for these local variations in size and shape of the upper airways. These results suggest that regardless of careful selection of inhalation flowrates and particle sizes to optimize deposition in a subject with a known (measured) global characteristic diameter, there will remain an unavoidable and considerable variation in deposition caused by geometric dissimilarities that are not captured in previously published simple algebraic correlations. As a consequence, the notion of individualized targeted aerosol delivery remains, for the time being, an elusive endeavor, a conclusion previously expressed by Clark and Hartman (2012).

A caveat of the above methodology involves the selection of appropriate values of inhalation flowrates and characteristic diameters for the population under consideration. Those wishing to adapt the above methodology toward predicting deposition of nebulized aerosols from novel devices must accurately define the parameters involved in the Golshahi et al. (2013) correlation; otherwise, the accuracy of the predictive correlation is reduced. While additional in vivo data would be welcome, the 19 subjects involved in the Yang et al. (2017) study represent a typical cross-section of the healthy adult population, and the presently observed ability of the Golshahi et al. (2013) correlation to predict deposition variability in an entirely unrelated group of subjects based on measurements of inhalation flowrates and characteristic diameters is promising.

While individualized targeted aerosol delivery remains out of reach, it appears that the proposed method outlined in the present work provides a relatively straightforward approach for accurately predicting the variability of extrathoracic deposition of nebulized aerosols in typical adult populations. Whether or not this method can be extended to other correlations, other types of devices that demonstrate different and often more complex behavior with regards to deposition in the respiratory tract (such as dry powder inhalers and pressurized metered dose inhalers), and other patient groups including those with compromised lung function, remains to be examined.

Acknowledgments

C. A. Ruzycki thanks Dr. Andrew Martin of the University of Alberta for constructive discussions during preparation of the manuscript.

Funding

CAR and WHF gratefully acknowledge funding from the Natural Sciences and Engineering Research Council of Canada, Alberta Innovates Technology Futures, and the University of Alberta. HKR and MY's research was supported under Australian Research Council's Discovery Projects funding scheme (DP150103953).