Knudsen transition effects on the thermophoretic properties of fractal-like aggregates: Implications for thermophoretic sampling of high-pressure flames

ABSTRACT

Aggregated particles nucleated and grown by Brownian encounters in atmospheric pressure gaseous flames, usually have primary particles (of radius R₁) smaller than the prevailing gas molecule mean-free-path, l_g. This simplifies their drift behavior in a strong temperature gradient, i.e., thermophoresis (TP), as has been exploited in the popular technique of TP/TEM soot sampling. Indeed, thermophoretic sampling has become the effective “calibration standard” because it also provides unambiguous aggregate morphology information and is independent of optical properties needed to interpret alternate “non-invasive” methods. However, we show here that at pressures of current engineering interest (e.g., 30–50 bar) the Knudsen number (Kn₁ l_g/R₁) is O(1) and the sensitivity of aggregate TP-behavior to pressure, morphology and, especially, aggregate size is altered considerably. While the recent gas kinetic theory results of Young reveal that the thermal force on each spherule should diminish as one leaves the free-molecule limit, large fractal-like aggregates receive the benefit of inter-particle “momentum shielding,” and we predict that larger aggregates drift faster than smaller ones in the same temperature gradient. We show that aggregate TP-diffusivity approximately scales with a Kn₁-dependent power, k, of the spherule number N, where the exponent k is as large as 0.44 for aggregates characterized by “dimension” D_f = 1.8, k_p/k_g = 1000 and Kn₁ below O(1). However, if the particle thermal conductivity far exceeds that of the carrier gas, the reduction in thermal force overwhelms the inter-particle momentum shielding below about Kn₁ = 0.7, with the aggregate TP-diffusivity becoming inadequate for TP-sampling near Kn₁ = 0.2. Based on these results we conclude that to infer accurate high-pressure mainstream aggregate size distributions and volume fractions via TP-sampling, it is necessary to correct observed TEM-information for the expected “over-representation” of large aggregates. These appreciable corrections (up to 40% for the number-mean aggregate size and approximately one-decade for the associated spherule volume fraction, φ_∞, at pressure near 50 bar), are shown to be straightforward to implement for sufficiently large mainstream and approximately log-normal aggregate populations.

Copyright © 2017 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction, motivation, and objectives

While admittedly an “immersion” method requiring post-sampling TEM-grid image analysis, the experimental technique known as “thermophoretic (TP) sampling” (to determine the nature and quantity of particulate matter in combustion gases, first implemented by Dobbins and Megaridis [1987]), has become the “gold-standard” in near-atmospheric- (or sub-atmospheric) pressure combustion studies. Its convenience for characterizing aggregated carbonaceous or inorganic “soots” has been based on the remarkable insensitivity of the TP-dominated capture efficiency to differences in aggregate size-, structure- (morphology) and even the intrinsic thermal conductivity of its constituent spherules (Rosner et al. 1991). Thus, if TP is indeed the dominant deposition mechanism (cf. Brownian diffusion or inertial impaction), relative abundances seen on the target often provide a sufficiently accurate picture of what must have existed in the local mainstream—independent of the often uncertain optical properties of such precipitates.

The principal reason for the abovementioned insensitivity has been the fact that the constituent spherules (often with radii of order only 10–20 nm) found themselves in the “free-molecule” domain of gas/solid momentum- and energy-transfer, i.e., the prevailing gas molecule mean free path far exceeded the individual spherule radii. Moreover, even large aggregates (containing thousands of primary particles) are often “open” enough to facilitate gas molecule “penetration,” i.e., their “internal” surface area is said to be quite “accessible” to the much smaller probing gas molecules (Rosner and Tandon 1994).

Our present theoretical extensions (Section 5) are motivated by current practical interest in the TP/TEM-sampling of high-pressure flames (Leschowski et al. 2014; Vargas and Gulder 2016), frequently well above 30 bar. Additionally, we anticipate the need for more realistic mathematical modeling of soot production and transport in practical high pressure combustion environments. This requires that we gain an understanding of the thermophoretic behavior of aggregates under gas-dynamic conditions in which the constituent spherules find themselves in the so-called Knudsen transition regime (Kn₁ < 1)¹ —if not the near-continuum regime (with Kn₁ ≪ 1).

In this article, we develop/report/illustrate a rational yet tractable method (Section 5) to predict the orientation-averaged TP-properties of large fractal-like aggregates (FA) over the entire expected range of Knudsen numbers and thermal conductivity ratios: k_p/k_g. As will be seen, our numerical results now suggest that the abovementioned remarkable insensitivities of the dimensionless thermophoretic diffusivity (when Kn₁ ≫ 1) are NOT expected to carry over to the more complex Knudsen transition regime in which primary particles of large fractal-like aggregates will find themselves in sampled, “sooting” high-pressure flames. Our present predictions will be seen to provide the basis for a rational/tractable “deconvolution” procedure (Section 6, Figure 4, and the Appendix) capable of systematically inferring local mainstream aggregate size distributions and corresponding total mainstream aggregate volume fractions from what is experimentally observed on TEM-grids immersed in combustion products at pressures even up to ca. 200 bar—probably the present upper limit considering our underlying assumption (Sections 2 and 5.8) of the relative dominance of thermophoretic transport (over Brownian diffusion).

2. Present assumptions and simplifications

To proceed with our prediction of the effects of high-pressure on the thermophoretic properties of aggregated precipitate particles in combustion gases, we now explicitly introduce the following assumptions and simplifications:

A1	The underlying molecular accommodation coefficients which determine gas/solid thermal creep and momentum and energy transfer, already near their theoretical upper limits for most gas/macroscopic surface interactions (Li and Wang 2005) even below 1 bar, will not be significantly altered when the carrier gas molecular volume fraction remains small enough to fall within the ideal gas domain.
A2	In the large N (N ≫ 1) aggregate size range being investigated here (nominally gyration radii exceeding ca. 0.2 micrometers and comprised of “nano-spherules” with diameters of the order of 30 nm, Brownian motion of the constituent primary particles will not appreciably affect the thermal force, even in the isolated sphere free-molecule (Waldmann-) limit: Kn1 ≫ 1 ( Li and Wang 2004).
A3	Estimates of the prevailing thermal force on each primary particle (at each Knudsen number Kn1 and thermal conductivity ratio) will be based on the Young correlation (Young 2011) for an isolated sphere–recently demonstrated to be in better agreement with available experimental data than earlier correlations (e.g., that due to Talbot et al. 1980), especially for thermally conductive particles within the Knudsen transition range [where “higher-order kinetic theory effects” (i.e., non [Navier–Stokes–Fourier] theory) become important.
A4	To approximately account for thermal shielding (Section 5.1) we further assume that the temperature gradient experienced by each such spherule within the FA is simply reduced from the maximum (imposed) value by the local factor (3/2)·{1 + [keff/(2 kg,eff)]}−1, where keff is the effective thermal conductivity of the local spherule suspension and kg,eff corrects the prevailing gas thermal conductivity for Knudsen sublayer effects in the vicinity of each primary spherule (Rosner and Papadopoulos 1996). For this purpose the orientation- averaged FA will be considered to be a radially non-uniform granular “porous medium”–as in the earlier mobility (inverse drag) calculations of Tandon and Rosner (1995).
A5	To estimate the more significant effects of multi-spherule momentum shielding (i.e., drag reduction) we simply exploit recent drag (mobility) results (Thajudeen et al. 2015; Melas et al. 2014) which relate the Knudsen transition regime drag on the FA to the drag on an equivalent (“adjusted”) solid sphere (Dahneke 1973a,b,c) whose radius is calculated from both the orientation-averaged projected area of the FA, written ≪PA≫, and the continuum-limit mobility radius—taken to be a structure-dependent fraction of the gyration radius of the FA (Sorensen 2011).
A6	To make use of available “isolated” single-sphere results (Young 2011) and for simplicity, we assume that the spherules comprising the aggregate are only “weakly necked” (i.e., have nearly point contacts with their [often two-] nearest neighbors) and are all of nearly the same material and radius, R1. (Thus, we currently preclude partially “sintered” [or “re-structured”] aggregates and/or “mixed” aggregates with unusually large primary particle “polydispersity.”)

This combination of plausible assumptions and simplifications will be shown to lead to a tractable “quadrature”-method (Sections 5.2 and 5.3) for predicting the significant amount by which the thermophoretic diffusivity of an N-particle FA (with N in the range 10²–10⁶) should exceed the corresponding thermophoretic diffusivity of an isolated primary particle in the same environment. Of particular interest will be our predictions of the dimensionless TP-diffusivity: ≪α_T·D_p/ν_g≫_N, for both Diffusion Limited Cluster Aggregates (DLCAs) and Reaction Limited Cluster Aggregates (RLCAs), with N-values in the frequently observed range: 10²–10⁶, k_p/k_g-values from, say, 10²–10³, and pressures so large that the prevailing Knudsen number Kn₁ is of order unity or less (even when the primary spherule radius R₁ is only ca. 10–20 nm).

Summarizing, our present focus is on the following question: At high pressures of current combustion interest what correction factors must be applied to TP/TEM sampling data to account for now-expected systematic differences in TP-dominated aggregate collection efficiency? Or, put another way: What quantitative correction factors must be applied to relative abundances observed on the TEM grid to predict actual relative abundances in the local mainstream? Provided the collection mechanism is, in fact, TP-dominated (for a convenient sufficient condition, see Section 5.8), our present tractable methods/preliminary results should now enable systematic corrections (Section 6 and the Appendix) for aggregate/spherule size (N,R₁), FA-morphology (e.g., DLCAs or RLCAs), k_p/k_g-values, at sampling pressures of current engineering interest. The “correction” to the apparent total volume fraction of aggregates is found (Appendix) to rise to the level of a 10-fold systematic overestimate for either mainstream DLCAs or RLCAs at sampling pressures near 50 bar.

3. Relevance of recent work on the thermophoretic properties of isolated spherical particles in non-isothermal gases

In comparing Young's theoretical analysis (Young 2011) of the thermophoretic diffusivity of an isolated spherical particle in a monatomic gas temperature gradient with that of Talbot et al. (1980) it becomes clear that while both results essentially possess the same Kn₁-asymptotes (i.e., the same values in the free-molecule limit [Kn₁ ≫ 1] and the [Navier-Stokes-Fourier] continuum limit [Kn₁ ≪ 1]) they differ quite significantly in the Knudsen transition region (e.g., for Kn₁-values between, say, 1 and 0.01), especially when the particle-to-gas thermal conductivity ratio: k_p/k_g is large, i.e., >>1. Indeed, as shown in Figure 1, when k_p/k_g is larger than about 35, as it often is for combustion-generated particles (especially ordinary carbonaceous “soot”), Young's method (which includes non-Navier-Stokes-Fourier effects in the gas phase² ) actually predicts a domain of small and ultimately negative (reverse-) thermophoresis before changing sign again and approaching from below the now-familiar (Epstein-) continuum limit value of the dimensionless TP-diffusivity {approx. (3/4)· [1 + (k_p/2k_g)] ⁻¹}.

Figure 1. Dimensionless thermophoretic diffusivity of an isolated spherical particle of thermal conductivity k_p in a non-isothermal ideal gas of thermal conductivity k_g; alternative predictions of expected Knudsen transition behavior (Young 2011; Talbot et al. 1980).

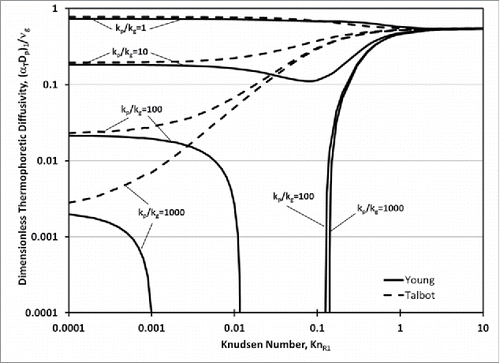
For Kn₁ = O(1), Young (2011) has critically reviewed available experimental data on the N = 1 thermal force reported by no less than 16 international groups over the time interval: 1952–1995, as well as N = 1 TP-drift velocity data reported by 9 groups between 1946 and 2009 (including microgravity experiments). On this basis Young (2011) has shown that his present non-monotonic interpolation recommendation (motivated in part by higher-order Boltzmann equation solutions, plotted in Figure 1 for the dimensionless TP-drift velocity, and adopted in Sections 5 and 6 for our present aggregate drift velocity predictions) is more accurate than the previously-used Talbot et al. (1980) monotonic interpolation—especially for the usually encountered case of thermally conductive spherules: k_p/k_g ≫ 1.

In what follows, we therefore make use of Young's correlation³ for the net thermal force—in effect, this enables our estimate of the dimensionless TP-“factor” (α_T)₁, defined here in such a way that the thermal force per spherule is:[1]

If this force acts on each of the N spherules in an aggregate, and if we invoke what is now known about the orientation-averaged mobility of FAs (Section 4) then we can infer the expected drift velocity of a FA in a gas of spatially non-uniform temperature. In Section 5 we use this approach to develop results for the expected orientation-averaged TP-diffusivity ≪α_T·D_p≫_N defined by the drift-velocity relation:[2]

To a first approximation (Rosner 2000; Appendix), TP-dominated particle deposition rates will be directly proportional to this scalar coefficient ≪α_T·D_p≫_N, with units m²/s. In Section 5 we develop our general method and use this method to estimate/ plot present values of the corresponding dimensionless aggregate TP-diffusivity, i.e., ≪α_T·D_p/ν_g≫_N, in terms of Kn₁ and N for both DLCAs (D_f = 1.8, k₀ = 1.3) and RLCA (D_f = 2.1, k₀ = 0.94) with, say, k_p/k_g = 1000. To open the door to a rational “deconvolution” procedure, in Section 6 we show how these predicted Knudsen transition effects would systematically distort the TP-sampled aggregate size distribution function, pdf_w(N), providing a numerical illustration for the case of TP-sampling from a 2000 K flame at a pressure of 50 bar. (Corresponding systematic over-estimates of the total aggregate volume fraction are dealt with in the Appendix). We conclude (Section 7) with a brief discussion of several immediate theoretical and experimental implications of these predictions, especially timely in view of current international interest in thermophoretic sampling from high-pressure flames (Leschowski et al. 2014; Vargas and Gulder 2016).

4. Recent work on the mobility properties of large fractal aggregates

As summarized by Sorensen (2011), useful scaling laws have been developed to facilitate calculations of the orientation-averaged drag on large FAs, both in the continuum limit (Kn₁ ≪ 1), and in the Knudsen transition regime (Kn₁ = O(1)).

Continuum results are conveniently stated in terms of the equivalent “mobility radius” of a FA, found to be expressible in the form:[3] i.e., due to “momentum shielding”, the low Reynolds number orientation-averaged drag on an FA containing N spherules is less than N-times the drag on a single isolated spherule in the same stream by the above mentioned dimensionless factor η_mom, which is a function of N for a given FA structure (i.e., k₀, D_f)⁴ .

To account for the drag reduction associated with gas rarefaction use is made of the Cunningham slip correction function (Allen and Raabe 1982) for an isolated solid sphere but using (in the definition of Kn) an effective aggregate radius which depends both upon the orientation-averaged projected area, ≪PA≫, of the FA and its continuum mobility radius, i.e.:[4]

This method, having roots in the small-chain aggregate “ASM”-work of Dahneke (1973a,b,c), has been shown to be successful for large FAs in the more recent computational work of Zhang et al. (2012); Thajudeen et al. (2015) and Melas et al (2014).

By balancing the total thermal force (Section 3) on an N-spherule FA against the transition regime total orientation-averaged aggregate drag, we are now in a position to predict N-dependent dimensionless aggregate TP-diffusivities when the prevailing gas pressures are high enough for the constituent spherules to enter the interesting Knudsen transition regime. Especially for large values of k_p/k_g (of practical interest) and FAs with large N, this method now leads to several previously unanticipated trends—as pointed out/explored in Sections 5 and 6.

5. Present predictions of ≪α_T·D_p/ν_g≫_N in the Knudsen transition regime

5.1. Total thermal force on a fractal-like aggregate

We now imagine that the (orientation-averaged-) fractal aggregate has a radial structure defined by the solid-fraction function:[5] except for a small “random-(nearly-) close packed” core (see Tandon and Rosner 1995 for details). The total thermal force on such an aggregate can then be formally written (Equation (6[6] )):[6] where we have neglected the small changes in Kn₁ within the FA interior and also explicitly factored out [grad T]_∞, the local temperature gradient in the carrier gas if the spherules comprising the aggregate were not present⁵ .

5.2. FA drift velocity via force balance

Equating this thermal force (Equation (6[6] )) to the total drag on the aggregate (Section 4), and making use of Equations (3[3] ) and (4[4] ) of Section 4, we are led to the following interesting separable representation for the aggregate dimensionless thermophoretic diffusivity, defined by Equation (2[2] ), i.e.⁸:[7]

Here we identify (α_TD_p/ν_g)₁ as the Young-predicted dimensionless thermophoretic diffusivity of an isolated spherical particle at the prevailing Kn₁ and k_p/k_g, (Figure 1) along with two non-dimensional multi-spherule “shielding factors” — one for momentum defined by:[8]

Introducing assumption A4 (Section 2) we are led to the following quadrature representation for the thermal shielding contribution:[9] a factor which is seen to be expressible as the ratio of two volume-averages over the radially symmetric (orientation-averaged) FA structure.

Because, for DLCAs, <φ> is so small (Table 1, which also summarizes our D_f, k₀ choices for the DLCA and RLCA parameters, as well as the correlations we have used for η_PA and η_mom) the internal effective thermal conductivity k_eff, say evaluated at <φ>, is not much larger than k_g,eff and we expect (and find⁹, Section 5.3) that S_h will be close to unity. Even for very large RLCAs, inter-spherule thermal shielding remains weak, e.g., for N = 10,000, k_p/k_g = 10³, Kn₁ = 1 and D_f = 2.1 we find (via Equation (9[9] )) that S_h = 0.987. Because <φ> is often ≪1, a useful rough first approximation to the thermal shielding factor S_h for situations with k_p/k_g≫1 is found to be: 1–3 <φ> (where use has been made of the classical Maxwell relation for the conductivity of a dilute suspension of spherical conductors). For DLCAs with N = 1000 the “quadrature” value of S_h (Equation (9[9] ))⁶ for k_p/k_g = 1000 is in fact 0.99 (cf. 1–3·(0.0051) = 0.985 with <φ> = 0.0051).

Table 1. Statistical parameters and normalized correlations chosen to characterize two important classes of fractal (-like) aggregates (FAs).

	Type of FA
Parameter	DLCA	RLCA
Df	1.8	2.1
k0	1.3	0.94
β	0.665	0.464
ηPA	0.478 + 0.5228·N^−0.23	0.644 + (1.78/N)
ηmom	N^−0.54 (N ≤ 74)	1.33·N^−0.572
	0.65·N^−0.44 (N > 74)
< φ > for N = 1000^*	0.51%	1.73%

* Volume-average particle volume fraction (calculated from the closed form approximation: (β)^3/Df· (N) ^{−[(3/Df) − 1]}).

5.3. Numerical predictions for ≪α_T·D_p/ν_g≫_N ; dependence on Kn₁, N, and fractal-like structure

For an important particular class of FAs, i.e., DLCAs with k_p/k_g = 1000, we depict in Figure 2 the result of applying the factor S_mom· S_h (defined by Equation (7[7] )) to the N = 1 Young-values of (α_T·D_p/ν_g)₁ displayed in Figure 1. To display the now appreciable N-dependence, the predicted Kn₁-dependence is shown (Figure 2) for each of the distinct N-values: 10ⁿ (2 ≤ n ≤ 6). Especially noteworthy is the now-expected increase in TP-diffusivity (for any N) as one leaves the free-molecule (Waldmann) limit—prior to the ultimate dramatic descent attributed to the Young-monomer contribution (Figure 1) as Kn₁ approaches values near 0.2. Peak aggregate TP diffusivities (favorable for the dominance of the TP-deposition mechanism over that of Brownian diffusion [Section 5.8], hence simplifying the deconvolution process) should be expected near Kn₁ = 0.7—which, for R₁ = 20 nm and T = 2000 K, corresponds to a combustor pressure of about 42 bar.

Figure 2. Predicted (Equation (7[7] )) dimensionless (orientation-averaged) thermophoretic diffusivity of a fractal aggregate (D_f = 1.8, k₀ = 1.3) containing N-spherules (Kn₁-transition behavior for N = 1 based on Figure 1; Young 2011).

Regarding the treatment of more “compact” aggregate structures, we note that similar calculations for RLCAs (with D_f = 2.1, k₀ = 0.94) lead to the results summarized in Figure 3. While qualitatively similar to Figure 2, significantly, the N-dependence of ≪α_T·D_p/ν_g≫_N for Kn₁ = O(1) is somewhat greater than that shown in Figure 2. This is quantified in Section 5.7, where we extract/report useful correlations for the power-law dependence of ≪α_T·D_p/ν_g≫_N on spherule number N. In Section 6 we demonstrate how these Kn₁-dependent exponents can be used to correct future experimentally reported TP/TEM high pressure data for the expected “falsification” of both pdf_∞(N) and the corresponding mainstream aggregate volume fraction.

Figure 3. Predicted (Equation (7[7] )) dimensionless (orientation-averaged) thermophoretic diffusivity of a fractal aggregate (D_f = 2.1, k₀ = 0.94) containing N-spherules (Kn₁ transition behavior for N = 1 based on Figure 1; Young 2011).

5.4. Predicted behavior of ≪α_T·D_p/ν_g≫_N in the free-molecule and continuum limits

It is clear from the discussion above that the principal Kn₁- dependencies are contained in the factors [α_T·D_p/ν_g]₁ (Figure 1) and the momentum shielding factor S_mom defined by Equation (8[8] ).The latter contains the nonlinear function C_slip(Kn₁) but for the present asymptotic limits the simple approximation mentioned by Sorensen (2011), i.e., C_slip(Kn₁) ≈ 1+ 1.612 Kn₁ will suffice.

5.4.1. Free molecule limit: Kn₁ ≫ 1

When Kn₁ ≫ 1 we find that, independent of the continuum limit function η_mom, S_mom approaches (η_PA)⁻¹, which for DLCAs is 1.67 for N = 10⁴ and for N ≫ 1 approaches the limiting value 2.09 (Meakin et al. 1989). These multipliers would then be applied to the dimensionless TP-diffusivity: 0.5385 for N = 1 (Waldmann value with diffuse molecular “reflection”). Our current predictions in this limit appear to be somewhat larger than those predicted by Mackowski (2006), who used a Monte Carlo-numerical scheme (obtaining (his Figure 4) ca. 1.1 for S_mom at N = 10⁴). In any case, even when using TP/TEM sampling from near- or sub-atmospheric pressure flames, modest systematic capture-fraction corrections appear to be warranted if the FAs are sufficiently large. It is interesting to also note that in the (less-likely) limiting case of specular molecular reflection, Zurita-Gotor (2006) has shown that, independent of N, all aggregates of any structure should exhibit ¾ for the dimensionless TP-diffusivity, corresponding to the complete absence of inter-spherule shielding, i.e., S_mom·S_h = 1, when Kn₁ ≫ 1.

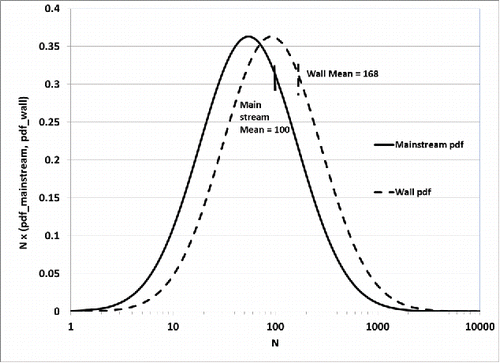
Figure 4. Predicted “falsification” of observed fractal-like aggregate distributions due to expected N-dependent thermophoretic diffusivities (Figure 2). Comparison between mainstream- and predicted wall- log-normal distributions for a p = 50 bar, T = 2000 K mainstream DLCA aggregate population characterized by = 100, D_f = 1.8 and σ_g = 3; see the Appendix for the corresponding over-estimate of the inferred mainstream total aggregate volume fraction.

5.4.2. Continuum limit: Kn₁ ≪ 1

When Kn₁ ≪ 1 we find that S_mom approaches 1/η_mom irrespective of η_PA, with correlations for η_mom summarized in Table 1 for both DLCAs and RLCAs. Moreover, the continuum limits of (α_T·D_p/ν_g)₁ for both Young (2011) and Talbot et al. (1980) become indistinguishable (Figure 1). However, as quantified in Section 5.5, all of the “low Kn_1” results presently collected in Figures 2 and 3 will be “inaccessible” if the primary spherules in the aggregates are in the frequently encountered 10–20 nanometer range. This is because the attainment of such small Kn₁ values would require pressures inconsistent with our restriction to the ideal gas law. Only if dealing with aggregates containing spherules which are of the order of micrometers in radii could this regime be accessed without violating our ideal gas constraint.

5.5. Restrictions associated with departures from gas ideality

The ideal gas kinetic theory expression for the gas mean-free-path can be re-written in terms of the molecular volume fraction: (φ)_molec = n_g· [(π) (σ)³]/6, where n_g = p/[k_B· T] for an ideal gas. If the ideal gas -law fails when (φ)_molec exceeds, say, 5%, then we find that the l_g cannot be less than about 2.4· (σ)_g,eff and therefore Kn₁ cannot be less than about 2.4· [σ/R₁]. Because (σ)_g,eff is near 0.4 nm (and only weakly T-dependent) and R₁ is typically near 15 nm, on this basis, Kn_1,min will be about 6.3 × 10⁻², almost independent of T. Thus, because of our present “Ideal Gas constraint” (see A1), we should not expect the “low Kn₁ branches,” formally displayed in Figures 2 and 3 to be “accessible.” However, we note that the precipitous fall in aggregate TP-diffusivity (after its notable rise well above fm-limit-values!) should be observable for combustion-generated “soot” at sufficiently high pressures w/o violating our near-ideal gas law “self-consistency” condition.

5.6. Relations between S_mom and ≪D≫_N ; S_h and (α)_T,N

We remark here that what we have called the momentum shielding factor, S_mom, bears a close relation to the Brownian diffusivity ratio [≪D≫_N]/D₁ which was calculated via our earlier “non-uniform porous sphere” model of a fractal aggregate (Tandon and Rosner 1995). Indeed, we find that the Einstein mobility equation and the FA relations in Section 4 imply:[10]

In this respect S_mom, shown by our numerical results to be significantly greater than unity (Section 5.3), quantifies the amount by which N ≪D≫_N exceeds the N = 1 diffusivity D₁.

Somewhat analogously, the thermal shielding factor S_h introduced above is closely related to the ratio of dimensionless TP-factors: ≪α_T≫_N/(α_T)₁, i.e.,[11]

Recalling the close relation between α_T and the net thermal force (Equation (1[1] )), this relation shows that the factor S_h quantifies the expected systematic difference between the actual FA TP-factor ≪α_T≫_N and N times the dimensionless TP factor for a single, isolated spherule, (α_T)₁.

Because S_h is near unity⁹ the prevailing value of ≪α_T≫_N will be about N-times the prevailing value of α_T,1. It is also useful to point out that in the free-molecule limit the Waldmann-value of α_T,1 can be shown to be expressible (via ideal gas kinetic theory) as:[12] which is itself ≫1 when R₁ ≫ σ_g,HS,eff —as in the ideal gas-applications of present interest.

5.7. Power-law correlations for the N-dependence of ≪α_TD/ν_g≫_N expected at high pressures

One of our objectives (Section 6) is to calculate and illustrate the expected “distortion” of sampled aggregate size distributions (ASDs) and inferred aggregate mainstream volume fractions that results when the FA deposition rate acquires a significant dependence on aggregate size N—all other factors remaining constant. If, as is often the case, measured ASDs are well fit by a log-normal representation then a particularly convenient representation of the N-dependence of ≪α_T·D_p/ν_g≫_N is the power-law form, i.e., an N^k dependence, where because Kn₁ = O(1), k > 0.

From the dimensionless TP diffusivity results displayed in Figure 2 (for D_f = 1.8, k₀ = 1.3, k_p/k_g = 1000) we find that the effective exponent k increases as we move away from the free-molecule (Kn₁ ≫ 1) limit, taking on the values: k(100) = 0.145 k(10) = 0.344 and k(1) = 0.432, k(0.2) = 0.442. A reasonable curve-fit to this behavior is:[13a]

A similar curve-fit to our D_f = 2.1 results (depicted in Figure 3) is:[13b]

These values will be shown to greatly facilitate the interpretation of future TP/TEM sampling data from high pressure flames. Our methods will be illustrated in Section 6 and the Appendix.

5.8. Sufficient condition for the dominance of the TP-deposition mechanism

Equation (11[11] ) also facilitates the development/use of a simple sufficient condition for the dominance of the TP-deposition mechanism. The respective laws governing deposition rates by thermophoresis or Brownian convective-diffusion (Rosner 2000) suggest that the following simple condition on ≪α_T≫_N will be sufficient to ensure TP-dominance:[14]

The diffusivity ratio Sc on the RHS of Equation (14[14] ) can be estimated via the gas kinematic viscosity and the use of the slip-corrected Stokes-Einstein relation:[15]

Whether ≪α_T≫_N actually meets condition (Equation (12[12] )) can be verified because ≪α_T≫_N will be simply the ordinate of Figures 2 or 3 multiplied by the prevailing Sc-value calculated via Equation (15[15] ).

6. Predicted “falsification” of observed aggregate size distributions (and corresponding mainstream particle volume fractions)

In this section, we calculate and illustrate the “distortion” of the sampled aggregate size distribution (ASD) that results when the FA deposition rate has a N^k power-law dependence on aggregate size N—all other factors remaining constant. This dependence will be seen to be particularly convenient if the measured ASDs are well fit by a log-normal (LN-) representation. From the DLCA dimensionless TP diffusivity results displayed in Figure 2 we find that the effective exponent k increases as we move away from the free-molecule (Kn₁ ≫ 1) limit, with the k(Kn₁) correlations for DLCA and RLCA given by Equations (13a[13a] ) and (13b[13b] ), respectively.

If, for sufficiently large N, the aggregate number flux to the cooler TEM grid is proportional to N^k then it is easy to show that if the mainstream normalized log normal (LN) aggregate size distribution (ASD) is written pdf_∞(N), i.e.,[16] then the normalized pdf_w(N) will also be log-normal and can be compactly written:[17] whereand we have exploited the fact that for ≫ 1 we can, in effect, replace the lower limit N = 1 by zero. A useful property of LN distribution functions is that any moment M_k can be expressed in closed-form via N_g and σ_g:[18]

Using these relations, as well as the LN-based relation between the pdf spread parameter and the pdf's moments: M₂, M₁ and M₀, it is possible to now prove that, irrespective of the magnitude of the exponent k, the wall ASD will have the same spread as the mainstream pdf, i.e.,[19]

However, as now expected, N_g,w will be larger than N_g,∞ and the enlargement factor is found to be:[20]

Because the mainstream and TEM grid ASD-spreads are equal this also implies that the number-average aggregate size on the TEM grid will be systematically larger than by this same factor: .

While high-pressure experimental results for aggregate size distributions via TP-sampling have not yet appeared in the combustion literature, we can illustrate this expected systematic ”ASD-falsification” with the help of a simple numerical special case. Consider that we are sampling from a LN- population of FAs with D_f = 1.8, and σ_g = 3, with = 100 comprised of, say, 12 nm radius spherules at p = 50 bar, 2000 K. Under these conditions we find that the gas mfp is about 11.7 nm so that Kn₁ based on R₁ is 0.975, i.e., quite close to unity. At this Knudsen number the exponent k is found to be about 0.43 and the corresponding pdfs are shown plotted in Figure 4, along with each value, with the sampled being 168. The corresponding values of parameter k are found to be 0.39 and 0.34 for Knudsen number Kn1 of 5 and 10, respectively, resulting in sampled of 160 and 151. Such corrections become particularly significant, because properly implemented TP/TEM sampling, being independent of material optical properties and morphological uncertainties, has assumed the role of a calibration standard in most experimental studies of flame-generated particulate matter. As shown in the Appendix the consequences for inferred mainstream total aggregate volume fraction, which involves an integral over all N, are even more dramatic—rising to the level of one order of magnitude under these same conditions.

As for the canonical “inverse” problem of de-convoluting observed pdf_w(N) data, when is sufficiently large (see, also, Section 7) the implications are now clear. To reconstruct the corresponding mainstream pdf_∞(N) our TP-diffusivity predictions (Figure 2) show that one can assume the same pdf spread, but both N_g,∞ and will be smaller than their TP- sample counterparts by the factor , where k is evaluated from either Figures 2 and 3 or Equations (13a[13a] ) and (13b[13b] ) at the prevailing Knudsen number based on the relevant gas mfp and .

Over the range of viable TP-sampling conditions considered here, we also expect that our principal conclusions (Sections 5 and 6) will not be significantly altered if our aggregate TP-diffusivity calculations are simply based on the number-mean R₁-value, i.e., . This expectation is based on the facts that: (a) recently observed spherule radius spread-parameters (Vargas and Gulder 2016; Leschowski et al. 2014) appear to be quite modest (apparently less than 1.5 (with 1.0 corresponding to strict R₁-uniformity), and (b) the condition for TP-dominance (Section 5.8) will likely rule out future Kn₁-values which are small enough to cause the spherule size-dependence of the thermal force on conductive spherules⁷ to become significant.

7. Conclusions, implications for TP/TEM sampling in high-pressure flames, and future work

Quite clearly, when flame conditions are such that the individual spherules found within aggregates are large enough to no longer find themselves in the “free-molecule” regime, the indicated dependencies of ≪α_T·D_p/ν_g≫_N on aggregate size (N), structure (D_f, k₀) and thermal conductivity (via k_p/k_g) are found to be no longer “modest”! We provisionally conclude that, especially because k_p/k_g is usually large, the quantitative interpretation of TP/TEM sampling data from high-pressure flames will normally require a non-trivial “deconvolution” with the help of ≪α_T·D_p/ν_g≫_N -results of the type shown for the first time in Figures 2 and 3, i.e., large aggregates would be appreciably “over-represented” on TEM grids. This is now explicitly illustrated in Section 6, with the expectation that suitable high-pressure experimental data on aggregate size distributions will soon become available. We find (Section 5.7) that over useful domains of Kn₁ and N, power-law representations of our numerical results are adequate, greatly facilitating systematic “corrections” to “falsified” TP-data both for back-calculating pdf(N)_∞ (Section 6) and the corresponding mainstream aggregate volume fraction, (φ)_{p, ∞} (Appendix).

Despite the fact that for intermediate Kn₁-values the nonlinearity of the presently accepted functions C_slip(Kn₁), η_PA, η_mom and S_h will normally preclude simple exponent power-law relations, when -values are sufficiently large, our present TP-diffusivity prediction methods are sufficiently tractable to enable a straightforward data-reduction procedure. However, we find (Section 6) that over useful domains of Kn₁ and N, power-law representations of our numerical results are adequate, greatly facilitating such systematic “corrections” to “falsified” TP-data, e.g., the Kn₁ dependence of k can be represented by Equation (13). (The N-dependence of ≪α_T·D_p/ν_g≫_N appears to be even greater [ca. N^0.57] for RLCAs when Kn₁ = O(1)). As shown in Section 6, if aggregate size distributions are well-fit by log-normal relations then these power-law representations make correcting “raw” TEM-observed abundances for the now-expected systematic differences in TP capture fraction rather straightforward.

As additional theoretical, numerical or experimental information becomes available (e.g., about the thermophoretic properties of isolated spherules, or the orientation-averaged mobility properties of spherule aggregates) it should be possible to incorporate these improvements in our present analysis. Of course, experimental confirmation of some or all of our present qualitative and quantitative predictions (Figures. 2 and 3) would build confidence in our underlying assumptions (Section 2). While our present rational approximation methods rely on the largeness of the mean spherule number in the mainstream population, it remains to be seen how small N can actually be before the associated systematic errors become unacceptable. Since there is also likely considerable interest in situations dominated by “small” aggregates (e.g., ≤O(10)) systematic “small N-1”-corrections to our present results will undoubtedly be of future value. In any case, our present analysis will, hopefully, motivate further advances in high-pressure thermophoretic sampling and perhaps have presently unexpected applications. In this regard, we note that the Kn₁-transition regime seems to be well-suited for exploiting thermophoresis for aggregate size separation—perhaps in combination with inertial effects. Thermophoresis in this Kn₁-domain may also prove to be practical for aggregate separations based on spherule thermal conductivity (Rosner and Arias-Zugasti 2011). In closing, we also conjecture that analogous inter-particle shielding effects may cause a similar size-dependence for the electrophoresis of large fractal-like aggregate in liquid solutions of biological interest—when one leaves the thin Debye sheath limit.

Added in Press

The dimensionless TP-diffusivity results shown plotted in Figure 2 for DLCAs were based on the η_mom(N;D_f = 1.8) correlation displayed in Table 1 (Sorensen 2011). However, our recent extensions (Rosner and Tandon 2017, Aerosol Sci. and Tech. submitted), carried out to demonstrate the role of “momentum shielding” for the rival aggregate transport mechanisms of isothermal convective-diffusion, or inertial impaction, have revealed that our “porous medium” approach (see, also, Footnote 4) leads to somewhat higher η_mom -factors—amounting to ca. 1.6-1.8 fold, depending upon N. On this basis we now believe that the dimensionless TP-diffusivity predictions displayed in Figure 2 should be systematically reduced by about this modest factor near Kn₁ = O(1). In this same follow-up paper our “porous sphere” model has also been generalized to independently validate the ‘Adjusted Sphere Method’ in the broad domain of N and Kn₁-values for which Kn_N ≪ 1, i.e., the “outer” flow is near-continuum. Finally, we wish to add that our present Kn₁-transition results for large aggregate thermophoresis will also be applicable to the TEM-analysis of thermally precipitated aggregated smokes sampled under near-atmospheric pressure conditions, especially at more modest (not flame-) temperatures, and when the spherule radii may reach ca. 50 nm. Examples of this type will evidently occur in sampling “pyrolysis smokes,” including those from orbiting spacecraft environments (Meyer et al. 2015; Mulholland et al. 2015).

Nomenclature

	=	molecular mean thermal speed, [8kBT/(πmg)]1/2
D	=	Brownian diffusivity
Df	=	fractal dimension (Table 1)
Cslip	=	Cunningham slip factor (Kneff-dependent)
FT,1	=	thermal force on a spherule
fB(κ)	=	Brinkman function (Tandon and Rosner 1995; their Equation (3.1-2[2] ))
k	=	Exponent in relation ≪αTDp/ν≫ ∼ Nk (Section 5.7, Equation (13))
kB	=	Boltzmann constant
k0	=	pre-factor (relating N to (Rgyr/R1)Df)
kg	=	gas thermal conductivity (Fourier)
kp	=	particle (spherule) thermal conductivity
Kn	=	Knudsen number (lg/R1)
l	=	molecular mean-free-path (in carrier gas), ≈ 2νg/
m	=	mass of one gas molecule
N	=	number of spherules in fractal aggregate (FA)
Np	=	aggregate number density; Equation (A1[A1] )
p	=	pressure (units:1 bar(105 Pa) unless otherwise specified)
R1	=	spherule radius
Rgyr	=	aggregate gyration radius, R1·(N/k0)1/Df
Rmob	=	mobility radius of FA containing N spherules; Equation (3[3] )
r	=	radial position within FA (from FA center-of-mass)
Sc	=	Schmidt number for particle diffusion in gas, νg/Dp,N
Smom	=	momentum shielding factor for aggregate (Equations (7[7] ) and (8[8] ))
Sh	=	energy (thermal) shielding factor for a FA (Equations (7[7] ) and (9[9] ))
T	=	absolute temperature (Kelvins)
U	=	thermophoretic drift velocity; Equation (2[2] )
V	=	total included volume of one FA (based on Rmax)

Greek

αT	=	thermophoretic factor (dimensionless); Equation (1[1] ))
β	=	prefactor relating N to (Rmax/R1)Df
χ	=	permeability of local granular medium
φ	=	local solid fraction within (orientation-avgd) FA; Equation (5[5] )
ηPA	=	normalized, orientation-avgd proj. area of FA; Equation (4[4] ) ≡ ≪PA≫/[N·(π R12)]
ηmom	=	normalized drag of FA (cf. N- individual spheres); Equation (3[3] ))
μg	=	Newtonian viscosity of carrier gas
κ	=	Rmax/χ1/2
ν	=	momentum diffusivity (kinematic viscosity)
σ	=	effective hard sphere diameter of molecule
σg	=	geometric mean spread parameter in LN pdf
Φ	=	dimensionless thermal force, N = 1 (Young 2011)
ψ	=	dimensionless drag on spherule (Young 2011)

Subscripts

c	=	continuum
eff	=	effective
fm	=	free-molecule
g	=	pertaining to the carrier gas
g	=	pertaining to geometric mean
h	=	pertaining to heat (energy) transfer
HS	=	effective “hard-sphere” value
N	=	pertaining to a FA with N spherules
p	=	pertaining to the (solid-like) particles
min	=	minimum value (consistent with A1)
mob	=	mobility (drift velocity per unit force)
molec	=	pertaining to the molecular gas
mom	=	pertaining to momentum transfer
1	=	pertaining to N = 1 (single, isolated spherule)
∞	=	in the gas far from the aggregate center of mass

Acronyms and abbreviations

ASD	=	aggregate size distribution
ASM	=	adjusted sphere model (Dahneke 1973a,b,c)
cf	=	short for confer meaning compare
DLCA	=	diffusion-limited cluster aggregate (Table 1)
FA	=	fractal (-like) aggregate
LN	=	log-normal (Equation (15[15] ))
mfp	=	mean free path in carrier gas
≪PA≫	=	projected area (orientation-averaged)
PDE	=	partial differential equation
pdf	=	probability density function
RLCA	=	reaction-limited cluster aggregate (Table 1)
TEM	=	transmission electron microscope
TP	=	thermophoretic

Operators

grad()	=	spatial gradient operator
|| grad T ||	=	magnitude of the local vector grad T
O( )	=	order-of-magnitude
< >	=	volume-averaged
≪ ≫	=	orientation-averaged
	=	average value of ( )

Acknowledgments

This article is dedicated to the memory of Prof. Richard A. Dobbins (Brown University, Division of Engineering), who (with his then graduate student C. M. Megaridis) put the experimental technique of “Thermophoretic Sampling” on the combustion-generated particle “map” nearly 3 decades ago (Langmuir, vol 3 (1987) loc cit). It is also our pleasure to acknowledge the helpful comments of our current and former Yale/SEAS colleagues: J. Fernandez de la Mora, A. Gomez, A. G. Konstandopoulos, D. W. Mackowski, M. Arias-Zugasti, and M. Zurita-Gotor, as well as C.M. Megaridis (U IL-Chicago, Mechanical Engineering.), C. Sorensen (KSU Physics), R. L. McGraw (Brookhaven National Laboratory, Aerosol Chemistry), and G. W. Mulholland (University of Maryland, Chemical Engineering).

Funding

This work was partially supported by the Industrial Affiliates of the Yale/ChE Sol Reaction Engineering Research Group.

Notes

¹ For present purposes, a useful preliminary estimate of the relevant mean-free-path (units: nm) will be l_g(p,T)= 66 · [p(bar)]⁻¹ · [(T(Kelvins)/300)^1.15. (This dimensional form results from the ideal gas kinetic theory expression for mfp, together with a numerical estimate of the [weakly temperature-dependent] effective hard-sphere diameter of molecular nitrogen, i.e., (σ)_N2,HS,eff.)

² Associated with “higher order” gas kinetic theory—i.e., beyond the Enskog–Chapman level of ideal gas kinetic theory.

³ In the notation of Young (2011), our (α_T·D_p/ν_g )₁ is Young's: Φ/ψ

⁴ As done in Tandon and Rosner (1995), by viewing the (orientation-averaged) FA as a quasi-spherical “porous” object with a radially variable permeability, it is possible to relate (η)_mom (N;D_f,k₀) to the closed-form Brinkman function f_B(κ) (Equation 3.1-2 in Tandon and Rosner, loc cit) associated with the Re ≪ 1 non-dimensional drag on a sphere of uniform permeability. On this basis we find that a reasonable, independent estimate of (η)_mom can be obtained from the relation:where (κ)_eff ≡ R_max/(χ_eff)^1/2 and (χ)_eff = (χ)_Happel evaluated at the volume-averaged solids fraction: <φ>( Table 1). See, also: “Added in Press.”

⁵ If the relative change in gas temperature over one molecular mean-free path is indeed small then transport coefficients defined by “linear” flux laws of the type used here for the aggregate TP-diffusivity: ≪ (α_T·D)≫_N in Equation (2[2] ), and calculated as we have done in Section 5 (subject to the assumptions stated in Section 2), will not have a dependence on ||grad T|| itself. Moreover, when the condition: l_g·||grad T||/T ≪ 1 is met then the dimensionless scalar coefficient transport coefficient ≪ (α_T·D)/ν_g)≫ _N , calculated and plotted in Figures 2 and 3, contains not only the entire dependence of the TP-drift velocity, U_T, on pressure and spherule radius R₁ (via Kn₁), but also its dependence on the thermal conductivity ratio: k_p/k_g (with the help of Figure 1) and the aggregate's fractal-like structure via its parameters: D_f and k₀. As a numerical example, available data on the pressure-dependence of laminar flame speeds (say, for pre-mixed CH₄/air) suggest that even at ca. 50 bar the product: l_g·||grad T||/T would be of the order of only 10⁻⁴, i.e., ca.1/100th %. Thus, the internal structure of such gaseous flames would remain amenable to a “pseudo-continuum” analysis, including the use of flux-laws compatible with the principles of linear irreversible thermodynamics. Moreover, based on currently available experimental data for individual spherules, and fractal-like assemblies of such spherules (Sections 2 and 3), we provide in Figures 2 and 3 the first available quantitative estimates for the relevant aggregate thermophoretic transport coefficients applicable in the Knudsen transition regime. Implications for investigators currently sampling aggregates from high pressure “sooting flames” are considered in Section 6.

⁶ Volume integrals needed for our estimates of the thermal shielding function, S_h (Equation (9[9] )) incorporated in Figures 2 and 3 were calculated numerically via the radial integral of {(2/3)[ 1 + (k_eff/2k_g,eff)]}⁻¹ · [φ(r;D_f,k₀)] · 4(π) r² dr where [φ(r) is given by Equation (5[5] ), 0 ≤ r ≤ R_max, and V = (4/3)(π)R_max³. For this purpose k_eff was taken to be the Maxwell-effective conductivity of the local suspension of uniform size conductive spherules, and both k_eff and k_g,eff were reduced to account for non-zero Kn₁ via the methods summarized in Rosner and Papadopoulos (1996). This quadrature approximation to S_h (see Assumption A4 and Equation (9[9] )), which circumvents solution of the heat diffusion PDE within the (orientation-averaged) aggregate, is expected to be adequate for large fractal-like aggregates because <φ> ≪1 (Table 1), causing S_h to remain close to unity. This expectation has been verified a posteriori for the DLCAs and RLCAs explicitly considered here.

⁷ While beyond the scope of the present manuscript, our analysis of the FA TP diffusivity via both the (R₁-dependent) individual particle thermal force (Young 2011)) and the drag on an assembly of N particles (Section 4) opens the door to quantitative estimates of the consequences of “spherule polydispersity.” Indeed, available high pressure TP-sampling data (Leschowski et al. 2014; Vargas and Gülder 2016) enable estimates of pdf_w(R₁) irrespective of N.

Appendix: Effect of predicted aggregate size-dependent thermophoretic velocity on inferred mainstream soot volume fractions

Underlying earlier “non-optical” estimates of absolute “soot” spherule volume fractions using TP-dominated flame sampling data (McEnally et al. 1997; Gomez and Rosner 1993; Tandon et al 2003) is the assumption of an aggregate size-insensitive TP-velocity, i.e., equivalent (Sections 5.7 and 6) to setting the exponent k = 0. However, as emphasized above (Section 5), we now find that this simplifying assumption fails badly when the sampling pressure is high enough to reduce the operative spherule Knudsen numbers (based on ) from ≫1 to O(1). Because the soot volume fraction is in fact calculated from the absolute total aggregate deposition rate on the cooler solid target, we turn our attention here to the theoretical correction factor associated with the calculable dimensionless deposition rate ratio—again assuming that the normalized mainstream aggregate size distribution (ASD), written pdf_∞(N), is approximately “log-normal” (as in Section 6).

If m₁ is the mass of one spherule and the total aggregate number density in the local mainstream being sampled then the total TP-dominated deposition rate can be approximated by:[A1]

But, suppose that most aggregates in the population contain many spherules, i.e., N_g ≫ 1 and, following Equation (7[7] ), we can write:[A2]

Here Equation (A2[A2] ) may be regarded as a local power-law fit to the behavior of ≪α_T*D_p≫_N/(α_TD)₁ near N = N_g,∞.

Equations (A1[A1] ) and (A2[A2] ) lead to the closed-form result:[A3]

Dividing by the corresponding expression when k = 0 then leads to the predicted deposition rate ratio, i.e.,[A4]

For example, when Kn₁ = 1 and k = 0.43 (for D_f = 1.8, k₀ = 1.3) we find that if N_g,∞ = 100 and σ_g = 3 this particular ratio is as large as ca. 1.9—larger than the previously calculated -ratio (Section 6). But as calculated above is itself larger than the corresponding spherule deposition rate by the factor [S_mom*S_h]_{N = Ng,∞}, which we estimate (using Figures 1 and 2) to be ca. 4.4. Thus, the overall enhancement in spherule deposition rate to the cold target is the product of 1.9 and 4.4, giving ca. 8.4—or nearly a one-decade correction.

On this basis we expect that the systematic corrections required to infer realistic mainstream soot volume fractions based on high-pressure TP/TEM flame sampling (often used as the calibration standard in this field) can rise to the level of necessary reduction factors by ca. one -decade. We note here that at the pressure levels of current combustion turbine interest (up to ca. 50 bar) this important conclusion would not be significantly altered if we had retained the earlier Talbot et al. (1980) thermal force law (for individual spherules)—as a reference to Figure 1 will confirm.

This calculation can be repeated for more compact fractal-like aggregates (e.g., with D_f = 2.1, k₀ = 0.94, as in Figure 3) using the important deposition rate ratio (Equation (A4[A4] )) in combination with Figures 1 and 2. The overall result is again a correction of ca. 10-fold. On this basis we conclude that apparent soot volume fractions calculated from total spherule counts on TEM grids at flame pressures near 50 bar using previously available methods would be systematically high by as much as one decade. This is but one dramatic consequence of the fact that such aggregates will no longer find themselves in the more familiar “free-molecule” regime, i.e., their spherules can take advantage of increased “momentum shielding” (Rosner and Tandon 2017).