Analytical expression for the rotational friction coefficient of DLCA aggregates over the entire Knudsen regime

ABSTRACT

We apply a self-consistent field method (Corson et al. 2017c) to calculate the rotational friction coefficient for fractal aerosol particles in the transition flow regime. Our method considers hydrodynamic interactions between spheres in a rotating aggregate due to the linear velocities of the spheres. Results are consistent with electro-optical measurements of soot alignment. Calculated rotational friction coefficients are also in good agreement with continuum and free molecule results in the limits of small (Kn = 0.01) and large (Kn = 100) primary sphere Knudsen numbers. As we previously demonstrated (Corson et al. 2017b) for the translational friction coefficient, the rotational friction coefficient approaches the continuum limit as either the primary sphere size and the number of primary spheres increases. We apply our results to develop an analytical expression Equation (26)[26] $\frac{{\zeta }_r}{8\pi \mu a^3}=\frac{1+5.988{\text{Kn}}_{\text{1}}}{C_r({\text{Kn}}_{\text{1}})}{\{{\left[0.713N^{1.63}+0.287\right]}^{-1}+5.988{\text{Kn}}_{\text{1}}{\left[1.184N^{2.02}-0.184\right]}^{-1}\}}^{-1}$[26] for the rotational friction coefficient as a function of the primary sphere size and number of primary spheres. One important finding is that the ratio of the translation to rotational diffusion times is nearly independent of cluster size. We include an extension of previous scaling analysis for aerosol aggregates to include rotational motion.

Copyright © 2018 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction

The rotational behavior of an aerosol particle can be characterized by the rotational friction and diffusion coefficients ${\zeta }_r$ and $D_r$, which are related by the Stokes-Einstein relationship ${\zeta }_r=kT/D_r$. The rotational behavior can be important to evaluating the average drift velocity (Li et al. 2014; Mulholland et al. 2016) and particle alignment in an external electric field and subsequent relaxation (Cheng et al. 1991; Weiss et al. 1992; Colbeck et al. 1997; Li et al. 2012, 2016).

For fractal aggregates that consist of many nanosized spheres in contact, determining the rotational friction/diffusion coefficient is a difficult problem. This is due to two principal factors: the complicated, fractal-like shape of the aggregates, and the fact that the particle size is often comparable to the mean free path of the molecules in the gas. The latter complication means that the particles are in the transition flow regime, where one must use kinetic theory to solve for the forces and torques exerted by the gas on the aggregates. For these fractal-like particles, the relationship between the number of spheres in the aggregate and its radius of gyration is[1] $N=k_0{\left(\frac{R_g}{a}\right)}^{d_f}$[1] where $d_f$ and $k_0$ are the fractal dimension and prefactor. For particles formed by diffusion-limited cluster aggregation (DLCA), which is the focus of this work, $k_0\approx 1.3$ and $d_f\approx 1.78$.

In this article, we build on our prior work on the rotational friction coefficient of aggregates (Corson et al. 2017c). Here, we apply our extended Kirkwood-Riseman (EKR) theory to determine the rotational friction coefficient of DLCA aggregates over a parameter range of interest to aerosol scientists. We use our results to generate a simple analytical expression for the rotational friction coefficient, as a function of primary sphere size and the number of spheres in the aggregate.

2. Theoretical methods

The force and torque on a rigid particle moving slowly relative to the surrounding fluid can be expressed as

[2] $\overrightarrow{F}=-{\overleftrightarrow{\xi }}_t\cdot {\overrightarrow{U}}_O-{\overleftrightarrow{\xi }}_{O,c}^{†}\cdot \overrightarrow{\omega }$[2] [3] $\overrightarrow{T}=-{\overleftrightarrow{\xi }}_{O,c}\cdot {\overrightarrow{U}}_O-{\overleftrightarrow{\xi }}_{O,r}\cdot \overrightarrow{\omega }$[3] where point O is the center of mass of the particle; ${\overrightarrow{U}}_O$ and $\overrightarrow{\omega }$ are the translational and rotational velocities of the particle; and ${\overleftrightarrow{\xi }}_t$, ${\overleftrightarrow{\xi }}_{O,r}$, and ${\overleftrightarrow{\xi }}_{O,c}$ are the translational, rotational, and translation-rotation coupling friction tensors. The translational, rotational, and coupling friction tensors relate the particle translational velocity to the force on the particle, the particle angular velocity to the torque on the particle, and the particle translational or angular velocity to the torque or force on the particle, respectively. Note that the subscript O indicates that the property is described relative to the particle's center of mass, while the dagger symbol represents the transpose of a tensor. These equations apply for creeping flow in the continuum, free molecule, and transition regimes, characterized by very small, very large, and intermediate Knudsen numbers, respectively. For spheres, the Knudsen number is defined as $\text{Kn}=\lambda /a$, where λ is the gas mean free path and a is the sphere radius.

Brenner (1967) demonstrated that a particle's friction and diffusion tensors are connected by a generalized Stokes-Einstein relationship,[4] ${\overleftrightarrow{D}}_O=kT{{\overleftrightarrow{M}}_O}^{-1}$[4] where the grand mobility and diffusion tensors ${\overleftrightarrow{M}}_O$ and ${\overleftrightarrow{D}}_O$ are defined as[5] ${\overleftrightarrow{M}}_O=\left[\begin{array}{ll}{\overleftrightarrow{\xi }}_t& {\overleftrightarrow{\xi }}_{O,c}^{†}\\ {\overleftrightarrow{\xi }}_{O,c}& {\overleftrightarrow{\xi }}_{O,r}\end{array}\right]$[5] [6] ${\overleftrightarrow{D}}_O=\left[\begin{array}{ll}{\overleftrightarrow{D}}_{O,t}& {\overleftrightarrow{D}}_{O,c}^{†}\\ {\overleftrightarrow{D}}_{O,c}& {\overleftrightarrow{D}}_r\end{array}\right]$[6]

The scalar friction and diffusion coefficients are obtained from the trace of the rotational diffusion tensor:[7] $D_r=kT/{\zeta }_r=\frac{1}{3}Tr\left({\overleftrightarrow{D}}_r\right)$[7]

Analytical expressions are available for the rotational friction/diffusion coefficient of simple shapes in the continuum (Happel and Brenner 1965; Brenner 1967; Ortega and Garcia de la Torre 2003) and free molecule regimes (Halbritter 1974; Williams and Loyalka 1991; Li et al. 2014), but more approximate methods are needed for fractal-like aggregates of touching spheres. The rotation problem has been studied extensively by Garcia de la Torre and colleagues for rigid particles in continuum flow (Bernal and Garcia de la Torre 1980; Carrasco and Garcia de la Torre 1999; Garcia de la Torre et al. 2007). Li et al. (2016) used a simplified approach in the free molecule regime that ignored shielding by other spheres in the aggregate. In principle, one could use a Monte Carlo approach in the free molecule regime analogous to that used to compute the translational friction coefficient (Chan and Dahneke 1981; Mackowski 2006; Larriba and Hogan 2013; Shrivastav et al. 2017) by replacing the linear velocity field by a rotating velocity field, though no one appears to have published any results using this approach.

Unfortunately, in many practical situations aerosol particles are fractal-like aggregates in the transition flow regime, so a different approach is needed to analyze their rotational behavior. Recently, we (Corson et al. 2017c) demonstrated that our extended Kirkwood-Riseman (EKR) method (Corson et al. 2017a,b) can be applied to the rotational problem.

2.1. Extended Kirkwood-Riseman method for the rotational friction coefficient

Kirkwood and Riseman (1948) developed a method to determine the force exerted by a fluid on a particle or macromolecule consisting of N spherical elements in continuum flow, whereby the force on each element is equal to the force on an isolated sphere minus the perturbations to the flow field caused by the other spheres:[8] ${\overrightarrow{F}}_i=-{\zeta }_{t0}{\overrightarrow{U}}_i-{\zeta }_{t0}{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{T}}_{ij}\cdot {\overrightarrow{F}}_j}$[8] [9] ${\overleftrightarrow{T}}_{ij}=\frac{1}{8\pi \mu r_{ij}}\left[\left(\overleftrightarrow{I}+\frac{{\overrightarrow{r}}_{ij}{\overrightarrow{r}}_{ij}}{r_{ij}^2}\right)+\frac{2a^2}{3r_{iij}^2}\left(\overleftrightarrow{I}-\frac{3{\overrightarrow{r}}_{ij}{\overrightarrow{r}}_{ij}}{r_{ij}^2}\right)\right]$[9]

Here, ${\zeta }_{t0}=6\pi \mu a$ is the monomer translational friction coefficient, ${\overrightarrow{U}}_i$ is the velocity of the ith sphere in the aggregate, and ${\overleftrightarrow{T}}_{ij}$ is the hydrodynamic interaction tensor that quantifies the effects of the jth sphere on the ith sphere. Applications of KR theory often use the Rotne-Prager-Yamakawa (RPY) tensor (Rotne and Prager 1969; Yamakawa 1970), Equation (9)[9] ${\overleftrightarrow{T}}_{ij}=\frac{1}{8\pi \mu r_{ij}}\left[\left(\overleftrightarrow{I}+\frac{{\overrightarrow{r}}_{ij}{\overrightarrow{r}}_{ij}}{r_{ij}^2}\right)+\frac{2a^2}{3r_{iij}^2}\left(\overleftrightarrow{I}-\frac{3{\overrightarrow{r}}_{ij}{\overrightarrow{r}}_{ij}}{r_{ij}^2}\right)\right]$[9] , for ${\overleftrightarrow{T}}_{ij}$, which is accurate to $O(r_{ij}^{-3})$, where $r_{ij}$ is the distance between the ith and jth sphere.

The product of the monomer friction coefficient and the RPY tensor is similar to the solution for Stokes' flow around a sphere ${\overleftrightarrow{V}}_{ij}$, where $\overrightarrow{u}(r_{ij})={\overleftrightarrow{V}}_{ij}\cdot {\overrightarrow{U}}_j$ is the velocity around a sphere moving with velocity ${\overrightarrow{U}}_j$. Noting this, we introduced our extended Kirkwood-Riseman (EKR) method by replacing ${\zeta }_{t0}{\overleftrightarrow{T}}_{ij}$ in Equation (8)[8] ${\overrightarrow{F}}_i=-{\zeta }_{t0}{\overrightarrow{U}}_i-{\zeta }_{t0}{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{T}}_{ij}\cdot {\overrightarrow{F}}_j}$[8] with the velocity tensor for flow around a sphere in the transition regime, ${\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)$ (Corson et al. 2017a,b):[10] ${\overrightarrow{F}}_i=-{\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right){\overrightarrow{U}}_i-{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)\cdot {\overrightarrow{F}}_j}$[10]

As noted in the above equation, both the velocity tensor and the monomer friction coefficient are functions of the primary sphere Knudsen number Kn₁. These functions are obtained by solving the Bhatnagar-Gross-Krook equation (Bhatnagar et al. 1954) using the approach of Loyalka and colleagues (Lea and Loyalka 1982, 1986).

To determine the rotational friction coefficient, we first apply Equation (10)[10] ${\overrightarrow{F}}_i=-{\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right){\overrightarrow{U}}_i-{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)\cdot {\overrightarrow{F}}_j}$[10] by substituting ${\overrightarrow{U}}_i=\overrightarrow{\omega }\times {\overrightarrow{r}}_i$, where $\overrightarrow{\omega }$ is the angular velocity of the aggregate and ${\overrightarrow{r}}_i$ is the vector from the center of mass to the center of the ith sphere. This gives the force on each sphere in the rotating aggregate. Next, we calculate the torque on each sphere about the center of mass and sum up these torques to determine the total torque on the aggregate:[11] ${\overrightarrow{T}}_O={\displaystyle \sum _{i=1}^N{\overrightarrow{r}}_i\times {\overrightarrow{F}}_i}$[11]

Performing this procedure for angular velocities about three mutually orthogonal axes, we obtain the rotation friction tensor. Finally, we obtain the rotational diffusion tensor and the rotational friction/diffusion coefficient from Equations (4)[4] ${\overleftrightarrow{D}}_O=kT{{\overleftrightarrow{M}}_O}^{-1}$[4] and (7[7] $D_r=kT/{\zeta }_r=\frac{1}{3}Tr\left({\overleftrightarrow{D}}_r\right)$[7] ). Note that the translational and coupling friction tensors that appear in the grand mobility tensor ${\overleftrightarrow{M}}_O$ are obtained by solving Equation (10)[10] ${\overrightarrow{F}}_i=-{\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right){\overrightarrow{U}}_i-{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)\cdot {\overrightarrow{F}}_j}$[10] for a uniform translational velocity in three orthogonal direction for the force and torque (via Equation (11)[11] ${\overrightarrow{T}}_O={\displaystyle \sum _{i=1}^N{\overrightarrow{r}}_i\times {\overrightarrow{F}}_i}$[11] ) on the particle.

One significant flaw in applying the above method to calculate the torque on a rotating particle is that it yields a value of zero for a sphere or for a straight chain rotating about its long axis. To address this flaw, Garcia de la Torre and Rodes (1983) proposed adding the torque of N rotating spheres to the torque computed using KR theory for a rotating aggregate in continuum flow (the so-called volume correction). We take the same approach with our EKR method, except now the monomer rotational friction coefficient is a function of Knudsen number:[12] ${\overrightarrow{T}}_O=-N{\zeta }_{r0}\left({\text{Kn}}_{\text{1}}\right)\overrightarrow{\omega }+{\displaystyle \sum _{i=1}^N{\overrightarrow{r}}_i\times {\overrightarrow{F}}_i}$[12]

There is very little experimental data available for the torque on a rotating sphere as a function of Knudsen number. Tekasakul et al. (1996) and Bentz et al. (2001) state that their experimental results are in good agreement with the linearized Boltzmann results of Loyalka (1992) but do not provide sufficient data for a meaningful comparison. Thus, we use the published computational results of Loyalka and fit those results to an analytical expression for ${\zeta }_{r0}\left({\text{Kn}}_{\text{1}}\right)$. Specifically, we posit that the functional form of the monomer rotational friction coefficient is analogous to the Cunningham slip correction factor that appears in the monomer translational friction coefficient:[13] ${\zeta }_{r0}=\frac{8\pi \mu a^3}{C_r\left(\text{Kn}\right)}=\frac{8\pi \mu a^3}{1+\text{Kn}\left[A_{1r}+A_{2r}\exp \left(-\frac{A_{3r}}{\text{Kn}}\right)\right]}$[13]

The numerator of the above expression represents ${\zeta }_{r0}$ in the continuum limit. For very large Knudsen numbers, Equation (13)[13] ${\zeta }_{r0}=\frac{8\pi \mu a^3}{C_r\left(\text{Kn}\right)}=\frac{8\pi \mu a^3}{1+\text{Kn}\left[A_{1r}+A_{2r}\exp \left(-\frac{A_{3r}}{\text{Kn}}\right)\right]}$[13] must reduce to the free molecule expression for ${\zeta }_{r0}$ (Epstein 1924; Williams and Loyalka 1991),[14] ${\zeta }_{r0}^{FM}=\frac{2\pi \alpha }{3}\rho \overline{c}{a}^4=\frac{2\pi \alpha }{3\left(0.499\right)}\frac{\mu }{\lambda }{a}^4$[14] where $\alpha$ is the fraction of gas molecules that are reflected diffusively from the sphere surface. In the last equality, we use the viscosity of a hard sphere gas, $\mu =0.499\rho \overline{c}\lambda$, where $\rho$ is the gas density and $\overline{c}$ the mean speed of gas molecules. Using the results from Table IV (“Present” column) and Equation (33) from Loylka (1992) and noting that for diffuse reflection $A_{1r}+A_{2r}=5.988$, we get the following values for the coefficients in the rotational slip correction factor: $A_{1r}=3.930$, $A_{2r}=2.058$, and $A_{3r}=0.3277$.

A second concern in employing the EKR method is that it ignores rotational and translation-rotation coupling interactions between spheres. Simply put, the linear and rotational motions of a sphere can induce a rotation or torque in another sphere, in accordance with Faxén's second law (Happel and Brenner 1965). The rotational and coupling hydrodynamic interaction tensors are (to order $r_{ij}^{-3}$) equal to the vorticity field around a rotating sphere and the vorticity field around a translating sphere, respectively. Thus, one would need to compute these fields as a function of Knudsen number to account for rotational and coupling effects. In addition, one would now need to invert a 6N-by-6N matrix (instead of a 3N-by-3N matrix, as in our current method) to obtain the translational, rotational, and coupling friction tensors. (See Corson et al. [2017c] for further discussion.) Rotational and coupling hydrodynamic interactions are weaker (i.e., lower order in $r_{ij}$) than the translational hydrodynamic interactions described by ${\overleftrightarrow{T}}_{ij}$, so we ignore these effects in our EKR method. The resulting error is appreciable (around 30–40%) for very small, dense (i.e., high fractal dimension) aggregates but decreases as the aggregate size (and thus the average distance between spheres) increases (Corson et al. 2017c). We will discuss this further later in this paper.

To apply our method for calculating the rotational friction coefficient, one simply needs the coordinates of the primary spheres in the particle (either from a cluster-cluster aggregation algorithm, as we use for this study, from a detailed Brownian simulation, or from a TEM image) and the velocity field around a sphere. (See Corson et al. [2017a] for velocity results at select Knudsen numbers.) Given this information, one forms a 3N-by-3N matrix where each 3-by-3 block is ${\overleftrightarrow{Q}}_{ij}=\left[{\delta }_{ij}\overleftrightarrow{I}+\left(1-{\delta }_{ij}\right){\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)\right]/{\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right)$ and ${\delta }_{ij}$ is the Kronecker delta. The tensor ${\overleftrightarrow{V}}_{ij}$ is a function of primary size and the vector connecting the i th and j th spheres. In other words, one solves Equation (10)[10] ${\overrightarrow{F}}_i=-{\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right){\overrightarrow{U}}_i-{\displaystyle \sum _{i\ne j}^N{\overleftrightarrow{V}}_{ij}\left({\text{Kn}}_{\text{1}}\right)\cdot {\overrightarrow{F}}_j}$[10] as a linear algebra problem to obtain the force on each sphere and uses these results and Equation (12)[12] ${\overrightarrow{T}}_O=-N{\zeta }_{r0}\left({\text{Kn}}_{\text{1}}\right)\overrightarrow{\omega }+{\displaystyle \sum _{i=1}^N{\overrightarrow{r}}_i\times {\overrightarrow{F}}_i}$[12] to determine the torque on the particle. Repeating this procedure for three mutually orthogonal angular velocities, one obtains the rotational friction tensor. See our previous paper for further discussion (Corson et al. 2017c).

2.2. Adjusted sphere method for the rotational friction coefficient

The extended Kirkwood-Riseman method can be applied to determine the friction tensors of an aggregate in the transition flow regime, given the coordinates of the spheres in the aggregate and the velocity around a sphere as a function of the primary sphere Knudsen number. From these friction tensors, one can obtain the rotational friction or diffusion coefficient. Here, we propose a parametric method of determining the rotational friction coefficient that does not rely on the EKR method. This parametric method is based on the adjusted sphere method (ASM) of Dahneke (1973) and Zhang et al. (2012) for determining the translational friction coefficient. Our preliminary results show that the adjusted sphere approximation can be applied to the rotational friction coefficient (Corson et al. 2017c).

Dahneke (1973) and Zhang et al. (2012) posited that there is a universal relationship between the translational friction coefficient of an aggregate and an aggregate Knudsen number:[15] ${\zeta }_t^{\text{ASM}}=\frac{6\pi \mu R_H}{C_c({\text{Kn}}_t^{\text{agg}})}$[15] [16] ${\text{Kn}}_t^{\text{agg}}=\frac{\pi \lambda R_H}{\text{PA}}$[16]

Here, the hydrodynamic radius $R_H$ and orientation-averaged projected area PA are continuum and free molecular measures of the particle size, respectively. The adjusted sphere method allows one to compute the translational friction coefficient of an aggregate given its hydrodynamic radius and projected area.

Melas et al. (2015) show that this aggregate Knudsen number is proportional to the ratio of continuum and free molecule expressions for the translational friction coefficient. We propose an analogous approach for the rotational friction coefficient:[17] ${\zeta }_r^{\text{ASM}}=\frac{{\zeta }_r^c}{C_r({\text{Kn}}_r^{\text{agg}})}$[17] [18] ${\text{Kn}}_r^{\text{agg}}=\frac{{\zeta }_r^c}{\left(A_{1r}+A_{2r}\right){\zeta }_r^{FM}}$[18]

Here, ${\zeta }_r^c$ and ${\zeta }_r^{FM}$ are the aggregate rotational friction coefficients computed using continuum and free molecular methods, respectively. The rotational slip correction factor formula is the same as $C_r$ defined in Equation (13)[13] ${\zeta }_{r0}=\frac{8\pi \mu a^3}{C_r\left(\text{Kn}\right)}=\frac{8\pi \mu a^3}{1+\text{Kn}\left[A_{1r}+A_{2r}\exp \left(-\frac{A_{3r}}{\text{Kn}}\right)\right]}$[13] and used to compute the monomer rotational friction coefficient; likewise, coefficients $A_{1r}+A_{2r}=5.988$, just as in the monomer formula.

The adjusted sphere method is useful if one wants to obtain the rotational friction coefficient without worrying about the details of the EKR method. However, ASM incorporates both the continuum and free molecule friction coefficients for an aggregate, and obtaining these expressions typically requires methods at least as complex as the EKR method.

2.3. Scaling laws for the rotational friction coefficient in the continuum and free molecule regimes

Given the complications involved in determining the rotational friction coefficient of fractal aggregates, it is useful to develop a simple relationship between the aggregate size and structure (i.e., the monomer size, the number of monomers, and the fractal dimensions) and its rotational friction coefficient. Here, we present some theoretical considerations for this relationship in both the continuum and free molecule regimes and use those considerations to develop upper bounds for the rotational friction coefficient. Later, we will use our results for the rotational friction coefficient of DLCA aggregates to improve these simple relationships in the continuum and free molecule regimes and to introduce a new expression for the transition regime.

We begin with the continuum regime, where we will use an analogy with the translational friction coefficient to develop the relationship between the aggregate size and structure and the rotational friction coefficient. As mentioned in the previous section, one can define the hydrodynamic radius as the radius of a sphere with the same translational friction coefficient as the aggregate. Computational studies have shown that this hydrodynamic radius is roughly proportional to the radius of gyration (Meakin et al. 1985; Sorensen 2011; Corson et al. 2017b), such that the translational friction coefficient can be estimated as ${\zeta }_t^c\sim 6\pi \mu R_g$. By the same rationale, we can replace the sphere radius in the expression for the rotational friction coefficient with the radius of the gyration of the aggregate:[19] ${\zeta }_r^c\sim 8\pi \mu R_g^3$[19]

Using Equation (1)[1] $N=k_0{\left(\frac{R_g}{a}\right)}^{d_f}$[1] , we obtain a scaling relationship between the aggregate size and structure and the rotational friction coefficient:[20] ${\zeta }_r^c\sim k_0^{-3/d_f}{\zeta }_{r0}^c{N}^{3/d_f}$[20]

For DLCA aggregates with $d_f\approx 1.78$, ${\zeta }_{t0}^c$ would scale with $N^{1.685}$ based on this simplified analysis.

For the free molecule regime, we use the approach introduced by Li et al. (2016) to estimate the rotational relaxation time of an aggregate. In this approach, one assumes that the drag on each sphere in a rotating aggregate is equal to the drag on an isolated sphere moving with linear velocity ${\overrightarrow{U}}_i=\overrightarrow{\omega }\times {\overrightarrow{r}}_i$. Computing the torque ${\overrightarrow{T}}_i={\overrightarrow{r}}_i\times {\overrightarrow{F}}_i$ on each sphere and summing over all spheres in the aggregate, the torque becomes $\overrightarrow{T}=-{\zeta }_{t0}^{FM}N{R}_{g1}^2\overrightarrow{\omega }$, where $R_{g1}$ is the radius of gyration about the axis of rotation and ${\zeta }_{t0}^{FM}$ is the free molecule translational friction coefficient. Replacing $R_{g1}$ with $R_g$ and using Equation (1)[1] $N=k_0{\left(\frac{R_g}{a}\right)}^{d_f}$[1] , we obtain a scaling relationship between the aggregate size and structure and the rotational friction coefficient in the free molecule regime:[21] ${\zeta }_r^{FM}\sim k_0^{-2/d_f}{\zeta }_{r0}^{FM}{N}^{1+\left(2/d_f\right)}$[21]

Note that we have also substituted the free molecule rotational friction coefficient for the product $a^2{\zeta }_{t0}^{FM}$, since the two expressions are related by a constant of order unity. For DLCA aggregates, ${\zeta }_r^{FM}$ would scale with $N^{2.124}$ based on this simplified analysis.

The above expressions are analogous to the power-law relationship between the translational friction coefficient and the number of spheres in the aggregate observed in numerous experimental and computational studies, as summarized by Sorensen (2011). However, the exponents in Equations (20)[20] ${\zeta }_r^c\sim k_0^{-3/d_f}{\zeta }_{r0}^c{N}^{3/d_f}$[20] and (21[21] ${\zeta }_r^{FM}\sim k_0^{-2/d_f}{\zeta }_{r0}^{FM}{N}^{1+\left(2/d_f\right)}$[21] ) are much higher than the exponents in the translational friction power laws (approximately 0.54 and 0.94 in the continuum and free molecule regimes, respectively [Sorensen 2011; Corson et al. 2017b]), resulting in a much larger variation in the rotational friction coefficient for increasing N.

3. Results and discussion

We have used our EKR method to determine the rotational friction coefficient for DLCA aggregates ($k_0\approx 1.3$ and $d_f\approx 1.78$) with between 5 and 2000 primary spheres and for primary sphere Knudsen numbers between 0.01 and 100. We have also independently calculated ${\zeta }_r^{\text{ASM}}$ for these aggregates. The free molecule rotational friction coefficients that appear in the aggregate rotational Knudsen number are calculated using a Monte Carlo algorithm (Corson et al. 2017c), while the continuum friction coefficients are calculated using a KR-based method that accounts for translational, rotational, and coupling hydrodynamic interactions between spheres in the aggregate. (Specifically, we use the 3RD method described by Carrasco and Garcia de la Torre [1999], which includes terms up to order $O(r_{ij}^{-3})$ in the hydrodynamic interaction tensors.) For each aggregate size, we determine the friction coefficients of 20 different aggregates generated by a cluster-cluster algorithm. Thus, each data point in the following graphs represents the average of 20 realizations of aggregates with the same fractal dimension, prefactor, and number of primary spheres.

3.1. Comparison to experimental data

There is unfortunately a very limited databased for comparison. Colbeck et al. (1997) determined the rotational relaxation time of soot from the combustion of gasoline and other fuels using electro-optic scattering. In this technique, one compares the intensity of scattered light for particles aligned in an electric field to that randomly-oriented. The measured relaxation time is related to the rotational diffusion coefficient by ${\tau }_r=1/\left(6D_r\right)$. For gasoline combustion generated soot the measured relaxation time was about 4 ms.

Colbeck et al. (1997) provide SEM images of soot from the various fuels they used in their study. Based on these images, we estimate the maximum aggregate length for the gasoline soot (Figure 2a of Colbeck et al. [1997]) is approximately 4000 nm. Since the largest aggregates dominate the light scattering, we base our calculations on the larger clusters. The authors do not specify the primary sphere size or the number of spheres in the aggregate, so we must estimate these properties based on information available in the literature. Köylü and Faeth (1992) measured the primary sphere diameter of soot from several gaseous and liquid hydrocarbons, including n-heptane (35 nm), isopropanol (30 nm), benzene (50 nm), and toluene (51 nm). Thus, the mean primary sphere diameter for soot from gasoline combustion is likely in the range of 30–50 nm, depending on the fraction of aromatics in the fuel blend.

Using primary sphere sizes of 35, 40, 45, and 50 nm; fractal dimension and prefactor of 1.78 and 1.3; and a radius of gyration equal to 25% or 37.5% of the maximum aggregate length,¹ we can estimate the number of primary spheres in the aggregate. Results for the rotational relaxation times for aggregates generated with the above properties are listed in Table 1. It is seen that the results are weakly dependent on the primary sphere size for a fixed radius of gyration. Our results based on these simple estimates of the aggregate properties for the larger radius of gyration are in good agreement with the experimental results.

Table 1. Comparison of EKR results to experimental data from Colbeck et al. (1997).

Primary sphere diameter (nm)	Radius of gyration (nm)	Number of primary spheres	Rotational relaxation time (ms)
N/A	N/A	N/A	4^a
35	1000	508	0.96
40	1000	400	0.96
45	1000	325	0.91
50	1000	269	0.88
35	1500	1045	3.6
40	1500	824	3.5
45	1500	668	3.6
50	1500	554	3.4

^a Experimental result for gasoline (petrol), from Table 3 of Colbeck et al. [1997].

3.2. Comparison to results in the continuum and free molecule limits

The continuum and free molecule results exhibit the following power-law relationship between the rotational friction coefficient and the number of spheres in the aggregate:[22] ${\zeta }_r^c=0.713{\zeta }_{r0}^c{N}^{1.627}$[22] [23] ${\zeta }_r^{FM}=1.184{\zeta }_{r0}^{FM}{N}^{2.019}$[23]

The exponents in these equations are within 5% of the exponents we derived from the simple scaling analysis in the previous section. In both the continuum and free molecule regimes, the exponent obtained from our KR and Monte Carlo results are slightly lower than the exponents from our scaling analysis. In the continuum, this may be due to the fact that the hydrodynamic radius of a rotating aggregate increases more slowly than the radius of gyration with increasing aggregate size. Note that this behavior is observed for the translational friction coefficient. In the free molecule regime, the exponent based on the MC calculations is lower than the exponent from our scaling analysis because the scaling analysis does not account for the effects of shielding by other spheres in the aggregate on the drag on each sphere. The effects of shielding increase with aggregate size, which explains the reduced exponent in Equation (23)[23] ${\zeta }_r^{FM}=1.184{\zeta }_{r0}^{FM}{N}^{2.019}$[23] versus Equation (21)[21] ${\zeta }_r^{FM}\sim k_0^{-2/d_f}{\zeta }_{r0}^{FM}{N}^{1+\left(2/d_f\right)}$[21] .

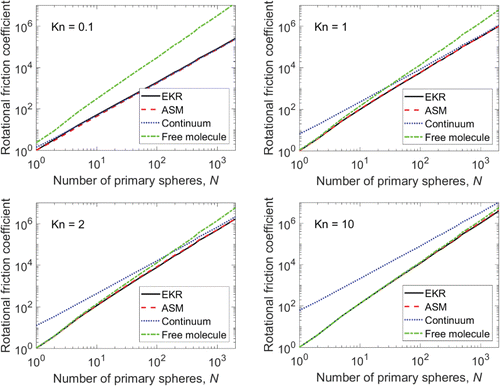
The large variation in the friction coefficient with N shown in Equations (22)[22] ${\zeta }_r^c=0.713{\zeta }_{r0}^c{N}^{1.627}$[22] and (23[23] ${\zeta }_r^{FM}=1.184{\zeta }_{r0}^{FM}{N}^{2.019}$[23] ) is evident in Figure 1. This figure also shows our EKR and rotational adjusted sphere method results at Knudsen numbers of 0.1, 1, 2, and 10. All results are normalized to the monomer rotational friction coefficient at the primary sphere Knudsen number specified in each plot. At Kn₁ = 0.1, the aggregates behave as if they are in the continuum, as expected. Likewise, at Kn₁ = 10 the aggregates exhibit free molecular behavior, though the EKR and ASM results begin to diverge from the free molecular limit at large N. At Kn₁ = 1 and Kn₁ = 2, the rotational friction coefficient approaches the continuum limit at large N. These trends are analogous to the trends in the translational friction coefficient as a function of primary sphere Knudsen number and the number of spheres (Corson et al. 2017b); the notable difference is that for the translational friction coefficient, the transition to continuum-like behavior occurs at a higher Knudsen number and for aggregates with fewer primary spheres. The reason for this is as follows. First, in the absence of any hydrodynamic interactions or any shielding by other monomers, the torque on each monomer is proportional to $r_i^2\cos \theta$, where $\theta$ is the angle between ${\overrightarrow{r}}_i$ and the axis of rotation. Second, the spheres furthest from the center of mass are less influenced by the other spheres, and thus behave more as if they are isolated. As a result, the spheres in the extremities of the aggregate experience a higher drag force than spheres in the interior of the particle. Combining these two effects, we see that the spheres furthest from the center of mass have the largest effect on the rotational friction coefficient, and these spheres behave most like they are isolated spheres whose drag force is given by ${\zeta }_{t0}\left({\text{Kn}}_{\text{1}}\right)\overrightarrow{\omega }\times {\overrightarrow{r}}_i$. The shielding effect is also evident for the translational friction coefficient, but since all the spheres move at the same translational velocity and are weighted equally (not by the distance from the center of mass), the behavior of the interior spheres dominates the aggregate translational friction coefficient. This explains why the rotational friction coefficient transitions to continuum-like behavior at lower Kn₁ and higher N relative to the translational friction coefficient.

Figure 1. Rotational friction coefficient results for Kn₁ = 0.1, 1, 2, and 10. Results are normalized by the monomer rotational friction coefficient for each Knudsen number.

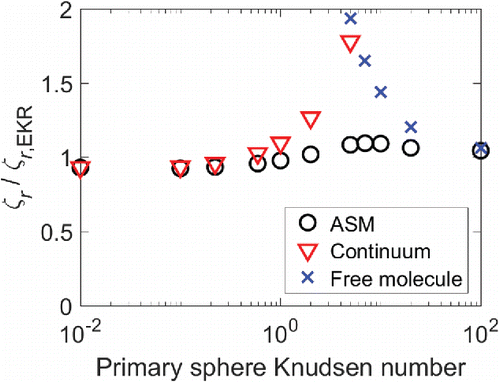
Given the nature of log-log plots in general and the six-order-of-magnitude variation in the rotational friction coefficient between N = 1 and N = 2000, it is difficult to ascertain the differences between the calculation results from the methods shown in Figure 1. For this reason, we have plotted the ratio of the adjusted sphere method, continuum, and free molecule rotational friction coefficients to the rotational friction coefficient calculated using the EKR method (Figure 2). Results are shown for N = 2000. For small Knudsen numbers, our EKR results are in good agreement with the continuum limit, while for very large Knudsen numbers, the EKR results are in good agreement with the free molecule limit. The EKR and ASM results are in good agreement for the entire Knudsen number range, which provides further evidence that there is a universal relationship for the rotational friction coefficient.

Figure 2. Ratio of the rotational friction coefficients for N = 2000 calculated using the rotational adjusted sphere method and in the continuum and free molecule limits to the rotational friction coefficient calculated using the EKR method.

3.3. Relative importance of translational and rotational diffusion

One consideration in many aerosol studies is the relative importance of rotational effects on aerosol transport properties. Studies often ignore rotational effects (e.g., on coagulation rates and the resulting shapes of aggregates [Mountain et al. 1986; Heinson et al. 2014]). This approach is valid if rotational diffusion is negligible relative to translational diffusion, i.e., if particle orientation changes very little in the time it takes for the particle to diffuse an appreciable distance. The relative importance of rotation on particle transport is captured by the ratio of a characteristic translation time to a characteristic rotation time. Defining the characteristic translation and rotation times as the time required for the particle to diffuse one radius of gyration and rotate one radian, this ratio becomes[24] $\frac{{\tau }_t}{{\tau }_r}=\frac{R_g^2/6D_t}{1/6D_r}=\frac{R_g^2{\zeta }_t}{{\zeta }_r}$[24]

Figure 3 shows this ratio as a function of primary sphere Knudsen number and the number of primary spheres, calculated using both our EKR results and analytic expressions for the translational and rotational friction coefficients (introduced in Section 3.5 below). Note that the choppy nature of the EKR plot is due to large variations in the rotational friction coefficient for a given set of aggregate parameters, as discussed in the next section. The exact magnitude of the results in this figure is insignificant since we are choosing arbitrary translational and rotational diffusion distances; nevertheless, the results show that in the time it takes an aggregate to diffuse one radius of gyration, it has rotated significantly. Simply put, translational and rotational diffusion are equally important. This is true for all of the primary sphere and aggregate sizes we have included in this study. These results do not imply that ignoring rotational behavior has a significant impact on the results of aerosol transport calculations (e.g., coagulation rates or filtration efficiency); nevertheless, our results suggest that this issue deserves further attention.

Figure 3. Ratio of the characteristic translational diffusion time to the characteristic rotational diffusion time for DLCA aggregates as a function of primary sphere size and the number of primary spheres. Each curve represents the results for the specified primary sphere Knudsen number. The plot on the left shows results of our EKR calculations, while the plot on the right shows results obtained using our analytic fits for the translational and rotational friction coefficients (Equations (25)[25] $\frac{\zeta }{6\pi \mu a}=\frac{1+1.612{\text{Kn}}_{\text{1}}}{C_c({\text{Kn}}_{\text{1}})}{\{{\left[0.852N^{0.535}+0.148\right]}^{-1}+1.612{\text{Kn}}_{\text{1}}{\left[0.843N^{0.939}+0.157\right]}^{-1}\}}^{-1}$[25] and (26[26] $\frac{{\zeta }_r}{8\pi \mu a^3}=\frac{1+5.988{\text{Kn}}_{\text{1}}}{C_r({\text{Kn}}_{\text{1}})}{\{{\left[0.713N^{1.63}+0.287\right]}^{-1}+5.988{\text{Kn}}_{\text{1}}{\left[1.184N^{2.02}-0.184\right]}^{-1}\}}^{-1}$[26] )).

It is also interesting to note that the ratio of translational to rotational relaxation times increases as a weak function of N in the continuum (low Kn) and free molecule (large Kn) limits. One can also arrive at this conclusion by substituting the power laws for the continuum and free molecule rotational friction coefficients (Equations (22)[22] ${\zeta }_r^c=0.713{\zeta }_{r0}^c{N}^{1.627}$[22] and (23[23] ${\zeta }_r^{FM}=1.184{\zeta }_{r0}^{FM}{N}^{2.019}$[23] )) and the power laws for the translational friction coefficients (N^0.54 and N^0.94 in the continuum and free molecule regimes, respectively) into Equation (24)[24] $\frac{{\tau }_t}{{\tau }_r}=\frac{R_g^2/6D_t}{1/6D_r}=\frac{R_g^2{\zeta }_t}{{\zeta }_r}$[24] .² In between, the situation is more complicated: the transition to continuum-like behavior happens at lower N and higher Kn₁ for translational transport compared to rotational transport, which explains the decrease in the characteristic diffusion ratio at moderate Knudsen numbers.

3.4. Uncertainty in the calculated rotational friction coefficients

In our previous paper (Corson et al. 2017b), we discussed the uncertainty in our calculated translational friction coefficients. There, we identified two main sources of uncertainty: the uncertainty in the calculated velocity tensor and monomer friction coefficient that appear in the EKR method, and KR theory itself. These factors also contribute to the uncertainty in the rotational friction coefficient. However, we must add two additional sources of uncertainty: the effects of neglecting rotational and coupling hydrodynamic interactions and variations in the friction coefficient for aggregates with the same number of primary spheres and the same fractal dimension and prefactor.

As we have mentioned, the linear and rotational velocities of each sphere in the aggregate can induce a torque in the other spheres. In the continuum, the rotational and coupling interactions are order $r_{ij}^{-3}$ and $r_{ij}^{-2}$, respectively, as compared to the translational hydrodynamic interaction tensor, which has leading terms of order $r_{ij}^{-1}$. As a result, we expect that the error in our EKR method would decrease with increasing aggregate size due to the increase in the average distance between monomers. Our results confirm this expectation: the difference between the EKR and continuum results at Kn₁ = 0.01 is approximately 25% for N = 5 and 8% for N = 2000. That 8% difference at N = 2000 mirrors the difference between our calculated monomer translational friction coefficient and the friction coefficient given by Stokes' law (Corson et al. 2017b), suggesting that the effects of coupling and rotational hydrodynamic interactions are negligible for large aggregates. Expressions for the rotational and coupling interaction tensors are unavailable for noncontinuum flow, so it is difficult to estimate the effects of neglecting these effects in the transition regime. However, we note that the EKR and free molecule results at Kn₁ = 100 are within 5% for the entire aggregate size range we studied. This suggests that rotational and coupling interactions decrease in importance with increasing Knudsen number, as well as for increasing aggregate size. As a result, the uncertainty in the rotational friction coefficients computed using our EKR method is comparable to the uncertainty in our computed translational friction coefficients (i.e., ∼10%) for all aggregates near the free molecule regime and for large aggregates for any flow regime. This uncertainty is larger (i.e., ∼25%) for small DLCA aggregates near the continuum regime.

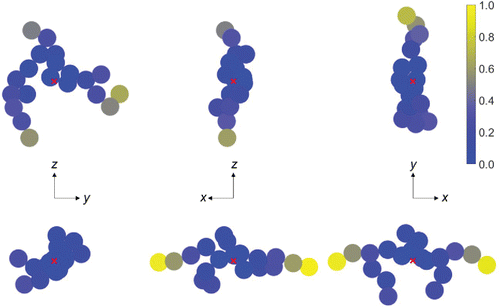
The sources of uncertainty discussed above might better be termed “sources of error,” since they represent differences between our results and the true rotational friction coefficient. The final source of uncertainty is just that: variability in the resulting rotational friction coefficient for the same input (namely, the primary sphere Knudsen number, the number of primary spheres, and the fractal dimension and prefactor). Our reported results represent averages of results from 20 trials for each set of inputs; here, the variability is due to differences in the coordinates of the spheres that comprise the aggregate. For the translational friction coefficient, this uncertainty is present, but it is very small: the standard deviation in the calculated friction coefficient is less than 2% of the mean for all primary sphere and aggregate sizes. However, for the rotational friction coefficient the standard deviation is as high as 20% of the mean, and the standard deviation varies with Kn: it is lowest near the continuum regime and largest near the free molecule regime. These variations can be understood in the context of our earlier discussion on the influence of peripheral spheres on the rotational friction coefficient: spheres far from the center of mass have a much larger impact on the rotational friction coefficient than spheres near the center of mass. Thus, variations in the coordinates of the spheres in the aggregate that have little impact on the translational friction coefficient are amplified when determining the rotational friction coefficient. (See online supplemental information for tables of rotational and translational friction coefficient results.) Figure 4 illustrates this point. In the figure, we show the torque on each sphere in two rotating 20-sphere aggregates for rotation about the three principal axes (i.e., the axes for which the rotational friction tensor is diagonal). The calculations are performed at Kn₁ = 10. The scale is the same for all six cases shown: the values indicate the torque on the sphere, divided by the largest torque among the six cases. These two aggregates have the same (i.e., within 0.5%) translational friction coefficient, but the rotational friction coefficient—essentially the harmonic average of the friction coefficient for each principal axis—of aggregate 2 is only 75% of the rotational friction coefficient of aggregate 1. Thus, even though the torque is highest for aggregate 2 rotating about the y- and z-axes, the torque about the x-axis is so low that the harmonic average is less than the harmonic average of the torque coefficients for aggregate 1. Again, these effects are dominated by spheres near the periphery of the aggregate, as indicated by figure.

Figure 4. Torque on each sphere of two 20-particle aggregates rotating about the x-, y-, and z-axes (left, middle, and right, respectively) for Kn₁ = 10. The rotation axis is out of the page. The torque is normalized by the maximum torque among the six cases. The rotational friction coefficient for aggregate 2 (bottom) is approximately 75% of the rotational friction coefficient for aggregate 1 (top).

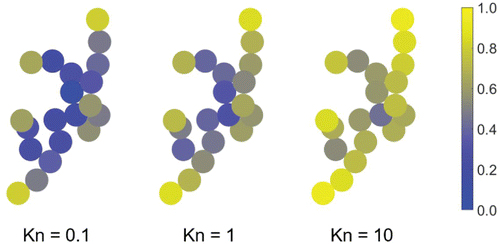
The effect of the peripheral spheres on the rotational friction coefficient is more significant near the free molecule regime because these spheres behave almost as if they are isolated, whereas in the continuum even the peripheral spheres are somewhat affected by the particle's overall effect on the flow field. This behavior is illustrated in Figure 5, which shows the ratio of the drag on each sphere in a 20-sphere aggregate to the drag on an isolated sphere (i.e., $F_i/\left[{\zeta }_0\left({\text{Kn}}_{\text{1}}\right)U_i\right]$) for three different Knudsen numbers. Note that the uncertainty due to variations in particle shape (as illustrated in Figure 4) does not affect our EKR results for individual particle realizations; rather it represents the variation in the rotational friction coefficient for the same set of inputs.

Figure 5. Ratio of the drag on each sphere in a 20-particle aggregate to the drag on an isolated sphere (i.e., the monomer momentum shielding factor). Here, the particle is rotating counter-clockwise. A value of unity indicates that the sphere behaves as if it is isolated, while a value near zero indicates that the perturbations caused by the other spheres have a significant impact on the drag.

3.5. Analytical expression for rotational friction coefficients of DLCA aggregates

Previously, we developed an analytical expression for the translational friction coefficient of DLCA aggregates (Equation (38) of Corson et al. [2017b]) that we verified with our EKR results:[25] $\frac{\zeta }{6\pi \mu a}=\frac{1+1.612{\text{Kn}}_{\text{1}}}{C_c({\text{Kn}}_{\text{1}})}{\{{\left[0.852N^{0.535}+0.148\right]}^{-1}+1.612{\text{Kn}}_{\text{1}}{\left[0.843N^{0.939}+0.157\right]}^{-1}\}}^{-1}$[25]

We will use the same approach to develop an analytical expression for the rotational friction coefficient, which may be used to quickly estimate the characteristic rotational relaxation time for a Brownian particle.

Our expression is based on the harmonic sum of the continuum and free molecule power-law expressions for the rotational friction coefficient (Equations (22)[22] ${\zeta }_r^c=0.713{\zeta }_{r0}^c{N}^{1.627}$[22] and (23[23] ${\zeta }_r^{FM}=1.184{\zeta }_{r0}^{FM}{N}^{2.019}$[23] )). In addition, we have added a term to each power law to give the correct value for the monomer friction coefficient, and we have corrected for the fact that the harmonic sum of the continuum and free molecule monomer friction coefficients differs from the monomer friction coefficient given by Equation (13)[13] ${\zeta }_{r0}=\frac{8\pi \mu a^3}{C_r\left(\text{Kn}\right)}=\frac{8\pi \mu a^3}{1+\text{Kn}\left[A_{1r}+A_{2r}\exp \left(-\frac{A_{3r}}{\text{Kn}}\right)\right]}$[13] . The resulting expression is[26] $\frac{{\zeta }_r}{8\pi \mu a^3}=\frac{1+5.988{\text{Kn}}_{\text{1}}}{C_r({\text{Kn}}_{\text{1}})}{\{{\left[0.713N^{1.63}+0.287\right]}^{-1}+5.988{\text{Kn}}_{\text{1}}{\left[1.184N^{2.02}-0.184\right]}^{-1}\}}^{-1}$[26]

Figure 6 shows the error in our fit relative to our EKR results:[27] $error=\frac{{\zeta }_r^{\text{fit}}-{\zeta }_r^{EKR}}{{\zeta }_r^{EKR}}$[27]

Figure 6. Error in our analytical expression for the rotational friction coefficient (Equation (26)[26] $\frac{{\zeta }_r}{8\pi \mu a^3}=\frac{1+5.988{\text{Kn}}_{\text{1}}}{C_r({\text{Kn}}_{\text{1}})}{\{{\left[0.713N^{1.63}+0.287\right]}^{-1}+5.988{\text{Kn}}_{\text{1}}{\left[1.184N^{2.02}-0.184\right]}^{-1}\}}^{-1}$[26] ) relative to our EKR results. This error is defined by Equation (27)[27] $error=\frac{{\zeta }_r^{\text{fit}}-{\zeta }_r^{EKR}}{{\zeta }_r^{EKR}}$[27] .

The error is within approximately 15% for much of the primary sphere Knudsen number and aggregate size range studied here, though the error for smaller aggregates near the continuum regime is higher. Again, this is because the continuum power-law expression is based on results from a more rigorous method of calculating the rotational friction coefficient, where we account for rotational and coupling hydrodynamic interactions. Thus, the error in Equation (26)[26] $\frac{{\zeta }_r}{8\pi \mu a^3}=\frac{1+5.988{\text{Kn}}_{\text{1}}}{C_r({\text{Kn}}_{\text{1}})}{\{{\left[0.713N^{1.63}+0.287\right]}^{-1}+5.988{\text{Kn}}_{\text{1}}{\left[1.184N^{2.02}-0.184\right]}^{-1}\}}^{-1}$[26] relative to the true rotational friction coefficient near the continuum regime is likely much lower than indicated by Figure 6, which shows the error relative to the EKR results that overestimate the rotational friction coefficient for small aggregates near the continuum regime. However, our fit does not account for uncertainties in the rotational friction coefficient due to variations in the aggregate shape. Thus, the true error in the fit may be as high as 30% for a given aggregate. This is still acceptable given the lack of alternative methods for estimating the rotational friction coefficient in the transition regime.

4. Conclusions

We have presented our self-consistent field results for the rotational friction coefficient of DLCA aggregates consisting of 5–2000 primary spheres with primary sphere Knudsen numbers between 0.01 and 100. Our results are in good agreement with the continuum and free molecule limits for small and large Knudsen numbers, respectively. Our computed relaxation times from an aligned to randomly oriented agglomerate are consistent with the measurements by Colbeck et al. (1997) for soot produced from gasoline. We estimate that our calculated rotational friction coefficients are within 30% of the true value for the range of parameters we have studied, with the greatest errors occurring for small aggregates near the continuum regime and significantly better agreement for all aggregates near the free molecule regime and for large aggregates in any flow regime.

We have used our EKR method to calculate the ratio of translational to rotational characteristic diffusion times. A potentially important finding is that this ratio is nearly independent of cluster size. Our results show that aggregates rotate significantly in the time it takes to diffuse one radius of gyration. This finding suggests that further study is needed to assess the importance of rotation on aerosol coagulation and deposition behavior.

We have introduced an analytic expression for the rotational friction coefficient of DLCA aggregates ($k_0\approx 1.3$ and $d_f\approx 1.78$). This simple model can be applied to quickly estimate the characteristic rotational relaxation time for studies involving particle alignment in an external field. We have extended scaling analyses for the continuum and free molecule friction coefficients to the rotational problem, which can also be used to estimate the rotational friction/diffusion coefficient of an aggregate in these limits.

We have also provided an expression for the monomer rotational friction coefficient as a function of Knudsen number, based on the computational results of Loyalka (1992). This expression includes a slip correction factor with the same general form as the Cunningham slip correction factor used for the translational friction coefficient of a sphere.

Notes

¹ These are bounding estimates. Note that the algorithm we use to generate our aggregates yields particles whose radii of gyration are ∼30–33% of the maximum length.

² Note that if one applies the simple scaling arguments from Section 2.3 (translational friction coefficient proportional to the radius of gyration in the continuum and to the number of primary spheres in the free molecule regime, and rotational friction coefficients given by Euations (20)[20] ${\zeta }_r^c\sim k_0^{-3/d_f}{\zeta }_{r0}^c{N}^{3/d_f}$[20] and (21[21] ${\zeta }_r^{FM}\sim k_0^{-2/d_f}{\zeta }_{r0}^{FM}{N}^{1+\left(2/d_f\right)}$[21] )), one predicts that the ratio is independent of N in the continuum and free molecule regimes.