Thermophoresis of a particle in a concentric cavity with thermal stress slip

ABSTRACT

The thermophoretic motion of a spherical particle situated at the center of a spherical cavity filled with a gaseous medium under a prescribed temperature gradient is studied analytically. The Knudsen number is small for the gas motion in the slip-flow regime, and the temperature jump, thermal creep, frictional slip, and particularly, thermal stress slip are allowed on the solid surfaces. After solving the equations of heat conduction and fluid motion, an explicit formula for the migration velocity of the confined particle is obtained for different temperature conditions of the cavity with arbitrary values of the particle-to-cavity radius ratio and other parameters. Contributions from the thermoosmotic flow along the cavity wall and from the wall-corrected thermophoretic force to the particle velocity are equivalently important and can be linearly superimposed. With either or both of these contributions, the particle velocity in general is a decreasing function of the particle-to-cavity radius ratio and vanishes in the limit. The effects of the thermal stress slip at the solid surfaces to the migration velocity of the confined particle can be significant and interesting, dependent on the thermal and interfacial properties of the particle and surrounding gas. The wall effect on the thermophoretic migration of the particle in a cavity is qualitatively different from that on the motion of the particle in a circular tube.

Copyright © 2018 American Association for Aerosol Research

EDITOR:

• Yannis Drossinos

1. Introduction

When a tangential temperature gradient exists in a rarified gas adjacent to a solid surface, a thin Knudsen layer of the fluid at the surface will flow along with the gradient (i.e., from cold to hot). This thermal creep phenomenon (Maxwell 1879) provides a mechanism in the slip-flow regime for the thermophoresis of aerosol particles and thermoosmosis of bounded gases with the Knudsen number of the order 0.1, where is the linear dimension of the particles or boundaries and is the mean free path of the gas molecules. Thermophoresis (viz., the Soret effect), which is the particle motion caused by a bulk-gas temperature gradient against its direction (i.e., from hot to cold), plays an important role in many practical applications such as aerosol sampling, air cleaning, microelectronic manufacturing, scale formation on heat exchanger surfaces, nuclear reactor safety, modified chemical vapor deposition, and catalysis-driven plasmonic nanomotors (Balsara and Subramanian 1987; Williams and Loyalka 1991; Chang and Keh 2010a,b; Hsieh and Keh 2012; Sagot 2013; Guha and Samanta 2014; Wu et al. 2015; Bhusnoor et al. 2017; Qin et al. 2017).

The kinetic theory of gases suggests a relation between the velocity slip at a solid surface across the Knudsen layer and the heat flux , viscous stress , as well as second-order temperature gradient in the slip-flow regime as (Maxwell 1879; Sone 1972; Lockerby 2004; Chang and Keh 2017)[1]

Here, , , , and are the thermal conductivity, viscosity, mass density, and absolute temperature, respectively, of the gas, , , and are the thermal creep, frictional slip, and thermal stress slip coefficients, respectively, about the particle-gas interface (all are dimensionless of the order unity), is the unit dyadic, and is the unit vector outwardly normal to the solid surface. Note that the thermal stress slip, whose effect was usually neglected, vanishes as .

The application of Fourier's law of conduction and Newton's law of viscosity to Equation (1[1] ) as the boundary condition for the fluid velocity , incorporating with the temperature jump at the particle surface [as shown in Equation (3[3] )], leads to the thermophoretic velocity of a spherical particle of radius in a uniformly prescribed temperature gradient (Chang and Keh 2012; Chen and Keh 2014),[2]

Here, the dimensionless coefficient accounts for the temperature jump (also of the order unity), is the thermal conductivity of the particle, and is the average absolute temperature of the fluid around the particle with . This particle velocity is a linear combination of the contributions from both effects of the thermal creep and thermal stress slip, and for large particle-to-gas thermal conductivity ratios reversed thermophoresis (i.e., from cold to hot) may occur (Dwyer 1967; Young 2011). As (i.e., in absence of thermal stress slip), Equation (2[2] ) becomes the well-known formula obtained by Brock (1962) that cannot predict reversed thermophoresis.

A set of kinetic-theory values of the jump/slip coefficients for complete energy and momentum accommodations of gas molecules with the hard-sphere pair potential appear to be , , and (Talbot et al. 1980), and the value of has been taken to be 1 (Lockerby et al. 2004; Li et al. 2010) or 3 (Bakanov 2004). According to Equation (2[2] ), particles with small Knudsen number and large thermal conductivity (e.g., and ) may undergo thermophoretic motion with velocities of 10–50 in a temperature gradient of 0.01 .

In most real applications of thermophoresis in microfluidic devices, the dimensions of the aerosol particles and confining microchannels are comparable, and it is needed to ascertain if the proximity of the channel wall significantly influences the particle velocity (Wang and Keh 2010). The thermophoretic motions of a spherical particle perpendicular (Chen and Keh 1995; Keh and Chang 2006) and parallel (Keh and Chen 2003) to a single plane wall or a pair of plane walls as well as along the axis of a circular tube (Lu and Lee 2003; Li and Keh 2017) were examined by using the methods of bipolar coordinates, boundary collocation, and successive reflections. Analytical and numerical solutions of the boundary corrections to Equation (2[2] ) with for the particle mobility were obtained extensively in these investigations.

The system of an aerosol sphere moving in a spherical cavity can be a simplified model for the capture of soot particles undergoing thermophoresis in porous filters composed of connecting spherical pores. The thermal and hydrodynamic interactions between the particle and the cavity wall determine the deposition behavior of the particle toward the wall, and thus relates closely to the capture efficiency of the particulate filter (Matte-Deschênes et al. 2016). Indeed, the thermophoretic motion of a spherical particle in a spherical cavity with has been theoretically studied to certain extent (Keh and Chang 1998; Lu and Lee 2001). In this article, the thermophoresis of an aerosol sphere in a concentric spherical cavity is analyzed, and the effects of temperature jump, thermal creep, frictional slip, and especially, thermal stress slip at the particle surface and cavity wall are incorporated. The geometric simplicity in this system allows closed-form solutions to the conservation equations and to the particle velocity to be obtained. Some interesting features of the wall effect on this thermophoretic migration are revealed from the results.

2. Analysis

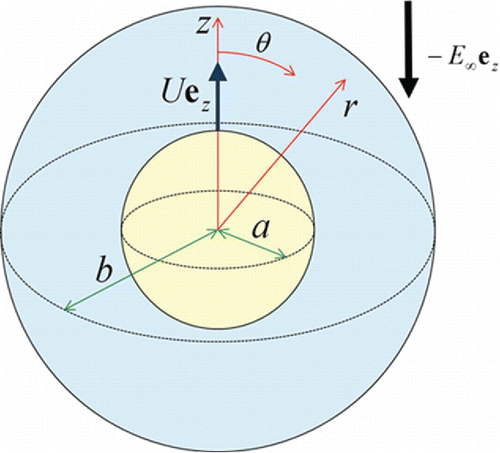
Consider the thermophoretic migration of a spherical particle of radius located at the center of a spherical cavity of radius filled with a gaseous medium in the slip-flow regime at quasi-steady state, as illustrated in Figure 1. The linear temperature distribution (with temperature gradient ) is applied at a distance from the particle, where is the unit vector in the direction, is a positive constant, and are the spherical coordinates with the origin at the cavity center and . The Epstein number is small in practice (Young 2011), so that all the physical properties in the system are taken to be constant. Our objective is to determine the correction to Equation (2[2] ) for the thermophoretic velocity of the confined aerosol particle caused by the proximity of the cavity wall.

Figure 1. Geometrical sketch for the thermophoresis of an aerosol sphere in a concentric spherical cavity.

2.1. Temperature field

The temperature distributions inside the particle (), for the fluid (), and in the cavity surroundings () are axially symmetric and governed by Laplace's equations for heat conduction (since the Peclet number is low in thermophoresis). The boundary conditions at the particle surface and cavity wall entail that the normal heat fluxes are continuous and the temperature jumps occur. Also, the temperature far from the particle in the surroundings approaches the linear imposed distribution. Thus (Brock 1962; Keh and Chen 1995),[3] [4] [5] where , , and , are the thermal conductivities of the fluid, particle, and surroundings, respectively; and are the temperature jump coefficients associated with the particle surface and cavity wall, respectively; is the mean free path of the gas molecules.

The solution of the temperature distributions satisfying Laplace's equations and Equations (3)–(5) is[6] [7] [8] where[9] [10] [11] [12]

If the linear temperature distribution is imposed along the cavity wall, then the boundary conditions in Equations (4[4] ) and (5[5] ) are combined into[13] and the temperature distribution in Equation (8[8] ) and thermal conductivity become trivial. For this case, the solution given by Equations (6[6] ) and (7[7] ) is still valid but the parameter in Equation (9[9] ) should be replaced by[14]

2.2. Fluid flow field

For the thermophoresis of a particle in a concentric cavity, the Reynolds number is small and the fluid motion is governed by the axisymmetric Stokes equation for the stream function (which is related to and , the and components, respectively, of the fluid velocity ),[15] where is the Stokes operator (Happel and Brenner 1983).

There exist thermal creep, frictional slip, and thermal stress slip along the gas-solid interfaces shown in Equation (1[1] ), the boundary conditions for the fluid velocity at the interfaces are[16] [17]

Here, , , and (as well as , , and ) are the thermal creep, frictional slip, and thermal stress slip coefficients associated with the particle surface (as well as cavity wall), respectively, τ_rθ is the nontrivial shear stress of the fluid, and is the unknown thermophoretic velocity of the confined particle (in the z-direction). The derivatives and in Equations (16[16] ) and (17[17] ) are calculated using the temperature distribution in Equation (7[7] ).

The solution to Equations (15)–(17) is obtained as[18] where[19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] and , which is a characteristic thermophoretic velocity.

2.3. Thermophoretic velocity

The drag force exerted on the freely suspended aerosol sphere by the fluid is calculated from (Happel and Brenner 1983)[33]

Using the constraint that this force vanishes (viz., ) to Equation (20[20] ), we obtain the particle velocity as[34] where[35] which is the thermophoretic velocity of the corresponding unconfined particle same as Equation (2[2] ),[36] featuring the particle velocity caused by the circulation of the thermoosmotic flow along the cavity wall, and[37] representing the normalized thermophoretic mobility of the confined particle. Note that the contributions from the thermoosmotic flow circulation and from the wall-corrected thermophoretic driving force to the particle velocity can be linearly superimposed. In the particular case of , Equations (34)–(37) reduce to the corresponding result obtained by Keh and Chang (1998) for an aerosol sphere in a concentric spherical cavity without effects of thermal stress slip.

Equations (34)–(37) indicate that, in the absence of the thermal stress slip at the solid surfaces (), the presence of the cavity enhances the thermophoretic migration of the particle; this enhancement, depending upon the particle-to-cavity radius ratio and other parameters, is attributed to the circulation of the thermoosmotic flow arising from the interaction between the imposed temperature gradient and the thermal-creep cavity wall. The thermal stress slip at the particle surface increases the thermophoretic velocity of the unconfined particle if (the heat conduction in the fluid is repulsed by the particle), decreases if (the heat conduction is attracted by the particle), and has no effect on if (the heat conduction is not influenced by the particle). In fact, the unconfined particle reverses the direction of its thermophoretic velocity (i.e., reversed thermophoresis occurs) (Dwyer 1967; Young 2011) if both and . On the other hand, the thermal stress slip at the cavity wall decreases the particle velocity induced by the thermoosmotic flow circulation if , increases if , and has no effect on if . The influence of the thermal stress slip at the cavity wall on disappears in the limit of (a small particle within a large cavity), although the enhancement on the thermophoretic migration of the particle due to the thermoosmotic flow circulation caused by the thermal-creep cavity wall still exists in this limit. The leading cavity wall effect on the normalized thermophoretic mobility is of the order and that on is of the order , in contrast to the order for the relevant settling mobility of the particle (Keh and Chang 1998), regardless of the existence of the thermal stress slip at solid surfaces.

3. Results and discussion

In this section, the closed-form result for the thermophoretic velocity of an aerosol sphere in a concentric spherical cavity obtained in Equations (34)–(37) is presented graphically, while typical sketches of the corresponding thermal and hydrodynamic streamlines described by Equations (6)–(8) and (18[18] ) were provided by Keh and Chang (1998) in absence of thermal stress slip. The Knudsen number, Peclet number, and Reynolds number are smaller than the order 0.1, thus our results are accurate for the size of aerosol particles in a broad range from 0.5 μm to 1 mm and the parameters and should be less than about unity. For convenience and conciseness, we only present graphical results for the case of (a rounded ratio of 2.18/1.14), (), (), and [, if Equations (4[4] ) and (5[5] ) are used for the temperature condition of the cavity], without loss of generality.

The normalized thermophoretic mobility of an aerosol sphere in a concentric spherical cavity given by Equation (37[37] ) is independent of the thermal creep and thermal stress slip at the solid surfaces. Typical values of are plotted versus the radius ratio in Figure 2 for the temperature conditions of the cavity specified by Equations (4[4] ) and (5[5] ) and by Equation (13[13] ) for various values of the normalized frictional slip coefficient and thermal conductivity . In general, decreases with an increase in (), increases with an increase in , decreases with an increase in , keeping the other factors uncharged, and vanishes as (the particle fills the cavity up completely). For the case of a cavity with the temperature condition specified by Equations (4[4] ) and (5[5] ), as (the cavity wall is at an infinite distance from the particle), while for the case of a cavity with the temperature condition specified by Equation (13[13] ), the value of is smaller than that for the former case for a combination of , , and , a weak increasing function of , and always equal to unity (the thermophoretic mobility of the aerosol sphere reduces to that of an unconfined particle as expected) as .

Figure 2. The normalized thermophoretic mobility of an aerosol sphere in a concentric spherical cavity versus the radius ratio for the case of , , and : (a) with as a parameter; (b) with as a parameter. The solid and dashed curves denote the temperature conditions of cavity specified by Equations (4[4] ) and (5[5] ) with and by Equation (13[13] ), respectively.

Typical values of the normalized migration velocity of the confined spherical particle caused by the circulation of the thermoosmotic flow along a cavity wall with the temperature condition of Equations (4[4] ) and (5[5] ) calculated from Equation (36[36] ) are plotted versus the radius ratio in Figure 3 for various values of , , and the thermal stress slip coefficient . The dashed and solid curves in Figure 3 denote the cases in absence of thermal stress slip (i.e., ) and in presence of it (with ), respectively. The thermal stress slip at the cavity wall decreases if and increases this velocity if , as expected. The influence of the thermal stress slip at the cavity wall on disappears in the limit of , but can be appreciable when the values of (or the Knudsen number ), , and are not too small (say, , , and ). Analogous to the tendency of the normalized thermophoretic mobility shown by the solid curves in Figure 2, decreases with an increase in , increases with an increase in , and decreases with an increase in from at to zero at , keeping the other factors uncharged. For the particle in a cavity with the temperature condition specified by Equation (13[13] ), the trend of , which can easily be examined from using Equation (36[36] ), is also similar to that of (always decreasing with an increase in from unity at to zero at ). The decrease in the value of with an increase in means that the approach of the cavity wall (with reducing surface area) to the particle diminishes the wall-induced thermoosmotic flow-circulation conveying effect on the particle.

Figure 3. The normalized migration velocity of an aerosol sphere caused by the thermoosmotic flow circulation in a cavity with the temperature condition specified by Equations (4[4] ) and (5[5] ) versus the radius ratio for the case of , , , and : (a) with as a parameter; (b) with as a parameter. The solid and dashed curves are computed with and , respectively.

The dimensionless net velocity of an aerosol sphere in a concentric spherical cavity with and calculated from Equations (34)–(37) as a function of the radius ratio for various values of , , and the ratio of the thermal stress slip and thermal creep coefficients (including the case , in absence of thermal stress slip) is presented in Figure 4 for both temperature conditions of the cavity. Only the typical case of and resulting in moderately positive values of the uncorrected thermophoretic velocity is plotted and discussed here, but other cases can easily be examined from using the closed-form formulas. Because of the thermoosmotic flow arising from the interaction between the prescribed temperature gradient and the cavity wall with thermal creep and thermal stress slip, no longer equals the normalized thermophoretic mobility illustrated in Figure 2. Nonetheless, in general decreases with an increase in , a decrease in , and an increase in (to zero at ), keeping the other factors uncharged. For constant values of , , and , the value of is an increasing function of and smaller for the case of a cavity with the temperature condition specified by Equation (13[13] ) than that specified by Equations (4[4] ) and (5[5] ). Note that the contribution to the particle velocity from the thermoosmotic flow circulation are at least equivalently important to that from the wall-corrected thermophoretic driving force. The fact that the confining cavity can greatly enhance the thermophoretic migration of the particle is qualitatively different from the wall effect on the thermophoretic motion of the particle along the axis of a circular tube (Li and Keh 2017), where the thermoosmotic flow induced by the confining wall diminishes the particle velocity.

Figure 4. The dimensionless velocity of a confined aerosol sphere versus the radius ratio with as a parameter for the case of , , , , and : (a) with the temperature condition of cavity specified by Equations (4[4] ) and (5[5] ) and the solid and dashed curves denoting and , respectively; (b) with the temperature condition of cavity specified by Equation (13[13] ) and the solid and dashed curves denoting and , respectively.

4. Concluding remarks

In this article, the thermophoretic migration of an aerosol sphere inside a concentric spherical cavity with an imposed temperature gradient is analyzed for the slip-flow regime. After solving the governing equations of heat conduction and fluid motion, the temperature distribution and fluid velocity field are determined in the presence of temperature jump, thermal creep, frictional slip, and thermal stress slip at the particle surface. An explicit expression for the migration velocity of the confined particle as a function of the relevant parameters is obtained for two different temperature conditions of the cavity, and the results are presented in Figures 2–4 for various values of the particle-to-cavity radius ratio and of other parameters. The thermoosmotic flow induced by the interaction of the imposed temperature gradient with the cavity wall can lead to a dominantly significant enhancement of the thermophoretic migration of the particle. The normalized particle velocity in general decreases with an increase in the normalized slip coefficient (), increases with an increase in the particle-to-gas thermal conductivity ratio , and decreases with an increase in . The effects of the thermal stress slip at the solid surfaces to the migration velocity of the particle can be significant and interesting, depending upon the thermal and interfacial properties of the particle and fluid. The wall effect on the thermophoretic migration of the particle in a cavity is quite different from that for a particle along the axis of a circular tube.

When is large (i.e., the particle is at near-uniform temperature), the thermal creep flow is negligible and the thermal stress slip flow dominates the thermophoretic motion (and reversed thermophoresis may occur). For the thermophoresis of an aerosol particle within a cavity under this condition, which often appears in practical applications (Matte-Deschênes et al. 2016), our findings are novel and important. In particular, this article's analytical nature provides some insight to the effects of various parameters including and the thermal stress slip coefficients and , that are not easy to gain in a purely numerical study, and allows readers to use our results as benchmark if needed.