Aggregation- and rarefaction-effects on particle mass deposition rates by convective-diffusion, thermophoresis or inertial impaction: Consequences of multi-spherule ‘momentum shielding’

ABSTRACT

At the same total spherule volume fraction in a gaseous mainstream, we predict the significant alteration of mass deposition rate attending extensive aggregation—illustrating our methods and results here not only for a mainstream of single-sized cluster aggregates, but also for coagulation-aged (near log-normal) distributions of large fractal-like aggregates (N_g = O(10³), D_f = 1.8 (DLCAs) or D_f = 2.1 (RLCAs)) compared to isolated spherule deposition in the same environment. Because of their drastically different sensitivities to aggregation, we consider, sequentially, the particle transport mechanisms of either: ordinary isothermal convective-diffusion, thermophoresis (to a cooled solid target) or inertial impaction (without rebound). Using a rather general formulation (which incorporates Knudsen transition effects expected at elevated pressures) but neglecting direct “interception” effects, we find that for, say, D_f = 2.1, N = O(10³), Kn₁: = mfp/R₁ = 1, if convective-diffusion (with Sc >> 1) were the dominant mechanism then mainstream aggregation would decrease expected mass deposition rates to much larger targets by somewhat more than one decade. However, for thermophoresis aggregation would increase deposition rates by approximately somewhat more than one decade, and, for, say, “eddy impaction” (in a fully turbulent duct flow) aggregation would increase deposition rates by as much as nearly 1.5 decades. Physically, these large aggregation enhancement-ratios for deposition by thermophoresis or particle Inertial Impaction are attributed to drag reduction (per spherule) associated with “momentum shielding”—analogous to the aerodynamic advantages that birds, fish, bicyclists, runners,… experience when “in formation”. Using this approach, other impaction geometries and Knudsen number situations are also readily treated, as well as more “compact” even porous (D_f = 3) aggregate populations. These predictive methods, illustrative results, and conclusions are expected to be useful to investigators seeking to maximize (or minimize) particle deposition rates on solid targets by exploiting control over the spherule aggregation process in the mainstream.

As an important corollary, our methods also enable the quantitative deconvolution of aggregated aerosol sampling data, i.e., correcting for the systematic distortion (falsification) of sampled aggregate size distributions, pdf_w(N), brought about by the size-dependent capture coefficients associated with momentum-shielding (nearly power-law: S_mom ∼ N^k) for each of the mechanisms considered here (C-D, T-P, or E-I; Section 5)). As demonstrated in Section 6.3, while we expect Log-Normal-type distributions to retain their shape, we predict the systematic correction factors needed to obtain the mean and median aggregate sizes ( and N_g) that must have existed in the mainstream (see Equation (30[30] )). These correction factors become quite significant for each of the mechanisms (especially thermophoresis and impaction) when the mainstream aggregate size-spread is large (e.g., σ_g > ca. 2) and the pressure is high enough to cause Kn₁ to drop to O(1).

For completeness, the systematic consequences of the appreciable effective size of N >> 1 cluster aggregates, briefly discussed in Section 6.2, will need to be included, especially for the deposition of D_f < 2 fractal-like aggregates on targets not much larger than the aggregates themselves (e.g., depth filter fibers,…). However, for capture by sufficiently large targets a noteworthy conclusion is that, of the distinct aerosol transport mechanisms considered here, isothermal convective-diffusion stands out as the only mechanism for which isolated spherules will deposit more efficiently than large-N cluster aggregates (when compared in the same flow environment at the same mainstream spherule volume fraction).

Copyright © 2018 American Association for Aerosol Research

EDITOR:

• Yiannis Drossinos

1. Introduction/Motivation

Our purpose is to answer the following important question: If one's goal is simply to maximize (or minimize) the total deposition rate on to a locally planar surface from a flowing dilute suspension of solid-like particles in a gas, is it advantageous to first allow the mainstream particles to coagulate to form fractal-like aggregates (each comprised of a large number, N, of “primary” particles)? Using what has recently been learned about the transport properties of fractal-like aggregates, we can now address/answer this interesting question even for the case of “coagulation-aged” mainstream aggregate populations which deposit principally by any one of the three eligible transport mechanisms: C-D: = isothermal convective diffusion, TP: = thermophoresis to a cooler solid target, or E-I: = ”eddy” impaction from a fully turbulent local flow. While this question arises in other contexts, because of current practical interest in high-pressure hydrocarbon-fueled combustors, for our illustrative calculations we focus here on large aggregates comprised of a narrow distribution of “primary” carbonaceous spherules with radii R₁ of the order of only 10 nm, including pressures high enough to cause the gas mean-free-path¹ to become comparable to R₁ without violating the ideal gas assumption. As will be seen, we find (Section 5) that, while aggregation is expected to reduce deposition rates due to convective-diffusion, aggregation will dramatically increase deposition rates for the mechanisms of thermophoresis and impaction, especially away from the free-molecule limit. In Section 6 this facilitation is attributed to spherule drag reduction due to “momentum shielding”—analogous to the aerodynamic benefits that birds experience when flying “in formation”. [This shielding effect also operates for convective-diffusion but it is not sufficient to overcome the intrinsically low Brownian diffusion coefficient of large (more massive) aggregates (Section 5.1)].

Regarding the structure of our present article, in Section 2 we first summarize what has been learned about the mobility of large fractal-like aggregates (FAs) suspended in a carrier gas, making use of the comprehensive review of Sorensen (2011) and several more recent computational studies. In Section 3 we review recent results for the thermophoretic (TP-) properties of large aggregates. As discussed in Rosner and Tandon (2017), these were obtained by combining the FA mobility results summarized in Section 2 with recent higher-order kinetic theory predictions (Young 2011) of the thermal force on an isolated spherule in a local temperature gradient. Because we ultimately seek deposition-rate results from “coagulation-aged” populations of aggregates or isolated, single-size spherules, in Section 4 we briefly review previous results for the “self-preserving” spreads of such aggregate size distributions, accounting for systematic effects of gas rarefaction. Combining the information presented above with several plausible assumptions enables the predictions summarized in Section 5 for each of the three deliberately idealized distinct deposition mechanisms: C-D, T–P, and E–I.

While the additional mechanism of “direct interception” (normally associated with effective CA size comparable to the target size when Re << 1, as in fibrous filtration (Rosner 2000; Friedlander 2000) is beyond our present scope (Rosner and Tandon 2017b) we call attention to such extensions in Section 6.2.

As discussed further in Sections 6 and 7, our present theoretical methods, computational results, and insights are expected to be useful to investigators seeking to:

(1)	maximize (or minimize) particle deposition rates (without regard to individual deposit microstructures; Tassopoulos et al. 1989) by exploiting available methods (carrier gas dilution, residence time,…) to control the mainstream spherule aggregation process and/or
(2)	correct aggregate sampling data for the size-bias (‘falsification’) intrinsic to each of the abovementioned deposition mechanisms—especially when the sampling pressure or spherule size is high enough to cause Kn1 to become of O(1)—with simple-to-use results presented in Section 6.3.

In the Appendix we briefly consider the transport properties of D_f = 3 aggregates having the property that their (radially uniform) solid fraction, φ, depends on N in the same manner as < φ > depends on N for D_f = 1.8 (Equation (A2[A2] )). While the “coagulation-aged” spread of such LN-populations remains to be investigated further (e.g., the dependence on Kn₁) the deposition rate behavior of such D_f = 3 aggregates is found to mimic that of D_f = 1.8 fractal-like aggregates. This will also be the case for D_f = 2.1 aggregates if the D_f = 3 calculations are based on the volume-averaged solid fraction associated with RLCAs (Table 1).

Table 1. Statistical parameters and normalized correlations chosen to characterize two important classes of fractal (-like) aggregates (FAs).

	Type of FA
Parameter	DLCA	RLCA
Df	1.8	2.1
ko	1.3	0.94
β	0.665	0.464
ηPA	0.478 + 0.5228^.N^−0.23	0.644 + (1.78/N)
ηmom	N^−0.54 (N ≤ 74)	1.33^.N^−0.572
(Sorensen 2011)	0.65^.N^−0.44 (N > 74)

2. Mobility of large fractal-like aggregates, including rarefaction effects

Useful scaling laws have been developed to facilitate calculations of the orientation-averaged drag on large FAs, both in the continuum limit (Kn₁ << 1), and in the Knudsen transition regime (Kn₁ = O(1)) (Sorensen 2011).

2.1. Fractal-like aggregates in the continuum limit

Continuum-limit results are conveniently stated using an equivalent (effective) FA- “mobility radius” expressible in the form:[1]

i.e., due to “momentum shielding” (discussed further below), the low Reynolds number orientation-averaged drag on an FA containing N spherules is systematically less than N-times the drag on a single isolated spherule in the same stream by the abovementioned dimensionless factor η_mom. In particular, for fractal-like aggregates characterized by pre-factor k_o and fractal dimension D_f then η_mom is a function of aggregate “size” N. Noticing that the gyration radius, R_g, of a FA is a more appropriate scale for R_mob,N;c, many authors have reported their results in terms of the ratio of R_mob,N;c, to R_g, which is often weakly N dependent (especially above N = 100). From Equation (1[1] ) it is easy to show that η_mom can be related to this (R_mob,N;c/ R_g) ratio by:[2]

For, say, DLCAs with D_f = 1.8 and k₀ = 1.3, available numerical results for η_mom have been approximated (Sorensen 2011) as: N^−0.54 (for N ≤ 74) and 0.65·N^−0.44 (N > 74) and this recommendation was, in fact, used in our previous analysis of aggregate thermophoresis (Rosner and Tandon 2017). However, we have noticed that there is an appreciable spread among recent estimates, with the numerical results of Filippov (2000) (for DLCAs with N = 100) leading to η_mom-values higher than this correlation by ca. 20 pct. Moreover, several authors base their effective FA mobility radius estimates on the explicit assumption that the more readily computed effective heat- (or mass-) diffusion radius of an orientation-averaged FA will be approximately equal to the momentum-based effective “mobility radius.” However, the underlying equations are by no means the same. Indeed, comparing the continuum momentum transfer results reported by Filippov (2000) with the energy transfer results reported in Filippov et al. (2000) suggests that the latter effective size (sometimes called the Smoluchowski radius) systematically underestimates the effective mobility radius.

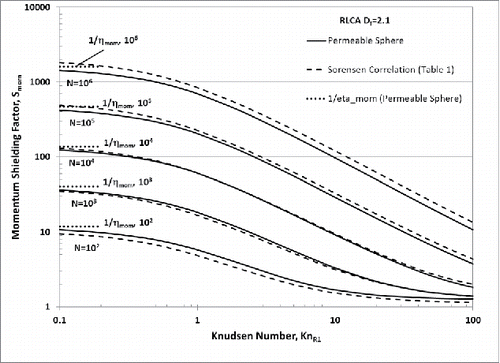
The abovementioned observations led us to re-investigate the consequences of viewing large multi-spherule aggregates as “permeable” solids—with the intrinsic “internal” permeability being spatially non-uniform within the CA (Tandon and Rosner 1995). This “effective medium” approach is rational and, as displayed immediately below, it leads to convenient closed-form analytic approximations which should be useful and capture the important parametric trends. While we ultimately chose this method to predict the deposition-rate consequences of inter-spherule momentum-shielding for the three dominant aerosol transport mechanisms: isothermal Convective-Diffusion, Thermo-phoresis and Inertia (Section 5 and Figures 3 and 4), it probably provides the most conservative estimates for “momentum shielding,” yielding η_mom-estimates ca. 40 pct higher than the DLCA correlation mentioned in Table 1 (Sorensen 2011). Because these two tractable alternative methods tend to bracket actual reported values for such CAs, predictions using both will be displayed (compared) in Figure 2, which also incorporates gas rarefaction effects (Section 2.2 below). It is interesting that these systematic differences become quite modest even for RLCAs (D_f = 2.1). The consequences of these modest differences for aggregate deposition rates (e.g., Figure 4, below) are easily calculated from the explicit equations presented in Section 5. For our subsequent predictions of the consequences of momentum shielding for the deposition behavior of FAs (compared to their isolated spherules in the same environment) on “large” targets we will adopt the “permeable sphere method,” corrected for rarefaction effects in the manner described in Section 2.2 which follows.

In accord with our modified permeable sphere method we can express η_mom in terms of the normalized drag on a permeable sphere in Re << 1 steady flow. For a “solid” sphere of uniform permeability, χ, and outer radius R_max this dimensionless drag is defined by what we call the Brinkman function (see Figure A1 and Equation (A1[A1] )), written f_B(κ). From their respective definitions, η_mom can be calculated from:[3]

The effective dimensionless radius appearing in the closed–form Brinkman function f_B(κ), (Appendix, Figure A1) is defined by R_max / [χ]^1/2.

A first approximation to the relevant dimensionless radius is provided by simply using the permeability, (χ_ref, corresponding to the volume-averaged solid fraction within the FA, i.e., Our “reference” sphere (with radially constant permeability [as in D_f = 3; see also the Appendix]) is one that has a spatially uniform solid fraction equal to the volume-averaged solid fraction of a “true” FA, i.e.:[4] where the relevant volume-averaged solid fraction is given by:[5]

To account for the fact that a real FA has a spatially non-uniform solid fraction we then make use of the finding that such a permeable particle will have an effective dimensionless radius: κ_eff, calculable from the known φ(r) (see, the recommendation of Tandon and Rosner [1995], Equation (3.1–4)). Exploiting the fact that φ << 1, this leads us to the final explicit closed-form (rather modest) correction to κ⁽⁰⁾, i.e:[6]

We note that this final correction would be unity when D_f = 3 (spatially uniform solid fraction) but for D_f = 1.8 (DLCAs) this ratio is 0.968 and, for D_f = 2.1 (RLCAs), we find κ_eff/κ⁽⁰⁾ = 0.984. These relations/results (the Appendix) were used to generate the η_mom-values underlying Figures 3 and 4 below—to be discussed in Section 6.

2.2. Momentum shielding in the presence of gas rarefaction effects

Drag reduction associated with gas rarefaction is calculated using the Cunningham slip correction function (Allen and Raabe 1982) for an isolated solid sphere but in the definition of Kn an effective aggregate radius is introduced which depends both upon the orientation-averaged FA-projected area, <<PA>>, and its (abovementioned) continuum mobility radius, i.e.:[7] where we have introduced the dimensionless ratio:[8] and for D_f = 1.8 aggregates, Meakin et al. (1989) recommend a correlation equivalent to:[9]

This convenient method, which we have adopted here, derives from the early small-chain aggregate “Adjusted Sphere Model” (ASM) work of Dahneke (1973a,b,c). It has been verified for large FAs in the more recent computational work of Zhang et al. (2012), Thajudeen et al. (2015), Melas et al. (2014) and Corson et al. (2017).²

In this present study, as well as Rosner and Tandon (2017), we have identified the following decisive dimensionless factor:[10] associated with what we call multi-spherule “momentum shielding.”

Its fundamental importance is made clear by the following simple argument: Keeping in mind the definitions above for η_mom and η_PA, consider the relation between the Re<<1 drag on an arbitrary assembly of N identical solid spherules (not necessarily a fractal-like aggregate) and the drag (in the same gaseous flow environment) on the same number of identical spherules if they were isolated from one another. Then, invoking the abovementioned equations for the continuum mobility radius R_N,c, and the choice R_N,eff for calculating C_slip,N, along with the abovementioned momentum shielding factor S_mom (Equation (10[10] )), we readily find:[11] or, in words: the drag on the assembly will be smaller than the sum of the drags on the N members (if isolated) by the factor (1/S_mom) for that configuration.³

We have calculated (and plotted in Figure 1 for D_f = 1.8) this decisive function S_mom(Kn₁; N; D_f) for the fractal-like arrangement of N-spherules as a function of Kn₁, revealing how S_mom grows when one leaves (e.g., via higher gas pressures for the same R₁ and gas temperature) the free-molecule (Kn₁ >>> 1) domain. This is a physical consequence of the growing importance of gas–gas molecular encounters as one leaves the free-molecule domain (where only gas molecule/solid encounters need be accounted for). Not surprisingly, at each Kn₁ the momentum shielding increases with N—nearly as a power-law (see Section 5.7 and Rosner and Tandon 2017). When dealing with coagulation-aged populations of aggregates, the illustrative calculations below includes predictions of the size distribution of deposited aggregates (in the absence of break-up’ Section 6.3).

Figure 1. Predicted behavior of aggregate “momentum shielding function”: S_mom(Kn₁; N); dependence on Knudsen number (based on spherule radius) and total spherule number n (>>1); unless otherwise specified results are for diffusion-limited cluster aggregates with D_f = 1.8. (See Section 2.3 for test of ASM; see the Appendix for a special case: D_f = 3 with uniform [low] solid fraction [dashed contours].)

This momentum shielding factor can readily be shown to be the ratio of N·⟨⟨D_N⟩⟩ to the N = 1 value of the isolated spherule Brownian diffusion coefficient, D₁. It also dominates the ratio between the aggregate thermophoretic diffusivity and that of its constituent spherules (if isolated in the same non-isothermal gaseous environment), as discussed in Section 5.2; cf. Equation (21[21] )). Invoking the Einstein relation between Brownian diffusivity and mobility one can also show that the characteristic “stopping time” (t_p)_N for an aggregate containing N-spherules must be greater than t_p,1 by this same factor: S_mom(Kn₁; N; D_f)—a result exploited in Section 5 dealing quantitatively with the deposition rate consequences of mainstream aggregation for each of the three mechanisms of particle transport considered here: convective-diffusion (C-D), thermo-phoresis (T-P), and inertial (e.g., eddy-) impaction (E-I).

2.3. Independent tests of the adjusted sphere method

The “porous sphere” perspective/model exploited in the Appendix to evaluate the continuum level of “momentum shielding” provides an independent route to test the widely used “adjusted sphere” method for including gas rarefaction effects on S_mom(Kn₁;N) provided Kn_N is small enough for C_slip,N to be near unity, i.e., if at least the “outer” flow is continuum-like. This is because the effect of gas rarefaction within the ‘granular’ porous medium can be incorporated in evaluating the medium permeability by simply introducing the factor C_s,1^−1/2 in the evaluation of κ, i.e.,[12]

Values of S_mom calculated in this way (only plotted where Kn_Rmax < 0.03) will be shown dashed on Figure 1 (for D_f = 1.8). The excellent agreement displayed between this “non-ASM” result (dashed) and the solid curves computed using Equation (10[10] ) with ASM (solid curves) provide an independent test of the success of ASM in the present context. The ability of ASM⁴ to span situations in which the outer viscous flow is also rarefied is, of course, a very desirable feature—which explains its adoption for the present work. In Section 5 the resulting values of S_mom (Kn₁; N) will be used to anticipate the consequences of spherule aggregation (in the mainstream) on aerosol deposition rates to solid surfaces by either the mechanism of isothermal convective-diffusion, thermophoresis (due to a temperature gradient), or particle inertia, as discussed/presented in Sections 5.1–5.3.

3. Recent estimates of the thermophoretic properties of large fractal-like aggregates

By balancing the total thermal force (as recently predicted /correlated for a single isolated spherule in a local temperature gradient by Young [2011]) on an N-spherule fractal aggregate against the transition regime total orientation-averaged aggregate drag (Section 2 above), we have recently predicted (Rosner and Tandon 2017) N-dependent dimensionless aggregate TP-diffusivities. In this work we deliberately considered gas pressures high enough for the constituent spherules to enter the currently important Knudsen “transition” regime.

The orientation-averaged thermophoretic diffusivity, written ⟨⟨α_T·D_p⟩⟩ is defined as the aggregate drift velocity per unit {–grad T)/T}. In brief, we found that this diffusivity should be greater than the N = 1 value (for an isolated spherule) by a calculable factor: S_mom·S_h, where the “momentum shielding” factor, often >>1, is already familiar from Section 2 above. The second factor, S_h, which accounts for “thermal shielding,” i.e., the reduction in |grad T| experienced by internal spherules—was found to be rather close to unity for D_f = 1.8 aggregates, even when the thermal conductivity ratio, k_p/k_g >> 1. In this way we generated (Figure 2 of Rosner and Tandon 2017) curves of the dimensionless <<α_TD_p>> (i.e., ⟨⟨α_T·D_p⟩⟩ made dimensionless by (ν)_gas) as a function of Kn₁ (from 100 down to ca. 0.301) over the range of N-values from 10² to 10⁶. However, our present estimates of S_mom*S_h, used in Section 5 to compute TP-dominated deposition rates, are based on what we believe is a more accurate correlation Equation (2[2] ), for the continuum function η_mom. It is also interesting to note that our present calculations of aggregate:monomer deposition rate ratios (see Sections 5.2 below) are actually independent of which rival theory of monomer TP-diffusivity is adopted. (But recall that the N = 1 results of JB Young [2011]—shown plotted in Figure 1 of Rosner and Tandon [2017] over a range of k_p/k_g-values, are believed to be more reliable than those of Talbot et al. [1980]—especially for k_p/k_g >> 1.) In any case, to facilitate deposition rate calculations from a log-normal distribution of aggregates (Appendix 1⁵ of Rosner and Tandon [2017] and Section 4 below) our values of S_mom·S_h were fit to the power-law form: from which the exponent k could be estimated at any Kn₁ in the abovementioned Kn₁- “transition” range. These results will be invoked in Section 5.2 below.

Figure 2. Predicted behavior of aggregate “momentum shielding function”: S_mom(Kn₁; N); dependence on Knudsen number (based on spherule radius) and total spherule number N (>>1) for reaction-limited cluster aggregates with D_f = 2.1; comparison between results of permeable sphere model (Section 2.1 and the Appendix) and correlation (Table 1 and Sorensen 2011).

4. “Coagulation-aged” populations of aggregates: Knudsen number dependence of LN-spreads

Our present goal is to ultimately predict mass deposition rates from coagulation-aged populations of fractal-like aggregates and compare them with the deposition rates from a mono-dispersed population of “un-aggregated” spherules with the same mainstream spherule volume fraction. For this purpose we need to invoke information on the expected shape of such aggregate size distributions (ASDs).

Brownian coagulation of aerosol particles usually leads to a broad distribution of sizes and the coagulation of fractal-like aggregates is no exception. Earlier work (Otto et al. 1994) has shown that such distributions are often well-described by the convenient 2-parameter “log-normal” form, with geometric spread parameters, (σ)_g, that are Kn-dependent. For fractal dimensions near 1.8 the spread (σ)_g has been reported to be as large as 4.1 in the free-molecule limit (Kn₁ >> 1) but only ca. 2.4 in the continuum (Kn₁ << 1) limit. Because the mid-point of this transition occurs near Kn₁ = 1, for our illustrative “poly-dispersed” calculations (Sections 5.1.2, 5.2.2, and 5.3.2) we will simply assume that our mainstream D_f = 1.8 coagulation-aged aggregates have a normalized ASD, pdf(N), which is log-normal with a spread parameter adequately described by:[13a]

Less is currently known about the spreads of coagulation-aged RLCA populations. For our present illustrative RLCA calculations we have provisionally adopted[13b] which is seen to vary (monotonically) between 3.6 (fm limit) and 2.36 (continuum limit). For all of our spherule deposition rate ratio (DRR) calculations involving multi-sized aggregates in the mainstream the explicit functional form of pdf (N; N_g, σ_g) for N ≥ 1 is given by:[14]

Our illustrative “aggregation-effect” calculations below will be made for situations with a number-mean aggregate size, of, say, 1,000 spherules, where:[15]

In this way we capture the principal effects of spherule transport in aggregates which are both much larger than and also smaller than . (Analogous calculations for the deposition rates of isolated but coagulation-aged rapidly coalescing spherules were reported in Rosner [1989].)

5. Consequences of aggregation for predicted mass deposition rates on large target for three idealized mechanisms

5.1. Deposition by Sc >> 1 convective-diffusion

Laminar forced-convection near-isothermal systems with dilute solute mass transfer to an immersed solid often exhibit a D^2/3 dependence on the solute Brownian diffusivity, especially when this diffusivity is much smaller than the momentum diffusivity of the host fluid (Levich 1962). For our comparisons below we will assume that all conditions (target geometry, flow velocity, host fluid properties) are the same for both aggregate and spherule transport, including the total spherule volume fraction (and hence suspended particle mass fraction) in the mainstream.

5.1.1. Mono-dispersed case: []_CD

If all aggregates in the mainstream had the same size, N, and Brownian diffusivity <<D_N>> then, for the same mainstream spherule volume (and mass) fraction we find:[16]

But, because N * <<D_N>>/D₁ = S_mom (N; D_f, k_o), we conclude that[17]

We note that while S_mom > 1 and increases monotonically with N, as will be seen, the ratio of S_mom to N decreases with increasing N. This “competition” implies that if convective-diffusion were the dominant transport mechanism aggregation would cause a net decrease in the rate of spherule transport to the solid surface, despite the presence of “momentum shielding”. This is clearly shown in Figure 3 for the case of DLCAs (D_f = 1.8), N = 10³ over the Knudsen transition range: 0.1 < Kn < 100. Corresponding results for RLCAs (D_f = 2.1), which exhibit greater “momentum shielding” (Figure 2), are shown in Figure 4—again for N = 10³ and over the same Kn₁-range. On this basis, even with increased momentum shielding, and even near the continuum limit, if convective-diffusion is the dominant mechanism then isolated spherules would be ca. 10 times more efficient in depositing spherules on a large target than compact cluster aggregates.

Figure 3. Predicted deposition rate ratios resulting from mainstream aggregation (at const total spherule volume fraction). Sensitivity to particle deposition mechanism and Knudsen number, (mfp)/R₁, for monodisperse mainstream aggregate population (all particle with N = 1000 and σ_g = 1) and coagulation-aged, “self-preserving” populations of DLCAs, = O(10³) with D_f = 1.8.

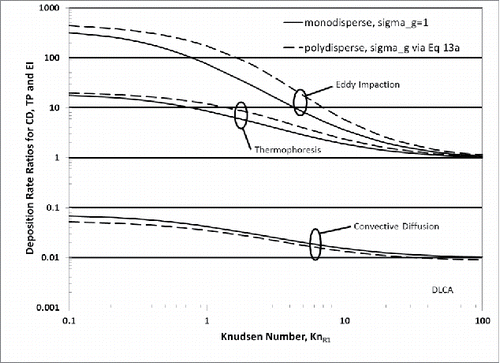
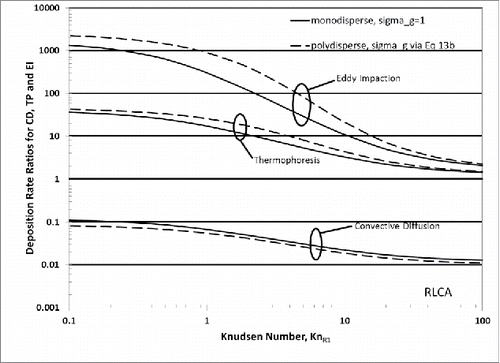
Figure 4. Predicted deposition rate ratios resulting from mainstream aggregation (at const total spherule volume fraction). Sensitivity to particle deposition mechanism and Knudsen number, (mfp)/R₁, for monodisperse mainstream aggregate population (all particle with N = 1000 and σ_g = 1) and coagulation-aged, “self-preserving” populations of RLCAs, = O(10³) with D_f = 2.1.

5.1.2. “Coagulation-aged” (polydispersed) aggregate populations: []_CD

If, instead, the mainstream aggregate population is “coagulation-aged” and has a normalized LN distribution with respect to N (as described in Section 4), then Equation (9[9] ) generalizes to:[18]

If we now introduce the curve fit: near N = and note that if >> 1 then the lower limit can be replaced by 0 without significant error, then a potentially useful closed-form approximation to deposition rate ratio we seek: can be written:[19]

The Knudsen number dependence of this deposition rate ratio, is also shown plotted in Figures 3 and 4 for in the range 0.1 < Kn₁ < 100, with results to be discussed in Section 6. Over this range, reasonable fits for parameter k are given by the expression:[20a] [20b]

Corresponding spherule DRR results for coagulation-aged distributions of RLCAs (D_f = 2.1) with = 10³ are shown (dashed) in Figure 4.

5.2. Deposition by thermophoresis

These cases have recently been treated in the abovementioned paper of Rosner and Tandon (2017), motivated by current needs to interpret TP-sampling data from high pressure flames (see the Appendix, loc cit.). Our principal results are summarized here, now using Equation (2[2] ) for constructing Figures 1 and 2.

5.2.1. Mono-dispersed case: []_TP

To a first approximation, thermophoretically dominated deposition rates are linearly proportional to the “thermophoretic diffusivity” (α_T·D_p) defined by the drift velocity per unit -grad(ln T). Rosner and Tandon (2017) have predicted that:[21] where S_mom is the abovementioned “momentum shielding” factor, and S_h (a “thermal shielding factor”) accounts for the expected reduction in ||grad T|| within the aggregate structure. Even when k_p/k_g >> 1 the solids fraction within large fractal aggregates appears to be small enough that S_h is only slightly less than unity. In any case, for the mono-dispersed case, i.e., mainstream aggregates of only a single size N (>>1), it follows that:[22]

Our calculations have included rational numerical estimates of the (small) thermal shielding contribution, S_h (see Rosner and Tandon [2017] for details). However, in no case presented here did S_h depart from unity by more than about 6 pct. Estimated values of []_TP based on Equation (22[22] ) are contained in Figure 3 for N = 10³ and 0.1 < Kn₁ < 100. Corresponding TP-results for RLCAs (D_f = 2.1) are shown in Figure 4. Note that in all of these T-P dominated cases spherule DRR-values exceed unity—indicating that aggregate T-P would be more efficient for depositing spherules on a large/cooled target than isolated (un-aggregated) spherules at the same mainstream spherule volume fraction. For RLCAs near the continuum limit the enhancement factor is seen to be ca. 1.5 decades.

5.2.2. “Coagulation-aged” (poly-dispersed) aggregate populations: []_TP

For TP-dominated deposition from a coagulation-aged distribution of fractal aggregates we therefore predict the expected effect of aggregation on total deposition rate to be:[23] where pdf(N) may often be represented by a 2-parameter log-normal function with a Kn₁-dependent spread parameter (Section 4). If we now represent S_mom·S_h by a local power-law (with exponent k) near , then a potentially useful closed-form approximation to deposition rate ratio: []_TP can be written:[24]

The Knudsen number dependence of this aggregation-induced ratio, also shown plotted in Figures 3 and 4 for , based on our most recent DLCAs and RLCAs calculations, is of particular relevance to combustion investigators exploiting the TP soot–sampling technique from high-pressure flames. As the pressure rises far above atmospheric (e.g., above 30 bar) the constituent spherules “leave” the Kn₁ >> 1 (“free-molecule”) limit, the aggregation effect on deposition rate rises to the level of an order of magnitude effect (near Kn₁ = 1). Evidentially, this N-dependence of the thermophoretic diffusivity has not yet been appreciated and will systematically reduce any simple deposition-based estimates of total soot volume fractions based on TP-sampling from high-pressure sooting flames. This systematic error is attributable to the expected “over-representation” of large aggregates on the cooler TEM grid targets.

5.3. Deposition by “eddy impaction”

Even more dramatic examples of the sensitivity of deposition rate to aggregation will occur when the dominant particle transport mechanism is “ballistic” impaction associated with suspended particle “inertia,” i.e., particle inability to rapidly respond to changes in host fluid speed and/or direction. Because (Section 2) the characteristic “stopping time” (t_p)_N for an aggregate containing N-spherules is greater than (t_p)₁ by the abovementioned momentum shielding factor: S_mom (Kn₁, N, ko, D_f). This will also be true for the relevant dimensionless stopping time, often written Stk (after G. Stokes).

When inertial particle deposition dominates rival mechanisms (see Section 8.2 in Rosner 2000) the particle capture fraction often increases monotonically with the “Stokes number,” Stk. For simplicity we first consider the case of particle deposition from a fully turbulent smooth-wall pipe flow where, in the “eddy impaction” (E-I) domain, the mass transfer coefficient depends quadratically on (t_p)_N (as displayed by McCoy and Hanratty [1977] this occurs for Stk-values between ca. 0.2 and 300, where (t_p)_N in this situation has been made dimensionless with the characteristic time⁶ ()⁻¹)) based on the time-averaged local shear rate at the fluid/solid interface. The “inertial” particle deposition rate law situation for aggregates in more general situations is briefly considered in Section 5.3.3, below.

5.3.1. Mono-dispersed case: []_EI

In the “eddy-impaction” domain particle mass deposition rates will be proportional to (t_p)², which leads us to immediately conclude that if all aggregates in the mainstream were of size N then:[25]

This sensitivity to aggregation, and reduced Kn₁ (e.g., due to high pressure) is found to be more extreme for impaction than for thermophoresis, as is immediately seen from the corresponding curves in Figures 3 and 4 for an aggregate mainstream with N = 1000.

5.3.2. Coagulation-aged (”polydispersed”) populations [] _EI

For EI-dominated deposition from a coagulation-aged distribution of fractal aggregates, we therefore predict the expected effect of aggregation on total deposition rate to be:[26] where, for large populations pdf(N) may often be represented by a 2-parameter log-normal function with a Kn1-dependent spread parameter (Section 4). If we now introduce the curve-fit: based on the local power-law behavior of S_mom near N = then a potentially useful closed-form approximation to the deposition rate ratio: []_EI can be written:[27]

The calculated Knudsen number dependence of this impressive ratio, is also shown plotted in Figure 2 for . Note that the effect of polydispersity is greatest for this (inertial) deposition mechanism because of its increased sensitivity to the momentum shielding (Figures 1 and 2).

5.3.3. Comments on other canonical impaction situations: Cylindrical target in a steady crossflow

The “eddy-impaction” case explicitly treated in Sections 5.3.1 and 5.3.2 above is exceptional in the sense that over an extended range of Stk-values the mass transfer coefficient (or suitably defined particle “capture fraction”) is a simple power-law (here with exponent 2). For most inertial impaction situations the function η_cap vs. Stk is not a simple power-law, and often exhibits a “critical” Stokes number, written Stk_crit, below which inertial impaction does not even occur (Friedlander 2000). Recalling that because the stopping time for an aggregate will be S_mom,N times that of a single spherule, the definition of Stk (essentially a dimensionless stopping time) implies that Stk_N will be S_mom,N times Stk₁. For the mono-dispersed case, this immediately leads to the following generalization of Equation (16[16] ) of Section 5.3.1:[28]

irrespective of the functional form of η_cap(Stk) for the geometry in question. An interesting implication of this result is that, in the immediate vicinity of (Stk)_crit,1, the sensitivity of inertial impaction rates to aggregation will be extremely large.

For the more general impaction situation in which the ASD is “poly-dispersed,” the counterpart of Equation (17[17] ) of Section 5.3.2 becomes:[29]

a result which will normally require numerical integration for the case at hand. When the mainstream aggregate size distribution is well-described by a log-normal, a finite-analytic method based on a “piecewise-power law” approximation to η_cap(Stk), as implemented in Rosner and Tassopolous (1989), may be a useful option⁷ . Illustrative calculations of the inertial impaction of a LN-population of “compact” cluster-aggregates (D_f > 2) on a large cylindrical target in Re >> 1 crossflow are included in Rosner and Tandon (2017a).

5.4. Comment on the dependence of aggregate deposition rate on mechanism at constant Kn₁ and mainstream spherule volume fraction

At first sight it might appear that a useful byproduct of the deposition rate ratio calculations summarized in Figure 2 might also be “direct” quantitative information on the mechanism-sensitivity of aggregate deposition rates at the same Kn₁ and mainstream spherule volume fraction. This is because a vertical line (at the Kn₁-value of interest) provides three ordinates whose ratios apparently provide the “mechanism sensitivity” irrespective of the “common” reference monomer deposition rate in the same environment. However, this would require that the monomer deposition rates in each case would be the same—which, e.g., fixes grad T for TP and the impaction environment for EI. Thus, our premise of “otherwise identical conditions” would be violated.

Instead, the sensitivity to deposition rate mechanism for aggregates of the same morphology at the same mainstream volume fraction would clearly be calculable from ratio of the corresponding dimensionless mass transfer coefficients: e.g., in forced-convection situations: St_m,EI: St_mTP: St_m,CD (Rosner 2000). When of interest this calculation can readily be made with the help of information on the transport properties of fractal-like aggregate summarized and exploited above.

Of course, if one happened to be comparing three different situations which did correspond to the same monomer deposition rates at the same mainstream spherule volume fraction and Kn₁, then our present results for the distinct mechanisms of CD,TP, and EI (plotted in Figures 3 and 4) would provide the correct relative aggregate deposition rates in each of those distinct environments. While this is not the application we had in mind in making these calculations, it is mentioned here for completeness.

6. Discussion of aggregation effects on mass deposition rates; practical implications

6.1. Principal consequences of momentum shielding for predictions of aerosol deposition rates

The illustrative results collected in Figures 3 and 4 demonstrate the effect of aggregation on aerosol deposition rates both for the case of single size aggregates (N = 10³) and for coagulation-aged distributions of aggregates with = 1000. While our polydispersed aggregates results are to LN distributions of D_f = 1.8 and 2.1 fractal-like aggregates having the same mainstream spherule volume fraction as for the reference case of isolated spherules, they clearly display the drastically different sensitivities to suspended spherule aggregation for each of the most familiar particle transport mechanisms: ordinary isothermal convective-diffusion, thermophoresis (to a cooled solid target) OR inertial impaction (without rebound)—especially when one leaves the “free-molecule” (Kn₁ >> 1) limit. These idealized calculations show that while mainstream aggregation is expected to decrease total deposition rates by convective-diffusion, in sharp contrast, aggregation should lead to significant increases for particle deposition rates dominated by the mechanisms of either thermophoresis or inertial impaction—especially when carrier gas pressures are high enough to reduce Kn₁-values to near O(1).

Physically, the large aggregation enhancement ratios for deposition for both TP and inertial impaction displayed in Figures 3 and 4 are directly attributable to drag reduction (per spherule) associated with “momentum shielding”—quite analogous to the advantages that birds experience when flying “in formation.” Using this approach, other Knudsen number situations and/or more “compact” (higher D_f-) aggregate populations could also be readily treated (including “low φ” D_f = 3 aggregates), as well as other impaction geometries (as indicated in Section 5.3.3).

From the shapes of the S_mom (Kn₁; N) results plotted in Figures 1 and 2 for DLCAs and RLCAs, and the three sets of deposition rate ratios plotted in Figures 3 and 4, it appears that when Kn₁ is as small as 0.1 we have nearly reached the corresponding “continuum” (Kn << 1) asymptotes. Indeed, in Figures 1 and 2 we have included (as short horizontal fine lines) the continuum asymptotes—readily found (from Equation (10[10] ) and the small Kn₁-behavior of C_slip) to be S_mom,c(0;N) = 1/η_mom(N). However, Figures 1 and 2 reveal that when Kn₁ is as large as 100 we have not reached the corresponding “free-molecule” asymptotes, i.e., the corresponding values of S_mom,fm = 1/η_PA (Equation (9b)).

It is hoped that our present methods, explicit results, and the insights that can be derived from these simple illustrations, will prove useful to investigators seeking to maximize (or minimize) particle deposition rates, possibly by introducing suitable control over the upstream spherule aggregation process.

6.2. Caveats regarding the addition of “interception” effects

Especially when predicting mainstream aggregation effects on aerosol deposition rates for D_f < 2, in extensions of our present analysis, it will normally be necessary to make systematic corrections to account for the non-zero effective physical size of the suspended aggregates themselves, i.e., they cannot be considered “point particles.”

Perhaps least obvious is the case of R_N,eff becoming much larger than the formally expected Brownian diffusion “sub”-layer thickness, δ_m at the prevailing Sc (>>1) -value. Recalling that the condition δ_m << δ_mom underlies the expected dependence of the C-D-dominated deposition rate on (D_N)^2/3 this aggregate size effect will reduce (below 2/3) the relevant exponent on the ratio (S_mom/N) in Equation (18[18] )—probably in the direction of (S_mom/N)^1/2. This alone will probably not alter our previous conclusion (Figures 3 and 4) that the spherule DRR for the C-D mechanism will fall below unity over the entire Kn₁-range even in the presence of momentum shielding (see Figure 1 for the relevant S_mom-values for D_f = 1.8).

More dramatic effects of non-zero CA-size are expected to occur for CA-capture by “targets” that are not much larger than the effective aggregate “interception radius” (itself probably of order R_N,gyr). This situation is likely to occur in the industrially important process of depth filtration using fibrous mattes (Friedlander 2000). While a more complete analysis of the simultaneous role of “direct interception” when using micron-scale filter fibers is beyond the scope of this present (initial) study, we have already found (Rosner and Tandon [2017b], in preparation) that the addition of the “direct interception” mechanism can actually produce continuum-limit DRR-values above unity for the C-D–based spherule deposition by D_f = 1.8 aggregates—thereby enabling spherules in aggregates to be more readily captured (by sufficiently small “targets”) than isolated spherules in the same environment. Recall that, for large targets (Figure 2), only (thermo-)phoresis and inertial impaction enabled spherule DRR-values to exceed unity—and this was true over the entire Knudsen transition regime.

6.3. Consequences of aggregation for the ‘falsification’ of sampled aerosol size distributions

Aerosol deposition is often carried out for sampling purposes, in which case an important issue is the expected distortion of the sampled size spectrum associated with the size-dependence of the capture mechanism utilized. Indeed, anticipating this ‘falsification’ was the primary motivation for our recent treatment of the thermophoretic properties of fractal-like aggregates (Rosner and Tandon (2017)—especially in view of current interest in extending the technique of thermophoretic sampling of soot aggregates from hydrocarbon/air flames (Dobbins and Megaridis 1987) to pressures high-enough to force the aggregates out of the free-molecule limit common for atmospheric pressure flames. Briefly, for TP-dominated large FA-deposition, we showed that momentum shielding, i.e., S_mom (Kn₁; N; D_f) via Equation (10[10] ), was far more important than its thermal shielding counterpart) and the fact that its size-dependence is adequately represented by a power-law with exponent k satisfying 0 < k < 1 (see Figure 1 over the entire Kn₁ transition) facilitated the following conclusions (see Section 6 of Rosner and Tandon (2017, loc cit):

C1 If the mainstream ASD is log-normal (with median size N_g,∞ and spread σ_g,∞) then the deposited ASD will also be log-normal

C2 Because of a T-P diffusivity bias in favor of large N aggregates, both the number-mean and the median sizes for the deposit ASD will be larger than the corresponding mainstream values by the factor: exp[k·ln²(σ_g,∞)] where k is the exponent (0 < k < 1) describing the N-dependence of S_mom at the prevailing Kn₁ (see Figure 1 and Equation (20))

C3 ASD_w will exhibit the same spread as in the mainstream—i.e., σ_g,∞ = σ_g,w

Our methods can now be generalized to include corresponding results for the alternative aggregate deposition mechanisms treated in Section 5, i.e., for isothermal convective-diffusion (C-D) and “eddy impaction” (E-I).

Irrespective of the capture mechanism, if η_cap(N) describes the relevant capture fraction (proportional to the relevant dimensionless mass transfer coefficient St_m(N) [Rosner 2000]), then, in the absence of aggregate breakup, we expect the sampled ASD_w when normalized to be related to the mainstream size distribution via:[30]

Now, if for purposes of illustration we limit ourselves to situations for which the relevant η_cap can be adequately expressed in the power-law form:[31] then in all such cases pdf_w(N) can be simplified to the common form:[32]

so that if pdf_∞(N) is LN then each such pdf_w(N) is also LN.

Returning to the alternative mechanisms of isothermal convective diffusion, i.e., C-D (Section), thermo-phoresis (T-P) and eddy impaction (E-I) in the absence of appreciable interception corrections we exploit the fact that each of our present illustrations can be approximated by a CA size-dependent capture fraction with an appropriate exponent n involving the abovementioned k(Kn₁). Based on our present formulation (Section 5) we see that n takes on the following values:[33]

By examining the moment-ratio: [M₂/(M₁)²] for pdf_w(N) we can show that, for any exponent n, [M₂/(M₁)²]_w = [M₂/(M₁)²]_∞ which, for LN distributions, leads to the conclusion that both pdf_w and pdf_∞ have the same spread parameter, σ_g. It follows that in each of the above cases, both N_g,w and will be larger than their mainstream counterparts by the factor:[34] which recovers our previously reported result (Rosner and Tandon 2017) for the T-P mechanism.

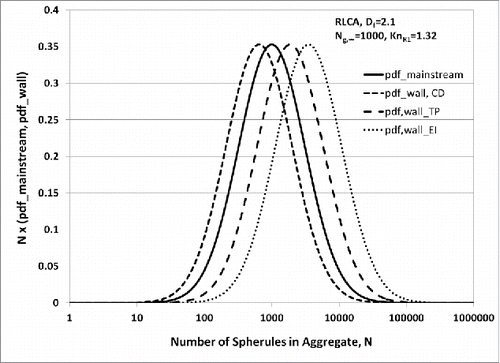
It is noteworthy that this latter ratio is less than unity for the C-D mechanism because the exponent n is itself negative (Equation (33[33] )). Thus, the relevant C-D mass transfer coefficient favors the capture of smaller aggregates, causing smaller aggregates to be “over-represented” in the deposit. However, for both T-P and, especially, E-I it is the larger aggregates that will be over-represented in the aggregate deposit. These expected trends are illustrated in Figure 5 (for DLCAs) and 6 (for RLCAs) by comparing both N*pdf_w and N*pdf_∞ (linear scale) vs. log₁₀(N) for each of the three mechanisms considered here. Because log-normality is preserved for “power-law” mass transfer coefficients, each of these curves is a suitably shifted Gaussian on these particular coordinates. In all cases shown, N_g,∞ = 10³.

Figure 5. Predicted mainstream and wall fractal-like aggregate distributions due to expected N-dependent convective diffusion, thermophoretic diffusivities and eddy impaction deposition rates. Comparison between mainstream- and predicted wall-log-normal distributions mainstream aggregate population characterized by N_g,∞ = 1000, D_f = 1.8 and Kn_R1 = 1.32.

For more general situations in which St_m and η_cap have a more complicated dependence on N (as for the canonical case of inertial impaction [without break-up] of “compact” aggregates [e.g., RLCAs]) on a large-diameter cylinder in Re >> 1 crossflow— treated in Rosner and Tandon [2017a]) then pdf_w(N) is no-longer log-normal and N·pdf_w(N) vs. log₁₀ N is no longer a symmetric Gaussian (see Figure 6 of that ref).

Figure 6. Predicted mainstream and wall fractal-like aggregate distributions due to expected N-dependent convective diffusion, thermophoretic diffusivities, and eddy impaction deposition rates. Comparison between mainstream- and predicted wall-log-normal distributions mainstream aggregate population characterized by N_g,∞ = 1000, D_f = 2.1, and Kn_R1 = 1.32.

7. Conclusions

We have here formulated and calculated (Section 5) the expected alterations in mass deposition rate from an aerosol-containing gas flow associated with extensive mainstream aggregation—illustrating our methods and results for single sized as well as for “coagulation-aged” populations of large fractal-like aggregates (N >> 1, D_f = 1.8 and 2.1). All reported rates have been compared to isolated spherule deposition rates in the same environment at the same mainstream spherule volume fraction. We have explicitly considered the deposition mechanisms of either: ordinary isothermal convective-diffusion, thermophoresis (to a cooled solid target) OR inertial impaction (without particle rebound), for the present ignoring “interception” effects that would normally be associated with capture by targets not much larger than the aggregates themselves.

Physically, our predicted enhancement ratios for the mechanisms of thermophoresis and impaction can be attributed to drag reduction (per spherule) associated with “momentum shielding”—analogous to the advantages that birds (and fish, bicyclists, runners,…) experience when “in formation.” This “shielding” also operates for convective-diffusion—indeed, without it C–D rates for aggregated situations would even be much lower than currently predicted (Figure 3 and 4). In any case, whether one seeks to maximize (or minimize) particle deposition rates in any particular application, our present findings suggest that this might be accomplished by exploiting control over the spherule aggregation process in the mainstream.

For the mechanisms of thermophoresis (even when k_p/k_g >> 1; Rosner and Tandon, 2017) and inertial impaction the sensitivity of deposition rates to mainstream aggregation is found to be significantly greater near the continuum limit (Kn << 1) than near the free-molecule (Kn >> 1) limit. This is consistent with the observation that for N >> 1 we find that S_mom,c ( = 1/η_mom) is significantly larger than S_mom,fm ( = 1/η_PA). Even at pressures high enough to cause Kn₁ = O(1), the aggregation effect on each of the deposition rate mechanisms is particularly dramatic. Indeed, when the gas mfp is comparable to the spherule radii (i.e., Kn₁ = 1) and = O(10³), we find the aggregation-induced spherule deposition rate ratios for D_f = 2.1 (Figure 4) are, respectively: ca. 0.08 for Sc >> 1 Convective–Diffusion, 20 for Thermophoresis and as much as 300 for “Eddy Impaction.”

As emphasized in Rosner and Tandon (2017), the nearly order-of-magnitude aggregation effect we predict for thermophoretically dominated deposition has immediate relevance for combustion researchers exploiting thermophoretic sampling of soot aggregates from high-pressure flames. This is because previous (non-optical) estimates of total soot volume fractions (e.g., in atmospheric pressure flames) have been based on the assumption that aggregate size does not appreciably influence aggregate capture fractions. This particular assumption, which was motivated by aggregate behavior in the Kn₁ >> 1 limit, fails for flame pressures near or above 40 bar and would lead to over-estimates of the mainstream soot volume fraction by ca. 10-fold.

More generally, for each of these aggregate transport mechanisms considered here these transport-consequences of “momentum shielding” (quantified by the function S_mom (Kn₁;N) in Figures 1 and 2) become more significant when the gas molecule mean-free-path is no longer large compared to the spherule radii, i.e., when gas–gas molecular encounters start to play a significant role in the momentum transfer.

An important consequence of the predicted size-dependence of cluster aggregate transport properties, especially for aerosol sampling applications, is the resulting “distortion” of the observed aggregate size distribution on solid targets (e.g., EM-grids, microscope slides,…). We have shown (Section 6.3) that the nearly power-law dependence of the “momentum shielding” function, S_mom(Kn₁; N; D_f), on spherule number N, i.e., S_mom ∼ N^k, facilitates the “deconvolution” of such measurements—i.e., reconstructing the ASD that must have prevailed in the local mainstream. For log-normal (LN-) type ASDs considered explicitly in Section 6.3, we found that only a calculable Kn₁-and mechanism-dependent shift in the N-scale is necessary (Equation (34[34] )), with no significant correction needed for the spread parameter, σ_g. More general situations (in which the aggregate capture fraction is no longer proportional a simple power of S_mom [as in Section 5.3.3] leading to non-LN ASDs) are illustrated for inertial impaction by “compact” cluster aggregates (with D_f = 2.1 or 3) in Rosner and Tandon (2017a).

Of course, even apart from the abovementioned caveats regarding “interception” (Section 6.2), some of our remaining simplifying assumptions (which include log-normal “coagulation-aged” ASDs, uniform spherule radii, large mean aggregate size (N >> 1), domination by one deposition mechanism, negligible particle rebound) will, in particular cases, require generalization. However, we believe that our present simplifications and illustrations capture the essential characteristics of this broad class of particle deposition rate problems. Hopefully, our methods and illustrations already suggest useful process control- or intensification-strategies, and will open the door to progress on commonly encountered complicating factors of particular interest to the aerosol- and particle technology-communities.

Nomenclature

	=	molecular mean thermal speed, [8kBT/(πmg)]1/2
CD	=	dimensionless drag coefficient (see Footnote 3)
Cf	=	skin friction coefficient (wall shear stress made dimensionless by (1/2) ρU2
Cslip	=	Cunningham slip factor (Kneff-dependent) (Equation (A5[A5] ))
D	=	Brownian diffusivity
Df	=	fractal dimension
DRR	=	Deposition Rate Ratio, [(N-mer):(Isolated monomer)], Section 5
fB(κ)	=	Brinkman function (Tandon and Rosner 1995, their Equations (3.1–2))
k	=	Exponent in local relation: Smom∼ Nk or, for T–P: Smom·Sh ∼ Nk
kB	=	Boltzmann constant
ko	=	pre-factor (relating N to (Rgyr/R1)Df)
kg	=	gas thermal conductivity (Fourier)
kp	=	particle (spherule) thermal conductivity
Kn	=	Knudsen number (lg/R1), unless otherwise specified
l	=	molecular mean-free-path (in carrier gas),≈ 2νg/
m	=	mass of one gas molecule
	=	mass deposition rate on a solid target
N	=	number of spherules in fractal aggregate (FA)
Np	=	aggregate number density
p	=	pressure (units: 1 bar(105 Pa) unless otherwise specified)
R1	=	spherule radius
Rgyr	=	aggregate gyration radius, R1.(N/ko)1/Df
RN,mob	=	mobility radius of FA containing N spherules
r	=	radial position within FA (from FA center-of-mass)
Sc	=	Schmidt number for particle diffusion in gas, νg/Dp,N
Smom	=	momentum shielding factor for aggregate (Equations (10[10] ) and (11[11] ))
Sh	=	energy (thermal) shielding factor for a FA
Stk	=	dimensionless stopping time, proportional to tp; Stokes number
T	=	absolute temperature (Kelvins)
tp	=	characteristic stopping time (for particle in viscous medium)
U	=	velocity vector (Equation (A3[A3] ))
	=	local time-averaged streamwise velocity
y	=	distance from deposition target surface

Greek

αT	=	thermophoretic factor (dimensionless)
β	=	prefactor relating N to (Rmax/R1)Df
χ	=	permeability of local granular medium; Equation (A4[A4] )
φ	=	local solid fraction within (orientation-avgd) FA
ηcap	=	capture fraction (for inertial impaction); PA-based
ηPA	=	normalized,orientation-avgd proj. area of FA; ≡ <<PA>>/[N.(π R12)]
ηmom	=	normalized drag of FA (cf.N- individual spheres) in continuum limit
μg	=	Newtonian viscosity of carrier gas
κ	=	dimensionless aggregate radius, Rmax/χ1/2
ν	=	momentum diffusivity (kinematic viscosity)
σg	=	geometric mean spread parameter in LN pdf

Subscripts

agg	=	pertaining to aggregates
c	=	continuum (Kn << 1)
CD	=	pertaining to Convective-Diffusion
crit	=	critical (threshold) value
eff	=	effective
EI	=	pertaining to eddy impaction
fm	=	free-molecule (Kn >> 1)
g	=	pertaining to the carrier gas
g	=	pertaining to geometric mean
h	=	pertaining to heat (energy) transfer
II	=	pertaining to inertial impaction
N	=	pertaining to an aggregate with N spherules
p	=	pertaining to the (solid-like) suspended particles
min	=	minimum value
mob	=	mobility (drift velocity per unit force)
molec	=	pertaining to the molecular gas
mono	=	“mono-dispersed” (single size) (or σg = 1.0)
poly	=	polydispersed (i.e., a distribution of sizes)
mom	=	pertaining to momentum transfer
1	=	pertaining to N = 1 (single, isolated spherule)
∞	=	in the gas far from the aggregate center of mass or far from deposition target (as in, e.g., Equation (23[23] ))

Acronyms and abbreviations

ASD	=	aggregate size distribution
ASM	=	adjusted sphere model (Dahneke 1973a,b,c)
CA	=	Cluster Aggregate
DLCA	=	diffusion-limited cluster aggregate
FA	=	fractal (-like) aggregate
LN	=	log-normal (Equation (14[14] ))
mfp	=	mean free path in carrier gas
mono	=	“mono-dispersed” (single size)
⟨⟨PA⟩⟩	=	projected area (orientation-averaged)
PDE	=	partial differential equation
pdf	=	probability density function
poly	=	“polydispersed” (i.e., a distribution of sizes)
RLCA	=	reaction-limited cluster aggregate
TEM	=	transmission electron microscope
TP	=	thermophoretic
1	=	pertaining to a single spherule
N	=	pertaining to an aggregate containing N-spherules

Operators

grad()	=	spatial gradient operator
|| grad T ||	=	magnitude of the local vector grad T
O()	=	order-of-magnitude
< >	=	volume-averaged
<< >>	=	orientation-averaged
	=	average value of ()

Acknowledgments

This article is dedicated to the memory of our late colleague John B. Fenn (Nobelist, Chemistry [2002]) on the 100th anniversary of his birth (June 1917). It is also our pleasure to acknowledge the helpful comments of our current and former Yale/SEAS colleagues: J. Fernandez de la Mora, A. Gomez, A.G. Konstandopoulos, D. W. Mackowski, M. Arias-Zugasti, and M. Zurita-Gotor, as well as G. M. Mulholland (University of Maryland), C. Sorensen (Kansas State University Physics), and R. L. McGraw (Brookhaven National Lab, Aerosol Chemistry).

Funding

This work was partially supported by the Industrial Affiliates of the Yale/ChE Sol Reaction Engineering Research Group.

Notes

¹ Estimated using the correlation: mfp (nm) = 66*[T(K)/300)]^1.15 /p(bar).

² This “ASM” approach can be put to the test for large (N >>> 1), D_f = 3 “porous” aggregates, as illustrated in the Appendix. This is because, for large N spherical aggregates of spatially uniform permeability a rigorous alternative approach is available provided the outer flow is that of a “creeping” (Re << 1) Newtonian continuum fluid.

³ An interesting corollary of Equation (11[11] ) and the conventional definition of the dimensionless aerodynamic drag coefficient, C_D (i.e., ratio of the fluid-dynamic drag to the reference force: ((1/2)ρU²·(PA)) is that the corresponding ratio of C_D,N to C_D,1 should be (η_PA ·S_mom)⁻¹. But, consistent with the adjusted sphere method (ASM) for estimating rarefaction effects on suspended aggregates, S_mom approaches the asymptote: 1/η_PA when Kn₁>>>1. (This free-molecule limit [often called the high-“vacuum limit”] is of particular interest to macromolecular mass spectroscopists.) Thus, in the near-“vacuum limit” ASM implies that C_D,N and C_D,1 should become identical, revealing the central role of the aggregate “projected area” (PA) in determining free-molecule regime drag and mobility (The corresponding result in terms of “mobility” is simply: (mobility)_N-mer ≈ {(mobility)₁/N}/η_PA.) While well-established as a useful first-approximation, this is now known to require significant corrections depending on the actual N-“spherule” configuration and the laws governing gas/solid “scattering.”

⁴ The efficient numerical method recently used by Corson et al. (2017) serves to verify the success of ASM over a wider range of conditions, but for N up to 100 (see the correlation shown in their Figure 4).

⁵ Indeed, for sufficiently narrow LN-size distributions, explicit approximate results could be obtained for any impaction geometry using only the logarithmic slopes {d ln η_cap)/d ln (Stk)} evaluated at the peak in the aggregate size distribution.

⁶ In Rosner and Fernandez de la Mora (1982) Appendix 1 we show that eddy impaction sets in when the prevailing particle stopping time, tp, is numerically equal to the time required to traverse the Brownian diffusion sublayer if a “point” particle is traveling at the “friction velocity”: [τ_w/ρ]^1/2 = U*(C_f/2)^1/2. Especially for D_f < 2, our present analysis must be revisited to allow for the large (non-zero) size of such aggregates (see Section 6.2).

⁷ Indeed, for sufficiently narrow LN-size distributions, explicit approximate results could be obtained for any impaction geometry using only the logarithmic slopes {d ln η_cap)/d ln (Stk)} evaluated at the peak in the aggregate size distribution.

⁸ A simple systematic improvement to C_slip^(o), convenient for hand-calculations, is the modification:

Appendix:

The Brinkman function and its application to predict the drag of aggregates of both spatially uniform and spatially variable solid fraction

Because of its importance in the rational estimation of the continuum function η_mom defined by Equation (1[1] ), and its use in Section 2.3 for testing the “adjusted sphere method” for making rarefaction corrections (at least when Kn based on R_max is sufficiently small) we display in Equation (A1[A1] ) and Figure A1 the Brinkman function f_B(κ) and briefly discuss below its asymptotic behavior for both small and large dimensionless radius: κ: ≡ R_max/χ^1/2.

Figure A1. Behavior of the Brinkman function, f_B(κ), describing the drag on a sphere of uniform permeability in Re << 1 Flow when Kn_N << 1; log-log representation of Equation (A1[A1] ) showing asymptotic behavior at small and large dimensionless radius, ≡ R_max/χ^1/2.

Explicitly the Brinkman function f_B(κ) quantifies the ratio of the actual drag on a rigid but permeable solid sphere in Re << 1 flow to the Stokes drag: (6πμUR_max) on a solid impermeable sphere of the same outer radius, i.e.:[A1]

This function f_B(κ) can be readily shown to have the small κ behavior: ∼ (2/9)κ² and the large κ behavior ∼ [1 – (1/ κ)]—asymptotes which are displayed dashed in Figure A1. Additionally, when κ is greater than ca. 2.65 then tanh(κ) can be replaced by unity to within 1 pct accuracy. When the granular permeability is radially variable (as in the numerical integrations associated with Tandon and Rosner [1995]), a successful choice of κ_eff, was found to be:[A2]

In adopting the closed-form Brinkman function for the dimensionless drag, our “reference” sphere (with radially constant permeability is one that has a spatially uniform solid fraction—in our cases equal to the volume-averaged solid fraction of a “true” FA. The small additional correction to this result is then obtained using Equation (6[6] ) of the text–derived directly from Equation (A2[A2] ).

In this connection we remind the reader that the permeability χ of an isotropic porous medium, with units length², is defined by the phenomenological expression:[A3] where U_o is the local area-averaged fluid velocity (vector) and μ the fluid Newtonian viscosity. In this work we have made use of the result that for a granular porous medium of low solid fraction φ made up of uniform size spheres of radius R₁ the permeability χ can be shown to be:[A4]

Throughout this work we have adopted the Cunningham-Millikan slip correction, C_slip(Kn) to the solid sphere (Stokes') drag in the form:[A5]

Because the second term, abbreviated ϵ(Kn), is seen to vanish in both Kn limits C_slip^(o) = 1+1.612*Kn is often chosen as a convenient first approximation to C_slip (Sorensen 2011)⁸ —which has the limiting behavior: C_slip(0) = 1 and C_slip ∼ 1.612 · Kn when Kn >>> 1.

While originally developed to account for rarefaction effects on the drag for an isolated solid sphere (Allen and Raabe 1982) the “ASM”-approach described in Section 2.2 enables its use to estimate the rarefaction effect on the drag experienced by large fractal-like aggregates. In accord with this ASM for dealing with the Knudsen transition for large aggregates (see Section 2.3), among other recent confirmations (Corson et al. 2017) for N up to 100), and our present notation, it follows that C_slip,N(Kn_N,eff) should be evaluated using the familiar Cunningham-Millikan Equation (A5[A5] ), but with Kn evaluated as: Kn_N,eff = Kn₁ * (η_mom/ η_PA), i.e., the N-mer will be considerably closer to the continuum limit (where C_slip approaches unity) for N >> 1.