Stationary characteristics in bipolar diffusion charging of aerosols: Improving the performance of electrical mobility size spectrometers

EDITOR:

• Matti Maricq

1. Introduction

Electrical mobility size spectrometers are widely used to measure particle number size distributions (PNSD) in the range of 1–1000 nm (Wang and Flagan 1990; Jiang et al. 2011). These instruments condition the charge state of aerosols using a neutralizer (bipolar diffusion charging), select positively or negatively charged particles using a differential mobility analyzer (DMA), and measure concentrations of these mobility-classified particles. The distribution of measured particles is referred to as the raw PNSD. Assuming known aerosol charge fractions, the original PNSD including charged and uncharged particles is estimated from the raw PNSD through data inversion. Variations in charge fractions can lead to significant uncertainties in the inverted PNSD. For instance, when using a widely used approximation (Wiedensohler 1988) for charge fractions of 20–300 nm particles, a 10% deviation was observed when measuring positively and negatively charged particles (Wiedensohler et al. 2018). Also, the difference between the PNSD-integrated total particle number concentration and a reference condensation particle counter (CPC) changed from −7% to +17% by simply increasing the solvent residue in the neutralizer carrier gas (Figure S3 in the online supplemental information [SI]).

During bipolar diffusion charging, particles acquire both positive and negative charges following collisions with positive and negative ions. Aerosols reach stationary charge states when the product of ion concentration and residence time is high enough. However, these states (charge fractions) are affected by ion properties, including mass, mobility, and concentration, and can vary with experimental conditions. For instance, ion properties can be influenced by the source of ionizing radiation, the mechanical design of the charger, flowrate, and the composition of the carrier gas including its relative humidity and trace constituents. These sensitivities can lead to variabilities in positive and negative charge fractions for instruments of different design, and with time for a given instrument. In this letter, we report a data acquisition and analysis procedure that avoids these sensitivities. Our approach is based on the finding that the sum of positive and negative charge fractions is nearly constant even when positive or negative charge fractions vary.

We hypothesize that if the spectrometer measures both positively and negatively charged particles (rather than measuring particles of only a single polarity, as is done conventionally), uncertainties caused by aerosol charging can be reduced by using both of them when inverting data. We test this hypothesis using both simulations and experiments.

2. Sum of positive and negative charge fractions

Bipolar charge fractions have often been examined separately for positively and negatively charged particles. As illustrated in Figure 5 in Jiang et al. (2014), the significant variations in reported charge fractions reflect the variations of ion properties under conditions used in these studies. These measured fractions were often compared to predictions using Fuchs’ model (Fuchs 1963; Hoppel and Frick 1986) and explained using various empirically-determined values for ion mobility and mass. As summarized by Tigges et al. (2015), values of ion mobility and mobility ratio of positive and negative ions that have been used are mostly in the ranges of 1.0–2.0 × 10⁻⁴ m²/(V·s) and 0.7–1.0, respectively. By using an interval of 0.05 × 10⁻⁴ m²/(V·s) for the above ion mobility range, we formed 143 combinations of positive and negative ion mobilities. Their masses were calculated using a fitted mass-mobility equation (Steiner et al. 2014). With these ion combinations, bipolar charge fractions for 1–1000 nm particles were estimated using Fuchs’ model. Despite variations of positive and negative charge fractions under various ion combinations (Figure 1 in Chen and Jiang [2018]), the size-dependent sums (f(+1) + f(−1) and f(+2) + f(−2)) are relatively stable (Figure 1; the same results are shown in Figure S1 in the SI with a linear scale for charge fractions). Furthermore, those sums are in good agreement with various measurements and with values calculated using Wiedensohler’s approximation. The sum of positive and negative charge fractions remains approximately constant for bipolar diffusion charging because a decrease in positive charge fraction is usually accompanied by an increase in negative charge fraction and vice versa. Accordingly, the fraction of neutral particles also remains approximately constant under various conditions.

Figure 1. The sum of positive and negative charge fractions estimated from modeling and from experiments, where q is the number of elementary charges carried by particles. For predictions using Fuchs’ model, 143 ion combinations were used. The box boundaries indicate the 25th and 75th percentiles, respectively; the line within the box marks the median; whiskers (error bars) above and below the box indicate the 90th and 10th percentiles, respectively; circles are 5th and 95th outlying points.

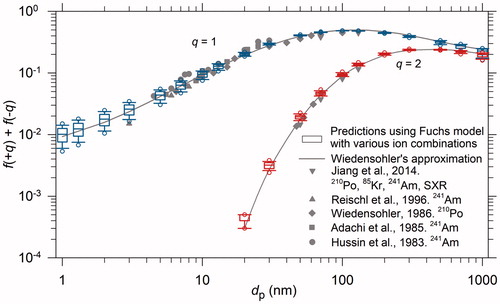
Figures 1 and S1 also reveal limitations of the finding. For 5–500 nm particles, the agreement among various datasets is generally good. For larger particles, however, multiple charging leads to more variations in charge fractions. For sub-5 nm particles, more variations were also observed since their collision rates with ions are significantly affected by ion properties. Fuchs’ model needs to be updated when evaluating these small particles (Lopez-Yglesias and Flagan 2013) and more charging experiments for particles below 5 nm and above 500 nm will help to better understand their charging behaviors.

Nevertheless, the invariance in the sum of positive and negative charge fractions can be utilized to improve the accuracy of the inverted PNSD and integral properties of the aerosols, such as total particle number concentration. This requires measurement of both positively and negatively charged particles. This can be readily achieved with bipolar high voltage suppliers for the DMA and by updated data inversion schemes.

3. Improve the performance of electrical mobility size spectrometers

Simulated aerosols were used to test the new approach. Lognormally-distributed aerosols with a geometric mean diameter of 100 nm and a geometric standard deviation of 1.5 were sent into a virtual spectrometer (including a neutralizer, a DMA, and a CPC) to measure the raw PNSDs for both positively and negatively charged particles. The non-diffusive transfer function was used for the DMA (Knutson and Whitby 1975). The particle penetration efficiency during transport through the spectrometer and the detection efficiency of the CPC were assumed to be unity. Similarly, 143 combinations of positive and negative ions were used for the neutralizer to condition the test aerosols into different stationary charge states using Fuchs’ model such that the measured raw PNSDs change accordingly. Details about this simulation can be found in Chen and Jiang (2018).

A linear inversion algorithm (Hagen and Alofs 1983) was used to recover the original PNSD. Two sets of aerosol charge fractions were used: one was calculated using Wiedensohler’s approximation; the other was estimated from the raw PNSDs for both positively and negatively charged particles using a method developed by Chen and Jiang (2018). Conventional inversion using charged particles of a single polarity was performed. In addition, two new inversions were explored to utilize the stationary characteristics in the sum of positive and negative charge fractions. One is simply averaging the conventionally inverted PNSDs from negatively and positively charged particles (average inversion). The other involves adding positively and negatively charged fractions and using this sum when inverting positively and negatively charged particles together (sum inversion). All the inverted PNSDs were compared to the input PNSD. A weighted deviation defined in Equation (1) was calculated to evaluate the difference between the inverted PNSD and the input PNSD (Chen and Jiang 2018). (1) where n_I,j and n_T,j represent the size distribution function of the jth size bin of the inverted PNSD and the input test PNSD, respectively; J is the total number of size bins.

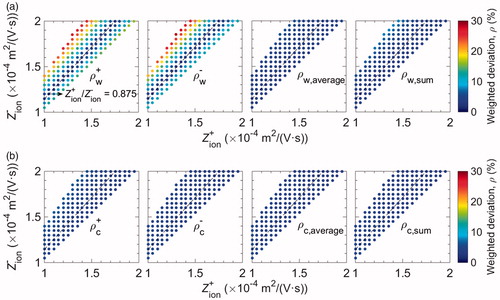
As expected, the inverted PNSDs based on either positive or negative charge fractions estimated using Wiedensohler’s approximation deviate significantly from the input PNSD when the neutralizer has an ion mobility ratio far from 0.875 (Figure 2a). Please note that this approximation was developed by fitting charge fractions estimated at the ion mobility ratio of 0.875 using Fuchs’ model (Wiedensohler 1988). However, both average inversion and sum inversion significantly reduce these deviations by canceling them out when adding positively and negatively charged particles together. Based upon charged particles of both polarities, Chen and Jiang’s method can capture the variations in ion properties and charge fractions under various conditions. Therefore, the inverted PNSDs using conventional, average, and sum inversions all have good agreement with the input PNSD (Figure 2b).

Figure 2. Weighted deviation between the input PNSD and inverted PNSD using various inversions. The subscripts “W” and “C” indicate that charge fractions were estimated using Wiedensohler’s approximation (a) and Chen and Jiang’s method, respectively (b). The superscripts “+” and “-” indicate that the inversion was based on positively and negatively charged particles, respectively. The subscripts “average” and “sum” correspond to average inversion and sum inversion, respectively. Z⁺_ion and Z^-_ion are the mobilities of positive and negative ions, respectively. The dashed line corresponds to an ion mobility ratio of 0.875.

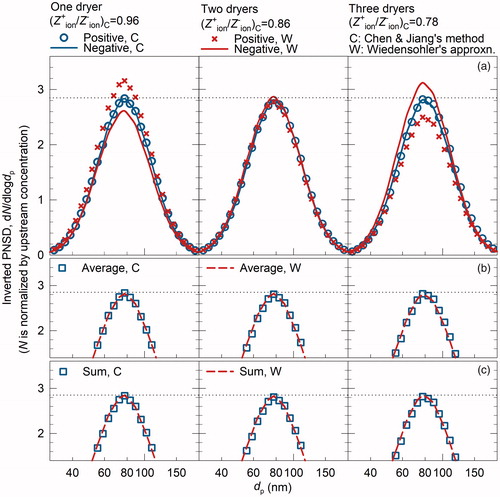
We have also carried out experiments to assess the robustness of our proposed sum inversion method when ion properties are affected by composition of the carrier gas. Dioctyl sebacate acid in isopropyl alcohol (IPA) was atomized to generate aerosols peaked at ∼80 nm (Figure S2 in the SI). Experiments with one, two, and three diffusion dryers in series were performed to adjust the raw PNSDs of IPA residue. A mobility spectrometer was used to measure the raw PNSDs of positively and negatively charged particles. The mobilities of positive and negative ions were affected by the number of dryers (Figure S3 in the SI). Using Chen and Jiang’s method, the ion mobility ratio was estimated to be 0.96, 0.86, and 0.78 for one, two, and three dryers, respectively, indicating that IPA residue affects the neutralizer ions and therefore, the aerosol charge fractions, although the peak diameter of aerosols was unaffected by the number of dryers (Figure S3). The same inversions used for simulated aerosols were performed.

With two dryers, the ion mobility ratio of 0.86 is close to that used to develop Wiedensohler’s approximation, and charge fractions estimated by this approximation are similar to those estimated using Chen and Jiang’s method. Therefore, all the inverted PNSDs are consistent with each other (Figure 3). When the ion mobility ratio is far different from 0.875, i.e., with one and three dryers, however, the inverted PNSDs based on positive and negative charge fractions estimated by Wiedensohler’s approximation are different from each other and are also different from the inverted PNSDs using conventional inversion with Chen and Jiang’s method for charge fractions, average inversion, and sum inversion. For conventional inversion with Wiedensohler’s approximation for charge fractions, the difference between the reference CPC and the PNSD-integrated total number concentrations changed from +17% to −7% for positively charged particles and from −4% to +15% for negatively charged particles, respectively, when increasing the number of dryers from one to three (Figure S3). In contrast, this difference is within 4% for all the inverted PNSDs using conventional inversion with Chen and Jiang’s method for charge fractions, average inversion, and sum inversion.

Figure 3. Inverted PNSDs using conventional inversion (a), average inversion (b), and sum inversion (c). “W” and “C” indicate that charge fractions were estimated using Wiedensohler’s approximation and Chen and Jiang’s method, respectively. The included ion mobility ratio was estimated using Chen and Jiang’s method. The horizontal dotted line corresponds to the same value (2.85) to guide the comparison among all the inverted PNSDs.

4. Conclusion

For bipolar diffusion charging of aerosols, the sum of positive and negative charge fractions was found to be relatively stable under typical conditions. We demonstrated that this can be readily utilized to improve the performance of electrical mobility size spectrometers. In contrast to conventional practices, charged particles of both polarities are measured and used by updated data inversion schemes. The accuracy of the inverted distributions and integral parameters is significantly improved even when positive and negative charge fractions vary with ion properties. After avoiding the sensitivities to ion properties using the sum inversion, we showed that the approximation by Wiedensohler (1988), which has been widely used for more than three decades, works for various tested conditions. The reported influences of neutralizer flowrate on singly and doubly charge fractions (Jiang et al. 2014) can be reduced when adding positively and negatively charged particles together (Figure S4). It also overcomes the inconvenience of using different sets of charge fractions for radioactive and soft X-ray neutralizers as recently practiced by several commercial spectrometers. In addition, we showed that the variations in ion properties and charge fractions can be well captured by a method based on charged particles of both polarities. It can be readily implemented in data inversion, especially for measurement with significant variations in the charge state of aerosols.

Additional information

Funding

Financial support from the National Key R&D Program of China [2017YFC0209503] and the National Science Foundation of China [21521064] is appreciated. PHM’s work was supported by the US Department of Energy’s Atmospheric System Research program under grant number [DE-SC0011780].