Characterization of a high-resolution supercritical differential mobility analyzer at reduced flow rates

Abstract

Classifying sub-3 nm particles effectively with relatively high penetration efficiencies and sizing resolutions is important for atmospheric new particle formation studies. A high-resolution supercritical differential mobility analyzer (half-mini DMA) was recently improved to classify aerosols at a sheath flow rate less than 100 L/min. In this study, we characterized the transfer functions, the penetration efficiencies, and the sizing resolution of the new half-mini DMA at the aerosol flow rate of 2.5–10 L/min and the sheath flow rate of 25–250 L/min using tetra-alkyl ammonium ions and tungsten oxide particles. The transfer functions of the new half-mini DMA at an aerosol flow rate lower than 5 L/min and a sheath flow rate lower than 150 L/min agree well with predictions using a theoretical diffusing transfer function. The penetration efficiencies can be approximated using an empirical formula. When classifying 1.48 nm molecular ions at an aerosol-to-sheath flow ratio of 5/50 L/min, the penetration efficiency, the sizing resolution, and the multiplicative broadening factor of the new half-mini DMA are 0.18, 6.8, and 1.11, respectively. Compared to other sub-3 nm DMAs applied in atmospheric measurements (e.g. the mini-cyDMA, the TSI DMA 3086, the TSI nanoDMA 3085, and the Grimm S-DMA), the new half-mini DMA characterized in this study is able to classify particles at higher aerosol and sheath flow rates, leading to a higher sizing resolution at the same aerosol-to-sheath flow ratio. Accordingly, the new half-mini DMA can reduce the uncertainties in atmospheric new particle formation measurement if coupled with an aerosol detector that could work at the corresponding high aerosol flow rate.

© 2018 American Association for Aerosol Research

EDITOR:

• Pramod Kulkarni

1. Introduction

Measuring aerosol size distributions accurately down to the cluster sizes (∼1.5 nm) is a key to study atmospheric new particle formation (Jiang et al. 2011c; Almeida et al. 2013; Kulmala et al. 2013; Yu et al. 2014; Kerminen et al. 2018) and anthropogenic emissions of nanoparticles (Sgro et al. 2008; Namgung et al. 2016; Rönkkö et al. 2017). Differential mobility analyzers (DMAs) classify submicron particles and nanoparticles according to their electrical mobility (Knutson and Whitby 1975) and determine the sizing resolution of an electrical mobility spectrometer (scanning mobility particle spectrometer, SMPS or differential mobility particle spectrometer, DMPS) that measures aerosol size distributions. Compared to other instruments that can evaluate the size of sub-3 nm particles, for example, the particle size magnifier (Lehtipalo et al. 2014), DMAs can have significant advantages in the sizing resolution. Theoretical analysis has suggested that enhancing the penetration efficiency, aerosol flow rate, and the sizing resolution of the DMA will reduce the uncertainties in the observed size distributions of sub-3 nm particles (Cai et al. 2018). Thus, to reduce the relatively large uncertainties in the present techniques measuring sub-3 nm aerosol size distributions during atmospheric new particle formation events (Kangasluoma and Kontkanen 2017), a DMA classifying sub-3 nm particles at a moderate aerosol flow rate (e.g. 2–5 L/min) with high penetration efficiency and resolution is preferred.

Several DMAs have been used to classify sub-3 nm particles in atmospheric measurements. The cylindrical nanoDMA (Chen et al. 1998) commercialized by TSI Incorporation (model 3085) was used to size 1–10 nm particles in a prototype diethylene glycol scanning mobility particle spectrometer (DEG-SMPS, Jiang et al. 2011b), later commercialized as the TSI 1 nm SMPS (model 3938E77). The sizing resolution of the TSI nanoDMA 3085 is relatively low, for example, 3.9 when classifying 1.48 nm molecular ions at an aerosol-to-sheath flow ratio of 2/20 L/min (Jiang et al. 2011a). Compared to the TSI nanoDMA 3085, the TSI DMA 3086 used in the commercialized TSI 1 nm SMPS improves the sizing resolution by 10%–20% via shortening the classification length (Stolzenburg et al. 2018). The penetration efficiency of the TSI nanoDMA 3085 for 1.48 nm molecular ions is 0.186 at the aerosol-to-sheath flow ratio of 2/20 L/min (Jiang et al. 2011a), whereas the penetration efficiency of the TSI DMA 3086 has not been reported. A miniature cylindrical DMA (mini-cyDMA) was specially designed for sub-3 nm particles and deployed in a prototype DEG-SMPS (Cai et al. 2017). Its aerosol flow rate range is 1–3 L/min. When classifying 1.48 nm molecular ions at the recommended aerosol-to-sheath flow ratio of 2.5/25 L/min, the penetration efficiency and the sizing resolution of the mini-cyDMA are 0.21 and 5.7, respectively. The Grimm S-DMA used in the DMA-train (Stolzenburg, Steiner, and Winkler 2017) has a higher resolution than the TSI nanoDMA 3085 and the TSI DMA 3086. However, the penetration efficiency of the Grimm S-DMA is much lower than the TSI nanoDMA 3085, the TSI DMA 3086, and the mini-cyDMA, for example, 0.066 when classifying 1.48 nm molecular ions (Jiang et al. 2011a). Other DMAs such as the Caltech nano-RDMA (Brunelli, Flagan, and Giapis 2009) and other instruments such as the radial opposed migration ion and aerosol classifier (ROMIAC, Mui et al. 2013, 2017) are also capable of sizing sub-3 nm particles, yet their applications in atmospheric measurements have not been reported.

In addition to the aforementioned DMAs that classify particles at low Reynolds numbers, the high-resolution supercritical DMAs (working at Reynolds numbers higher than 2,000) developed at Yale University can also classify sub-3 nm particles (e.g. Rosser and Fernández de la Mora 2005; Fernández de la Mora and Kozlowski 2013). However, these supercritical DMAs were mainly used in laboratory calibrations in previous studies because of their high flow rates of several hundred or thousand liters per minute and the corresponding high maintaining expenses. There were attempts to apply the high-resolution DMA at reduced flow rates in atmospheric measurements. A high-resolution DMA, known as the half-mini DMA (Fernández de la Mora and Kozlowski 2013), was operated at an aerosol-to-sheath flow ratio of 5/100 L/min to classify atmospheric aerosols (Kangasluoma et al. 2018). Compared to other DMAs working at low Reynolds numbers, the half-mini DMA can increase the total number of particles passing through the DMA and thus the raw counts recorded by the downstream counter simply via classifying particles at a higher aerosol flow rate. In addition, the sizing resolution of a DMA increases with the increasing sheath flow rate when keeping the same aerosol-to-sheath flow ratio and the same DMA geometry. Recently, the aerosol injection slit of the half-mini DMA was improved for better performance at reduced sheath flow rates (Fernández de la Mora 2017). Applying this new half-mini DMA at reduced flow rates in atmospheric measurements may improve the accuracy of the measured size distributions of sub-3 nm particles.

The performance of the new half-mini DMA, especially the penetration efficiency, needs to be characterized before deploying it in atmospheric measurements. The characterizations of the new half-mini DMA (Fernández de la Mora 2017), the classical half-mini DMAs with the original aerosol inlets (Fernández de la Mora and Kozlowski 2013), and other high-resolution DMAs (Kangasluoma et al. 2016) in previous studies were mainly focused on their resolutions and transmission efficiencies. Transmission efficiency is defined as the ratio of particles passing through a DMA and the maximum transmission efficiency is determined by both particle losses and diffusional broadening effect. In contrast, penetration efficiency characterizes only the particle losses when pass through the DMA. To retrieve aerosol size distributions from the raw counts recorded by an SMPS/DMPS, penetration efficiency is necessary even using the conventional one-to-one inversion method (Knutson 1976; Stolzenburg and McMurry 2008). In addition to penetration efficiency, the transfer functions of the half-mini DMA at different particle sizes are often required (or inferred using electrical transfer theory) when using other inversion methods (Kandlikar and Ramachandran 1999; Ramachandran and Cooper 2011).

In this study, we evaluate the performance of a new half-mini DMA equipped with the improved aerosol injection slit (Fernández de la Mora 2017) and a classical half-mini DMA using the original aerosol injection slit (Fernández de la Mora and Kozlowski 2013). The characterized aerosol and sheath flow rate ranges are 2.5–10 and 25–250 L/min, respectively. Sub-5 nm molecular ions and particles were generated using an electrospray and a wire generator, respectively, to calibrate the penetration efficiencies and transfer functions of the half-mini DMAs. Their empirical transfer functions and sizing resolutions are evaluated in comparison to a theoretical diffusing transfer function (Stolzenburg 2018). The penetration efficiencies of the new half-mini DMA at various flow rates and particle diameters are inferred according to the measured transfer functions. An empirical formula is then fitted to the inferred penetration efficiencies. The recommended configuration of the aerosol and sheath flow rates is discussed according to a multiplicative broadening factor and a parameter of Π that characterizes the performance of an SMPS/DMPS. The performance of the new half-mini DMA is compared with other sub-3 nm DMAs used for atmospheric measurements.

2. Methods

The two test DMAs are long/fat-model half-mini DMAs (Fernández de la Mora and Kozlowski 2013). The outer radius of the central electrode is 4 mm. The inner radius of the DMA outer cylinder is 7 mm. The length of the classification region is ∼20 mm. The long models classify larger particle sizes than the short models (i.e. short/fat and short/thin model) at the same flow rate and voltage configuration, which suits the need for the maximum classified particle size in atmospheric measurements better. The maximum electrical mobility diameter classified by the long/fat model at the sheath flow rate of 25 L/min is ∼24 nm when assuming a safe voltage of 5 kV (see Figure 3). Note the characterization results reported in this study should not be used for the other three models (long/thin, short/fat, and short/thin) without verification. One of the test half-mini DMAs is deployed with a 24-hole perforated ring between the aerosol inlet chamber and the aerosol injection slit (Fernández de la Mora 2017, referred as the new half-mini DMA), and the other half-mini DMA is a classical version without the perforated ring (referred as the classical half-mini DMA). The pressure drop between the aerosol inlet and outlet of the new half-mini DMA was 2.4 kPa and negligible at the aerosol-to-sheath flow ratio of 10/200 and 5/100 L/min, respectively. Both DMAs were checked and cleaned before the calibration. There are two opposite aerosol inlets on each half-mini DMA, however, the aerosols entered the half-mini DMA via only one aerosol inlet to avoid potential aerosol losses due to flow splitting and extended tubing.

According to the evaluated transfer functions using 1.48 nm molecular ions, the calibrated resolution of the classical half-mini DMA is sensitive to the aerosol injection slit width and the position of the central electrode. The optimum resolutions at different aerosol and sheath flow rates correspond to different slit widths and electrode positions. Because it was difficult to obtain the optimum resolution at each flow rate configuration, we adjusted the slit width and the electrode position of the classical half-mini DMA by tuning the mounting screws to obtain a (local) optimum resolution at the aerosol-to-sheath flow ratio of 5/100 L/min. Note that the slit widths at different positions of the circumference were not necessarily the same because the mounting screws were not tuned uniformly. Thus, the reported resolutions of the classical half-mini DMA at other flow rates can potentially be improved.

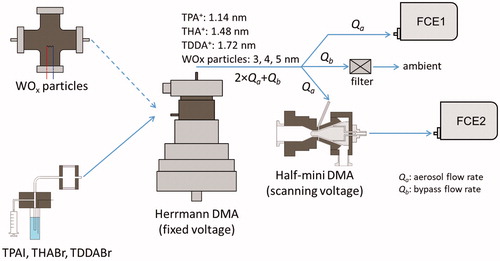
The half-mini DMAs were characterized using a tandem DMA system. As shown in Figure 1, standard molecular ions were produced using an electrospray. A Herrmann DMA (Herrmann et al. 2000; Kangasluoma et al. 2016) operated at a fixed voltage was used to select the monodisperse ions. The electrical mobility diameters of the selected TPAI (tetra-propyl ammonium iodide, N[C₃H₇]₄I), THABr (tetra-heptyl ammonium bromide, N[C₇H₁₅]₄Br) and TDDABr (tetra-dodecyl ammonium bromide, N[C₁₂H₂₅]₄Br) cations were ∼1.14, ∼1.48, and ∼1.72 nm, respectively (Ude and Fernández de la Mora 2005). There may be some uncertainties in these estimated electrical mobility diameters due to the assumed parameters when converting electrical mobility into electrical mobility diameters. However, we used the inverse electrical mobility values when fitting the transfer functions, which are reliable according to Stolzenburg et al. (2018). Only monomers were used to test the half-mini DMAs so that the influence of multi-charged ions with larger molecular weights was minimized (Attoui et al. 2013). These classified tetra-alkyl ammonium cations can be approximately regarded as strictly monodisperse ions. A glowing wire generator was used to produce tungsten oxide (WO_x) particles larger than 2 nm (Peineke, Attoui, and Schmidt-Ott 2006; Kangasluoma et al. 2013). The electrical mobility diameters of the classified positively charged WO_x particles were 3, 4, and 5 nm. Note that the classified WO_x particles were not strictly monodisperse because of the finite resolution of the Herrmann DMA. Two Faraday cage electrometers (FCEs, model TSI 3068B) were used to record the particle or ion number concentrations upstream and downstream of the test half-mini DMA. The sampling flow rates of the FCEs were calibrated using a bubble flow meter. The particle concentrations reported by the two FCEs, when measuring the same aerosol population, were compared at various flow rates. The total line lengths between the flow splitter and the FCEs are equal for the two FCEs (excluding the test DMA). A factor of 1.08 was used to correct the systematic difference between the two FCEs. When calibrating the transfer functions and penetration efficiencies, the voltage of the test half-mini DMA increased linearly. Each calibration scan took 10 min, which was sufficiently slow indicated by the fact that there was no significant difference among the transfer functions calibrated at the scanning time of 5, 10, and 20 min.

Figure 1. Schematic diagram of the experimental setup for calibrating half-mini DMAs. The systematic error in flow splitting was included in the correction factor for the ratio of the aerosol concentrations recorded by the two FCEs.

The empirical transfer functions and the penetration efficiencies of the half-mini DMAs were analyzed using the data inversion routine presented in Jiang et al. (2011a) and Cai et al. (2017) with updates reported by Stolzenburg (2018). The corrected ratio of the aerosol concentrations recorded by the two FCEs, N₂/N₁, is equal to the product of penetration efficiency and transfer function: (1) where N₁ and N₂ are the aerosol number concentrations upstream and downstream of the test half-mini DMA, respectively; η_pene is the penetration efficiency characterizing particle losses inside the DMA; d_Z is the electrical mobility diameter; is the dimensionless electrical mobility defined as the ratio of the particle electrical mobility, Z, to the centroid electrical mobility, Z*; and Ω is the DMA transfer function. Note that the N₂/N₁ value in Equation (1)(1) is already corrected using the factor 1.08. The diffusion losses over the paths to the upstream FCE and the downstream FCE (excluding the test DMA) are assumed equal. According to this assumption, the fitted η_pene characterizes the particle losses inside the DMA. Different from maximum transmission efficiency, which is defined as the peak height of N₁/N₂, penetration efficiency is theoretically equal to the area between the N₁/N₂ and the horizontal axis. When using the conventional one-to-one inversion method, penetration efficiency can directly relate the aerosol size distribution function and the total number concentration of the classified aerosols (Knutson 1976; Stolzenburg and McMurry 2008; Cai et al. 2018).

The DMA transfer function used in this study is a diffusing transfer function (Stolzenburg 1988, 2018; Stolzenburg and McMurry 2008): (2) where σ is the broadening parameter; β is the aerosol-to-sheath flow ratio; δ characterizes the difference between the aerosol inlet flow rate and the classified aerosol flow rate; f_v is an adjustable multiplier to correct the ratio between the electrical mobility of the input aerosol and that inferred by the test DMA measurements; and ε is a function of , σ, β, and δ. It should be clarified that the fitted transfer function, Ω, in Equation (1)(1) is different from the classically defined transfer function with varying Z at a constant voltage, although the difference is usually not significant. For each fitted transfer function, σ is constant because the challenge aerosol is monodisperse while DMA voltage varies. In contrast, for the classically defined transfer function, σ is a function of Z. The fitted transfer functions presented in this study (in Figures 2 and 8) are determined using Equation (1)(1) . When estimating the classically defined transfer functions using the fitted parameters, one should use Equation (2)(2) where σ depends on Z. For the details on this diffusing transfer theory, please refer to Stolzenburg (2018).

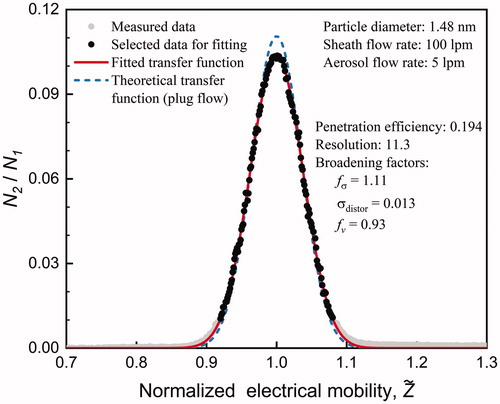
Figure 2. The fitted and theoretical transfer functions of the new half-mini DMA when classifying 1.48 nm molecular ions at the aerosol-to-sheath flow ratio of 5/100 L/min.

The value of f_v ranges from 0.69 to 0.98 in the test conditions is described in the online supplementary information (Table S1). The relatively large discrepancies were also observed when charactering the transfer functions in the sub-3 nm size range in previous studies (e.g. 0.84–0.94 in Stolzenburg et al. 2018). The value of f_v in this study is positively related to sheath flow rate and particle electrical mobility diameter, indicating potential offsets in DMA voltage and sheath flow rate, although voltages and flow rates had been checked before the experiments.

The broadening parameter can be theoretically predicted. A multiplicative broadening factor, f_σ, and an additive broadening factor, σ_distor, can be used to characterize the difference between the empirical broadening parameter, σ, and the theoretical broadening parameter, σ_theo: (3)

The additive broadening factor, σ_distor, indicates the broadening due to flow distortion and asymmetry. The multiplicative broadening factor, f_σ, characterizes the errors due to the assumptions of the diffusing transfer theory better than σ_distor. However, it is usually difficult to separate these two kinds of affects (Stolzenburg 2018). Thus, both broadening factors are used in this study. The fitted f_σ can be smaller than 1.0 because σ_theo is calculated based on a series of assumptions and approximations. For instance, the central electrode of the half-mini DMA downstream of the aerosol outlet holes is conical cylindrical with an increasing diameter along the flow direction rather than circular cylindrical, which may contribute to the distortion of the electrical field. Note that the broadening factors calibrated using WO_x particles are not reported in this study because the WO_x particles were not strictly monodisperse and the fitted σ values were thus overestimated. However, it is reasonable to assume that the accuracies of penetration efficiencies were negligibly affected by the nonstrictly monodisperse WO_x particles.

The flow inside the classification region was assumed to be plug flow when calculating σ_theo. The dimensionless geometry and flow field dependent coefficient, G, was 2.26 and 2.47 at the aerosol-to-sheath flow ratio of 0.05 and 0.10, respectively (Stolzenburg 2018). The half-mini DMA is a supercritical DMA. Although the test flow rates were reduced compared to the original design, the Reynolds number inside the classification region is larger than 2,000 when the sum of aerosol and sheath flow rates exceeds 33 L/min. Turbulence is suppressed because the flow scheme is not fully developed inside the classification region. Thus, the plug flow model should approximate the flow inside the classification region better than the Hagen–Poiseuille flow model.

The sizing resolution of the DMA, R, is defined as the ratio of the centroid electrical mobility, Z*, and the full width at half maximum for the transfer function, ΔZ_FWHM (Flagan 1999): (4)

Fernández de la Mora (2017) proposed a new method to characterize the sizing resolution of the half-mini DMA, that is, , where is the smaller electrical mobility at half-height of the transfer function. However, for the convenience of understanding and comparison, we use the conventional definition of the sizing resolution as shown in Equation (4)(4) in this study.

3. Results and discussion

3.1. Sizing resolution

The transfer function and the sizing resolution of the new half-mini DMA can be approximated using the theoretical transfer function at relatively low flow rates. For instance, when classifying 1.48 nm aerosols at an aerosol-to-sheath flow ratio of 5/100 L/min which was the flow rate configuration for the half-mini differential mobility particle spectrometer (HFDMPS, Kangasluoma et al. 2018), the empirical transfer function agreed well with the theoretical transfer function and the multiplicative broadening factor (f_σ) was 1.11 (Figure 2). The f_σ for 1.14 and 1.72 nm particles calibrated at the same flow rates were 1.01 and 1.11, respectively. Considering the experimental uncertainties and the relatively good agreement between the empirical transfer function and the theoretical transfer function, it is reasonable to approximate the empirical transfer function using the theoretical transfer function in practical applications when f_σ is close to 1.0.

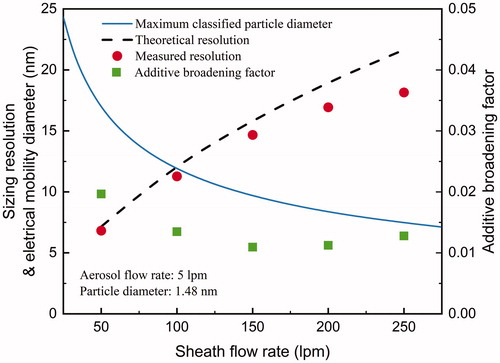
However, the transfer functions of the new half-mini DMA are non-negligibly broadened at relatively high flow rates. The influence of the sheath flow rate on the sizing resolution of the new half-mini DMA was tested using 1.48 nm molecular ions at the aerosol flow rate of 5 L/min. As shown in Figure 3, the measured resolution decreased from 95% to 84% that of the theoretical resolution when the sheath flow rate increased from 50 to 250 L/min. The f_σ values were ∼1.10 at the sheath flow rates less than 150 L/min and increased to 1.22 when the sheath flow rate increased to 250 L/min. However, turbulence might not be the reason of the significantly broadened transfer function at relatively high sheath flow rates because σ_distor was at a relatively constant value (∼0.012) when the sheath flow rate increased from 150 to 250 L/min. The increase of f_σ was due to the decrease of σ_theo with the increasing sheath flow rate. At the sheath flow rates higher than 150 L/min, the nonideality of the new half-mini DMA or the diffusing transfer theory cannot be neglected.

Figure 3. The classified electrical mobility diameter at maximum voltage (5,000 V), empirical resolution, theoretical resolution, and the additive broadening factor of the new half-mini DMA as functions of the sheath flow rate. The empirical and theoretical resolutions were obtained according to the fitted and theoretical transfer functions, respectively.

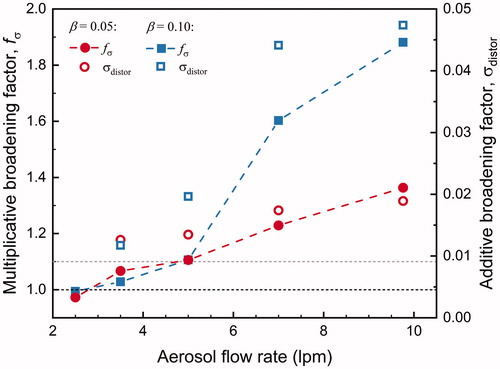
A high aerosol flow rate will also lead to the broadening of the transfer function. When classifying 1.48 nm molecular ions at a sheath flow rate of 100 L/min, the σ_distor of the new half-mini DMA increased monotonically with the aerosol inlet flow rate (Figure 4). The influence of the aerosol flow rate on f_σ and σ_distor was larger compared to the sheath flow rate. The broadening effect was significant when the aerosol flow rate was higher than 5 L/min (e.g. f_σ = 1.30 at 7 L/min). The turbulence caused by the mixing of the aerosol flow and the sheath flow might partially explain the broadening effect, while the asymmetric aerosol injection stream at a high aerosol flow rate might also contribute.

Figure 4. The measured resolutions, theoretical resolutions, and additive broadening factors of the new half-mini DMA and the classical half-mini DMA as functions of the aerosol flow rate. The theoretical maximum relative resolution (1.0) is indicated using the gray-dashed line.

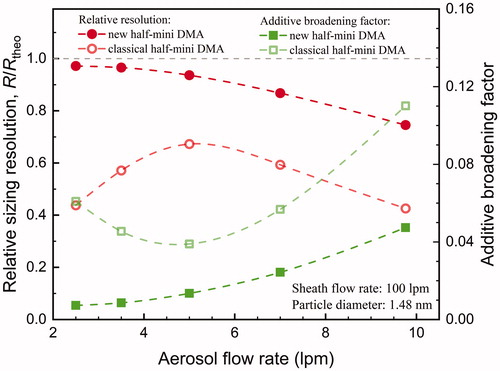
The significant influence of aerosol flow rate on f_σ can be illustrated using the calibration results of the classical half-mini DMA. As shown in Figure 4, the sizing resolution of the classical half-mini DMA always deviated significantly from the theoretical resolution at the test aerosol flow rates. For instance, the measured resolution was 44% that of the theoretical resolution at the aerosol flow rate of 2.5 L/min when classifying 1.48 nm molecular ions. The value of f_σ increased from 1.68 to 3.84 with the increase of the aerosol flow rate from 5 to 10 L/min. Note that the highest resolution appearing at an aerosol flow rate of 5 L/min was an artifact because the resolution was specially tuned to be the highest at the aerosol-to-sheath flow ratio of 5/100 L/min. The central electrode might be off-axis in this configuration. Split peaks were observed when injecting the aerosol from the opposite aerosol inlet tube. The distribution of the aerosol injection stream varies with the aerosol flow rate, thus the DMA geometrical configuration corresponding to the highest resolution at 5/100 L/min could hardly correspond to the highest resolutions at other flow rates. The maximum available resolutions of the classical half-mini DMA should be higher than the reported values, yet we tested the DMA using the same geometry configuration. Although the DMA was adjusted toward the highest resolution at 5/100 L/min, the corresponding f_σ value of 1.69 indicates that the aerosol injection stream was still not symmetrically distributed. According to Fernández de la Mora (2017), some previous unpublished studies also found that tuning the width of the aerosol injection silt cannot avoid this resolution loss.

A low aerosol-to-sheath flow ratio helps to reduce the broadening effect. When the transfer function of the new half-mini DMA for 1.48 nm molecular ions was significantly broadened (at an aerosol flow rate higher than 5 L/min), the f_σ at an aerosol-to-sheath flow ratio of 0.05 was lower than the f_σ at the aerosol-to-sheath flow ratio of 0.10 (Figure 5). Similar results can also be concluded from the results reported in Fernández de la Mora (2017). However, a high aerosol-to-sheath flow ratio is usually preferred in atmospheric measurements especially in sub-3 nm size range because it corresponds to a high total number concentration of the classified aerosol (yet low resolution), as discussed in Section 3.3.

Figure 5. The multiplicative and additive broadening factors of the new half-mini DMA at the aerosol-to-sheath flow ratio of 0.05 and 0.10. The black and gray lines indicate f_σ = 1.0 and f_σ = 1.1, respectively.

3.2. Penetration efficiency

The effective length method was used in some previous studies to characterize the particle diffusional losses inside the DMA (e.g. Reineking and Porstendörfer 1986; Jiang et al. 2011a) while the electrostatic particle loss was assumed to be a constant value (Karlsson and Martinsson 2003). However, it should be noted that using a single effective diffusion length to characterize the particle losses was for practical purpose without theoretical support. Cai et al. (2017) reported that the fitted effective length for the mini-cyDMA was different at different flow rates. We tested the formula characterizing the diffusional losses in the cylinder tubing (Cheng 2011) and the semi-empirical particle loss formula considering the diffusional loss and the electrostatic loss (Bezantakos et al. 2015). However, neither of the two formulas could describe the penetration efficiencies of the new half-mini DMA at various flow rates and particle diameters. 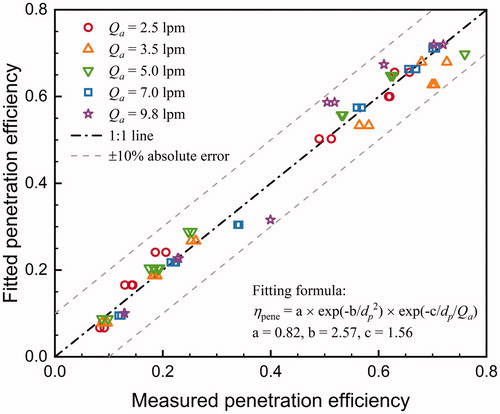Thus, an empirical formula, corresponding to the smallest sum of squared residuals among the tested empirical formulas, was fitted to the penetration efficiencies of the new half-mini DMA: (5) where a = 0.82, b = 2.57, c = 1.56, d_p is the electrical mobility diameter in nm, and Q_a is the aerosol flow rate in L/min. The penetration efficiency was negligibly affected by the sheath flow rate (as shown in Figure 6). The fitted penetration efficiencies agreed with the calibrated penetration efficiencies within an absolute error of 10%. The penetration efficiencies calibrated using the WO_x particles were also included although the WO_x particles were not strictly monodisperse because it is reasonable to assume that penetration efficiency does not vary significantly in a relatively narrow size range.

Figure 6. The measured and fitted penetration efficiencies of the new half-mini DMA at various flow rates and classified particle diameters. d_p is electrical mobility diameter in nm. Q_a is the aerosol flow rate in liters per minute. The electrical mobility diameters of challenge particles were 1.14, 1.48, 1.72, 3, 4, and 5 nm. The different measured penetration efficiencies at the same fitted penetration efficiency were evaluated at the same aerosol flow rate but different sheath flow rates.

3.3. Recommended flow rate configurations for atmospheric measurements

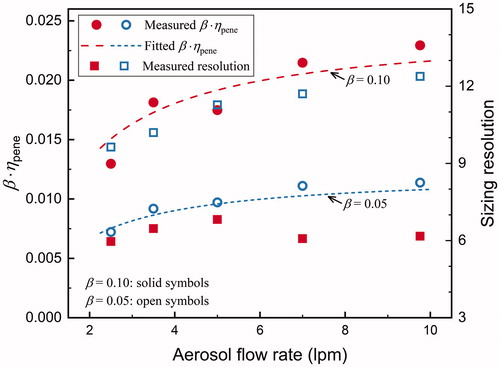
The Π parameter and DMA resolution are two important parameters governing the performance of an SMPS/DMPS system for measuring aerosol size distributions down to ∼1 nm (Cai et al. 2018). Π is linearly proportional to the overall detection efficiency of the SMPS/DMPS, the measurement time, the effective aerosol flow rate, and the aerosol-to-sheath flow ratio, β. Accordingly, Π is linearly proportional to β and the penetration efficiency, η_pene, of the DMA. Thus, we use the product of β and η_pene, β·η_pene, and the sizing resolution to characterize the performance of the half-mini DMA in this study. A smaller β corresponds to a higher resolution but a lower β·η_pene at the same aerosol flow rate (Figure 7). Although designed to classify particles with a resolution higher than 15 (Fernández de la Mora 2017), the new half-mini DMA can also work at a resolution smaller than 10 to obtain a relatively large β·η_pene value. A large β·η_pene value is preferred in atmospheric measurements because the raw counts of the aerosol detector are usually low when measuring sub-3 nm particles. For typical atmospheric new particle formation events, the ideal resolution corresponding to the minimum uncertainties was found to be ∼5–8 (Cai et al. 2018). Thus, we consider the β of 0.1 better than 0.05 when using the new half-mini DMA to classify atmospheric particles.

Figure 7. The β·η_pene and measured sizing resolution of the new half-mini DMA as functions of the aerosol flow rate, where β is the aerosol-to-sheath flow ratio and η_pene is the penetration efficiency.

We recommend the new half-mini DMA to classify atmospheric particles at the aerosol-to-sheath flow ratio of 5/50 L/min. As shown in Figures 3–5, the transfer functions for the new half-mini DMA can be approximated using the theoretical diffusing transfer function when the aerosol flow rate was less than 5 L/min and the sheath flow rate was less than 150 L/min. The sizing resolution at the aerosol flow rate of 5 L/min was the highest among the measured resolutions at the β value of 0.1. However, considering the aerosol sampling flow rate of the particle detector (e.g. a condensation particle counter, CPC) are usually lower than 5 L/min, it is also an option to determine the aerosol flow rate of the new half-mini DMA according to the particle detector to avoid potential particle losses when splitting the aerosol stream. The classical half-mini DMA is not recommended for atmospheric measurements because of its significantly broadened transfer function.

3.4. Comparison with other DMAs

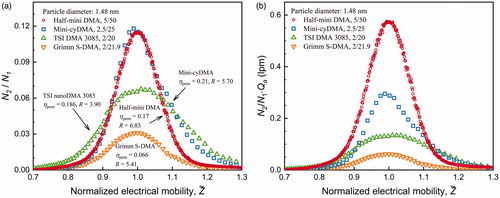
The performance of the new half-mini DMA was compared to other DMAs at their own typical scenario when the aerosol-to-sheath flow ratios were ∼0.1. As shown in Figure 8a, the sizing resolution of the new half-mini DMA was the highest among the four DMAs due to its geometry design and the comparatively high sheath flow rate. The TSI DMA 3086 is not included in Figure 8 because its penetration efficiency was not reported, yet its sizing resolution for 1.48 nm particles was less than 5.3 (Stolzenburg et al. 2018). The penetration efficiency of the new half-mini DMA was lower than the mini-cyDMA and the TSI nanoDMA 3085. The maximum sheath flow rates of the mini-cyDMA, the TSI DMA 3086, and the TSI nanoDMA 3085 are no higher than 30 L/min to prevent flow turbulence. For a given measurement time, the Π parameter for an SMPS/DMPS is proportional to N₂/N₁⋅Q_a when assuming the effective aerosol flow rate is equal or proportional to Q_a. The potential advantage of the new half-mini DMA over the other DMAs is that it can work at higher flow rates corresponding to larger Π values (Figure 8b). Since both Q_a and the flow rate passing through the optical detector of particle counter limit the effective aerosol flow rate, a particle counter operated at this high aerosol flow rate is needed to realize this advantage, though the effective aerosol flow rate of most present commercial CPCs is less than 2.5 L/min.

Figure 8. The calibrated (a) transfer functions and (b) products of the transfer functions and the aerosol flow rates of the new half-mini DMA, the mini-cyDMA, the TSI nanoDMA 3085, and the Grimm S-DMA at their typical scenario when the aerosol-to-sheath flow ratios were ∼0.1. N₂/N₁ is the corrected ratio of the aerosol concentrations measured upstream and downstream of the test DMA (Equation (1)). Q_a is the aerosol flow rate of the DMA. The data for the mini-cyDMA were from Cai et al. (2017). The data for the TSI nanoDMA 3085 and the Grimm S-DMA were from Jiang et al. (2011a). The transfer function of the TSI DMA 3086 is not included because its penetration efficiency has not been reported while its sizing resolution for 1.48 nm particles was less than 5.3 (Stolzenburg et al. 2018).

4. Conclusions

We characterized the penetration efficiency and transfer function of a new half-mini DMA equipped with an improved aerosol injection slit (Fernández de la Mora 2017) at reduced sheath flow rates ranging from 25 to 250 L/min. An empirical formula was fitted to the measured penetration efficiencies within an absolute error of 0.1. The empirical transfer function of the new half-mini DMA agreed well with the theoretical diffusing transfer function (Stolzenburg 2018) when the sheath flow rate was less than 150 L/min and the aerosol flow rate was less than 5 L/min with a multiplicative broadening factor smaller than 1.11. When classifying particles at a higher aerosol or sheath flow rate, the difference between the measured and theoretical transfer functions was significant due to the asymmetrical distribution of the aerosol stream and other nonidealities of the new half-mini DMA or the diffusing transfer theory. Based on our results, the recommended aerosol flow rate of the new half-mini DMA is 5 L/min at the aerosol-to-sheath flow rate of 0.1 when classifying sub-3 nm particle during atmospheric new particle formation events. Compared to the mini-cyDMA, the TSI DMA 3086, the TSI nanoDMA 3085, and the Grimm S-DMA at their own typical scenario with the aerosol-to-sheath flow ratio of ∼0.1, the new half-mini DMA has a higher sizing resolution. A classical half-mini DMA using the original aerosol injection slit was also tested. However, we do not recommend it for atmospheric measurements because its transfer function was found to be significantly broadened due to the asymmetrical aerosol injection stream. The new half-mini DMA provides a possibility to reduce the uncertainties in measuring the size distribution of sub-3 nm atmospheric particles by improving the Π parameter if an aerosol detector that could work at the corresponding high aerosol flow rate is available.

Acknowledgments

We thank Prof. Juan Fernández de la Mora at Yale University for helpful discussions on extending the high-resolution DMAs to lower flow rates.

Additional information

Funding

Financial support from the National Key R&D Program of China (2017YFC0209503), National Science Foundation of China (21876094 and 41730106), ACTRIS-2 (grant agreement No. 654109), the Academy of Finland (project No. 307331), and Faculty of Science, University of Helsinki is acknowledged. R. Cai appreciates the support from China Scholarship Council (CSC) for his visit to University of Helsinki.