A numerical aerosol model Fractal Aggregate Moment Model (FAMM) to simulate simultaneous nucleation, coagulation, surface growth, and sintering of fractal aggregates

Abstract

Particles generated from high-temperature processes often attain an aggregate structure, with physical and chemical properties and health impacts dependent on the particles’ size and morphology. A numerical aggregate model is a useful tool to produce well-controlled ceramic particles and to predict the production of particulate air contaminants. Although extensive efforts have been directed at developing accurate and fast-running numerical aerosol codes that can model the formation and growth of aerosol aggregates using the framework of the log-normal (LN) moment method, none developed thus far can account for the bimodal particle size distribution and aggregate morphology simultaneously. In this study, two previous models, a bimodal LN model for spherical particles and a unimodal LN model for fractal aggregates, are extended to fabricate a bimodal LN model for fractal aggregates. By tracing five time-dependent variables for the particle phase, the present model can predict the formation of nucleus particles from a gas precursor and the change in the particle size distribution and morphology. Nucleation, surface growth, intramodal and intermodal coagulation, sintering, and condensational obliteration are taken into account. Numerical experiments performed for validating the new model showed that it is a robust and efficient tool for predicting both aggregate particle size distribution and morphology. The proposed model is expected to be a useful tool for simulating the formation and growth of fractal aggregate particles in multidimensional spatial domains requiring a fast-running aerosol model.

Copyright © 2019 American Association for Aerosol Research

1. Introduction

Particles generated from high-temperature processes, e.g., ceramic particles produced from gas-phase reactions or soot particles produced from combustion of fuels, often attain aggregate structure. The size and morphology of these aggregate particles are determined by competition of several mechanisms including coagulation, surface growth and sintering. Because the physical and chemical properties and health impacts of the aggregate particles are dependent on their size and morphology, it is important to predict and control the particle growth processes. In this regard, a numerical aggregate model is a useful tool to produce well-controlled ceramic particles and to predict the production of particulate air contaminants (soot).

The most rigorous way of modeling the formation and growth of aggregate particles is to use a two-dimensional (2D) sectional model (e.g., Xiong and Pratsinis 1993, 283–300; Nakaso et al. 2001, 929–947), in which aggregate particles are characterized by two quantities representing particle size and morphology (e.g., volume and surface area). The 2D sectional models require long computation time and hence can hardly be used as an aerosol module included in a larger model for solving chemistry and transport issues (e.g., combustion models). One-dimensional (1D) sectional models substantially reduced the computing time, compared to the 2D models, by taking two independent variables, e.g., particle volume and surface area (Tsantilis and Pratsinis 2000, 407–415; Jeong and Choi 2001, 565–582), or particle volume and number of primary particles (Park and Rogak 2003, 947–960) for each section. Nevertheless, even the 1D sectional models reportedly suffer from computational load when applied to multidimensional problems (Jeong and Choi 2003a, 713–732).

Jeong and Choi (2003b, 965–976; 2004, 1071–1090; 2005, 351–359) reported a series of model developments to predict the change in particle size and shape in high-temperature particle formation and growth processes. Jeong and Choi (2003b, 965–976) developed a bimodal model, consisting of a monodisperse nuclei mode and a monodisperse accumulation mode, for fractal aggregates undergoing nucleation, coagulation, and sintering. While the nuclei mode was assumed to contain spherical nuclei particles with a fixed volume, the accumulation mode was allowed to contain fractal aggregates with time-dependent particle volume and surface area. Later the same authors improved the model by allowing the accumulation mode particle volume to change according to surface growth in order to simulate simultaneous nucleation, coagulation, sintering and surface growth (Jeong and Choi 2005, 351–359). Although these models were very effective in predicting the average particle volume and surface area, they could not predict the particle size distribution in the accumulation mode. Therefore, Jeong and Choi (2004, 1071–1090) developed a bimodal log-normal (bi-LN) model, in which the accumulation-mode particle size distribution is described by a time-dependent LN function. By tracing four dependent variables, the nuclei-mode particle number and three moments of the accumulation mode, this model could predict the change in the particle size distribution resulting from simultaneous nucleation, coagulation, and surface growth. Sintering could not be modeled by this model, however, because the particle shape was assumed to be spherical.

The first effort to simulate simultaneous coagulation and sintering within the LN model framework was reported by Park et al. (2011, 1664–1667). By assuming unimodal LN (uni-LN) particle size distribution and taking the average primary particle radius as an additional dependent variable, they could trace the fractal structure of the aggregates and the particle size distribution. This model showed very good agreement with a sectional model of Park and Rogak (2004, 1385–1404) in predicting the average primary particle size and the aggregate particle size distribution. Later, the effects of surface growth and condensational obliteration were added to the model (Park, Jung, and Park 2013, 2008–2011). However, this model has a clear limitation that the particle nucleation cannot be simulated because it assumes a unimodal particle size distribution. In order to simulate simultaneous nucleation, coagulation, sintering, and surface growth of fractal aggregates in a time-efficient way, a bi-LN model accounting for the fractal morphology of aggregate particles needs to be developed, which, to the best of our knowledge, has never been reported thus far.

In this study, the bi-LN model for spherical particles of Jeong and Choi (2004, 1071–1090) and the uni-LN model for fractal aggregates of Park et al. (2011, 1664–1667; 2013, 2008–2011) are extended to fabricate a bi-LN model for fractal aggregates, named Fractal Aggregate Moment Model (FAMM). By tracing five time-dependent variables, FAMM can predict the change in the aggregate particle size distribution and morphology, as well as the number of the nuclei-mode particles. Nucleation, surface growth, intramodal and intermodal coagulation, sintering, and condensational obliteration are taken into account.

2. Theory of the log-normal moment method

The particle size distribution of an aerosol undergoing simultaneous nucleation, coagulation, and surface growth is governed by the following integro-differential equation (Seinfeld and Pandis 1998): (1) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{coag}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=\frac{1}{2}{\int }_0^v\beta \left(v-\overline{v},\mathrm{}\overline{v}\right)n\left(v-\overline{v},\mathrm{}t\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-n\left(v,\mathrm{}t\right){\int }_0^{\mathrm{\infty }}\beta \left(v,\mathrm{}\overline{v}\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}+J\left(v\right)\delta (v-v_1)$$(1) where $n(v,\mathrm{}t)$ is the particle size distribution function, expressed in terms of particle volume v, at time t, $\beta \left(v,\mathrm{}\overline{v}\right)$ is the collision kernel for two particles of volume $v$ and $\overline{v},$ $I\left(v\right)=\frac{\mathit{dv}}{\mathit{dt}}$ is the surface growth rate, $J\left(v\right)$ is the nucleation rate, and $v_1$ is the nucleus particle volume.

In this study, we are interested in an aerosol that retains a bimodal size distribution, which is composed of a monodisperse nuclei mode (Mode 1) with the fixed particle volume $v_1$ and an LN accumulation mode (Mode 2). Then the particle size distribution can be represented by the following equation: (2) $$n\left(v,\mathrm{}t\right)=n_1\left(v,\mathrm{}t\right)+n_2\left(v,\mathrm{}t\right)=N_1\left(t\right)\delta \left(v-v_1\right)+\frac{1}{3v}\frac{N_2\left(t\right)}{\sqrt{2\pi }\mathrm{}\hspace{0.17em}\text{ln}\hspace{0.17em}\sigma \left(t\right)}\mathrm{e}\mathrm{xp}\left[\frac{-\hspace{0.17em}{\text{ln}}^2\left\{v/v_g\left(t\right)\right\}}{18\hspace{0.17em}{\text{ln}}^2\sigma \left(t\right)}\right]$$(2) where $N_1\left(t\right)$ is the particle number concentration of the nuclei mode and $N_2\left(t\right),$ $\sigma \left(t\right),$ and $v_g\left(t\right)$ are the particle number concentration, the geometric standard deviation of volume-equivalent particle diameter, and the geometric number mean particle volume, respectively, of the accumulation mode. The assumption that the accumulation-mode particles form an LN size distribution has widely been employed theoretically and experimentally.

Equation (2)(2) $$n\left(v,\mathrm{}t\right)=n_1\left(v,\mathrm{}t\right)+n_2\left(v,\mathrm{}t\right)=N_1\left(t\right)\delta \left(v-v_1\right)+\frac{1}{3v}\frac{N_2\left(t\right)}{\sqrt{2\pi }\mathrm{}\hspace{0.17em}\text{ln}\hspace{0.17em}\sigma \left(t\right)}\mathrm{e}\mathrm{xp}\left[\frac{-\hspace{0.17em}{\text{ln}}^2\left\{v/v_g\left(t\right)\right\}}{18\hspace{0.17em}{\text{ln}}^2\sigma \left(t\right)}\right]$$(2) indicates that the above-described bimodal particle size distribution can be represented by four time-evolving variables, $N_1,$ $N_2,$ $\sigma ,$ and $v_g,$ if the particle volume is the only particle size parameter (e.g., for spherical particles). If the aerosol particles are aggregates, however, at least one additional variable is required to describe the aggregate morphology in Mode 2. Park et al. (2011, 1664–1667; 2013, 2008–2011) took the average primary particle radius ($r_p$) as the additional variable representing particle morphology. The adoption of the average primary particle radius as the additional variable, however, appeared to lead to complications when a nuclei mode was added. Therefore, here we adopt the number concentration of primary particles present in the aggregates in Mode 2 ($N_p$), instead of $r_p,$ as the variable representing particle morphology. In this case, $N_p/N_2$ is the average number of primary particles per aggregate. We also need another additional variable $N_{\mathrm{vap}},$ which represents the number concentration of precursor vapor molecules, to account for the consumption of precursor vapor due to nucleation and condensation. Therefore, we have five variables for aerosol particles and one variable for gaseous precursor.

In the next section, we apply the LN moment method (LNMM) to Equation (1)(1) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{coag}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=\frac{1}{2}{\int }_0^v\beta \left(v-\overline{v},\mathrm{}\overline{v}\right)n\left(v-\overline{v},\mathrm{}t\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-n\left(v,\mathrm{}t\right){\int }_0^{\mathrm{\infty }}\beta \left(v,\mathrm{}\overline{v}\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}+J\left(v\right)\delta (v-v_1)$$(1) to convert it into a set of differential equations for six variables. In the LNMM, the kth moment of the accumulate-mode particle size distribution is defined as (3) $$M_k={\int }_0^{\mathrm{\infty }}{v}^k{n}_2\left(v,\mathrm{}t\right)dv$$(3) where $k$ is an arbitrary real number. According to the properties of an LN function, any moment can be written in terms of $M_0$ ($=N_2$), $v_g$ and $\sigma$ as (4) $$M_k=M_0{\nu }_g^k{Z}^{k^2/2}$$(4) where $Z=\exp \left(9{\ln }^2\sigma \right).$

From Equation (4)(4) $$M_k=M_0{\nu }_g^k{Z}^{k^2/2}$$(4) with $k=$ 1 and 2, $\sigma$ and ${\nu }_g$ can be solved in terms of $M_0,M_{1,}\text{and}{M}_2$ as follows: (5) $$Z=\frac{M_0{M}_2}{M_1^2}$$(5) (6) $${\nu }_g=\frac{M_1^2}{M_0^{3/2}{M}_2^{1/2}}$$(6)

The particle diameter of Mode 1 ($d_1$) and the volume-equivalent geometric mean particle diameter of the Mode 2 ($d_g$) are defined as (7) $$d_1={\left(\frac{6{\nu }_1}{\pi }\right)}^{1/3}$$(7) (8) $$d_g={\left(\frac{6{\nu }_g}{\pi }\right)}^{1/3}$$(8)

The average-mass primary particle volume ($v_p$) and diameter ($d_p$) in the Mode 2 are given by (9) $$v_p=\frac{M_1}{N_p}$$(9) (10) $$d_p={\left(\frac{6{\nu }_p}{\pi }\right)}^{1/3}$$(10)

For the whole particle size distribution (i.e., Mode 1 plus Mode 2), the volume-equivalent geometric mean particle diameter $d_{\mathit{gt}},$ the geometric standard deviation ${\sigma }_t,$ and the average-mass primary particle diameter $d_{\mathit{pt}}$ can be calculated as (11) $$d_{\mathit{gt}}=\exp \left(\frac{M_0\ln d_g+N_1\ln d_1}{M_0+N_1}\right)$$(11) (12) $${\sigma }_t=\exp \left\{\sqrt{\frac{M_0\left({\ln }^2\sigma +{\ln }^2\frac{d_g}{d_{\mathit{gt}}}\right)+N_1{\ln }^2\frac{d_1}{d_{\mathit{gt}}}}{M_0+N_1}}\right\}$$(12) (13) $$d_{\mathit{pt}}={\left(\frac{6}{\pi }·\frac{v_1{N}_1+M_1}{N_1+N_p}\right)}^{1/3}$$(13)

The main dependent variables and some important auxiliary variables used in this article are summarized in Table 1.

Table 1. Definition of variables.

$N_1$	Particle number concentration of Mode 1 (nuclei mode)
$M_0$ (=$N_2$)	Particle number concentration of Mode 2 (accumulation mode)
$M_1$	Particle volume concentration of Mode 2
$M_2$	Particle volume-squared concentration of Mode 2
$N_p$	Primary particle number concentration of Mode 2
$N_{\mathrm{vap}}$	Number concentration of precursor vapor molecules
$d_1$ and ${\nu }_1$	Particle diameter and volume of Mode 1
$d_g$ and ${\nu }_g$	Volume-equivalent geometric mean particle diameter and volume of Mode 2
${\nu }_2$ ($=M_1/M_0$)	Average particle volume of Mode 2
$\sigma$	Geometric standard deviation of volume-equivalent particle diameter of Mode 2
$Z$	$\mathrm{Exp}\left(9{\ln }^2\sigma \right)$
$d_p$ and ${\nu }_p$	Average-mass primary particle diameter and volume of Mode 2
$d_{\mathit{gt}}$	Volume-equivalent geometric mean particle diameter of the whole particle size distribution (Modes 1 and 2)
${\sigma }_t$	Geometric standard deviation of volume-equivalent particle diameter of the whole particle size distribution
$d_{\mathit{pt}}$	Average-mass primary particle diameter of the whole particle size distribution

3. Development of the bimodal moment model FAMM

In this section, a set of differential equations for six variables, $N_1,$ $N_2,$ $\sigma ,$ $v_g,$ $N_p,$ and $N_{\mathrm{vap}},$ which are solved numerically in FAMM, is derived. Five mechanisms that change the particle size distribution and morphology are taken into account: nucleation, surface growth, coagulation, sintering, and condensational obliteration.

3.1. Nucleation

When we consider only nucleation, Equation (1)(1) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{coag}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=\frac{1}{2}{\int }_0^v\beta \left(v-\overline{v},\mathrm{}\overline{v}\right)n\left(v-\overline{v},\mathrm{}t\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-n\left(v,\mathrm{}t\right){\int }_0^{\mathrm{\infty }}\beta \left(v,\mathrm{}\overline{v}\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}+J\left(v\right)\delta (v-v_1)$$(1) becomes (14) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=J\left(v\right)\delta (v-v_1)$$(14)

For the monodisperse Mode 1, Equation (14)(14) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=J\left(v\right)\delta (v-v_1)$$(14) can be translated into the derivatives of $N_1$ and $N_{\mathrm{vap}}$ as follows: (15) $${\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{nucl}}=J\left(v_1\right)$$(15) (16) $${\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{nucl}}=-J\left(v_1\right)$$(16)

3.2. Surface growth

If surface growth is the only mechanism under consideration, Equation (1)(1) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{coag}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=\frac{1}{2}{\int }_0^v\beta \left(v-\overline{v},\mathrm{}\overline{v}\right)n\left(v-\overline{v},\mathrm{}t\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-n\left(v,\mathrm{}t\right){\int }_0^{\mathrm{\infty }}\beta \left(v,\mathrm{}\overline{v}\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}+J\left(v\right)\delta (v-v_1)$$(1) becomes (17) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}$$(17)

The surface growth rate $I$ is dependent on particle volume. For example, if the surface growth mechanism is condensation of vapor molecules, $I$ is proportional either to $v^{1/3}$ in the continuum regime or to $v^{2/3}$ in the free-molecule regime (Pratsinis 1988, 416–427). For aggregate particles consisting of equal-sized primary particles that grow due to surface reaction, $I$ is proportional to the particle surface area, and hence, to the particle volume $v.$ Here we assume that (18) $$I\left(v\right)=\frac{\mathit{dv}}{\mathit{dt}}=I_0{v}^m$$(18) to achieve generality, where $m$ is an arbitrary real number.

3.2.1. Surface growth in Mode 1 (surf 1)

A particle that has grown due to surface growth during an infinitesimal time falls between the nuclei volume ($v_1$) and the average volume of the accumulation-mode aggregates ($v_2=M_1/M_0$). Jeong and Choi (2003b, 965–976) suggested an apportioning scheme, which puts a part of the grown particles into Mode 2 with volume $v_2$ and the remainder back into Mode 1 with volume $v_1$ while conserving total particle number and volume. However, this apportion scheme leads to the establishment of unrealistic bimodal particle size distribution composed of two monodisperse particles in the case of simultaneous nucleation and condensation because the particles added to Mode 2 always have the same volume as the preexisting particles. Therefore, we propose here a slightly modified apportioning scheme, in which the particles put into Mode 2 have a volume of $2v_1$ instead of $v_2.$ In the early stage of surface growth of nuclei particles $2v_1$ is equal to $v_2.$ As the particles in Mode 2 also grow, however, $v_2$ becomes larger than $2v_1$ and the addition of particles with volume $2v_1$ to Mode 2 leads to a polydisperse particle size distribution of Mode 2, which is more realistic. Using this apportioning scheme, Equation (17)(17) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}$$(17) combined with Equation (18)(18) $$I\left(v\right)=\frac{\mathit{dv}}{\mathit{dt}}=I_0{v}^m$$(18) can be translated into the following four equations: (19) $${\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{surf}1}=-I_0{v}_1^{m-1}{N}_1$$(19) (20) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{surf}1}=2^k{I}_0{v}_1^{m+k-1}{N}_1$$(20) (21) $${\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{surf}1}=I_0{v}_1^{m-1}{N}_1$$(21) (22) $${\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{surf}1}=-I_0{v}_1^{m-1}{N}_1$$(22)

3.2.2. Surface growth in Mode 2 (surf 2)

The aggregate particles in Mode 2 that have grown by surface growth are assumed to remain in Mode 2. Then, for this mechanism Equation (17)(17) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}$$(17) is written as (23) $${\left.\frac{\partial n_2\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}2}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n_2\left(v,t\right)\right\}$$(23)

By multiplying Equation (23)(23) $${\left.\frac{\partial n_2\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}2}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n_2\left(v,t\right)\right\}$$(23) by $v^k,$ integrating it from 0 to $\mathrm{\infty },$ and using Equations (18)(18) $$I\left(v\right)=\frac{\mathit{dv}}{\mathit{dt}}=I_0{v}^m$$(18) and (4)(4) $$M_k=M_0{\nu }_g^k{Z}^{k^2/2}$$(4) , we have (24) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{surf}2}=k{I}_0{M}_0{v}_g^{m+k-1}{Z}^{\frac{{\left(m+k-1\right)}^2}{2}}$$(24)

The consumption of vapor molecules can be expressed as (25) $${\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{surf}2}=-\frac{{\left.\frac{d{M}_1}{\mathit{dt}}\right|}_{\mathrm{surf}2}}{v_1}=-\frac{I_0{M}_0{v}_g^m{Z}^{m^2/2}}{v_1}$$(25)

3.3. Coagulation

3.3.1. Intramodal coagulation in Mode 1 (coag1)

The number of collisions per unit time due to simple monodisperse coagulation in Mode 1 is $\frac{1}{2}\beta \left(v_1,v_1\right)N_1^2.$ In the case of coagulation, the apportioning scheme that Jeong and Choi (2003b, 965–976) suggested appeared to be superior to the one that we used for surface growth in this study. The Jeong and Choi (2003b, 965–976)’s scheme apportions the resulting particles of volume $2v_1$ between Modes 1 and 2, in such a way that total particle number and mass are conserved: $(\gamma -2)/\left(\gamma -1\right)$ of them to Mode 1 with particle volume $v_1$ and $1/\left(\gamma -1\right)$ of them to Mode 2 with particle volume $v_2.$ Then, every intramodal coagulation event in Mode 1 results in the consumption of two particles in Mode 1 and the production of $(\gamma -2)/\left(\gamma -1\right)$ particles in Mode 1 and $1/\left(\gamma -1\right)$ particles in Mode 2. Therefore, the following equations are obtained: (26) $${\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}1}=-\frac{\beta \left(v_1,v_1\right)N_1^2\mathrm{\gamma }}{2\left(\mathrm{\gamma }-1\right)}$$(26) (27) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}1}=\frac{\beta \left(v_1,v_1\right)v_2^k{N}_1^2}{2\left(\mathrm{\gamma }-1\right)}$$(27) (28) $${\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{coag}1}=\frac{\beta \left(v_1,v_1\right)N_1^2\mathrm{\gamma }}{2\left(\mathrm{\gamma }-1\right)}$$(28) where $\gamma =\frac{v_2}{v_1}.$

The particles in Mode 1 are so small and thus belong to the free-molecule regime, in which the collision kernel is given as (Matsoukas and Friedlander 1991, 495–506) (29) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)={\left(\frac{8\pi k_{B}T}{{\rho }_p}\right)}^{1/2}{\left(\frac{d_c}{2}+\frac{\overline{d_c}}{2}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(29) where $k_B$ is the Boltzmann constant, T is the absolute temperature, ${\rho }_p$ is the particle density, and $d_c$ and $\overline{d_c}$ are the collision diameters of the two colliding particles. For the collision between two particles in Mode 1, $d_c=\overline{d_c}=d_1$ and $v=\overline{v}=v_1$ hold, resulting in (30) $$\beta \left(v_1,v_1\right)=4\sqrt{2}{K}_{\mathit{fm}}{v_1}^{1/6}$$(30) where $K_{\mathit{fm}}$ ($={(3/4\pi )}^{1/6}{(6k_{B}T/{\rho }_p)}^{1/2}$) is the collision coefficient for the free-molecule regime.

3.3.2. Intramodal coagulation in Mode 2 (coag2)

For this mechanism, Equation (1)(1) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{coag}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}+{\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{nucl}}=\frac{1}{2}{\int }_0^v\beta \left(v-\overline{v},\mathrm{}\overline{v}\right)n\left(v-\overline{v},\mathrm{}t\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-n\left(v,\mathrm{}t\right){\int }_0^{\mathrm{\infty }}\beta \left(v,\mathrm{}\overline{v}\right)n\left(\overline{v},\mathrm{}t\right)d\overline{v}-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}+J\left(v\right)\delta (v-v_1)$$(1) has only the first two terms in the right hand side and $n=n_2.$ Multiplying this equation by $v^k$ and integrating it from 0 to $\mathrm{\infty },$ we have the following for $k=$ 0 and 2: (31) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left\{{\left(v+\overline{v}\right)}^k-v^k-{\overline{v}}^k\right\}\beta \left(v,\mathrm{}\overline{v}\right)n_2\left(v,\mathrm{}t\right)n_2\left(\overline{v},\mathrm{}t\right)dvd\overline{v}$$(31)

For $k=1,$ Equation (31)(31) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left\{{\left(v+\overline{v}\right)}^k-v^k-{\overline{v}}^k\right\}\beta \left(v,\mathrm{}\overline{v}\right)n_2\left(v,\mathrm{}t\right)n_2\left(\overline{v},\mathrm{}t\right)dvd\overline{v}$$(31) becomes ${\left.\frac{d{M}_1}{\mathit{dt}}\right|}_{\mathrm{coag}2}=0,$ which simply means that coagulation is a mass-conserving process. The evaluation of Equation (31)(31) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left\{{\left(v+\overline{v}\right)}^k-v^k-{\overline{v}}^k\right\}\beta \left(v,\mathrm{}\overline{v}\right)n_2\left(v,\mathrm{}t\right)n_2\left(\overline{v},\mathrm{}t\right)dvd\overline{v}$$(31) depends on the functional form of $\beta \left(v,\mathrm{}\overline{v}\right),$ which in turn depends on the particle size regime.

3.3.2.1. Free-molecule regime

Equation (29)(29) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)={\left(\frac{8\pi k_{B}T}{{\rho }_p}\right)}^{1/2}{\left(\frac{d_c}{2}+\frac{\overline{d_c}}{2}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(29) can also be used when two colliding particles are fractal aggregates if the collision diameter ($d_c$ and $\overline{d_c}$) can be expressed as a function of particle volume. The aggregates formed from coagulation among solid particles often show the following power-law relation between the collision diameter and particle volume (Matsoukas and Friedlander 1991, 495–506): (32) $$\frac{v}{v_p}={\left(\frac{d_c}{d_p}\right)}^{D_f}$$(32) where $D_f$ is the mass fractal dimension, which is usually within the range of 1.7–2.5 (Forrest and Witten 1979, L109–L117; Samson, Mulholland, and Gentry 1987, 272–281; Schmidt-Ott 1988, 954–956; Zhang et al. 1988, 867–871; Megaridis and Dobbins 1990, 95–109), having a typical value of ∼1.8 when cluster-cluster collision is the dominant growth mechanism (Mountain, Mulholland, and Baum 1986, 67–81). Although intensive sintering may alter the value of $D_f$ during the particle growth, we assume here that $D_f$ remains constant, i.e., sintering is not so intensive as to change the fractal dimension, for the sake of simplicity.

Using Equation (32)(32) $$\frac{v}{v_p}={\left(\frac{d_c}{d_p}\right)}^{D_f}$$(32) , Equation (29)(29) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)={\left(\frac{8\pi k_{B}T}{{\rho }_p}\right)}^{1/2}{\left(\frac{d_c}{2}+\frac{\overline{d_c}}{2}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(29) can be rearranged into (33) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathit{fm}}{v}_p^{2/3-2/D_f}{\left(v^{1/D_f}+{\overline{v}}^{1/D_f}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(33)

Substituting Equation (33)(33) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathit{fm}}{v}_p^{2/3-2/D_f}{\left(v^{1/D_f}+{\overline{v}}^{1/D_f}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(33) into Equation (31)(31) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left\{{\left(v+\overline{v}\right)}^k-v^k-{\overline{v}}^k\right\}\beta \left(v,\mathrm{}\overline{v}\right)n_2\left(v,\mathrm{}t\right)n_2\left(\overline{v},\mathrm{}t\right)dvd\overline{v}$$(31) and using Equations (4)–(6), we have the following for $k=$ 0 and 2: (34) $${\left.\frac{d{M}_0}{\mathit{dt}}\right|}_{\mathrm{coag}2}={\left.\frac{d{M}_0}{\mathit{dt}}\right|}_{\mathit{fm}2}=-{\xi }_2{K}_{\mathit{fm}}{M}_0^2{v}_p^{\frac{2}{3}-\frac{2}{D_f}}{v}_g^{\frac{2}{D_f}-\frac{1}{2}}{Z}^{\frac{2}{D_f^2}-\frac{1}{2D_f}+\frac{1}{8}}\left(Z^{\frac{1}{2D_f}}+2Z^{-\frac{1}{D_f^2}}+Z^{-\frac{1}{2D_f}}\right)$$(34) (35) $${\left.\frac{d{M}_2}{\mathit{dt}}\right|}_{\mathrm{coag}2}={\left.\frac{d{M}_2}{\mathit{dt}}\right|}_{\mathit{fm}2}=2{\xi }_2{K}_{\mathit{fm}}{M}_0^2{v}_p^{\frac{2}{3}-\frac{2}{D_f}}{v}_g^{\frac{2}{D_f}+\frac{3}{2}}{Z}^{\frac{2}{D_f^2}+\frac{3}{2D_f}+\frac{5}{8}}\left(Z^{\frac{1}{2D_f}}+2Z^{-\frac{1}{D_f^2}}+Z^{-\frac{1}{2D_f}}\right)=-2v_g^2{Z}^{\frac{2}{D_f}+\frac{1}{2}}{\left.\frac{d{M}_0}{\mathit{dt}}\right|}_{\mathit{fm}2}$$(35) where ${\xi }_2$ is a coefficient dependent on $\sigma$ and $D_f,$ as was presented in Table 1 of Park and Lee (2002, 85–91). Recently, Park (2018) approximated ${\xi }_2$ as a function of $\sigma$ and $D_f$ as the following: (36) $${\xi }_2=1-f\left(D_f\right)\exp \left(-2\sigma \right)+\left\{f\left(D_f\right)-\left(1-\frac{1}{\sqrt{2}}\right)\exp \left(2\right)\right\}\exp \left(-0.5{\sigma }^2-1.5\right)$$(36) where $f\left(D_f\right)=5.19-5.7D_f+0.864D_f^2.$

3.3.2.2. Continuum plus near-continuum regime

In the continuum plus near-continuum regime, the collision kernel is given as (Rogak and Flagan 1992, 203–224) (37) $${\beta }_{\mathrm{co}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathrm{co}}\left(d_c+\overline{d_c}\right)\left\{\frac{C\left(d_m\right)}{d_m}+\frac{C\left(\overline{d_m}\right)}{\overline{d_m}}\right\}$$(37) where $K_{\mathrm{co}}$ ($=2k_{B}T/3\mu$) is the collision coefficient in the continuum plus near-continuum regime, $\mu$ is the gas viscosity, d_m is the mobility-equivalent diameter, and C is the slip correction factor given by (Lee, Lee, and Han 1997, 486–492) (38) $$C\left(d_m\right)=1+1.591\frac{2\lambda }{d_m}$$(38) where $\lambda$ is the mean free path length of gas molecules.

It has been assumed in the continuum regime that both the mobility-equivalent and the collision diameters are proportional to $v^{1/D_f}$ (Mountain, Mulholland, and Baum 1986; Kaplan and Gentry 1988), as was expressed in Equation (32)(32) $$\frac{v}{v_p}={\left(\frac{d_c}{d_p}\right)}^{D_f}$$(32) . Thus the collision kernel is rewritten as follows: (39) $${\beta }_{\mathrm{co}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathrm{co}}\left(v^{1/D_f}+{\overline{v}}^{1/D_f}\right)\left\{\frac{1+B{v}_p^{1/D_f-1/3}{v}^{-1/D_f}}{v^{1/D_f}}+\frac{1+B{v}_p^{1/D_f-1/3}{\overline{v}}^{-1/D_f}}{{\overline{v}}^{1/D_f}}\right\}$$(39) where $B=1.591\lambda {\left(4\pi /3\right)}^{1/3}.$ Substituting Equation (39)(39) $${\beta }_{\mathrm{co}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathrm{co}}\left(v^{1/D_f}+{\overline{v}}^{1/D_f}\right)\left\{\frac{1+B{v}_p^{1/D_f-1/3}{v}^{-1/D_f}}{v^{1/D_f}}+\frac{1+B{v}_p^{1/D_f-1/3}{\overline{v}}^{-1/D_f}}{{\overline{v}}^{1/D_f}}\right\}$$(39) into Equation (31)(31) $${\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left\{{\left(v+\overline{v}\right)}^k-v^k-{\overline{v}}^k\right\}\beta \left(v,\mathrm{}\overline{v}\right)n_2\left(v,\mathrm{}t\right)n_2\left(\overline{v},\mathrm{}t\right)dvd\overline{v}$$(31) , we have the following for $k=$ 0 and 2: (40) $${\left.\frac{d{M}_0}{\mathit{dt}}\right|}_{\mathrm{coag}2}={\left.\frac{d{M}_0}{\mathit{dt}}\right|}_{\mathrm{co}2}=-K_{\mathrm{co}}{M}_0^2\left\{1+Z^{\frac{1}{D_f^2}}+B{v}_p^{\frac{1}{D_f}-\frac{1}{3}}{v}_g^{-\frac{1}{D_f}}{Z}^{\frac{1}{2D_f^2}}\left(1+Z^{\frac{2}{D_f^2}}\right)\right\}$$(40) (41) $${\left.\frac{d{M}_2}{\mathit{dt}}\right|}_{\mathrm{coag}2}={\left.\frac{d{M}_2}{\mathit{dt}}\right|}_{\mathrm{co}2}=2K_{\mathrm{co}}{M}_1^2\left\{1+Z^{\frac{1}{D_f^2}}+B{v}_p^{\frac{1}{D_f}-\frac{1}{3}}{v}_g^{-\frac{1}{D_f}}{Z}^{\frac{1}{2D_f^2}-\frac{1}{D_f}}\left(1+Z^{\frac{2}{D_f^2}}\right)\right\}$$(41)

3.3.2.3. Transition regime

In the transition regime we use the harmonic mean of each moment equation (Pratsinis 1988, 416–427): (42) $${\left.\frac{d{M}_k}{dt}\right|}_{\mathit{coag}2}=\frac{{\left.\frac{d{M}_k}{dt}\right|}_{\mathit{co}2}\times {\left.\frac{d{M}_k}{dt}\right|}_{\mathit{fm}2}}{{\left.\frac{d{M}_k}{dt}\right|}_{\mathit{co}2}+{\left.\frac{d{M}_k}{dt}\right|}_{\mathit{fm}2}}$$(42) which is valid for the entire particle size range.

3.3.3. Intermodal coagulation (coag12)

The coagulation between a nuclei particle of volume $v_1$ and an aggregate particle of volume $v$ results in the formation of an aggregate particle of volume $v+v_1.$ Therefore, the rates of change in $N_1,$ $M_1,$ $M_2,$ $N_p$ are given as the following: (43) $${\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}=-N_1{\int }_0^{\mathrm{\infty }}\beta \left(v_1,v\right)n_2\left(v,t\right)dv=-N_1{\mathrm{\Phi }}_1$$(43) (44) $${\left.\frac{d{M}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}=N_1{\int }_0^{\mathrm{\infty }}\left\{\left(v+v_1\right)-v\right\}\beta \left(v_1,v\right)n_2\left(v,t\right)dv=-v_1{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}$$(44) (45) $${\left.\frac{d{M}_2}{\mathit{dt}}\right|}_{\mathrm{coag}12}=N_1{\int }_0^{\mathrm{\infty }}\left\{{\left(v+v_1\right)}^2-v^2\right\}\beta \left(v_1,v\right)n_2\left(v,t\right)dv=2N_1{v}_1{\int }_0^{\mathrm{\infty }}v\beta \left(v_1,v\right)n_2\left(v,t\right)dv-v_1^2{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}=2N_1{v}_1{\mathrm{\Phi }}_2-v_1^2{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}$$(45) (46) $${\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{coag}12}=-{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}$$(46) where (47) $${\mathrm{\Phi }}_1={\int }_0^{\mathrm{\infty }}\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(47) (48) $${\mathrm{\Phi }}_2={\int }_0^{\mathrm{\infty }}v\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(48)

In order to evaluate the above two integrals, the same approach as that used for the intramodal coagulation in Mode 2 is used in the following subsections.

3.3.3.1. Free-molecule regime

In the case of intermodal coagulation, a spherical particle in the nuclei mode and a fractal aggregate collide. Therefore, Equation (29)(29) $${\beta }_{\mathit{fm}}\left(v,\mathrm{}\overline{v}\right)={\left(\frac{8\pi k_{B}T}{{\rho }_p}\right)}^{1/2}{\left(\frac{d_c}{2}+\frac{\overline{d_c}}{2}\right)}^2{\left(\frac{1}{v}+\frac{1}{\overline{v}}\right)}^{1/2}$$(29) becomes (49) $${\beta }_{\mathit{fm}}\left(v_1,v\right)=K_{\mathit{fm}}{\left(v_1^{1/3}+v_p^{1/3-1/D_f}{v}^{1/D_f}\right)}^2{\left(\frac{1}{v_1}+\frac{1}{v}\right)}^{1/2}\cong {\xi }_{12}{K}_{\mathit{fm}}{\left(v_1^{1/3}+v_p^{1/3-1/D_f}{v}^{1/D_f}\right)}^2\left(\frac{1}{v_1^{1/2}}+\frac{1}{v^{1/2}}\right)$$(49)

The factor ${\xi }_{12}$ was suggested by Jeong and Choi (2004, 1071–1090) as (50) $${\xi }_{12}=\frac{{\left(\frac{1}{v_1}+\frac{1}{v}\right)}^{1/2}}{\frac{1}{v_1^{1/2}}+\frac{1}{v^{1/2}}}\cong \frac{{\left(1+\gamma \right)}^{1/2}}{1+{\gamma }^{1/2}}$$(50)

Substituting Equation (49)(49) $${\beta }_{\mathit{fm}}\left(v_1,v\right)=K_{\mathit{fm}}{\left(v_1^{1/3}+v_p^{1/3-1/D_f}{v}^{1/D_f}\right)}^2{\left(\frac{1}{v_1}+\frac{1}{v}\right)}^{1/2}\cong {\xi }_{12}{K}_{\mathit{fm}}{\left(v_1^{1/3}+v_p^{1/3-1/D_f}{v}^{1/D_f}\right)}^2\left(\frac{1}{v_1^{1/2}}+\frac{1}{v^{1/2}}\right)$$(49) into Equations (47)(47) $${\mathrm{\Phi }}_1={\int }_0^{\mathrm{\infty }}\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(47) and (48)(48) $${\mathrm{\Phi }}_2={\int }_0^{\mathrm{\infty }}v\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(48) and using Equation (4)(4) $$M_k=M_0{\nu }_g^k{Z}^{k^2/2}$$(4) , we have the following: (51) $${\mathrm{\Phi }}_{1,\mathit{fm}}={\xi }_{12}{K}_{\mathit{fm}}{M}_0{v}_1^{\frac{1}{6}}\left\{1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{\frac{1}{8}}+2v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}{Z}^{\frac{1}{2D_f^2}}\left(1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{\frac{1}{8}-\frac{1}{2D_f}}\right)+v_1^{-\frac{2}{3}}{v}_p^{\frac{2}{3}-\frac{2}{D_f}}{v}_g^{\frac{2}{D_f}}{Z}^{\frac{2}{D_f^2}}\left(1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{\frac{1}{8}-\frac{1}{D_f}}\right)\right\}$$(51) (52) $${\mathrm{\Phi }}_{2,\mathit{fm}}={\xi }_{12}{K}_{\mathit{fm}}{M}_1{v}_1^{\frac{1}{6}}\left\{1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{-\frac{3}{8}}+2v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}{Z}^{\frac{1}{D_f}+\frac{1}{2D_f^2}}\left(1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{-\frac{3}{8}-\frac{1}{2D_f}}\right)+v_1^{-\frac{2}{3}}{v}_p^{\frac{2}{3}-\frac{2}{D_f}}{v}_g^{\frac{2}{D_f}}{Z}^{\frac{2}{D_f}+\frac{2}{D_f^2}}\left(1+v_1^{\frac{1}{2}}{v}_g^{-\frac{1}{2}}{Z}^{-\frac{3}{8}-\frac{1}{D_f}}\right)\right\}$$(52)

3.3.3.2. Continuum plus near-continuum regime

For the collision between a spherical particle in Mode 1 and a fractal aggregate in Mode 2, Equation (37)(37) $${\beta }_{\mathrm{co}}\left(v,\mathrm{}\overline{v}\right)=K_{\mathrm{co}}\left(d_c+\overline{d_c}\right)\left\{\frac{C\left(d_m\right)}{d_m}+\frac{C\left(\overline{d_m}\right)}{\overline{d_m}}\right\}$$(37) becomes (53) $${\beta }_{\mathit{co}}\left(v_1,v\right)=K_{\mathit{co}}\left(v_1^{1/3}{v}_p^{1/D_f-1/3}+v^{1/D_f}\right)\left(\frac{1+B{v}_1^{-1/3}}{v_1^{1/3}{v}_p^{1/D_f-1/3}}+\frac{1+B{v}_p^{1/D_f-1/3}{v}^{-1/D_f}}{v^{1/D_f}}\right)$$(53)

The substitution of Equation (53)(53) $${\beta }_{\mathit{co}}\left(v_1,v\right)=K_{\mathit{co}}\left(v_1^{1/3}{v}_p^{1/D_f-1/3}+v^{1/D_f}\right)\left(\frac{1+B{v}_1^{-1/3}}{v_1^{1/3}{v}_p^{1/D_f-1/3}}+\frac{1+B{v}_p^{1/D_f-1/3}{v}^{-1/D_f}}{v^{1/D_f}}\right)$$(53) into Equations (47)(47) $${\mathrm{\Phi }}_1={\int }_0^{\mathrm{\infty }}\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(47) and (48)(48) $${\mathrm{\Phi }}_2={\int }_0^{\mathrm{\infty }}v\beta \left(v_1,v\right)n_2\left(v,t\right)dv$$(48) yields the following: (54) $${\mathrm{\Phi }}_{1,\mathit{co}}=K_{\mathit{co}}{M}_0\left[2+B{v}_1^{-\frac{1}{3}}+B{v}_1^{\frac{1}{3}}{v}_p^{\frac{2}{D_f}-\frac{2}{3}}{v}_g^{-\frac{2}{D_f}}{Z}^{\frac{2}{D_f^2}}+Z^{\frac{1}{2D_f^2}}\left(1+B{v}_1^{-\frac{1}{3}}\right)\left\{v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}+{\left(v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}\right)}^{-1}\right\}\right]$$(54) (55) $${\mathrm{\Phi }}_{2,\mathit{co}}=K_{\mathit{co}}{M}_1\left[2+B{v}_1^{-\frac{1}{3}}+B{v}_1^{\frac{1}{3}}{v}_p^{\frac{2}{D_f}-\frac{2}{3}}{v}_g^{-\frac{2}{D_f}}{Z}^{-\frac{2}{D_f}+\frac{2}{D_f^2}}+Z^{\frac{1}{2D_f^2}}\left(1+B{v}_1^{-\frac{1}{3}}\right)\left\{v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}{Z}^{\frac{1}{D_f}}+{\left(v_1^{-\frac{1}{3}}{v}_p^{\frac{1}{3}-\frac{1}{D_f}}{v}_g^{\frac{1}{D_f}}{Z}^{\frac{1}{D_f}}\right)}^{-1}\right\}\right]$$(55)

3.3.3.3. Transition regime

In the transition regime we again use the harmonic mean of each moment equation: (56) $${\Phi }_1=\frac{{\Phi }_{1,\mathit{co}}\times {\Phi }_{1,\mathit{fm}}}{{\Phi }_{1,\mathit{co}}+{\Phi }_{1,\mathit{fm}}}$$(56) (57) $${\Phi }_2=\frac{{\Phi }_{2,\mathit{co}}\times {\Phi }_{2,\mathit{fm}}}{{\Phi }_{2,\mathit{co}}+{\Phi }_{2,\mathit{fm}}}$$(57) which are valid for the entire particle size range.

3.4. Sintering

Here we use the following two-sphere neck growth model of Koch and Friedlander (1990, 419–427) to predict the growth of primary particles by sintering of an aggregate particle: (58) $$\frac{\mathit{da}}{\mathit{dt}}=-\frac{1}{{\tau }_s}\left(a-a_f\right)$$(58) where $a$ is the surface area of the aggregate particle, $a_f$ is the surface area of the volume-equivalent sphere, and ${\tau }_s$ is the characteristic sintering time dependent on temperature and $d_p.$ Park and Rogak (2003, 947–960) derived the following equation from Equation (58)(58) $$\frac{\mathit{da}}{\mathit{dt}}=-\frac{1}{{\tau }_s}\left(a-a_f\right)$$(58) : (59) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{3}{{\tau }_s}\left(n_p-n_p^{2/3}\right)$$(59) where $n_p$ is the number of primary particles in the aggregate particle. In the sectional model that we use for the validation of the moment model, Equation (59)(59) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{3}{{\tau }_s}\left(n_p-n_p^{2/3}\right)$$(59) is used. In the moment model, however, Equation (59)(59) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{3}{{\tau }_s}\left(n_p-n_p^{2/3}\right)$$(59) must be modified so that the change of the total number of primary particles ($N_p$) can be deducted. We assume that Equation (59)(59) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{3}{{\tau }_s}\left(n_p-n_p^{2/3}\right)$$(59) holds for the average $n_p,$ i.e., $N_p/M_0.$ By replacing $n_p$ with $N_p/M_0$ in Equation (59)(59) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{3}{{\tau }_s}\left(n_p-n_p^{2/3}\right)$$(59) , we have (60) $${\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{sint}}=-\frac{3}{{\tau }_s}{N}_p\left\{1-{\left(\frac{M_0}{N_p}\right)}^{1/3}\right\}$$(60)

3.5. Condensational obliteration

Park and Rogak (2003, 947–960) derived the following equation for the primary particle growth due to condensational obliteration: (61) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{D_f}{v_p\left(3-D_f\right)}\left(1-n_p^{-1/D_f}\right)I\left(v\right)$$(61)

We assume that Equation (61)(61) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{D_f}{v_p\left(3-D_f\right)}\left(1-n_p^{-1/D_f}\right)I\left(v\right)$$(61) holds for the average $n_p$ ($=N_p/M_0$) and $v$ ($=M_1/M_0$). Substituting Equation (18)(18) $$I\left(v\right)=\frac{\mathit{dv}}{\mathit{dt}}=I_0{v}^m$$(18) into Equation (61)(61) $$\frac{d{n}_p}{\mathit{dt}}=-\frac{D_f}{v_p\left(3-D_f\right)}\left(1-n_p^{-1/D_f}\right)I\left(v\right)$$(61) and replacing $n_p$ and $v$ with $N_p/M_0$ and $M_1/M_0,$ respectively, we have (62) $${\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{obli}}=-\frac{D_f{I}_0{M}_0}{v_p\left(3-D_f\right)}{\left(\frac{M_1}{M_0}\right)}^m\left\{1-{\left(\frac{M_0}{N_p}\right)}^{1/D_f}\right\}$$(62)

3.6. Overall conservation equation

When the five mechanisms described above take place simultaneously, the overall conservation equations for the six dependent variables can be expressed as the following. (63) $$\frac{d{M}_k}{\mathit{dt}}={\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{surf}1}+{\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{surf}2}+{\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}1}+{\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}2}+{\left.\frac{d{M}_k}{\mathit{dt}}\right|}_{\mathrm{coag}12}$$(63) for $k$ = 0, 1, and 2 (64) $$\frac{d{N}_p}{\mathit{dt}}={\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{surf}1}+{\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{coag}1}+{\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{coag}12}+{\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{sint}}+{\left.\frac{d{N}_p}{\mathit{dt}}\right|}_{\mathrm{obli}}$$(64) (65) $$\frac{d{N}_1}{\mathit{dt}}={\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{nucl}}+{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{surf}1}+{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}1}+{\left.\frac{d{N}_1}{\mathit{dt}}\right|}_{\mathrm{coag}12}$$(65) (66) $$\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}={\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{nucl}}+{\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{surf}1}+{\left.\frac{d{N}_{\mathrm{vap}}}{\mathit{dt}}\right|}_{\mathrm{surf}2}$$(66)

4. Validation of FAMM

In this section, our new moment model FAMM is validated against a very accurate sectional aggregate model (SAM) of Park and Rogak (2003, 947–960; 2004, 1385–1404), as well as against available exact solutions or experimental results.

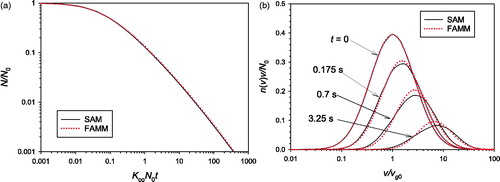
4.1. Coagulation of aggregate particles

Coagulation of aggregate particles was simulated by FAMM and SAM and the results are compared in Figure 1. $D_f=1.8$ and $d_p=0.01\mathrm{\mu }\mathrm{m}$ were assumed and $d_{g0}=0.1\mathrm{\mu }\mathrm{m},$ $N_0={10}^{15}\mathrm{}{\mathrm{m}}^{-3},$ and ${\sigma }_0=1.4$ were used as the initial condition. For the sectional model, 100 sections with the section spacing factor, which is the particle volume ratio between the neighboring sections, of 1.2 were used for sufficiently accurate calculation. The two models showed excellent agreement for the number concentration decay and reasonable agreement for the particle size distribution.

Figure 1. Comparison of the predictions of SAM and FAMM for the aggregate coagulation: (a) number concentration decay; (b) particle size distribution change.

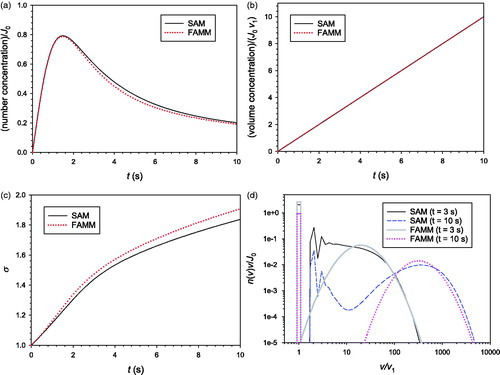
4.2. Surface growth of aggregate particles

Surface growth of aggregate particles was simulated by FAMM and SAM with two different values of $m.$ The same assumptions and initial conditions as those used for the coagulation were used here. The results obtained with $m=1$ and $m=2/3$ are compared in Figures 2 and 3, respectively. In many cases the surface growth rate of aerosol particles is proportional to the particle surface area, which corresponds to $m=1$ for aggregate particles with a uniform primary particle size and to $m=2/3$ for spherical particles. When the surface growth is the only ongoing mechanism, the exact solution of Equation (17)(17) $$\frac{\partial n\left(v,t\right)}{\partial t}={\left.\frac{\partial n\left(v,t\right)}{\partial t}\right|}_{\mathrm{surf}}=-\frac{\partial }{\partial v}\left\{I\left(v\right)n\left(v,t\right)\right\}$$(17) can be obtained using the method of characteristics for partial differential equations (see, for example, Seinfeld and Pandis 1998). In Figures 2 and 3 the solutions of FAMM and SAM are compared with the exact solution.

Figure 2. Comparison of the predictions of SAM and FAMM for the surface growth of aggregate particles with $m=1:$ (a) mass concentration; (b) $\sigma ;$ (c) $v_g;$ (d) particle size distribution.

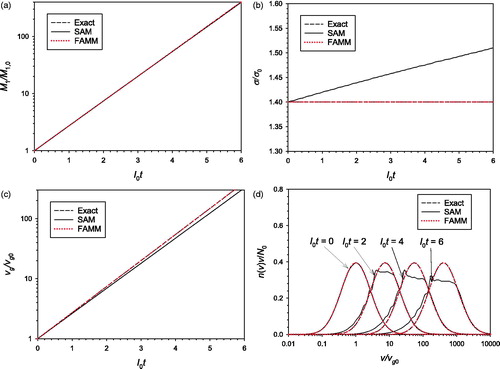
Figure 3. Comparison of the predictions of SAM and FAMM for the surface growth of aggregate particles with $m=2/3:$ (a) mass concentration; (b) $\sigma ;$ (c) $v_g;$ (d) particle size distribution.

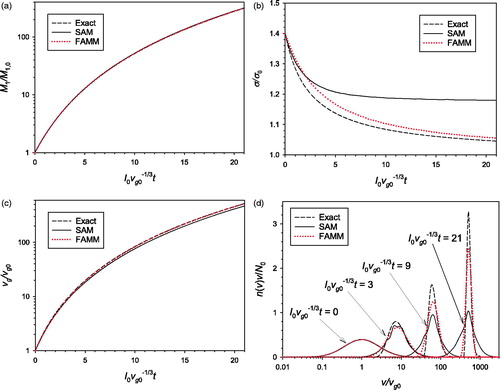
When $m=1$ (Figure 2), the LN particle volume distribution shape does not change except for the increase in the geometric mean particle volume as the particle growth rate is proportional to particle volume. Because the assumption of LN size distribution is valid throughout the whole simulation time, FAMM yields very accurate results. On the other hand, SAM suffers from significant numerical diffusion although the sectional model used in this study is known to be able to significantly reduce numerical diffusion compared with the conventional 2-point sectional model (Park and Rogak 2004, 1385–1404) and a very small section spacing factor 1.2 was used. While the total particle volume concentration is not affected by the numerical diffusion (Figure 2a), $\sigma$ is overpredicted (Figure 2b) resulting in the underprediction of $v_g$ (Figure 2c). It is also noted that spurious oscillations appears in the SAM-predicted particle size distribution (Figure 2d). This phenomenon stems from the nature of the 3-point scheme adopted in the SAM of Park and Rogak (2004, 1385–1404) to reduce the numerical diffusion.

As the accuracy of SAM increases indefinitely with decreasing section spacing factor, it is possible to obtain the SAM result very close to the exact solution by adopting an extremely small section spacing factor (and a very large number of sections). However, we did not do so because 1.2 is already a very small value compared to the normally used section spacing factor values (∼2) and because the strength of FAMM over SAM for surface growth simulation can be demonstrated effectively by using a reasonably small section spacing factor for SAM. Another way to enhance the accuracy of SAM is to use a more careful numerical method, such as the moving-sectional (Gelbard 1990, 399–412; Kim and Seinfeld 1990, 185-199) or the moving-center (Jacobson 1997, 131–144) methods. However, in these methods the representative size for each section is dependent on the growth rate, which can cause complications when applied to a multidimensional grid system.

When $m=2/3$ (Figure 3), the particle size distribution does not retain an LN shape during the surface growth, and hence, FAMM creates some error compared to the exact solution. Nevertheless, the error of FAMM is much smaller than that of SAM created owing to numerical diffusion. Based on the results shown in Figures 2 and 3, we conclude that FAMM can be superior to SAM, at least with the model parameters used in this study, in modeling surface growth.

4.3. Simultaneous nucleation and coagulation

Figure 4 compares the predictions of FAMM and SAM for the simultaneous nucleation and coagulation with a constant nucleation rate $J_0.$ Because coagulation does not alter the total particle mass and the particle mass created by nucleation is not affected by the aerosol model type, the mass concentrations predicted by the two models are identical (Figure 4b). Although FAMM appears to reasonably reproduce the bimodal nature of the particle size distribution (Figure 4d), it fails to model the particles existing between the two modes (e.g., dimer, trimer, etc.), which can account for a significant amount immediately after the nucleation burst. The neglect of these intermediate-sized particles in FAMM led to the overprediction of $\sigma$ (Figure 4c) and hence the underprediction of particle number (Figure 4a). Nevertheless, the overall agreement between FAMM and SAM appears reasonable.

Figure 4. Comparison of the predictions of SAM and FAMM for the simultaneous nucleation and coagulation: (a) number concentration; (b) mass concentration; (c) $\sigma ;$ (d) particle size distribution.

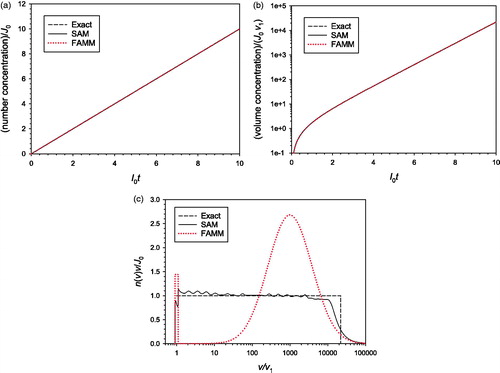
4.4. Simultaneous nucleation and surface growth

Simultaneous nucleation and surface growth with a constant nucleation rate $J_0$ was modeled using FAMM and SAM (Figure 5). Only the case of $m=1$ was tested because the exact solution exists for this case. FAMM, which assumes a bimodal distribution, clearly fails to predict accurately the change in particle size distribution in this case, although it predicts the total number and mass concentrations very accurately, because the particle size distribution is not bimodal but flat.

Figure 5. Comparison of the predictions of SAM and FAMM for the simultaneous nucleation and surface growth: (a) number concentration; (b) mass concentration; (c) particle size distribution.

4.5. Simultaneous nucleation, surface growth, and coagulation

The most realistic pathway of aerosol particle formation and growth is the simultaneous nucleation, surface growth, and coagulation. The synthesis of titania nanoparticles in a tubular flame aerosol reactor reported in Tsantilis et al. (2002, 21392156) was simulated using FAMM and SAM (Figure 6). According to the analysis of Tsantilis et al. (2002, 2139–2156), nucleation and surface growth ended before the first 0.04 cm and 0.4 cm, respectively, of the reactor. Detailed process conditions can be found in Tsantilis et al. (2002, 2139–2156). Contrary to the case of simultaneous nucleation and coagulation, the addition of surface growth led to a smaller $\sigma$ predicted by FAMM than that predicted by SAM (Figure 6c), probably owing to the numerical diffusion of SAM. The particle number and volume concentrations, geometric mean particle volume, and particle size distribution predicted by FAMM showed very good agreement with those predicted by SAM, demonstrating that FAMM is a reliable tool in modeling the particle formation and growth by simultaneous nucleation, surface growth, and coagulation.

Figure 6. Comparison of the predictions of SAM and FAMM for the flame synthesis of titania nanoparticles undergoing simultaneous nucleation, coagulation and surface growth (Tsantilis, Kammler, and Pratsinis 2002, 2139–2156): (a) number concentration; (b) mass concentration; (c) $\sigma ;$ (d) $v_g;$ (e) particle size distribution.

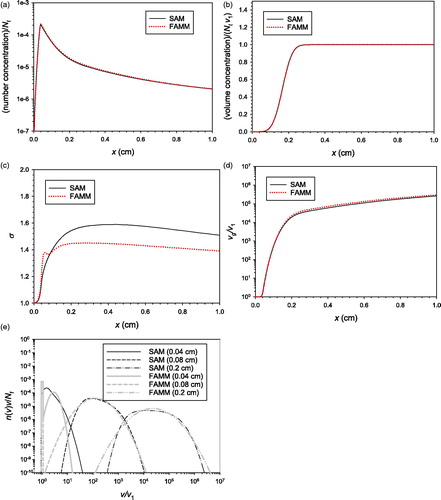
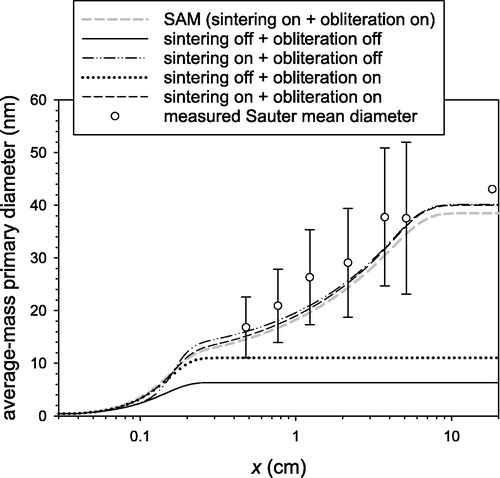
One of the strengths of FAMM is that it can model the growth of primary particles due to sintering and condensational obliteration. Figure 7 shows the primary particle diameter of average mass predicted by FAMM under different simulation conditions with sintering and obliteration switched on or off. The results are compared with the measured data (Tsantilis, Kammler, and Pratsinis 2002, 2139–2156) as well as with the prediction of SAM. The primary particle diameter measured by Tsantilis et al. (2002, 2139–2156) was the Sauter mean diameter representing the ratio between the mean particle volume and the mean particle surface area (=$\sum n{d}^3/\sum n{d}^2$), which is always larger than or equal to the diameter of average mass (=${\left(\sum n{d}^3/\sum n\right)}^{1/3}$). For example, for an LN particle size distribution with $\sigma =1.5,$ the Sauter mean diameter is 18% larger than the diameter of average mass. By considering the discrepancy between the Sauter mean diameter and the diameter of average mass and the uncertainty indicated by the error bars for the measurement, the prediction of FAMM shows excellent agreement not only with that of SAM but also with measured data when sintering was taken into account. When only obliteration was taken into account, the model considerably underestimated the primary diameter because surface growth ended relatively early in this experiment and thus the primary particle growth was dominated by sintering after $x=\sim 0.2$cm. Nevertheless, the predicted primary particle diameter with only obliteration switched on was significantly larger than that predicted with both sintering and obliteration switched off, implying that condensational obliteration can be an important primary particle growth mechanism where surface growth is the dominant aggregate growth pathway under appropriate conditions of precursor concentration and temperature (e.g., in soot particle growth).

Figure 7. Primary particle diameter of average mass predicted by FAMM compared with measured data and the SAM prediction.

5. Conclusions

A new numerical model capable of tracing the formation and growth of fractal aggregates in the course of simultaneous nucleation, surface growth, coagulation, sintering, and condensational obliteration in the framework of LNMM was developed. The new model can predict the changes in the bimodal size distribution and morphology of fractal aggregate particles by tracing five time-dependent variables (and an additional variable for the amount of gas precursor). A bimodal size distribution composed of a monodisperse nuclei mode for spherical nucleus particles with a fixed particle size and an LN accumulation mode for fractal aggregates was assumed. The new model showed good agreement with a more accurate sectional model and with available measured data, except for an imaginary case in which ceaseless nucleation and no coagulation were assumed.

Addendum

The code FAMM is an intellectual property of Sunchon National University (SCNU). Upon request (email to: Sung Hoon Park, [email protected]), the code will be provided for scientific and academic purposes with the approval of SCNU.

Additional information

Funding

This research was supported by the National Strategic Project–Fine particle of the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT), the Ministry of Environment (ME), and the Ministry of Health and Welfare (MOHW) (NRF-2017M3D8A1092022). This research was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2016R1D1A3A03916423).