High potential, near free molecular regime Coulombic collisions in aerosols and dusty plasmas

Abstract

Determination of the particle charge in aerosols and dusty plasmas requires an accurate calculation of the particle-ion collision kernel taking into account the particle-ion Coulombic coupling and ion-neutral gas molecule collisions. While the effect of Coulombic interactions of any strength is described accurately in the continuum limit and free molecular limit, an accurate physical description at intermediate collisional regimes remains elusive. Specifically, the Coulomb influenced collisions between oppositely charged particles and ions have evaded accurate theoretical description in the past. We use Langevin dynamics (LD) calculations to infer the non-dimensional collision kernel $H$ as a function of the electrostatic potential energy to thermal energy ratio ${\Psi }_E$ and the diffusive Knudsen number ${Kn}_D,$ the index of ion-neutral collisionality in a finite pressure system. The LD approach yields a simple, approximate treatment of particle charging in the entire ion-neutral collision regime under the assumption that $Z\equiv \frac{m_i}{m_g}\to \mathrm{\infty },$ where $m_i$ is the mass of an ion and $m_g$ is the mass of the background gas molecules. We show that the Gumbel distribution accurately describes the underlying distribution of $H$ calculated using LD. The effect of high ion concentrations (at which screening of particle by free charges in space is important) on $H$ is parameterized through a non-dimensional screening length parameter $S_D.$ Analysis of the dependence of the distribution parameters on ${\Psi }_E,\mathrm{ }{Kn}_D,$ and $S_D$ leads to a regression for $H$ that is valid for ${0<\Psi }_E\le 60$ and ${Kn}_D\le 2000$ plasmas. Inter-comparison of current model with select models from the literature shows that the current model and the model published by Gatti and Kortshagen (that assumes $Z\to 0$) yield similar predictions for a wide range of ${\Psi }_E,\mathrm{ }{Kn}_D,$ and $S_D.$

Copyright © 2019 American Association for Aerosol Research

Editor:

• Yannis Drossinos

Introduction

The electric charge of micro- and nanoparticles determines their long-range electrostatic interaction, electrical mobility, growth kinetics and collective behavior in aerosols and dusty plasmas. Determination of the particle charge distribution is necessary for the inversion of measured electrical mobility distribution to obtain particle size distribution (Hagen and Alofs 1983; Hogan et al. 2009) and for the description of size-resolved growth dynamics in aerosols (Gelbard, Tambour, and Seinfeld 1980; In Jeong and Choi 2001; McMurry 2000; Wu and Flagan 1988). In dusty plasmas characterized by highly charged particles suspended in a partially ionized gas, self-assembly of particles (or grains) over mesoscopic length scales has been observed in controlled experiments (Molotkov et al. 2015; Nefedov et al. 2003; Pustylnik et al. 2016) and natural contexts (interplanetary nebulae, planetary rings). These “Coulombic crystals” are formed due to long- and short-range interactions between particles, primarily determined by their electric charge and plasma conditions (ion, electron concentrations, and electric fields). In both aerosol and plasma science, determination of the electric charge on particles plays a pivotal role in the theoretical description of the spatial and temporal dynamics of particulate populations.

The particle charge in gas-phase systems (aerosols/dusty plasmas) can vary by a variety of mechanisms—ion and electron fluxes collected by the particles via collisions and charge transfer (Khrapak and Morfill 2009), photoionization (Han et al. 2003; Jiang et al. 2007; Yun et al. 2009), thermionic emission (Autricque et al. 2018) and photoelectron emission by UV radiation, chemical ionization and so on (Fortov et al. 2005). In this article, we focus on particle charging by collisions with ions driven by the combined electrostatic motion and Brownian diffusion in the gas phase and in the absence of external electric fields. In typical aerosol systems, ions of both polarities have similar masses (∼50–600 amu) and electrical mobilities ($\sim 2–10\times {10}^{-4}\mathrm{ }{\mathrm{m}}^2{\text{ s}}^{-1} {\mathrm{V}}^{-1}$). The particle charge varies nominally between ±20 in the sub-1 µm size range at atmospheric pressure (Gopalakrishnan, McMurry, and Hogan 2015; Gopalakrishnan, Meredith, et al. 2013; Wiedensohler 1988). Contrastingly, in non-thermal dusty plasmas, electrons are hotter than the positive ions ($k_B{T}_e\sim 1\mathrm{ }\mathrm{eV}\gg k_B{T}_i\sim 0.03\mathrm{ }\mathrm{eV}$) while the ions are equilibrated via collisions with neutral gas molecules ($k_B{T}_i\sim k_B{T}_g$) at a common temperature (Lieberman and Lichtenberg 2005). Further, electrons are also ∼10,000 times lighter than the ions that are typically derived from the ionization of the background gas molecules (${\mathrm{Ar}}^{+},\mathrm{ }{\mathrm{Ne}}^{+},\dots ).$ Thus, initially uncharged particles receive a higher electron current than ion current from the bulk plasma and rapidly attain a negative charge. The extent of the negative particle charge $z_p$ on the particle roughly scales with the electron temperature and particle size ($z_p\sim k_B{T}_e,\mathrm{ }{d}_p$). When the particle is sufficiently negatively charged, slow moving electrons are repelled causing a reduction in the electron current and thereby the ion flux eventually catches up with the electron flux leading to a stationary state charge on the particles. As a result, 0.1–10 µm particles carry $\sim {10}^2–{10}^4{e}^{-}$ units of negative charges in typical low pressure, non-thermal dusty plasmas, making the collisions between highly negatively charged particles and positive ions the dominant charge transfer process. In both types of particulate systems, the collisions between unlike charged entities (particle and ion) in a background gas are dominated by attractive Coulomb interactions and Brownian diffusion. We restrict our scope to the collisions between particles and ions at thermal equilibrium with the gas. Collisions between particles and non-equilibrium ions/electrons are beyond our scope here.

By virtue of their high negative charge level ($\sim {10}^2–{10}^4{e}^{-}$), grains/particles in a dusty plasma hold a finite number of positively charged ions in metastable orbits around them. These ions effectively shield the grain of its charge and the extent of screening is dependent on the ion concentration. While this effect is negligible at low ion concentrations (typical of atmospheric aerosols or low-strength bipolar neutralizers), high ion concentrations are routinely found in dusty plasmas, unipolar aerosol chargers, flames/plasmas generated for material synthesis, and cosmic environments (planetary nebulae, ionosphere, etc.). The charging of particles in high ion concentration environments where electrostatic screening of the particle is appreciable has been routinely considered by dusty plasma modelers (Khrapak and Morfill 2009). The screening of grains/particles by free charges in the gas phase leads to a non-trivial electrostatic potential around the particle that can be self-consistently calculated by simultaneously solving the ion and electronic concentration profile and the Poisson equation for the electrostatic potential (Bystrenko and Zagorodny 1999; Daugherty, Porteous, and Graves 1993; Khrapak and Morfill 2009). As an approximation, at low particle concentrations, the electrostatic potential around an isolated particle is often modeled using a Debye–Huckel potential that retards the classic $r^{-1}$ Coulomb potential exponentially with an effective Debye length ${\lambda }_D$ (Gatti and Kortshagen 2008; Lampe et al. 2003; Zobnin et al. 2008). The Debye screening length ${\lambda }_D\equiv {\left(\frac{{\epsilon }_{o{k}_B{T}_i}}{n_i{e}^2}\right)}^{1/2}$ is obtained from the linearization of the Poisson–Boltzmann equation to describe ion concentration and the electrostatic potential around the particle (Lieberman and Lichtenberg 2005). A screened Coulomb potential with a distance-dependent screening length has been recently shown to be a reasonable approximation for the electrostatic potential around a particle with strong particle-ion coupling (Semenov, Khrapak, and Thomas 2015). The continuous ion absorption and electron emission from the particle surface and ion flux conservation give rise to long range power-law asymptotes for the electrostatic potential around the particle. A bi-directional coupling between the particle surface electric potential (charge) and the ion and electron concentration near the particle using coupled Poisson–Boltzmann equation and species concentration equation has been used to infer the electrostatic potential (Daugherty et al. 1992; Fortov et al. 2005; Hutchinson and Patacchini 2007; Khrapak and Morfill 2009; Semenov, Khrapak, and Thomas 2015). The complex electrostatic potential deviates from a simple Coulomb form, especially at large particle-ion separations. However, in close proximities, although not entirely accurate, the modeling of the particle-ion electrostatic potential via a prescribed screened Coulomb potential allows physical insight into the effect of charge screening at high ion concentrations without much computational cost associated with simultaneously solving for the spatial ion concentration and the electrostatic potential around a particle. A complete analysis of particle charging taking into account the temporally changing, self-consistent electric potential and non-linear charge fluxes to the particle surface would require numerical calculations using diffusion-based approaches (Tarasov and Veshchunov 2018) or particle-in-cell (PIC) methods (Hutchinson and Patacchini 2007). In aerosol science, by virtue of relatively dilute ion concentrations and low charge levels ($\sim \pm 20$ units of charge), the charging of particles at high ion concentrations has been scarcely investigated experimentally (Adachi et al. 1989; Pui, Fruin, and McMurry 1988). The focus has largely been on the effect of image potential on the attachment of small ions onto aerosol particles due to electrostatic attraction. In addition to the thermal energy and electrostatic energy of the ion, charge screening due to excess space charge (ion) concentration also determines the particle charge distribution by reducing the effective charge on the particles and needs to be described accurately. In this article, we focus on electrostatic interactions between particle and ion due to a simple Coulomb potential in the presence of background gas molecules. Further theoretical development to include image potential interactions and other short-range interactions may be built upon using the approach and results described in this article.

The charging rate $R\mathrm{ }\left({\mathrm{m}}^{-3}{\mathrm{s}}^{-1}\right)$ of particles of a certain size per unit volume per unit time is calculated as the product of the particle concentration $n_p\mathrm{ }\left({\mathrm{m}}^{-3}\right),$ ion concentration $n_i\mathrm{ }\left({\mathrm{m}}^{-3}\right)$ and the particle-ion collision kernel ${\beta }_i\mathrm{ }\left({\mathrm{m}}^3{\mathrm{s}}^{-1}\right)$ that describes the particle-ion interaction: $R={\beta }_i{n}_p{n}_i.$ The unperturbed (positive/negative) ion concentration $n_i$ and particle concentration $n_p$ is obtained from Langmuir probe measurements (Hopkins and Graham 1986; Merlino 2007) or optical diagnostics (Melzer et al. 2018) in a dusty plasma (Bonitz, Henning, and Block 2010; Chaudhuri et al. 2011; Mann et al. 2011; Molotkov et al. 2015; Shukla and Eliasson 2009). In aerosol systems, condensation particle counters (CPCs) allow the direct measurement of particle concentration (Stolzenburg and McMurry 1991) and the ion concentration is obtained via electrometer measurements. Tandem ion mobility spectrometry-mass spectrometry (IMS-MS) techniques have been employed to obtain the mass-mobility distribution of charging ions as well (Gopalakrishnan, McMurry, and Hogan 2015; Maißer et al. 2015). The collision kernel ${\beta }_i$ encompasses the collision physics and is calculated from a suitable model of particle-ion collision in the presence of a background gas. Development of models for ${\beta }_i$ has been the subject of many prior investigations in the field of aerosol science and dusty plasmas. We begin by reviewing important theoretical developments with appropriate context to the respective field.

The orbital motion limited (OML) theory (Allen 1992; Mott-Smith and Langmuir 1926), based on the conservation of energy and angular momentum of an ion colliding with a particle, is widely used in the field of dusty plasmas to calculate the collision kernel ${\beta }_i.$ Ion-neutral collisions destroy conservation of these quantities and make OML inapplicable for particle charging in moderate and high-pressure dusty plasmas. ${\beta }_i$ (${\mathrm{m}}^3\mathrm{ }{\mathrm{s}}^{-1}$) is referred to as ion flux coefficient in the plasma literature and defined as the ratio of the ion current $I_i$ ($\mathrm{C}\mathrm{ }{\mathrm{s}}^{-1}$) collected by the particle to the ion concentration $n_i$ multiplied by the charge on an electron ($\mathrm{C}\mathrm{ }{\mathrm{m}}^{-3}$) (Khrapak and Morfill 2009; Morfill and Ivlev 2009; Shukla and Eliasson 2009). By construction, OML assumes transport of the charges to the particles without considering collisions with neutral background gas molecules via purely ballistic motion making it strictly applicable only in perfect vacuum (gas pressure → 0). The ions are assumed to have a Maxwell–Boltzmann distributed velocity in their approach towards the particle (Allen 1992). The application of OML theory to the calculation of (positive) ion currents collected by (negatively charged) particles in dusty plasmas leads to significant differences between the predicted and measured charge on the particles at pressures ∼10–1000 Pa. The most significant assumption of the OML theory that is not met in moderate pressure dusty plasmas is the neglect of ion-neutral gas molecule collisions. Ion trajectories around a particle are distorted by collisions with neutral gas molecules (Goree 1992). The neutrals scatter momentum and energy that destroys deterministic ion orbits and lead to a higher ion current than predicted by OML. This effect has been observed in many computational investigations (Gopalakrishnan and Hogan 2012; Hutchinson and Patacchini 2007; Vaulina, Repin, and Petrov 2006; Zobnin et al. 2000) and it is expected that the particle charge would be less negative than if the ion current were calculated using collision-less OML. The mean charge on the particles is seen to be about 2–4 times lower than the value predicted by OML. Fortov et al. (2004) report that the mean charge on 1.8 and 12.7 µm particles is nearly 4 times smaller than the predictions of OML in a RF neon discharge of frequency 100 MHz operated between 20 and 50 Pa. Ratynskaia et al. (2004) investigated the charging of 0.6 µm particles between 20 and 100 Pa and found that the charge is systematically lower than the OML prediction. They attribute the reduction in particle charge to ion-neutral collisions that increase ion collection by the particles. Khrapak et al. extended the pressure range to 150 Pa and remark that their measurements are systematically lower than OML predictions (Khrapak et al. 2005, 2012), reaffirming the over-prediction of particle charge (or under-prediction of the ion flux coefficient).

Analytic modeling has been undertaken to account for the ion-neutral gas molecule collisions in particle charging. The idea of dividing the space around a charged particle into two zones, a highly collisional outer zone in which ion transport can be described via a Fokker–Planck type diffusion equation and an inner zone of very low collisionality close to the particle wherein a vacuum picture can be applied, has led to several avatars of the flux matching model (Bricard 1962; D’Yachkov et al. 2007; Fuchs 1963; Hoppel and Frick 1986; Lopez-Yglesias and Flagan 2013; Lushnikov and Kulmala 2004; Marlow 1980). The continuum and ballistic fluxes are matched at the surface of a limiting sphere to idealize the transition from continuum transport of ions to a rarefied motion near the particle. This idealization of the ion motion to purely ballistic motion is in practice realized when the ion is much lighter compared to the background gas molecules, thereby making the model exact in the limit of the ratio $Z,$ comparing mass of the ion $m_i\mathrm{ }$to mass of the background gas molecules $m_g,$ approaching zero, i.e., $Z\equiv \frac{m_i}{m_g}\to 0.$ However, the increase in kinetic energy of the ion as it arrives at the surface of the limiting sphere, and within the limiting sphere due to the particle-ion attractive potential is not accounted for in this model (Filippov 1993; Gopalakrishnan and Hogan 2012; Gopalakrishnan, Thajudeen, et al. 2013; Ouyang, Gopalakrishnan, and Hogan 2012). Further, when the motion of the ion inside the limiting sphere was assumed collision-less, a first order correction was necessary to account for ion-neutral collisions (also referred to as resonant charge exchange collisions in the dusty plasma literature and three-body trapping in the aerosol science literature) and later it was recognized that higher order corrections may be necessary as well (Hoppel and Frick 1986). This model requires the estimation of the probability of ion capture by the particle while moving inside the limiting sphere making it dependent on free parameters such as the radius of the limiting sphere and the capture probability. In the field of aerosol science, the flux matching model by Fuchs (1963) has been tested against measured charge fractions (Adachi, Kousaka, and Okuyama 1985; Hussin et al. 1983; Porstendörfer et al. 1984; Reischl, Scheibel, and Porstendörfer 1983; Wiedensohler et al. 1986) and often free parameters in the model are chosen to force agreement with predictions (Reischl et al. 1996; Stober, Schleicher, and Burtscher 1991; Wiedensohler and Fissan 1988), thereby clouding the validity of the theory itself (Gopalakrishnan, McMurry, and Hogan 2015; Liu and Pui 1974).

Gatti and Kortshagen (2008) recognized that in order to scatter enough momentum for an ion to be eventually trapped by the particle, a very small number of collisions with neutrals is sufficient. Based on this idea, they proposed that the ion current can be calculated by accounting for just three types of transport: collision-less capture of ions that is described by the classical OML result (Allen 1992), the continuum or infinitely collisional limit (Fuchs 1964) and as an intermediate case—the capture of ions due to exactly one collision with a neutral in its approach towards the particle. Similar to the flux matching model, Gatti and Kortshagen’s model also implicitly assumes that the ion is much lighter than the background gas molecules, i.e., $Z\equiv \frac{m_i}{m_g}\to 0.$ They calculated the ion current as the sum of the current due to each of the three transport mechanisms weighted by their respective probabilities (Varney 1971) based on the ion mean free path relative to a “capture radius” $R_c$ and obtained excellent agreement with dusty plasma charging experiments cited before. They advanced the notion that the capture radius $R_c\mathrm{ }$calculated as the radial distance at which the ion’s mean kinetic energy $\frac{3}{2}{k}_B{T}_i\mathrm{ }$equals to the electrostatic potential energy $\left|e{\phi }_p\right|$ is the appropriate length scale for describing the particle-ion interaction (Lushnikov and Kulmala 2004): $\left|e{\phi }_p\left(R_c\right)\right|=\frac{3}{2}{k}_B{T}_i.$ At moderate gas pressures, an ion’s motion could still be influenced by multiple collisions with neutrals and an accurate book keeping of ion-neutral collisions is necessary to capture the enhancement in the ion current accurately.

Semi-empirical expressions have been proposed to fit the results of ab initio molecular dynamics (MD), PIC, and Langevin dynamics (LD) calculations of particle-ion collisions in the presence of background gas molecules (Gopalakrishnan and Hogan 2012; Hutchinson and Patacchini 2007; Iza and Lee 2006; Lampe et al. 2003; Lampe and Joyce 2015; Taccogna, Longo, and Capitelli 2003; Trunec et al. 2004; Vaulina, Repin, and Petrov 2006; Zobnin et al. 2000). Hutchinson and Patacchini (2007) derived an empirical fit to the ion current obtained from PIC calculations for a wide range of gas pressures or ion-neutral collisionalities including interactions between ions and electrons. They show good agreement with the calculations by Lampe et al. (2003) in which the presence of neutrals is accounted for by solving ion-neutral collision integrals. Zobnin et al. (2008) solved the Boltzmann equation with a constant ion-neutral collision frequency and developed a fit to their results across a wide range of collisionalities. Their fit also converges to the OML limit as collision frequency → 0 and to the current calculated by continuum models (Yaroshenko et al. 2004) that take into account ion drift and diffusion at high gas pressures (i.e., strongly collisional plasma). It must be noted that approaches based on solutions to various approximations of the Boltzmann equation implicitly or explicitly assume that the ions are much lighter than the background gas $\left(Z\equiv \frac{m_i}{m_g}\to 0\right).$

Vaulina, Repin, and Petrov (2006) pioneered the application of LD, that implicitly accounts for ion-neutral collisions via the drag force on the ion due to neutrals and the rapidly fluctuating impulses in ion velocity and position due to Brownian diffusion in addition to electrostatic interactions, to compute the steady state charge on a non-emitting grain immersed in a non-thermal dusty plasma. They probed the effect of electron temperature, grain size and charge concentration and produced a simple parameterization for the mean charge (average potential) of the particle. They showed that LD greatly simplifies the determination of particle charge and ion current received by the particle for a wide range of ion-neutral collisionalities. The expression for the ion current put forward by Vaulina, Repin, and Petrov (2006) from theoretical considerations was tested against the predictions of LD calculations of the mean charge on a non-emitting dust grain immersed in a non-thermal dusty plasma. Contrastingly, by analyzing LD calculations of the particle-ion collision time in the dilute limit ($n_i^{-1/3}\to \mathrm{\infty }$), Gopalakrishnan and Hogan (2012) have proposed a model for the particle-ion collision kernel ${\beta }_i.$ The inverse of the non-dimensional particle-ion collision time in a periodic domain was interpreted as a non-dimensional collision kernel ${\beta }_i$ (which is elaborated upon shortly and referred to as $H$). Both Vaulina, Repin, and Petrov (2006) and Gopalakrishnan and Hogan (2012) have used LD to infer ${\beta }_i$ by considering particle-ion collisions. The simulations of Vaulina, Repin, and Petrov (2006) allowed the particle charge to equilibrate in the presence of positive ion and electron collisions without considering ion-ion, ion-electron or electron-electron interactions. Gopalakrishnan and Hogan (2012) took a similar approach in which only particle-ion interactions were considered along with the effect of neutrals using the Langevin equation. As will be discussed later, these models yield similar predictions for a wide range of particle-ion collision parameters. The Langevin-inferred $H$ is accurate in the limit of the ratio $Z,$ comparing mass of the ion $m_i\mathrm{ }$to mass of the background gas molecules $m_g,$ approaching infinity, i.e., $Z\equiv \frac{m_i}{m_g}\to \mathrm{\infty }.$ The LD approach provides an approximate treatment for the collision kernel in the entire transition regime and has been applied to derive an expression for the collision kernel that describes coagulation (Gopalakrishnan and Hogan 2011; Thajudeen, Gopalakrishnan, and Hogan 2012), vapor condensation (Gopalakrishnan, Thajudeen, and Hogan 2011; Ouyang, Gopalakrishnan, and Hogan 2012), and unipolar charging (Gopalakrishnan, Thajudeen, et al. 2013) of arbitrarily shaped particles. Gopalakrishnan and Hogan (2012) laid out a phase space diagram of ion-neutral gas molecule collisionality (parameterized by a diffusive Knudsen number ${Kn}_D$) and particle-ion electrostatic energy (parameterized by an electrostatic potential to thermal energy ratio of the ion ${\Psi }_E,$ ${\Psi }_E>0$ for attractive Coulombic interactions). ${Kn}_D$ is defined as the ratio of the average distance traveled by the ion before it completely changes direction, i.e., the mean persistence distance of the ion motion relative to the particle size. At high pressures, the particle-ion motion is dominated by Brownian diffusion and results in small persistence distances (${Kn}_D\to 0).$ At low pressures, the ion motion is nearly ballistic and is dominated by inertial effects (${Kn}_D\to \mathrm{\infty }).$ ${Kn}_D,$ by definition, is an index of the collisionality or collision frequency between ions and neutral gas molecules and is used to parameterize the effect of ion-neutral collisions on the ion transport onto the surface of the particle (and lead to particle charging). We note that, in the plasma literature the ion collisionality index is usually defined as the ratio of the ion mean free path to the plasma screening length. Our definition of ${Kn}_D$ parameterizes the ion-neutral collisionality in comparison to the particle size as a length scale. Likewise, particle-ion interactions dominated by thermal energy or absence of any electrostatic interaction corresponds to low ${\Psi }_E$ while interaction between highly charged particles and ions lead to high values of ${\Psi }_E.$ Gopalakrishnan and Hogan (2012) developed models for the non-dimensional collision kernel $H$ for the cases of hard spheres interactions (${\Psi }_E<0.5$ and all ${Kn}_D$), high potential near continuum regime (large ${\Psi }_E$ and small ${Kn}_D$) and repulsive interactions (${\Psi }_E<0$ and all ${Kn}_D$). The high potential, near free molecular regime (large ${\Psi }_E$ and large ${Kn}_D$), was not parameterized in their model development as they were not able to derive a model that converged to the correct free molecular (or OML limit) as ion-neutral collisionality approaches zero (or ${Kn}_D\to \mathrm{\infty }).$ The charging of sub-20 nm particles at atmospheric pressure, charging of ∼1 µm particles in a ∼100 Pa dusty plasma are a few instances wherein the collision between particles and ion leads to a ${Kn}_D$> 100 and ${\Psi }_E>30.$ In this article, we develop a model for ${\beta }_i$ for a wide range of ion-neutral collisionalities and particle-ion coupling strengths, especially those corresponding to the high potential, near free-molecular charging regime. In contrast with prior work on the use of LD to develop collision kernel expressions, our approach here consists of parameterizing the underlying distribution of particle-ion collision times inferred from LD. A description of the underlying distribution and its dependence on ${Kn}_D,\mathrm{ }{\Psi }_E$ allows the calculation of ${\beta }_i$ as a function of properties of the colliding particle and ion. We develop approximate, easy-to-use expressions for the flux coefficient ${\beta }_i$ for both Coulomb and screened Coulomb (also known as retarded Coulomb or Debye–Huckel) potentials for $0<{\Psi }_E\le 60$ and ${Kn}_D\le 2000.$

Computational methods

Theoretical analysis of Coulombic particle-ion collisions

We consider a spherical particle of radius $a_p,$ charge $z_p$ and a point ion of mass $m_i,$ charge $z_i,$ and friction factor $f_i$ (related to the low-field ion mobility ${\mu }_i=\frac{z_{i}e}{f_i}$ and diffusion coefficient $D_i$= $\frac{k_B{T}_i}{f_i}$) in the presence of neutral gas molecules that are in thermal equilibrium with the ions at a common temperature ${k_{B}T}_i.$ The particle and ion interact through the classical Coulomb potential $\phi \left(\overrightarrow{r}\right)=\frac{z_p{z}_i{e}^2}{4\pi {\epsilon }_{o}r}$ and in dilute conditions (Debye length ${\lambda }_D\to \mathrm{\infty }$). By choosing the particle radius $a_p$ as the length scale of the particle-ion Coulomb coupling, the relative importance of the particle-ion electrostatic potential energy to the ion’s thermal energy is parameterized by ${\Psi }_E=-\frac{z_p{z}_i{e}^2}{4\pi {\epsilon }_o{a}_p{k_{B}T}_i}.$ In the continuum or infinitely collisional limit of ion motion, continuum modeling has been employed to derive ${\beta }_i$ in the presence of Brownian diffusion and electrostatic drift of point-like ions towards a large, spherical particle. In this regime, ${\beta }_i$ is given by the classic Smoluchowski equation that depends on the ion friction factor $f_i,$ particle radius $a_p,$ and an enhancement factor ${\eta }_c\left({\Psi }_E\right):$ (1a) $${\beta }_i=4\pi \frac{{k_{B}T}_i}{f_i}{a}_p{\eta }_c\left({\Psi }_E\right).$$(1a)

The enhancement factor ${\eta }_c\left({\Psi }_E\right)$ can be evaluated using the Fuchs integral (Friedlander 2000; Fuchs 1963) for the Coulomb potential $\phi \left(\overrightarrow{r}\right)=\frac{z_p{z}_i{e}^2}{4\pi {\epsilon }_{o}r}$ as: (1b) $${\eta }_c\left({\Psi }_E\right)=\frac{{\Psi }_E}{1-\exp \left(-{\Psi }_E\right)}.$$(1b)

In the collision-less or free molecular limit, methods of kinetic theory of gases have been applied to derive a model for ${\beta }_i$ assuming that the ions start far away from the particle with a Maxwell–Boltzmann distributed velocity and do not suffer any collisions with neutrals until they are collected by the particle. ${\beta }_i$ is dependent on the mean thermal speed of the ion and the effective free molecular particle-ion collision cross section. Analogous to the continuum enhancement factor, a free molecular enhancement factor ${\eta }_f\left({\Psi }_E\right)$ is used to account for the electrostatic potential: (2a) $${\beta }_i={\left(\frac{8{k_{B}T}_i}{\pi m_i}\right)}^{\frac{1}{2}}\pi a_p^2{\eta }_f\left({\Psi }_E\right).$$(2a)

By considering the conservation of angular momentum and kinetic energy of the ions, an expression for the free molecular enhancement factor is derived as (Allen 1992; Mott-Smith and Langmuir 1926): (2b) $${\eta }_f\left({\Psi }_E\right)=\left\{\begin{array}{c}1+{\Psi }_E, {\Psi }_E\ge 0\\ \exp \left({\Psi }_E\right), {\Psi }_E\le 0\end{array}\right..$$(2b)

The LD calculation of ${\beta }_i$

Equations (1) and (2) describe the continuum (infinitely collisional) and free molecular (collision-less) limits of ${\beta }_i$ respectively and offer an important physical insight. The continuum limit depends only on the ion’s diffusivity (or friction factor $f_i$) while the free molecular limit depends only on the ion’s inertia (mass $m_i$), while both limits depend on the particle size $a_p,$ gas temperature ${k_{B}T}_i,$ and the particle-ion electrostatic energy ratio ${\Psi }_E.$ At intermediate pressures or collisionalities, ${\beta }_i$ depends only on the parameters that affect it in continuum and free molecular limits. In such instances, the ion motion is neither entirely diffusive nor ballistic to be accurately described by continuum or kinetic approaches (Gopalakrishnan and Hogan 2012). For such circumstances, a Langevin description of ion motion has been successfully employed in the past to derive approximate collision rate coefficients or kernels, and to predict the dilute transport of species in a background gas (Gopalakrishnan and Hogan 2011; Narsimhan and Ruckenstein 1985). The Langevin treatment is strictly applicable only in instances wherein the ratio of the mass of the ion $m_i$ to the mass of the background gas molecules $m_g$ approaches infinity, i.e., $Z\equiv \frac{m_i}{m_g}\to \mathrm{\infty }$ (Mazur and Oppenheim 1970). In practice, $Z\sim 2-10$ for ions found in typical aerosol charging environments with typical mass of positive ions ∼100 g/mole and negative ions ∼50 g/mole (Adachi, Kousaka, and Okuyama 1985; Gopalakrishnan, McMurry, and Hogan 2015; Maißer et al. 2015) in air or nitrogen. In non-thermal dusty plasmas, $Z=1$ for ${\mathrm{Ar}}^{+}$ or simple ions formed by the direct ionization of the discharge gas. In the continuum regime, it is known that continuum based approaches ($Z=\mathrm{\infty }$) and approximations to the Boltzmann equation (that assume $Z=0)$ yield identical expressions for the collision kernel (Veshchunov 2010, 2011; Veshchunov 2012; Veshchunov and Azarov 2012). The influence of $Z$ on the electrostatically influenced diffusion of ions to the particle surface in the transition and free molecular transport regimes remain hitherto unexplored. However, the effect of $Z$ and ion-neutral collisions can be indirectly inferred by comparing the predictions of transition regime collision kernel expressions derived under drastically different assumptions of $Z$ and computational approaches. Gopalakrishnan and Hogan (2011) compared, for hard sphere interactions between two spheres and a sphere and a point mass, the predictions of several collision kernel expressions that assume $Z\to \mathrm{\infty }$ or $Z\to 0$ in their construction. LD (Gopalakrishnan and Hogan 2011), diffusion theory (Veshchunov 2010) and other approaches (Dahneke 1983; Fuchs 1964) that assume $Z\to \mathrm{\infty }$ yield predictions that are neither systematically different nor differ more than $\pm 5\mathrm{\%}$ from the predictions of the models derived by solving the Boltzmann equation to model vapor transport to an absorbing particle with $Z\to 0$ (Fuchs and Sutugin 1970; Loyalka 1982). Although this comparison was made for hard sphere interactions, it is instructive that the influence of $Z$ on the collision kernel is presumably no larger than the statistical variation associated with LD computations. Clearly, further work is necessary to clarify the role of $Z$ further and that if the collision kernel is a stronger function of $Z$ as $Z\to 0$ and in the presence of potential interactions. The charging of particles by ions in non-thermal dusty plasmas are typically due to ions that are of the same mass of the background gas molecules (for example, ${\mathrm{Ar}}^{+}$ in $\mathrm{Ar}$ leading to $Z=1$). In aerosol systems, heavier bipolar charging ions lead to $Z>2.$ The charging by electron collisions or ions lighter than the background gas, for which $Z<1,$ is beyond the scope of the modeling here. Due to the lack of a significant difference between the predictions of collision kernels that assume $Z\to 0$ and $Z\to \mathrm{\infty }$ in prior work, we use the Langevin equation to describe the particle-ion collision in the frame of reference of the particle to describe particle charging in the $Z\to \mathrm{\infty }$ limit. A rigorous treatment of ion transport onto the surface of a charge particle suspended in a background gas should be treated via the Boltzmann equation. This fact notwithstanding, the Langevin description applied here is later justified by qualitative and reasonable quantitative agreement between Langevin-inferred $H$ (assuming $Z\to \mathrm{\infty }$) and the predictions of models that assume $Z\to 0$ in a posteriori comparison: (3) $$m_i\frac{d\overrightarrow{v}}{\mathit{dt}}=-f_i\overrightarrow{v}+{\overrightarrow{F}}_o+\overrightarrow{X}\left(t\right).$$(3)

Here, $\overrightarrow{v}$ is the relative velocity of the ion with respect to the particle, ${\overrightarrow{F}}_o$ is the sum of all external forces on the ion and $\overrightarrow{X}\left(t\right)$ is a fluctuating impulse force term used to model the thermal diffusion of the ion (Chandrasekhar 1943). To scale the equations and express them in physically significant units, length is expressed in multiples of the particle radius $a_p,$ time in terms of the ion relaxation time $\frac{m_i}{f_i}$ and $a_p\frac{f_i}{m_i}$ is identified as a reference velocity. By non-dimensionalizing the solution to Equation (3)(3) $$m_i\frac{d\overrightarrow{v}}{\mathit{dt}}=-f_i\overrightarrow{v}+{\overrightarrow{F}}_o+\overrightarrow{X}\left(t\right).$$(3) originally derived by Ermak and Buckholz (1980), we track the ions in the space around the particle using an explicit equation for its non-dimensional velocity ${\overrightarrow{v}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)$ and position ${\overrightarrow{r}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right):$ (4a) $${\overrightarrow{v}}^{\mathrm{*}}\left(t^{\mathrm{*}}+\Delta t^{\mathrm{*}}\right)={\overrightarrow{v}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)\mathrm{e}\mathrm{xp}\left(-\Delta t^{\mathrm{*}}\right)+{\overrightarrow{F}}_o^{\mathrm{*}}\left(1-\exp \left(-\Delta t^{\mathrm{*}}\right)\right)+{\overrightarrow{A}}_1,$$(4a) (4b) $$〈A_1^2〉=3{Kn}_D^2\frac{{\eta }_f^2}{{\eta }_c^2}\left(1-\exp \left(-2\Delta t^{\mathrm{*}}\right)\right),$$(4b) (4c) $${\overrightarrow{r}}^{\mathrm{*}}\left(t^{\mathrm{*}}+\Delta t^{\mathrm{*}}\right)={\overrightarrow{r}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)+\left({\overrightarrow{v}}^{\mathrm{*}}\left(t^{\mathrm{*}}+\Delta t^{\mathrm{*}}\right)+{\overrightarrow{v}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)-2{\overrightarrow{F}}_o^{\mathrm{*}}\right)\left(\frac{1-\exp \left(-\Delta t^{\mathrm{*}}\right)}{1+\exp \left(-\Delta t^{\mathrm{*}}\right)}\right)+{\overrightarrow{F}}_o^{\mathrm{*}}\Delta t^{\mathrm{*}}+{\overrightarrow{A}}_2,$$(4c) (4d) $$〈A_2^2〉=6{Kn}_D^2\frac{{\eta }_f^2}{{\eta }_c^2}\left(\Delta t^{\mathrm{*}}-2\left(\frac{1-\exp \left(-\Delta t^{\mathrm{*}}\right)}{1+\exp \left(-\Delta t^{\mathrm{*}}\right)}\right)\right).$$(4d)

${\overrightarrow{A}}_1$ and ${\overrightarrow{A}}_2$ are normally distributed random displacement and velocity vectors that are added to the solution at each time step to capture the effect of Brownian fluctuations (Ermak and Buckholz 1980). ${\overrightarrow{A}}_1$ and ${\overrightarrow{A}}_2$ have a mean of zero and variances given by Equations (4b)(4b) $$〈A_1^2〉=3{Kn}_D^2\frac{{\eta }_f^2}{{\eta }_c^2}\left(1-\exp \left(-2\Delta t^{\mathrm{*}}\right)\right),$$(4b) and (4d)(4d) $$〈A_2^2〉=6{Kn}_D^2\frac{{\eta }_f^2}{{\eta }_c^2}\left(\Delta t^{\mathrm{*}}-2\left(\frac{1-\exp \left(-\Delta t^{\mathrm{*}}\right)}{1+\exp \left(-\Delta t^{\mathrm{*}}\right)}\right)\right).$$(4d) . Ermak and Buckholz (1980) solved Equation (3)(3) $$m_i\frac{d\overrightarrow{v}}{\mathit{dt}}=-f_i\overrightarrow{v}+{\overrightarrow{F}}_o+\overrightarrow{X}\left(t\right).$$(3) as a stochastic differential equation with vectors ${\overrightarrow{A}}_1$ and ${\overrightarrow{A}}_2$ added to the deterministic part of the solution to capture the thermal fluctuations in the velocity and position, respectively, due to ion-neutral gas molecule collisions. ${\overrightarrow{F}}_o^{\mathrm{*}}$ is the non-dimensional force acting on the ion and is an explicit function of the ion position ${\overrightarrow{r}}^{\mathrm{*}}\left(t^{\mathrm{*}}\right).$ For the case of unscreened Coulomb interaction between the particle and ion, ${\overrightarrow{F}}_o^{\mathrm{*}}{(Kn}_D,$ ${\Psi }_E)=-{\Psi }_E{Kn}_D^2\frac{{\eta }_f^2}{{\eta }_c^2}\frac{\widehat{r}}{{r^{\mathrm{*}}}^2}$ and ${\eta }_c,{\eta }_f$ are given by Equations (1b)(1b) $${\eta }_c\left({\Psi }_E\right)=\frac{{\Psi }_E}{1-\exp \left(-{\Psi }_E\right)}.$$(1b) , (2b)(2b) $${\eta }_f\left({\Psi }_E\right)=\left\{\begin{array}{c}1+{\Psi }_E, {\Psi }_E\ge 0\\ \exp \left({\Psi }_E\right), {\Psi }_E\le 0\end{array}\right..$$(2b) respectively. From the non-dimensionalization, we recognize that the ion’s motion depends on two dimensionless numbers—the potential energy ratio ${\Psi }_E$ and the diffusive Knudsen number ${Kn}_D,$ an index of ion-neutral collisionality: (5) $${Kn}_D=\frac{\sqrt{m_i{k}_B{T}_i}{\eta }_c}{f_i{a}_p{\eta }_f}.$$(5)

The expression for the diffusive Knudsen number ${Kn}_D,$ well established as a parameter in diffusion-limited mass transfer (Dahneke 1983; Loyalka 1976; Rogak and Flagan 1992), is a ratio of the mean ion persistence distance $\frac{\sqrt{m_i{k}_B{T}_i}}{f_i}$ and an effective length scale characterizing the particle-ion electrostatic interaction$\mathrm{ }\frac{a_p{\eta }_f}{{\eta }_c}.$ In the continuum (infinitely collisional) limit, the mean persistence path is much smaller than the length scale of the particle-ion interaction, i.e., ${Kn}_D\to 0.$ Likewise, ${Kn}_D\to \mathrm{\infty }$ denotes the free molecular (collision-less) limit of ion motion. Finally, we non-dimensionalize ${\beta }_i$ to derive $H=\frac{{\beta }_i{m}_i{\eta }_c}{f_i{a}_p^3{\eta }_f^2}.$ Normalizing Equations (1a)(1a) $${\beta }_i=4\pi \frac{{k_{B}T}_i}{f_i}{a}_p{\eta }_c\left({\Psi }_E\right).$$(1a) and (2a)(2a) $${\beta }_i={\left(\frac{8{k_{B}T}_i}{\pi m_i}\right)}^{\frac{1}{2}}\pi a_p^2{\eta }_f\left({\Psi }_E\right).$$(2a) yield the continuum and free-molecular limits for $H$ in ${Kn}_D$ space: (6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) (6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b)

At intermediate collisionalities, the non-dimensional collision kernel $H$ is a function of both ${Kn}_D$ and ${\Psi }_E$ and should converge to the limits given by Equation (6) at the respective limits of ${Kn}_D.$ To infer ${H(Kn}_D,$ ${\Psi }_E),$ we employ the rate constant calculation procedure developed by Hogan and coworkers (Gopalakrishnan and Hogan 2011; Gopalakrishnan and Hogan 2012; Gopalakrishnan, Thajudeen, and Hogan 2011; Ouyang, Gopalakrishnan, and Hogan 2012; Thajudeen, Gopalakrishnan, and Hogan 2012). Briefly, the ion is initialized on the surface of a sufficiently large periodic box ($500a_p–8000a_p$) with a velocity sampled from the Maxwell–Boltzmann distribution and tracked using Equation (4) until it collides with the particle $\left(r^{\mathrm{*}}=1\right)$ at the origin to obtain the collision time. The inverse of the mean binary particle-ion collision time $\tau$ normalized by the simulation box volume $L_{\mathrm{box}}^3$ is interpreted as $H$ based on statistically significant number (2000 here) of trials of the particle-ion collision: (7) $$H=\frac{L_{\mathrm{box}}^3}{\tau }\frac{{\eta }_c}{{\eta }_f^2}.$$(7)

The time step $\Delta t^{\mathrm{*}}$ is chosen by the empirical condition that compares the diffusional and electrostatic force to determine the optimum timestep for computational efficiency: $\Delta t^{\mathrm{*}}=0.005\frac{{r^{\mathrm{*}}}^2}{{Kn}_D^2}\min \left(1,\frac{{\eta }_c^2}{{\Psi }_E{\eta }_f^2}\right).$ The effect of the parameter 0.005 was empirically tested and chosen to balance computational accuracy and expense. The domain size was chosen as large as necessary to ensure that the ion started in conditions where its electrostatic potential energy is approximately zero. The following condition was used to determine $L_{\mathrm{box}}$ for each ${\Psi }_E:$ $L_{\mathrm{box}}=\max \left(500,\mathrm{ }\frac{400}{3}{\Psi }_E\right).$

${H(Kn}_D,$ ${\Psi }_E)\mathrm{ }$model development for Coulombic collisions

For ${\Psi }_E=0$ (hard-sphere interactions), prior work (Gopalakrishnan and Hogan 2011) has shown that $H$ has the following functional form valid for all ${Kn}_D$ and converges to the limits of Equations (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) and (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) : (8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8)

Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) also describes $H$ including the effect of short-range, singular contact potentials (Ouyang, Gopalakrishnan, and Hogan 2012), and repulsive Coulombic $\left({\Psi }_E<0\right)$ potential (Gopalakrishnan and Hogan 2012; Gopalakrishnan, Thajudeen, et al. 2013) when the appropriate enhancement factors ${\eta }_c$ and ${\eta }_f$ are calculated for the respective potentials and used in the definition of ${Kn}_D$ and $H.$ For each ${Kn}_D$ and ${\Psi }_E,$ 2000 independent trials of the particle-ion collision were simulated to build a histogram for $w=\log \left(\frac{H\left({Kn}_D,{\Psi }_E\right)}{H_{\mathit{HS}}\left({Kn}_D\right)}\right).$ Here, $H$ is calculated based on the particle-ion collision time for an individual trial (1$,\mathrm{ }2,\mathrm{ }3,\mathrm{ }\dots ,2000).$ $w$ is the logarithm of the enhancement in $H$ at a given ${Kn}_D$ due to ${\Psi }_E$ compared to the corresponding hard sphere value $H_{\mathit{HS}}\left({Kn}_D\right)$ predicted by Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) . 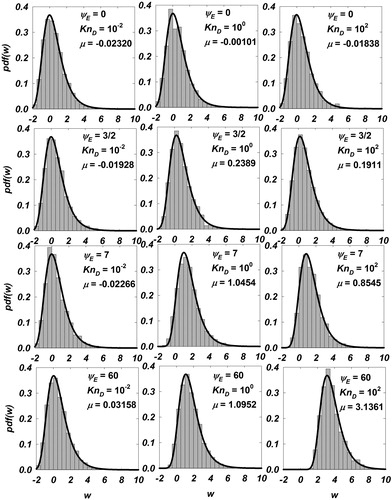Figure 1 shows the normalized frequency histogram of $w$ for ${\Psi }_E=0,\mathrm{ }\frac{3}{2},\mathrm{ }7,\mathrm{ }60$ at high $({Kn}_D={10}^{-2}$), intermediate (${Kn}_D={10}^0)\mathrm{ }$and low (${{Kn}_D=10}^2)$ collisionalities. It is seen that the distributions are translated along the abscissa as ${\Psi }_E$ and ${Kn}_D$ are varied, with their shape and magnitude intact. A Gumbel distribution (Coles 2001) with one location parameter $\mu$ is found to describe the probability density function $\mathit{pdf}\left(w\right)$ with high statistical confidence (regression details in Section S1 of the online supplementary information [SI]): (9) $$\mathrm{pdf}\left(w\right)=e^{-(w-\mu )}{e}^{-e^{-(w-\mu )}}.$$(9)

Figure 1. Histograms of $w$ inferred from Langevin simulations are shown for ${\Psi }_E=0,\mathrm{ }\frac{3}{2},\mathrm{ }7,\mathrm{ }60\mathrm{ }$for ${Kn}_D={10}^{-2},\mathrm{ }{10}^0,\mathrm{ }{10}^2.$ The gray bars represent the normalized counts $\mathrm{pdf}\left(w\right)$ of $w=\log \left(\frac{H\left({Kn}_D,{\Psi }_E\right)}{H_{HS}\left({Kn}_D\right)}\right)$ and the solid black line is the Gumbel distribution function (Equation (9)(9) $$\mathrm{pdf}\left(w\right)=e^{-(w-\mu )}{e}^{-e^{-(w-\mu )}}.$$(9) ) with the corresponding value of location parameter $\mu$ fitted for each case.

The Langevin simulation is a means to sample $H$ from an ensemble of infinite trajectories. The periodic domain restricts the sampling of $H$’s that represent the minimums from a possible infinite sequence of ion trajectories that also includes those in which the ion spends a long time away from the particle but are eliminated in the computer experiments. According to the Fisher–Tippett–Gnedenko theorem (Gnedenko 1948), these $H$ values, the minimums of infinite sequences of $H,$ follow the Gumbel distribution which is a special case of the generalized extreme value distribution (Coles 2001). Using $\mathrm{pdf}\left(w\right)$ of Equation (9)(9) $$\mathrm{pdf}\left(w\right)=e^{-(w-\mu )}{e}^{-e^{-(w-\mu )}}.$$(9) , $H$ can be computed through the mean value of $w:$ (10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10)

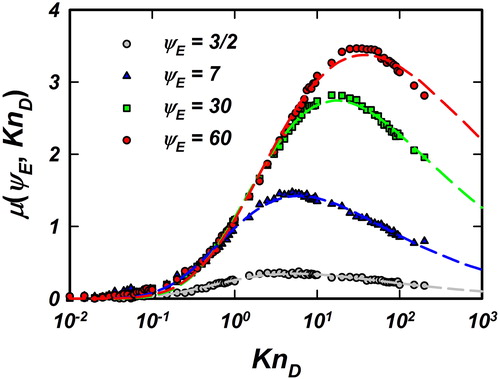
To use Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) for a given combination of ${Kn}_D$ and ${\Psi }_E,$ we fit $\mathrm{\mu }$ as a functional form. Figure 2 shows $\mathrm{\mu }$ for ${Kn}_D={10}^{-2}-2000$ and ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,60.$ A function with four fit constants $A,\mathrm{ }B,C,\mathrm{ }k$ accurately fits the data: (11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11)

Figure 2. Fitted values of the location parameter $\mu$ for ${\Psi }_E=\frac{3}{2},7,\mathrm{ }30,\mathrm{ }60$ for ${Kn}_D={10}^{-2}-2000$ shown as data points. The corresponding fit for $\mu$ (Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) ) is shown as dashed lines of the same color.

Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) captures the dependence of $\mu$ for $0<{\Psi }_E\le 60,\mathrm{ }{Kn}_D\le 2000$ and approaches 0 as ${Kn}_D\to 0$ and ${Kn}_D\to \mathrm{\infty }$ ensuring that $H\left({Kn}_D,{\Psi }_E\right)$ converges to the limits of Equation (6). Regression fit for $A,\mathrm{ }B,C,\mathrm{ }k$ are described in Section S2, SI. Thus, Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) can be used with Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) to predict $H$ for $0<{\Psi }_E\le 60,\mathrm{ }{Kn}_D\le 2000.$

In Figure 3a, $H$ calculated using the mean collision time for 2000 collisions (Equation (7)(7) $$H=\frac{L_{\mathrm{box}}^3}{\tau }\frac{{\eta }_c}{{\eta }_f^2}.$$(7) ) for ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,\mathrm{ }60$ are plotted as a function of ${Kn}_D.$ Also shown on the plots are the continuum limit (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and free-molecular limit (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ). The model developed in this article (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) with appropriate value of ${\Psi }_E$) is presented to show the comparison with the Langevin-inferred $H.$ Using Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) in (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) , dashed curves corresponding to each ${\Psi }_E$ were generated and compared against the Langevin-inferred $H$ (Equation (7)(7) $$H=\frac{L_{\mathrm{box}}^3}{\tau }\frac{{\eta }_c}{{\eta }_f^2}.$$(7) ) to calculate the % difference as $\frac{H_{\mathrm{eq}.10}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}.$ This comparison is plotted in Figure 3b for each case of ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,\mathrm{ }60.$ Immediately evident is that the model describes the Langevin-inferred $H$ to within $\pm 10\mathrm{\%}$ accuracy for most data points, with few data points within $\pm 15\mathrm{\%}.$ More importantly, the model of Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) is designed to approach the free molecular limit (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ), which has been the deficiency of the prior work on this topic by Gopalakrishnan and Hogan (2012). Figure S3a and b presents additional simulation results corresponding to ${\Psi }_E=3–50$ with differences between $\pm 10\mathrm{\%}$ for all the cases of ${Kn}_D$ and ${\Psi }_E$ examined here. The high ${\Psi }_E,$ high ${Kn}_D$ particle-ion collisions are the most challenging to model and expensive to compute. Physically, these cases represent highly charged particles at low pressure/temperature such as those in dusty plasmas. They also correspond to sub-10 nm particles at atmospheric pressures typical of aerosol systems. Thus, we have parameterized the Coulombic collisions between particles and ion in the low ion concentration limit and for intermediate ion-neutral collisionalities, i.e., ${Kn}_D$ is neither low nor high enough to be described by continuum or free molecular approaches. Coulombic collisions in the presence of neutrals are further used as a limiting case to examine the effect of particle charge screening due to high ion concentrations.

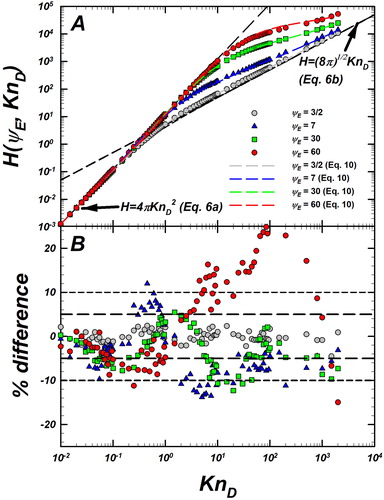
Figure 3. (a) Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and prediction of Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) (dashed lines with the same color as the symbols) are plotted as a function of ${Kn}_D$ for ${\Psi }_E=\frac{3}{2},7,\mathrm{ }30,\mathrm{ }60.$ Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collisionless (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as black dashed lines. (b) Plot showing the % difference between the prediction of Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) and $H_{\mathrm{Langevin}}$ defined as $\frac{H_{\mathrm{model}}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}\left(\mathrm{\%}\right).$ The same symbols are used in both plots to denote different values of ${\Psi }_E.$ Reference lines at $\pm 10\mathrm{\%}$ are included to guide the eye. A compilation of more the datasets and their deviations from predictions of Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) are provided in Figure S3, SI.

${H(Kn}_D,$${\Psi }_E,\mathrm{ }{S}_D)\mathrm{ }$model development for screened Coulombic collisions

Typical to dusty plasmas and other high ion concentration environments, is the screening of negatively charged particles by positive ions that are caught in metastable orbits around individual particles. These ions effectively shield the charge on the particle at distances much longer than the particle radius and the Debye screening length. This effect is often modeled using a screened Coulomb potential of the form: $\phi \left(\overrightarrow{r}\right)=\frac{z_p{z}_i{e}^2}{4\pi {\epsilon }_{o}r}\exp \left(-\frac{r}{{\lambda }_D}\right),$ where ${\lambda }_D$ is Debye screening length that depends on the concentration of free charges (ions/electrons) around the particle. Independent of the method of calculating$\mathrm{ }{\lambda }_D,$ it enters the picture of particle-ion collision as another length scale. In the limit of low ion concentration ${\lambda }_D\gg a_p,$ this represents an unscreened particle. This case has been parameterized in the previous section for the unscreened Coulomb potential (Eq. (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ). On the other hand, high ion concentrations (free space charges) lead to ${\lambda }_D\ll a_p$ or ${\lambda }_D\sim a_p$ and the particle is effectively screened completely to behave like a hard sphere. The effect of finite $S_D=\frac{{\lambda }_D}{a_p}$ along with ${Kn}_D,$${\Psi }_E$ are encoded in $\mu$ through the fit constants $A,\mathrm{ }B,C,\mathrm{ }k$ which now depend on $S_D$ along with ${\Psi }_E\mathrm{ }$and will have to be derived taking into account the screened Coulomb potential. The $S_D\to \mathrm{\infty }$ limit represents an ion moving in the Coulomb potential due to a charged particle only and in the presence of ion-neutral collisions as was discussed in the previous subsection. For $S_D\to 0$ or high ion concentrations, an individual ion moves in the resultant electric field due to the absorbing particle and other ions in space. Nominally, the electric potential experienced by the ion is subjected to rapid spatial and temporal fluctuations due to space charge. The approximation of the electrostatic potential by a screened Coulomb functional form assumes that the ensemble average of such fluctuations is nearly zero and that the potential is spatially continuous. This assumption allows us to derive a collision kernel in a closed form by analyzing Langevin trajectories. The root-mean squared local field could be significant for very high ion concentrations near surfaces (Mayya and Sapra 2002), warranting a detailed treatment of interacting ions (through a field approach or a discrete approach) and background gas molecules. Nevertheless, the theory developed here for screened Coulomb potential is potentially instructive about the charge screening of particles in high ion concentration environments through a simple, physically motivated albeit approximate computational approach.

Firstly, for the screened Coulomb potential, the dimensionless force acting on the ion is computed as ${\overrightarrow{F}}_o^{\mathrm{*}}{(Kn}_D,$${\Psi }_E,\mathrm{ }{S}_D)=\nabla \left(-\frac{{\Psi }_E}{r^{\mathrm{*}}}\exp \left(-\frac{r^{\mathrm{*}}}{S_D}\right)\right)$ to be used in the Langevin tracking (Equation (3)(3) $$m_i\frac{d\overrightarrow{v}}{\mathit{dt}}=-f_i\overrightarrow{v}+{\overrightarrow{F}}_o+\overrightarrow{X}\left(t\right).$$(3) ). Likewise, the continuum enhancement factor ${\eta }_c$ is calculated by numerically solving the Fuchs integral with the screened Coulomb potential: (12a) $${\eta }_c\left({\Psi }_E,\mathrm{ }{S}_D\right)={\left(\underset{1}{\overset{\mathrm{\infty }}{\int }}\frac{1}{{r^{\mathrm{*}}}^2}\exp \left(-\frac{{\Psi }_E}{r^{\mathrm{*}}}\exp \left(-\frac{r^{\mathrm{*}}}{S_D}\right)\right)d{r}^{\mathrm{*}}\right)}^{-1}.$$(12a)

The free molecular enhancement factor ${\eta }_f$ is obtained from OML theory as: (12b) $${\eta }_f\left({\Psi }_E\right)=\left\{\begin{array}{c}1+{\Psi }_E\exp \left(-\frac{1}{S_D}\right), {\Psi }_E\ge 0,\\ \exp \left({\Psi }_E\exp \left(-\frac{1}{S_D}\right)\right), {\Psi }_E\le 0.\end{array}\right.$$(12b)

These updated enhancement factors are used in the definition of ${Kn}_D$ and $H.$ The limits of Equations (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) and (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) are invariant to the form of the potential interaction and can be generalized to any potential provided ${\eta }_c$ and ${\eta }_f$ are calculated appropriately. With the unscreened Coulomb limit (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) valid for $0<{\Psi }_E\le 60$ and $S_D=\mathrm{\infty }$) and hard sphere limit (Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) valid for ${\Psi }_E=0$) known, the effect of the non-dimensional screening length $S_D$ is probed by varying it from ${10}^{-1}-\mathrm{ }{10}^4$ in the range of $0<{\Psi }_E\le 60,\mathrm{ }{Kn}_D\le 2000$ 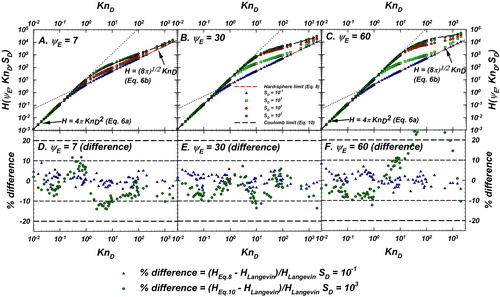analogous to unscreened Coulomb potential model development. Figure 4 shows results for ${\Psi }_E=7,\mathrm{ }30,\mathrm{ }60$ in panels (a–c). On each panel, the continuum and free molecular limits are shown (dotted lines) and the simulation results converge to these limits for low and high values of ${Kn}_D.$ Also shown are the hard sphere fit (Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) ) and the Coulomb model developed in the previous section (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) as dashed lines. For clarity, the data points of $S_D={10}^4$ are not shown as they are indistinguishable from $S_D={10}^3.$ The Langevin simulation results for $S_D={10}^{-1},\mathrm{ }{10}^1,\mathrm{ }{10}^2,\mathrm{ }{10}^3$ are shown as discrete data points of various colors. Panels D, E, F of Figure 4 show the difference between the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and (1) the prediction of the hard sphere fit (referred to as $H_{\mathrm{Eq}.8}$) for $S_D={10}^{-1}$ shown as blue triangles and (2) the prediction of Coulomb model developed in the previous section (referred to as $H_{\mathrm{Eq}.10}$) for $S_D={10}^3$ shown as green circles. Reference lines for denoting difference levels of $\pm 10\mathrm{\%}$ and $\pm 20\mathrm{\%}$ are shown to guide the eye. Figures S4 and S5 present $H\mathrm{ }$and % difference values for an expanded dataset with ${\Psi }_E=3–60$ to further illustrate the trends shown in Figure 4. For ${\Psi }_E=3–60,$ the hard sphere fit describes the simulation results $S_D={10}^{-1}$ within $\pm 10\mathrm{\%}$ nominally. Likewise, the agreement between the Langevin-inferred $H$ and the Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) is within $\pm 10\mathrm{\%}$ for all ${\Psi }_E$ values with a few outliers at high ${\Psi }_E.$ We attribute this to the higher uncertainty in fitting at the end of the ${\Psi }_E$ range. Overall, this establishes that for $S_D\le {10}^0,$ the Langevin-inferred $H$ approaches the hard sphere fit and for $S_D\ge {10}^3,$ they approach the Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ). As $S_D$ is varied between ${10}^0\text{ and }{10}^3,$ $H$ transitions between the hard sphere fit and the Coulomb model. This variation of $H$ is captured by the underlying variation in the $\mu$ parameter introduced through Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) . A fit for the fit constants $A,\mathrm{ }B,\mathrm{ }C,\mathrm{ }k$ that appear in Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) is provided in Table S1 (SI). These fits depend on ${\Psi }_E,\mathrm{ }{S}_D$ and can be used to calculate $H{(Kn}_D,$${\Psi }_E,\mathrm{ }{S}_D)$ for both the unscreened and screened Coulomb potentials.

Figure 4. Plot showing the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) for ${\Psi }_E=7,\mathrm{ }30,\mathrm{ }60.$ Panels (a–c) present $H_{\mathrm{Langevin}}$ for $S_D={10}^{-1},\mathrm{ }{10}^1,\mathrm{ }{10}^2,\mathrm{ }{10}^3$ as data points. The continuum limit (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and free molecular limit (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) are shown as black dotted lines. Also shown is the hard sphere fit (Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) ) and the unscreened Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ). The common legend for panels (a–c) is given in panel (b). Panels (d–f) plot the comparison of the difference between the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and (1) the prediction of the hard sphere fit (referred to as $H_{\mathrm{Eq}.8}$) for $S_D={10}^{-1}$ shown as blue triangles and (2) the prediction of Coulomb model (referred to as $H_{\mathrm{Eq}.10}$) for $S_D={10}^3$ shown as green circles. Reference lines for denoting difference levels of $\pm 10\mathrm{\%}$ and $\pm 20\mathrm{\%}$ are shown to guide the eye. The common legend for panels (d–f) is given at the bottom.

Results and discussion

The Langevin-inferred $H$ values have been analyzed to develop Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) for $H$ in the presence of attractive unscreened (${{\Psi }_E>0,\mathrm{ }S}_D\to \mathrm{\infty }$) and screened (${\Psi }_E>0,\mathrm{ }$finite $S_D$) Coulomb potentials between a particle and an ion. The ${H(Kn}_D, {\Psi }_E)$ model developed here, valid in the limit of $\mathrm{Z}\equiv \frac{m_i}{m_g}\to \mathrm{\infty },$ based on prior evidence about the weak sensitivity of the collision kernel on $Z$ (Gopalakrishnan and Hogan 2011), can be used to describe charging of particles by simple atomic and molecular ions of equal or greater mass than the background gas molecules. Their application to describe charging of particles by ions that are lighter than the background gas molecules remains to be investigated. In this section, we present inter-comparison of the predictions of models available in the literature against Langevin-inferred $H.$ We choose six models from the literature along with the model developed in this paper (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ). The analytical models that represent different approaches and assumptions about the ion to gas molecule mass ratio $Z$ ($Z\to 0$ or $Z\to \mathrm{\infty }$) discussed in the introduction: limiting sphere model pioneered by Fuchs and derived for the Coulomb potential by D’Yachkov et al. (2007) assuming $Z\to 0,$ the linear combination model derived by Gatti and Kortshagen (2008) assuming $Z\to 0,$ the expression developed by Zobnin et al. (2008) based on solutions to the Boltzmann equation with an ion-neutral collision term (assuming $Z\to 0$), and Vaulina, Repin, and Petrov (2006) and Gopalakrishnan and Hogan (2012) based on LD ($Z\to \mathrm{\infty }$), Hutchinson and Patacchini (2007) based on PIC calculations (assuming $Z\to 0$) are chosen for comparison. Here, the model of Zobnin et al. (2008) is analogous to models of vapor condensation derived by solving the Boltzmann equation without involving force potentials (Fuchs and Sutugin 1970; Loyalka 1982). Thus, the models chosen here for comparison represent both the limits of ion-neutral mass ratio $Z$ to assess the sensitivity of the collision kernel to the same. The models of D’Yachkov et al. (2007), and Gopalakrishnan and Hogan (2012), by construction, are applicable only for unscreened Coulomb potential ($S_D\to \mathrm{\infty }$) and are thus not included in the comparison for screened Coulomb potential calculations. The original formulation of Gatti and Kortshagen’s model and Hutchinson and Patacchini’s fit has a drift-diffusion expression built as the continuum or strongly collisional limit. We have replaced the continuum limit used by those authors with Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) to ensure that those models converged to the continuum limit in the absence of systematic ion drift. For all comparisons with Langevin-inferred $H,$ these adjusted expressions of Gatti and Kortshagen’s model and Hutchinson and Patacchini’s fit are used throughout this paper. The fit developed by Hutchinson and Patacchini (2007) was developed for finite electron and ion Debye lengths (as opposed to infinite Debye lengths or unscreened interactions). Following Khrapak and Morfill (2008), we set an interpolation exponent in their model to 1 and apply it for finite screening lengths cases for comparison. Further, the ion to electron temperature parameter in their fit equation is set to zero to approximate a non-thermal dusty plasma, although it is noted this is not strictly true. The current model calculates the ion current to an isolated grain in the presence of neutrals with a fixed screened or unscreened Coulomb interaction potential. Hutchinson and Patacchini’s fit, however, self-consistently calculates the particle-ion interaction potential that also renders the comparison approximate to illustrate the transition of ion current from the continuum limit to the free molecular limit as a function of ion-neutral collisionality. Finally, the current model and the model put forward by Vaulina, Repin, and Petrov (2006) are both based on LD and are compared on a one-to-one basis instead of comparison with models derived using other approaches. Thus, to represent the LD approach to collision kernel development, the current model is compared with other models and Langevin-inferred $H.$ The equations of the respective models used for comparison in this paper in terms of ${Kn}_D,$${\Psi }_E,\mathrm{ }{S}_D$ can be found in Sec. S3, SI.

Unscreened Coulomb ($S_D\to \mathrm{\infty }$) potential driven particle-ion collisions

In Figure 5, we present the Langevin-inferred $H$ values and model predictions for ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,\mathrm{ }60$ as 4 panels. In each panel, the Langevin-inferred $H$ for a fixed ${\Psi }_E$ is shown as light green circles with black outline. Predictions of the models considered are shown as dashed lines including the current model in blue, D’Yachkov et al. (2007) in orange, Gatti and Kortshagen (2008) in pink, Gopalakrishnan and Hogan (2012) in dark green and Zobnin et al. (2008) in red. Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collision-less (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as dotted black lines. Figure 6 shows the % difference between the predictions of each model and the Langevin-inferred $H.$ % difference is defined as $\frac{H_{\mathrm{model}}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}\left(\mathrm{\%}\right).$ Figure 6 has 4 panels that correspond to the difference of each model for corresponding value of ${\Psi }_E.$ Immediately apparent from Figures 5 and 6 is the agreement of $H_{\mathrm{Langevin}}$ values with Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) as ${Kn}_D\to 0.$ At low ${\Psi }_E=\frac{3}{2}$ (i. e), when the ion potential energy and thermal energy are nominally equal, the current model, D’Yachkov model and Gatti-Kortshagen’s model have very low difference within ∼5% nominally for the entire ${Kn}_D$ range. However, the model developed by Gopalakrishnan and Hogan (2012) has significant difference as ${Kn}_D$ increases and does not converge to the collision-less limit of Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) as ${Kn}_D\to \mathrm{\infty }.$ This model was designed by fitting simulation results to a rational function of ${Kn}_D.$ Gopalakrishnan and Hogan (2012) postulated that a correct form of the capture radius (discussed in the Introduction section) should be used to calculate the diffusive Knudsen number ${Kn}_D$ and used while describing attractive Coulombic collisions. Their choice of the non-dimensional capture radius of $\frac{2}{3}{\Psi }_E$ works well only when $H_{\mathrm{Langevin}}$ is well described by the continuum limit (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) as well. It can be seen from Figure 6 all the models agree with each other and have low difference when $H_{\mathit{Langevin}}$ is well described by the continuum limit. The ${Kn}_D$ at which $H_{\mathit{Langevin}}$ departs from Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) is dependent on ${\Psi }_E.$ Figure 5 shows that for ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,\mathrm{ }60,$ the maximum ${Kn}_D$ at which ${\mathrm{ }H}_{\mathrm{Langevin}}$ is well described by Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) is approximately 0.2, 2, 9, and 20, respectively. If a particle-ion collision is calculated to have a certain ${Kn}_D,$ depending on ${\Psi }_E,$ the transport could be continuum or free molecular. The ${Kn}_D$ value itself is only weakly dependent on ${\Psi }_E$ and hence, the attraction between particle and ion effectively increases the particle’s ability to capture ion from far—making the transport more continuum than if it were a hard-sphere interaction. Thus, the continuum limit represents the limit for $H$ as ${\Psi }_E\to \mathrm{\infty }$ as evidenced by ${\Psi }_E=30,\mathrm{ }60$ datasets. For ${\Psi }_E=7,\mathrm{ }30,\mathrm{ }60,\mathrm{ }$the Gopalakrishnan and Hogan (2012) model improperly approaches a false collision-less limit as ${Kn}_D\to \mathrm{\infty }.$ The current model, which is also built by analyzing Langevin simulations, parameterizes the underlying distribution of the particle-ion collision times (Equations (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) and (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) ). This approach based on the analysis of the particle-ion collision time distribution leads to differences within $\pm 10\mathrm{\%}$ as shown in Figure 6 for the entire ${Kn}_D,\mathrm{ }{\Psi }_E$ space investigated here. Physically, ${Kn}_D\sim 2000$ represents the collision between a 2 nm particle and an ${\mathrm{Ar}}^{+}$ ion (300 K) at ∼100 Pa pressure. For these conditions, for a singly charged particle, ${\Psi }_E\sim 55.$ For larger particles, ${Kn}_D$ decreases with size, and depending on the electron temperature in plasmas, the current model can be applied for ${\Psi }_E\le 60.$ The flux-matching model of D’Yachkov et al. (2007) does not account for ion-neutral collisions within the limiting sphere in their formalism and thereby predicts that the collision kernel $H$ falls much faster than the $H_{\mathrm{Langevin}}\mathrm{ }$values. This makes this model inaccurate at low ion-neutral collisionalities (high ${Kn}_D$) and highly charged particles (high ${\Psi }_E$). The model of Zobnin et al. (2008) also has a similar mismatch in the rate at which the predictions approach the collision-less limit (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ). Finally, the Gatti and Kortshagen model over predicts when compared to $H_{\mathrm{Langevin}}.$ Their model distinguishes between collision-less ion capture by the particle and that in which there is exactly one collision between ion and neutral gas molecule. However, for sufficiently energetic ions, more than one collision with neutrals may be necessary for its kinetic energy to become less than the attractive potential energy, thereby resulting in capture by the particle. Overall, the Gatti and Kortshagen model captures the physical trends but the degree of over-prediction increases with increasing ${\Psi }_E.$ Figures S6 and S7 present additional $H_{\mathrm{Langevin}}$ and model predictions for ${\Psi }_E=3–50$ to further the discussion presented here. Overall, the current model can be seen to describe the Langevin-inferred $H_{\mathrm{Langevin}}$ values to within $\pm 10\mathrm{\%}$ with few instances where the difference is within $\pm 20\mathrm{\%}$ making it accurate for describing particle charging in dusty plasmas and aerosol systems in which the Debye screening length is much larger than the particle size.

Figure 5. Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$ shown as green circles with black outline) and the predictions of various models considered for evaluation are plotted as a function of ${\mathit{Kn}}_D$ for ${\Psi }_E=\frac{3}{2},7,\mathrm{ }30,\mathrm{ }60.$ In each panel, the predictions of the unscreened Coulomb ($S_D=\mathrm{\infty }$) model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) , blue dashed line), D’Yachkov et al. (2007) in orange, Gatti and Kortshagen (2008) in pink, Gopalakrishnan and Hogan (2012) in dark green, and Zobnin et al. (2008) in red are shown. Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collision-less (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as dashed black lines. For comparison of the difference between model predictions and $H_{\mathrm{Langevin}},$ see Figure 6.

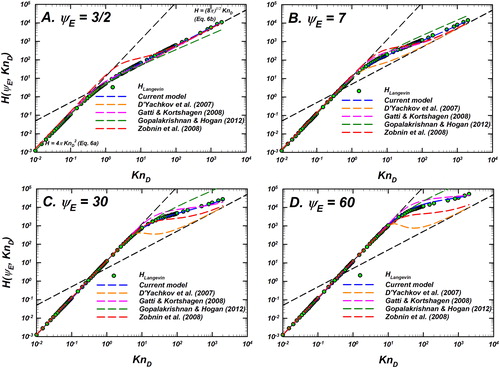
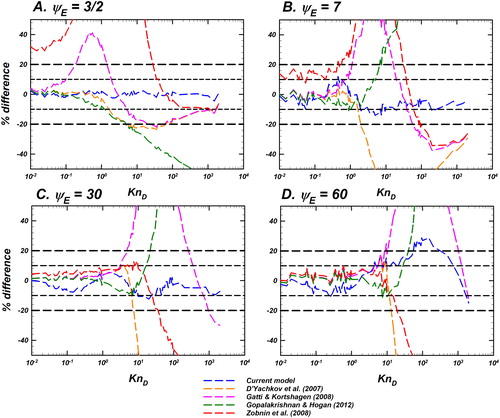
Figure 6. Comparison of the difference between the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and the prediction of various models as noted in the legend for ${\Psi }_E=\frac{3}{2},\mathrm{ }7,\mathrm{ }30,\mathrm{ }60$ as a function of ${Kn}_D.$ Differences of the models considered are shown as dashed lines including the current model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) with $S_D=\mathrm{\infty }$) in blue, D’Yachkov et al. (2007) in orange, Gatti and Kortshagen (2008) in pink, Gopalakrishnan and Hogan (2012) in dark green, and Zobnin et al. (2008) in red. The y-axis shows the % difference between the predictions of each model and $H_{\mathrm{Langevin}}.$ % difference is defined as $\frac{H_{\mathrm{model}}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}\left(\mathrm{\%}\right).$ Reference lines for denoting difference levels of $\pm 10\mathrm{\%}$ and $\pm 20\mathrm{\%}$ are shown to guide the eye. This plot is to be read in conjunction with Figure 5.

Screened Coulomb (finite $S_D$) potential driven particle-ion collisions

The Debye screening of individual particles by ions in the gas phase is parameterized by the normalized screening length $S_D=\frac{{\lambda }_D}{a_p}.$ In Figures 4, S4, and S5, we showed that the effect of finite $S_D$ is important in the range of $S_D={10}^{-1}–{10}^3.$ For $S_D\le 10,$ we find that the hard sphere fit reasonably predicts $H_{\mathrm{Langevin}}.$ Likewise, for $S_D\ge {10}^3$ the unscreened Coulomb model describes $H_{\mathrm{Langevin}}$ well. $S_D={10}^1-{10}^3$ represents the dynamic range wherein $H$ is sensitive to both $S_D$ and ${\Psi }_E.$ Hence, we pick $S_D={10}^1,\mathrm{ }{10}^2$ and ${\Psi }_E=3–60$ to evaluate the accuracy of the models considered. For purpose of comparison, we select the model developed in this paper (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) with $\mu$ from Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(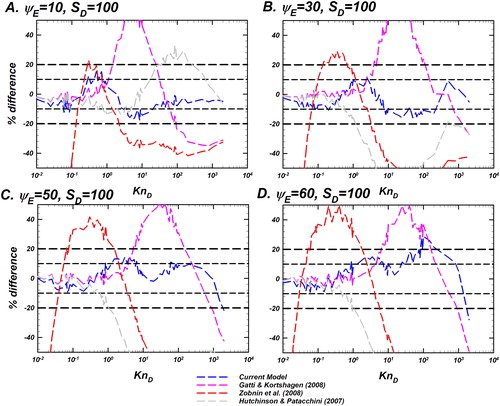11) and fit constants from Table S2, SI), the model of Gatti and Kortshagen, model of Zobnin et al., and Hutchinson and Patacchini’s fit for comparison. Figure 7 shows $H_{\mathrm{Langevin}}$ calculations and model predictions for ${\Psi }_E=10,\mathrm{ }30,\mathrm{ }50,\mathrm{ }60$ and for fixed $S_D={10}^1.$ Likewise, Figure 9 shows the same for $S_D={10}^2$ with other parameters being identical to Figure 7. $H_{\mathrm{Langevin}}$ values are shown as green circles with black outline, the current model predictions in blue dashed line, Gatti and Kortshagen’s model in pink dashed line, Zobnin et al.’s model in red dashed line, and Hutchinson and Patacchini’s fit in gray dashed line. Immediately apparent is the excellent agreement of the current model and Gatti and Kortshagen’s expression with continuum limit as ${Kn}_D\to 0.$ Gopalakrishnan and Hogan (2012) remark that the Gatti and Kortshagen’s expression was adjusted to ensure that it converges to the continuum limit that is consistent with diffusive transport of ion in the ${Kn}_D\to 0$ limit (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) as opposed to their original formulation of the drift-diffusion equation. Zobnin et al.’s model does not approach the continuum limit as it is seen to make predictions for $H$ that are non-positive as well. Both observations lead to inference that the usage of these models at moderate or higher pressures (${Kn}_D\le 1)$ is problematic. In this regime, the current model describes the data to within $\pm 10\mathrm{\%}.$ Zobnin et al.’s model shows improved agreement with the continuum limit at $S_D={10}^2$ and very good agreement with $S_D=\mathrm{\infty }$ (unscreened Coulomb as shown in Figures 5, 6, S6, and S7). Thus, Zobnin et al.’s model is prone to error at small screening lengths or high ion concentrations. The current model and Gatti and Kortshagen’s model, on the other hand, capture the trends of $H_{\mathrm{Langevin}}$ quite closely. For $S_D={10}^1,$ as can be seen from Figure 8, the difference profiles of two models are similar and within $\pm 20\mathrm{\%}$ for ${\Psi }_E\le 30.$ For ${\Psi }_E=50$ and ${\Psi }_E=60,$ Gatti and Kortshagen’s model over predicts $H_{\mathit{Langevin}}$ at $10<{Kn}_D<1000$ to about ∼40%. The current model on the other hand has higher difference at the edge of the fitting interval near ${Kn}_D\sim 2000,$ but overall captures the data well. Zobnin et al.’s model has high difference in the low ${Kn}_D$ range and has a similar difference profile to the Gatti and Kortshagen’s model at high ${Kn}_D.$ Hutchinson and Patacchini’s fit, for both $S_D={10}^1,\mathrm{ }{10}^2,$ is similar in trend to the model of Zobnin et al. as the difference profiles of Figures 8 and 10 indicate. The similarity between the two models was also seen in the comparison done by Khrapak and Morfill (2008). When compared to $H_{\mathrm{Langevin}},$ Hutchinson and Patacchini’s fit is lower by up to ∼40% (Figure 8) at $S_D={10}^1.$ Also, the predictions of all the models compared in Figure 7 are reasonably close to each other. Physically, $S_D={10}^1$ represents high ion concentration or well-screened particles that behave more like hard spheres than charged entities. We note an inherent difference in the treatment of ion transport to the particle in the PIC calculations of Hutchinson and Patacchini. PIC takes into account the space charge effect around the particle and obtains the solution to the ion and electron concentration profile around the particle as well. The difference between PIC and LD calculations reveal the need for further work to probe the effect of space charge as well as the complex electrostatic potential around the particle, as noted in the Introduction. Among the models compared, including the model developed in this paper, Hutchinson and Patacchini’s model is the only approach that takes into account the floating potential on the particle and interactions between ions and electrons in calculating ion transport to the grain. While we have shown a reasonable description of the collision kernel for isolated particle-ion interactions without other charges being present in the vicinity, the difference between Hutchinson and Patacchini’s fit and other models reveal a further need to parameterize the space charge effect. Based on this we conclude that in high ion concentration environments, Gatti and Kortshagen’s model and the current model can be reasonably used to calculate $H$ for the entire ${Kn}_D$ range for dilute space charge environments ($n_i^{-\frac{1}{3}}\gg {\lambda }_D,\mathrm{ }{a}_p$) wherein ion-ion interactions can be ignored while still considering screening of particle charge. More sophisticated treatment of the particle potential will be presumably necessary to expand the applicability of LD-based models to high concentration of space charges ($n_i^{-\frac{1}{3}}\sim {\lambda }_D,\mathrm{ }{a}_p$). Figures S10 and S11 also show similar results of $H_{\mathrm{Langevin}}$ and model predictions for lower ${\Psi }_E$ values such as ${\Psi }_E=5,\mathrm{ }7,\mathrm{ }20,\mathrm{ }40.$

Figure 7. Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$ shown as green circles with black outline) and the predictions of various models considered for evaluation are plotted as a function of ${Kn}_D$ for ${\Psi }_E=10,\mathrm{ }30,\mathrm{ }50,\mathrm{ }60$ and a fixed $S_D=10.$ In each panel, the predictions of the unscreened Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) , blue dashed line), Gatti and Kortshagen (2008) in pink, Zobnin et al. (2008) in red and Hutchinson and Patacchini (2007) in gray are shown. Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collision-less (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as black dashed lines. For comparison of the difference between model predictions and $H_{\mathrm{Langevin}},$ see Figure 8.

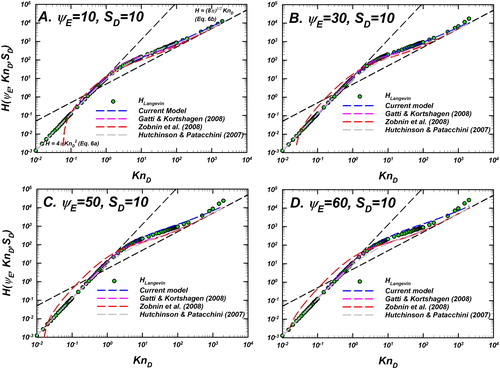
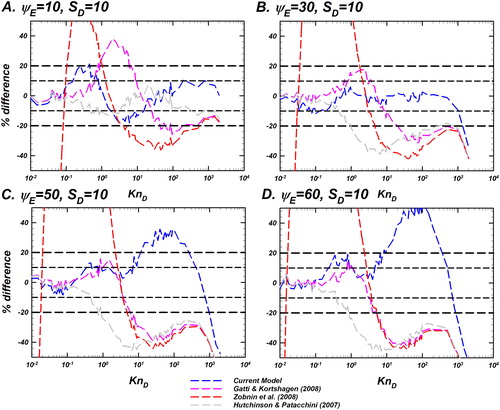
Figure 8. Comparison of the difference between the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and the prediction of various models as noted in the legend for ${\Psi }_E=10,\mathrm{ }30,\mathrm{ }50,\mathrm{ }60$ and a fixed $S_D=10.$ Differences of the models considered are shown as dashed lines including the current model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) in blue, Gatti and Kortshagen (2008) in pink, Zobnin et al. (2008) in red, and Hutchinson and Patacchini (2007) in gray. The y-axis shows the % difference between the predictions of each model and $H_{\mathrm{Langevin}}.$ % difference is defined as $\frac{H_{\mathrm{model}}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}\left(\mathrm{\%}\right).$ Reference lines for denoting difference levels of $\pm 10\mathrm{\%}$ and $\pm 20\mathrm{\%}$ are shown to guide the eye. This plot is to be read in conjunction with Figure 7.

At $S_D={10}^2,$ the differences between predictions and $H_{\mathrm{Langevin}}$ are lower than the previous case and the current model and Gatti and Kortshagen’s model capture the data quite well. As seen in Figure 9, the two models capture the rise and fall of the $H_{\mathrm{Langevin}}$ values and their approach towards the free molecular limit of Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) as ${Kn}_D\to \mathrm{\infty }.$ Figure 10 confirms the agreement as the difference is within $\pm 10\mathrm{\%}$ throughout the ${Kn}_D$ range investigated. Zobnin et al.’s model has a systematic error built in it at intermediate and low ${Kn}_D$ values. For $S_D={10}^2,$ Hutchinson and Patacchini’s fit is consistently lower than $H_{\mathrm{Langevin}}$ (Figure 9). Beyond ${Kn}_D\sim 10,$ where the predictions of the model begin to diverge from $H_{\mathrm{Langevin}},$ up to a factor of 2 lower, as seen from the difference in Figure 10. Additional data to support this observation is presented in Figures S10 and S11. Overall, the current model leads to a difference of ∼$\pm 10\mathrm{\%}$ for $S_D\ge {10}^2$ for all ${Kn}_D$ values (0.01–2000). For $S_D=10,$ it leads to good agreement (∼$\pm 10\mathrm{\%})$ for up to ${\mathrm{K}n}_D\sim 200.$ Between 200 and 2000, the difference increases up to ∼50% due to poor quality of curve fitting in this range. However, that is readily redressed by the fact that for $S_D\le 10,\mathrm{ }{H}_{\mathrm{Langevin}}$ is well described by the hard sphere fit of Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) , as evidenced in Figures 4, S4, and S5. Gatti and Kortshagen’s model does not differ significantly from $H_{\mathrm{Langevin}}$ and current model’s predictions. That model, however has a ∼40% over prediction at mid ${Kn}_D$ range ($1\le {Kn}_D\le 100$). Combined with the fact that the original formulation presented in their paper has a drift-diffusion expression built as the continuum or strongly collisional limit, this makes the model problematic to apply at intermediate or moderate pressure dusty plasmas.

Figure 9. Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$ shown as green circles with black outline) and the predictions of various models considered for evaluation are plotted as a function of ${Kn}_D$ for ${\Psi }_E=10,\mathrm{ }30,\mathrm{ }50,\mathrm{ }60$ and a fixed $S_D=100.$ In each panel, the predictions of the unscreened Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) , blue dashed line), Gatti and Kortshagen (2008) in pink, Zobnin et al. (2008) in red, and Hutchinson and Patacchini (2007) in gray are shown. Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collision-less (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as black dashed lines. For comparison of the difference between model predictions and $H_{\mathrm{Langevin}},$ see Figure 10.

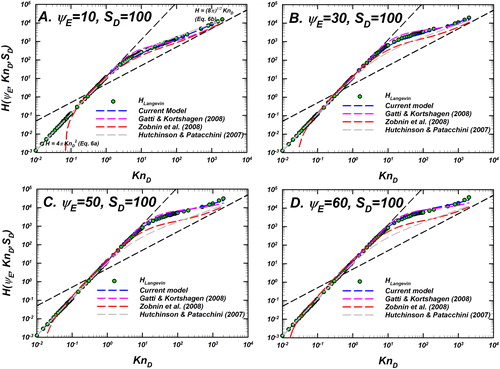
Figure 10. Comparison of the difference between the Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$) and the prediction of various models as noted in the legend for ${\Psi }_E=10,\mathrm{ }30,\mathrm{ }50,\mathrm{ }60$ and a fixed $S_D=100.$ Differences of the models considered are shown as dashed lines including the current model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) in blue, Gatti and Kortshagen (2008) in pink, Zobnin et al. (2008) in red, and Hutchinson and Patacchini (2007) in gray. The y-axis shows the % difference between the predictions of each model and $H_{\mathrm{Langevin}}.$ % difference is defined as $\frac{H_{\mathrm{model}}-H_{\mathrm{Langevin}}}{H_{\mathrm{Langevin}}}\left(\mathrm{\%}\right).$ Reference lines for denoting difference levels of $\pm 10\mathrm{\%}$ and $\pm 20\mathrm{\%}$ are shown to guide the eye. This plot is to be read in conjunction with Figure 9.

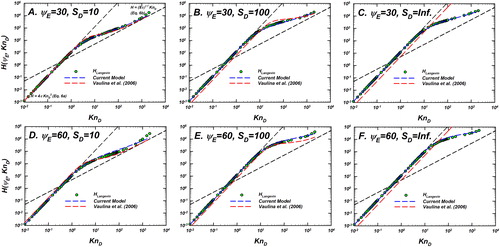
The model developed in this paper and the model of Vaulina, Repin, and Petrov (2006), both based on LD calculations of particle-ion collisions, are compared to illustrate the similarity in their predictions and formulation. Figure 11 shows the predictions of the current model (blue dashed line) and Vaulina et al.’s expression (red dashed line) along with ${\mathrm{H}}_{\mathrm{Langevin}}$ values (green filled circles with black outline). In panels A, B, C, for ${\psi }_E=30$ and $S_D={10}^1,{10}^2,\mathrm{ }\mathrm{\infty },$ the two models are qualitatively similar—the transition of $H$ from the continuum limit (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) onto the collisionless/free molecular limit is seen around similar ${Kn}_D$ value. However, for the case of unscreened Coulomb interaction ($S_D=\mathrm{\infty }$), Vaulina et al.’s expression predicts $H$ to be equal to the continuum limit (only differing by a constant), as is seen from Figure 11c. the same is true at ${\psi }_E=60,$ as can be seen from panels (d–f). For finite values of $S_D,$ the two models qualitatively predict the same variation of $H,$ while for unscreened Coulomb interactions (low ion concentrations, finite ${\psi }_E$), Vaulina et al.’s fit does not approach the OML limit as the disagreement with $H_{\mathrm{Langevin}}$ shows. Nevertheless, the similarity in the methodology of constructing the two models is the reason for qualitative, if not quantitative similarity.

Figure 11. Langevin-inferred $H$ (referred to as $H_{\mathrm{Langevin}}$ shown as green circles with black outline) and the predictions of Langevin dynamics based models—the current model and the model of Vaulina, Repin, and Petrov (2006) are plotted as a function of ${\mathit{Kn}}_D$ for ${\Psi }_E=30,\mathrm{ }60$ and $S_D=10,\mathrm{ }100,\mathrm{ }\mathrm{\infty }.$ In each panel, the predictions of the current model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) , blue dashed line) and Vaulina, Repin, and Petrov (2006) (red dashed line) are shown. Also shown are the infinitely collisional (Equation (6a)(6a) $${Kn}_D\to 0:\mathrm{ }H=4\pi {Kn}_D^2,$$(6a) ) and collision-less (Equation (6b)(6b) $${Kn}_D\to \mathrm{\infty }:\mathrm{ }H=\sqrt{8\pi }{Kn}_D.$$(6b) ) limits as black dashed lines.

Finally, we note that among the models that were compared with each other for both the unscreened and screened Coulomb potentials, the closest agreement in the predictions are found between the model presented in this paper and Gatti and Kortshagen’s model. It may be recalled that the model derived here based on Langevin tracking of ion trajectories is valid in the limit of $Z\to \mathrm{\infty }$ and that Gatti and Kortshagen’s model is derived assuming $Z\to 0.$ The other models compared here also assume $Z\to 0.$ Similar to Gopalakrishnan and Hogan (2011), we find here that models derived assuming $Z\to 0$ and $Z\to \mathrm{\infty }$ lead to qualitatively similar predictions (within ∼40% maximum deviation). Further work will be necessary to probe the sensitivity of the collision kernel to $Z,$ for which the current work provides some justification to believe, if any, that the collision kernel only weakly depends on $Z.$

Conclusions

1. We have used LD to simulate Coulomb potential driven spherical particle-ion collisions and the associated collision kernel or ion flux coefficient. LD provides an approximate, yet physical, treatment of potential driven collision across the entire transition regime of ion-neutral collisionality. The Gumbel distribution accurately describes the underlying distribution of the particle-ion collision times and the non-dimensional ion flux coefficient $H$ and can be derived as a simple expression (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) that depends on a single location parameter $\mu .$ $\mu$ has been parameterized for $0<{\Psi }_E\le 60$ and ${Kn}_{\mathrm{D}}\le 2000$ via Equation (11)(11) $$\mu \left({Kn}_D,{\Psi }_E\right)=\frac{C}{A}{\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}-1}\exp \left({-\left(1+k\frac{\log {Kn}_D-B}{A}\right)}^{-\frac{1}{k}}\right),\mathrm{ }k\ne 0.$$(11) . The developed model has been shown to be accurate to within $\pm 10\mathrm{\%}$ for the parameter range investigated here.

2. The effect of particle screening has been parameterized by calculating $H$ while a screened Coulomb potential is employed to describe the interaction between the particle and ion as a function of the Debye screening length ${\lambda }_D$ relative to the particle size $\left(S_D\equiv \frac{{\lambda }_D}{a_p}\right).$ The use of a screened Coulomb potential provides a relatively inexpensive approach to parameterizing charge screening following precedent in the dusty plasma literature (Gatti and Kortshagen 2008; Lampe et al. 2003; Zobnin et al. 2008). It is seen that the Langevin-inferred $H_{\mathrm{Langevin}}$ is well described by the hard sphere fit (Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) ) for $S_D\le {10}^1$ and by the Coulomb model (Equation (10)(10) $$H({Kn}_D,{\Psi }_E)=e^{\mathrm{\mu }}{H}_{\mathit{HS}}\left({Kn}_D\right).$$(10) ) for $S_D\ge {10}^3.$ For ${10}^1<S_D<{10}^3,$ a regression to the dependence of the $\mu$ parameter is presented for ion flux coefficient evaluation in high ion concentration dusty plasma and aerosol systems.

3. For the unscreened Coulomb potential, the current model and four selected models from the literature were compared against the Langevin-inferred $H_{\mathrm{Langevin}}$ values. These models were derived from various approximations to the Boltzmann equation or assume that $Z\equiv \frac{m_i}{m_g}\to 0$ in contrast to the Langevin modeling of ion motion that assumes $Z\to \mathrm{\infty }.$ The current model and model developed by Gatti and Kortshagen yield similar predictions and are reasonably accurate throughout the range of ${Kn}_D$ and ${\Psi }_E$ considered here. The ion to gas molecule mass ratio $Z$ is seen to exert a weak influence on the collision kernel due to two models with widely different assumptions of $Z$ yielding similar predictions. Further work is necessary to completely delineate the dependence of the particle-ion collision kernel ${\beta }_i$ on the ion to gas molecule mass ratio $Z$ in the presence of potential interactions.

4. For the screened Coulomb potential, the current model and two other models were compared against the Langevin-inferred $H_{\mathrm{Langevin}}$ values. The current model has an accuracy of $\pm 10\mathrm{\%}$ for $S_D={10}^2$ for the entire ${Kn}_D$ considered here. For $S_D={10}^1,\mathrm{ }$the difference increases up to $50\mathrm{\%}$ beyond ${Kn}_D\sim 200\mathrm{ }$due to poor quality of regression fitting. However, this problem can be easily addressed because for $S_D\le \mathrm{ }{10}^1,\mathrm{ }{H}_{\mathrm{Langevin}}$ is also well described by the hard sphere fit (Equation (8)(8) $$H({Kn}_D,{\Psi }_E=0)=H_{\mathit{HS}}\left({Kn}_D\right)=\frac{4\pi {Kn}_D^2+25.836{Kn}_D^3+\sqrt{8\pi }{Kn}_D\left(11.211{Kn}_D^3\right)}{1+3.502{Kn}_D+7.211{Kn}_D^2+11.211{Kn}_D^3}.$$(8) ). The model of Gatti and Kortshagen also accurately describes $H_{\mathrm{Langevin}}$ but has a consistent overprediction of up to ∼40% at intermediate ${Kn}_D$ values between 1 and 100, making it problematic to apply for moderate to atmospheric pressure plasmas. The model of Zobnin et al. (2008) is also reasonably accurate as $S_D\to \mathrm{\infty },$ making it more suitable to low ion concentration plasmas than those in which the screening length is comparable or smaller than the particle size. The empirical fit to PIC calculations developed by Hutchinson and Patacchini yields predictions that are similar to $H_{\mathrm{Langevin}}\mathrm{ }{S}_D={10}^1$ and up to a factor of 2 lower at $S_D={10}^2.$ The differences with PIC calculations highlight the need for accounting of the space charge effect and floating particle potential, that is self-consistently accounted in the PIC calculations by Hutchinson and Patacchini (2007). The LD approach can be potentially used to develop simple, physical expressions if further complexity in particle charging beyond the dilute limit of ion concentrations is considered in future investigations. The comparison between the model developed in this paper and the model of Vaulina, Repin, and Petrov (2006) reveal similar predictions by both the models based on LD calculations of the particle-ion collision kernel. The current model accurately predicts Langevin-inferred particle-ion collision kernel for both screened (finite $S_D$) and unscreened ($S_D\to \mathrm{\infty }$) Coulomb potential-influenced collisions in the presence of neutral gas molecules.

5. Finally, we present a self-contained model for the calculation of the ion flux coefficient ${\beta }_i$ in a non-dimensional form $H.$ The presented model is analyzed for accuracy and is presented in algebraic form (Section S2, SI). Section S4 of the SI presents the steps to carry out calculations to obtain ${\beta }_i$ as a function of particle, ion and neutral gas parameters. Based on the inherent assumption in the Langevin formulation of $Z\to \mathrm{\infty },$ the presented model can be used to describe particle charging by ions that are of the same mass or higher mass than background gas molecules.

Acknowledgments

We are indebted to our three anonymous reviewers and to our editor, Dr. Yannis Drossinos, all of whose constructive criticism greatly helped shape our thinking on this topic.