Evolution dynamics of fractal aggregates in continuously stirred tank aerosol reactors using generalized condensation exponents

Abstract

Understanding the evolution of aerosol metrics in Continuously Stirred Aerosol Reactors (CSTAR) is of considerable importance for the generation and synthesis of aerosol particles with controlled size and morphological properties. Generally, the dynamic equations governing the depletion of precursor monomer species as well as the evolution of aerosol metrics are solved by method of moments. These provide a simpler, alternative system of ordinary differential equations in place of the complicated integro-partial differential system of general dynamics equation for the entire size distribution function. A fundamental question pertains to the existence of closure of the moment equations, consistent with aerosol processes. In this article, we derive constraints on the values of condensation exponent in the pre-coagulation regime of CSTAR, which lead to a system of closed moment equations. The relevant condensation processes on fractal aggregates corresponding to some of these exponents are also identified. Stability analysis for these systems is carried out by formulating and solving their characteristic equations. The solutions are examined by numerically integrating the moment equations, which show interesting non-monotonic behavior with respect to ventilation rate (reciprocal of residence time). The study not only highlights the general features of the aerosol evolution equation, but also demonstrates its usefulness for optimizing the yield of particles across a range of growth exponents.

Copyright © 2020 American Association for Aerosol Research

Editor:

• Nicole Riemer

1. Introduction

Aerosol reactors are used for synthesizing various materials for technological applications. The materials synthesized have diverse particle characteristics such as concentration, size, shape and degree of polydispersity (Lang-Yona et al. 2010; Kuwata and Martin 2012; Boje et al. 2017), depending upon the application. Among different types of reactors, Continuously Stirred Tank Aerosol Reactor (CSTAR) is a homogeneous, isothermal, constant volume tank, in which particles are formed from the nucleation of a vapor maintained under constant flow. This system is used for the production of particles at industrial scale (Pratsinis 1998) and to study aerosol formation processes by nucleation of reactant gases/vapors under constant flow conditions (Adkins et al. 1988; Friebel and Mensah 2019; Kuwata and Martin 2012; McMurry and Li 2017). Subsequent to nucleation, the particles further grow in size due to either vapor condensation or coagulation, and are removed from the system either by outflow or by deposition on walls of the reactor. The kinetics of growth crucially depends on the shape and structure of the particles, which in turn depend upon the material properties and temperature conditions in the reactor. The assumption of spherical shape may be a good approximation for droplet formation, but would be inadequate for formation of solid-like particles. In fact, considerable evidence exists for the formation of fractal aggregates with fractal dimension varying widely from 1.3 to 2.7. When growth is dominated by collision-coalescence of spherical primary particles in the free-molecular and transition regimes, aggregates of mass fractal dimension in the range 2.2–2.5 (Saunders and Plane 2006) are formed. Athanassiou, Grass, and Stark (2010) showed that particles with a fractal dimension of 1.7–1.9 representing a very open aggregate structure are formed in a flame reactor. Other experimental observations (Saathoff et al. 2003) show that particles of fractal dimension in the range of 1.9–2.1 and 2.0–2.3 are formed for diesel soot and spark generated “Palas” soot, respectively, in an aerosol chamber. In the case of high temperature reactors, particle shape continuously evolves during the production process, where the structure of aggregates is largely determined by the interplay of particle collision and coalescence (Eggersdorfer et al. 2011).

In order to understand the evolution of the particle characteristics in CSTAR systems, mutually coupled equations for vapor depletion and aerosol general dynamics equations are solved using either analytical or numerical techniques. These equations involve integro-differential terms in particle volume and time, and are difficult to solve for the detailed particle volume distribution function. An often-used alternative approach is based on the method of moments, which has been effectively implemented for the aerosol reactor system producing spherical aerosol particles (Friedlander 1983; McGraw and Saunders 1984; Pratsinis, Friedlander, and Pearlstein 1986; Whitby and McMurry 1997). Furthermore, few researchers (McGraw and Saunders 1984; Pratsinis, Friedlander, and Pearlstein 1986) carried out the stability analysis of CSTAR systems to explain the oscillatory behavior of the output variables in the aerosol system for spherical aerosol particles. The mechanisms considered include nucleation of vapor injected into the reactor, condensation of vapor on the particles and flow-controlled, size-independent, removal process from the system. The present study aims at extending this formulation to include generalized condensational growth, corresponding to various possible fractal dimensions and rate control mechanisms, in the CSTAR systems. As particles collide with each other, they undergo coalescence or aggregation, which is termed as coagulation. However, coagulation being a relatively late stage process, is not included in the present study, and in this respect, the system under consideration is similar to that discussed by McGraw and Saunders (1984) and Pratsinis, Friedlander, and Pearlstein (1986). McGraw and Saunders (1984) formulated the equations for CSTAR with simultaneous nucleation and condensation using Becker-Doring approach and further used method of moments to obtain closed system of equations under approximation of negligible evaporation flux for a critical cluster. A linearized normal mode analysis is then carried out to study the oscillatory behavior and obtain stability diagram for the system. A similar study is carried out by Pratsinis, Friedlander, and Pearlstein (1986) for spherical particles. However, fractal structures, such as diffusion limited aggregates (DLAs) with varying fractal dimensions, can still emerge depending upon the mechanisms of attachment and the post sticking rearrangement of the attached monomers. Such situations can arise in cold processes such as the formation of solid particles from monomers produced through vapor phase chemical reactions (e.g., ammonium chloride). The study intends to throw light on the stability and evolutionary characteristics of the generalized system (stable oscillations, damped, etc.) and the dependence of the yield of particles on the parameters such as the removal rate.

2. Problem formulation

Let us consider a system in which vapor of condensable material is continuously introduced into a large well stirred chamber, maintained at a uniform temperature. Quick and uniform mixing is assumed so that there is no spatial dependence of vapor concentration inside the reactor. Once the injected monomers (vapor molecules) reach super-saturation level, they undergo nucleation to generate new particles. Some of the vapor molecules may condense on the existing particles. The condensation rate of vapors on pre-formed particles depends on the monomer concentration and the cluster diameter (Tsang and Brock 1982) which is related to the critical mass, via the fractal dimension. The effect of monomer concentration may be separated from that of cluster mass by defining a second order rate constant, $\beta \left(m\right),$ which we refer to as condensation coefficient. $\beta \left(m\right)$ multiplied by the monomer concentration yields the condensation rate on a given particle. $\beta \left(m\right)$ is essentially a function of particle mass (Tsang and Brock 1982) scaled in terms of mass of the vapor molecule (i.e., it is a function of the number of monomers in the cluster). Although the condensation coefficient can have different functional forms depending on the size of the cluster and the process of condensation, a power-law form is generally adapted for convenience (Friedlander 2000): (1) $$\beta \left(m\right)={\beta }_0{\left(\frac{m}{m_1}\right)}^{\nu }$$(1) where, m and m₁ are the mass of the cluster and the vapor molecule, respectively. ${\beta }_0$ is a size-independent pre-factor and $\nu$ is the exponent, known as the condensation exponent. The quantity $\nu$ is a real positive number which depends on the fractal dimension ($d_f$) of the particle and the kinetic regime in question for the condensation rate (free-molecular regime, $\nu =2/d_f;$ continuum regime, $\nu =1/d_f$). It is presumed that the structure of the cluster cannot be determined from the kinetic models, as they depend on the process followed in aggregation and internal forces (such as due to reordering and sticking post deposition of monomers). The cases corresponding to $\nu \le 1$ only are studied as a part of this work as it represents most of the physical problems. The cases of $\nu >1$ correspond to situations of super growth rates, which are not encountered generally and are beyond the scope of this study. Furthermore, the aerosol particles may be removed either by size dependent wall deposition processes or due to size independent ventilation process. Generally, due to presence of maintained outflow, the ventilation rate will be larger than the wall deposition rate by several orders of magnitude and hence a size-independent total removal rate of the system is considered in this analysis.

Upon considering nucleation and condensation as the dominant mechanisms governing the conversion of vapor molecules into particles, the rate of change of monomer concentration (n₁) in the system is given by, (2) $$\frac{d{n}_1\left(t\right)}{dt}=R-J\left(t\right)k_c\left(t\right)-\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right){\beta }_0\mathrm{ }A\left(t\right)-\lambda \mathrm{ }{n}_1\left(t\right)$$(2) where, R is the monomer/vapor injection rate, J is the nucleation rate (i.e., rate of formation of fresh particles), $k_{\mathrm{c}}$ is number of molecules in the critical cluster, n_∞ is equilibrium monomer concentration, $A(t)$ is the particle size-integrated condensation rate factor and λ is ventilation rate which is related to the residence time of the particles in the system. The first term on the RHS of Equation (2)(2) $$\frac{d{n}_1\left(t\right)}{dt}=R-J\left(t\right)k_c\left(t\right)-\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right){\beta }_0\mathrm{ }A\left(t\right)-\lambda \mathrm{ }{n}_1\left(t\right)$$(2) represents the source term, i.e., rate of injection of monomer/vapor in the system (R), the second term represents the removal of monomers due to nucleation. The third term accounts for the loss of monomers due to their condensation on the pre-formed particles. The last term stands for the removal of monomers from the system (due to outflow of monomers from the reactor).

The particles formed due to nucleation at different times grow at different rates and this result in a polydisperse distribution with respect to particle masses. Let $f\left(m,t\right)$ denote the number concentration distribution function for particles in the mass range around m. In analogy with Equation (2)(2) $$\frac{d{n}_1\left(t\right)}{dt}=R-J\left(t\right)k_c\left(t\right)-\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right){\beta }_0\mathrm{ }A\left(t\right)-\lambda \mathrm{ }{n}_1\left(t\right)$$(2) , the equation governing the rate of change of $f\left(m,t\right)$ may be written as, (3) $$\frac{\partial f\left(m,t\right)}{\partial t}+{\beta }_0\mathrm{ }\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right)\frac{\partial }{\partial m}\left[{\left(\frac{m}{m_1}\right)}^{\nu }\mathrm{ }f\left(m,t\right)\right]=J\left(t\right)\mathrm{ }\delta \left(m-m_1{k}_c\left(t\right)\right)-\lambda \mathrm{ }f\left(m,t\right)$$(3) where, the nucleation rate in the Equations (2)(2) $$\frac{d{n}_1\left(t\right)}{dt}=R-J\left(t\right)k_c\left(t\right)-\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right){\beta }_0\mathrm{ }A\left(t\right)-\lambda \mathrm{ }{n}_1\left(t\right)$$(2) –(5)(5) $$A\left(t\right)={\int }_0^{\mathrm{\infty }}{\left(\frac{m}{m_1}\right)}^{\nu }\mathrm{ }f\left(m,t\right)\mathrm{ }dm$$(5) is given by (Friedlander 1983), (4) $$J\left(t\right)=J_0{S\left(t\right)}^2\exp \hspace{0.17em}\left(-\frac{k_c^0}{2\mathrm{ }{\left(\ln \hspace{0.17em}\left[S\left(t\right)\right]\right)}^2}\right)$$(4) where, ${J_0=\frac{1}{3}\left(\frac{\mathrm{ }{\sigma }_s\mathrm{ }}{\pi \mathrm{ }}\right)}^{1/2}{\beta }_0{n}_{\mathrm{\infty }}^2,$ $S(t)=\frac{n_1(t)}{{\mathrm{ }n}_{\mathrm{\infty }}},$ is the super saturation ratio, ${\sigma }_s=\frac{\sigma s_1}{kT}$ is the interfacial tension between the particle surface and the host fluid, $\sigma$ is surface tension of the particle, $s_1$ is surface area of monomer, k is Boltzmann constant, T is temperature and $k_c^0={\left(\frac{2{\sigma }_S\mathrm{ }}{3}\right)}^3.$ The number of monomers in a critical cluster at a given super-saturation ratio $S(t)$ is given by, $k_c\left(t\right)=\frac{\mathrm{ }{k}_c^0}{{\left\{\ln \hspace{0.17em}\left[S\left(t\right)\right]\right\}}^3}.$ The condensation term in Equation (2)(2) $$\frac{d{n}_1\left(t\right)}{dt}=R-J\left(t\right)k_c\left(t\right)-\left(n_1\left(t\right)-n_{\mathrm{\infty }}\right){\beta }_0\mathrm{ }A\left(t\right)-\lambda \mathrm{ }{n}_1\left(t\right)$$(2) depends on the particle size integrated condensation rate factor and is given by, (5) $$A\left(t\right)={\int }_0^{\mathrm{\infty }}{\left(\frac{m}{m_1}\right)}^{\nu }\mathrm{ }f\left(m,t\right)\mathrm{ }dm$$(5)

For simplicity, the system of equations (Equations (2-5)) are re-cast in terms of dimensionless variables defined in Table 1, as follows: (6) $$\frac{dS\left(t^{\mathrm{*}}\right)}{d{t}^{\mathrm{*}}}=R^{\mathrm{*}}-\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }{A}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)-{\lambda }^{\mathrm{*}}\mathrm{ }S\left(t^{\mathrm{*}}\right)$$(6) (7) $$\frac{\partial f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}+\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\frac{\partial }{\partial m^{\mathrm{*}}}\left[m^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\right]=\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{k_c\left(S\left(t^{\mathrm{*}}\right)\right)}\mathrm{ }\delta \left[m^{\mathrm{*}}-k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]-{\lambda }^{\mathrm{*}}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)$$(7) where, $\varphi \left(S(t^{\mathrm{*}})\right)=\mathrm{ }\left(\frac{1}{3}\sqrt{\frac{{\sigma }_s}{\pi }}\right)\frac{k_{c\mathrm{ }}^0{S(t^{\mathrm{*}})}^2}{{\left(\ln \hspace{0.17em}S(t^{\mathrm{*}})\right)}^3}\mathrm{ }\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\frac{k_c^0}{2\mathrm{ }{\left(\ln \hspace{0.17em}S(t^{\mathrm{*}})\right)}^2}\right).$

Table 1. Scaling of parameters in terms of dimensionless parameters.

Mathematical Relation	Physical quantity
$m^{\mathrm{*}}=m/m_1$	Scaled mass of the particle
$R^{\mathrm{*}}=R/J_c$	Scaled monomer injection rate
${\lambda }^{\mathrm{*}}=\lambda \mathrm{ }{t}_c$	Scaled reciprocal residence time (ventilation rate)
$t^{\mathrm{*}}=t/t_c$	Scaled time
$t_c=\frac{1}{{\beta }_0{n}_{\mathrm{\infty }}}\mathrm{ }=\frac{n_{\mathrm{\infty }}}{J_c}$	Characteristic time
$J_c={\beta }_0{n}_{\mathrm{\infty }}^2$	Characteristic nucleation rate
$f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)=\frac{m_1}{n_{\mathrm{\infty }}}f\left(m,t\right)$	Scaled particle mass distribution function
$A^{\mathrm{*}}(t^{\mathrm{*}})={\int }_0^{\mathrm{\infty }}{m}^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\mathrm{ }d{m}^{\mathrm{*}}$	Scaled condensation rate factor

Equations (6)(6) $$\frac{dS\left(t^{\mathrm{*}}\right)}{d{t}^{\mathrm{*}}}=R^{\mathrm{*}}-\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }{A}^{\mathrm{*}}\left(t^{\mathrm{*}}\right)-{\lambda }^{\mathrm{*}}\mathrm{ }S\left(t^{\mathrm{*}}\right)$$(6) and (7)(7) $$\frac{\partial f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}+\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\frac{\partial }{\partial m^{\mathrm{*}}}\left[m^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\right]=\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{k_c\left(S\left(t^{\mathrm{*}}\right)\right)}\mathrm{ }\delta \left[m^{\mathrm{*}}-k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]-{\lambda }^{\mathrm{*}}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)$$(7) are nonlinearly coupled differential equations in the size variable, m* and time, t*. Although possible in principle, their direct solutions for the detailed size distribution function involve numerical complexity and associated uncertainties of numerical diffusion. An elegant approach is to develop appropriate system of moment equations, for the main quantities of interest such as the mass concentration and number concentrations of the system. From mass and number concentrations, characteristic size of the distribution can be inferred. Hence, moment equations are constructed in a closed form for certain class of values of ν. The general moment of order “q” is defined as (8) $$F_q\left(t^{\mathrm{*}}\right)={\int }_0^{\mathrm{\infty }}{m}^{\mathrm{*}q}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\mathrm{ }d{m}^{\mathrm{*}}$$(8) where, q is a real positive number. Special values corresponding to q = 0, 1 and ν have the following physical interpretation: (9) $$\text{Total number concentration }\left(\text{zeroth moment}\right):\mathrm{ }{F}_0\left(t^{\mathrm{*}}\right)={\int }_0^{\mathrm{\infty }}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\mathrm{ }d{m}^{\mathrm{*}}=N\left(t^{\mathrm{*}}\right)$$(9) (10) $$\text{Total mass concentration }\left(\text{first moment}\right):\mathrm{ }{F}_1\left(t^{\mathrm{*}}\right)={\int }_0^{\mathrm{\infty }}{m}^{\mathrm{*}}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\mathrm{ }d{m}^{\mathrm{*}}=M\left(t^{\mathrm{*}}\right)$$(10) (11) $$\text{Total condensation rate factor }\left(\nu \text{th moment}\right):F_{\nu }\left(t^{\mathrm{*}}\right)={\int }_0^{\mathrm{\infty }}{m}^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\mathrm{ }d{m}^{\mathrm{*}}$$(11)

By noting these identities (Equations (9–11)), multiplying Equation (7)(7) $$\frac{\partial f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}+\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\frac{\partial }{\partial m^{\mathrm{*}}}\left[m^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\right]=\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{k_c\left(S\left(t^{\mathrm{*}}\right)\right)}\mathrm{ }\delta \left[m^{\mathrm{*}}-k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]-{\lambda }^{\mathrm{*}}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)$$(7) with $m^{\mathrm{*}\nu }$ and integrating it from 0 to ∞, we get an equation for F_ν$\left(t^{\mathrm{*}}\right),$ (12) $$\frac{\partial F_{\nu }\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\nu \mathrm{ }{F}_{2\nu -1}\left(t^{\mathrm{*}}\right)=a\mathrm{ }\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{1-\nu }}-{\lambda }^{\mathrm{*}}{F}_{\nu }\left(t^{\mathrm{*}}\right)$$(12) where, $a=\left(\frac{1}{3}\sqrt{\frac{{\sigma }_s}{\pi }}\right).$

Equation (12)(12) $$\frac{\partial F_{\nu }\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\nu \mathrm{ }{F}_{2\nu -1}\left(t^{\mathrm{*}}\right)=a\mathrm{ }\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{1-\nu }}-{\lambda }^{\mathrm{*}}{F}_{\nu }\left(t^{\mathrm{*}}\right)$$(12) requires an equation for $F_{2\nu -1}\left(t^{\mathrm{*}}\right),$ and it is obtained by multiplying Equation (7)(7) $$\frac{\partial f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}+\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\frac{\partial }{\partial m^{\mathrm{*}}}\left[m^{\mathrm{*}\nu }{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)\right]=\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{k_c\left(S\left(t^{\mathrm{*}}\right)\right)}\mathrm{ }\delta \left[m^{\mathrm{*}}-k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]-{\lambda }^{\mathrm{*}}{f}^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right)$$(7) with $m^{\mathrm{*}\left(2\nu -1\right)}$ and integrating from 0 to ∞, (13) $$\frac{\partial F_{2\nu -1}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\left(2\nu -1\right)F_{3\nu -2}\left(t^{\mathrm{*}}\right)=a\mathrm{ }\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{2-2\nu }}-{\lambda }^{\mathrm{*}}{F}_{2\nu -1}\left(t^{\mathrm{*}}\right)$$(13)

Equation (13)(13) $$\frac{\partial F_{2\nu -1}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\left(2\nu -1\right)F_{3\nu -2}\left(t^{\mathrm{*}}\right)=a\mathrm{ }\frac{\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{2-2\nu }}-{\lambda }^{\mathrm{*}}{F}_{2\nu -1}\left(t^{\mathrm{*}}\right)$$(13) requires an equation for $F_{3\nu -2}\left(t^{\mathrm{*}}\right)$ and so on. Hence, for general power of the surface growth term, i.e., condensation exponent ν, moment equations lead to an open hierarchy, having an infinitely coupled system of equations with lower moments depending upon higher moments of $f^{\mathrm{*}}\left(m^{\mathrm{*}},t^{\mathrm{*}}\right).$ The general term will be $F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right),$ given by, (14) $$\frac{\partial F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\left[\left(n+1\right)\nu -n\right]\mathrm{ }{F}_{\left(n+2\right)\nu -\left(n+1\right)}\left(t^{\mathrm{*}}\right)=\mathrm{ }\frac{a\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{\left(n+1\right)\left(1-\nu \right)}}-{\lambda }^{\mathrm{*}}{F}_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)$$(14) where, n = 0, 1, 2,… Equation (14)(14) $$\frac{\partial F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\left[\left(n+1\right)\nu -n\right]\mathrm{ }{F}_{\left(n+2\right)\nu -\left(n+1\right)}\left(t^{\mathrm{*}}\right)=\mathrm{ }\frac{a\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{\left(n+1\right)\left(1-\nu \right)}}-{\lambda }^{\mathrm{*}}{F}_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)$$(14) yields a hierarchy of fractional moment equations for different integer values of n. In general, as n increases, this hierarchy of moment equations will not terminate into a closed set. Inspection of Equation (14)(14) $$\frac{\partial F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\left[\left(n+1\right)\nu -n\right]\mathrm{ }{F}_{\left(n+2\right)\nu -\left(n+1\right)}\left(t^{\mathrm{*}}\right)=\mathrm{ }\frac{a\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{\left(n+1\right)\left(1-\nu \right)}}-{\lambda }^{\mathrm{*}}{F}_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)$$(14) shows that closure is possible for special situations corresponding to following cases: (15) $$\left(n+1\right)\nu -n=0$$(15)

That is, closure occurs only when the condensation exponent is expressible as the ratio of consecutive integers: (16) $$\nu =\left(\frac{n}{n+1}\right),\mathrm{ }n\mathrm{ }=\mathrm{ }0,\mathrm{ }1,\mathrm{ }2,\mathrm{ }\dots$$(16) i.e., ν = 0, 1/2, 2/3, 3/4, 4/5, …

Under the explicit assumption that $\nu =2/d_f$ and $\nu =1/d_f$ for free molecular and the continuum regimes, respectively, one may note that the above exponents correspond to a wide range of fractal dimensions lying between 1 and 3. The sequence denoted in Equation (16)(16) $$\nu =\left(\frac{n}{n+1}\right),\mathrm{ }n\mathrm{ }=\mathrm{ }0,\mathrm{ }1,\mathrm{ }2,\mathrm{ }\dots$$(16) includes the special case of $\nu =2/3$ ($d_f=3$), discussed by Pratsinis, Friedlander, and Pearlstein (1986). The behavior of the CSTAR system for other closure cases may be examined by explicitly constructing the moment equations from Equation (14)(14) $$\frac{\partial F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\left[\left(n+1\right)\nu -n\right]\mathrm{ }{F}_{\left(n+2\right)\nu -\left(n+1\right)}\left(t^{\mathrm{*}}\right)=\mathrm{ }\frac{a\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{\left(n+1\right)\left(1-\nu \right)}}-{\lambda }^{\mathrm{*}}{F}_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)$$(14) and solving the corresponding characteristic equations.

3. Results and discussion

Equations (14–16) show that there are infinite number of closure systems possible; however, the physically realizable systems are possible up to n = 4. The number of equations required for closure increases with n and the respective closure equations up to n = 4 are presented in the Table 2. The case of ν = 0 (or n = 0) requires only two equations for closure, one for saturation ratio and other for the number concentration. This is an unphysical system in which the condensation rate is independent of the size of the particles and hence, not very useful. Similarly, ν = 1 is an exceptional case (limit of the sequence corresponding to n = ∞ in Equation (16)(16) $$\nu =\left(\frac{n}{n+1}\right),\mathrm{ }n\mathrm{ }=\mathrm{ }0,\mathrm{ }1,\mathrm{ }2,\mathrm{ }\dots$$(16) ) which corresponds to a condensation process on a fractal particle with d_f = 2 in the free molecular regime. In this case, the condensation rate factor is exactly equal to the mass concentration (A(t) = M(t)). It possesses closure with just two equations and is a remarkably simple, physically meaningful case.

Table 2. System of coupled equations with closure for possible value of ν.

n	ν	No. of equations	System of equations	Characteristic equation	Remarks
0	0	2		–	Trivial system, Not very useful
1	1/2	3			Diffusion limited, fractal particle system, df – 2, solid aggregates (Area (A) – F1/2 Number (N) – F0)
2	2/3	4			Kinetic limited, compact particle system, df – 3, droplet model (Area (A) – F2/3 Mass (M) – F1/3 Number (N) – F0)
3	3/4	5			Kinetic limited, fractal particle system, df − 2.67 (Area (A) – F3/4 Number (N) – F0)
4	4/5	6			Kinetic limited, fractal particle system, df – 2.5, aggregation model (Area (A) – F4/5 Number (N) – F0)
–	1	2			Kinetic limited, fractal particle system, df - 2, solid aggregate model (Area (A)/Mass (M) – F1 Number (N) – F0)

The case with n = 1 leads to a system of three coupled equations; namely, the equations for saturation ratio, surface area and number concentration. The corresponding value of ν = 1/2 corresponds to condensation occurring in diffusion limited regime (continuum) on solid fractal aggregates having d_f = 2. As mentioned, the spherical droplet model belongs to the case of n = 2 (ν = 2/3) which requires four closed set of equations as shown in Table 2. This particular case belongs to kinetic limited regime and was analyzed in greater detail by Pratsinis, Friedlander, and Pearlstein (1986).

The case of n = 3 (ν = 3/4) requires five coupled equations to describe the evolution of aerosol metrics (condensation rate factor (A) – F_3/4; number (N) – F₀). The fractal dimension (d_f) of the aerosol aggregate in this system is estimated as 2.67 using the condensation rate exponent applicable in the kinetic limited regime. Also, there is a possibility of fractal dimension of 1.33 if one uses the exponent (1/d_f) in the condensation rate expression; however, physically this fractal dimension is not possible.

Another case of n = 4 (ν = 4/5) also belongs to the fractal particle system in the kinetic regime with a fractal dimension (d_f) of 2.5. This system requires six coupled equations for closure and the important metrics such as condensation rate factor (A – F_4/5) and number concentration (N – F₀) are estimated from their solutions.

All the coupled system of equations for the above-mentioned cases are derived and summarized in the Table 2.

3.1. Evolution of number concentration

The above-mentioned systems of coupled equations (from Table 2) are numerically solved using Mathematica (Wolfram Inc. 2004) for a typical reactor system producing NH₄Cl particles (Henry, Gonzalez, and Peters 1982). Typical parameter values of surface tension of the particles $\left({\sigma }_s\right),$ initial saturation ratio S($0$), and reaction/production rate of the monomers ($R^{\mathrm{*}}$) are assumed as 2, 1.01, and 100, respectively, in terms of non-dimensional parameters for production of NH₄Cl particles (Dahlin, Su, and Peters 1981; Pratsinis, Friedlander, and Pearlstein 1986). In terms of dimensional variables, these values translate to a surface tension of 0.03 N/m and residence time of 1.8 s (for ${{\lambda }^{\mathrm{*}}}^{-1}$ = 1000) at a temperature of 293 K. 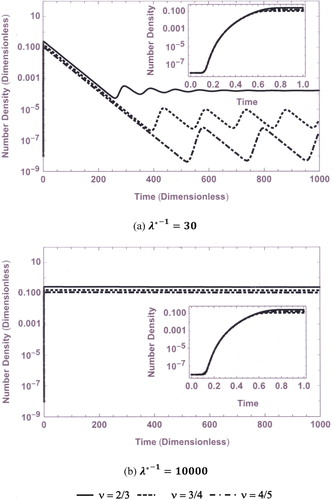Keeping all these parameters same, the numerical simulations are carried out for different residence times $\left({{\lambda }^{\mathrm{*}}}^{-1}\right)$ and fractal dimensions. The evolution of total number concentration (N($t^{\mathrm{*}}$)) for three different exponent values (ν) are presented in Figure 1.

Figure 1. Number concentration (N($t^{\mathrm{*}}$)) Vs Time ($t^{\mathrm{*}}$). (S(0) = 1.01; R* = 100; ${\sigma }_s$ = 2.

From Figure 1, it is observed that the maximum number concentration is obtained for the $\nu =2/3\mathrm{ }$ case (spherical aerosol particles) compared to other exponents (fractals). Figure 1a (${{\lambda }^{\mathrm{*}}}^{-1}$ = 30), shows that the number density attains steady-state for $\nu =2/3$ (continuous curve, spherical) as the small perturbations in the number concentration die out after sometime while in the case of fractals, number density oscillates and becomes unstable corresponding to the same set of parameters. However, in the case of large residence time (${{\lambda }^{\mathrm{*}}}^{-1}$= 10,000), steady state is achieved immediately for all cases. More details of stability analysis are presented in the next section.

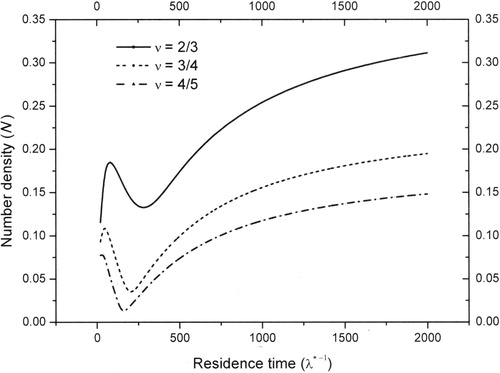
Further numerical simulations are carried out as a function of residence time for different d_f and the large time number density values are plotted in Figure 2. From Figure 2, it is observed that with increase in the residence time (${{\lambda }^{\mathrm{*}}}^{-1}$), number concentration first increases, then reduces and after a certain residence time it increases monotonically. The dip in the number concentration with increase in residence time may be attributed to the dominance of condensation. With further increase in residence time, vapor removal rate reduces, thereby increasing the nucleation rate and hence the number concentration in the reactor. These results may be used to optimize throughput of the reactor by adjusting the residence time for a given set of operating conditions and material properties in a CSTAR.

Figure 2. Variation of aerosol number concentration with residence time.

3.2. Stability analysis

In the present study, the characteristic equations are obtained for the standard fractal systems and other possible values of $\nu ,$ and tabulated in the Table 2. These characteristic equations are then solved analytically for stability analysis by introducing perturbations to the system under steady-state conditions. For an unstable system, even a small perturbation in the parameter leads to oscillations; while in the stable region, the introduced perturbation dampens out after sometime. This stability is quantified by evaluating the eigenvalues of the characteristic equation and mapping them on stability diagram for a given set of parameters. The movement of eigenvalues of the linearized system toward the origin indicates that the system is attaining the stable steady-state when the real and imaginary parts of the eigenvalues are plotted as a function of residence time.

To illustrate the application of stability analysis for a fractal system, a linear stability analysis is performed for a typical case of ν = 4/5 (Figure 3). From this stability curve, it is evident that the eigenvalues approach the origin of the complex plane as the residence time (${{\lambda }^{\mathrm{*}}}^{-1}$) increases. This is observed in Figure 1; the oscillations of number density vanish as the residence time increases. Initially, the system is in an unstable state and tends toward the stable steady-state asymptotically as the eigenvalues approach origin of the complex plane. The present case ($\nu =4/5,\mathrm{ }{d}_f=2.5$) is different from the case of $\nu =2/3$ (Pratsinis, Friedlander, and Pearlstein 1986) as there is no crossover of the eigenvalues from Left Half Plane (LHP) to Right Half Plane (RHP) and it directly moves toward origin of the complex plane.

Figure 3. Movement of eigenvalues as a function of residence time (${{\lambda }^{\mathrm{*}}}^{-1}$) in the complex plane (ν = 4/5).

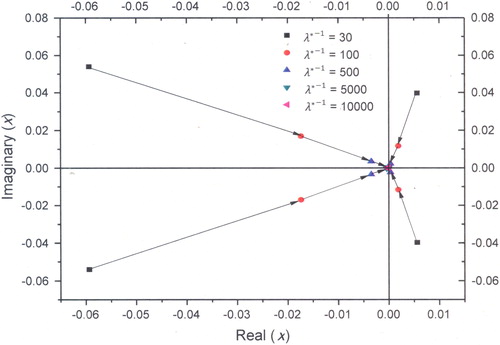
Similar movement of eigenvalues is observed in the stability analysis of system with ν = 3/4, i.e., a system with fractal dimension of 2.67 in the kinetic limited regime. The analysis is carried out by solving five coupled linear equations and found that eigenvalues of the characteristic equations directly move toward origin of the complex plane as residence time increases, similar to $\nu =4/5\mathrm{ }(d_f=2.5$) case. The study thus demonstrates the usefulness of stability analysis in identifying the domains in which stable output is expected from the CSTAR.

It may be noted that the cases described in the present work deal with the systems for which closed moment equations exist, and therefore are limited to the family of the condensation exponents expressible as ratio of consecutive integers. However, there exist important physical systems, which are not covered by these exponents. For example, $\nu$ value for condensation on spherical cloud drops in the diffusion-controlled growth regime is, 1/3. In this case, closure is not possible using conventional method of moments (Equation (14)(14) $$\frac{\partial F_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)}{\partial t^{\mathrm{*}}}-\left(S\left(t^{\mathrm{*}}\right)-1\right)\mathrm{ }\left[\left(n+1\right)\nu -n\right]\mathrm{ }{F}_{\left(n+2\right)\nu -\left(n+1\right)}\left(t^{\mathrm{*}}\right)=\mathrm{ }\frac{a\mathrm{ }\varphi \left(S\left(t^{\mathrm{*}}\right)\right)}{{\left[k_c\left(S\left(t^{\mathrm{*}}\right)\right)\right]}^{\left(n+1\right)\left(1-\nu \right)}}-{\lambda }^{\mathrm{*}}{F}_{\left(n+1\right)\nu -n}\left(t^{\mathrm{*}}\right)$$(14) ). Hence, approximate closure methods such as Quadrature Method of Moments (QMOM) and Taylor-Expansion Method of Moments (TEMOM) needs to be employed. McGraw (1997) applied QMOM for the closure of system of equations for $\nu =1/3$ case, by representing the moments in terms of appropriate weights and abscissas. Alternatively, one might also explore TEMOM based approach involving Taylor expansion of the terms about the ratio of first moment to the zeroth moment to force a closed system of equations (Yu et al. 2015; Yu and Lin 2017). The present work provides an impetus to set up generalized moment equations by including coagulation, similar to the studies carried out by Barrett and Webb (1998) and Rosner, McGraw, and Tandon (2003). It is hoped that the construction of moment equations by combining generalized condensation exponents and the coagulation kernels would offer a simplified system of ordinary differential equations for solving a broad range of aerosol evolution problems.

4. Conclusion

The Continuously Stirred Tank Aerosol Reactor offers a simple framework for examining the formation and evolution of aerosol particles from vapor phase and has been investigated extensively (Bau et al. 2017; McGraw 1997; Pratsinis, Friedlander, and Pearlstein 1986) for specific cases. The condensation process is central to this system as it introduces a fascinating feedback mechanism inducing oscillatory growth (McGraw and Saunders 1984). The present study revisits this system from the perspective of closure and stability of the moment equations for a family of generalized condensation exponents. These exponents arise in the context of fractality of the aggregates covering a wide range of growth laws applicable to both free-molecular and diffusion regimes. It is shown that there exists a set of exponents for which one can develop a system of closed moment equations. This set assumes significance since some of these exponents correspond closely to the known growth laws of aerosol particles.

The study also includes stability analysis of the CSTAR for these exponents, corresponding to fractal systems with different fractal dimensions. Also, the dependence of the throughput of the system on input and operating parameters is examined. It is found that the number concentration output has non-monotonic dependence on the ventilation rate (reciprocal residence time) for a broad range of physically realizable exponents. It increases initially, followed by a decrease and then increases again. This complex behavior is the result of competition between nucleation rate and scavenging of vapor molecules by pre-formed clusters. From a practical standpoint, the model can be used for designing and optimizing the throughput of the reactor by controlling the flow rate for a given set of initial and operating conditions. Although limited to early stage growth, we believe that these results contribute in a fundamental way, toward improving our understanding of the dynamics of evolution of an aerosol system formed from vapor phase.

Nomenclature

$\beta \left(m\right)$	=	condensation rate coefficient
${\beta }_0$	=	pre-factor independent of particle size
$m$	=	mass of the particle
$m_1$	=	monomer mass
$\nu$	=	condensation exponent
$d_f$	=	fractal dimension
$n_1\left(t\right)$	=	monomer concentration at time t
$R$	=	monomer/Vapor injection rate
$J\left(t\right)$	=	nucleation rate per molecule at time t
$J_c$	=	characteristic production rate density
$k_c\left(t\right)$	=	number of molecules in the critical cluster
$n_{\mathrm{\infty }}$	=	monomer concentration at saturation condition
$A\left(t\right)$	=	particle size-integrated condensation rate factor; represents area in case of spherical particles
$\lambda$	=	ventilation rate/removal rate of the system
$f\left(m,t\right)$	=	particle mass distribution function
$S(t)$	=	super-saturation ratio
σ	=	interfacial tension between the particle surface and the host fluid
k	=	Boltzmann constant
T	=	temperature
$s_1$	=	surface area of the monomer
$t_c$	=	characteristic time
x	=	Eigen value