A Solution to the Problem of Nonequilibrium Acid/Base Gas-Particle Transfer at Long Time Step

Abstract

A stable numerical solution to the unsolved problem of nonequilibrium growth/evaporation at long time step of multiple dissociating acids (e.g., nitric acid, hydrochloric acid, carbonic acid, sulfuric acid, etc.) and a base (ammonia) is discussed. The solution eliminates most oscillatory behavior observed in previous solutions at long time step. The solution is applicable across the entire relative humidity range, both in the presence and absence of solids and among multiple aerosol size bins and distributions. It involves solving growth/evaporation of semivolatile acids with a dissolutional growth scheme at high liquid water content (LWC), semivolatile acids with a condensational growth scheme at low LWC, involatile acids with a condensation scheme at all LWCs, then equilibrating ammonia and pH simultaneously between gas and solution phases at all LWCs based on updated acid contents, and finally solving internal-aerosol composition, final pH, and LWC with an operator-split equilibrium calculation. The new method at long time step (150–300 s) compares well with, and is 10–60 times faster than, a previous solution at short time step over the entire size distribution. Solutions at short and long time steps converge to equilibrium solutions when unique equilibrium solutions exist, even in the presence of calcium, magnesium, potassium, and carbonate. The new scheme is referred to as PNG-EQUISOLV II, where PNG is Predictor of Nonequilibrium Growth. Analysis with the scheme suggests that, under some conditions of high relative humidity and concentration, some coarse-mode particles (< 6 μ m diameter) may reach equilibrium on time scales < 1 h.

INTRODUCTION

The transfer of a gas to and from a population of particles is a time-dependent process. The numerical treatment of this process is complicated by the fact that several gases transfer simultaneously and may interact with each other chemically in particle solutions or on particle surfaces. In particular, the simultaneous transfer of acids such as nitric acid, hydrochloric acid, and sulfuric acid, and a base such as ammonia, results in the instantaneous adjustment to pH, particle composition, and vapor pressure that renders the resulting set of equations stiff and difficult to solve at long time step.

Several studies of the simultaneous nonequilibrium transfer of acids and bases have been carried out. Wexler and Seinfeld (1990) derived expressions and time scales to equilibrium for the transfer of NH₃, HNO₃, and HCl to a population of solid particles containing NH₄Cl(s) and NH₄NO₃(s). Jacobson et al. (1996) derived expressions for the transfer of any soluble gas to a population of particles containing liquid water, where the solution accounted for the instantaneous change in vapor pressure over the surface due to dissolution, and for the operator-split hydration of liquid water and formation of solids and ions. The growth equations were solved with a sparse-matrix ordinary differential equation solver. Meng and Seinfeld (1996) solved growth expressions of Wexler and Seinfeld (1990) at short time step and found that the fine mode of particles was closer to equilibrium than the coarse mode.

Jacobson (1997a, b, c) derived and applied to Los Angeles a noniterative, mass-conserving, and unconditionally stable solution to dissolutional growth of a gas to a population of particles containing any amount of liquid water on their surfaces. The growth solution allowed vapor pressures to adjust instantaneously as a gas dissolved in solution and was operator split from a chemical equilibrium solution that calculated liquid water content (LWC), pH, ion dissociation, activity coefficients, and solid composition within each particle size bin. After gases dissolved in even a tiny amount of water during the growth step, solids formed during the equilibrium step. It was found that, when the operator-split time interval between growth and equilibrium was < 15 s, the numerical solution was relatively smooth. At longer time step, though, the solution “produced oscillations” due to delays in feedback between the equilibrium and growth calculations. For example, at long time step the delay in the update to pH and sulfuric acid dissociation caused too much or too little growth during the step that was overcompensated for during the next time step. Another drawback was that, at low liquid water contents (e.g., < 0.01 μ g m^{− 3}, summed over all particles), solids took too long to reach equilibrium because the LWC allowed only a small amount of gas to dissolve each growth time step, and a 15 s time step between growth and equilibrium delayed the gas-to-solid conversion. Jacobson (2002) tried to address this latter issue by solving growth of solid-forming gases as a condensation instead of dissolution process in size bins where solids already existed.

Meng et al. (1998) solved nonequilibrium growth in a modeling study of Los Angeles. Vapor pressures, which were fixed during the growth calculation, were determined from an operator-split equilibrium calculation. The time step for growth was variable and dependent on the stiffness of the system, thereby limiting it.

Sun and Wexler (1998a, b) discuss the same time step limitation found in Jacobson (1997c), stating that a “very small time step” is necessary to integrate the stiff growth equations for HCl, HNO₃, and NH₃. They proposed calculating the growth rates of all three gases independently, then recalculating the growth rate of one of the gases assuming that pH stays constant during growth. Pilinis et al. (2000) also discussed the oscillatory behavior of acid/base growth at long time step. They postulated that holding pH constant to resolve this issue might cause errors in the growth solution and proposed calculating a “flux” of hydrogen ion to each particle size bin equal to the net change in ion concentration due to the fluxes of all acid and base gases, including HNO₃, HCl, NH₃, and H₂SO₄. To minimize oscillations, the hydrogen ion flux was limited, forcing a limit on the flux of one or more acid or base gases as well. They solved the growth equations with a stiff ODE solver, which still required a short time step. The time constraint was significant enough that Capaldo et al. (2000) developed a hybrid scheme that solved fine-mode sizes with an equilibrium solution and coarse-mode sizes with a nonequilibrium solution. Koo et al. (2003) compared these two approaches with a pure equilibrium approach.

Here, a scheme is developed that solves nonequilibrium growth operator split from equilibrium chemistry with remarkably stability and accuracy at long time step (e.g., 150–300+ s), at all relative humidities across the entire size distribution. The growth portion of the scheme is referred to as the predictor of nonequilibrium growth analytical predictor of dissolution (PNG) scheme. The equilibrium scheme is EQUISOLV II. The coupled scheme is PNG-EQUISOLV II.

NUMERICAL METHOD

The PNG-EQUISOLV II scheme involves the solution of five processes: (1) dissolutional growth of semivolatile acid gases at high and moderate LWCs; (2) condensational growth of semivolatile acid gases at low LWCs; (3) condensational growth of involatile gases at all LWCs; (4) equilibration of NH₃/NH₄ ⁺and pH between the gas phase and all particle size bins while conserving charge and moles; and (5) equilibration of internal-aerosol liquid, ion, and solid composition, pH, liquid water content, and activity coefficients.

The method described here differs from that of Sun and Wexler (1998a, b) in that this method allows vapor pressures to adjust instantaneously as a gas dissolves, and it equilibrates ammonia and pH with all particle sizes following acid growth rather than fixing pH and readjusting the growth rate of an acid or NH₃ at the fixed pH, as was done in that study. The method also differs from that of Pilinis et al. (2000) in that this method equilibrates ammonia and pH after acid growth, whereas that method allowed acids and NH₃ to grow independently and then adjusted the pH based on the change in charge-balance alone, while limiting the pH change and growth rates of acids and bases with a stability limiter. Here no stability limits are necessary, and the pH adjustment conserves charge among acid gases following their growth, and it also satisfies mole conservation and the NH₃/NH₄ ⁺ equilibrium constraint among all size bins. In addition, the ammonia equilibration technique here is applied during both liquid and solid formation. Below, the five steps in the procedure are described.

Dissolutional Growth of Semivolatile Gases at High LWC

When a liquid solution pre-exists on a particle surface, the growth of semivolatile gases onto the particle is controlled by dissolution. The growth equation for a semivolatile acid gas, such as hydrochloric acid (HCl), that dissolves then dissociates (in this case to the hydrogen ion, H⁺, and the chloride ion, Cl⁻) in solution, may be written as

[1]

where

[2]

is the mole concentration (mol cm^{− 3}-air) of dissolved, undissociated hydrochloric acid plus that of the chloride ion in particles of size i at time t, k _{HCl,i,t − h} is the mass transfer rate (s^{− 1}) of HCl vapor to particles of size i (e.g., Jacobson 1999a, Equation (17.62)), C _HCl,t is the gas-phase mole concentration of HCl (mol cm^{− 3}-air), S′_{HCl,i,t − h} is the equilibrium saturation ratio of the condensing gas (Jacobson, 1999a, Equation (17.45)), and C _HCl,s,i,t is and the saturation mole concentration (SMC) over the surface of particles of size i. The subscript t identifies values that are currently unknown, and the subscript t−h (where h is the time step size) identifies values that are known from the beginning of the time step.

The gas concentration of each growing species is linked to its aqueous concentration among all size bins through the mole-conservation relationship,

[3]

where N _B is the number of size bins.

The mole concentration of any dissolved species q in size bin i is related to its molality (m _q,i , mol kg^{− 1}) by

[4]

where m _v is the molecular weight of water (0.01802 kg mol^{− 1}) and c _w,i is the mole concentration (mol cm^{− 3}-air) of liquid water in bin i. LWC is obtained from the operator-split equilibrium calculation. The mole concentration of any gas q is related to its partial pressure (p _q , atm) by

[5]

where R* is the universal gas constant (82.06 cm³ atm mol^{− 1} K^{− 1}) and T is absolute temperature (K).

In the case of HCl, its saturation mole concentration is calculated by considering the equilibrium equations, HCl ⇔ HCl(aq) and HCl(aq) ⇔ H⁺ + Cl⁻. The equilibrium coefficient relations for these equations are

[6]

[7]

where p _HCl,s,i is the saturation vapor pressure of HCl over the surface of particles of size i; γ _i,H⁺/Cl⁻ is the mean mixed activity coefficient of HCl in a solution containing multiple components, determined from a mixing rule during the operator-split equilibrium calculation; H _HCl is the Henry's constant of HCl dissolution (mol kg⁻¹ atm^{− 1}); and K _HCl is the first dissociation constant of HCl(aq) (mol kg^{− 1}). Combining Equations (2), (6), and (7), then substituting Equations (4) and (5) into the result and rearranging, gives

[8]

where

[9]

(mol cm^{− 3}) is the adjusted equilibrium coefficient determined at the beginning of the growth step from known parameters. Adding time subscripts to Equation (8) and substituting it into Equation (1) gives the growth equation for HCl to one size bin as

[10]

This equation has two unknowns for each size bin: the gas concentration and the total dissolved chlorine concentration. For the growth of acids, the hydrogen ion concentration (used in Equation (9)) is taken from the beginning of the time step. For the corresponding growth of the base, ammonia, pH will adjust in a manner that conserves charge exactly.

Integrating Equation (10) gives the growth solution for the chloride ion to a size bin as

[11]

where the gas concentration in the equation is still unknown. Substituting Equation (11) into Equation (3) and solving gives the final acid gas concentration as

[12]

(Jacobson, 1997c, 1999a). Substituting Equation (12) back into Equation (11) gives the final total chlorine concentration in each size bin. The solution is unconditionally stable (where a stable solution is defined as one in which the difference between the numerical and exact solution is bounded regardless of the time step or integration time) and mole conserving. The unconditional stability and mole conservation of Equations (11) and (12) are demonstrated in Table 18.5 of Jacobson (1999a).

An alternative to the exponential solution given in Equations (11) and (12) is the semiimplicit solution, given here as

[13]

[14]

respectively. Although the exponential solution is barely more accurate at typical concentrations, it is more prone to roundoff error when concentrations vary significantly over a size distribution. The semi-implicit solution eliminates nearly all such roundoff error and takes slightly less computer time (due to the lack of an exponential). It is also unconditionally stable and mole conserving.

Growth equations for other semivolatile acid gases, such as nitric acid, carbon dioxide, formic acid, etc. are solved in the same manner as those for hydrochloric acid. In the case of carbon dioxide, the adjusted equilibrium coefficient (Equation (9)) must include a second dissociation constant. Equations for all gases can be written to treat dissolution into multiple aerosol size distributions in a manner similar to that done in Jacobson (2002).

Condensational Growth of Semivolatile Gases at Low LWCs

Equations (13) and (14) can be solved for any finite amount of liquid water on a particle surface. However, when the total (over all sizes) aerosol LWC decreases to below about 0.01 μ g m^{− 3}, solid formation from dissolution proceeds slowly at long time step since solids form only during the operator-splitting equilibrium calculation. If the time-interval between growth and equilibrium is long, the little gas that dissolves in a small amount of water during each growth step cannot convert to a solid rapidly each equilibrium calculation. This problem is addressed here by treating HCl and HNO₃ growth as condensation rather than dissolution processes when the LWC is below 0.01 μ g m^{− 3}. At such low water contents, growth of CO₂ and other acids are still modeled as dissolution processes since (1) such acids are less important with respect to solid formation than are HCl or HNO₃, and (2) the dissolution scheme, which still allows solids to form through the equilibrium calculation, is unconditionally stable for any nonzero LWC.

When an acid gas grows onto particles to eventually form a solid, it is modeled as first condensing as a liquid, but with its saturation mole concentration determined from gas-solid equilibrium to ensure that the correct amount of acid gas transfers to particle surfaces for solid formation. Unlike with dissolution where the SMC of the gas is an instantaneous function of its molality in solution, the SMC for a condensing gas is held constant during a growth time step.

During condensation, liquids (or their dissociation products) enter into the small (nonzero) amount of liquid water on the particle surface. The amount of ammonia that condenses simultaneously is discussed in section “Equilibration of NH₃ with Growing Acids at all LWCs” below. Because the particle solution is now supersaturated with respect to the solid phase, solids readily form from the solution during the subsequent internal-aerosol equilibrium calculation. During that calculation, the molalities of the solution components (e.g., liquids and ions) quickly drop (due to solid formation) to satisfy solution–solid equilibrium constraints so that they are well within the range of molalities for which solute activity coefficients are valid. This holds true even if the LWC drops to machine precision (10^{− 40}μ g m^{− 3} on some computers and 10^{− 250}μ g m^{− 3} on others) because the numerical equilibrium solver (EQUISOLV II) always converges, and the converged solution between ions and solids requires that the solubility product of a given solid equals the product of the activities of the ions making up the solid. At equilibrium, these activities (molalities multiplied by activity coefficients) are relatively small or modest, regardless of the LWC.

It should be noted here that, although the method of acid nonequilibrium growth is changed from a dissolution to a condensation process at a fixed LWC (0.01 μ g m^{− 3}), the water content may decrease to machine precision during the subsequent equilibrium calculation. In such cases, all liquids or ions effectively convert to solids while solid-solution equilibrium is maintained. Because equilibrium is maintained, the solute concentration (e.g., moles cm^{− 3}-air) in the trivial amount of liquid water is also trivial, whereas the solute molality (moles kg^{− 1}-water) is nontrivial and satisfies equilibrium constraints. In sum, this numerical solution is physically realistic, since it allows the water content naturally to tend toward zero. All other numerical treatments of solid formation assume that water either exists or doesn't exist in the particle, which results in an error in composition when this assumption is incorrect.

The SMCs of HCl, and HNO₃ are solved here simultaneously by considering the two gas–solid equilibrium reactions, NH₄NO₃(s) ⇔ NH₃ + HNO₃ and NH₄Cl(s) ⇔ NH₃ + HCl. Either solid may form within aerosol particles when either (1) the relative humidity (RH) is increasing and less than the deliquescence relative humidity (DRH) of the solid, or (2) the RH is decreasing and less than the crystallization relative humidity (CRH) of the solid. DRHs and CRHs and references are given in Jacobson (1999a, Table 18.4). Although a solid can form when the RH is below the solid's DRH or CRH, the solid may or may not form. When multiple ions are present in solution and multiple solids can form, some may form below their DRH/CRH and others may not. When solids do form, all equilibrium constraints are satisfied (solution charge balance, solution–solid equilibrium, solution–solution equilibrium, mass balance).

For determining whether acid gases will be allowed to condense in the model eventually to form solids, one other criterion must be satisfied. Namely, for ammonium nitrate and/or ammonium chloride to form, the equations,

[15]

[16]

respectively, must be satisfied, where the ps are partial pressures of the gases (atm) and the Ks are gas–solid equilibrium coefficients (atm²). At equilibrium, the relation between the SMC and the equilibrium coefficients of the two reactions can be obtained by substituting Equation (5) into Equations (15) and (16) and rewriting the equation as an equality, giving

[17]

[18]

respectively. If Equations (15) and (16) are satisfied, SMCs are calculated by solving Equations (17) and (18) together with the mole-balance equation,

[19]

The analytical solution to these 3 equations and 3 unknowns for the ammonia gas SMC is

[20]

where

[21]

The SMCs of nitric acid and hydrochloric acid are now trivially found from Equations (17) and (18), respectively. The solution assumes that all three SMCs are independent of particle size.

If only ammonium nitrate can form, Equation (20) is solved by removing K _NH4Cl and setting C ₀ = C _{NH3, t − h} − C _{HNO3, t − h} . If only ammonium chloride can form, the equation is solved by removing K _NH4NO3 and setting C ₀ = C _{NH3, t − h} − C _{HCl,t − h} .

Once the SMCs for HNO₃ and HCl are calculated, they are substituted into condensational growth equations and solved with the noniterative, unconditionally stable condensation solver described by Equations (13)–(17) of Jacobson (2002) with D _Ni = 0.

Condensational Growth of Involatile Gases At All LWCs

Condensation/evaporation of relatively involatile (extremely low vapor pressure) gases, such as sulfuric acid and high molecular weight organics, is solved as a condensation process among all size bins at low and high LWC (Equations (13)–(17)) of Jacobson 2002 with D _Ni = 0). In this case, the SMCs are determined a priori from data or parameterizations that are a function of temperature.

Equilibration of NH ₃ with Growing Acids At All LWCs

Following the growth calculation for all acid gases, ammonia is equilibrated with all size bins, conserving charge among all ions, including those entering solutions during the dissolution and condensation steps of the three preceding sections. The calculation conserves moles and satisfies the gas–aerosol equilibrium constraint for ammonia. With the present method, the quantity of ammonium added to each size bin each time step is the exact amount necessary to balance charge among all ions in solution as determined after the growth calculation for such ions. Because the equilibration of ammonia is calculated after the diffusion-limited growth of all acids, ammonia growth is effectively a nonequilibrium growth process. This technique allows smooth solutions and convergence at long time step among all growing species. The alternative to equilibrating ammonia is to solve the same nonequilibrium equations for HNO₃ or HCl, but this leads to oscillations in the solution at long time step, as discussed in the introduction.

With the present method, the charge balance equation for ammonium within each size bin is

[22]

where c _{NH4 ⁺,i,t} and c _H⁺,i,t are unknown, and

[23]

consists of known values. The terms outside the summation in Equation (23) are concentrations of the ions NO₃ ⁻, Cl⁻, HSO₄ ⁻, and SO₄ ^{2 −} from the end of the current time step (time t). The dissolutional and condensational growth equations solved in the preceding sections gave total nitrate [HNO₃(aq) + NO₃ ⁻], total chloride [HCl(aq) + Cl⁻], and total sulfate [S(VI) = H₂SO₄(aq) + HSO₄ ⁻ + SO₄ ^{2 −}] in solution. The partitioning of total S(VI) into ions following S(VI) growth for Equation (23) is obtained by applying the ratios, HSO₄ ⁻/S(VI) and SO₄ ^{2 −}/S(VI), determined from the equilibrium calculation at the beginning of the operator-split time interval, to the total S(VI) following growth. The partitionings of total chloride and total nitrate to the chloride ion and the nitrate ion are calculated in a similar manner. The terms inside the summation in Equation (23) are mole concentrations (c) multiplied by charge (z = ±1,2,3) of all ions, except those outside the summation, that are present in solution.

The mole balance equation between gas-phase ammonia and the ammonium ion within each aerosol size bin is

[24]

Finally, the gas-aerosol equilibrium relations for ammonia are NH₃(g) ⇔ NH₃(aq) and NH₃(aq) + H⁺ ⇔ NH₄ ⁺. The equilibrium coefficient relations for these equations are

[25]

[26]

respectively, where the pressure in the denominator of Equation (25) is assumed to be a partial pressure, rather than a saturation vapor pressure over a size bin. The single-ion activity-coefficient ratio in Equation (26) is calculated in terms of mixed binary solute activity coefficients with, for example,

[27]

In mole concentration units, Equations (25) and (26) simplify to

[28]

[29]

respectively. Equations (22), (24), (28), and (29) represent a system of 3N _B + 1 equations and unknowns. These equations are solved exactly as follows.

Combining Equations (28) and (29) gives an expression for the hydrogen ion concentration as

[30]

Substituting this expression into Equation (22) gives

[31]

where the gas concentration on the right side of this equation is still unknown. This equation requires c _{±, i,t} = min (c _{±, i,t} ,0). If c _{±, i,t} > 0, then the size bin following acid growth and before re-equilibration has a net positive charge without H⁺ or NH₄ ⁺, which is not physically possible unless acid evaporates from the bin in a quantity greater than the H⁺ + NH₄ ⁺ present in the bin (since at the beginning of each growth step, the bin is in charge balance). If c _{±, i,t} = } 0 due to such an occurrence, c _{NH4 ⁺,i,t} = 0 for the bin and time step.

Substituting Equation (31) and c _{NH3 (aq),i,t} = C _NH3,t H′_{NH3,i,t − h} into the mole balance equation, Equation (24), gives

[32]

This nonlinear equation has only one unknown, C _NH3,t . It can be solved with a Newton-Raphson iteration,

[33]

where n is the iteration number and

[34]

[35]

This iteration always converges to a positive number and almost always within ≤12 iterations when the first guess of the ammonia gas concentration is zero (C _NH3,t,0 = 0). The computer time for iteration is relatively trivial in comparison with the computer time saved by taking a long time step for growth among all growing acids and between growth and equilibrium calculations. Once C _NH3,t is obtained, it is substituted back into Equation (31) to obtain the updated ammonium concentration, into c _{NH3 (aq),i,t} = C _NH3,t H′_{NH3,i,t − h} to update the liquid ammonia concentration, and into Equation (30) with ammonium to obtain the updated pH. However, pH is updated more completely during the operator-split equilibrium calculation, described shortly.

This procedure works for any LWC above zero. Thus, when HNO₃ and/or HCl condense (section “Condensational Growth of Semivolatile Gases at Low LWCs” below) at negligible LWC, the procedure calculates the amount of ammonia transferred to each bin to ensure mole and charge balance and satisfaction of the ammonia/ammonium equilibrium constraint. During the subsequent equilibrium calculation supersaturated nitrate, chloride, and ammonium may crystallize to form solids through the ion–solid equilibrium equations, NH₄NO₃(s) ⇔ NH₄ ⁺ + NO₃ ⁻ and NH₄Cl(s) ⇔ NH₄ ⁺ + Cl⁻. Alternatively, the ions may hydrate liquid water if conditions are right. Thus, the resulting particle can consist of both aqueous and solid components.

Operator-Split Equilibrium Calculation

Following the ammonia calculation, an operator-split internal aerosol equilibrium calculation is performed to recalculate aerosol ion, liquid, and solid composition, activity coefficients, and LWC, accounting for all species in solution in each size bin. The equilibrium solution is obtained with EQUISOLV II (Jacobson 1999b), which is iterative, positive-definite, and mole and charge conserving, regardless of the number of iterations taken. Since all growth solutions discussed are positive-definite and mole conserving between the gas phase and all particle size bins, and since equilibrium is solved after growth, the entire PNG scheme is mole and charge conserving and positive-definite regardless of the time step size for growth or between growth and equilibrium.

RESULTS

The PNG-EQUISOLV II scheme is analyzed here by comparing time-dependent results from it at long time step with results from the scheme under the same conditions at short time step and with results from simulations in which only gas-aerosol equilibrium (except as described shortly) was considered. In all cases, including the equilibrium-only cases, 60 aerosol size bins were used. In the equilibrium-only cases, sulfuric acid was allowed to condense in a nonequilibrium manner onto all size bins, but all other gases were equilibrated with the size distribution during and after condensation. A unique solution exists to equilibrium among multiple size bins in all cases except when a solid forms from two gases (e.g., NH₄NO₃(s) and NH₄Cl(s)). In such cases, there is no unique size bin to which the solids go (e.g., Wexler and Seinfeld 1990). This constraint does not apply to solids such as NaNO₃(s) or (NH₄)₂SO₄(s) that form from one gas and one involatile liquid/ion (Jacobson 1999b). When NH₄NO₃(s) or NH₄Cl(s) form, the equilibrium solution is also not the correct solution with respect to total mass (although it is close) because the formation of these solids in random size bins affects the rate of sulfuric acid condensation, which depends on particle size, and the relative amount of sulfate in a bin affects the equilibrium partitioning of bases and other acids to that bin.

Figure 1 shows the initial number and mass aerosol distribution for all cases except one (Figure 7). Aerosol particles were initialized with 10 μ g m^{− 3} NaCl(s) and 20.4 μ g m^{− 3} of inert material. The temperature in all cases was 298 K.

FIG. 1 (a) Initial model size distribution for all simulations, except those for Figure 7. The distribution consists of 10 μ g m^{− 3} NaCl(s) and 20.4 μ g m^{− 3} of inert particulate matter, spread over 60 size bins.

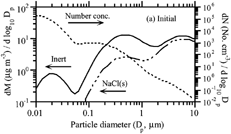
FIG. 7 (a) and (b) Same as Figures 2a and 2b, respectively, except when the initial particle size distribution contained 0.5, 0.5, and 0.5 μ g m^{− 3} K₂CO₃(s), CaCO₃(s), and MgCO₃(s), respectively, in the accumulation mode and 1.0, 3.0, and 3.0 μ g m^{− 3} K₂CO₃(s), CaCO₃(s), and MgCO₃(s), respectively, in the coarse mode.

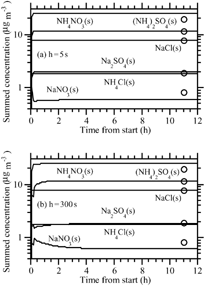
Several simulations were run for different initial gas concentrations and relative humidities. Figure 2 shows results for the first case, in which initial gas concentrations were 30 μ g m^{− 3} HNO₃(g), 10 μ g m^{− 3} NH₃(g), 0 μ g m^{− 3} HCl(g), and 10 μ g m^{− 3} H₂SO₄(g), and the RH was 90%. During the simulation period, H₂SO₄ condensed, HCl and HNO₃ dissolved/dissociated, and NH₃ equilibrated with dissolved and dissociated species, as described in section “Numerical Method” above. Water uptake and aerosol composition were calculated during each operator-split equilibrium calculation. Figures 2a and 2b show time-series of the aerosol concentrations, summed over all size bins, when the operator-split time interval between growth and equilibrium was 5 s and 300 s, respectively. The figures also show results from the equilibrium-only calculation. Results from both operator-split time steps matched each other and the equilibrium solution fairly accurately, although the longer time step resulted in a small error during the first 15 min. Equilibrium was reached within about 6 h in both simulations.

FIG. 2 (a) Time series of aerosol component concentrations, summed over all size bins, from a simulation of dissolutional growth coupled with chemical equilibrium (solved with PNG-EQUISOLV II) when the operator-split time interval between growth and equilibrium was h = 5 s. The circles are equilibrium solutions, found from EQUISOLV II alone (except that sulfuric acid condensed as a nonequilibrium process). Initial gas concentrations were 30 μ g m^{− 3} HNO₃(g), 10 μ g m^{− 3} NH₃(g), 0 μ g m^{− 3} HCl(g), and 10 μ g m^{− 3} H₂SO₄(g). In addition, RH = 90% and T = 298 K. (b) Same as Figure 2a, but with h = 300 s.

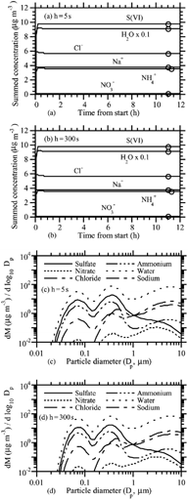
Figure 3 shows results under the same conditions as Figure 2, except the initial nitric acid gas concentration was 0.1 μ g m^{− 3} instead of 30 μ g m^{− 3}. Whereas, Figure 2 examined how the scheme performed under high nitrate conditions, this test examines how it performed under low nitrate conditions. In this case, the scheme demonstrated near-perfect accuracy at 300 s, even during the first 15 min. Figures 3c and 3d show the mass size distributions of individual components after 12 h when h = 5 s and h = 300 s, respectively. The distributions also matched accurately.

FIG. 3 (a) Same as Figure 2a (h = 5 s case), except HNO₃(g) = 0.1 μ g m^{− 3} initially. (b) Same as Figure 2b (h = 300 s case), except HNO₃(g) = 0.1 μ g m^{− 3} initially. (c) Size distribution after 12 h of the h = 5 s case shown in Figure 3a. (d) Size distribution after 12 of the h = 300 s case shown in Figure 3b.

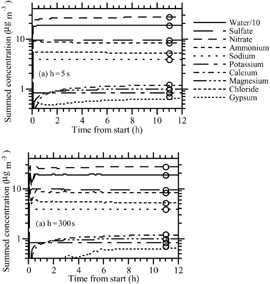
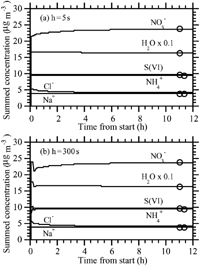
Figure 4 shows results under the same conditions as Figure 2, except the initial ammonia gas concentration was 0.1 μ g m^{− 3} instead of 30 μ g m^{− 3}. This test examines how the scheme performed under extremely low ammonia conditions. This test is of particular interest and possibly the toughest test of the code, since the PNG scheme is premised on the assumption that ammonia equilibrates with all sizes following acid growth. If ammonia is extremely low, one might think that the scheme would fail or result in severe oscillations. Figure 4a shows that, with a 5 s time step, the solution was perfectly smooth and matched the equilibrium solution within 6–8 h. Figure 4b shows that, with a 150 s time step, the solution was slightly oscillatory but not unstable. It was also slightly less accurate than the 5 s solution after 12 h. Despite the slight errors, this test demonstrates the ability of the code to perform well under an extreme condition. At a 300 s time step (not shown) the solution converged to values similar to those at 150 s but with greater oscillation for some species. Figures 4c and 4d show the size distribution from the equilibrium calculation and from the 5 s nonequilibrium calculation after 12 h. The figures are nearly identical, suggesting that the nonequilibrium solution converged to the equilibrium solution at all sizes.

FIG. 4 (a) Same as Figure 2a (h = 5 s case), except NH₃(g) = 0.1 μ g m^{− 3} initially. (b) Same as Figure 2b, except NH₃(g) = 0.1 μ g m^{− 3} initially and h = 150 s. (c) Size distribution from the equilibrium calculation corresponding to the circles in Figures 4a and 4b. (d) Size distribution after 12 h of the h = 5 s case shown in Figure 4a. (e) Size distribution of nitrate and chloride ions after 15 mins, 1 h, and 12 h of the h = 5 s case shown in Figure 4a. (Continued on next page)

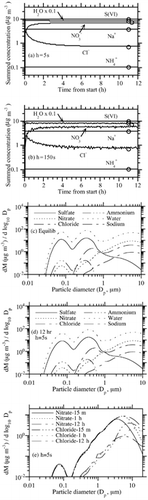
Figure 4 is also of interest physically for two reasons. First, it shows the time dependence of the well-known process of sea-spray acidification. Sea-spray acidification is the depletion of chloride from sea-spray drops when acid gases dissolve into them, reducing their pH and causing HCl to become supersaturated and evaporate (e.g., Ericksson 1960; Hitchcock et al. 1980). Figure 4a shows that the addition of these acids caused a 60% reduction in the chloride ion after 15 min, a 76% reduction after 1 h, and an 87% reduction after 12 h. Thus, chloride loss was relatively fast under the conditions tested (RH = 90%; high acid concentrations). Figure 4d shows that the greatest percentage loss in chloride occurred in submicron-sized particles. Several studies have shown that chloride depletion from acidification occurs more in small than large particles (e.g., Junge 1957; Wilkniss and Bressan 1972; Martens et al. 1973).

Second, Figure 4e shows that, under the conditions tested, particles smaller than 3 μ m diameter reached equilibrium within 15 min, particles smaller than 6 μ m diameter reached equilibrium within an hour, and the rest reached equilibrium within 12 h. Several studies have suggested or calculated that small particles are more likely to be in equilibrium than large particles (e.g., Meng and Seinfeld 1996; Capaldo et al. 2000; Pilinis et al. 2000; Fridlind and Jacobson 2000, Moya et al. 2001). Figure 4e supports these results but also suggests that, in some situations (e.g., at high RH and at high gas concentration), large particles smaller than 6 μ m in diameter may reach equilibrium on the time scale of less than an hour. Thus, some exceptions may exist to the previously established result that coarse-mode particles are not in equilibrium. This conclusion is not unexpected because previous studies did not examine all possible cases.

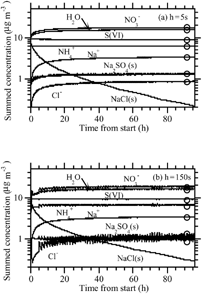
Figure 5 shows results under the same initial concentration conditions as Figure 1, but with RH = 50% and assuming solids formed only if the RH was less than the crystallization RH of the solid (e.g., the RH was decreasing). In this case, NaCl(s) was present initially and gradually disappeared, replaced in part by Na₂SO₄(s). The nonequilibrium solutions at both time steps (5 s and 150 s) approached the equilibrium solution nearly exactly, not only with respect to solid composition but also with respect to ion composition and LWC. The solution at a time step of 150 s showed small oscillations for Na₂SO₄(s) and a small error but remained stable. Oscillations grew at time steps > 150 s (not shown), but the solution converged to final values similar to those at 150 s.

FIG. 5 (a) Same as Figure 2a (h = 5 s case), except with RH = 50%. (b) Same as Figure 2b, except with RH = 50% and h = 150 s.

Figure 6 shows results under the same initial concentration conditions as Figure 1, but at RH = 10%. At this RH, the LWC was always trivially small, and growth of ammonia and nitric acid was calculated as a condensation process (section “Condensational Growth of Semivolatile Gases at Low LWCs” below). Solids formed during the operator-split equilibrium calculation. The figure shows that the result with a 300 s growth time step and growth-equilibrium splitting interval was nearly the same as at 5 s. The equilibrium solution matched the nonequilibrium results relatively well. However, as discussed at the beginning of this section, the equilibrium solution is not the correct solution in this case, since NH₄NO₃(s) and NH₄Cl(s) formed, and there is no unique equilibrium solution to the size bins in which they form.

FIG. 6 (a) and (b) Same as Figures 2a and 2b, respectively, except with RH = 10%.

Finally, Figure 7 shows a case under the same conditions as Figure 2, except the initial particle size distribution contains K₂CO₃(s), CaCO₃(s), and MgCO₃(s) in the accumulation and coarse modes in addition to NaCl(s) and inert material. As acids entered the particles, the carbonates dissolved, forcing carbon dioxide to the gas phase. Some of the calcium reassociated with sulfate to form gypsum (CaSO₄). The rest remained unassociated. The numerical solution with a 300 s time step approached that at 5 s, and both nearly matched the equilibrium solution after about 8 h, although complete equilibrium did not occur until about 24 h in this case.

SUMMARY

A new method of solving nonequilibrium acid/base gasparticle transfer at long time step was derived. The method involves solving dissolutional or condensational growth equations for acids, then equilibrating ammonium and pH between the gas phase and all aerosol size bins at the end of each growth time step for acids, then updating aerosol composition, pH, and LWC with an operator-split internal-aerosol equilibrium calculation. The scheme was applied to cases at several RHs and concentration regimes, including in the presence of calcium, magnesium, potassium, and carbonate. Solutions at long time step (150 or 300 s) were compared with solutions at 5 s time step. Results in all cases matched remarkably well and converged to equilibrium solutions. Since nonoscillatory solutions to nonequilibrium growth across an entire size distribution for liquids and solids were limited previously to time steps of 5–15 s, the new scheme allows for a factor of 10–60 speedup in comparison with such solutions. A physical finding from this study was that under at least some conditions (e.g., high RH, high concentrations, and in the absence of solid formation) particles smaller than 6 μ m diameter reached equilibrium within less than 1 h and those smaller than 3 μ m in diameter reached equilibrium within less than 15 min. Equilibrium took longer for coarse particles in several other cases. Thus, in some cases, some coarse-mode particles may be in equilibrium, suggesting that some caveats may exist to the result found in previous studies that coarse-mode particles are not in equilibrium.

Acknowledgments

This work was supported, in part, by the NASA Earth Sciences Program, the Environmental Protection Agency Office of Air Quality Planning and Standards, the National Science Foundation Atmospheric Chemistry Division (ATM 0101596), and the Global Climate and Energy Project.