Computational Models for Simulating Multicomponent Aerosol Evaporation in the Upper Respiratory Airways

Abstract

An effective model for predicting multicomponent aerosol evaporation in the upper respiratory system that is capable of estimating the vaporization of individual components is needed for accurate dosimetry and toxicology analyses. In this study, the performance of evaporation models for multicomponent droplets over a range of volatilities is evaluated based on comparisons to available experimental results for conditions similar to aerosols in the upper respiratory tract. Models considered include a semiempirical correlation approach as well as resolved-volume computational simulations of single and multicomponent aerosol evaporations to test the effects of variable gas-phase properties, surface blowing velocity, and internal droplet temperature gradients. Of the parameters assessed, concentration-dependent gas-phase specific heat had the largest effect on evaporation and should be taken into consideration for respiratory aerosols that contain high volatility species, such as n-heptane, at significant concentrations. For heavier droplet components or conditions below body temperatures, semiempirical estimates were shown to be appropriate for respiratory aerosol conditions. In order to reduce the number of equations and properties required for complex mixtures, a resolved-volume evaporation model was used to identify a twelve-component surrogate representation of potentially toxic JP-8 fuel based on comparisons to experimentally reported droplet evaporation data. Due to the relatively slow evaporation rate of JP-8 aerosols, results indicate that a semiempirical evaporation model in conjunction with the identified surrogate mixture provide a computationally efficient method for computing droplet evaporation that can track individual toxic markers. However, semiempirical methodologies are in need of further development to effectively compute the evaporation of other higher volatility aerosols for which variable gas-phase specific heat does play a significant role.

INTRODUCTION

Reliable dose assessments of multicomponent aerosols in the respiratory tract require accurate analyses of droplet heat and mass transfer characteristics. Applications in which multicomponent liquid respiratory aerosol evaporation is of significance include the inhalation of potentially toxic pollutants (Broday and Georgopoulos 2001; Zhang et al. 2004), as well as the generation and delivery of inhaled therapeutics (Finlay 2001; Edwards and Dunbar 2002). In either case, the dose received depends on the characteristics of the inhaled liquid aerosol, biophysical transport (ICRP 1994), and the surface conditions at the local site of aerosol deposition or vapor absorption, e.g., mucus or surfactant covering and thickness, metabolic reactions, etc. (Miller et al. 1985; Cohen Hubal et al. 1996; Overton et al. 2001; Kimbell et al. 2001). Evaporation of respiratory aerosols affects the diameter and density of the particle, thereby significantly affecting transport including deposition (Martonen et al. 1982; Stapleton et al. 1994; Broday and Georgopoulos 2001; Martonen and Schroeter 2003; Zhang et al. 2004). Moreover, individual chemical species of multicomponent aerosols are often of interest due to particular toxic or therapeutic effects, making it necessary to differentiate among chemical components. Hence, accurate dose assessments require an effective model for the evaporation of multicomponent respiratory aerosols that is capable of predicting the formation of individual vapors as well as determining the remaining droplet characteristics and liquid mass fractions.

The effects of water condensation and evaporation (hygroscopicity) on aerosols in the respiratory tract have been considered in a number of studies as reviewed by Morrow (1986) and Hiller (1991). More recently, Finlay and Stapleton (1995) showed that two-way coupling between aerosol droplets and the continuous phase, due to water evaporation and condensation, significantly affects respiratory deposition. Due to high relative humidity, studies that have considered the effects of evaporation and condensation on droplet transport and deposition in the respiratory tract have predominately focused on water vapor. For these conditions, simplifying assumptions often include spatially and temporally constant droplet temperature profiles, constant gas and liquid properties, and no effect from surface blowing. However, the evaporation and condensation of multiple component droplets and compounds with higher volatilities than water may violate the assumptions typically made for respiratory aerosol hygroscopicity.

Respiratory aerosols are characterized by low-to-moderate particle Reynolds numbers and relatively mild variations in temperature. In contrast to combustion applications (Landis and Mills 1974; Law 1982; Aggarwal et al. 1984), evaporation of multicomponent droplets for a range of volatilities under conditions consistent with the respiratory tract has been considered in relatively few studies. For moderate Reynolds number conditions (Re _p < 130) and mild temperature variations, Chen et al. (1997) and Runge et al. (1998) both considered the evaporation of single and multicomponent fuel droplets. Chen et al. (1997) showed that a semiempirical rapid mixing model (RMM), which assumes spatially constant droplet temperatures and concentrations, performed well for the moderate evaporation rates considered. The model employed by Chen et al. (1997) was based on the solution of ordinary differential equations (ODEs) for droplet heat and mass conservation with empirical Nusselt and Sherwood number correlations used to account for gas-phase transport. Similarly, Runge et al. (1998) showed that a semiempirical ODE-based solution could be used to match their experimental results; however, relations for the product of gas-phase density and diffusivity were derived empirically for each fuel mixture considered.

For low temperature evaporation of multicomponent fuel blends, a homogeneous mixture model has been developed based the process of batch distillation (Gauthier et al. 1996) and applied to respiratory aerosol conditions (Zhang et al. 2004). This model assumes rapid mixing of the components and implements composite properties for the fuel mixture of interest that are calculated based on the method of Bardon and Rao (1991) and that depend on the fraction of mass evaporated (Catorie et al. 1999; Benaissa et al. 2002). As such, the fuel can be considered a single-component or homogeneous mixture, and only one conservation of mass equation is necessary to predict droplet evaporation. However, a constant effective diffusivity must be empirically determined for the mixture, and the model is not designed to differentiate among chemical compounds, as may be of interest in dose assessments.

For cases in which empirical correction factors are not available to describe the gas-phase transport, direct numerical simulations may be conducted. These resolved-volume techniques can directly account for the effects of droplet arrays, shear in the underlying fluid media, and variable thermo-physical properties of the gas-phase. Due to the small diameter of respiratory aerosols, surface tension is much greater than other forces on the droplet such that a spherically symmetric geometry may be assumed (Sadhal et al. 1997). For combustion applications, several researchers have numerically simulated the evaporation characteristics of spherical droplets including variable thermo-physical properties, transient heating, internal liquid circulation, and droplet rotation (Xin and Megaridis 1996; Kleinstreuer et al. 1993; Chiang and Kleinstreuer 1992a, b). For instance, Chiang and Kleinstreuer (1992a, b) considered collinear interacting and vaporizing single-component fuel droplets in a heated air stream, under high pressure, and for particle Reynolds numbers of approximately Re _p = 100. Assuming a spherical interface, gas- and liquid-phase flows were coupled and fully resolved. In a similar study, Kleinstreuer et al. (1993) found that for single-component hydrocarbon fuels the Lewis number is greater than unity and variable during the initial phase of evaporation.

Studies dealing with respiratory aerosols typically focus on particle diameters less than 10 μm. This is based on the effective filtering mechanism of the lung as well as supporting evidence that only a small percentage of particles greater than 10 μm reach the alveolar or pulmonary region during moderate breathing conditions. However, studies have shown that particles on the order of 100 μm are frequently inhaled through the mouth and nose, i.e., an inhalation efficiency of approximately 50% (ACGIH 1997; Hinds 1999). Nearly all of the inhaled particles in this size range are deposited in the nasal and oral cavities or the pharynx (Stahlhofen et al. 1989). Analysis of toxic and therapeutic doses within these extrathoracic regions requires accurate assessments of aerosol transport and deposition, which are largely influenced by evaporation. Moreover, larger particles deliver a significantly greater amount of the toxic or therapeutic compound. For instance, deposition of a 100 μm particle provides 8,000 times more dose than a 5 μm particle on a volumetric basis. While clearance is typically rapid in the extrathoracic airways, absorption through the mucus lining into the blood may occur depending on the local metabolic characteristics. Desorption resulting in vapor formation may also occur after the liquid droplet deposits, resulting in gas-phase transport to other regions of the lung. In this study, droplet diameters ranging from 5 to 100 μm within the upper respiratory tract will be considered. Particle diameters less than 5 μm have been excluded to avoid the influence of noncontinuum effects on heat and mass transfer.

An effective model for predicting multicomponent aerosol evaporation in the respiratory system that is capable of differentiating among individual components for a range of volatilities and that does not require an empirically derived effective gaseous diffusivity is needed for accurate dosimetry estimates. Considering the broad range of inhalable particles and the significance of deposition in the upper airways, models appropriate for dosimetry applications should be valid up to aerosol diameters on the order of 100 μm and for low-to-moderate particle Reynolds numbers, i.e., 0 < Re _p ≤ 30. In this study, the performance of droplet evaporation models for multicomponent respiratory aerosols over a range of volatilities is evaluated based on comparisons to available experimental results for similar conditions. Models considered include a semiempirical ODE-based approximation as well as resolved-volume simulations of single and multicomponent aerosol evaporation rates to test the effects of variable gas-phase properties, surface blowing velocity, and droplet temperature gradients. Sherwood and Nusselt number correlations for respiratory aerosol heat and mass transfer under uniform flow conditions have also been evaluated. The primary disadvantage of the heterogeneous evaporation models considered is the complexity introduced by the physiochemical constants required for each species present in multicomponent mixtures. In order to reduce the number of required properties while maintaining the capability to track individual components of interest, the appropriate multicomponent evaporation models can be used to define surrogate blends of complex mixtures. To illustrate this concept, jet propellant-8 (JP-8) aviation fuel has been selected as a potential toxicant due to its wide use and chemical complexity. JP-8 is a kerosene-based fuel consisting of over 200 hydrocarbons spanning a wide range of volatilities that is exclusively used by the U.S. Air Force and may present a prevalent exposure hazard to maintenance personnel (ATSDR 1998; Bakshi and Henderson 1998). An appropriate droplet evaporation model has been used to identify a twelve-component representative or surrogate mixture for JP-8 fuel based on comparisons to the experimentally reported droplet evaporation data of Runge et al. (1998). The selected evaporation models and surrogate mixture can be used to simplify computational toxicokinetic analyses in which tracking specific chemical markers, e.g., benzene, contained within multicomponent aerosols is imperative. The evaporation models evaluated are capable of accounting for the effects of rarefied flow and relative humidity; however, these factors have not been directly considered in this study.

METHODS

Evaporation Models and Assumptions

To model the evaporation of multicomponent aerosols in the upper respiratory tract, semiempirical and resolved-volume treatments of the gas-phase have been employed. As with the classic d ² law (Spalding 1953), the semiempirical approach implements Nusselt and Sherwood number correlations to account for heat and mass transfer at the droplet surface. The other approach considered in this study directly simulates (or fully resolves) the gas-phase field around the droplet, including heat and mass transfer. Due to relatively slow evaporation rates of droplets that are consistent with respiratory aerosols, it is hypothesized that both approaches may employ rapid mixing assumptions for the liquid phase (Chen et al. 1997). That is, infinite conduction and diffusion may be assumed within the droplet such that liquid temperature and concentration are spatially constant but vary with time, i.e., the lumped capacitance method (Sirignano 1999). To test the validity of the rapid mixing model assumption for respiratory aerosols, resolved-volume simulations have also been conduced with a diffusion-limited model in which droplet temperatures are assumed to vary temporally and radially.

The semiempirical approach requires solution of a coupled set of ordinary differential equations (ODEs) for heat and mass conservation, which can be numerically computed very efficiently. However, this ODE-based approach may not be valid for conditions that violate the assumptions of the underlying empirical approximations. For instance, empirical correlations may not be valid across a range of chemical volatilities and may be inaccurate for the low-to-moderate Reynolds number conditions of respiratory aerosols. Furthermore, thermophysical properties of the gas-phase are assumed spatially constant, which may not effectively account for concentration dependence near the droplet surface.

To assess the implicit limitations of the ODE-based semiempirical model applied to respiratory aerosols, resolved-volume simulations have been employed. As indicated in Table 1, the resolved-volume models considered are of increasing complexity to allow for the isolation and evaluation of a number of critical assumptions. The first three resolved-volume approaches include rapid mixing assumptions for the liquid phase, denoted as RMM1 through RMM3. Specifically, the effects of calculating the gas-phase flow field (RMM1), spatially variable gas-phase specific heat (RMM2), and surface blowing (RMM3) are evaluated. The fourth resolved-volume model accounts for radial droplet temperature gradients that may arise for rapid evaporation conditions, i.e., a diffusion-limited model (DLM). In reality, spatial variations arise for both temperature and concentration fields within the droplet; however, the interdiffusion of more than two chemical species at similar concentrations is difficult to predict (Bird et al. 1960). As such, this study will focus on the effects of temperature gradients and use comparisons to empirical droplet evaporation data to assess the assumption of infinite mass diffusion within the droplet.

TABLE 1 Description of computational models implemented for droplet evaporation

Conditions: Model	Solution of the flow field	Spatially variable gas specific heat	Surface blowing	Internal droplet temperature gradient
ODE			X ^a
RMM1	X
RMM2	X	X
RMM3	X	X	X
DLM	X	X	X	X

In addition to the RMM and DLM approximations, a number of other simplifying assumptions can be applied for respiratory aerosol conditions. The relatively small droplet diameters of interest and low-to-moderate particle Reynolds numbers result in dominate surface tension forces, allowing for the assumption of spherically symmetric droplets with no internal vortex motion (Clift et al. 1978; Sadhal et al. 1997). Constant surface temperature and concentration values have been assumed based on expected rapid mixing within the droplet and the results of Chen et al. (1997). In addition, Niazmond et al. (1994) have shown that the thermal Marangoni effect induces significant surface flows, arising from temperature-dependent variations in surface tension, that aid in equalizing droplet surface temperatures and concentrations (Dwyer et al. 2000). For the gas-phase the assumptions of low mass fluxes and dilute chemical species, which simplify the mass transport equations, were made. Reynolds and Mach number conditions as well as moderate temperature variations allow for the assumptions of laminar incompressible flow. For the resolved-volume models, beginning with RMM2, the gas-phase specific heat is calculated at each location in the flow field and is based on weighted contributions from each mass fraction. All gas-phase properties have been calculated at the current film temperature.

Governing Equations and Numerical Methods

Conservation of energy for an immersed droplet, indicated by the subscript d, under rapid mixing model conditions can be expressed as

[1]

In the above equation m _d is the droplet mass, C _pd is the composite liquid specific heat, q _conv is the convective heat flux, n _s is the mass flux of each evaporating chemical species at the droplet surface, and L _s is the latent specific heat of each liquid component. The integrals are performed over the droplet surface area, A. Conservation of mass for an immersed droplet based on evaporating fluxes can be expressed as

[2a]

Implementing the chain rule, Equation (2a) is often rewritten in terms of droplet radius (Aggarwal et al. 1984):

[2b]

with r(t = 0) = R _o . For the semiempirical ODE-based model, surface-averaged heat and mass fluxes are assumed such that the surface integrals in Equations (1 and 2) may be written as

[3a]

and

[3b]

The primary difference between the semiempirical and resolved-volume solutions is defined by the method used to calculate the surface heat and mass flux values. For the semiempirical solution, heat and mass fluxes can be determined from appropriate correlations available for uniform flow. Based on 56 observations with particle Reynolds numbers from 2 to 200 and temperatures up to 220°C, Ranz and Marshall (1952) established the widely used correlation

[4a]

Blowing effects are absent in this expression, which is attributed to the fact that the observations by Ranz and Marshall (1952) were mostly below 90°C (Renksizbulut et al. 1991). At nonzero Reynolds numbers, experimental observations show a strong analogy between heat and mass transfer allowing for a corresponding Nusselt number correlation of

[4b]

The analogy between heat and mass transfer expressions is not exact largely due to property variations in the gas-phase associated with moderate to high flux rates (Clift et al. 1978). In a more recent analysis, Clift et al. (1978) correlated available data for Re _p < 400 with the expressions:

[5a]

and

[5b]

Once Nusselt and Sherwood numbers have been determined, the associated dimensional heat and mass transfer parameters can be computed from

[6a]

and

[6b]

where k _g is the thermal conductivity of the gas and D _s is the binary diffusion coefficient of species s with air. For the semiempirical ODE-based solution, these transport coefficients are employed to evaluate the mean fluxes at the droplet surface, i.e.,

[7]

and accounting for the convective effect of droplet evaporation (blowing velocity)

[8a]

where ω _s is the gas-phase mass fraction of each species and ρ _g is the gas mixture density, assumed to be that of air. Surface mass flux is often expressed in the following equivalent form

[8b]

which arises from an ambient solution (Re _p = 0) of the species conservation equation.

Provided evaporation-induced convective effects (blowing velocity) can be neglected and assuming low evaporation rates, the surface mass flux reduces to

[8c]

For the resolved-volume approach, heat and mass fluxes at the liquid-gas interface are determined from a solution of the surrounding flow field. The gas-phase conservation equations for laminar incompressible flow on a moving mesh in strong conservation law format can be written (Hawkins and Wilkes 1991)

Conservation of mass

[9a]

Conservation of momentum

[9b]

Conservation of energy

[9c]

Conservation of dilute chemical species

[9d]

In these equations, represents the moving mesh location and is the metric tensor determinate of the transformation, i.e., the local computational control-volume size. As such, terms of the form account for the gain or loss of the variable due to control-volume motion. For a stationary mesh, and .

In the resolved-volume approach, heat and mass fluxes are computed at the gas–liquid interface using the gas-phase surface gradients, i.e.,

[10a]

and

[10b]

These flux values are then applied to determine the area-averaged transient heat and mass transfer parameters,

[11a]

and

[11b]

which are written in non-dimensional form as the Nusselt (Nu = h d/k_g ) and Sherwood (Sh = h _m,s d/D _s ) numbers. For low mass flux cases in which blowing velocity may be neglected (i.e., RMM1), the term (1-ω _s,surf ) is absent in Equations (10b) and (11b).

For the resolved-volume solution with rapid mixing model assumptions (RMM1–RMM3), the area-averaged heat and mass fluxes may be substituted directly into Equation (1). If spherical droplet conduction is assumed, as with the DLM, conservation of energy for the droplet is governed by

[12]

The area-averaged surface flux values determined from the resolved-volume simulation are then used to establish the interface boundary conditions, and Equation (12) is numerically solved to establish the internal droplet temperature gradient at the current time.

For both the semiempirical and resolved-volume solutions, assumptions of thermodynamic equilibrium at the droplet surface, ideal gas conditions, and Raoult's law have been made, such that the gas-phase surface concentrations can be expressed as

[13]

In the above expression, x _s is the liquid-phase mole fraction of component s, R _s is the gas constant, and P _{sat, s} (T _d ) is the temperature dependent saturation pressure. To estimate the saturation pressure of each component on the surface, the Clausius-Clapeyron equation has been employed, i.e.,

[14]

where P _o,s and T _o,s represent saturation conditions at a reference state.

Statements for the conservation of energy and mass—Equations (1) and (2)—represent a coupled set of ordinary differential equations that can be solved for droplet temperature and radius over time. With the semiempirical approach, heat and mass transfer parameters are readily available for a specified particle Reynolds number such that multiple-point predictor-corrector algorithms can easily be used to solve the coupled ODE set. As such, a fourth-order Runge Kutta algorithm (Press et al. 1992) has been implemented for the ODE-based semiempirical solution to compute droplet flux values, temperature, radius, and mass over time for single and multicomponent droplets. Variable time-step and error control routines were included to ensure efficient and accurate solutions. The error control algorithm ensures that differences among solutions calculated using variable time increments Δt and 2 × Δt/2 are negligible at each step (Press et al. 1992; Longest et al. 2004).

Solution of the droplet heat and mass transport equations with the resolved-volume approach is complicated by the numerical evaluation of the surrounding flow field. The computational fluid dynamics program CFX 4.4 (ANSYS, Inc.), which is a finite-volume code that allows for multiblock structured meshes, was implemented to solve the flow field conservation equations. Mesh deformation was included to account for the effects of droplet evaporation. To improve computational accuracy on the scales of interest, a cgs (centimeters, grams, and seconds) system of units and double precision calculations were employed. A dimensionally based code was selected to avoid complications associated with geometry motion occurring due to droplet evaporation. All flow field equations were discretized to be at least second-order accurate in space. The third-order QUICK scheme was employed for the advection terms in order to better resolve the upstream diffusional effects that arise for the lower Reynolds number flows of interest. The use of moving grids to resolve droplet evaporation limits temporal discretization to first-order accuracy, i.e., a fully implicit backward Euler scheme. However, time-step size and not method order determine solution accuracy, such that an acceptable solution can be achieved for a sufficiently small time-step.

Once the gas-phase heat, mass, and flow fields were determined for a time-step, effects on the particle are evaluated. Convective and mass fluxes are computed at the droplet surface using Equations (10a) and (10b). Surface gradients of temperature and mass fraction were computed to be second-order accurate on the deformable nonuniform grid surrounding the droplet (Tannehill et al. 1997). Given the use of a first-order method in time for the flow field equations, a first-order Euler approximation was also used to determine the droplet temperature and component mass at each solution step. Total droplet mass and liquid mass-fraction can then be directly computed. Due to numerical accuracy, it is most effective to determine next the new droplet volume, composite density, and finally the diameter and mixture specific heat. Equations (11a) and (11b) are then used to calculate the area-averaged heat and mass transfer parameters at the current time-step. Based on the new spherical diameter, the mesh resolving the flow field around the droplet is adjusted. The solution is then advanced by setting the new droplet temperature and mass fraction at the spherical surface and repeating the flow field solution.

The solution of the parabolic expression for droplet conduction, Equation (12), was computed using a Crank-Nicholson scheme. Singularity at the droplet center was addressed by only considering the second derivative spatial term at this location (Tannehill et al. 1997). To minimize numerical diffusion, spatial discretization and time-steps were selected to satisfy the condition α Δt/Δr ² = 0.5, where α is the composite liquid thermal diffusivity.

Properties that must be set for each of the chemical species contained in a droplet include liquid density (ρ_l ), molecular weight (M_l ), liquid mass fraction (ω_l ), gas constant (R _s ), latent heat of vaporization (L _s ), liquid specific heat (C _p,l ), reference saturation pressure and temperature (P _sat,s (T _d )), and the binary gas diffusivity constant of each component with air (D _s ). The initial droplet diameter and temperature are also explicitly set. For a specified initial set of liquid mass fractions and a diameter based on spherical volume (V), the liquid mixture density of the droplet (ρ _d ) is determined by solving a coupled equation set of the form

[15]

where V_s is the volume of each component. For the gas-phase, the local concentration-dependent specific heat depends on the mass fractions of air and the n dilute chemical species present in vapor form, i.e.,

[16]

To resolve diffusion on the micron-size spatial scales of the droplets, a very small time-step is needed. Furthermore, the use of moving grids and the fully implicit backward Euler scheme severely limit the allowable time-step size. Using numerical experimentation, it was found that initial resolution of the developing gas-phase temperature and mass concentration profiles, along with accurate prediction of droplet temperature changes, required a time-step on the order of Δt = 2 × 10⁻⁴ s for the resolved-volume approach. Considering that droplet evaporation often requires minutes to several hours, the associated number of time-steps is unreasonable. However, it was found that once pseudosteady temperature and concentration fields developed, time-steps could be increased significantly as further evaporation occurs. The upper limit for time-step size after pseudosteady concentration fields have developed was found to be on the order of Δt ≈ 0.1 s.

The external flow system of an isolated droplet represents a large flow environment with a relatively small disturbance field, especially for the higher Reynolds number flows considered. As such, significant residual reductions of all equations are required to ensure convergence. Numerical experimentation indicates that convergence could be assumed, based on a 1% relative local error criterion on all variables, once initial global residual values have been reduced by five to six orders of magnitude. In addition, the rate of residual reduction was also observed and used to establish convergence for all equations. While strict residual criteria had to be enforced for the external flow field compared to typical internal conditions, increased under-relaxation factors allowable for the low Reynolds number solutions reduced the number of iterations required to reach convergence, thereby decreasing solution time.

Geometry and Boundary Conditions

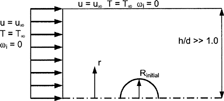
To assess the resolved-volume evaporation models considered, a system consisting of a two-dimensional spherical axisymmetric droplet in an infinite gas was employed (Figure 1). A closed system was formulated for numerical analysis by specifying walls far from the droplet in a manner that does not interfere with heat and mass transfer characteristics. Uniform flow was specified sufficiently far upstream from the droplet, representing motion relative to the surrounding air, i.e., particle slip. Zero mass concentration and ambient temperature conditions was specified on the lateral boundaries and upstream of the droplet. While slip is allowed on the boundary walls, the droplet surface is considered rigid due to high relative surface tension forces, resulting in a no-slip boundary condition. Droplet surface temperature is assumed spatially constant and is specified according to initial and previous time-step conditions. Based on droplet temperature, saturation pressure is determined for each species from the Clausius-Clapeyron relation, Equation (14), and is used to calculate the constant gas-phase surface concentration, Equation (13).

FIG. 1 Axisymmetric two-dimensional geometry of a spherical droplet in a nearly infinite media (from Longest and Kleinstreuer 2004 with permission).

Comparisons to Empirical Data

Respiratory aerosols are characterized by a wide range of particle diameters and Reynolds numbers. Particles inhaled into the extrathoracic region may vary from the nanometer range to several hundred microns (ACGIH 1997; Hinds 1999). Respiratory aerosols on the order of 5 μm have a momentum response time of approximately 0.08 ms, indicating nearly instantaneous acceleration to surrounding conditions and resulting in a particle Reynolds number of nearly zero. In contrast, the momentum response time of a 100 μm liquid aerosol is on the order of the mean residence time within the upper airways through the trachea, i.e., approximately 30 ms. For an inhaled 100 μm droplet initially at rest, the particle Reynolds number is approximately Re _p = 30 in the mid-oral cavity region and Re _p = 10 in the orthopharynx. In addition, near-wall drag may significantly increase particle Reynolds numbers for respiratory aerosols of all sizes (Dahneke 1974; Loth 2000; Longest et al. 2004).

In this study, particle diameters less than 5 μm are not considered to avoid the influence of noncontinuum effects on heat and mass transfer. Hence, droplet diameters ranging from 5 to 100 μm within the upper respiratory tract with particle Reynolds numbers ranging from 0 < Re _p ≤ 30 are of interest. Empirical data satisfying these diameter and Reynolds number specifications was not found for evaporating multicomponent aerosols of variable volatility. However, evaporation model performance is expected to be similar for spherical droplets below the onset of external vortex shedding (Re _p  ≈ 130) and internal liquid vortex formation (Clift et al. 1978). In addition, relatively low evaporation temperatures are necessary. Based on these specifications, the empirical results of Runge et al. (1998), which are characterized by 30 ≤ Re _p ≤ 127, d ≤ 600 μm, and T ≤ 300 K, have been selected as an acceptable match to the respiratory aerosol conditions of interest. For the maximum particle Reynolds number and diameter considered, the droplet Weber number is approximately 10⁻⁴, which indicates dominance of the surface tension over inertial forces, such that spherical droplets may be assumed.

RESULTS

Representative computational solutions of the flow field equations for an n-heptane droplet (T _∞ = 298 K and Re _p = 30.2) are shown in Figures 2a and b, including velocity vectors, contours of velocity magnitude, and mass fractions. Moderate momentum diffusion due to viscous forces results in noticeable influences on the flow field upstream of the droplet and rapid downstream recovery of a uniform velocity profile. Upstream mass diffusion is much less pronounced due to the relatively high Schmidt number of n-heptane in air (Sc = 2.4) and the contour levels selected.

FIG. 2 Representative computational flow field results: (a) Velocity vectors, contours of velocity magnitude, and (b) mass fraction for an axisymmetric 480 cm n-heptane droplet far from the wall with T_∞ = 298 K, u_∞ = 100 cm/s ω_∞ = 0, and Re _p = 30.2 (from Longest and Kleinstreuer 2004 with permission).

Resolved-volume simulations were used to evaluate the available Sherwood and Nusselt number correlations that are needed for the semiempirical ODE-based solution approach. Results are compared to the empirical relations of Ranz and Marshall (1952) and Clift et al. (1978) for respiratory aerosol conditions (0 ≤ Re _p ≤ 30) in Figures 3a and b. Numerical estimates have been computed using RMM1 due to the absence of variable property effects and blowing velocity in the low-to-moderate flux correlations. Considering Sherwood number values, the correlation of Clift et al. (1978) provides the best fit to the numerical data. The Ranz and Marshall (1952) correlation marginally overpredicts the Sherwood values for particle Reynolds numbers less than approximately 2. Retaining the widely used form of the Ranz and Marshall (1952) correlation, a best fit to the numeric Sherwood data in the range of 0 ≤ Re _p ≤ 30 results in

[17a]

FIG. 3 Comparison of two-dimensional simulation results for uniform flow to (a) Sherwood and (b) Nusselt number correlations of Clift et al. (1978) and Ranz and Marshall (1952).

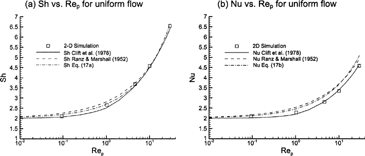
This relation provides an improved representation of the data (r ² = 0.99 and p-value ≤ 0.01), especially in the critical range of Re _p ≈ 1. Considering Nusselt number values, the more complex expression of Clift et al. (1978) provides the best fit to the numerical results. Applying the heat and mass transfer analogy, a Nusselt number relation comparable to Equation (17a), can be written

[17b]

This expression results in improved Nusselt number predictions in the range of Re _p ≈ 1 compared to the Ranz and Marshall (1952) correlation. While Nusselt number estimates calculated using Equation (17b) are marginally higher than the simulated values, the effect on the evaporation solution is not expected to be large considering the relatively mild temperature variations of interest. As such, Equations (17a) and (17b) have been used in the semiempirical calculation of droplet evaporation based on their simplicity and familiar form. The effects of implementing the more exact expressions of Clift et al. (1978) were also assessed, as discussed below.

Based on similarity to multicomponent respiratory aerosol conditions, the evaporation models considered were compared to the experimental results of Runge et al. (1998) for single- and two-component droplets (Figures 4a–d). Considering a relatively volatile droplet of n-heptane at near body temperature conditions (T_∞ = 298 K), the models considered predict evaporation consistent with one of two rates (Figure 4a). The ODE and RMM1 solutions significantly overpredict droplet evaporation. Minor differences between these two models arise due to variations in the empirical and computed Nusselt numbers shown in Figure 3b. In fact, implementing the expression of Clift et al. (1978) in the semiempirical ODE approximation results in a solution that is practically indistinguishable from the RMM1 prediction. In contrast to the ODE and RMM1 solutions, the remaining models all predict the empirical droplet evaporation rate of n-heptane inline with experimental results (Figure 4b). The only difference between the RMM1 and RMM2 solutions is that the latter accounts for concentration-dependent gas-phase specific heat throughout the flow field. As such, it appears that an accurate estimate of variable specific heat is a significant factor, resulting in the improved prediction of the RMM2 approximation. Accounting for the blowing velocity (RMM3) only marginally increases the evaporation rate compared to RMM2, largely due to a marginal increase in wet-bulb temperature. Inclusion of a radial droplet temperature gradient (DLM) in addition to the blowing velocity results in a reduction in the evaporation rate arising from a more accurate prediction of droplet surface cooling; however, this effect appears negligible.

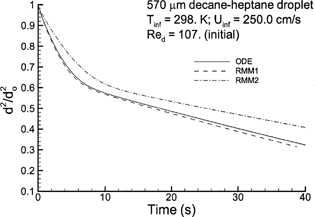
FIG. 4 Computational estimates of normalized droplet surface area (d ²/d _o ²) over time compared to the experimental results of Runge et al. (1998) for (a) high volatility n-heptane with T_∞ = 298 K and Re _p = 30.2; (b) high volatility n-heptane with T_∞ = 272  K and Re _p = 107.3; (c) low volatility n-decane with T_∞ = 272  K and Re _p = 94.1; and (d) multicomponent 50:50 heptane-decane mixture with T_∞ = 272 K and Re _p = 107.0. Descriptions of the numerical models are given in Table 1.

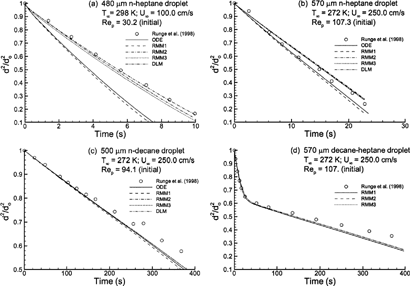
In comparison to Figure 4a, Figure 4b illustrates evaporation of a similar 570 μm n-heptane droplet in a lower temperature environment, as may occur in the upper respiratory airways under cold external conditions. Despite a significant in Reynolds number (107.3 versus 30.2), the lower temperature environment results in a significant reduction in the droplet evaporation rate (Figure 4b). For n-heptane with Re _p = 107.3 and T _∞ = 272 K, differences between the constant and variable specific heat models remain evident but are less pronounced than in Figure 4a. The constant property assumption of the ODE and RMM1 solutions results in a marginal overprediction of the evaporation rate. In contrast, the models that do account for variable gas-phase specific heat result in a marginal underprediction of the evaporation rate. Furthermore, the reduced evaporation rate has also largely eliminated differences among the RMM2, RMM3, and DLM solutions.

The effects of further decreasing the evaporation rate by considering a much lower volatility compound are shown in Figure 4c. Due to the high boiling point of n-decane, evaporation at T_∞ = 272 K and Re _p = 94.1 requires on the order of 400 s for the droplet surface area to be reduced by a factor of two. Under these conditions, differences among the evaporation models considered are much less pronounced. Moreover, all models considered appear to predict the evaporation rate effectively.

Evaporation results for a 570 μm droplet consisting of a 50:50 or 50% heptane-decane mixture are shown in Figure 4d in comparison to the results of Runge et al. (1998). Due to considerable overlap in the results, ODE and DLM solutions are not shown. For the relatively low temperature environment (T_∞ = 272 K) and moderate Reynolds number (Re _p = 107) considered, all models match experimental results and indicate two distinct phases of evaporation. First, a majority of the lighter heptane evaporates resulting in a rapid diameter reduction during the initial 30 s. Thereafter, the droplet is primarily composed of heavier (or less volatile) decane, resulting in a more gradual evaporation rate. Beyond 250 s, the models moderately overpredict the evaporation rate. However, this minor discrepancy is consistent with the results for pure decane (Figure 4c). Inclusion of mass concentration gradients within the droplet will slow the initial evaporation of lighter components, thereby increasing droplet evaporation at later times. This increase in droplet evaporation rate will further separate the numeric and experimental results. Therefore, effects of internal mass gradients are expected to be negligible for this scenario.

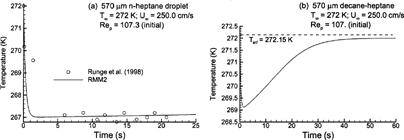
Considering droplet temperature, rapid cooling occurs until the droplet wet-bulb condition is reached, and then remains relatively constant due to the balance between evaporative heat loss and convective effects. In comparison to the experimental results of Runge et al. (1998) for the n-heptane droplet considered in Figure 4a, the RMM2 solution matches the observed droplet temperatures very well (Figure 5a). Similar performance is also observed for all other solutions considered. For the 50% heptane-decane mixture, cooling associated with rapid n-heptane evaporation initially results in a large temperature decline (Figure 5b). As the heptane is depleted, evaporative cooling effects are reduced, and the droplet temperature rises. Eventually, the droplet temperature remains constant at the wet-bulb state for a decane droplet evaporating under the specified conditions.

FIG. 5 Variable property (RMM2) estimates of droplet temperature over time for: (a) n-heptane with T_∞ = 272 K and Re _p = 107.3; and (b) multicomponent 50:50 heptane–decane mixture with T_∞ = 272 K and Re _p = 107.0.

Due to relatively cold temperatures and resulting slow evaporation rates, little difference was observed among the evaporation models applied to the heptane-decane mixture considered in Figure 4d. However, comparison of Figures 4a and b indicates the significance of temperature on factors affecting droplet evaporation. The computed evaporation rate of a multicomponent 50% heptane–decane droplet for near body temperature conditions (T_∞ = 298 K) and Re _p = 107 is shown in Figure 6. For this variable volatility configuration, significant differences are observed in the simulated evaporation rate due to inclusion of concentration-dependent gas-phase specific heat (i.e., RMM1 versus RMM2). Results for the RMM3 and the DLM solutions were practically indistinguishable from the RMM2 approximation. Therefore, it may be necessary to account for variable gas-phase specific heat when computing multicomponent respiratory droplet evaporations where relatively high volatility components are present at significant concentrations.

FIG. 6 Semiempirical and resolved-volume simulations of droplet evaporation for a multicomponent 50:50 heptane–decane mixture with T_∞ = 298 K and Re _p = 107. Results for RMM3 and the DLM are practically indistinguishable from the RMM2 solution.

Accounting for variable gas-phase specific heat resulted in significantly slower evaporation rates in some cases due to variation in droplet temperature conditions. Considering the n-heptane droplet at T_∞ = 298 K and Re _p = 30.2 (Figure 4a), droplet temperatures calculated with RMM1 and RMM2 were 284.2 and 275.4, respectively. The reduced droplet temperature of the variable specific heat case results in lower surface mass fractions, which produce a reduced evaporation rate. Viewed another way, the inclusion of variable gas-phase specific heat for this high volatility compound effectively insulates the droplet, thereby reducing heat transfer from the surrounding environment, which drives evaporation. This variable property effect results in a significantly reduced Nusselt number compared to predictions from the empirical correlations considered. For instance, the Nusselt numbers computed from constant (RMM1) and variable (RMM2) property models applied to the n-heptane droplet are approximately 4.0 and 2.1, respectively. In contrast, little variation was observed in calculations of the Sherwood number. It would be highly advantageous if this variable property effect could be approximated using the semiempirical ODE-based approach. However, incorporation of a mass-fraction-weighted gas-phase specific heat on the droplet surface, which enters the ODE solution through the Prandtl number, affected the final result by less than 2%. Moreover, inclusion of blowing velocity had a negligible effect on all solutions considered.

Relevant to respiratory aerosol conditions, Runge et al. (1998) considered the evaporation of a JP-8 droplet in a 294  K environment with a Re _p of 120.3. Solutions of selected evaporation models (i.e., RMM1 and RMM2) have been evaluated for a 12-component surrogate mixture suggested by Edwards and Maurice (2001) (Table 2) and are compared to the experimental results of Runge et al. (1998) (Figure 7). The significant discrepancy between the computed and empirical results is likely due to an incorrect surrogate mixture for droplet evaporation or inaccuracy of the rapid mixing models for droplets consisting of a significant number of compounds. Inclusion of concentration gradients in the droplet will slow the initial evaporation rate by limiting transport of high volatility compounds to the surface, in the absence of Hill vortex formation. However, evaporation at later times will be increased due to continued availability of the lighter components. It appears that the slopes of the predicted evaporation curves remain greater than or equal to the experimental data. This indicates that internal gradients may not be responsible for the discrepancy between predicted and experimental values, which is consistent with the computed results for a binary heptane–decane droplet. Based on calculations with the RMM2 approximation, a surrogate mixture that accurately predicts droplet evaporation is defined in Table 2, and evaporation rates are shown in Figure 7. For the suggested surrogate model, differences among the RMM1 and RMM2 solutions are largely negligible, which indicates that either a reduced presence of volatile hydrocarbons or a reduced evaporation rate associated with multiple components minimizes the need to account for variable gas-phase specific heat in this case. As such, the ODE-based semiempirical solution used with the suggested surrogate mixture provides a computationally effective method for evaluating the evaporation of potentially toxic JP-8 aerosols in the respiratory tract.

FIG. 7 Computational estimates of normalized droplet surface area (d ²/d _o ² ) over time compared to the experimental results of Runge et al. (1998) for a twelve-component JP-8 surrogate mixture.

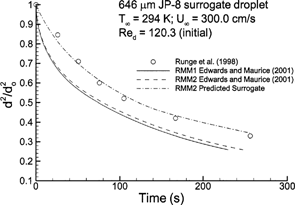
TABLE 2 Twelve component JP-8 surrogate

Component	Wt % Edwards and Maurice (2001)	Wt % Computed with RMM2
iso-octane	5.0	0.25
Methyl cyclohexane	5.0	0.25
m-xylene	5.0	0.25
Cyclooctane	5.0	0.25
Decane	15.0	7.0
Butyl benzene	5.0	3.0
1,2,4,5 tetramethyl benzene	5.0	14.0
Tetralin	5.0	15.0
Dodecane	20.0	23.0
1-methyl naphthalene	5.0	8.0
Tetradecane	15.0	17.0
Hexadecane	10.0	12.0

DISCUSSION

In this study, semiempirical and resolved-volume evaporation models were assessed based on comparisons to empirical data for conditions consistent with inhalable multicomponent aerosols in the upper respiratory tract. The effects of implementing empirical correlations, variable gas-phase specific heats, blowing velocity, and internal droplet temperature gradients in computing the evaporation of multicomponent respiratory aerosols were evaluated. Of the parameters considered, variable gas-phase specific heat had the largest effect on evaporation, which was realized for high volatility compounds at near body temperature conditions. Accounting for this phenomenon, an appropriate representative or surrogate mixture of a complex multicomponent hydrocarbon fuel (JP-8) was identified for future toxicological analysis. In addition, other factors that may influence the evaporation of multicomponent inhaled respiratory aerosols include hygroscopic and rarefied flow effects, as well as reduced internal droplet convective transport for aerosols smaller than those considered in this study.

Other studies have shown the importance of including variable gas-phase properties for evaporating volatile droplets in moderate-to-high temperature combustion applications (T ≥ 400 K; Chen et al. 1997; Chiang and Kleinstreuer 1993). However, due to a relatively low temperature environment, variable gas-phase properties are typically neglected for respiratory aerosols (Finlay 2001; Zhang et al. 2004). Results of this study indicate that concentration dependent gas-phase specific heat should be taken into account for respiratory aerosols that contain species of similar volatility to heptane at significant concentrations. For instance, variable gas-phase specific heat is expected to influence the evaporation rate of droplets with significant amounts of toxic single-ring aromatic compounds, e.g., benzene, and medical aerosol propellants, e.g., HFA 134a. However, evaporation of multicomponent JP-8 aerosols was not largely affected by variable gas-phase properties for the conditions studied. This is largely due to the wide range of volatilities present in which heavier compounds limit the availability of the lighter fractions on the surface, via Equation (13), thereby reducing the evaporation rate. As such, a semiempirical ODE solution is appropriate for the evaporation of potentially toxic JP-8 aerosols in the respiratory tract. To compute effectively the evaporation of other aerosols for which variable gas-phase specific heat does play a significant role, semiempirical methodologies are in need of further development. Furthermore, effects of a solid particle core surrounded by a liquid layer, as may occur with aerosols generated by metered dose inhalers, warrants additional investigation.

Due to wide use and potentially toxic effects of JP-8 fuel, other studies have modeled the low temperature evaporation of these aerosols. Catoire et al. (1999) and Benaissa et al. (2002) compared results of the homogeneous mixture model of Gauthier (1996) for JP-8 to the low-temperature suspended-droplet evaporation results of Runge et al. (1998). Results of their homogeneous mixture model were in moderate agreement (10–30%) over an indicated time period of 80 s. However, the predicted evaporation curve diverges from the experimental results such that significant discrepancies will occur over the longer time period measured by Runge et al. (1998). To correct this divergence, Zhang et al. (2004) implemented a modified composite gaseous diffusion coefficient. Still, the homogeneous mixture model is unable to differentiate among the evaporation of lighter potentially toxic components and heavier inert carriers. In contrast, the evaporation models assessed in this study, in conjunction with the surrogate mixtures, can be used to effectively compute multicomponent droplet evaporation, which affects deposition, and identify the vaporization of individual potentially toxic markers. As such, the local deposition and absorption of individual chemical species can be modeled, which is a critical component for accurate dosimetry estimates and toxicokinetic analysis.

Variations in the computed JP-8 surrogate blend and the formulation suggested by Edwards and Maurice (2001) may be attributed to several factors. The surrogate of Edwards and Maurice (2001) was established for combustion applications and is based on the oxidation characteristics of JP-8, which does not ensure an equivalent distillation curve or comparable droplet evaporation rates. In addition, the composition of a JP-8 fuel droplet is continually changing due to evaporation. In the experiments of Runge et al. (1998), droplet evaporation data may not have been recorded before some of the lighter components were removed by ambient diffusion from either the droplet or the original batch fuel. This observation emphasizes the need to model both aerosol and vapor transport for accurate dose assessments.

Compared to the time required for droplet evaporation, mean residence times in the upper airways are very brief (e.g., 30 ms). However, Zhang et al. (2004) showed that droplet evaporation had a significant effect on the deposition of 5 and 10 μm JP-8 fuel aerosols in the upper respiratory tract. This effect is largely due to the increased residence time of near-wall particles in comparison to mean flow. The presence of the wall creates an additional drag force on the particle (Dahneke 1974; Loth 2000; Longest et al. 2004), which effectively increases the particle Reynolds number and results in enhanced evaporation rates. Flow characteristics within the upper respiratory tract may also alter droplet evaporation rates. Enhanced conduction and diffusion due to near-wall proximity and shear stress have been shown to significantly increase heat and mass transfer in large droplets (Longest and Kleinstreuer 2004). Furthermore, turbulent eddies that may arise in the upper respiratory tract will likely increase evaporation rates, potentially leading to appreciable internal heat and mass gradients.

For the droplets considered in this study, thermal Biot numbers are on the order of unity, which indicates that the rate of conduction within the liquid droplet is comparable to external convection. In contrast, comparisons of the numerical models to empirical results indicate that thermal concentration gradients within the droplets considered are largely negligible. The validity of the rapid mixing assumption is therefore due to convective mixing effects within the droplets driven by inertial or viscous surface forces. However, Hill vortex formation is not expected for the droplet sizes and Reynolds numbers considered due to some degree of surface contamination (Clift et al. 1978; Sadhal et al. 1997). Therefore, an alternative internal convention mechanism may exist within the droplet that results in well-mixed temperature and concentration profiles. Further studies are required to quantify internal convective mechanisms and evaluate their persistence for droplets smaller than those considered here. Should the prediction of internal convective effects become necessary, an effective conduction model could be formulated to enhance numerical efficiency.

Both hygroscopic and rarefied flow effects, which frequently arise for respiratory aerosols, can be accounted for with the models evaluated in this study. Considering a droplet in air, noncontinuum effects begin to become significant for diameters less than 5 μm (Clift et al. 1978). Similar to the Cunningham correction factor for drag in rarefied flows, theoretical and empirical expression are available for heat and mass transfer. Clift et al. (1978) suggested an empirical correlation that reduces the Nusselt number value of a 5 μm droplet in air by approximately 5%. Alternatively, corrections for the heat and mass flux terms are proved by Qu et al. (2001a, b). The presence of water vapor will also impact droplet evaporation rates in the respiratory tract. Gas-phase conditions, including specific heat, can be approximated from knowledge of the spatially and temporally variable local respiratory humidity. Diffusion coefficients for each hydrocarbon in an air-water mixture can be approximated from the Stefan-Maxwell relations (Bird et al. 1960). Furthermore, water vapor condensation onto an evaporating droplet may be approximated as an additional species in the multicomponent models described.

In conclusion, effective models for predicting multicomponent aerosol evaporation in the upper respiratory airways that are capable of identifying individual compounds for a range of volatilities were assessed. Resolved-volume simulations indicated that a semiempirical ODE solution including a rapid mixing model assumption is appropriate for large respiratory aerosols except in cases where high volatility compounds affect the local gas-phase specific heat. In conjunction with appropriately selected surrogate mixtures, the models considered provide an effective method for computing droplet evaporation of complex multicomponent hydrocarbon mixtures in a manner that can track individual chemical species for computational dosimetry analysis. The significant effect of variable gas-phase specific heat on respiratory aerosol evaporation identified in this study obviates the need for improved semiempirical models that can account for this phenomenon. Further experimental and numerical studies are also necessary to better assess the evaporation behavior of multicomponent respiratory aerosols smaller than those considered in this study, especially for low particle Reynolds number conditions in which internal convection may be reduced.

Acknowledgments

This effort was sponsored by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under graft number F49620-01-1-0492 (Dr. Walt Kozumbo, Program Manager). The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright notation thereon. Use of the software package CFX4 from ANSYS, Inc. (Canonsburg, PA, USA) and access to the SGI Origin 2400 at the North Carolina Supercomputing Center (Research Triangle Park, NC) are gratefully acknowledged.

Notes

^a Not included in ODE solution shown.