An Improved Model for Anisotropic Dispersion of Small Particles in Turbulent Shear Flows

In order to investigate the dispersion of small particles in a turbulent shear flow, a new model based on accurate modelling of the directional dependence of the fluid Lagrangian time scales is proposed and tested against experimental data in a gas–solid channel flow. The continuum phase is described by a nonlinearlow-Reynolds k-ϵ model, thus allowing a fine description of turbulence anisotropy and near-wall effects. The dispersed phase is described by a Lagrangian stochastic method, which is formulated in order to take into account the nonhomogeneity and the anisotropy of turbulence. The fluid Lagrangian time scales in each direction are assessed following a recent proposal supported by channel flow DNS computations. The integral time scales of the fluid seen by the particles are then estimated in taking the inertia and crossing trajectory effects into account. The numerical predictions (particle and fluid statistical quantities) obtained by means of this time scale model and previously available time scale models are compared and confronted to recent experimental data from the literature about the motion of small solid particles in a turbulent vertical channel flow. It is shown that the new Lagrangian time scale formulation leads to very satisfactory results compared to the measurements.

INTRODUCTION

Modelling of gas–solid or gas–droplet turbulent flows is a key issue for industrial, environmental, or biomedical engineering. Numerical simulation of such two-phase flows is generally dealt with using two kinds of approaches. In the two-fluid (also called Eulerian–Eulerian) approach, the two phases are considered as interacting and interpenetrating continua, whereas the Eulerian–Lagrangian method involves Lagrangian monitoring of solid particles or droplets in the gaseous flow. Comparisons between these two descriptions have been proposed by many authors (Crowe 1991; Durst et al. 1984; Stock 1996). These studies show that although the two-fluid approach is less time consuming and more efficient, the Lagrangian description of the solid phase allows better consideration of the physical phenomena that govern particle motion. In the particular case of confined flows, the latter technique enables better modelling of the near-wall behavior, for instance.

In this work, an improved Eulerian–Lagrangian numerical model is proposed to describe the transport of solid particles in a fully developed turbulent channel flow. The fluid flow is described by the usual Reynolds-averaged Navier–Stokes (RANS) equations. In order to describe the near-wall region accurately, an anisotropic k-ϵ low Reynolds closure model is selected. The trajectories of a large number of solid particles injected in the gas flow are then numerically tracked in the computational domain. The motion of each particle is described by a set of six equations expressing the linear and angular momentum conservation, the rotational motion being taken into account owing to the high angular velocities induced by frictional particle–wall collisions. Such conservation equations involve several fluid–particle interaction forces and torques (described later) that require the calculation of the instantaneous velocity of the fluid at the particle location. Since a RANS model is used to describe the fluid flow, only mean quantities such as the mean velocity field or the mean turbulence characteristics are directly available. It is thus necessary to reconstruct from these data the random nature of the motion along the particle trajectory.

Two main ways of evaluating the instantaneous fluid velocity at the particle location have been developed in the literature. In the so-called eddy interaction models (Ormancey and Martinon 1984; Graham 1996) it is considered that the particle successively crosses several random discrete eddy structures, each of them defined by its lifetime, influence zone, and intensity. Such models, which have been widely developed and discussed, are able to render complex physical phenomenon such as the so-called crossing trajectory effect, which reduces the particle dispersion in case of nonzero mean relative velocity, and the additional decrease in the transverse directions called continuity effect. However, it still cannot handle anisotropy or inertia effects properly.

A more recent family of models involves first-order autoregressive stochastic processes to correlate the fluid velocity seen by a particle at its new location with the fluid velocity at the previous position. Among such models, two-step methods have been developed during the past decade (Berlemont et al. 1990; Lu et al. 1993; Burry and Bergeles 1993; Zhou and Leschziner 1996; Pascal and Oesterlé 2000), in which the new velocity fluctuation is predicted by means of a first-order time series for the fluid particle path followed by a spatial step, which is written in a similar manner using a given Eulerian length scale. The drawbacks of such two-step methods, as identified and discussed by Pozorski and Minier (1998), result from the inconsistency of the spatial step which leads to incorrect prediction of the kinetic energy of the fluid seen and of the inertia effect on the particle dispersion.

In contrast with these two-step approaches, the model in use in this study is a one-step correlation model that requires the evaluation of the integral time scales of the fluid seen by the particle in each direction, T _i *, in order that the instantaneous fluid velocity seen at time level t can be predicted directly from the fluid velocity seen at time level t + Δ t, tracking the same discrete particle (Simonin et al. 1993; Pozorski and Minier 1999; Pétrissans et al. 2002). Unfortunately, there is no general expression so far to evaluate such integral scales, which are only available in some limited cases by means of direct numerical simulation. Even though methods have been suggested to estimate the time scales of the fluid motion seen by the particles, the proposed correlations are still restricted to homogeneous isotropic turbulence. Wang and Stock (1993), as well as Pozorski and Minier (1998) or Derevich (2000), proposed expressions of T* accounting for the inertia effect depending on T _L and T _mE , the fluid Lagrangian and moving Eulerian integral time scales, respectively (leaving out the index due to the isotropy assumed by these authors). The crossing trajectory effect can be introduced in such models following the principle of Csanady's derivation (Csanady 1963; Wang and Stock 1993). Making the assumption that these expressions, validated only in the case of isotropic homogeneous turbulence, can be extended to shear flow cases, the fluid time scales in each direction, T _Li and T _mEi , are the remaining unknowns to be evaluated.

The main purpose of this work is therefore to assess the performance of an anisotropic dispersion model based on a recent proposal for the prediction of the directional dependence of the fluid Lagrangian integral time scales (Rambaud et al. 2002). This model is compared to the anisotropic formulation used by Berlemont et al. (1990) or Zhou and Leschziner (1996) and to an isotropic model. Numerical computation of statistical quantities using these three formulations are then compared to the experimental data resulting from the study of the motion of small glass beads in a fully developed turbulent vertical channel flow (Khalitov and Longmire 2003).

MODEL DESCRIPTION

Fluid Phase

As briefly mentioned in the introduction, the gas flow is calculated by means of a Reynolds-Averaged Navier Stokes (RANS) model, thus requiring some closure assumptions to express the Reynolds stresses ⟨u _i u _j ⟩. Here we introduce the classical concept of turbulent kinetic energy k and its dissipation rate ϵ, whose transport equations are modelled and solved to predict the mean flow dynamics. Closure is achieved using the Nonlinear Eddy Viscosity Model (NEVM) proposed by Speziale (1987), in which turbulence anisotropy is taken into account in the expressions of the Reynolds stresses. In the present fully developed channel flow configuration—denoted by x, y, z in the streamwise, wall-normal, and spanwise directions, respectively—the normal Reynolds stresses determined from this nonlinear model are

where ⟨U _x ⟩ is the local mean velocity in the channel, ν _t is the turbulent viscosity, and the model constants are C _μ = 0.09 and C _D = 1.68 (Speziale 1987). The turbulent shear stress obeys the usual form,

In order to improve precision in the near-wall region where the viscosity effects have to be taken into account, modifications of the standard k-ϵ model have been proposed by several authors (e.g., Lai and So 1990; Myong and Kasagi 1990; Yang and Shih 1993). These models generally introduce “damping” functions that allow the transport equations of k and ϵ to be valid close to the wall. From a study by Hrenya et al. (1995), the model elaborated by Myong and Kasagi (1990) was shown to offer the best performance for fully developed pipe flow. Therefore this model, which the reader is referred to for details, has been selected here and implemented in the Eulerian description of the fluid phase flow.

Discrete Phase Modelling

In order to predict the discrete phase motion, the trajectories of a large number of particles released in the gas flow field are computed. The particles are assumed to be spherical and rigid. Calculation of trajectories is performed through integration of the particle equations of motion along the channel. Due to the particle–wall interactions, which are not supposed to be frictionless, particles may be subjected to significant rotational motion, which is to be taken into account in expressing the particle–fluid interactions. The particle motion is, therefore, described by a set of six scalar equations expressing the linear and angular momentum conservation:

where V and Ω are the linear and angular velocity vectors of the particle; m _p and d _p denote the particle mass and diameter, respectively; and g is the gravitational acceleration. Besides the quasi-stationary drag force F _D , which is expressed according to usual standard correlations for the drag coefficient in terms of the sphere Reynolds number, particles experience a torque Γ and a lift force F _L that may be of significant importance, particularly for large particles. The lift force is calculated through the correlation proposed by Oesterlé and Bui Dinh (1998), valid for a large range of Reynolds numbers, and the torque is expressed according to the correlation of Dennis et al. (1980). Owing to the high particle-to-fluid density ratio, nonstationary contributions to the drag force such as history force, added mass force, and displaced force, can be neglected.

In case of particle–wall collision, the new components of the translational and rotational velocities are calculated as a function of the velocity components before collision using the linear and angular momentum equations and Coulomb's law during the very short contact duration. The parameters needed for the processing of collisions are the coefficient of restitution e and the coefficients of static and kinetic friction f and f ₀. Additionally, in order to take into account the effects of wall roughness and possible nonsphericity of particles, the virtual wall model proposed by Sommerfeld (1992) is used, i.e., the actual wall is replaced by a virtual wall whose inclination is selected from a centered Gaussian distribution with given standard deviation σ_γ. The so-called shadow effect is properly handled by discarding any unphysical rebound.

The particle-to-air mass loading in the experiments of Khalitov and Longmire (2003) being of order 10%, the collisions between particles are not considered in this study. For similar reasons, the solid phase can be assumed to have negligible influence on the fluid flow, so that the only coupling effect is the fluid-to-particle one, i.e., one-way coupling.

From a practical point of view, after the Eulerian computation of the fluid flow field, the Lagrangian step is performed by tracking a large number of particles, with the fluctuating quantities of the fluid flow being calculated at each particle location by means of the dispersion model described below, using the data provided by the Eulerian calculation.

Dispersion Model

Because the fluid–particle interactions involve the instantaneous velocity of the fluid at the particle location, which is not available from RANS modelling of the turbulent fluid flow, a reconstruction method is needed to properly build the fluctuating velocity in accordance with the given first- and second-order statistical moments of the turbulence. As mentioned above, a stochastic one-step method is used to predict the fluid velocity seen by a discrete particle at time t in terms of the value of the fluid velocity at time t + Δ t and at the previous location of the same solid particle. In case of homogeneous turbulence, the corresponding first-order autoregressive process would take the simple form

where u _{i n} * is the i component of the velocity fluctuation of the fluid at the discrete particle location at time t = nΔ t, T _i * is the integral time scale of the fluid seen in the i direction, and the ψ _{i n} are centered Gaussian variables satisfying ⟨ψ _{i n} ψ _{i n − p} ⟩ = 0 for any integer p ≠ 0. In order to take turbulence anisotropy into account and to be consistent with the fluid Reynolds stress tensor, the components of the covariance matrix of the white noise disturbances ψ _{i n} have to be linked with the values of the Reynolds stresses given by the Eulerian computational step,

under the local homogeneity assumption in order that the process be stationary. A simple procedure to generate such random numbers ψ _{i n} is to select ψ_{1 n} from a normal p.d.f. with zero mean and variance ⟨ψ_{1 n} ²⟩ = (1 − exp (− 2Δ t/T ₁*)) ⟨ u ₁ ² ⟩, and to build ψ_{2 n} and ψ_{3 n} by ψ_{2 n} = a ₀ ϕ + a ₁ ψ_{1 n} and ψ_{3 n} = b ₀ χ + b ₁ ψ_{1 n} + b ₂ ψ_{2 n} , where ϕ,χ are independent Gaussian variables with zero mean and variance unity, and the coefficients a _k , b _k are deduced from Equation (6).

In case of nonhomogeneous turbulence, the formulation in Equation (5) has to be corrected by taking the variations of the fluid Reynolds stresses into account to avoid any spurious drift of the fluid particles towards the low turbulence intensity regions (Legg and Raupach 1982; McInnes and Bracco 1992). In the channel flow configuration, the y derivatives of the fluid Reynolds stresses are involved, leading to the following final expressions for the fluid velocity generation process in each direction:

The integral Lagrangian time scales T _i * of the fluid seen by the discrete particles are evaluated following the proposals of Wang and Stock (1993), which may yield acceptable estimates even in the case of nonhomogeneous anisotropic flow, provided that the fluid Lagrangian time scales T _Li and moving Eulerian time scales T _mEi (measured in a frame moving with the mean fluid velocity) are properly assessed in terms of the y location along the channel height, as described later. The first step of the calculation is the evaluation of the integral time scales under the hypothesis that no external force is acting by means of the following expression:

where the inertia effect is taken into account through the particle Stokes numbers St _i = τ _p /T _mEi , τ _p being the particle relaxation time. Then, the crossing trajectory effect, which is due to the gravity-induced mean relative velocity V _r (directed in the streamwise direction x), is introduced by expressing the time scales T _x *,T _y *,T _z * in terms of T _0i * and V _r , again following Wang and Stock (1993):

where L _f is the longitudinal integral length scale defined here by L _f = T _mEx .

At this point the Eulerian and Lagrangian time scales of the fluid in each direction, namely T _mEi and T _Li , are the key quantities that have to be evaluated. The quality of this evaluation will determine the accuracy of the particle motion description. Several models have been developed in the literature to estimate the Lagrangian time scales in anisotropic turbulent flows and to account for the directional dependency of these quantities. The available proposals are

with C _L = 0.2 to 0.25, according to Berlemont et al. (1990) or Zhou and Leschziner (1996), who normalized the velocity correlations by the root mean square (rms) velocities in directions i and j (so that it is not surprising to obtain negative values for the off-diagonal time scales), or alternatively

according to Burry and Bergeles (1993), who normalized the velocity correlations by the corresponding Reynolds stress.

Besides the lack of any physical ground (except dimensional arguments), the main drawback of such proposals is the assumed symmetry in i and j, which is not correct in turbulent shear flows. From any of the above expressions, the ratios of the streamwise and spanwise Lagrangian integral scales to the wall-normal scale would be

If we focus on the wall-normal direction, other expressions are available, e.g., the empirical formulation proposed by Ushijima and Perkins (1999), who started from the expression arising out of the Langevin model in stationary homogeneous isotropic turbulence, T _L = 4k/(3C ₀ ϵ) and used a wide range of experimental and numerical results to propose an empirical expression of the “constant” C ₀ as a function of the wall distance to obtain a more accurate evaluation of T _Ly in pipe or channel flows. Another way is to make use of the eddy-viscosity-based expression of T _Ly , which will be applied in the following. This method is based on the identification of the eddy viscosity ν _t with the long time turbulent diffusivity of Taylor's theory, i.e., ν _t = ⟨u _y ²⟩ T _Ly , leading to the following expression for T _Ly :

From comparison with DNS and LES results, it has been shown recently by Rambaud et al. (2002) that predictions of T _Ly using Equations (13) and Equation (14) are from being satisfactory, and that the the only acceptable estimates of T _Ly are by the formulation of Ushijima and Perkins (1999) or by the eddy-viscosity-based expression in Equation (16).

The present approach is based on a recent proposal, derived from the Generalized Langevin Model (Haworth and Pope 1986), for the prediction of the streamwise and spanwise Lagrangian time scales by Rambaud et al. (2002). This model, supported by comparison with available channel flow LES and DNS computations, was shown to yield significant improvement over the generally used empirical expressions in Equation (15). In the suggested formulation, the ratios of the streamwise and spanwise time scales to the wall-normal one are expressed in terms of the local Reynolds stress tensor components by

with

Starting from these estimations of the Lagrangian time scales, the moving Eulerian time scales are deduced by simply considering a fixed and constant value of the ratios β _i = T _Li /T _mEi , namely β _i ≅ 0.6, which seems to be an acceptable estimate according to available LES and DNS results in channel flows (Rambaud et al. 2002; Wang et al. 1995).

In the following section, we investigate the impact of the new anisotropic model for the Lagrangian time scales by means of comparisons between numerical calculations and experimental data using, respectively, the isotropic formulation, the formula in Equation (13) of Berlemont et al. (1990), and the new expressions in Equations (17) and (18) with T _Ly from Equation (16).

NUMERICAL RESULTS AND DISCUSSION

Domain Geometry and Model Parameters

As mentioned in the introduction, the simulation results are compared with the experimental results of Khalitov and Longmire (2003; hereafter denoted by KL03), who presented many results obtained in a fully developed vertical channel flow loaded with small solid particles. The fluid and particle velocities were measured simultaneously by two-phase PIV (Khalitov and Longmire 2002). The channel dimensions were h = 7.5 mm and l = 110h for the half-width and the dynamic length respectively, and the depth dimension was sufficiently large to avoid wall proximity effects in that direction and to suppose a two-dimensional flow. Five sets of monodisperse spherical solid particles were tested with mean diameter d _p ranging from 20 to 160 μm. The particle density was 2500 kg m⁻³. The fluid centerline velocity was equal to 10 ms^{− 1}, the Reynolds number based on this velocity and the channel half-width h was Re _h = 4500, and the estimated Stokes numbers based on integral time scale at the channel center varied in the range 0.2–10. The particle-to-air mass loading was about 10% for each experiment, so that the particles did not significantly affect the gas mean and rms velocity profiles.

Accordingly, the present numerical simulations have been performed using one-way coupling, i.e., the gas flow is assumed not to be affected by the dispersed phase. To ensure fully developed flow conditions, periodic boundary conditions are used for the trajectory calculations between the inlet and the outlet section of the channel. To improve the description of the gas flow in the near-wall region by the Eulerian model, a stretched grid is adopted in the wall-normal direction, following a logarithmic distribution law with 50 nodes along the channel half-width, the first node being located at y ⁺≅ 0.4 (dimensionless wall distance in wall units). For each nominal particle diameter, namely d _p = 20, 30, 60, and 100 μm, the Lagrangian simulation has tracked as many as 10⁶ particles to ensure sufficient statistical information in each cell of the domain to calculate the mean velocities and covariances. Due to the lack of available experimental data, the 160 μm case was not studied here. Preliminary numerical tests showed that increasing the number of particles or the number of cells does not modify the results significantly.

The particle–wall collision parameters were set to the following values: kinetic friction factor f = 0.2, static friction factor f ₀ = 0.3, coefficient of restitution e = 0.95. As pointed out by Lain et al. (2002), the standard deviation of the virtual wall inclination depends not only of the wall structure but also on the particle diameter. Here we used the values of σ_γ recommended by these authors for low roughness, namely: σ_γ = 0.064 for d _p = 20 μ m, σ_γ = 0.061 for d _p = 30 μ m, σ_γ = 0.052 for d _p = 60 μ m, and σ_γ = 0.043 for d _p = 100 μ m.

Three models for the Lagrangian time scales T _Li were tested in each case: the present new model, the anisotropic expressions in Equation (13) suggested by Berlemont et al. (1990) with C _L = 0.2, and an isotropic model in which the time scales in each direction are assumed to be equal to the wall-normal time scale computed by Equation (16).

Comparison with Experimental Results

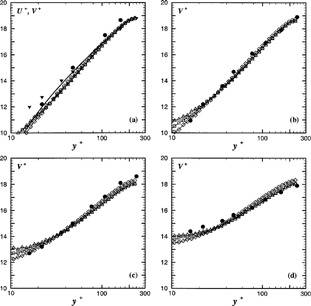
The dimensionless mean velocities (in wall units) of the fluid, U ⁺, and of the particles, V ⁺, are plotted in Figure 1 as a function of the wall distance y ⁺ for the various particle diameters investigated in KL03. All four plots show relatively good agreement between the measured and predicted velocities. The Eulerian predictions for the mean gas velocity (only shown in Figure 1a) are very satisfactory in the channel core region. Nevertheless, a slight discrepancy for U ⁺ is noticed very close to the wall, where the Eulerian model seems to underestimate the experimental data. This difference, which never exceeds 10%, seems to be independent from the wall treatment, and can be partly explained by the variations of the measured fluid velocity in the experiments. According to KL03, this velocity was found to vary within 2.3% from one case to another in the experiments; however, no systematic effect of the particle size was observed. Despite this difference close to the wall, the mean particle velocity V _x ⁺ is well predicted by the three Lagrangian models, which are seen to differ very slightly in the near-wall region. All of the numerical results within the whole channel, from wall to centerline, are very close to the experimental data except for the case d _p = 60 μ m, where the experimental results are somewhat underestimated by the simulation in the neighborhood of the channel centerline. The model clearly reproduces the experimental trend of the velocity profile, becoming flatter with increasing particle size, a well-known behavior that has been observed in many previous observations of gas–solid pipe or channel flows. From these comparisons, it may be noticed that the mean particle velocity predictions obtained using the three time scale models are very similar. This is not surprising because the strongest influence of the choice of the time scale model is expected to be on the particle dispersion and fluctuating velocities.

figure 1Profiles of dimensionless particle and gas mean velocities. Comparison between the simulations and the experimental results of Khalitov and Longmire (2003). (a) Unladen gas and d _p = 20 μm; (b)d _p = 30 μm; (c) d _p = 60 μm; (d) d _p = 100 μm. Experimental data:, unladen gas;, particles. Numerical results: ——, unladen gas; — —, particles, present model; — —, particles, isotropic model; ——, particles, Berlemont's model.

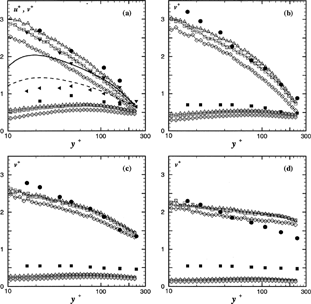
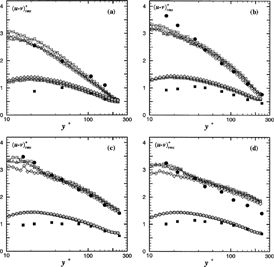
A comparison between the measured and computed profiles of the gas and particle rms velocities (u ⁺ and v ⁺, respectively) is presented in Figure 2. As shown by Figure 2a, the predicted rms velocities of the gas are in good agreement with experimental observations, except in the near-wall region (y ⁺ < 40) where the streamwise fluctuating velocity is somewhat underestimated. It shows a local maximum at y ⁺ ≅ 20 that is not visible in the measurements. In contrast, the spanwise fluctuating velocity is a little bit overpredicted. In spite of this difference between the results of KL03 and the present predictions of the gas fluctuating velocity near the wall, the rms velocities of the particles are quite well described by the Lagrangian models, as shown by Figures 2a–d. However, in the case of d _p = 100 μ m, the three models tend to overestimate the streamwise particle rms velocity in the channel center. Here the present model leads to improved agreement with the measured values. It is interesting to note that the model with isotropic Lagrangian time scales yields better results than the anisotropic model based on Equations (13) and (15). The difference between the three models, which may exceed 20% for the 20 μm particles, decreases with increasing particle diameter. Even if the computed values of the spanwise particle velocity fluctuations from the present model are very satisfactory for the smallest particles, they can be observed to underestimate the experimental results regardless of which model is used for the Lagrangian time scales, especially for larger particles. It can be concluded from Figure 2 that the present anisotropic model is more accurate for the prediction of the particle fluctuating velocities.

figure 2Profiles of dimensionless rms velocities. Comparison between the simulations and the experimental results of Khalitov and Longmire (2003). (a) Unladen gas and d _p = 20 μm; (b) d _p = 30 μm; (c) d _p = 60 μm; (d) d _p = 100 μm. Experimental data: ▾ gas, streamwise direction; ▵, gas, spanwise direction; •, particles, streamwise direction; ▪, particles, spanwise direction. Numerical results: ——, gas, streamwise direction; — — —, gas, spanwise direction; —▵—, particles, streamwise direction, present model; —□—, particles, streamwise direction, isotropic model; —□—, particles, streamwise direction, Berlemont's model; —▴—, particles, spanwise direction, present model; —▪—, particles, spanwise direction, isotropic model; —□—, particles, spanwise direction, Berlemont's model.

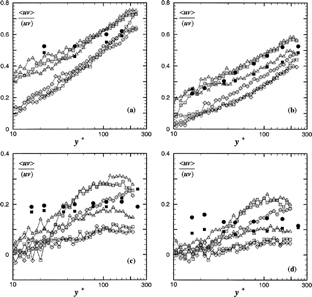
Additional information about the accuracy of the estimated time scales can be obtained by examining the reduced gas–particle velocity covariances, ⟨u _α v _α⟩/(u _α v _α) (α ≡ x,z), whose profiles are displayed in Figure 3. On the whole, the streamwise and spanwise gas–particle covariances, ⟨u _x v _x ⟩/(u _x v _x ) and ⟨u _z v _z ⟩/(u _z v _z ), computed by means of the proposed model are in acceptable agreement with the experiments. For heavier particles (d _p = 60 and 100 μm), however, the computed spanwise velocity correlations, ⟨u _z v _z ⟩/(u _z v _z ), are found to exceed the streamwise ones for all models of the time scales, contrary to the measurements. Nevertheless, the newly proposed model can be seen to enhance the predictions significantly compared to the two other Lagrangian time scale models, especially for the streamwise gas–particle velocity correlation, even though the spanwise velocity correlation in the channel core can be seen to be overestimated by our model and by the isotropic model as well.

figure 3Profiles of dimensionless gas–particle covariances. Comparison between the simulations and the experimental results of Khalitov and Longmire (2003). Same caption as in Figure 2. (a) d _p = 20 μm; (b) d _p = 30 μm; (c)d _p = 60 μm; (d) d _p = 100 μm.

The numerical and experimental profiles of the dimensionless mean slip velocity are compared in Figure 4. The mean slip velocity is obtained by averaging the instantaneous relative velocity, which is the difference between the velocity of the fluid seen by the particle and the velocity of the particle. Qualitatively, the numerical predictions show the same trend as the experimental data; however, the mean slip velocity is systematically overestimated in the core region, except for d _p = 100 μm, and underestimated close to the wall. Significant discrepancies can be observed for smaller particles, revealing a possible effect of preferential concentration that cannot be reproduced by means of this kind of Lagrangian simulations. The best agreement for the mean slip velocity is obtained for the 60 and 100 μm particles. The comparison between the experimental and numerical evaluations of the rms slip velocity in the streamwise and spanwise directions is presented in Figure 5. For all particle sizes examined, the three models yield nearly identical results that are in very satisfactory agreement with the measurements, although the rms spanwise relative velocity is slightly overestimated in the near wall region.

Figure 4Profiles of dimensionless mean slip velocities. Comparison between the simulations and the experimental results of Khalitov and Longmire (2003). Same caption as in Figure 2. (a) d _p = 20 μm; (b) d _p = 30 μm; (c)d _p = 60 μm; (d) d _p = 100 μm.

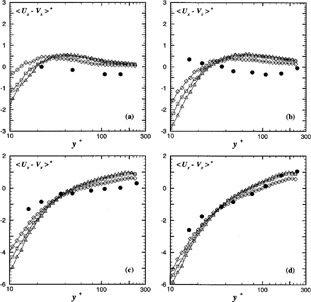
Figure 5Profiles of dimensionless rms slip velocities. Comparison between the simulations and the experimental results of Khalitov and Longmire (2003). Same caption as in Figure 2. (a) d _p = 20 μm; (b) d _p = 30 μm; (c)d _p = 60 μm; (d) d _p = 100 μm.

From the comparisons presented for this channel flow test case, it can be concluded that the prediction of the fluctuating motion of particles suspended in a wall-bounded turbulent flow can be improved by the proposed anisotropic dispersion model, especially with regards to the particle fluctuating velocity variances and the fluid–particle velocity covariances.

CONCLUSION

An improved Lagrangian model for the computation of turbulent gas–solid or gas–droplet flows was presented. By means of accurate modelling of the directional dependence of the fluid Lagrangian time scales, the proposed dispersion model is able to take into account the nonhomogeneous and anisotropic character of the turbulence. Through comparison with recent experimental data obtained in a channel flow by Khalitov and Longmire (2003), the method was shown to be a useful tool for the simulation of the dispersed phase motion in a gas–solid turbulent flow. Evaluation of the second-order statistical moments of the fluid and particle velocities appears to be significantly improved when compared to the predictions obtained by means of previous models for the fluid Lagrangian time scales.

However, some discrepancies between the predictions and the observations remain, showing that there is still scope for improvement in anisotropic dispersion models. Further investigations are needed to obtain new numerical data about the integral time scales of the fluid flow, including the moving Eulerian time scales, and about the relationships expressing the time scales of the fluid seen by discrete particles in terms of their Stokes number and mean slip velocity.