Use of Numerical Calculations to Simulate the Sampling Efficiency Performance of a Personal Aerosol Sampler

Numerical calculations were conducted to simulate air and particle behavior near and into the inlet of an aerosol sampler in order to determine sampling efficiency performance. This was done with the pre-verified commercial computational fluid dynamics (CFD) software package, FLUENT (Fluent, Inc., Lebanon, NH, US). Air flow behavior was calculated for steady-state conditions approaching and flowing into 3D geometries of an aerosol sampler free in the air that was similar in dimension to two commercial samplers, namely the Gesamtstaubprobenahme sampler (GSP) and the conical inhalable sampler (CIS). Particle trajectories were calculated in a Lagrangian reference frame on the resulting velocity fields. Based on the particle trajectories, sampling efficiencies were calculated and compared to those reported in the literature for a CIS aerosol sampler. They were found to have similar overall trends for particle sizes up to 21 μ m. Using a correction factor, agreement was observed to be very good for smaller particles, but less so for larger particles.

INTRODUCTION

Exposure to airborne dust is directly responsible for an estimated 31,000 deaths over the past 10 years (NIOSH 2003). Dust generated by surface and sub-surface mining machines is implicated in a large proportion of these deaths. In addition, there are many more sources of dust exposure including: welding and pipe cutting (NIOSH 2003), foundry work, asbestos mitigation, brick and cement work, abrasive blasting (OSHA 2004), and many other occupations. Therefore, controlling workers' exposures to airborne dust contaminants is an important concern in many workplaces.

In order to monitor workers' exposures to potentially harmful dusts, industrial hygienists use personal aerosol samplers to collect samples of the airborne particles. The samplers may be used to collect the inhalable, thoracic, and/or respirable fraction of aerosol particles that penetrate into the human airway. Inhalable aerosols include the range of particles penetrating into the airway from the nose and mouth to the alveoli. Thoracic particles include those that penetrate past the thoracic region of the lung, and respirable particles include only those that penetrate to the gas-exchange region, that is, to the alveoli.

Personal sampling of aerosols is used as a regulatory tool in enforcement of the permissible exposure limits of aerosols by OSHA. Control of aerosols by reducing their concentrations leads to improved health of workers. Thus, an accurate measure of the type and amount of the aerosol is important in determining the likelihood of exposure as well as the degree by which it should be controlled. This is dependent on knowing how well the samplers perform in a variety of conditions, which can be learned through performance evaluations.

Performance studies of aerosol samplers have traditionally been conducted with experimental measurements in wind tunnels and calm-air chambers. For example, to name only a few, the following have done work in wind tunnels: Badzioch (1959), Belyaev and Levin (1972), Ogden and Birkett (1977), Mark and Vincent (1986), Okazaki et al. (1987), Aizenberg et al. (2000a, b), and Li and Lundgren (2002). There have been fewer experiments conducted in calm-air chambers, including Davies (1968), Breslin and Stein (1975), Kenny et al. (1999), and Feather and Chen (2003).

Use of numerical simulation for studying aerosol samplers, although less prevalent, has received growing attention. Use of inviscid approaches to numerically simulate airflow and particle behavior has been investigated by Vitols (1966), Ingham (1981), Dunnett and Ingham (1986), Chung and Dunn-Rankin (1992), and Dunnett (1999). The work by Chung and Dunn-Rankin (1992) compared both inviscid and viscous results and found that there were small but detectable differences between the two approaches. On the viscous side, work has also been done by Griffiths and Boysan (1996), Gao et al. (1999, 2002), Baron and Bennett (2002), and Lo Savio et al. (2003).

The above research includes both reference samplers and personal samplers. Reference samplers, also called probe samplers, are used to determine the true concentration of aerosols in performance evaluations conducted in wind tunnels. A fair amount of research has been done on reference samplers including, Watson (1954), Badzioch (1959, 1960), and Belyaev and Levin (1972, 1974). However, it was Belyaev and Levin's work that became the foundation for determination of the reference concentration. They found two conditions for “thin-walled” sampling. First, if the ratio of outside probe diameter to inside diameter was less than 1.1, then the probe is thin-walled, no matter what the sharpness was. Second, if the ratio of outside diameter to inside diameter was greater than 1.1, then the probe sampler was “thin walled” only if it had an angle of sharpness no greater than 15 degrees and a wall thickness to probe diameter ratio not greater than 0.05. When operated isoaxially (in line with the approaching flow) and isokinetically (same velocity as freestream), such a reference sampler should collect the true concentration. Sampling efficiency is then determined from the ratio of mass or number of particles collected by the sampler being evaluated to that of the reference sampler.

Currently the performance evaluations of aerosol samplers are limited to experimental measurements. To date, there have been no complete performance evaluations conducted of inhalable aerosol samplers for direction-averaged, mannequin-mounted conditions using numerical simulations. There have, however, been several investigations of specific conditions including Griffiths and Boysan (1996), where the CFD code FLUENT was used to simulate flow in cyclone samplers; Gao et al. (1999), where the CFD code FIDAP (Fluent, Inc., Evanston, IL, US) was used to calculate airflow entering a bio-aerosol sampler; and Lo Savio et al. (2003), who used CFX (AEA Technology, Oxfordshire, England) with the renormalized group k−ε turbulence model to simulate airflow entering and passing around samplers free in the air at 0- and 90-degree orientations to the approaching airflow. Thus, there is a need to continue research in this area and expand the collective knowledge. The work presented in this paper brings numerical simulation closer to being a complete tool for performance evaluations of personal aerosol samplers.

METHODS

Geometries

In this work, numerical simulations were made of an aerosol sampler free in the air that had a computational geometry similar to those of two inhalable aerosol samplers: GSP (Gesamtstaubprobenahme; Gesellschaft für Schadstoffmesstechnik GmbH, Germany) and CIS (Conical Inhalable Sampler, BGI, Inc., Waltham, Massachusetts, USA). These samplers were chosen based on their simplistic geometries and the presence of experimental values in the literature for these samplers. The methods applied for these samplers will be considered in future work for other types including respirable and thoracic samplers.

Computational geometries were created using the 3D CAD software package GAMBIT (Fluent, Inc., Lebanon, New Hampshire, USA), and were based on dimensions of the above two samplers. A sharp-edged reference probe was included in the geometry in order to recreate the wind tunnel testing environment as closely as possible.

The aerosol sampler was not mounted on a mannequin or other torso-like object in order to minimize the total number of computational cells required by the geometry. A maximum of 5 million cells were possible due to the limitation of memory allocation of the 32-bit computers used in this work. Including a full-size bluff body for the grid densities used would have resulted in greater than the maximum number of cells allowed.

3D geometries were filled with tetrahedral-shaped cells in order to mesh them. A minimum of three grids of differing densities were made for each geometric scenario, which included orientations of 0, 90, and 180 degrees. A common metric in the field of CFD for determining an acceptable range of grid densities is defined by the grid refinement factor, r = h _coarse/h _fine, where the grid density, h, is found from the following

such that N is the total number of cells and Δ V _i is the cell volume (JFE 2004). Grid refinement factors greater than 1.3 are desirable (JFE 2004). This metric was used to guide the total number of cells used to fill computational domains (see Table 1).

Table 1 Cell numbers used in computational grids

Grid	Total	Volume	Normalized grid
type	cells	(m^3)	density (h)
Coarse	752,720	0.035708	0.00362
Medium	989,911	0.035708	0.00330
Fine	2,251,923	0.035708	0.00251
Superfine	4,343,013	0.035708	0.00201

Calculation of Flowfield

Velocity flowfields were calculated using the FLUENT CFD solver for the computational domains described in the previous section in conditions of 0.5 and 1 m/s freestream wind speeds. The FLUENT solver is based on a finite-volume discretization of the Navier-Stokes equations. The implementation used for these simulations is described in White (1991) and Versteeg and Malalasekera (1995) and is at most second-order accurate in time and space. For the steady-state application in this work, only space coordinates are considered.

Since these calculations are viscous based, turbulence may play a role in the simulation of accurate velocity fields. To capture turbulence effects, the k−ε model was applied. This two-equation turbulence model approximates the production (K) and dissipation (ε) of turbulent energy from the instantaneous Navier-Stokes equations (Reynolds-ensemble approach), which for energy and dissipation are

where σ _K = ν _t /ν _k , σ_ε = ν _t /ν_ε, ν _t ≈ , C _μ = 0.09, C ₁ = 1.44, C ₂ = 1.92, σ _k = 1.0, and σ_ε = 1.3.

These relations and values are appropriate for many high-speed, high-Reynolds numbers flows away from walls and surfaces. For the application in this work—low-speed, low-Reynolds number flows, and near walls—a more precise viscous treatment is needed. The method selected in the FLUENT solver for this work is the renormalized group (RNG) analysis method, which is based on an analytically derived differential formula (Choudhury 1993; Fluent, Inc. 2003). The turbulent transport equations used in the RNG k−ε model, based on Yakhot and Orszag (1986) and Choudhury (1993), are

where G _k is generation of turbulence kinetic energy from mean velocity gradients, G _b is generation of turbulence kinetic energy from buoyancy, S represents source terms, C _1ε = 1.42, C _2ε = 1.68, C _3ε is dependent on contribution of buoyancy, and C*_2ε = C _2ε+ . In order for this application of RNG theory to correctly model low-Reynolds-number flows, the following is used to calculate turbulent viscosity

where and C _ν≈ 100. Finally, there is an additional energy dissipation term in the RNG method not used in the standard k−ε equation, R _ε, which is found from

with η = Sk/ε, η₀ = 4.38, and β = 0.012.

The renormalized group (RNG) k−ε turbulence model was used with near-wall enhancement. This results in application of the RNG k − ε model for fully turbulent regions just outside the boundary layer transition zone, and then a switch to application of the one-equation Wolfstein model, which is applied for the transition zone between the viscous sublayer (essentially at the surface) and the fully turbulent region further away from the wall (Fluent, Inc. 2003). The Wolfstein model calculates a new turbulent viscosity as follows

such that the new length scale, l _μ is calculated from

Particle Trajectories

To calculate particle trajectories, a Lagrangian reference frame is used where the force-balance equation is integrated in order to find the direction and magnitude of the particle velocity. The force balance equation is

where F _D (u−u _p ) is the drag per unit particle mass and

For turbulence treatments, the stochastic tracking (random walk) model is used to include the effect of instantaneous turbulent velocity fluctuations on the particle trajectories.

Boundary and Operating Conditions

All calculations were conducted under environmental operating conditions that included the effect of gravity equal to 9.81 m/s² and the ambient pressure equal to 1 atmosphere (101,325 Pascals). In addition, this work focused on steady-state solutions in order to simplify the simulations and approximate the time-averaging event of workplace and wind tunnel aerosol sampling.

A constant sampler exit velocity of 0.082525 m/s was set for the simulations of the tested aerosol sampler geometry. This was based on the GSP and CIS manufacturers' recommendations that those samplers should be operated at 3.5 L/min. For sharp-edged reference samplers included with the test sampler, inlet velocity was varied according to the freestream velocity, 0.5 or 1.0 m/s, so that isokinetic conditions were maintained.

As previously described, turbulence was calculated using the RNG k−ε model. Turbulence intensity at the inlets and within the sampler, provided it is less than about 10%, should have little effect on the sampling efficiency for aerosol particles with Stokes numbers less than 1 (Vincent et al. 1985; Wiener et al. 1988), which is the case for these simulations. Turbulence intensity in the simulations was maintained at 5% at the inflow of the computational domain, and 3% inside the sampler based on experimental values of similar flows (Smith and Bird 2002). The range of potential length scales was defined by estimates of the Kolmogorov microscales and experimental values (Vincent et al. 1985). They were defined to be 0.01 m at the inflow to the domain (maximum), and equivalent to the minimum grid size at the respective sampler outlet, which was 0.0005–0.0010 m. These lengths are expected to cover the range of possible scales that will evolve for these flow scenarios.

Methods to Evaluate Simulations

The CFD results were evaluated by examining calculated cell values from a number of different simulations in comparison to each other. Parameter space analysis, grid convergence studies, and near-wall cell adaption were conducted on converged solutions. Converged solutions included only those that met the iterative convergence criteria of a 10-orders-of-magnitude decrease in residual values below initial conditions for each of the flow parameters. These included three components of velocity, the continuity term, pressure, turbulence generation, and turbulence dissipation.

Parameter Space Analysis

Parameter space analysis is presented here as a non-statistical method used to explore the influence that input parameters (boundary conditions, turbulence models, etc.) have on the results of a deterministic simulation. It is based on factorial analysis used in the design of experiments (DOE) applications (Montgomery, 2001). CFD data are deterministic, and thus it is not possible to demonstrate the presence of a normally distributed random error with a mean of zero. Therefore, classical statistics may not be performed on the results of CFD simulations.

Statistical inferences are based on the assumption that the error of a system is random, has a mean of zero, and is normally distributed. CFD simulations, by their nature, do not yield data that have these characteristics. If the simulation is conducted over and over again using the same input parameters each time, the exact same result will occur. There will be no difference between results if the simulation is conducted an infinite number of times, because there is no randomness in the simulation itself. However, changing of input parameter values, which is not a random process, may lead to differences in results. This is where parameter space analysis may be used.

A parameter space is defined by the “region” separating two deterministic results obtained from different input parameters. For example, the computational geometry will have several grids of varying densities in order to determine if the grids give different or the same answers. Comparing two grid densities will reveal the parameter “space” between them, if any, which is simply the delta of two nonstatistical averages of spatial or temporal data. There may be any number of parameter-space deltas between spatial or temporal averages, although the most important ones will often be the order of the numerical method and the grid density. The parameter-space “spread” of scalar difference between data taken from the center of the reference probe and from the wall was also calculated. This was done to determine a starting point for the sensitivity of the metric used as a measure for further analysis of parameter-space values.

Parameters were broken into two levels, high and low (see Table 2). To determine the average delta due to the particular factor, the difference of values in vertical alignment are found and then the average is taken. Thus for the case of the grid parameter,

where D1 represents average delta. The designation of “lll” means “low, low, low,” “llh” means “low, low, high,” “lhh” means “low, high, high,” etc. These designations represent the scalar value obtained when parameters are at these levels. The result obtained (see Table 2) when the grid is “low,” i.e., a lower density grid, the solver is “high,”—a 2nd-order solver—and the spread is “low,”—center of tube—is placed in this box. The same form is used for each parameter and parameter combination, and the influence of that parameter's contribution to solutions can be measured through the differences between spatial averaging.

Table 2 Low- and high-level coding map for parameter space analysis

Parameter	Grid	Solver	Spread	Result
	−	−	−	lll
	−	−	+	llh
	−	+	−	lhl
	−	+	+	lhh
	+	−	−	hll
	+	−	+	hlh
	+	+	−	hhl
	+	+	+	hhh
Avg. Delta	D1	D2	D3
Grid: − = lower density, + = higher density; Solver: − = first-order, + = 2nd-order; Spread: − = center of tube, + = near wall of tube

Grid Convergence Studies

Grid convergence studies were conducted in order to evaluate the rate of decrease of the uncertainty due to the grids, and were based on the Grid Convergence Index (GCI) method by Roache (1998). This method allows a measure of the effect of grid refining or coarsening on the solutions of a simulation. It is done to determine if the grid is independent from the solution for a particular class of flows with the result being a normalized relative percent uncertainty. The method is premised on a fundamental assumption of numerical analysis that if the computational grid becomes infinitely dense, the calculated solution will be exact. To actually do this would be impossible. Therefore, the grids are resolved to the point of “engineering efficiency,” in order that accurate solutions can be obtained for reasonable cost.

Based on the above assumption, the value of the resulting GCI is an uncertainty about the solution obtained from a respective grid of specific density. As grid density increases, uncertainty due to the grid is expected to decrease. In this application, the grid convergence uncertainty is determined from three grids and for two theoretical orders of the hybrid numerical method used in FLUENT.

The GCI method, applied for an identical computational grid domain of two different densities is

where “dense2” is the more dense grid; “dense1” is the less dense grid; F _s is a “factor of safety,” according to Roache (1998), which is defined conservatively as 3, but can be smaller; ε is the relative difference between scalar values from the different grids; r is the ratio of differing grid densities, that is, r = (more dense grid)/(less dense grid); and p is the apparent order of the numerical method from which the solution was obtained. The characteristic density, h, of the grid (“dense1” and “dense2” from above) can be obtained according to Equation 1.

In considering the orders of the numerical method, FLUENT does not have a true first-order solver, therefore the apparent order of the hybrid method applied in FLUENT is actually in the range of 1 < P < 2. This is a result of the advection terms being solved in a second-order discretization, while upwinding is solved in first order. Even so, if it is assumed that use of P = 1 for 1 < P < 2 is conservative, then comparisons can be made between the two theoretical applications of numerical solver, P = 1 and P = 2. This assumption is grounded by order comparisons made with the parameter-space analysis method and qualitative plots presented in Bird (2004). This approach of limiting P = 1 for hybrid methods is also recommended in the peer-reviewed literature (JFE 2004). Convergence analyses were conducted using Roache safety factors of 1, 1.25, and 3.

Near-Wall Cell Adaption

Mesh elements within the computational domain were evaluated for adherence to RNG k − ε requirements at two primary regions in the domain: near-wall and near-inlet. Near-wall grid element sizes were chosen based on two requirements: (1) there must be at least 10 cells between a cell with the value of Re _Turb = 200 and the wall, and (2) y ⁺ _wall must be less than 5, preferably less than 2, at a point just beside the wall (Fluent, Inc. 2003). If cell values were found to be out of range, the tetrahedral cell grids were refined in a step-wise process with cell adaption. This is a method used to split existing mesh cells into smaller cells, in order to yield a mesh that gave cell values within the acceptable ranges.

Particle Trajectory Calculations

Evaluation of the personal aerosol sampler with simulation was based on the method used to calibrate the computational domain for sampling efficiency calculations of the reference sampler. Results were obtained for the computational sampler free in the air and compared to those obtained by Li (1999) for the CIS sampler in experimental wind tunnel work.

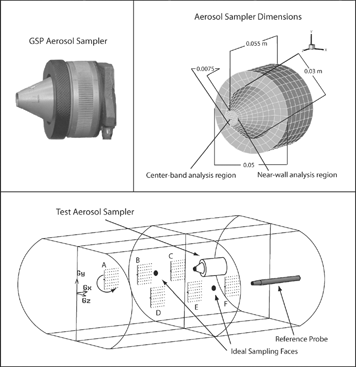
The aerosol sampler was evaluated by placing it in the same computational domain as the reference probe sampler (Figure 1). The samplers were situated in the domain so that their inlets were located at the same X distance downstream from the inflow face, and at equidistant Y and Z locations from the walls and centerline of the domain. Spatially the samplers were far enough apart so there was no effect from the presence of one on the other. Ideal reference faces were defined 0.1 m upstream of both the aerosol and probe samplers, which is beyond where any distortion of flow occurs due to the presence of the samplers.

Figure 1 Upper left: Photo of GSP sampler. Upper right: Dimensions of Computational Test Aerosol Sampler, surface mesh is for illustrative purposes. Bottom: Layout of Computational Aerosol Sampler, Reference Probe, Ideal Sampling Faces, and Particle Release Locations.

Particles were released from specific locations within the computational domain based on trajectory path parameters determined for the reference sampler (see Figure 1). Particles interacted with the external boundary of the samplers by rebounding then being reentrained into the flow, then rebounding again (if the flow brought them to the surface) up to a maximum of three times. Particles that interacted with the internal boundaries of the sampler were considered “collected” on first contact and did not rebound again.

Sampler flux ratio, (test sampler flux)/(reference probe flux), was determined for each scenario evaluated. Particle flux ratio into the aerosol sampler was determined for filter-only conditions and for total flux, which included filter collection + wall losses. The GSP and CIS samplers are intended by their manufacturers to be used with filter-only collection. However, it was deemed useful in this work to collect wall-loss information in order to make complete comparisons with existing experimental data. The results of wall loss data are reported in Bird (2004).

Particle source faces were chosen based on their location in the geometry so that a desired spread of particles was achieved upstream of a particular sampler location. Typically ten particle injections were made for each particle size calculation. Particles were set to originate from faces or lines in amounts of 250–1000 per grouping. To account for turbulence effects, a stochastic treatment was applied resulting in three particles being released from the same location. The total number of particles released, depending on the simulation, ranged from many thousands to over 100,000.

The particles were spherically shaped and had a density equal to that of anthracite (1,550 kg/m³). They were distributed in monodisperse groups of 1, 5, 10, 20, 30, and 40 μm in aerodynamic diameter. Release faces and concentrations require calibration so that isokinetic, isoaxial probe samplers yield aspiration efficiencies of unity. This was achieved by releasing particles from a variety of faces and locations throughout the computational domain until there was equality between the freestream concentration and inlet concentration. Release lines could be rotated in 360 degrees in order to yield dense particle distributions (A through F, Figure 1).

In a CFD simulation, the concentration of aerosols (particle tracks) must be calibrated in order that the thin-walled, sharp-edged probe sees the same number of particles as does an arbitrarily thin disk (referred to as an “ideal sampling face,” see Figure 1) in the undisturbed freestream flow. When this occurs, it is confirmation of sampling the true airborne concentration, which is sampling approximately with unity.

A trial-and-error approach was used to determine the best combination of release faces and concentrations in order to achieve unity between the concentrations seen by the aerosol aspiration faces. For aerosol aspiration in freestream flow, i.e. determination of the true concentration in undisturbed flow, the numbers of particles travelling across the face were counted and this number was used as the value for concentration. Particle fate was noted for the reference probe and the aerosol sampler for particles hitting walls as well as for particles exiting the samplers through their outflow faces, which is equivalent to filter sampling.

Sampling efficiency was determined from use of a flux ratio, in which particle capture by the test aerosol sampler and the reference probe was normalized by flux across an “ideal sampling face.” Sampling efficiency was calculated from the following

where N _aero is the number of particles collected by the test sampler, N _f1 is the number of particles crossing the ideal sampling face upstream from the test sampler, N _probe is the number of particles collected by the reference probe, and N _f2 is the number of particle crossing the ideal sampling face upstream from the reference probe.

RESULTS

Simulation Analysis

Parameter Space Analysis

Comparisons were made for two-grid combinations with results from coarse, medium, and fine grids compared to superfine grids at both orders of solver (1st and 2nd) and for both windspeeds (0.5 and 1m/s). Location comparisons were made from results taken from the center of the sampler inlets and at the walls of the samplers (Figure 1). All combinations were analyzed, however, only space values that had a 10% or larger deviation from the ideal values (0.5 or 1.0) were identified. They are shown in Table 3, which is broken into two sections. The top portion, consisting of only results for the probe sampler, is for freestream velocities of 0.5 m/s. The lower portion, consisting of both probe and GSP results, is for freestream velocities of 0.5 and 1.0 m/s. In the table, it can be seen that the observation location (spread) has the largest average deltas. It is expected that large differences would be seen here for the well-known fact that the fluid units in the center of a tube travel at a higher rate than those at the walls. The average delta due to spread is 15%, with the values for the probe sampler being less than those for the test aerosol sampler. Differences due to grid density and order of method have an average of 5%.

Table 3 Values determined from parameter space analysis to yield 10% or greater influence on desired results are shown in bold

			Avg. delta	Avg. delta	Two-	Avg. delta
	Wind speed	Two-grid	due to grid	due to order	location	due to spread
Sampler	(m/s)	comp.	(m/s)	(m/s)	comp.	(m/s)
Probe Samp.	0.5	Med, Sup	−0.05224	−0.006118	WN, WE	−0.07672
Probe Samp.	0.5	Fin, Sup	−0.02225	−0.0088159	WN, WE	−0.09295
Probe Samp.	0.5	Med, Sup	−0.038255	−0.008232	CB, WE	−0.10511
Probe Samp.	0.5	Fin, Sup	−0.017407	−0.012712	CB, WE	−0.130601
Probe Samp.	1.0	Fin, Sup	−0.063286	−0.02147	WN, WE	−0.118312
Probe Samp.	1.0	Med, Sup	−0.052210	−0.019425	CB, WE	−0.134302
Probe Samp.	1.0	Fin, Sup	−0.030947	−0.026591	CB, WE	−0.162006
Aero. Samp.	0.5	Crs, Sup	0.053560	0.021395	WN, WE	−0.224005
Aero. Samp.	0.5	Med, Sup	0.0103025	−0.081303	WN, WE	−0.153488
Aero. Samp.	0.5	Fin, Sup	0.0414425	0.018475	WN, WE	−0.283675
Aero. Samp.	0.5	Med, Sup	−0.033602	−0.135593	CB, WE	0.0732193
Aero. Samp.	0.5	Crs, Sup	0.0091545	0.088936	CB, WN	0.229158
Aero. Samp.	0.5	Med, Sup	0.1537645	0.187043	CB, WN	0.106906
Aero. Samp.	0.5	Fin, Sup	0.0034945	0.083846	CB, WN	0.265883
Aero. Samp.	1.0	Crs, Sup	0.100556	0.0558038	WN, WE	−0.091769
Probe Samp. = Reference Probe Sampler, Aero. Samp. = Test Aerosol Sampler, CRS = Coarse-Density Grid, MED = Medium-Density Grid, FIN = Fine-Density Grid, SUP = Superfine-Density Grid, WN = Wall-Near (Spatial Avg.), WE = Wall-edge, CB = Center-Band (Spatial Avg.)

Iterative Convergence

Simulations were iterated until all residuals had decreased by at least 10 orders of magnitude from initial conditions. This required approximately 2000 iterations for each of the flow parameters including three components of velocity, the continuity term, pressure, turbulence generation, and turbulence dissipation. Comparisons of calculated scalar values were made at 601, 1000, 2000, and 3800 iterations. Residuals were observed to decrease significantly between 601 and 2000 iterations. However, from 2000 to 3800 iterations there was a decrease of only 3 orders of magnitude at a cost of 3 additional days of computing time.

Grid Convergence Studies

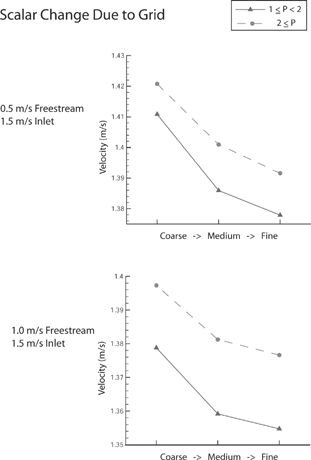
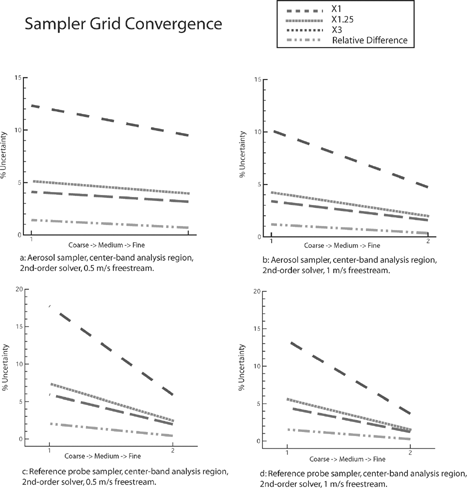
Figure 2 shows the decrease of uncertainty as determined using the GCI method. The lines in the plots represent the percent relative difference and grid convergence uncertainty at a Roache (1998) safety factor, F _s , of 1, 1.25, and 3. From the graphs, it appears the asymptotic approach, described in the GCI method, has not been reached. However, all of the graphs do demonstrate continually decreasing GCIs. Thus, the conservative safety factor of 3 is assumed to yield a measure of the numerical uncertainties for the simulations.

Figure 2 Plotted uncertainties determined from grid convergence studies on three grid densities of simulation results of the test aerosol sampler and the reference probe sampler at 0.5 and 1 m/s wind speeds for the 0-degree orientation.

Figure 3 contains velocity scalar values plotted against grid density used in the grid convergence study. The scalar value is seen to decrease sharply from coarse to medium density grids, then less sharply for the medium to fine grids. This suggests a likely trend toward convergence of the scalar value. Furthermore, the deltas between scalars of differing density grids are quite small, which suggests that the grids are independent from the solution for realistic applications.

Figure 3 Scalar values for center-band comparison region at the inlet of the GSP sampler plotted against increasing grid density.

Wall-Mesh Considerations

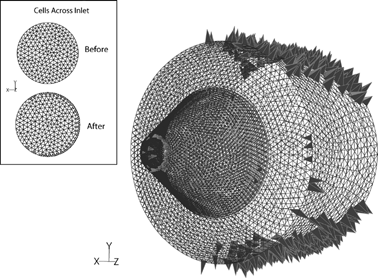
To ensure results are accurate at the walls, simulations were checked for consistency with requirements for use of the RNG k − ε turbulence model. Analysis showed that scalar values for near-wall cells to be slightly out of the acceptable ranges for use of the RNG k − ε model, so adaption (splitting) of the mesh was done resulting in cells 50% the size of the previous cell. Figure 4 shows a 3D view of the cells that were tagged for splitting. For freestream velocity conditions of 0.5 m/s, this mesh adaption and refinement resulted in a turbulent Reynolds number of 31.7 at a point 10 cells outside of the sampler's wall, and 14.5 at 10 cells within the sampler. Both values are within the required ranges. For freestream velocity of 1.0 m/s, turbulent Reynolds numbers were 33.7 and 30.1, also both within required ranges. The values of y ⁺ _wall were 2.7 and 4.01 for the 0.5 and 1.0 m/s freestream flows. This suggests the near-wall mesh was well resolved for this class of flow using the particular solver and turbulence models applied.

Figure 4 Computational surface mesh and grid elements on inside and outside surfaces of test aerosol sampler for nonconforming turbulent y ⁺ values tagged for adaption. Box: 2D slice of inlet cells before and after adaption.

Sampling Efficiency Comparison

Simulations of Reference Sampler

A minimum threshold number of particles was found by releasing them in numbers of 2000 to over 100,000 from discrete locations within the domain (see Figure 1). The particles were then tracked across two faces: (1) an ideal sampling face located in the freestream flow, and (2) the inlet face of the sharp-edged reference probe. Numbers of particles released were increased until there was agreement between the ideal sampling face and the inlet of the reference sampler. This value was found to be about 100,000 particles.

Near-unity agreement was found for the reference sampler for particle sizes up to 40 μm in freestream windspeeds of 0.5 and 1.0 m/s (Figure 5). For larger particle sizes, there was significant under-sampling depending on the combination of release faces, concentrations, and particle sizes. Thus, the optimal condition of near-unity agreement was not achieved for particle sizes larger than 40 μm. However, the inhalability convention curve (based on experiment) shows transition at the 40 μm level, therefore it is not unexpected that a transition would also be seen in simulation.

Figure 5 Sampling efficiency of sharp-edged probe sampler from FLUENT calculations at freestream velocities of 0.5 and 1.0 m/s.

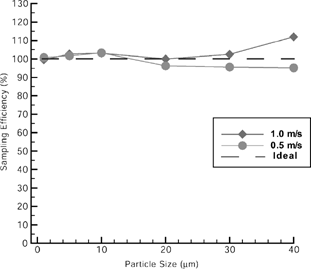
Sampler wall losses were also accounted for, and were found to be less than 1% for particle sizes up to 40 μm. This is expected to be due to the slight acceleration of the fluid within the probe, which leads to a concentrating effect of particles into the center flow region of the tube (Rao et al. 1993). For particle sizes larger than 40 μm, wall losses were significant, which is an expected result.

Sampling Efficiency Simulations of Personal Aerosol Sampler

Sampling efficiency data are shown in Table 4 for CFD simulations of the aerosol sampler at 0.5 m/s for all three orientations and for particle sizes from 1 to 40 μm. Also shown in Table 4 are the sampling efficiencies measured in a wind tunnel for the CIS sampler by Li (1999) for particle sizes from 1.6 to 68 μm in similar orientations and windspeeds. For this physical scenario, CFD simulation overpredicted experimental sampling efficiencies by nearly two times. Thus, a tuning correction factor of 0.7 was used to adjust the data down so comparison with experiment was possible. Tuning of the simulation results was done with a constant correction factor determined from the average of the ratios of values from experiment divided by those obtained from simulation. The average tuning correction factor for the particle size range from 1 to 20 μm was used for all of the particle sizes in a particular physical orientation and wind speed. Once this was done, no further adjustments were made to the simulation results so that the tune step did not replace simulation as a modeling method.

Table 4 Calculated and corrected “filter-only” sampling efficiencies from CFD simulation of the test aerosol sampler free in the air in 0.5 m/s freestream airflow with corresponding experimental data from the CIS sampler (Li 1999)

0 Degrees, 0.5 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)	COM	CFD	EXP
PS	AS	X 0.7	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/− U	(μm)	% SE	% SE	DIS	AGREE?
1	138.4 +/− 10%	96.8	1.6	98.4 +/− 1.9%	1.6	97.3*	98.4	1.14	YES
5	142.5 +/− 10%	99.8	5	99.7 +/− 3.5%	5	99.8	99.7	0.05	YES
10	133.2 +/− 10%	93.2	10	93.6 +/− 1.3%	10	93.2	93.6	0.42	YES
20	129.0 +/− 10%	90.3	21	88.1 +/− 1.2%	21	92.8*	88.1	5.36	YES
30	165.2 +/− 10%	115.6	41	50.5 +/− 3.4%	40	103.7	52.4*	98.01	NO
40	148.2 +/− 10%	103.7	68	15.0 +/− 8.9%
90 Degrees, 0.5 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)		COM	CFD	EXP
PS	AS	X 1.92	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/− U	(μm)	% SE	% SE	DIS	AGREE?
1	59.2 +/− 10%	113.6	1.6	−	1.6	−	−	−
5	51.2 +/− 10%	98.4	5	84.3 +/− 6.7%	5	98.4	84.3	16.7	Somewhat
10	36.3 +/− 10%	69.8	10	75.3 +/− 0.1%	10	69.8	75.3	7.3	YES
20	21.5 +/− 10%	41.3	21	44.0 +/− 1.8%	21	38.4*	44	12.7	Likely
30	6.01 +/− 10%	11.5	41	4.0 +/− 38.9%	40	1.4	6*	76.1	NO
40	0.8 +/− 10%	1.4	68	4.8 +/− 56.0%
180 Degrees, 0.5 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)		COM	CFD	EXP
PS	AS	X 14.8	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/−U	(μm)	% SE	% SE	DIS	AGREE?
1	7.2 +/− 10%	106.4	1.6	−	1.6	−	−	−
5	3.5 +/− 10%	52.4	5	94.6 +/− 4.7%	5	52.4	94.6	44.6	NO
10	6.8 +/− 10%	100.0	10	80.6 +/− 0.5%	10	100.0	80.6	24.07	NO
20	7.3 +/− 10%	107.8	21	41.6 +/− 0.9%	21	106.2*	41.6	155.3	NO
30	6.3 +/− 10%	92.6	41	9.7 +/− 23.9%	40	29.1	11.3*	157.9	NO
40	2.0 +/− 10%	29.1	68	6.9 +/− 12.3%

Also shown are the uncertainties from the experimental measurements and from the computational grids for simulations. Sampling efficiency agreement for the 0.5 m/s freestream velocity condition was good at the 0-degree orientation for smaller particle sizes. However, for the larger particle sizes and the 90- and 180-degree orientations, disagreement was large. Results for the aerosol sampler free in the air at all three orientations and for the 1 m/s windspeed are shown in Table 5.

Table 5 Calculated and corrected “filter-only” sampling efficiencies from CFD simulation of the test aerosol sampler free in the air in 1 m/s freestream airflow with corresponding experimental data from the CIS sampler (Li 1999)

0 Degrees, 1 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)		COM	CFD	EXP
PS	AS	X 0.8	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/− U	(μm)	% SE	% SE	DIS	AGREE?
1	115.1 +/− 5	92.1	1.6	97.2 +/− 0.8	1.6	91.6*	97.2	5.8	YES
5	110.7 +/− 5	88.6	5	94.5 +/− 4.8	5	88.6	94.5	6.3	YES
10	113.3 +/− 5	90.6	10	88.1 +/− 2.1	10	90.6	88.1	2.9	YES
20	105.8 +/− 5	84.6	21	78.0 +/− 1.8	21	85.4*	78.0	9.5	Likely
30	115.7 +/− 5	92.6	41	61.0 +/− 20.9	40	101.2	61.9*	63.0	NO
40	126.5 +/− 5	101.2	68	40.0 +/− 27.4
90 Degrees, 1 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)		COM	CFD	EXP
PS	AS	X 1.92	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/− U	(μm)	% SE	% SE	DIS	AGREE?
1	15.4 +/− 5	101.6	1.6	95.9 +/− 0.5	1.6	99.3*	95.9	3.6	YES
5	13.1 +/− 5	86.7	5	81.2 +/− 1.9	5	86.7	81.2	6.8	YES
10	8.2 +/− 5	54.3	10	64.7 +/− 2.6	10	54.3	64.7	16.1	Somewhat
20	1.3 +/− 5	8.4	21	7.8 +/− 9.9	21	7.6*	7.8	2.6	YES
30	0.1 +/− 5	0.8	41	0.7 +/− 49.5	40	0.3	1.06*	71.8	NO
40	0.1 +/− 5	0.3	68	1.3 +/− 36.7
180 Degrees, 1 m/s
CFD			Experiment		Comparison
		CORR	(Li 1999)		COM	CFD	EXP
PS	AS	X 30	PS	CIS	PS	AS	CIS	% REL
(μm)	% SE +/− U	% SE	(μm)	%SE +/− U	(μm)	% SE	% SE	DIS	AGREE?
1	3.2 +/− 5	97.2	1.6	95.9 +/− 0.7	1.6	96.3*	95.9	0.4	YES
5	3.1 +/− 5	91.4	5	89.0 +/− 6.0	5	91.4	89.0	2.7	YES
10	2.6 +/− 5	78.7	10	80.4 +/− 4.2	10	78.7	80.4	2.2	YES
20	2.9 +/− 5	87.7	21	13.7 +/− 0.5	21	85.4*	13.7	523.6	NO
30	2.2 +/− 5	64.5	41	1.9 +/− 0.0	40	12.7	2.49*	411.3	NO
40	0.4 +/− 5	12.7	68	0.7 +/− 66

DISCUSSION AND CONCLUSIONS

Parameter-Space Analysis: A Method to Evaluate Changes in User-Defined Parameters

In this work, the calculated velocity fields were analyzed using a parameter-space analysis method based on non-statistical application of factorial analysis. The method is essentially a measure of the differences between spatially averaged results from subsequent solutions. It was applied here specifically to determine if there were differences between grid densities and numerical orders, and if so, to determine how large they were. In addition, the method itself was tested to see if it would detect the expected differences between simulation results from the center of a tube and at the sampler wall. In this capacity it worked very well. Thus there was confidence in applying it to grid and numerical order measurements as well.

Grid densities were compared for results from coarse, medium, and fine grids to results from superfine grids. Comparisons between coarse to superfine and medium to superfine showed many cases greater than 5% deviation and fewer cases with 10% deviation. However, comparisons from fine to superfine grids showed rather small deviations. Also compared were differences between the numerical orders. Except for two comparisons between medium and superfine grids, the numbers of deviations were rather small at the 10% metric, and there were more if 5% is used. Use of this method gives a quantitative measure of the influence that major parameters of the simulation have on the results, and is useful in combination with other analysis methods to identify parameters that have an appreciable influence on final results. In this capacity, it can be used for optimizing input parameters. In this application, parameter-space analysis identified differences between orders of numerical method. Further analysis is necessary to determine if one method is better than the other. However, as previously mentioned, it may not be used for statistical analysis of CFD results because such deterministic data do not meet the criteria for analysis through statistical inference.

Discussion of the Numerical Uncertainty and Comparisons with Experiment

The grid convergence analysis method is well established in the literature (Celik and Karatekin 1997; Roache 1998), and in the peer-reviewed publishing arena (JFE 2004). Application of the method as presented by these sources should lead to useful results for determination of numerical uncertainties from solutions on grids of varying densities.

In this work, although iterative convergence is well established and the important scalar variable (velocity) exhibits convergence-like behavior, the asymptotic approach for the grid convergence index does not appear to have been reached, Therefore, the numerical uncertainty of the simulations obtained from the grid convergence index may not be indicative of the true quantitative uncertainty. Thus, it was necessary to temper these uncertainties with comparisons of the simulation results against experimental results.

The comparisons were made using sampling efficiency values, which were determined—both from the experimental data and the numerical results—as the ratio of collection by the aerosol sampler to collection by an ideal reference. Agreement between the CFD simulations and experiment values was found to be very good for the simple flow fields surrounding and entering the aerosol samplers. This included the orientation of sampler to freestream flow of 0 and 90 degrees for particle sizes up to 21 μm. Agreement was poor for the 180-degree orientation (most complex flow field) and for the larger particle sizes. Also, in this orientation, the correction factor needed to achieve any amount of agreement was quite large.

The above findings arguably suggest that the numerical model is quite adequate, with an uncertainty of around 10%, for correctly solving the simplified physical systems of the aerosol sampler oriented at 0 or 90 degrees to freestream flow and for particle sizes from 1 to 21 μm. However, the model breaks down for solving the more complex cases of a 180-degree orientation and for large particle sizes.

Additional work is necessary to improve the model for systems of greater complexity. Specifically, additional meshes of greater density, and/or larger differences between mesh densities will be needed in order to find the asymptotic approach of the grid convergence index. Also, further calibration steps are required to determine the numbers and locations of particle releases for particle sizes larger than 21 μm. Finally, it would be quite useful to compare velocities calculated in the CFD model to those from experiments for similar physical systems.

Acknowledgments

The author is grateful to the Health Effects Laboratory Division (HELD) of the National Institute for Occupational Safety and Health (NIOSH) for support of this research. The author also wishes to thank the diligent reviewers in NIOSH for their constructive comments. Specifically from the Health Effects Laboratory Division: Dr. Martin Harper, Chief, Exposure Assessment Branch; Dr. Vladimir Hnizdo, Allergy and Clinical Immunology Branch; and Dr. Michael Andrew, Biostatistics and Epidemiology Branch. A thank you also goes to Dr. James Bennett, Engineering and Physical Hazards Branch, Division of Applied Research Technologies. It must be noted that this work would not have been possible without the software and hardware expertise of Norma McKee and John Barnett, both from CDC's Information Technology Services Office. Finally, the author wishes to thank the journal's reviewers for their helpful and to-the-point comments.

The findings and conclusions in this report are those of the author and do not necessarily represent the views of the Centers for Disease Control and Prevention or the National Institute for Occupational Safety and Health. Mention of a commercial product or trade name does not constitute endorsement by the Centers for Disease Control and Prevention or the National Institute for Occupational Safety and Health.

Notes

* = Interpolated, PS = Particle Size, AS = Test Aerosol Sampler, SE = Sampling Efficiency, U = Uncertainty CORR = Corrected, CIS = CIS Sampler, COM = Common, EXP = Experiment, REL DIS = Relative Disagreement.

* = Interpolated, PS = Particle Size, AS = Test Aerosol Sampler, SE = Sampling Efficiency, U = Uncertainty CORR = Corrected, CIS = CIS Sampler, COM = Common, EXP = Experiment, REL DIS = Relative Disagreement.