Abstract
The objective of this study was to develop a method for reconstruction of parametrically described whorls and knots from data possible to extract from industrial scanning of logs, using X-ray scanners. The method was conceived using the logs in the Swedish Pine Stem Bank as a foundation, and was based on a few predictor features extracted from these logs; namely whorl volume, distance between whorls and distance between pith and surface. These features were not measured in images but calculated from existing parameterised knots. Simulated test sawing shows that the reconstruction method results in a representative model of the knot structure in the log, when considering the grade distribution of the sawn timber produced by the simulation program. The results of this study could, for instance, be used for improved online quality predictions at sawmills. One step in this direction is to use industrial X-ray data to enlarge the amount of log data available for sawing simulation research. Future work can, therefore, focus on developing a practical application of the results presented here.
Introduction
For many years it has been of interest to be able to predict the properties of sawn wood products from tree features. To facilitate this, different approaches have been tried; one example in recent times is the Swedish Pine Stem Bank (SPSB), which is a database that consists of properties for 198 Scots pine (Pinus Sylvestris L.) trees (Grönlund et al., Citation1995). The SPSB provides input data for the sawing simulation software Saw2003, described by Nordmark (Citation2005), and a large amount of the data used in this sawing simulation is based on computed tomography (CT) scanning of the logs in the SPSB. In forest research, a number of statistical models for predicting whorl and knot attributes from a number of measurable features have been developed. Several types of features for prediction of knots are used in these models, and they can roughly be divided into site, stand, tree and internal features. Site, stand and tree features are measured in the forest before felling and bucking, while internal features are measured in sawlogs, by destructive or non-destructive means. There are models, such as those described by Mäkelä et al. (Citation1997), Mäkinen and Colin (Citation1998), Björklund and Moberg (Citation1999) and Moberg (Citation2006), that take into account both tree features and site or stand features, to predict the properties of Scots pine knots. Other models are based on tree features and internal features; for instance, those presented by Pietilä (Citation1989) and Peterson (1998), which were made on Scots pine as well. Studies of knot characteristics that are based solely on internal features are uncommon. However, Moberg (Citation2006) found positive correlations between number of knots per whorl and distance to the previous whorl; knot length and diameter; and branch angle and diameter, respectively. These models are also based on stand features not connected to the single tree.
The studies made on whorl and knot models are unfortunately mainly done in Scandinavia. There are, however, studies from other countries where knot measurements have been made, for instance, by Fenton (Citation1960) on Corsican pine (Pinus laricio Poiret), Benjamin et al. (Citation1999) on Black spruce (Picea mariana Miller) and Pinto et al. (Citation2002) on Maritime pine (Pinus pinaster Aiton).
Grundberg and Grönlund (Citation1992, Citation1997) described models for extracting features, such as knot volume per whorl, dead knot volume per whorl, log type and distances between whorls, from simulated two-directional X-ray images of logs.
The possibility to perform sawing simulation on virtual models of sawmill logs in real time could be one way of improving log quality prediction. However, if the logs are scanned by a two-directional X-ray scanner it is difficult to determine the knot and whorl structure within the logs, since there is much less knot information available than in, for instance, CT data. Another problem, with using sawing simulation for research purposes, is the relatively small amount of available data today. Since the SPSB is limited to 198 trees, it is difficult to evaluate the validity of results of sawing simulation based on this material.
Thus, there is a need to:
| • | estimate knot structure in sawlogs online with a two-directional X-ray scanner, thus using less information than has been done earlier with CT data; | ||||
| • | enlarge the data available for sawing simulation with more logs. | ||||
One prerequisite for this is to be able to find the overall knot structure in sawmill logs, using data from industrial two-directional X-ray log scanning. Since there are few existing knot models based solely on two-dimensional internal log features, this requires a novel method of reconstructing knots from these features, which are far scarcer than features extracted from CT scanning. A method capable of this could be used to enhance the quality prediction of sawlogs and provide a source which would make it possible to add a significant number of new virtual logs to simulations, since a large number of logs are scanned in sawmills on a daily basis.
The reconstructed knots should be represented in the same parametric fashion as in the stem bank, to allow for sawing simulation. The shape of the logs, which is also necessary for creating logs for sawing simulation, can be obtained from optical three dimensional (3D)-measurements at sawmills, an issue which is not addressed here.
In a study by Grundberg et al. (Citation1999), a reconstruction of the knots in the SPSB based on simulated two-directional X-ray data was made, and property- and experience-based methods were evaluated. Two methods were tested using sawing simulation, and the best of these resulted in the same grade for the board produced by CT-scanning and the one based on two-directional X-ray scanning in 60% of the cases, when sawing 45 logs. In 3% of the cases it differed by more than one grade. The conclusion from the study was that the developed methods were in need of further development.
Thus, this study aims at developing improved reconstruction methods, and the objective of this study was to recreate knot data for logs, equivalent to those in the stem bank today, based on a small amount of features that are possible to extract from industrial X-ray images and to calculate from the knots in the SPSB. In a first step, the models used to recreate knot data will be developed, not using actual X-ray images, but based on features calculated from the SPSB data. These features are ones that are possible to extract from X-ray images. The modelled knots should be representative of the real knot population at large in the logs, and produce sawing simulation results similar to those of a CT-scanned log. Measuring the knot and whorl features in actual two-directional X-ray images will be addressed in future work.
Materials and methods
This study was based on 628 Scots pine logs from the SPSB, originating from 198 trees. The stem bank trees, from well-documented sites at different locations in Sweden, have been documented thoroughly regarding both tree properties and silvicultural treatments. They have been scanned with a medical CT scanner to record internal properties such as knots, pith location and sapwood/heartwood border. The SPSB knot database is based on 11 parameters named A to K, derived from CT-images of logs (Grundberg et al., Citation1995). The geometry of each knot is described by these parameters and the parametric description makes it possible to describe knots in a tree with a minimal amount of data. shows how a knot is represented geometrically in the SPSB, and the functions describing the geometrical features using the knot parameters are presented below. A further description of the knot parameters is included in Grönlund et al. (Citation1995).
Θ p =radial knot angle in radians,
r p =radial distance from the pith in pixels along the knot axis.
Ωaxis=angle position in radians of the knot axis,
Figure 1. Description of the key geometrical features for SPSB knots. These features are calculated using the 11 Swedish Pine Stem Bank knot parameters A–K.
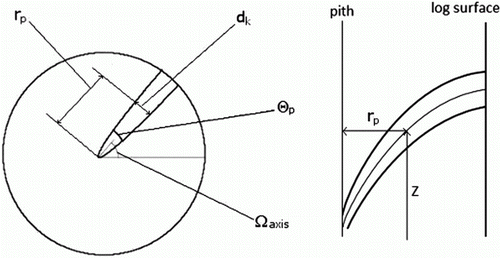
The parameters E and F are equivalent to the parameters A and B, but for the longitudinal diameter of the knot.
Z=Height position of the knot axis in cm, from the butt end of the log,
I=Distance from the pith to the end of the knot in millimetre,
J=Distance from the pith to the dead knot border in millimetre,
K=Distance from the pith to where the knot axis hits the log surface, in millimetre.
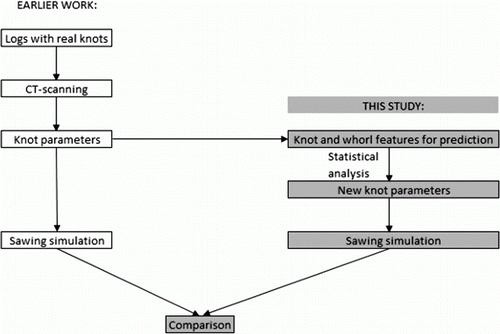
A summary of the stages involved in this study is presented in . The left-hand side of the chart represents the work that has been done in the SPSB (Grönlund et al., Citation1995) in addition to sawing simulation, while the right-hand side is the work presented in this article. The latter involves pre-processing of the SPSB knots to extract the desired features, reconstruction of the parameterised knots using only these features and sawing simulation to compare the two sets of knots, which are the same physical knots but constructed using different features.
Figure 2. Description of the main structure of this study. Note the distinction between the physical knots in the log, the knots as represented in the Swedish Pine Stem Bank by parameters, and the knot features used for reconstructing the knots. Furthermore, at the last step the sawing simulation is made on the same set of physical knots, but reconstructed in two separate ways. The original SPSB knots (left) are considered ground truth and are the foundation for the new parameterisation of the SPSB knots (right).
The models should be based on features that are possible to extract (Grundberg & Grönlund 1992, 1997; Nordmark Citation2005) from industrial X-ray images. The features tabulated in satisfy this condition and were extracted from the SPSB parameter files for each whorl, that is, these features are not measured in X-ray images, but calculated from parameter files created by CT-scanning and image analysis.
Table I. Features used for reconstructing knots. These features are possible to extract using two-directional X-ray scanning, and in this study were calculated for the SPSB knots.
Feature extraction from the SPSB knots
The first step of this study (right-hand side in ) was to extract features from the SPSB, WhorlHeight, ΔHeight, Whorl volume and SurfaceDist. In this study, 45,834 knots from the SPSB were analysed. The knots were sorted into whorls according to the following definition:
| • | If the height to a knot, measured from the butt end of the log to the starting position of the knot at the pith of the tree, is within 8 cm from the height of the whorl, the knot is added to the whorl. Eight centimetres was chosen because this conforms well to an earlier definition made by Björklund (Citation1997) on the SPSB whorls; see for more detail. Note that he excluded some of the whorls in his study, so the absolute numbers are different but the overall distribution of whorls is roughly the same. | ||||
| • | WhorlHeight is continuously updated each time a knot is added, and is defined as the average of the height, at the pith, of each included knot. | ||||
| • | If a knot cannot be assigned to a whorl, this knot forms a new whorl with height equal to the knot height (at the pith). | ||||
| • | “Whorls” with only one knot were omitted from the model. | ||||
Table II. Number of whorls with different knot frequencies, according to the definition used in this study. The sets of data in the two rows are both from the Swedish Pine Stem Bank; the first row is the number of whorls obtained with the above method, the second row is the number of whorls obtained by a method used in an earlier study by Björklund (Citation1997).
The result of this definition is presented in . Note that only whorls with 12 or less knots are presented here. In the SPSB, there are whorls with up to 23 knots, but the whorls with more than 12 knots account for less than five per mil of the total whorl population, so they are omitted in for more convenient reading.
WhorlHeight was calculated as already described, while ΔHeight was the height distance between a whorl and its predecessor. If the whorl was the first in the log, ΔHeight was set to WhorlHeight. The Whorl volume was the sum of the volumes of each individual knot in the whorl, which were calculated using the function for knot diameter. The knots were, in this case, assumed to have a circular cross-section, using the parameters A and B that describe the knot size in the log cross section plane, since these are better described in the SPSB than their longitudinal counterparts E and F (Grönlund et al., Citation1995). Thus, the volume of each knot was calculated using the following equations:
from Nordmark (2005), see Equation Equation1.
Equations 1 and 2:
V=knot volume in mm3
L=knot length (SPSB knot parameter I)
scale = magnification in computer tomograph/256
A, B=knot parameters describing knot propagation angle
r p =radial distance from the pith in pixels along the knot axis.
See and Equation Equation1 for details.
SurfaceDist in this study was already given in the stem bank for each knot, by parameter K.
Parameter reconstruction method
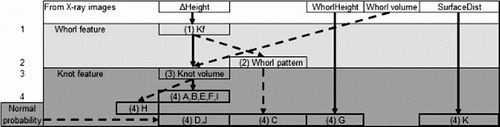
Reconstruction of parameters was the second step in the study; see . This was made by statistically analysing the extracted features of the SPSB knots. The features that needed to be predicted, from the calculated features in , to reconstruct the knots from the SPSB were K f =knot frequency or knots per whorl, and all 11 SPSB knot parameters A–K.
A method for reconstructing the knot parameter files of the SPSB from the measurable features in was constructed. The reconstruction method involved four main steps: assignment of K f to each whorl, assignment of cardinal direction pattern to the whorl, assignment of volume to each knot and assignment of SPSB knot parameters to each knot. The first step was based on a linear function predicting the number of knots of a whorl using ΔHeight. The second step was performed for each whorl, and was done to decide the cardinal direction of each knot in the whorl. In the SPSB logs, a small amount of typical patterns for cardinal direction of knots were very common. Thus, a whorl was given a certain chance of being sorted into a specific pattern depending on the relative distribution of these typical patterns. After this, the knots in the whorl were given a cardinal direction according to the pattern. The third step, distribution of the whorl volume over the knots in the whorl, tried to imitate the size distribution of the knots in the SPSB whorls, which was not even. This was done by randomly assigning each knot in the whorl a size order, and then distributing the knot volume according to the size order. The fourth and final step utilised a linear model relating the SPSB knot parameters to the knot volume when applicable, and in other cases the parameters were randomly chosen from a normal distribution. The linear models were chosen as the ones among several tested, that yielded the best coefficient of determination (R 2), when applied on the SPSB material. If R 2 was lower than 0.3 a stochastic method was chosen, for the most crucial parameters A, I and J. presents a summary of the reconstruction strategy. Dashed arrows denote connections with a random or a stochastic element, while solid arrows denote direct or linear relationships.
Figure 3. Reconstruction of knot parameters, from measurable log properties. From the features ▵Height, WhorlHeight, Whorl volume and SurfaceDist, each whorl is reconstructed (i.e. number of knots in the whorl and a typical pattern for cardinal direction of the knots). The individual knots are finally modelled in a parametric fashion from the whorl features. Note: solid arrows denote direct or linear relations; dashed arrows denote models with some sort of random element involved. K f =number of knots per whorl, A–K=SPSB knot parameters. Darkest area: knot features/parameters, semi-dark area: whorl features, light area: features from the SPSB. The numbers represent the different steps in the overall model, numbered 1–4.
The resulting knot models are thus described in exactly the same manner as the original SPSB knots, with the same set of parameters (but with other values), to allow sawing simulation and comparison with the original SPSB knots.
Validating the method by simulation
The SPSB can be used for sawing simulation using the simulation software Saw2003, developed by Nordmark (Citation2005). In Saw2003, the CT-scanned logs of the SPSB provide input, and the software allows the user to view and manipulate logs and boards in 3D. It models a sawmill that uses cant sawing with two sawing machines, edging and trimming. The latter two are value-optimised according to timber prices and grading criteria, and the simulation results in virtual boards with information about knots, value, dimensions and so forth.
The reconstruction method was thus tested using sawing simulation in Saw2003 of logs with the reconstructed knots from this study, which are the same knots as in the SPSB but parameterised in a different way using less information, that is, in the way that it would be done if the information was from a two-directional X-ray scanner instead of CT scanning. The results from this simulation were compared with sawing simulation of logs with the original stem bank knots, obtained from a medical CT-scanner. The latter knots are defined as the ground truth in this study.
Since the model involved random elements, three reconstructions and subsequent test sawings were made, with the same in-data. The simulations used the default sawing pattern for each individual log, which was chosen based on sawing class assignment of the log according to the top diameter.
In this comparison, log shape and heartwood/sapwood border were the same for both sets of logs. The resulting boards were graded A, B or C according to the Nordic Timber Grading Rules (Anon., Citation1994). Grades are ordinally scaled, with grade A considered as the one with the strictest rules. Concerning knots, grading is done according to size of and number of knots per board surface. Also, different criteria are used for sound knots and dead knots in grades A and B. One of the decisive quantities that are regarded when grading boards is the size of the largest knot on each board surface.
In the sawing simulations, the price list shown in was used. Because Saw2003 utilises value optimising in edging and trimming, a sensitivity analysis with regard to pricing was performed. This was done to investigate whether the prices for sawn timber affect the end result, since price is a quantity that constantly changes, and is subject to other factors than the raw material itself. The different prices are presented in . In the price sensitivity analysis, only one set of reconstructed knots was evaluated.
Table III. Sawn timber prices used in this study.
Results
Within this section, results of the four main steps are presented in ; models for K f, cardinal direction, knot volume and finally the knot parameters themselves. The models are based on the features extracted from the SPSB.
Knots per whorl
In this study, the prediction model for knot frequency per whorl (K f ) was based on distance between whorls, ΔHeight. A linear model using the natural logarithm of ΔHeight was used, and the least square regression function between K f and ln(ΔHeight) was calculated as K f =1.570 + 0.988×ln(ΔHeight). This model resulted in a coefficient of determination (R 2) of 0.13. However, when using this model and rounding the result to the nearest integer, which is necessary since knot frequency is a discrete quantity, the result differed from the SPSB whorl by less than or equal to one knot in 70% of the cases. In comparison, a normally distributed random function only achieved this in 49% of the cases, on average. For the whorls with 3–6 knots, which are by far the most common cases, accounting for around 4/5 of the whorl population, this number was higher: 86%. An untransformed model was slightly worse than the one using the natural logarithm of the intercept, with 66% of the whorls predicted within one knot. Furthermore, a model not using the natural logarithm of ΔHeight resulted in whorls with three or more knots only, thus not accounting for the two-knot whorls.
Cardinal direction of knot
Many of the whorls in the SPSB behave in a similar manner with regard to the cardinal direction of the knots near the pith. Whorls with five or more knots usually have their knots symmetrically distributed around the radial plane. Thus, a number of typical patterns () for whorls with three or four knots were defined. The special case of whorls with two knots can be handled in a more simplified way. Nine and 13 respective patterns were defined for whorls with three knots and whorls with four knots (in total 22 typical patterns). This classification was made to decide the parameter C for each knot in a whorl, based on the number of knots in the whorl.
Figure 4. Three examples of typical whorl patterns, from the Swedish Pine Stem Bank, for whorls with four knots. This figure shows the cross-sectional view of a log, seen from the top end. Note: The zero-degree direction corresponds to north in the standing tree. Each straight line corresponds to the cardinal direction, at the pith, of a knot. The uppermost right degree-interval limits the direction of the first knot, clock-wise, from the northern direction. All other degree-intervals limit the angular distances between knots.
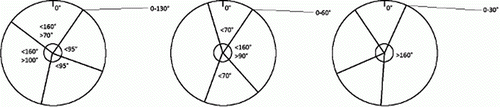
The typical patterns start with the first knot in a clock-wise direction (viewed from the top end of the log) from the 0° direction, which is the same as the north direction in the standing tree. The C parameter of this knot was defined within a specific interval of positions for each pattern, as shown in . All other knots were defined in relation to this first one, also within a degree-interval. These 22 type patterns represent 88% of the CT-scanned SPSB whorls. Reconstruction of whorls could thus be made using these typical patterns, randomising the actual position of the knot within the pattern intervals. Each three- or four-knot whorl was randomly assigned a typical pattern based on how common the case was, and then the knot direction was randomised within the pattern restrictions.
For whorls with more than four knots, it was more convenient to begin with the southernmost knot, since the northernmost knot could have either very high values (slightly below 360) or very low values (slightly above 0) of the parameter C, which makes it more difficult to handle. In the entire SPSB, the direction of this knot was, in general, approximately normally distributed around 180°, with a standard deviation that decreases with the number of knots in the whorl, but is around 26° on average.
The other knots were, in general, spread out with a distance of 360°/K f . In this case as well the standard deviation decreases with the amount of knots in the whorls, but on average it is around 28°. This meant that the reconstruction of the whorls with a knot frequency over four could be made by first defining the direction of the southernmost knot, using a normal distribution function with expected value 180° and standard deviation of 26°. Then the other knots were spread out, starting from the southernmost knot. The angular distance between a knot and the next one was decided according to a normal distribution function with an expected value of 360°/K f and a standard deviation of 28°.
Lastly, the whorls with just two knots were handled in a separate way. Here, the orientation of knots was evenly distributed, but the angle between the two knots was normally distributed with an expected value of 104° and a standard deviation of 44°. The consequence of this was that the first knot in a whorl with two knots could be randomly assigned a C-parameter (0–360), while the second knot could be positioned according to a normal probability function in relation to the first.
The value of the parameter D (i.e. bending of the knot in the radial plane) was normally distributed around 0.25 in the entire stem bank, with a standard deviation of 5.1. No significant differences due to cardinal direction or size could be found in the material; nor were there any clear similarities within the whorls or logs. All knots were thus assigned a D-parameter according to a normal probability function.
Distribution of knot volume
The total volume of a whorl was not evenly distributed among the knots in the whorl. The largest knot in the whorl had on average 183% of the average knot volume in the whorl, in a whorl with four knots. This percentage was approximately linearly related to the number of knots in the whorl; see .
Figure 5. The largest knot's percentage of the average knot volume, plotted against number of knots in the whorl. The vertical lines show the distance of one standard deviation around the average.
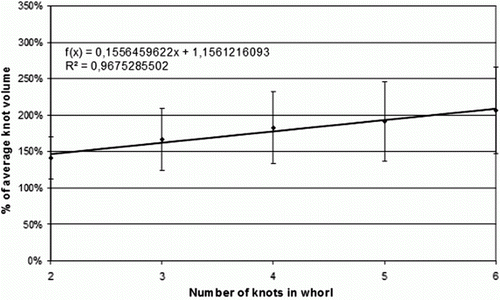
Similar relationships existed for knots of other size orders (second largest knot in whorl, third largest knot in whorl, etc.).
There was no correlation (correlation coefficient R=0) between knot volume and cardinal direction found in the material. The knot volume was thus decided by randomly giving each knot a size order, and assigning the volume according to this rank and the average knot volume in the whorl. This was made using the linear model above.
Parameter reconstruction
The parameters, A, B, E, F and I, are related to the size of the knot, that is, diameter and length. Hence, it was possible to predict the values of these parameters using the knot volume. shows the coefficient of determination (R 2) values for linear models of each of these parameters, using the knot volume as a predictor. Remember that parameters, C, D, G and K, are determined using other features than knot volume. The models tabulated are the ones among several tested, with different transformations of the data that yielded the highest R 2. Parameters H and J are also included, as well as dead knot percentage, which is expressed as (I–J)/I, that is, the dead knot length divided by total length.
Table IV. Models for reconstructing knot parameters from the knot volume (V). Note that the models for parameters H, J and dead knot percentage were not used in the final method.
Parameter H was reconstructed using a normal probability function with expected value along the regression model line, and a standard deviation equal to the root mean square error (RMSE = 0.59) of the model compared with the SPSB data. J was created purely by a normal probability function, but using dead knot percentage. This method is preferred over a direct approach since the knot length limits the dead knot length, thus making the value of the latter highly dependent on the value of the former. The expected value for this normal probability function is 0.43 and standard deviation 0.11. Parameters E and F, also with low R 2, are deemed as less important since they are poorly modelled in the SPSB itself, and are thus not crucial for the sawing simulation results. Hence, the models for these can be accepted even with such a low R 2.
In this study, the parameter G was set to the height of the whorl in the log, and the parameter K was set as the parameter K from one of the knots in the whorl which knots were reconstructed from, and copied to all the reconstructed knots in the whorl.
Validating the method by simulation
Using the strategy described, the whole SPSB was analysed and all whorls were reconstructed. Sawing simulation using the software Saw2003 was done on logs with the original knots, obtained from a medical CT-scanner, as well as logs with the reconstructed knots. This was done on all 628 logs of the SPSB. The result showed that the resulting boards with reconstructed knots had the same grade as the boards with the original knots in 63.5% of the cases, on average over three test runs using different but equivalent random sets for the knot reconstruction. In 10.4% of the cases, the difference was more than one grade.
The grade distributions of boards for the three different test runs were very similar, despite the random elements in the model. The average numbers of boards in each grade for the reconstructed and original knots, respectively, are presented in .
Table V. Comparison of the grades assigned to boards which have knots reconstructed by the method described, and the original SPSB knots.
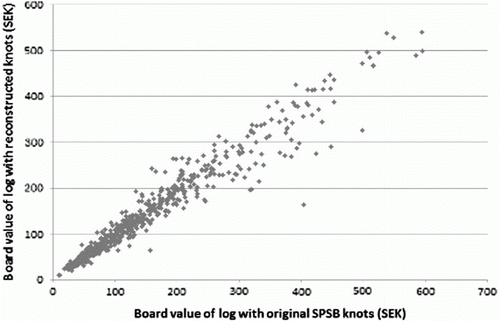
presents the value of boards produced by sawing simulation, for each log in the SPSB, for the first simulation run. The horizontal axis shows the value produced when using the original SPSB knots, and the vertical axis the value when using reconstructed knots.
Figure 6. Simulated value of logs with reconstructed knots, plotted against the simulated value of logs with the original SPSB knots; values in Swedish Crowns (SEK).
A sensitivity analysis with regard to prices of the sawn timber was made. Only one sawing simulation was performed here, since the variation in overall grade distribution is very low between different runs. The grade distribution with the changed prices is shown in for original SPSB logs, as well as those with reconstructed knots. In this case, the sawing simulations produced boards of the same grade as in the original SPSB in 60.9% of the cases.
Table VI. Comparison of grade distribution between reconstructed and original knots, when using a different pricelist than in . Note that the amount of C grade boards is much smaller since these are valued much lower than in the first simulation run.
Discussion
Reconstruction of knots requires data to work with; in this case internal knot features extracted from two-directional X-ray scanners. It also requires knowledge about how knots and whorls are structured within a log. Building this knowledge has been in focus with this study.
The results of this study are very promising, with a prediction rate (the amount of boards which were given a correct grade using the reconstructed knots) of almost 64%. This is higher than the figures presented in Grundberg et al. (Citation1999), and indicates that the model is worthy of future attention. The values of boards are similar when comparing simulations on logs with original knots with logs with reconstructed knots, as shown in . The difference to Grundberg et al. is mainly that the model presented here is, to a large degree, based on geometrical measurements, whereas the earlier study was feature and knowledge based. Geometrical considerations thus seem to play a major role in proper knot modelling. Since one of the key features considered when grading boards is size of the largest knot on each board side, the knot volume distribution is probably a crucial part of the model presented.
The typical whorl patterns (whorls with three or four knots) for cardinal direction are based on quite large intervals in degrees. This is a balancing issue, between covering enough whorls with the patterns, and introducing a random element in the whorl generation, which makes the reconstructed whorls differ more from the real ones. Moreover, the whorls are assigned a typical pattern in a random way. This strategy could be replaced with a more elaborate approach, and there is probably room for some fine-tuning regarding both these issues. The results of the sawing simulation are a strong indicator that the balancing has been performed quite well in this case, however. The last issue regarding cardinal direction is that all whorl patterns are defined in relation to the northern or southern direction. This is not a piece of information that is available in a practical application. However, this could be solved either by randomly assigning each log a “south” direction or by some distinguishable feature of the log. The choice of solution is open for future discussion and research.
There is also room for improvement with regard to the amount of knots per whorl. For instance, one might consider using the knot bumps on the surface of the log instead of ΔHeight, which is a rather weak indicator.
Many of the correlations used in the model are weak, due partly to the biological origin of the data, but also to the small amount of features available for prediction. This does not seem to be a large problem in this case though, since the overall quality of the logs in terms of knot features seem to be predicted quite well despite this. Furthermore, this study is based on data which is possible to extract from X-ray images using image analysis. In this study, the data have been extracted from the stem bank logs, but in an industrial application the data is expected to show a larger degree of noise. The consequence of this is that the model presented in this study needs to be verified and/or calibrated using real material.
Finally, the decision to build the models based on the logs in the SPSB can be considered as a bit dubious. One of the intended applications of the study is to be able to increase the size of the SPSB with more representative logs, using industrial X-ray data. If we do so by using models that are based on these trees, will they be valid for the real material? This is probably the case, since care has been taken to treat the trees in a varied fashion to achieve a population representative of the results of common practice today. The trees were, furthermore, located at a wide range of geographical locations, albeit limited to Sweden. This is, however, a matter that needs to be addressed in future work, again by testing on real X-ray data. Also, one has to bear in mind that the results presented here are only tested on Swedish data which is why a general conclusion regarding these knot characteristics is difficult to make from this study. Another issue is that the developed model recreates knots that are representative of the average tree, but it is not known what happens when a tree that differs significantly from the rest of the population is used as in-data to the model. This is shown in the correlation coefficient for some of the sub-models, which is low, not due to a lack of trend or linearity of the data, but due to a large spread around the average line. Whether this is an important issue depends on the intended application of the model.
Overall, the models predict the grade of the sawn timber to a very high degree on a larger scale with several logs, while on the single board level the error is larger. The conclusion of the study is that it is possible to use data obtainable from a two-directional industrial X-ray scanner to reconstruct realistic whorls and knots for sawlogs, to facilitate improved online sawing simulation, in sawmills with a two-directional X-ray scanner together with an optical three dimensional scanner. A secondary application is to enlarge the amount of data available for sawing simulation for research purposes. The method needs to be tested using measurements made in actual two-directional X-ray images, however.
Acknowledgements
This work was financially supported by TräCentrum Norr, a research programme jointly funded by industrial stakeholders, the European Regional Development Fund (ERDF) and the county administrative boards of Norrbotten and Västerbotten. The author would like to thank Olof Broman, Anders Grönlund, Micael Öhman and Johan Skog for commenting on the manuscript.
References
- Anonymous 1994 . Nordiskt trä. Sorteringsregler för sågat virke av furu och gran . [Nordic timber. Sorting rules for sawn timber from pine and spruce.] , Stockholm : Arbor publishing . (In Swedish.)
- Benjamin , J. G. , Kershaw , J. A. , Weiskittel , A. R. , Chui , Y. H. and Zhang , S. Y. 1999 . External knot size and frequency in black spruce trees from an initial spacing trial in Thunder Bay, Ontario . The Forestry Chronicle , 85 ( 4 ) : 618 – 624 .
- Björklund , L. 1997 . The interior knot structure of Pinus Sylvestris stems . Scandinavian Journal of Forest Research , 12 ( 4 ) : 403 – 412 .
- Björklund , L. & Moberg , L. 1999 . Modelling the inter-tree variation of knot properties for Pinus sylvestris in Sweden . Studia Forestalia Suecica, 207 , 23 pp .
- Fenton , R. 1960 . Timber-grade studies on Corsican pine in the Tapanui district and their silvicultural implications . New Zealand Journal of Forestry , 8 ( 2 ) : 218 – 230 .
- Grönlund , A. , Björklund , L. , Grundberg , S. & Berggren , G. 1995 . Manual för furustambank [Manual for pine stem bank] . Technical report 1995:19T. 25 s. ISSN 0349-3571 . Sweden : Luleå University of Technology . (In Swedish with English abstract.)
- Grundberg , S. & Grönlund , A. 1992 . Log scanning – Extraction of knot geometry . Seminar/workshop on Scanning Technology and Image Processing on Wood , August 30–September 1, 1992, Skellefteå .
- Grundberg , S. and Grönlund , A. 1997 . Simulated grading of logs with an X-ray log scanner – Grading accuracy compared with manual grading . Scandinavian Journal of Forest Research , 12 : 70 – 76 .
- Grundberg , S. , Grönlund , A. & Grönlund , U. 1995 . The Swedish Stem Bank – A database for different silvicultural and wood properties . Technical report 1995:31. ISSN 0347-0881 . Sweden : Luleå University of Technology .
- Grundberg , S. , Grönlund , A. , Oja , J. & Israelsson , M. 1999 . Log models reconstructed from X-ray LogScanner signals . In : G. Nepveu , Connection between Silviculture and Wood Quality through Modelling Approaches and Simulation Software . Proceedings of the Third Workshop, September 5–12, La Londe-Les Maures, France, IUFRO S5.01.04 , pp. 394 – 398 .
- Mäkelä , A. , Vanninen , P. and Ikonen , V. P. 1997 . An application of process-based modelling to the development of the branchiness in Scots pine . Silva Fennica , 31 ( 3 ) : 369 – 380 .
- Mäkinen , H. and Colin , F. 1998 . Predicting branch angle and branch diameter of Scots pine from usual tree measurements and stand structural information . Canadian Journal of Forest Research , 28 : 1686 – 1696 .
- Moberg , L. 2006 . Predicting knot properties for Picea abies and Pinus Sylvestris from generic tree descriptors . Scandinavian Journal of Forest Research , 21 ( 1 ) : 49 – 62 .
- Nordmark , U. 2005 . Value recovery and production control in the forestry-wood chain using simulation technique . Doctoral Thesis, Division of Wood Technology, Luleå University of Technology, 2005, 21. ISSN 1402-1544 .
- Petersson , H. 1998 . Prediction of branch variables related to timber quality in Pinus Sylvestris . Scandinavian Journal of Forest Research , 13 ( 1 ) : 21 – 30 .
- Pietilä , J. 1989 . Shape of Scots pine knots close to the stem pith . Silva Fennica , 23 ( 4 ) : 287 – 299 .
- Pinto , I. , Pereira , H. and Usenius , A. 2002 . Analysis of log shape and internal knots in twenty Maritime pine (Pinus pinaster Ait.) stems based on visual scanning and computer aided reconstruction . Annals of Forest Science , 60 ( 2 ) : 137 – 144 .