Analysis of normal tissue complication probability of the lung using a reliability model

Abstract

The volume effect of normal tissues and organs is an important factor for predicting normal tissue complication probability (NTCP) following partial, heterogeneous irradiation of organs at risk, and reducing the late sequela by conformal radiation therapy. We have previously developed a reliability model for calculation of NTCP, assuming a parallel architecture of functional subunits (FSU), where a critical number (k) out of the total number of FSUs (N) must be intact for the organ to maintain its function. Published data on radiation-induced lethal pneumonitis and altered breathing rate following partial volume irradiation of the mouse lung were analysed, and critical fraction and corresponding spatial density distribution of FSUs were estimated using this model. The critical fraction (k/N) seemed to be similar for the two endpoints, and a value of 0.7 was found to provide good fit to the experimental data. The critical fraction did not vary throughout the lung, and variation in volume effect cannot therefore be attributed to heterogeneous tissue architecture. On the other hand, our analysis revealed that the observed variation in volume effect of mouse lung may be attributed to heterogeneous spatial distribution in FSU density or also the spatial variation in inactivation probability of the FSUs.

In modern radiotherapy, a common strategy for improving the therapeutic ratio, i.e. the probability of local tumour control or survival vs. late toxicity, is to reduce the irradiated volume of normal tissues and organs. The underlying assumption for this strategy is that the organ or tissue in question possesses a fair volume effect. Different strategies have been pursued in the modelling of normal tissue complication probability following partial volume irradiation at different dose levels [1–9]. The established models can be classified as either phenomenological or biological/mechanistic. The phenomenological models are characterized by a limited number of parameters and are as such appealing as the clinical data may be limited, whereas the biological models may require a number of parameters in order to describe the most predominant mechanisms. Most of the biological or mechanistic founded models assume that the organ consists of functional subunits – FSUs, organized in a functional architecture.

We have previously published a reliability model for calculation of the normal tissue complication probability assuming a parallel architecture of FSUs, but where a given fraction, k out of the total number of FSUs (N), must be intact for the organ to maintain its function [4]. The k-out-of-N may also be denoted the critical fraction. In this model the tissue volume effect is thus attributed to variations in the fraction of FSUs that must be intact for the organ to maintain its function, i.e. the critical fraction. The assumption of a critical fraction has also been implemented in other authors’ models, e.g. the model suggested by Yorke and colleagues [6]. In contrast, the relative seriality model, suggested by Källman et al. [1], assumes that the volume dependence of irradiated normal tissue is attributed to various combinations of parallel and serial structures. The above-mentioned models take into account partial organ irradiation and heterogeneous dose distribution. An additional feature of the purposed reliability model is the dual inactivation principle, i.e. indirect effects on non-irradiated parts of the organ can be taken into account [4], [10].

The lung is generally regarded as a dose-limiting organ and significant with respect to morbidity associated with radiation therapy in the thorax. Curative radiation therapy involving high dose levels may thus result in unacceptable high probability of late sequela. Reduced volume of irradiated lung may, however, reduce the toxicity, as the probability of most late endpoints in lung is dependent on the irradiated volume as well as the dose level. Still, the tolerance dose to partial volume irradiation and the impact of irradiated volume is not known to the full extent [11]. The mouse lung has been regarded as a reasonable model for studies on late sequela of the human lung. Travis and colleagues [11–13] have in particular contributed to the investigation of the nature of the volume effect in lung and the tolerance doses by their experiments in mouse lung, and they have demonstrated a spatial heterogeneity in the radiosensitivity of the mouse lung. A pronounced variation in radiation sensitivity throughout the lung was demonstrated also in rats by Novakova-Jiresova and colleagues [14]. There may be different explanations for the observed volume effects; a spatial heterogeneity in FSU distribution, a spatial heterogeneity in radiation sensitivity of the individual FSUs, and lastly, a spatial heterogeneity in tissue architecture.

In the current paper, we have analysed the data on radiation-induced altered breathing rate and lethal pneumonitis following partial volume irradiation of the mouse lung published by Travis et al. [11] and Liao et al. [12]. In this analysis, the reliability model was applied in order to establish the critical fraction (k/N) for the two endpoints, as well as spatial distribution of FSUs, and spatial distribution of FSU inactivation probability.

Material and methods

Experimental data

The present analysis was based on data published by Travis et al. [11] and Liao et al. [12]. Their studies addressed the effect of partial-volume lung irradiation on the incidence of radiation pneumonitis in mice, as assessed by elevated breathing rate 22 weeks after irradiation and lethality within 28 weeks. In those studies, different subvolumes were irradiated in the apex, base, and the middle region of the lung, as described by Travis et al. [11].

NTCP model

The calculation of normal tissue complication probability (NTCP) for uniform irradiation was performed according to Olsen et al. [4], based on a reliability model, assuming that tissue and organs can be described as structures consisting of a number, N,of functional subunits (FSUs)-N. A partial volume irradiated corresponds to a number of irradiated subunits, n, in our reliability model. Complications will not occur unless sufficiently large fractions of the irradiated FSUs (n/N) are inactivated. We assume therefore that the lung consists of N identical FSUs, and that k of these subunits must be intact for the lung to maintain its function. In contrast, for strictly parallel organs it is sufficient that only one single FSU is intact for the organ to maintain its function. For organs with a highly serial functional architecture, on the other hand, k is close to N, i.e. the critical fraction k/N is close to unity. If the FSUs are arranged in a more parallel structure, as suggested for the lung, k is less than N, and no complication will ever occur if k is below N−n. We also, for simplicity, assumed that the probability p for a single FSU to be inactivated is a function of dose only. Then the normal tissue complication probability was calculated using Equation 1 in Olsen et al. [4]:1 The NTCP is calculated as one minus the FSU survival probability. The model calculates the sum of survival probabilities for all combinations of n and k, assuming at least k survivors, i.e. enough FSUs to maintain the organ function. The lower bound of summation is then k minus the unirradiated units (N−n), so y_min=k−(N−n)=k+n-N. The upper bound of the summation represents when all irradiated units survive, hence y_max=n. Based on appropriate values of p, N, k, and n, complication probabilities were calculated and compared to the experimental data. The model was implemented in Java (Sun Microsystems, Inc., California).

FSU inactivation model

Tucker et al. [13] used the lethality data [11], [12] to estimate the spatial distribution of target cells. In their analysis, all target cells were assumed to have the same radiosensitivity. The cell survival after dose D was given by the surviving fraction: SF=exp(ln K−D/D₀). In the following analysis, this model was assumed also valid for calculation of the inactivation probability of functional subunits. The inactivation probability p for every FSU was then calculated using Equation 2:2 where D≥D₀ ln K, and the radiosensitivity parameter D₀ and K are optimized for the two different endpoints.

Determination of parameters

A severe limitation of the non-empirical models addressing the normal tissue volume effect is the large number of parameters. Numerous parameters are in particular a problem when data is scarce. To reduce the number of parameters in the model we have introduced the relative number of FSUs, i.e. we normalize the total number of FSU to 100. The number of critical FSUs (k) and the number of irradiated FSUs (n) will then represent the percentage of the total number of FSUs. The NTCP model given by Equations 1 and 2 was fitted to data published by Travis et al. [11]. First, the radiosensitivity parameters were estimated, and then the number of irradiated subunits and the critical fraction. A possible distribution of inactivation probability was also estimated. These processes are described below.

Optimal parameter combinations were obtained using the principle of minimizing the sum of the squared deviations. For all combinations of the parameters under consideration, the sums of squared differences between the calculated complication probability and the experimentally observed responses were calculated according to Equation 3:3 where the sum is taken over all experimental data points considered. By dividing the sum of the squared deviations by the corresponding number of observations, M, the mean squared deviation was obtained. The root-mean-square (rms) error was then calculated according to Equation 4:4 This rms error served as a goodness of fit criterion, and should be as low as possible.

Radiosensitivity parameters (K and D₀)

The best combinations of the inactivation parameters K and D₀ were obtained by analysing the experimentally observed responses for 100% organ irradiation. This corresponded to n=N in the model, and represented the most reliable volume fraction. Assuming a non-uniform distribution of the FSUs throughout the lung, whole organ irradiation ensured correct irradiated fraction (n/N=1), and thus the impact of the critical fraction k/N turned out to be almost negligible as long as k/N < 0.9, which is plausible for an organ with a more parallel structure. For doses where responses of the 100% subvolume were observed, K and D₀ were varied, restricted to provide a non-negative FSU inactivation probability, p(K, D₀, D), and a minimal rms error.

Irradiated FSUs and critical fraction (n and k)

The best combinations of critical number of survivors (k) and number of irradiated FSUs (n) were calculated for all data sets (apical and basal data on lethality and elevated breathing rate), using already established values of K and D₀ for the given endpoints. The lower bound of summation in Equation 1 depends on both n and k; therefore, the best estimates of n (1–100) for different irradiated subvolumes in a data set were obtained for every possible value of k (1–100) by minimizing the rms error. As the inactivation probability was independent of location, our model did not account for the location of the irradiated subvolume. We also assumed that the critical fraction did not depend on location, i.e. it was irrelevant which of the irradiated FSUs that were contained in the surviving subset k.

Spatial distribution of FSU inactivation probability (p)

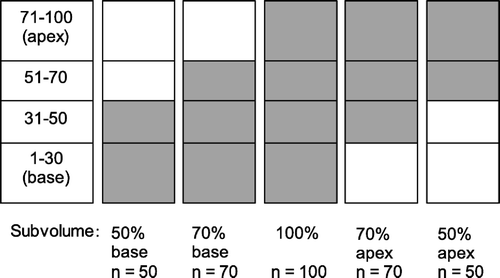
A possible spatial distribution of FSU inactivation probability was addressed by assuming a homogeneous distribution of the FSUs, i.e. n/N=subvolume, and a critical number (k) as estimated by the preceding optimizations. Due to the very large number of possible combinations of inactivation probabilities of the FSUs, we made some simplifications. Only basal and apical elevated breathing rate data corresponding to subvolumes 50% (n=50), 70% (n=70), and 100% (n=100) were used in the calculations. For each of these five different subvolumes (Figure 1), we obtained the combination of K and D₀ producing the lowest rms error comparing calculated complication probability and experimental data. Then p(K, D₀, D) was calculated for five different doses from 14 to 22 Gy for each of the subvolumes. Next, the 100 FSUs of the lung was divided into four different compartments from base to apex (numbered 1–30, 31–50, 51–70, and 71–100), as illustrated in Figure 1. The subvolumes 50%, 70%, and 100% then consisted of two, three and four compartments, respectively. For every dose, the inactivation probabilities for the four compartments were varied, and for every subvolume, a value of p was obtained using a weighted average of the inactivation probabilities for the corresponding compartments. This value was compared to the previously calculated p(K, D₀, D) for calculation of the rms error.

Figure 1.  The 100 FSUs of the lung divided into four compartments of different sizes, illustrated for five subvolumes.

Results

Determination of K and D₀

Determination of the FSU inactivation probability parameters K and D₀ was based on responses following whole organ irradiation. However, the two different endpoints do not necessarily correspond to the same set of K and D₀. For the elevated breathing rate data we found K=1.47 and D₀=27.5 Gy, and for the lethality data K=1.55 and D₀=24.9 Gy. These values were used in the calculations of inactivation probability for the two endpoints.

Determination of n and k

The best estimates of n for all irradiated subvolumes in a data set were obtained for every possible value of k (1–100) by minimizing rms errors. As can be seen in Table I, low and stable rms values corresponding to stable n values for all subvolumes and both endpoints were found for values of k in the range of 59–83, however only the range 66–75 was shared by all data sets. In Figure 2, the rms errors for different values of k can be seen. The intervals with stable rms values did not contain the lowest rms values. These were located at larger values of k. However, these lowest rms values corresponded to quite different distributions of n and the rms values were only about 1% lower than the stable values. Therefore we focused on the stable interval and decided to use k=70 for NTCP calculations. For all data sets, this value of k represented a unique value of n for every subvolume, except for the subvolumes where no complications were observed.

Figure 2.  The best rms error for each of the four data sets (elBR=elevated breathing rate data, dead=lethality data) as a function of the critical number of survivors, k, when the total number of FSUs is 100. Circles indicate the k with the least rms error for each of the four data sets. The stable intervals are given in the last row of Table I.

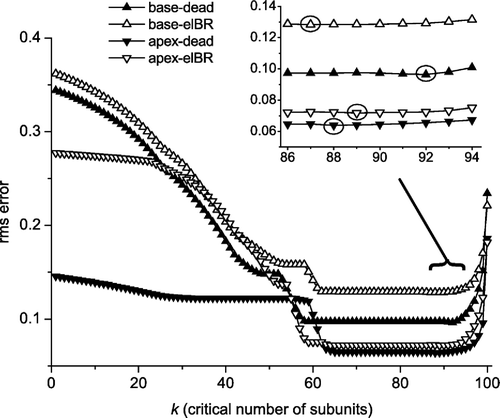
Table I.  Numbers of irradiated FSUs (n) and corresponding ranges of the critical number of FSUs (k) for the two endpoints and different irradiated subvolumes of the mouse lung.

	Optimized nbase			Optimized napex
Basal subvolume (%)	lethality	breathing	Apical subvolume (%)	lethality	breathing
18	-*	35	19	-*	-*
32	-*	39	30	36	37
40	-*	47	50	36	42
50	42	57	70	38	48
70	52	62	75	38	49
84	53	61	84	42	47
90	61	79	94	68	81
100	100	100	100	100	100
rms error	0.097	0.129	rms error	0.065	0.072
k	59–82	66–79	k	65–75	64–83

*No observed complications, hence n could not be estimated.

FSU distribution

In Figure 3, the number of FSUs (n) is plotted as a function of volume measured from the lung base, indicating a larger density of FSUs near the upper and lower ends of the lung. For the basal subvolumes the number of FSUs is displayed as a function of the respective subvolumes (v_base), while for the apical subvolumes the plotted values are N−n_apex as a function of v=100%−v_apex, where N=100. The results of the four data sets, as described in Table I, are shown together with the target-cell distribution obtained by Tucker et al. [13] and a uniform (linear) distribution for comparison. Tucker's distribution seemed to agree better with our obtained distributions for the elevated breathing rate data than with the lethality distributions (Figure 3), although Tucker's distribution was derived from the lethality data.

Figure 3.  Cumulative number of target cells or FSUs as a function of v% subvolume measured from the lung base, FSU inactivation probability assumed independent of localization. Data (elBR=elevated breathing rate data, dead=lethality data) are derived from Tucker's estimates [13] and from Table I (our optimizations assuming N=100), with basal data plotted as n_base(v_base) and apical data plotted as 100-n_apex as a function of v=100%-v_apex. Subvolumes with no observed complications are excluded from this figure.

Dose-response

Dose-response curves were generated using Equation 2 with the obtained K and D₀ for FSU inactivation probability, and Equation 1 for NTCP calculations, with k=70 and N=100 and the obtained distributions of n as input. The elevated breathing rate data are presented in Figure 4, and the lethality data in Figure 5. For the apical lethality data there were overlapping complication curves as n=36 for both subvolumes 30% and 50% and n=38 for both 70% and 75%. For some subvolumes, both for basal and apical data on elevated breathing rate, the value of n was decreasing as the volume increased, as seen in Table I. For some of the smaller subvolumes there were no observed complications, and the value of n could not be estimated. Therefore n=30 (i.e. N−k) was used for these subvolumes.

Figure 4.  Calculated NTCP (solid curves) using elevated breathing rate data (symbols) from Travis et al. [11] and Equation 1 with N=100, k/N=0.7, K=1.47 and D₀=27.5 Gy. The NTCP for the apical subvolumes 19, 30, 50, 70, 75, 84, 94, and 100% were calculated using n=30, 37, 42, 48, 49, 47, 81, and 100, respectively, with a total rms error of 0.072. The calculations of NTCP for the basal subvolumes 18, 32, 40, 50, 70, 84, 90, and 100% were performed using n=35, 39, 47, 57, 62, 61, 79, and 100, respectively, with a total rms error of 0.129.

Figure 5.  Calculated NTCP (solid curves) using lethality data (symbols) from Travis et al. [11] and Equation 1 with N=100, k/N=0.7, K=1.55 and D₀=24.9 Gy. The NTCP for the apical subvolumes 19, 30, 50, 70, 75, 84, 94, and 100% were calculated using n=30, 36, 36, 38, 38, 42, 68, and 100, respectively, with a total rms error of 0.065. The calculations of NTCP for the basal subvolumes 18, 32, 40, 50, 70, 84, 90, and 100% were performed using n=30, 30, 30, 42, 52, 53, 61, and 100, respectively, with a total rms error of 0.097.

Spatial distribution of p

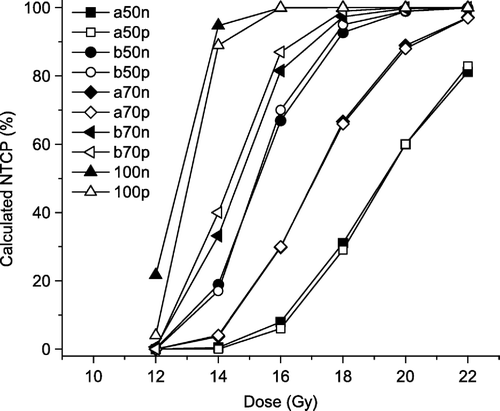
By assuming a homogeneous distribution of the FSUs, and dividing the FSUs into four compartments, it was possible to obtain a spatial distribution of the inactivation probability. The estimates clearly indicated an increased sensitivity towards the base and apex of the lung. This is demonstrated in Figure 6 (left axis), where also the FSU density is shown (right axis), with increased density towards the base and the apex of the lung. For the upper, central part of the lung (FSUs 51–70, as seen in Figure 1), only doses of at least 20 Gy resulted in a non-zero inactivation probability. In Figure 7, NTCP values are calculated for five subvolumes, using the heterogeneous inactivation probability distribution (open symbols) and the heterogeneous FSU distribution (filled symbols). Both approaches are able to illustrate the volume effect and predict the complication levels (NTCP_100%>NTCP_70%,base>NTCP_50%,base>NTCP_70%,apex>NTCP_50%,_apex).

Figure 6.  Inactivation probability (p) for FSUs at different doses for different regions of the lung assuming homogeneous FSU density distribution (left axis), compared to the FSU density distribution assuming uniform FSU radiosensitivity (right axis), both based on elevated breathing rate data.

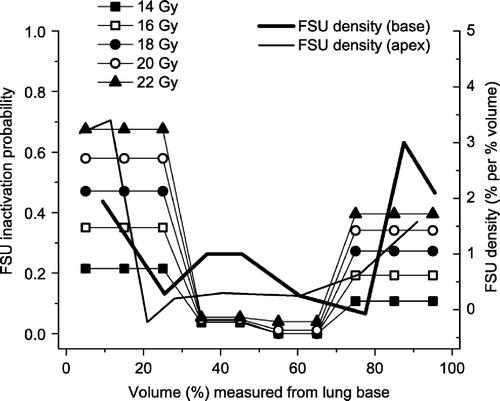
Figure 7.  Calculated NTCP values (elevated breathing rate) for 12, 14, 16, 18, 20, and 22 Gy for five subvolumes (50% apex, 50% base, 70% apex, 70% base, and 100%), based on a heterogeneous distribution of FSUs (filled symbols), and based on heterogeneous distribution of FSU inactivation probability (open symbols).

Discussion

For optimization of the therapeutic ratio and dose escalation studies, it is necessary to be able to assess the predicted risk for radiation-induced lung fibrosis, chronic pneumonitis, and other late endpoints following irradiation of tumours in the thorax. Robust and valid models as well as reliable parameters are thus required. The FSU concept on which the biological models are based, assume that all FSUs are equally important and homogeneously distributed throughout the entire organ [16]. The data from Travis et al. [11] indicate however, different radiosensitivity for the lung apex and the lung base. Such spatial difference may be caused by: 1) spatial heterogeneous distribution of FSUs, 2) heterogeneous FSU radiation sensitivity, 3) spatial differences in physiological functionality [16], or a combination of the three above-mentioned phenomena.

The present calculations, assuming all FSUs have the same inactivation probability, show a heterogeneous FSU density distribution for all four data sets. Figure 3 indicates that the FSU density in the middle of the lung is quite low. Most of the FSUs seem to be located in the 20% upper and the 20% lower parts of the lung. These observations are in general agreement with the conclusions of Tucker et al. [13]. However, this distribution does not show a pronounced increase in the number of FSUs in the lung base compared to the lung apex, and cannot explain the larger amount of damage caused by base irradiation compared to apex irradiation. If the obtained distribution of FSUs was correct, the corresponding basal and apical values of n for a given volume, n_base(v_base)+n_apex(100%-v_base), would sum up to N, and corresponding curves (with the same endpoint) would overlap. Our results indicate that the sum is less than N. The estimated values of n for the different basal subvolumes and/or the estimated values of n for the different apical subvolumes, as given in Table I, are thus too low.

An alternative explanation to the heterogeneous sensitivity is difference in FSU inactivation probability, p, in the different parts of the lung. Tucker et al. [13] have argued that target cells located in certain anatomical regions of the lung may possess different radiation sensitivity, and spatial variation in FSU radiation sensitivity can thus not be ruled out as a contributing factor to our observations. In our first calculations, the parameters K and D₀ were fitted to the 100% subvolume data, which include both apical and basal cells/FSUs, and p(K,D₀) then represents an effective value of the FSU inactivation probability. These estimated values of K and D₀ may not necessarily be representative for the smaller subvolumes. In Figure 6 the spatial distribution of inactivation probabilities, assuming homogeneous FSU density, is illustrated (left axis) together with the spatial density distribution of FSUs, assuming homogeneous radiosensitivity (right axis). The two distributions generally follow the same heterogeneous pattern. Both distributions may, alone or in combination, contribute to the difference in radiation sensitivity for the lung apex and the lung base.

Differences in physiological functionality may also explain the spatial variation in the effect of partial lung irradiation. Different part of the lung may play different roles in overall lung function. This may be described by different critical fractions for different parts of the organ. Our analysis assuming all FSUs having the same radiosensitivity revealed, however, that the values of k (and hence the critical fraction) that resulted in the best fit to the experimental data, covered the same interval for both apical and basal regions of the lung, as seen in Figure 2. Repeated calculations of the distribution of n and rms error, as a function of k, using groups of smaller or larger subvolumes showed only minor deviations from the values obtained using all subvolumes, providing no indication of any difference in critical fraction for the basal and apical part of the lung. Consequently, we have no indication for attributing the observed differences in partial volume effect to spatial variations in tissue architecture and thus distribution of critical fraction in the lung.

Clearly, the aim of non-empirical models is to establish a link between the parameters and the underlying biological and physiological characteristics, i.e. the value of the parameters are inherently of importance. Thus, normalizing the total number of FSUs to a fixed value in order to reduce the number of parameters is inconsistent with the concept of non-empirical models. However, when data is scarce this may still become a necessity. It is evident from Equation 1 that the NTCP is not only dependent on the critical fraction of FSUs, but also the absolute number of critical FSUs as well as the total number of FSUs. Normalizing the total number of FSUs to 100 and thereby introducing the critical fraction of FSUs may thus have an impact on the simulations. Clearly, a low number of FSUs is inconsistent with the number of alveoli of the mouse lung; however, Stavrev et al. [15] have estimated that the number of FSUs of the mouse lung is between 70 and 550. They argue that the actual number of terminal bronchioles may be as small as 550 and that the low value of FSUs in fact may reflect an anatomical structure of the mouse lung. Although the aim of non-empirical models is to link parameters and underlying biological and physiological characteristics, one must bear in mind the FSU concept is strictly a mathematical construct. The appropriate parameters are thus those that predict response most accurately, even though the parameter values themselves do not correspond to the number of any known anatomical structure.

Alternatively, the spatial variation in the effect of partial lung irradiation may be attributed to inactivation of non-irradiated FSUs. Khan et al. [17] reported some effects after partial irradiation of rat lung: out-of-field effects were observed as DNA damage in the lung apex following base irradiation, and cells in the lung base sustained more DNA damage than cells in the lung apex when either region was irradiated (in-field effect). Moiseenko et al. [18] analysed data from Liao et al. [12] and found that the elevated sensitivity to base irradiation can be interpreted with a hypothesis of in-field and out-of-field effects for cellular response. Their conclusion is thus in accordance with the suggested extension of the reliability model [4] assuming also a non-zero probability of FSU inactivation of non-irradiated units. According to Wiegman et al. [19], the increased responses for basal relative to apical irradiation may be caused by radiation damage to the liver or to the heart after basal irradiation. However, Khan et al. [20] ruled out the possibility that irradiation of parts of the abdomen (inferior to the lung) might be responsible for the out-of-field damage in rat lung. Novakova-Jiresova et al. [14] observed higher frequency of lung complications in the apex of rat lung as compared to the lung base using a functional endpoint. However, they failed to identify corresponding variations in histo-pathological damage. They conclude that regional variations in response to radiation, using a functional endpoint, is not due to hyperradiosensitivity of the cells or tissue in these regions, rather anatomic or physiologic reasons may underlay the regional differences. These data contradict those of Travis et al. on mouse lung [11–13]. However, both studies indicate that regions containing the largest proportion of parenchymal tissue are the most sensitive regions. These findings may indicate that the distribution of FSUs, rather than the distribution of FSU inactivation probability, may be the primary cause of varying response to partial lung irradiation.

This work was supported financially mainly by the Centre for Research and Training in Radiotherapy at The Norwegian Radium Hospital and partly by The Research Council of Norway.