Three-dimensional spatial modelling of the correlation between abdominal motion and lung tumour motion with breathing

Abstract

The aim of this research was to investigate whether a spatial correlation could be found between an external 3-D respiratory signal and the tumour trajectory. The respiratory signal was obtained by tracking the abdominal movement and the tumour trajectory was obtained by automatically determining the tumour position in a series of portal images. Three different models, based on Systems Identification, are presented to model the correlation using a 1-D respiratory signal, a 3-D respiratory signal and a 3-D respiratory signal together with previously determined tumour positions. Adequate correlation was found for all models in the direction of the tumour movement with standard deviations of 0.89 mm, 0.72 mm and 0.75 mm, respectively, and model fit of R_t²=0.19, 0.63 and 0.82, respectively. Increasing the frame rate for the acquisition of portal images from 3 to 15 frames per second improved the standard deviation and model fit. In summary, it is possible to spatially correlate a 3-D respiratory signal with the tumour trajectory using this approach. The models presented provide a framework that can be extended to include more information if required. A 3-D respiratory signal is preferable to a 1-D signal in modelling the tumour motion that is not along the main axis of tumour movement.

Intra-fractional tumour motion in the lung introduces uncertainties in treatment planning and delivery [1], [2]. Tumour movement can be considerable and peak-to-peak distances of up to 3 cm have been reported in the literature [3], [4]. The mobility of the tumour may be reduced by, for example, abdominal compression; however, some residual motion always remains. The standard method to deal with tumour motion is to add sufficiently large safety margins around the clinical target volume (CTV) on the planning CT. This has the disadvantage of delivering a high dose to a large volume of surrounding healthy tissue. The dose prescribed to the tumour is limited by the tolerance dose of the healthy tissue. There is clear evidence from clinical data that higher radiation doses lead to a survival benefit [5], [6] and also that the complications increase with the mean lung dose [7], [8]. To minimize toxicity the margins around the CTV should be as small as possible without compromising tumour control. Patients with poor lung function and patients with large tumours are most likely to benefit from reduced margins.

A number of approaches have been described in literature to deal with tumour movement, namely breathing control [9], respiratory gating [10] and tumour tracking [11]. For all of these techniques it is desirable to have some real-time feedback on the actual tumour position to verify that the beam and the tumour are aligned during irradiation [12]. According to Murphy [11] this information may be acquired by imaging the tumour itself, imaging anatomical structures rigidly connected with the tumour, imaging passive [13] or active [14], [15] fiducials/markers implanted near or in the tumour or by tracking surrogates that move in synchrony with the tumour.

An alternative method currently under scrutiny by the authors [16], [17] attempts to image the tumour directly by continuously acquiring megavoltage (MV) portal images at a high acquisition rate during irradiation. Note that this method neither requires implanted markers, an approach also considered by other researchers [18], nor does it expose the patient to additional radiation for imaging purposes. Each frame of the portal image sequence, with the tumour embedded in the image, is automatically compared to a reference image using an appropriate algorithm. At the same time the respiratory signal of the patient is acquired by placing a tool on the abdomen of the patient and tracking it by means of an infrared (IR) tracking camera resulting in a three-dimensional (3-D) respiratory signal. The intention is to have two independent and redundant data sets available regarding the position of the tumour, i.e. the tumour trajectory obtained from direct imaging of the tumour and the indirect respiratory signal, referred to as the primary and secondary signal, respectively. In this paper it is investigated whether a spatial correlation exists between the secondary and the primary signal and to find an appropriate model for the correlation.

Methods and materials

The approach described here to model the spatial correlation between tumour motion and the 3-D respiratory signal is based on least-squares parameter estimation and System Identification [19], [20]. System Identification is a powerful tool usually utilized in control engineering to identify the behaviour of industrial plants for which the internal behaviour is unknown or just partially known, also denoted black box or grey box approach, respectively. The methodology has also been successfully applied previously to model radiotherapy problems [21], [22]. To gather knowledge about the system characteristic sample data, consisting of both input and output data, are required from measurements. The sample data need to be rich in information and represent the complete range of possible states of the input/output dependency. Erroneous data must be eliminated or truncated in advance since they can affect the quality of the outcome. To relate the input/output data a system model has to be determined which consists of a number of mathematical equations with parameters that are to be estimated. While the system model is generally applicable for a particular problem the estimated parameters are characteristic for a particular set-up. With regards to the current work the general “problem formulation” relates to the spatial correlation between abdominal motion and tumour motion with breathing. The set-up relates to a particular patient and radiation beam from a certain gantry angle. The input to the model is the respiratory signal of the patient and the output is the tumour movement. Due to measurement inaccuracies in the sample data and inaccuracies in the mathematical description of the system model the parameter estimation problem becomes one of statistical estimation [20].

System description

The system is illustrated in Figure 1. The respiratory (secondary) signal is obtained by placing a base plate with three infra-red (IR) reflectors, henceforth referred to as the tracking tool, on the abdomen of the patient. The exact position of the tool is detected at f_r=25 Hz by means of an IR stereo camera (Polaris®, NDI, Waterloo, Ontario, Canada) mounted on the ceiling of the treatment room. Based on the exact dimensions of the tool and the location of the camera the relative displacements of the tracking tool are calculated. The resulting respiratory signal, representing the input data for the model, is then transformed into Cartesian room co-ordinates. The orientation of the right-handed co-ordinate system used throughout this work is as follows: x, y, and z refer to the lateral, superior-inferior and the anterior-posterior direction, respectively.

Figure 1.  System diagram illustrating the acquisition of both the data for the 3-D abdominal movement and the tumour trajectory as well as the time synchronisation.

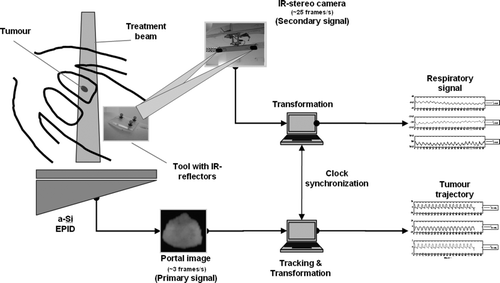
The tumour trajectory, representing the output data (primary signal), is extracted from portal images (Figure 2). The electronic portal imaging device (EPID) consists of an amorphous silicon (a-Si) flat panel attached to an Elekta Synergy S linear accelerator. The acquisition is carried out at an acquisition rate of f_t=∼3 Hz. The actual detection and tracking of the tumour trajectory from portal images without markers has been described elsewhere [16], [17]. In summary, a mask is placed over a representative portal image in which the tumour has been identified. This mask serves as reference window. In each of the series of portal images the reference window is compared with the portal image and the position in the portal image that best resembles the reference window is recorded as the current tumour position. The resulting curve is a 2-D trajectory in the plane of the electronic portal imaging device (EPID) perpendicular to the treatment beam. For the modelling the 2-D data are converted into the same Cartesian room co-ordinate system as mentioned above, taking into account the beam angle at which the data were acquired.

Figure 2.  Comparison of the digitally reconstructed radiograph (DRR) and portal image. Left: DRR generated in planning system to simulate a 6 MV beam (showing the position of the multileafs and the gross target volume); right: inverted portal image frame with window and levelling adjusted to make the tumour visible.

In order to correlate the two data sets accurately in time the internal clock of the two PCs was synchronized using in-house software (see also Figure 1). The synchronization is based on the internal high performance timer of the PCs, with a clock rate of approximately 260 ns, and the elapsed time for sending a certain number of packets between the PCs over the network using the User Datagram Protocol (UDP). Also considered was the drift between the two high performance timers. The achieved synchronization between the two PCs was ≤ 1 ms per hour.

General System Model

The principle of the System Identification approach is illustrated by means of an example. A simple linear model relates the output, v, at time t  =  i … m linearly to a set of n variables u  =  (u₁, u₂, … , u_n), e.g. the input to the model, with the equation1 where the parameter theta is θ  =  θ₁, θ₂, …, θ_n. Equation (1) is also referred to as the regression function and the elements in θ are called the regression coefficients. A more general description of the model including all observations is the matrix form2 whereIn order to solve Equation 2 it is necessary to involve at least n observations. However, due to random errors and inaccuracies in the sample data it is necessary to arrange that the number of observations is much larger than the number of unknowns, i.e. m≫n. This leads to a non-unique set of characteristic parameters θ and hence the need for a least-squares approach to find the best estimate for θ to fit the data sets. Solving Equation 2 for θ results in the expression3 where the expression [U^TU]⁻¹U^T is referred to as the “pseudo-inverse” and the expression [U^TU]⁻¹ is known as the covariance matrix. The pseudo-inverse is a generalization for any (m,n) matrix with m>n. The inverse U⁻¹ of the matrix U exists only if U is square (m  =  n) and has full rank. Then the solution to Equation 2 is. Inserting the estimated parameters in Equation 2 results in the estimated output4

The entire system identification approach can be summarized in three steps:

1. Establishing a system model that describes the physics of the system as well as possible (Equation 1).

2. Estimating the characteristic parameter vector based on a set of representative training data (Equation 3).

3. Applying the model to a set of input/output data not used in step 2 to see how well the model performs (Equation 4).

Sample data

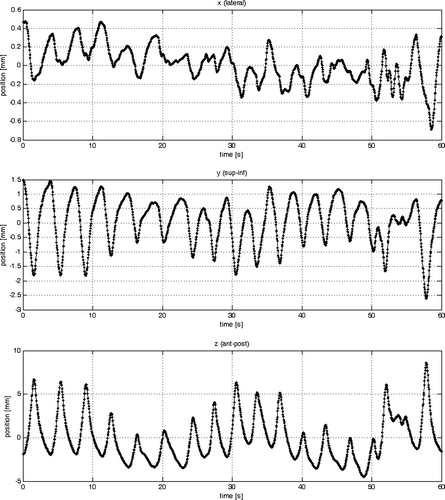
Characteristic sample data where obtained with the method illustrated in Figure 1. To demonstrate the approach a conformal coplanar beam at gantry angle 35° for an extra cranial stereotactic lung treatment was selected. The patient was a 65 year old male patient with a large peripheral pulmonary metastasis (CTV: 92 cm³ and PTV: 176 cm³) located near the hilum. The respiratory signal for this data set is shown in Figure 3. This data set was selected because the patient showed an irregular breathing pattern which is more challenging for the model. For the modelling both data sets needed to be available in the same resolution. This was accomplished by linearly interpolating the tumour trajectory with a frame rate of f_t=∼3 Hz to the resolution of the respiratory signal with f_r=25 Hz.

Figure 3.  Input data (respiratory signal) used for estimating the theta parameters.

System Equations

The example in Equation 1 used for illustration was a straightforward one dimensional system model. In the case of correlating the three dimensional respiratory signal with the tumour trajectory each data point for both the input and output data consists of three Cartesian co-ordinates each, i.e. each output v(i) in Equation 2 becomes v(i)=[v_xv_yv_z]^T. Therefore the model parameters were split into , and and were estimated independently for x, y and z, respectively, using the same system model equations. Note that all input data points, i.e. the respiratory signal, but also previously predicted output data points, i.e. the tumour trajectory, are possible candidates for use in the model. Different system models were investigated and the quality of the models was evaluated using standard model order identification techniques [19], [20], [23] with results obtained using the coefficient of determination, R_T². This criterion, together with the standard deviation (s.d.), the Akaike Information Criterion (AIC) and the Young Information Criterion (YIC) [24] was used as an aid to determine how many data points and parameters were to be included in the model. R_T² is a statistical measure to express the fit of a particular model to a certain set of data; a value close to unity is desirable. AIC and YIC criteria are means, which help to determine the effective model order. These two methods yield relative values and consist of two terms. The first term is a measure of how well the model explains the data, i.e. the smaller the better. The second term can be considered as a form of penalty, which becomes larger as more parameters are used [24]. In this paper only three of a number of system models that were investigated were selected and analysed: Model #1 assumed a one-dimensional (1-D) breathing signal by only including the z-co-ordinate of the 3-D respiratory signal. The system equation possessed an offset term, corresponding to θ₁, and a term for the anterior-posterior motion of the tool (z-co-ordinate), corresponding to θ₂:5 The 1-D respiratory signal resembles other common methods to record breathing motion over time such as e.g. a pressure sensor in an abdominal belt, spirometer or a temperature sensor to record the change in exhale air due to breathing. For each output component two theta parameters, θ₁ and θ₂, had to be estimated. The current and five previous inputs were grouped together to achieve some smoothing and to be less susceptible to outliers and erroneous measurements. Model #2 was similar to model #1 except that all three co-ordinates of the respiratory signal were included resulting in four theta parameters (only the x-component of the output is shown):6 Model #3 is an extension to model #2. In addition to the current and previous respiratory data points previously estimated, output data points are also included in the model resulting in seven theta parameters (only the x-component of the output is shown):7 where after every time interval i = round(f_r/f_t) the previously estimated output data in the observation matrix was replaced by the actual value determined directly from the portal image directly. This was simulated two times for portal image acquisition rates of f_t=3 Hz and f_t=15 Hz, referred to as model #3a and b, respectively.

Results

The results of the parameter estimation are summarised in Table I. The standard deviation was calculated from the 3-D error vector resulting from the difference between the sample data and the estimated output of the model as shown in Figures 4–6 for Model #1, #2 and #3, respectively.

Figure 4.  Comparison of the sample data with the estimated output from model #1 in each cardinal direction (x, y, z) individually (from top to bottom). At the very bottom the absolute of the 3-D error vector is plotted.

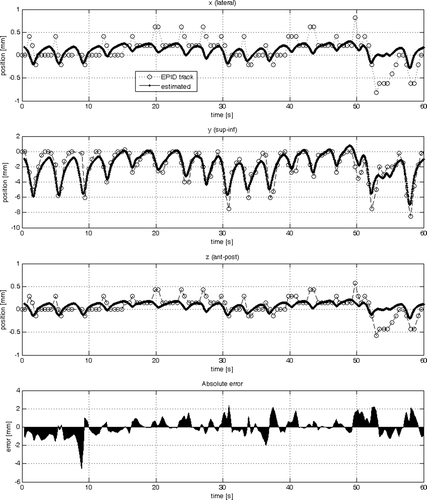
Figure 5.  Comparison of the sample data with the estimated output from model #2 in each cardinal direction (x, y, z) individually (from top to bottom). At the very bottom the absolute of the 3-D error vector is plotted.

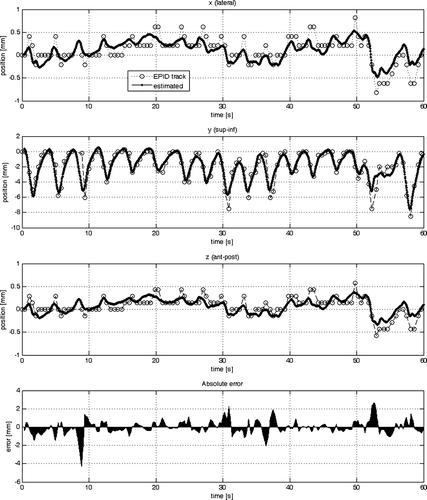
Figure 6.  Comparison of the sample data with the estimated output from model #3 in each cardinal direction (x, y, z) individually (from top to bottom). At the very bottom the absolute of the 3-D error vector is plotted.

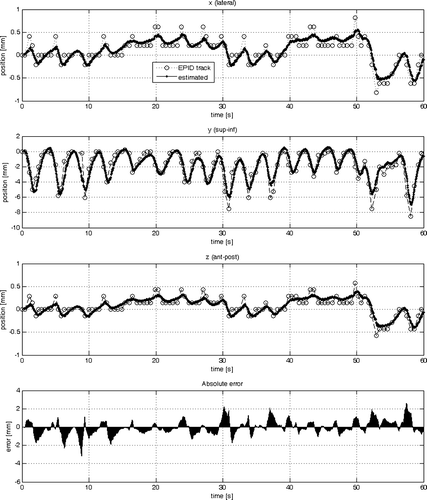
Table I.  The results of the least-squares estimation summarized for the three different models.

		RT^2			AIC			YIC
model #	STD in [mm]	x	y	z	x	y	z	x	y	z
1	0.89	0.19	0.75	0.19	−4162	−332	−5221	−5.8	−10.0	−5.8
2	0.72	0.63	0.84	0.63	−5327	−922	−6386	−7.6	−7.7	−7.6
3a (3 images/s)	0.75	0.82	0.82	0.82	−6425	−797	−7489	0.0	−3.4	0.0
3b (15 images/s)	0.44	0.95	0.94	0.95	−8283	−2370	−9342	−2.8	−5.5	−2.8

Firstly model #1 was compared with model #2. The R_T² value of 0.19 mm in x and z for model #1 indicates that the model finds a poor correlation between the sample data and the estimated tumour trajectory in those two dimensions. Extending the 1-D respiratory input to a 3-D respiratory signal (model #2) increases the fit to 0.63 in x- and z-direction and from 0.75 to 0.84 in y-direction. The overall standard deviation decreased from 0.9 mm to 0.7 mm. The AIC and YIC values also indicate that the increase in the number of theta parameters from two to four was justified since the tendency was that the values become more negative. This is true except for the YIC value in y-direction. The YIC criterion penalizes an increase in complexity in the model more than the AIC criteria. The interpretation for the increase from − 9.8 to − 7.7 is that only a slight increase in the model fit in the y-direction was achieved by a considerable increase in complexity of the model, i.e. doubling of the theta parameters.

The theta parameters in Table II reflect that the values corresponding to the y- contributed most to the output. This makes sense considering that the 1-D respiratory signal corresponded to the z-direction which is the anterior-posterior movement of the tool on the abdomen of the patient. The main direction of the tumour movement, however, is in the y-direction (superior-inferior) along the patient axis. A similar observation can be made for model #2 (see Table III). The fact that all parameters are within the same order of magnitude indicates that the model describes the data well and that no input to the model dominates.

Table II.  Estimated theta parameters for model #1.

	θx	θy	θz
θ1	0.099	−1.946	0.069
θ2	0.045	−0.602	−0.032

Table III.  Estimated theta parameters for model #2.

	θx	θy	θz
θ1	0.101	−1.950	0.070
θ2	0.528	1.904	0.370
θ3	−0.449	0.633	−0.314
θ4	−0.150	−0.383	−0.105

With respect to model #3 two different acquisition rates for portal images were considered. Comparing model #2 with model #3a shows that there is a considerable improvement in the R_T² value in the x- and z-direction from 0.63 to 0.82 (see also Figure 6), whereas in the y-direction the R_T² value is slightly lower. This is expressed in the slight deterioration from 0.75 to 0.72 in the standard deviation. The same trend is expressed by the AIC values. The YIC values penalise the overall increase in complexity from four to seven theta parameters. It is interesting to note that the theta parameters in Table IV indicate that for all three co-ordinates (x, y, z) θ₅ and θ₇ dominate with the highest contribution from the y co-ordinate. Increasing the sample rate for the acquisition of portal images from 3 to 15 Hz reduces the overall error which is expressed in the lowest standard deviation of 0.44 mm, high R_T² values of 0.94–0.95 and lower AIC and YIC values.

Table IV.  Estimated theta parameters for model #3a (3 frames/s).

	θx	θy	θz
θ1	0.023	−0.322	0.016
θ2	−0.005	−0.441	−0.003
θ3	−0.012	0.397	−0.009
θ4	−0.008	−0.045	−0.006
θ5	379.650	10482.000	265.160
θ6	0.009	0.819	0.006
θ7	−540.850	−14970.000	−377.750

Discussion

The modelling described here is part of a project that aims to correct intra-fractional tumour movement in real time [17], [25], [26] with a robotic treatment couch [27], [28] (HexaPOD, Medical Intelligence, Schwabmünchen, Germany). Determining the tumour position by means of two independent methods, namely MV imaging and modelling the 3-D abdominal breathing motion, provides redundant information that can be used to safely adjust the couch position. Two different strategies for the adaptation of the couch are envisaged to be considered. The first is to continuously correct for tumour movement above a certain threshold, e.g. 1 – 2 mm. However, it is to be investigated how the permanent rhythmical movement of the table will be tolerated by the patients. The second strategy is to monitor the mean tumour position and only correct for baseline shifts, which is a more tolerable option for the patient and less demanding for the control system. In addition, the approach can also be applied to gate the treatment.

In general when dealing with moving tumours it is essential to have a reliable model that can estimate the tumour position. For the specific case of tracking tumours in portal images without markers [17] it is crucial to have a model to be able to verify that the tumour trajectory determined is within a certain tolerance of the model predictions. This is necessary to verify the trajectory with an independent method. Analysis of the first few patients has indicated that, for instance for lateral beams, the diaphragms can mislead the algorithm if the tumour is in a disadvantageous position near the diaphragm, whereas solid lesions in the centre of the lung surrounded by lung tissue can be detected with a high degree of probability. In case of discrepancies between imaging and the model certain action, such as switching off the radiation beam, has to be taken. As a further option, different weightings could be assigned to the trajectory determined directly from the portal image and the estimated tumour position from a model. If, for instance, the quality of the position determined in the portal image can be quantified, e.g. with a parameter between zero and unity, this can be incorporated into balancing the weight between the two signals. As an example, if the tumour is clearly detectable on the portal images, perhaps 80% percent of the weight could be given to the position determined in the portal image and 20% to the estimation from the model. On the other hand, if the tumour reaches a position where it is hidden by another structure the tracking algorithm might fail to detect the exact position. In such a case the model is still able to estimate the tumour position since the external signal is independent of internal organ structures.

In the current work different system models have been presented and analysed. Only linear terms were discussed since no significant improvement was seen by using higher model order with quadratic terms (data not shown) but the model complexity increased considerably. There is also potential to include more information such as the normal vector perpendicular to the area between the three reflectors of the tool or to consider mathematical equations describing the tumour movement as a damped oscillation to improve the correlation even more.

The results from model #1 (see Figure 4 and Table I) have shown that tumour motion in one direction (e.g. superior-inferior) correlates well to a 1-D respiratory signal. However, the model resulted in a poor correlation in lateral (x) direction and anterior-posterior (z) direction of the respiratory signal with the tumour. Utilizing all dimensions of the respiratory signal improved the model fit and demonstrated the advantages of a 3-D respiratory signal over a 1-D one. The main direction of lung tumour movement is in superior-inferior but the anterior-posterior direction should not be neglected. From the beams-eye-view of a posterior beam from 0° only superior-inferior movement is seen. The same applies to the 35° beam selected for the training data. In a lateral beam from gantry angle 90° or 270° the amplitude of the anterior-posterior movement is at a maximum. Previously tracked lung tumours in our institution have shown up to 5 mm peak-to-peak movement in anterior-posterior direction despite using an abdominal compression device. In such cases model #2 would be preferable to model #1. Model #3 provides a framework to include previously determined estimates from the primary signal (portal image). This makes the modelling less dependent on the respiratory signal alone. The model has the potential for better fits of the data, especially when considering a high frame rate.

The training data utilised were based on a respiratory signal acquired with the Polaris camera, which is clinically used for accurate positioning [27], and on tracking data automatically generated from portal images [16], [17]. As was mentioned at the beginning of the methods and material section, it is important to have training data that are accurate. More accurate training data could have been obtained from tracking implanted markers with kV imaging [13], [29] but also, with respect to the current approach, by having an experienced radiation oncologist contour the tumour on each portal image manually [25], track on kV images [30] and/or by smoothing the data before they were used as training data to filter the noise in the signal. However, the overall aim of this paper was to examine whether it is principally possible to spatially correlate the 3-D respiratory signal with the tumour trajectory by means of System Identification and to investigate and compare different models. Although the data is not shown the system parameters for model #2 and #3 were also estimated for some of the other beams for the same patient and also to data from other patients and adequate model fits were obtained. This indicates that the system models are robust and generally applicable.

With regards to implementing this model for tumour tracking it would be necessary to estimate the characteristic system parameters for each beam direction prior to treatment and real-time tracking of the tumour. This means that a certain number of monitor units would need to be given to the patient prior to starting the actual treatment, which is not desirable. One alternative, which would expose the patient to less radiation, would be to obtain sample data from kV images from each beam direction prior to treatment on a linac with cone-beam CT [27]. The most desirable approach would be to determine one model for the entire 3-D tumour trajectory independent of the beam direction and to project the estimated trajectory onto the respective plane perpendicular to the beam corresponding to the EPID. This could be accomplished by installing the same stereo tracking camera in the CT room or using 4D cone-beam CT [31] and recording the respiratory signal during acquisition of 4D CTs. The acquired projections would then have to be reconstructed based on the spatial position of the tracking tool corresponding to the respiratory signal. Note that it would be essential, in this approach, that the tracking tool is placed in exactly the same position as during treatment. Having obtained such a CT data set the tumour trajectory could be determined automatically as demonstrated by Vences et al. [32] and then correlated with the respiratory signal. This remains an area of further work as well as extensive testing of the approach. Currently, efforts are underway to verify the approach with a phantom designed in-house with which realistic non-symmetrical tumour motion can be simulated by means of an industrial robot capable of movements in six degrees of freedom.

Last but not least, for adaptation of the treatment couch or the radiation beam to the actual position of the tumour it would be desirable not just to estimate the current position of the tumour but also to predict the tumour position a number of instances ahead of time to account for delays in the control system. This requires predictive control [33–36] and is currently an area of investigation.

Conclusion

A model approach has been presented that provides a framework to correlate a respiratory signal with the tumour trajectory. It has been shown that a 3-D respiratory signal has advantages over a 1-D respiratory signal in terms of modelling tumour movement that is not along the main axis of movement. By updating the observation matrix with previously estimated tumour positions as well as tumour positions obtained from the primary data set the model fit can be improved and makes the approach less dependent on the respiratory signal alone. Further work includes the verification of this approach by applying this methodology to patient data acquired over several fractions as well as obtaining a general 4D-CT model with the reconstructions sorted according to the spatial position of the tool to make the approach independent of the beam direction.

This work was partially supported by a grant from the ‘Bayerische Forschungsstiftung’, Germany and Elekta Oncology Systems, Crawley, UK. Presented in part at the 3rd Acta Oncologica Symposium on Stereotactic Body Radiotherapy (SBRT2006) in Copenhagen, Denmark in 2006.