Treatment planning optimisation based on imaging tumour proliferation and cell density

Abstract

Functional imaging could provide valuable information on the distribution of biological factors that influence the outcome of radiation therapy. Tumour proliferation and cell density in particular could be imaged with dedicated metabolic tracers and could thus be used for the biological optimisation of the treatment plans. The feasibility of individualising treatment planning using proliferation and density information has been investigated through simulations of heterogeneous tumours taking into account the cell density and proliferation rates. The predicted outcome was used to estimate the success of the individualisation of dose distributions. The results have shown that tumour control could be increased through the escalation of doses to proliferating foci with a relative reduction of doses to slowly proliferating regions of the tumour. This suggests that individualisation of treatment planning taking into account proliferation information creates the premises for further reduction of the doses to the surrounding regions which would consequently lead to an increased sparing of the normal tissues. Cell density has been shown to be another important factor that could be used for optimisation, albeit of a lower weight than proliferation. However, associated with proliferation it could lead to treatment failure if the trouble foci are underdosed. In conclusion, treatment optimisation based on imaged proliferation could improve both tumour control and normal tissue sparing.

Cancer diagnosis and treatment have been significantly improved with the appearance of advanced imaging methods that increased the accuracy of visualisation and delineation of tumours. Morphological imaging with computed tomography (CT), magnetic resonance imaging (MRI) and ultrasounds is routinely used in clinical practice to localise the tumour in relation to the surrounding normal structures. More recent advances in imaging techniques have led to the appearance of a broad array of methods that could provide information on metabolic, biochemical or other physiological aspects of the normal and tumour tissues in individual patients. This information could be used to define biological targets [1] that may lead to an individualisation of the treatment by targeting the regions with a high concentration of adverse factors known to contribute to the failure of the treatment. This individualisation could be achieved with advanced radiation delivery techniques, such as intensity modulated radiotherapy with photons, electrons, protons or heavier ions, some of which are entering routine clinical practice. Furthermore, functional imaging methods can also be used as tools to monitor the tumour response to the delivered treatment [2].

Among the physiological factors that influence the response to treatment, tumour cell proliferation has been identified rather early as a factor that reduces treatment effectiveness. Indeed, in the early days of radiotherapy it has been suggested that rapidly growing tumours may compensate the radiation damage faster than slowly proliferating normal tissues [3] and this argument was used by the proponents of the treatment delivery schemes with short duration [4]. A more systematic analysis came with the correlations between the duration of treatment and cure rates [5] when it was recognised that cell proliferation and especially accelerated repopulation could lead to a loss of treatment efficiency as they increase the population of tumour cells that need to be sterilised thus also increasing the probable number of survivor cells that could regrow the tumour after the end of the treatment. Consequently, the kinetic parameters of tumours were investigated through techniques such as flow cytometry [6] using biological material obtained from the patients through biopsies or following surgery. However, the invasive and laborious procedures required made these techniques rather cumbersome to use on individual patients. Furthermore, the values provided characterised the average behaviour of the tumour, while the spatial distribution of the measured parameters was generally lost. This is a rather serious limitation for the individualisation of treatment.

Technological advances in imaging methods like positron emission tomography (PET) or magnetic resonance imaging (MRI) have made possible the investigation of the magnitude and the spatial distribution of the physiological factors with adverse effects on treatment effectiveness in general and proliferation in particular. These methods are less invasive as they use dedicated tracers that follow the usual metabolic pathways of the organism. The versatility of the methods is enhanced by the availability of several tracers with different sensitivities and metabolic pathways to image the same physiological aspect. This opens up the prospect of using physiological information from functional imaging together with morphological information from traditional techniques to customise treatment plans to address the adverse effects identified in individual patients. However, the value of incorporating physiological information into treatment planning has to be investigated before it is put into practice as the success of treatment planning depends on many factors that have to be taken into consideration. Proposals have been made recently with respect to the heterogeneity and dynamics of tumour hypoxia that influence the inclusion into treatment planning of information on this tumour microenvironmental aspect [7]. Comparatively little attention has been paid to the inclusion of proliferation information into treatment planning. The present study plans to address this aspect and to investigate the feasibility of individualising treatment planning using proliferation and cell density information.

Materials and methods

The study was performed on three dimensional tumour models with heterogeneous proliferation features. Thus it was assumed that clinically-sized tumours may have two foci with higher proliferation rates than the bulk of the tumour. A mathematical algorithm was used to create a gradual transition from the proliferation in the foci to the bulk proliferation, the result being a realistic appearance similar to spatial infiltrations of the two regions. Several assumptions were made about the proliferation rates and cell density throughout the tumour in order to study their influence on the optimisation process and the treatment outcome.

Treatment effectiveness was evaluated in terms of the tumour control probability (TCP) given by a Poisson function from the distribution of initial cell density n₀(r) and cell survival SF(r) (Equation 1).1

Cell survival was calculated with the linear quadratic (LQ) model [8–11] adapted for proliferation [12]. Thus, the equivalent cell survival in a point in tumour is given by Equation 2.2

where n is the number of fractions, d(r) is the dose per fraction in the point of calculation, α and β are the radiosensitivity parameters, T is the time available for repopulation after the time T_k at which compensatory repopulation is assumed to begin in a two phase repopulation model and TD(r) is the cell doubling time at the point of calculation. No variation in radiosensitivity due to microenvironmental factors was taken into consideration, as the issue has been addressed elsewhere [7]. This is a reasonable assumption as experimental studies with fluorescent markers have shown that there is no spatial correlation between proliferation and hypoxia [13], [14]. It allowed only the study of the effects of proliferation and variations in radiosensitivity could be easily included in the model in the future by the corresponding modification of Equation 2.

The model used the generic radiosensitivity parameters SF₂=0.5 and α/β = 10 Gy that are considered relevant for the irradiation of tumours with doses in the clinical range [15] and therefore suitable for the simulations of clinical radiation treatments described in this paper. It was also assumed that the total tumour cell population was 10⁸ cells which corresponds to an average cell density of approximately 10⁷ cells per cm³ for clinically sized tumours 2–4 cm in diameter.

In order to avoid confusions that might be introduced by the simultaneous analysis of multiple factors it was assumed that the treatment duration is limited to 39 days (as required to give 30 fractions with a delivery schedule of 1 fraction per day, 5 days per week). The time delay for the onset of compensatory proliferation was assumed to have a minimum value of 14 days. The influence of the treatment duration or the fractional delivery frequency could be treated separately as described by Fowler [16].

The dose distribution required to ensure a given level of local control was calculated using equations 1 and 2 for tumours with different distributions of proliferation rates TD(r) and cell densities n(r). It was thus possible to investigate separately as well as together the effects of these two aspects.

The effectiveness of planning the dose distribution according to the proliferation information was assessed through comparisons with the effectiveness of uniform doses delivered to the tumour.

Results

Heterogeneous proliferation

Figure 1 shows a section through a three-dimensional tumour relatively quiescent (TD = 75 days) with two proliferating foci, one with TD = 15 days and one with TD = 3 days. The resulting proliferation rate of the whole tumour was described by an average doubling time of 44 days. The dose response curve predicted for this tumour for uniform target irradiation and uniform cell density at the beginning of the treatment is shown in Figure 2.

Figure 1.  A section through a simulated three-dimensional tumour relatively quiescent (TD = 75 days) with two proliferating foci, one with TD = 15 days and one with TD = 3 days.

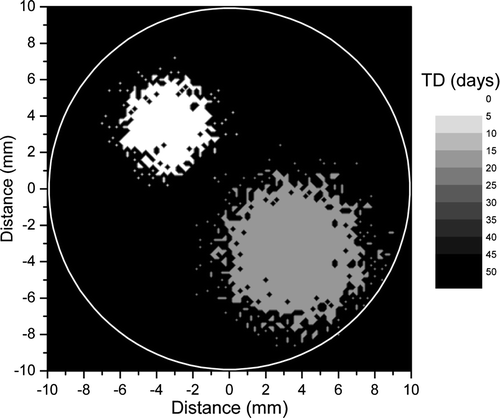
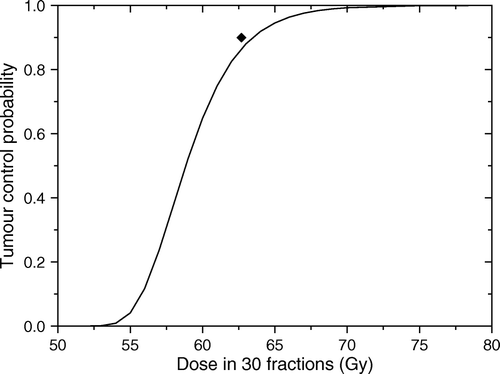
Figure 2.  Predicted response for the tumour in Figure 1. Solid line shows the predicted dose response curve for uniform target irradiation. The solid symbol shows the average dose for an optimal dose distribution required to lead to a local control of 90%.

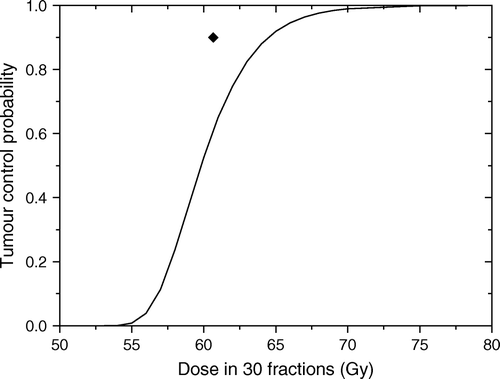
The results in Figure 2 show that even for a relatively quiescent tumour rather high doses are required in order to achieve good control rates. Thus, the uniform dose required to lead to a very high control rate of 90% for the tumour in Figure 1 would be about 65 Gy. This interesting result could be explained by the fact that high local control could be achieved only if all the tumour regions are effectively sterilised. Thus, for uniform dose delivery the total dose level has to account for the increase in cell numbers in the proliferating regions that could easily regrow the tumour if not sterilised. At the same time, the high doses delivered to the regions with low proliferation while not needed to increase the local control, do raise the collateral dose burden for the normal tissues surrounding the tumour. It thus appears that the dose required to lead to a given level of local control could be optimised to account for the regional characteristics of the target in the attempt to reduce the dose burden to the normal tissues.

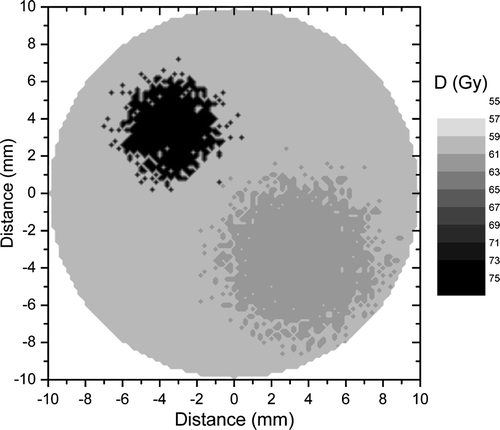
The optimal dose distribution calculated for the tumour in Figure 1 on the assumption that the cell density at the end of the treatment should be uniform [17] would have a non-uniformity given by the heterogeneity of the proliferation pattern. Indeed, as illustrated in Figure 3, a very high control rate of 90% could be achieved with a dose distribution that delivers up to 74 Gy to the highly proliferating focus, while the doses to the other regions are 63 and 60 Gy respectively. Thus, the average target dose that would lead to the given level of local control would be only 61 Gy in comparison to the 65 Gy predicted for the uniform target irradiation. The predicted reduction of the dose to the bulk tumour volume creates the premises for increased sparing of the normal structures around the target as the dose could be reduced from the proliferating foci towards the more quiescent regions of the tumour.

Figure 3.  Optimal dose distribution calculated for the tumour in Figure 1 to lead to a local control of 90%. The non-uniformity of the distribution is given by the heterogeneity of the proliferation pattern.

Figure 4 shows a tumour with a different proliferation pattern from that in Figure 1. Thus it was assumed that the bulk tumour proliferates with TD = 16 days, while the highly proliferating foci have TD = 8 days and TD = 4 days respectively. The resultant average proliferation rate of the tumour corresponded to an average doubling time of 14 days, hence a faster proliferation in comparison to the tumour in Figure 1. The corresponding dose response curve is shown in Figure 5 which predicts that a uniform dose required to lead to a very high control rate of 90% for the tumour in Figure 1 would be about 64 Gy. The reduction in total dose required for this rather rapidly proliferating tumour in comparison to the more quiescent tumour in Figure 1 might seem surprising, but it only strengthens the statement that the uniform dose required to achieve a certain control level is correlated with the highest proliferation subregion of the tumour. Indeed, the shortest doubling time in the tumour in Figure 1 was only 3 days in comparison to 4 days in the tumour in Figure 4.

Figure 4.  A section through a simulated three-dimensional tumour with moderate proliferation. The bulk of the tumour proliferates with TD = 16 days, while the proliferating foci have TD = 8 days and respectively TD = 4 days.

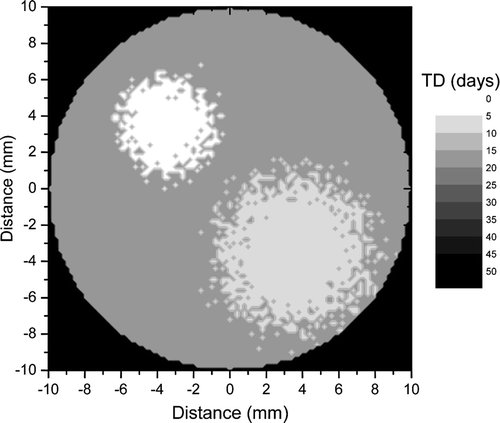
Figure 5.  Predicted response for the tumour in Figure 4. Solid line shows the predicted dose response curve for uniform target irradiation. The solid symbol shows the average dose for an optimal dose distribution required to lead to a local control of 90%.

Optimising the dose distribution according to the proliferation features of the tumour in Figure 4 for the same control rate of 90% leads to regional doses of 70 Gy, 65 Gy and 62 Gy, respectively. In comparison to the case in Figure 3, the dose levels reflect the different proliferation pattern of the two tumours. The average target dose for the tumour in Figure 4 is 63 Gy, again reflecting the increased proliferation of the tumour.

Heterogeneous cell density

For the simulations in Figures 1–5 it was assumed that the cell density at the beginning of the treatment was uniform throughout the tumour. Hence, the results in the mentioned Figures reflect only the effect of heterogeneous proliferation. Similar simulations were performed to investigate the effect of cell density throughout the tumour. More modest dose increases were required if the optimisation was done only according to the cell density indicating that initial cell density has a lower weight than proliferation (data not shown).

It appears that both factors giving the heterogeneity in tumour cell population throughout the treatment, proliferation and cell density, should be taken into consideration for optimisation of the treatment plans. Furthermore, the two factors are probably coupled in reality. It would therefore be interesting to see what would be the predictions when regions with high proliferation also have high pre-treatment cell densities. Thus, it was assumed that the proliferation follows the pattern in Figure 1 and that the pre-treatment cell density is proportional to the proliferation rate. This was considered a reasonable assumption regarding the spatial correlation between the two factors. Indeed, an exponential growth of the cells could lead to huge differences between the populations of compartments with different proliferation rates, but in reality one also has to take into account the cell loss from the proliferating compartments due for example to migration to the nearby regions or cell death through starvation. A more complex relationship could be considered when more experimental data on these aspects become available.

The predicted dose response curve of the tumour described above to uniform doses is that given in Figure 6. It should be noted the dramatic reduction in responsiveness in comparison to the case presented in Figure 2. The difference between the two curves is the effect of associating the cell density with proliferation and indicates strongly that this association could rapidly lead to treatment failure if the trouble foci are underdosed.

Figure 6.  Predicted response for the tumour in Figure 1 assuming that cell density is related to the proliferation rate. Solid line shows the predicted dose response curve for uniform target irradiation. The solid symbol shows the average dose for an optimal dose distribution required to lead to a local control of 90%.

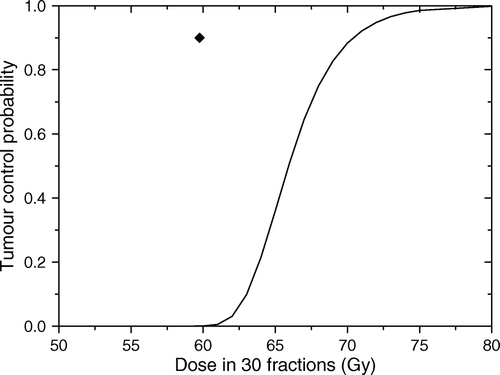
The combined effect of associating the two factors can also be seen from the heterogeneous distribution of doses that results from the optimisation process that targets proliferation. Thus, the doses required to the three regions of the tumour are 59, 65 and 80 Gy respectively. As expected, the combination of the two factors leads to an increase of the doses required to counteract their adverse effects. The differences in the dose levels required in the proliferating regions compared to the quiescent region are considerable and indicate that significant therapeutic gains could be achieved from targeting proliferation in the optimisation process.

Discussion

In curative radiotherapy the aim is to deliver the highest possible dose to the tumour that leads only to a small fraction of complications in the surrounding normal tissues. The consequence is that the tolerance of the normal tissues around the tumour dictates the dose that could be delivered to the target. For uniform irradiation of the target, this limitation could lead to cases when the tumour does not receive enough dose to ensure the effective sterilisation of the cells and therefore to a failure to achieve high control rates. One possible solution to avoid this situation and to increase the cure rates is to define biological targets [1] according to the metabolic aspects of the tumour and to plan heterogeneous dose distributions that will target the potentially troublesome regions. This individualisation of the treatment planning has the potential to increase the effect in the target while keeping the dose to the normal tissues at acceptable levels.

Tumour proliferation and cell density are among the physiological factors that could lead to a loss of treatment effectiveness and could therefore be used as criteria for the individualisation of treatments. The first attempts in this direction were based on the identification of the patients with increased proliferation which could become candidates for more aggressive therapies [18]. This approach was first determined by the characteristics of the experimental methods available to determine the kinetic parameters of the tumour and the relationship to treatment outcome. These were rather laborious and provided only a global characterisation of the tumour without the spatial distribution of the proliferation pattern. Advances in imaging methods provided new opportunities to determine both the intensity and the spatial localisation of the proliferating regions. It was the aim of the present study to investigate the benefits of including proliferation information from imaging modalities into treatment planning and the potential gains that could be achieved with this approach.

Both positron emission tomography (PET) and magnetic resonance imaging (MRI) have been proposed as possible imaging methods to provide information on tumour proliferation. One of the most used tracers for PET investigations is fluorodeoxyglucose (FDG) which is a glucose analogue that makes use of the increased glycolitic metabolism of tumours compared to normal tissues [19]. The uptake of FDG is governed by the energy requirement of the cells, which is high for tumour cells, and therefore FDG-PET has been used for improving the detection and staging of cancers [20–22]. FDG has also been shown to have a lower uptake in slowly proliferating tumours than in rapidly growing ones [2], but it has to be noted that it is a tracer for glycolitic metabolism, not proliferation and therefore the relationship between marker uptake and cell kinetics may not be straightforward.

3′-deoxy-3′-fluorothymidine (FLT) is another PET tracer that has been proposed for imaging the proliferation in tumours as the marker is phosphorylated by thymidine kinase (TK), an enzyme closely tied to cellular proliferation. It is therefore expected that the uptake of FLT in tissues will provide a measure of cellular proliferation. Patient studies have indeed shown good correlations between FLT uptake and the Ki-67 labelling index in lung nodules [23] and in colorectal cancer [24], in support of the use of the marker to investigate tumour proliferation. Animal studies have shown increased uptake in organs with high proliferation rates [25] thus strengthening the relationship to proliferation, but also indicating possible confounding factors if the investigated tumours are close to such organs.

Other PET markers with potential for imaging tumour proliferation are acetate and methionine labelled with the shorter-lived isotope ¹¹C. Indeed, experimental studies have shown that acetate is involved in the lipid synthesis and therefore could be used to estimate the proliferation activity of the cells [26]. Furthermore, clinical studies have shown several advantages of using acetate for the imaging of head and neck tumours [27]. Methionine has been suggested as a proliferation marker in gliomas [28], [29], even though a direct correlation with proliferation has not been mentioned.

Proliferation in gliomas has also been investigated with magnetic resonance spectroscopy that has been shown to correlate with Ki-67 labelling or other proliferation parameters [30–32]. Similarly, diffusion weighted imaging with magnetic resonance has been proposed as a technique to investigate cellular density for malignant tumours [33–35].

It therefore appears that several methods exist for imaging proliferation in various tumour types and that the uptake could be directly related to proliferation parameters. Information provided by the imaging modalities are generally used for qualitative clinical decisions like predicting the general response to chemotherapeutical agents targeting proliferation or selecting the patients for different treatment protocols. However, there is considerable potential for improvement of treatments if imaging information is used together with an optimisation approach like the one described in this study to calculate on deterministic bases the doses needed to counteract the proliferation pattern in each patient. As shown by the results of this study, this creates the premises for reducing the average dose to the target and implicitly to reduce the dose burden to the surrounding normal tissues. This could lead either to an increase of the control for the same complication levels or to a decrease of the complication rates for the same level of local control.

The strategy of defining subtargets according to the proliferation pattern and to devise heterogeneous plans to take into consideration their expected response is quite appealing, but it has to be noted that its success depends on several aspects that have to be carefully taken into consideration. One of the most important aspects is the accuracy of the imaging method in highlighting the proliferation pattern. Thus, dedicated tracers like FLT, acetate and methionine that have been shown to correlate directly with the proliferation index have more potential than metabolic markers like FDG that could provide only an indirect measure of proliferation. Furthermore, the success of the method depends on the correct determination of the uptake properties of the tracers and their relationship to the kinetic properties for many tumour types as this would eventually determine the prescribed doses. Another aspect directly linked to imaging is the geometrical resolution of the imaging methods which involve averaging over rather large volumes. The geometry of proliferating foci could also become an issue from the point of view of the technical methods used to deliver radiation to the targets. Methods to take into account these limitations are being developed, but the influence of the geometry aspect for proliferation could be investigated when more patient information will become available. Nevertheless, the potential gains from targeting proliferation appear to warrant further studies that may deal with the practical aspects of imaging it.

An important aspect that could interfere with the efficiency of the optimisation strategy and has therefore to be investigated closely is the relationship between the pre-treatment proliferation pattern and the accelerated repopulation triggered by the treatment itself [5]. Not enough data exist to state with certainty whether the accelerated repopulation is caused by the original proliferation foci when the cell loss decreases following the debulking of the tumour in the first weeks of the treatment or whether new foci are created with increased proliferation rates. The possible modification of the proliferation pattern, either in terms of the kinetics of the original foci or in terms of the spatial distribution of the proliferating regions is an important aspect that needs to be investigated in order to secure the success of the optimisation method proposed in the present study. The timescale of this possible modification is another aspect that has to be taken into consideration. Thus, an early modification would most likely need to be addressed with adaptive therapy as it could imply a mismatch with the planned high dose regions. A later modification on the other hand would probably not have the same impact as the whole tumour cell population is reduced and the effects of differences in dosage would probably not be that large.

Also of interest would be to combine the information on multiple physiological factors. It has been shown in the present study that correlating proliferation and cell density creates situations where high gains could be achieved with dose optimisation. A similar situation might also be encountered when adding information on tumour hypoxia as this might also lead to a synergistic effect with respect to the efficiency of optimisation if it correlates with proliferation. This will make the subject of future studies investigating the feasibility of image guided optimisation of radiation therapy taking into account multiple factors.

The results in this study have also highlighted another interesting aspect regarding the influence of proliferation on treatment outcome. Thus, it appears that the global characterisation of the proliferation in a tumour could hide the potentially detrimental effects of the proliferating cells. As could be seen from the comparison of Figures 2 and 5, relatively quiescent tumours with few foci of high proliferation like that presented in Figure 1 could have poorer response to uniform irradiation than tumours with almost uniform, though moderate proliferation like the case presented in Figure 4. An interesting question is whether this could be the explanation for the clinical studies that failed to show that global pre-treatment proliferation parameters could predict the treatment outcome [36]. This is an interesting aspect that highlights once again the need for accurate information regarding the distribution of proliferation rates in tumours.

Another interesting finding that could be inferred from the comparison of the dose response curves in Figures 2 and 5 is that most benefit from optimisation approaches could be obtained for tumours with heterogeneous distributions of the proliferation pattern. Thus, for the highly heterogeneous tumour in Figure 1 going from a uniform irradiation with 61 Gy to a heterogeneous one with the same average resulted in a treatment gain of more than 30%, while for the tumour with generally high proliferation in the whole volume the equivalent difference was less than 5%. The trend is however much enhanced if cell density is correlated with the proliferation rate as illustrated in Figure 6. These observations could be explained by the fact that a more homogeneous proliferation pattern could in principle be easily counteracted by a uniform target dose of a corresponding level if the surrounding normal tissues could bear the associated dose burden. At the same time, this finding indicates the importance of taking into consideration the individual features of the patients and could even indicate the need for a rethinking of the treatment approach to take into consideration these individual features.

The results in this study have shown the power of theoretical modelling to investigate rather quickly the impact of various treatment approaches. They have also highlighted some interesting features regarding the effects of proliferation that were not obvious from experimental investigations. Some aspects were not included into the model for lack of reliable data, like the possible modification by radiation of the proliferation pattern, but the model could be easily adapted to include them when details will become available. Nevertheless, the results have shown the potential benefit that could be brought by optimising the treatment according to proliferation parameters.

Conclusions

The results in this study have shown the potential gave that could be achieved by optimising the treatment according to proliferation. Thus, tumour control could be increased through the escalation of doses to proliferating foci with a relative reduction of doses to slowly proliferating regions of the tumour. Cell density is another factor that could be used for optimisation together with proliferation as they both could lead to treatment failure if not taken into consideration. Treatment optimisation based on imaged proliferation has therefore the potential to improve both tumour control and normal tissue sparing.

Acknowledgements

The author would like to acknowledge support from the Cancer Research Foundation in Northern Sweden. Thanks are also addressed to Prof. Jack F. Fowler for discussions regarding the modelling of proliferation in tumours.