Modeling in vivo relative biological effectiveness in particle therapy for clinically relevant endpoints

Abstract

Background: The relative biological effectiveness (RBE) of particle therapy compared to photon radiotherapy is known to be variable but the exact dependencies are still subject to debate. In vitro data suggested that RBE is to a large extend independent of ion type if parametrized by the beam quality Q. This study analyzed the RBE dependence of pre-clinical data on late toxicity with an emphasis on the beam quality.

Material and methods: Published pre-clinical RBE dose-response data of the spinal cord following one and two fractions of photon and carbon ion irradiation were compiled. The beam quality for each treatment condition was obtained from Monte Carlo simulations. The α_p and β_p parameters of the linear-quadratic (LQ) model for particle irradiation were determined from the pre-clinical data and was provided as a function of Q. An introduced model proposed α_p to increase linearly with Q and β_p to remain constant. RBE values predicted by the model were compared to the published data.

Results: The α_p parameter was highly correlated with Q (R² = 0.96) with a linear slope of 0.019 Gy⁻¹. No significant variation of β_p with Q was found. RBE and Q were also highly correlated (R² = 0.98) for one and two fractions. The (extrapolated) RBE at Q = 0 (theoretical photon limit) for one and two fractions was 1.22 and significantly larger than 1 (p = .004). The model reproduced the dependence of RBE on fractionation well.

Conclusions: Fraction dose and beam quality Q were sufficient to describe the RBE variability for a late toxicity model within a carbon ion treatment field. Assuming the independence of the identified RBE parameters on the ion type might suggest the translation of variable (pre-) clinical RBE data from carbon ion to proton therapy.

Introduction

Particle therapy i.e., carbon ion and in particular, proton therapy is increasingly used to treat numerous cancer types given its potential to better spare normal tissue than photon-based radiotherapy. It has, relative to photons, a higher biological effect e.g., increased cell killing, quantified by the relative biological effectiveness (RBE). The RBE is defined as the ratio between photon and particle doses resulting in a biological isoeffect. In conventional photon-radiotherapy, dose prescription, fractionation schedules and treatment planning rely on long term experiences from the dose response to photon irradiation, which are usually expressed in terms of tumor- and organ-specific threshold dose levels. The transfer of this established clinical knowledge to particle therapy requires the accurate knowledge of the RBE, since the irradiation dose in particle therapy results from dividing the photon dose by the RBE.

The RBE, however, is known to be variable and the exact dependence on potential influencing factors such as tissue type, clinical end point, treatment regimen, but also ion type is still subject to debate. In precise terms, a variable RBE is routinely used for dose prescription and treatment planning in carbon ion therapy, while in current clinical practice, protons are considered to uniformly express a 10% higher biological efficacy than photons. This is in contrast to the recently reported clinical evidence of a variable RBE in proton therapy [1]. Consequently, these treatment planning routines need to be optimized with gaining much more valid (pre-) clinical data especially on late toxicity endpoints of surrounding normal tissues. Towards this aim, it is of high relevance to increase the understanding of RBE in particle therapy, reduce the complex interdependencies associated with the RBE and therewith improve RBE-weighted dose prescription in particle therapy treatment planning- as recently discussed for proton therapy [2–4].

To appropriately elucidate RBE variations caused by the above mentioned influencing factors, in vitro studies comparing dose response of photon to particle irradiation under well controlled experimental conditions are needed [5–8]. Resulting RBE data are usually parametrized by the linear energy transfer (LET), which is a measure of the ionization density caused by the irradiation. A drawback of such a LET parametrization is, however, that it introduces a dependence of RBE on the type of ion irradiation. Our recent analysis of in vitro data emphasized the fact that RBE is to a large extend independent of ion type if considered as function of beam quality instead of the LET [9]. The translation of such basic understanding is essential for an apparent clinical RBE calculation. To increase robustness of RBE modeling only a small number of clinically accessible input parameters should be included that reflect patient treatment relevant endpoints such as functional organ response to fractionated irradiation. Experimentally, these endpoints can be studied with pre-clinical models, for example late toxicity.

In this study, pre-clinical literature data on dose response of the spinal cord to fractionated photon and carbon ion irradiation were analyzed to identify the essential parameters for an apparent clinical RBE description with special emphasis on the beam quality Q. Furthermore, it was elucidated how to assess the relevant input parameters directly from (pre-) clinical data. An analytical RBE expression based on these parameters was formulated that may also be useful for proton therapy.

Material and methods

Pre-clinical literature data

Pre-clinical literature data from a set of experiments on radiation-induced spinal cord injury were compiled for carbon ion and photon irradiation [10–14]. In brief, in all experiments the cervical spinal cord of rats was irradiated using single dose fractions (n = 1) or split dose irradiation (n = 2). The dose values at 50% complication probability, TD₅₀, were determined according to dose-response curves for the development of myelopathy (paresis grade II) within an observation time of 300 days. Irradiation with carbon ions was performed at six positions for a 6 cm spread-out Bragg peak (SOBP, dose-averaged LET range 16–99 keV/μm) for n = 1 [12,14] and n = 2 [13]. The RBEs were calculated using TD₅₀ values from comparable earlier experimental studies using 15 MV photon irradiation [10,11]. The extracted experimental parameters and RBE data used in the present study are listed in Table 1. The studied late toxicity endpoint of the serially organized spinal cord allowed for a well-defined toxicity scoring of a non-transient radiation-induced complication.

Table 1. Experimental literature data compiled for the irradiation of the rat spinal cord [10–14].

		n = 1		n = 2
Depth	LET	TD50	RBE	TD50	RBE
(mm)	(keV/μm)	(Gy)		(Gy)
Carbon ion irradiation
35	16	19.5	1.26	26.7	1.28
65	21	18.4	1.33	24.0	1.43
80	36	17.7	1.39	22.5	1.52
100	45	16.1	1.52	20.1	1.71
120	66	14.6	1.68	17.7	1.94
127	99	13.4	1.83	14.9	2.30
Photon irradiation
–	–	24.5	–	34.3	–

LET: Linear energy transfer; n: number of fractions; RBE: relative biological effectiveness; TD₅₀: dose at 50% probability of paresis grade II.

Calculation of the beam quality

In this work, the radiation response of ion irradiation was considered as a function of the dose-averaged LET – which will only be denoted as LET throughout the manuscript – as well as the dose-averaged beam quality Q defined as, (1) $$Q=\frac{Z^2}{E}\mathrm{ }$$(1) with Z and E being the charge and kinetic energy of an ion, respectively. In this work, Q was defined to be a dimensionless parameter and E had to be given in units of MeV per nucleon. The beam quality Q parametrizes the shape of the dose distribution deposited around an ion track. More specifically, it directly determines (as a factor) the height of the energy spectrum curve for the electrons that are produced by an ion track independently of ion type. A radiation field with a small Q corresponds to a more uniform dose within the area of a cell nucleus while a large Q implies high dose heterogeneity on that level.

The dose, LET and beam quality Q distributions as a function of depth in water were obtained from Monte-Carlo simulations optimized for carbon ion treatment using SHIELD-HIT12A [15,16]. For this purpose, the same 6 cm SOBP ranging from 70 to 130 mm water-equivalent depth was used for the published irradiation experiments [12–14] and was optimized using the treatment planning system TRiP [17]. The resulting treatment plan was imported into the Monte-Carlo tool to simulate particle-resolved energy spectra as function of depth in water. These spectra were used to determine dose-averaged LET and Q values similar as described in [18], using the stopping power routine libdEdx [19]. Simulated dose and LET distributions were compared to those applied for the rat irradiation experiments.

Analysis of the radiation response from fractionated irradiation

In the framework of the linear-quadratic (LQ) model, the dependence of the radiation effect ɛ is expressed by the linear and quadratic dose-response parameters α and β, respectively [20]. If each successive fraction with dose d in a multidose schedule is equally effective, the effect ɛ of n fractions can be expressed as, (2) $$\varepsilon =\alpha D+\beta dD\mathrm{ }$$(2) with the total dose D = n d. The biological endpoint expressed as 50% complication probability for radiation-induced myelopathy (paresis grade II) within 300 days after irradiation has been assumed as full effect (ɛ = 1) as suggested in [20]. The α and β values for the in vivo data were obtained using the graphical method [20] both for photon irradiation and each of the six carbon ion treatment positions as described in more detail in the Supplementary material.

Modeling the dose response and RBE

The LQ parameters α_p and β_p for particle irradiation vary with beam quality. An analysis of in vitro cell survival studies using particle irradiation with different ions suggested a linear increase for α_p with Q, while β_p remained approximately constant for the interval Q < 2.5 [9]. In this study, the simple parametrization, (3) $${\alpha }_p=\alpha \left(Q\right)={\alpha }_0+{\beta }_0{D}_{\text{L}}Q\mathrm{ }$$(3) (4) $${\beta }_p=\beta \left(Q\right)\approx {\beta }_0$$(4) was used which was found to be useful to describe previously analyzed in vitro data (not shown here). It is motivated by the local effect assumption combined with the LQ model as used, e.g., in the local effect model (LEM) [21] and the microdosimetric-kinetic model (MKM) [22], which are both in use for patient treatment with carbon ion therapy.

The constants α₀ and β₀ represent the limiting LQ parameters for Q approaching zero, which is the theoretical photon limit. They could potentially be approximated by the photon LQ parameters α_X and β_X. The limiting dose D_L is a model parameter, which is assumed to depend on the biological system but to be independent of ion type. It is conceptually related to the threshold dose, D_T, above which the LQ model is assumed to enter into a linear dose response again. Following the local effect approximation, the increase of biological effectiveness (assuming the validity of the LQ model) results from the inhomogeneous dose distribution irradiation on the cellular level of particle. However, this increase of effect is then limited to local doses up to values around the threshold dose D_T, i.e., a higher D_T may result in a higher D_L. The relationship, (5) $$D_{\text{T}}=1.1\left(\frac{{\alpha }_X}{{\beta }_X}+3.64\mathrm{ }\text{Gy}\right)\mathrm{ }$$(5) had been found empirically to match survival data with LEM simulations [21,23], which only depends on the photon α_X/β_X ratio.

The RBE in particle therapy is defined as the ratio of a reference photon dose, D_X and a particle test irradiation dose, D_p. (6) $$\text{RBE}=\left.\frac{D_X}{D_p}\right||\begin{array}{c}\\ \text{isoeffect}\end{array},$$(6) resulting in the same biological effect. For fractionated irradiation with the same number of fractions n for photon and particle irradiation, Equation (6)(6) $$\text{RBE}=\left.\frac{D_X}{D_p}\right||\begin{array}{c}\\ \text{isoeffect}\end{array},$$(6) is reduced by n and the RBE depends solely on the ratio of doses per fraction. The RBE for an endpoint achieved with n fractions (i.e., ɛ = 1 after n fractions) of the photon dose d_X and proton dose d_p = $\frac{1}{2{\beta }_p}\left(\sqrt{{{\alpha }_p}^2+\frac{4{\beta }_p}{n}}-{\alpha }_p\right)$ obtained by solving Equation (2)(2) $$\varepsilon =\alpha D+\beta dD\mathrm{ }$$(2) for d_p – is given by, (7) $$\text{RBE}=\frac{{2d}_X}{\sqrt{{\left(\frac{{\alpha }_p}{{\beta }_p}\right)}^2+\frac{4}{n{\beta }_p}}-\frac{{\alpha }_p}{{\beta }_p}} .$$(7)

Removing the dependence on fraction number n and using the model description as proposed in Equations (3)(3) $${\alpha }_p=\alpha \left(Q\right)={\alpha }_0+{\beta }_0{D}_{\text{L}}Q\mathrm{ }$$(3) and (4)(4) $${\beta }_p=\beta \left(Q\right)\approx {\beta }_0$$(4) results in (8) $$\text{RBE}=\frac{{2d}_X}{\sqrt{{\left(\frac{{\alpha }_0}{{\beta }_0}+D_{\text{L}}Q\right)}^2+4\frac{d_X}{{\beta }_0}\left({\alpha }_X+{\beta }_X{d}_X\right)}-\left(\frac{{\alpha }_0}{{\beta }_0}+D_{\text{L}}Q\right)} .$$(8)

For this model, the dependence of the RBE on the characteristics of the irradiation field (physics) is determined by the dose of the reference irradiation per fraction, d_X and the beam quality Q. The dependence on the biological system including the considered endpoint (biology) is approximated by α₀, β₀ and D_L.

In the case the parameters α₀ and β₀ can be approximated by the respective photon values α_X and β_X, the RBE expression further simplifies, (9) $$\text{RBE}=\frac{{2d}_X}{\frac{{\alpha }_X}{{\beta }_X}\left(\sqrt{{{\text{RBE}}_Q}^2+{\left(1+2{\frac{{\beta }_X}{{\alpha }_X}d}_X\right)}^2-1}-{\text{RBE}}_Q\right)},$$(9) with ${\text{RBE}}_Q=1+\frac{{\beta }_X}{{\alpha }_X}{D}_{\text{L}}\mathrm{Q.}$ Then the dependence of RBE on the biology is parametrized only by the photon α_X/β_X ratio and D_L.

For comparison with the measurements, modeled RBE values for the spinal cord were determined at the six positions within the SOBP using the photon irradiation doses d_X for n = 1 and n = 2 fractions and the RBE model given in Equation (8)(8) $$\text{RBE}=\frac{{2d}_X}{\sqrt{{\left(\frac{{\alpha }_0}{{\beta }_0}+D_{\text{L}}Q\right)}^2+4\frac{d_X}{{\beta }_0}\left({\alpha }_X+{\beta }_X{d}_X\right)}-\left(\frac{{\alpha }_0}{{\beta }_0}+D_{\text{L}}Q\right)} .$$(8) . The α₀/β₀ ratio was approximated as 2 Gy resembling the value often used clinically for comparable late toxicities in radiotherapy. All statistical data analyzes were performed using SPSS version 23.0 (IBM Corp.) and for the regression analysis p values <.05 were considered significant.

Results

Simulation of the beam quality in a SOBP

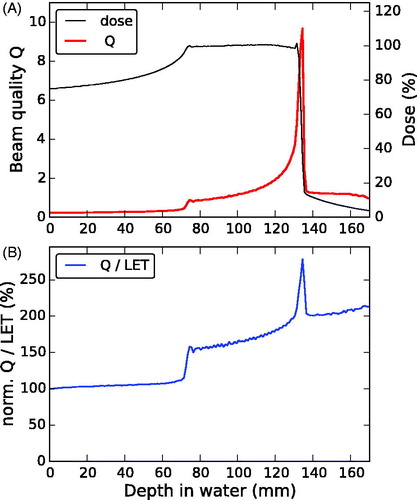
The Monte Carlo simulations of the 6 cm carbon ion SOBP reproduced the depth-dose and depth-LET distributions used for the rat spinal cord irradiation experiments well (Figure 1). The ranges of the SOBPs differed by less than 0.3 mm and the relative dose differences were well below 1% for all but the most proximal irradiation position where it was about 1%. The relative difference in LET increased toward the distal edge of the SOBP with the high LET gradient ranging between about 1 and 6%. The ratio between beam quality Q and LET was correlated but not constant and increased monotonously with depth toward the distal end of the SOBP (Figure 2). Three depth intervals could be distinguished, between which the Q/LET ratio clearly differed: proximal to the SOBP, within the SOBP dose plateau and in the distal fall-off region. Within each of the first two intervals (containing all six irradiation positions), the relative change between Q and LET was found to be small for the considered carbon ion treatment field.

Figure 1. Comparison of the depth-dose (black) and LET (blue) distributions as used in the considered experimental studies [12–14] (dashed lines) based on TRiP and obtained from SHIELD-HIT (SH) Monte-Carlo simulations in the present study (solid lines). The treatment positions are indicated by the (red) symbols on the experimental dose (circles) and LET (squares) curve.

Figure 2. (a) Monte-Carlo simulation of the beam quality Q as a function of depth in water compared to the simulated dose. (b) Relative ratio of the beam quality Q over the LET normalized to 1 at the depth = 0 mm.

Analysis of α and β as a function of Q

All α and β values obtained from the analysis of the experimental data are listed in Table 2. The α parameter for carbon ion irradiation increased linearly with Q (R² = 0.96, Figure 3) and also with LET (Figure S2 in Supplementary Material). Linear regression (including the photon data) yielded for α a slope (95% confidence limit) of 0.019 (0.015–0.023) Gy⁻¹ and a constant of 0.0052 (−0.0006–0.0111) Gy⁻¹. In contrast, no significant slope was found for the β data. Therefore, β₀ was approximated by the mean value 0.0019 Gy⁻² (Figure 3). This resulted in the values 9.9 Gy and 0.0038 Gy⁻¹ for the model parameters D_L (product of β₀ and the slope of α_p) and α₀ (product of β₀ and α₀/β₀ = 2 Gy), respectively. For photons, the α/β ratio determined from the one and two fraction data was 1.2 Gy with α_X = 0.0019 Gy⁻¹ and β_X = 0.0016 Gy⁻².

Figure 3. The parameters α and β of the linear quadratic model are shown in (a) and (b) respectively, as a function of the beam quality Q. The experimental data from photon and carbon ion irradiation are compared to the proposed model description.

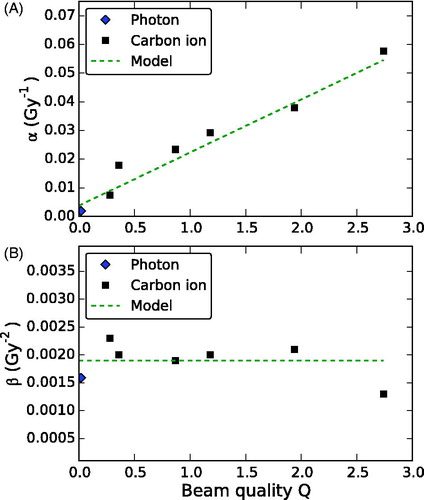
Table 2. Simulated beam quality Q at the six experimental depths positions of the rat spinal cord as well as α and β parameters extracted from the experimental data and calculated with the presented model approach. For the model, β is assumed to be constant with β = 0.0019 Gy⁻².

		Experimental data			Model
Depth	Q	α	β	α/β	α	α/β
(mm)		(Gy^−1)	(Gy^−2)	(Gy)	(Gy^−1)	(Gy)
Carbon ion irradiation
35	0.27	0.0074	0.0023	3.3	0.0090	4.7
65	0.36	0.0179	0.0020	9.0	0.0104	5.5
80	0.87	0.0234	0.0019	12.5	0.0199	10.5
100	1.18	0.0292	0.0020	14.3	0.0257	13.5
120	1.94	0.0380	0.0021	18.2	0.0397	20.9
127	2.74	0.0577	0.0013	45.8	0.0546	28.7
Photon irradiation
–	–	0.00194	0.00159	1.2	0.0038	2.0

Q: beam quality; α, β: linear and quadratic dose response parameters, respectively.

RBE analysis and model prediction as a function of Q

The experimental RBE data increased linearly with Q (Figure 4). Linear regression showed an equally high degree of correlation between RBE and Q (R² = 0.98) for both fractionation schedules. The slope increased with number of fractions (i.e., decreasing fraction dose) from 0.23 (0.19 – 0.27) to 0.39 (0.32 – 0.46).

Figure 4. The relative biological effectiveness (RBE) as a function of the beam quality Q. Comparison of experimental RBE data for 1 and 2 fractions with (a) linear fits of the experimental data and (b) the proposed RBE model. See text for details.

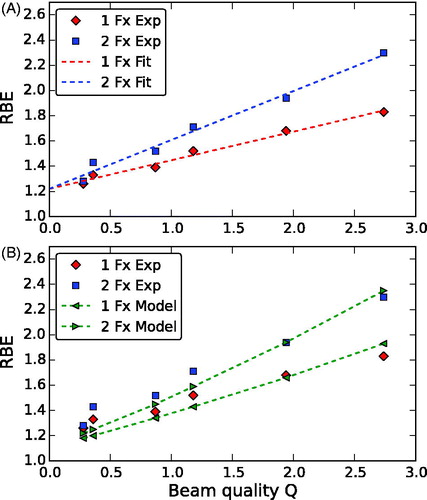
The dependence of RBE on fraction dose increased with increasing Q. For Q → 0 (limit of less densely ionizing high-energy radiation), both fractionation schemes showed the same (extrapolated) RBE value of 1.22 at Q = 0, which was significantly higher than a RBE of 1 (p = .004).

RBE values were calculated with the presented model for one, two and six fractions as well as for a photon fraction dose of 2 Gy (Table 3), using the parameters D_L = 9.75 Gy, α₀/β₀ = 2 Gy and β₀ = 0.0019 Gy⁻² (cf. previous section). The model reproduced the dependence on fractionation well (Figure 4). The overall match with the experimental data was reasonable. For small Q (especially for Q < 0.5, i.e., depths proximal to the SOBP) the model predictions were smaller than the experimental RBE values with a tendency to become larger than the measured RBE data for Q > 2.5. While the experimental data could be fitted well with a linear curve, the RBE model showed a slightly upward bended slope.

Table 3. Modeled RBE values using Equation (8). The values for 1 and 2 fractions can be compared to the experimental data in Table 1. Extrapolated RBE values are also provided for six fractions and a (clinically more relevant) photon fraction dose of 2 Gy.

			RBE
Depth (mm)	Q	dX (Gy)n	24.51	17.22	9.76	297
35	0.27		1.18	1.22	1.32	2.11
65	0.36		1.20	1.25	1.37	2.34
80	0.87		1.34	1.45	1.76	4.07
100	1.18		1.43	1.59	2.01	5.16
120	1.94		1.66	1.94	2.69	7.86
127	2.74		1.93	2.35	3.46	10.7

Q: beam quality; d_X: photon fraction dose; n: number of fractions; RBE: relative biological effectiveness.

Discussion

The analyzed organ response to fractionated irradiation in terms of radiation-induced side effects depends on fractionation dose and beam quality Q of the radiation or, in precise terms, on the macroscopic dose and the shape of the microscopic dose distribution on the level of the cell nucleus, respectively. For a carbon ion treatment field, as it was used for the published experimental data, the dose is optimized to be uniform in the treatment volume. The beam quality increases monotonously until the distal edge of the SOBP and can be described as a function of depth. Accordingly, the RBE for late toxicity increases toward the distal end of a particle therapy treatment field, too.

The linear increase of the RBE with the beam quality results primarily from the pronounced linear increase of α with Q. On the other hand, the quadratic term of the LQ model, β remains approximately constant. The same dependence of RBE and α on Q as well as the weak variation of β, which was observed here for the pre-clinical data, has recently also been noticed in our reanalysis [9] on a number of in vitro experiments such as [5,6,24]. The consistent outcome of these different in vivo and in vitro experiments suggests that the observed linear increase of α as well as RBE with Q is a systematic effect. The driving factor for the observed RBE variation is the linear slope of α with Q.

It is important to note, that the simple linear relation between RBE and Q may only hold true in a finite range (approximately Q ≤ 2.5 corresponding to LET ≤120 keV/μm for carbon ions). For larger Q, the overkill effect might gain importance, which is known to occur at high LET (for carbon ions typically >100 keV/μm) leading eventually to a vanishing β and decreasing α [23]. The analyzed data demonstrate that in practical terms this Q range is sufficient to cover the proximal 95% of the considered carbon treatment field (SOBP). However, in clinical situations, it might be that parts of the remaining distal fall-off region are placed inside an organ at risk. Therefore, the use of the proposed model could become problematic since it might estimate too large RBE values. Then the observed toxicity would be lower than estimated, i.e., the model prediction had to be considered as conservative estimate. While this has to be clarified based on experimental data, it has to be acknowledged that performing pre-clinical experiments and dose–response modeling around the distal dose fall-off of the SOBP is challenging, also due to various uncertainties, such as the range uncertainty.

In patient treatment, information on the dose response of clinical relevant endpoints is usually only accessible through the analysis of the response to different doses per fraction. For tumor response, those data can be obtained, e.g., from the analysis of clinical studies with different fractionation schedules. For normal tissue, patient-specific anatomy and treatment plans result inherently in a variation of dose distribution per fraction and among patients within an organ at risk. Those variations can be assessed through an analysis based on normal tissue complication probability models (e.g., for the spinal cord [25]).

The present investigation demonstrates that the LQ model parameters α and β – obtained by fractionation analysis – are in principle sufficient to model pre-clinical RBE. The same approach could also be used to analyze the clinical dose response. The use of such clinically derived data would be an important step to lower the uncertainties associated with RBE predictions that rely on experimental input data only. Additionally, the calculation of RBE from (predictions of) α and β as function of Q – as demonstrated here – has the advantage that the distinct dose-dependence of RBE is taken correctly into account.

It should be noted that the agreement of the modeled and the analyzed experimental data was sensitive to the values used for α₀ and β₀. In particular, a direct approximation by the photon α_X and β_X values [Equation (9)(9) $$\text{RBE}=\frac{{2d}_X}{\frac{{\alpha }_X}{{\beta }_X}\left(\sqrt{{{\text{RBE}}_Q}^2+{\left(1+2{\frac{{\beta }_X}{{\alpha }_X}d}_X\right)}^2-1}-{\text{RBE}}_Q\right)},$$(9) ] that were obtained here (α_X/β_X = 1.2 Gy) would have led to a diminished agreement, in particular, for small Q with modeled RBE values close to 1. While the experimental RBE values for one as well as two fractions extrapolated to Q = 0 (theoretical photon limit) were significantly larger than 1, RBE results compatible with 1 for Q = 0 would have implied isoeffectiveness for high-energy carbon ion and photon irradiation (i.e., α₀ = α_X and β₀ = β_X). On the other hand, the analysis of in vitro RBE data for different cell lines irradiated with carbon ions [9] and protons [26] suggested that RBE for particle irradiation in the limit Q = 0 might be compatible with a RBE of 1. An earlier analysis of the same photon data pooled with data for eight and 16 fractions suggested a higher photon α_X/β_X ratio of 2.8 Gy [11].

Disagreement was reported between the predictions by the LEM, which is used to determine the RBE for patient treatment with carbon ion therapy in Europe and the same set of experimental data as considered here [13]. For the comparison, LEM I [21] had been applied with the α and β values as input that are in use for actual patient treatment (α = 0.1 Gy⁻¹, β = 0.05 Gy⁻²) while for LEM IV [27] the applied values (α = 0.003 Gy⁻¹, β = 0.0015 Gy⁻²) were close to the photon α_X and β_X that were obtained in the present study. LEM I fitted best at the lowest Q (LET = 16 keV/μm) and deviated progressively toward higher LET values while LEM IV agreed best at the highest Q (LET = 99 keV/μm) and showed increasing deviations below. While the measured increase of RBE with LET could neither be fully described by LEM I nor by LEM IV, the systematic increase of the fractionation dependence of the RBE at higher LET values was better described by LEM IV. The observed deviations in this and earlier studies indicate the need for further experimental as well as biophysical modeling studies to improve the reliability of treatment planning software for particle therapy.

The present study of the experimental α and β parameters was limited by the fact that only published data for one and two fractions were available for the analysis. Determining a straight line from two experimental data points results in great uncertainties which propagate to the extracted parameters – specially, in the extrapolation to derive α as the intersection of the vertical axis. With only two points the straight line is given by default and the uncertainties are large. It is also known that the method used to extract α and β parameters is inefficient to estimate the α/β ratio [28]. Instead of one isoeffective dose point (here TD₅₀) per treatment condition, in a more direct regression approach, the entire experimental dose response curves – if available – should be used. However, the obtained α and β values fully reproduced all experimental RBE data using Equation (7(7) $$\text{RBE}=\frac{{2d}_X}{\sqrt{{\left(\frac{{\alpha }_p}{{\beta }_p}\right)}^2+\frac{4}{n{\beta }_p}}-\frac{{\alpha }_p}{{\beta }_p}} .$$(7) ), i.e., no modeling. Experimental data for six fractions may become available in the near future and serve as a validation data set (Table 3). For carbon ion irradiation, the observed response showed the anticipated systematic behavior (linear increase of α and constant β with Q) as shown in Figure 3. For photon irradiation, the analyzed α/β values appeared to be different whether one and two or in addition data with eight and 16 fractions (with the same isoeffect) were considered [11].

The parameter Q is closely related to a second commonly used parameter for radiation quality, namely the square of the effective ion charge divided by its relativistic velocity, ${\left(Z_{\text{eff}}/\left(\frac{v}{c}\right)\right)}^2$, which is known to provide a lower dependence of radiation-induced effects on the particle type than the LET [29]. This is in-line with our earlier analysis of in vitro cell survival data indicating that experimental α, β and RBE data were practically independent of the type of ion irradiation (e.g., proton, helium, carbon, neon) when parametrized by Q [9]. The present study suggests furthermore that the remarkably simple linear dependence of radiation response on dose and Q also holds true for (pre-) clinical endpoints. Assuming correctness, results from carbon ion irradiation could then be directly transferred to particle therapy with other ions. From a clinical point of view, this would allow for a direct translation of (clinically obtained) RBE data gathered in carbon ion therapy to application in proton therapy. This would be a major step toward improving the simplistic clinical RBE modeling currently in use in proton therapy (constant RBE = 1.1) by profiting from long term clinical experience with a variable RBE in carbon ion therapy. However, this implies that in future α and β as well as RBE will be provided as a function of Q instead of LET, due to the dependence on the type of ion irradiation introduced by LET. Such an approach would also imply the need for extrapolation of carbon ion RBE data (here obtained for Q ≥ 0.25) down to smaller values of Q ≤ 0.25 (i.e., proton energies ≥ 4 MeV), which are typically found in a proton SOBP. The applicability of such an extrapolation needs to be proven prior to application. Therefore, further research on the dependence of RBE, especially under pre-clinical and clinical conditions, is mandatory to realize a successful translation of this concept to proton therapy.

In conclusion, we showed for the first time that the fraction dose and beam quality Q are sufficient to describe the RBE variability for a late toxicity model and different fractionation schedules within a carbon ion treatment field. The variable RBE could be modeled in a simple way, although, photon dose response data alone were insufficient to explain the considered experimental data. The independence of the relevant RBE parameters on the type of ion irradiation suggests the translation of RBE data from carbon ions to protons to reduce the uncertainties currently associated with radiobiology in proton therapy.

Acknowledgments

The authors thank Christian Karger for discussions on the RBE dependence and for kindly providing treatment plans that had been used in the analyzed rat irradiation experiments.

Disclosure statement

No potential conflict of interest was reported by the authors.