Geometrical tracking accuracy and appropriate PTV margins for robotic radiosurgery of liver lesions by SBRT

Abstract

Purpose: To assess the geometrical accuracy and estimate adequate PTV margins for liver treatments using the Synchrony respiratory tracking system.

Material and methods: Treatment log files are analyzed for 72 liver patients to assess tracking accuracy. The tracking error is calculated as the quadratic sum of the correlation, the predictor and the beam positioning errors. Treatment target rotations and rigid body errors reported by the system are also evaluated. The impact of uncorrected rotations is assessed by rotating the planned dose distribution and reassessing target coverage. Total PTV margins are estimated by summing in quadrature tracking errors and rigid body errors. Relationships are explored between tracking errors, model linearity and motion amplitudes of internal and external markers.

Results: Margins of 3, 2, 2 mm in SUP-INF, LT-RT and ANT-POST directions, respectively, are sufficient to account for tracking and beam positioning errors for 95% of patients. If rigid body error is also considered, margins increase to 4 mm isotropic. Rotations could not be corrected for 92% of patients due to imperfect fiducial implantation and limitations in the magnitude of corrections that the system can apply. Uncorrected rotations would lead to average estimated dose reductions of 2.7% ± 5.8% of the prescribed dose for D99 of GTVs (5 mm PTV expansion) in which the target was well covered in the original plan (28 of 31 GTVs). 80% of tracking models exhibit near linear correlation between internal and external marker motions with small tracking errors (<2.2 mm).

Conclusions: Isotropic PTV margins considering tracking errors and target rigid body errors could be used for liver SBRT treatments if rotational corrections can be calculated accurately so that systematic rotational offsets can be avoided. The linearity of the internal and external breathing motions might be useful for other types of treatment modalities for liver cancer.

Introduction

Organ motion management for tumors that move with respiration is a challenge for accurate dose delivery during radiotherapy treatments [1,2]. It can lead to unacceptably high dose to healthy tissues and insufficient dose to tumors [3,4]. The liver is a highly deformable organ, and studies have shown that the liver can move in a complicated fashion due to respiration and other physiological motions [5,6]. The radiosensitivity of hepatocellular carcinoma, a primary malignancy of the liver, makes it a suitable candidate for hypofractionated radiation treatments [7]. Many multi-center studies have evaluated the outcomes of liver SBRT using a variety of treatment techniques [8–14]. Stereotactic body radiation therapy (SBRT) by the CyberKnife^® (Accuray Inc., USA) using Synchrony^® respiratory motion compensation is a promising technique to treat liver cancer, especially for patients who are not eligible for radio-frequency ablation or surgical resection [15].

Planning target volume (PTV) margins should consider motion tracking errors [16–18], target rotations [19] and deformations [20,21], and estimates of the overall delivery accuracy for static targets [22]. Researchers have used treatment log files to estimate treatment margins for thorax [21], lung [23–25] and liver [26–28] lesions treated with CyberKnife SBRT treatments. This work has assessed a relatively large cohort of 72 patients with comprehensive filtering to exclude all data not directly used during treatments (e.g., exclusion of data acquired during setup, beam-off periods and manually rejected by radiation therapy technologists). Details of inter- and intra- patient variations in tracking errors, effects of uncorrected rotations, and target deformations were not evaluated in most of those earlier studies. Some research groups assessed the deformations [29] and the resulting dosimetric effects [30,31] using either 4DCT or CBCT data. One study using CBCT data for 29 livers patients [32] suggested that large day-to-day variation of rotations (up to 16.9° and 28.6° in roll and yaw, respectively) may be important for liver treatments, especially without abdominal compression as is typical for CyberKnife treatments. At our center we do not typically add a CTV margin for our liver SBRT treatments. The PTV is most often a 5 mm expansion of the GTV target determined from a fused secondary MRI dataset. The use of ‘no margin’ for presumed microscopic extension is based upon the approach adopted for lung SBRT trials by the Radiation Therapy Oncology Group [33]. Treatments tracking errors, target rotations, rigid body errors, as well as linearity of tracking models that potentially affect the geometric tracking accuracy for liver SBRT treatments, are assessed in our study. We investigated if non-isotropic margins are warranted based on our data.

Material and methods

Principles of system operation and log file data

The Synchrony tracking system (henceforth referred to as ‘the system’) compensates for tumor motion in real time based on a model that correlates the positions of fiducials and external LED markers [34–36]. Before the treatment, fiducials (platinum seeds, ∼1.0-mm diameter by 3.0 mm length) are implanted inside or adjacent to a tumor under ultrasound image guidance. The fiducial positions are determined at different phases of the respiratory cycle by orthogonal X-ray planar images, which are typically acquired every 1 to 2 minutes [35]. The system uses these data to predict the tumor motion based on external marker motions. At least 8 X-ray image pairs are required to build a valid model, and the subsequent X-ray image data are used to update the model to account for intra-fractional changes in breathing motions [35,37]. The model predicts the target position 115 m in the future to overcome the latency between the hardware and software involved in beam delivery [34,37].

Treatment log files have been assessed for 72 patients (67%/33%: liver metastases/liver primaries, 70 ± 11 years old, 46 males/26 females, typically 3 to 6 fractions) treated between 2011 and 2017. All data were collected with the informed consent of the patients as a part of the Research Ethics Board (REB) approved local clinical trial.

During that time, different versions of the planning system (from v.3.5 to v.4.6) and delivery system (from v.9.0 to v.9.6) were used. The CT resolution used at our center was 1.0 × 1.0 × 1.0 mm³ or smaller, depending on the size of a patient. Recommended margins are rounded up to the nearest integer in mm due to partial volume effects associated with contour expansions in the CyberKnife planning system. Data analyses are performed using MATLAB 2018b (MathWorks Inc., Natick, MA).

Synchrony errors

The tracking error also referred to as the Synchrony error, is defined as the quadratic sum of correlation, predictor, and beam positioning errors [26]. The correlation error is the difference between the predicted and the measured target positions determined per X-ray image pair. The predictor error is the difference between the target position predicted 115 m earlier and the predicted target position inferred from the Synchrony model using the current LED positions which are sampled at a frequency of 26 Hz. According to quality assurance guidance documents [38,39], the beam positioning error (end-to-end error) for static phantoms should be maintained at less than 1 mm in any direction.

The correlation error per model is calculated as the root-mean-square (RMS) of correlation errors reported within the model. The predictor error per model is the RMS of predictor errors during beam-on periods within a model, following the approach of Pepin et al. [24]. To assess the intra-fractional variation of the predictor, the RMS predictor error over each beam is also calculated. The radial Synchrony error per patient is calculated as the mean value across models. We extract the marker position and split the external respiratory traces into eight equal-width time bins to investigate the phase dependence of the signed correlation and predictor error per patient (i.e., to see how the direction of these errors change during breathing).

Rotational corrections

During the treatment, fiducials may be disabled when the system cannot identify them in the X-ray image data or when acquired image data cannot match the digitally reconstructed radiographs. Accurate rotational corrections can be calculated only when three conditions are met for each X-ray image pair [28]: three or more fiducials are detectable, the minimum spacing between any fiducial pair is 20 mm, and the minimum angle formed by three fiducials is 15°, according to specifications stated in the CyberKnife treatment planning manual. Only rotational corrections calculated using fiducial positions that meet all these criteria are assessed. For all treatments using the Synchrony system at our center, the patient is initially set up using Xsight^® spine tracking setup plan. If the criteria for accurate rotational corrections are not met or the magnitude of rotational variation exceeds system limits, rotational corrections are turned off and the couch rotations are not changed from the spine setup values. The system is limited in the magnitude of rotational corrections that it can apply during the treatment. For body treatments using recommended planning settings, the system can correct for ± 1.5° for roll and pitch, and ± 3.0° for yaw. According to the treatment delivery manual, rotation corrections about the imaging system isocenter are applied (if they can be calculated, are correctable by the system and are enabled) based on the last X-ray image acquired before the beam delivery.

The contours and planned dose distributions are extracted from DICOM files for 72 patients, and the DVHs for the planned dose distributions are calculated. To estimate the dosimetric impact of rotations, we rotate the planned dose distributions about the imaging isocenter using the inverse of the rotation correction matrix and recalculate the DVHs. The changes to the D99 and D95 are assessed for targets (CTV and/or GTV) after rotation as a fraction of the prescribed dose (R_x) for each patient. These cases were planned using typically a 5 mm isotropic PTV margin. To verify this approach, we have rotated CTs for three patients, whose rotation corrections at the time of treatment were larger than 3° in at least one direction on average across the entire treatment course, by the average rotations and recalculated the dose in the planning system. 3D gamma analysis [40,41] is performed using an absolute dose difference criteria (2%/2 mm and 3%/3 mm) for the three patients to assess the impact of neglecting changes in attenuation (rotating the entire CT volume assuming the patient is a rigid body). The correlation between the dosimetric change to the targets and the distance between the imaging isocenter and the center of fiducials (from planning CT images) is also investigated. By applying ± 3°and ± 5° to 98 GTVs for 72 patients in any rotational direction, the sensitivity of change in percentage D99/R_x is investigated.

Rigid body errors

According to specifications stated in the CyberKnife treatment delivery manual, the rigid body error calculated by the system when an X-ray image pair is acquired, is defined as the absolute change in the inter-fiducial distance per active fiducial pair during the treatment compared to that determined in the CT volume [21]. However, the user cannot distinguish between target contraction and expansion by these absolute quantities. Hence, we calculate signed rigid body errors where positive and negative values indicate target expansion or target contraction, respectively. The rigid body error that represents the average change of inter-fiducial distances across all active fiducial pairs is assessed per X-ray image pair. Rigid body errors of 66 patients (with >1 fiducial enabled) are assessed. The number of fiducials that were used for tracking and implanted inside the GTV contours is investigated.

Correlations of errors with model linearity and motion amplitude

Since the system models the relationship between external and internal motions as either linear or curvilinear [34,37], the linearity between internal and external motions (hysteresis effect) is investigated. The target and marker positions are determined per X-ray image acquisition and reported in a log file. A linear fit is determined for the marker and target positions as a function of time across the entire model, and the drift component is corrected. We also quantify the correlations among Synchrony errors, peak-to-peak amplitudes of target SUP-INF motions, and marker radial motions for all models. The multiple correlation coefficient [42] is used to evaluate how well the internal and external motions can predict Synchrony errors. The R² value per model is used as an indicator of model linearity between SUP-INF positions of the target and the average radial positions of external markers within a model. Inter-patient and intra-patient (inter-model) target and marker motions are also assessed to evaluate variations in the amplitudes of internal and external breathing motions.

Hypothesis testing

Two-tailed Student’s and Welch’s t-tests [43,44] are used to calculate statistical significance (p ≤ .05), and the 95% confidence interval for the mean difference between two samples. Spearman correlation coefficients (Spearman r) are used [45] if Lilliefors statistics test p > .05. The impact on tracking accuracy of patient age, gender, and lesion position: left or right side of the liver, as well as the distance along the superior/inferior direction to the maximum superior slice of the liver contour (dome-to-target distance), is assessed. Also investigated is the relationship between the magnitude of rigid body errors and the number of fiducials used for tracking. Most statistical tests and figure generation are performed using OriginPro 2018b (OriginLab Corp., Northampton, MA).

Results

Synchrony errors

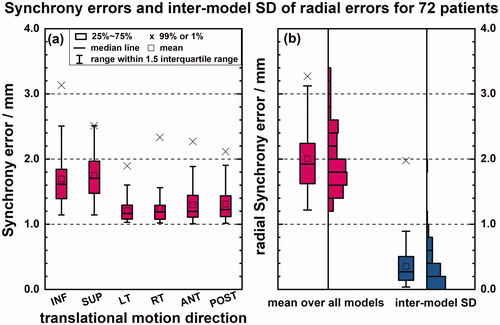
No significant differences in Synchrony errors (95% CI −0.1 to 0.0 mm, p ≤ .05 for SUP-INF, LT-RT, and ANT-POST directions) are observed along the positive and negative anatomical directions (Figure 1(a)). The errors in the SUP-INF direction are significantly different from those in the other two directions (95% CI +0.4 to +0.5 mm, p ≤ .0001 for LT-RT direction; 95% CI +0.3 to +0.5 mm, p ≤ .0001 for ANT-POST direction). The 95th percentiles of the Synchrony errors in SUP-INF, LT-RT, and ANT-POST directions for our patient population, are 2.3 mm, 1.6 mm, and 1.8 mm, respectively. Figure 1(b) illustrates the inter-patient and intra-patient (inter-model) variations in Synchrony errors. Supplementary Figure 1 shows inter- and intra- fractional variations of correlation errors per X-ray image pair and RMS predictor errors per treatment beam.

Figure 1. Synchrony errors and inter-model SD of radial errors for 72 patients. Synchrony errors are shown in different anatomical directions (a) and radially (b). Red boxplots (a, b) indicate the mean error for each patient across all their models while the blue boxplot (b) indicates the inter-model standard deviations (SD) across all models for each patient. (b) The length of the bar is proportional to the number of patients within each bin.

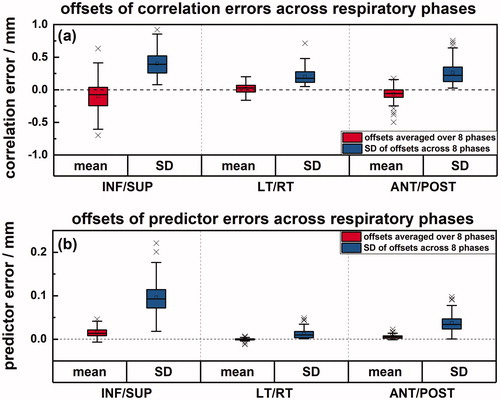
Figure 2 shows for all patients the average and SD of signed correlation and predictor errors across the respiratory phases per patient. The systematic effect for both correlation and predictor errors across all respiratory phases approximately cancels out within ± 0.5 mm and ± 0.05 mm, respectively for most patients. The average SD of correlation errors across respiratory phases in SUP-INF, LT-RT, and ANT-POST directions are 0.4, 0.2 and 0.3 mm, respectively.

Figure 2. The offsets of correlation (a) and predictor errors (b) across eight respiratory phases for 72 patients. The red boxplots indicate the mean error across eight respiratory phases across all patients while the blue boxplots indicate the inter-phase SD across eight respiratory phases for each patient.

Rotational corrections

Geometric target rotations are an independent source of error [19] which should be considered in determining treatment margins, especially when rotational corrections cannot be applied. Fiducial placements for only 23 out of 72 patients (32%) meet all the criteria for accurate calculation of rotations (for total 84 fractions). In 18 out of the 23 patients (78%) more than three fiducials were used for tracking which is also recommended for lower uncertainty in rotation corrections [46]. Rotational corrections for each fraction of 23 patients are shown to illustrate inter- and intra- fractional variations (Figure 3). Supplementary Figure 2 shows the inter-patient and intra-patient (inter-x-ray) variation of rotational corrections. The average rotational errors for the 23 patients are −0.1° ± 3.3° in roll, −1.0° ± 3.7° in pitch, and 0.5° ± 3.8 in yaw. The rotational corrections are found to be uncorrelated with Synchrony errors (Spearman r < 0.3).

Figure 3. Inter- and intra- fractional variations of rotational corrections for 23 patients in roll (a), pitch (b) and yaw (c). Rotational corrections per X-ray image pair are grouped by fraction for these patients. Each vertical data cluster represents the 5^th to 95^th percentile of the rotational corrections per fraction. Clusters belonging to individuals alternate between red and blue. The dashed lines indicate the thresholds of rotations for which the system can correct. Three patients with the largest rotational corrections had 2 to 3 distinct large lesions with fiducials in the most inferior segment (VI) of the liver closest to the bowel structures. (d) The changes to D95 and D99 as a fraction of the prescribed dose for the 23 patients (31 targets) with accurate rotations. The arrows indicate three targets that were treated with compromised plans.

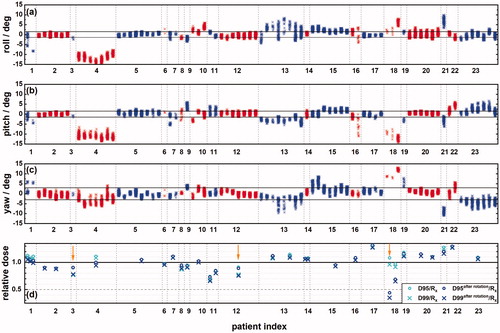
Only 6 (patient 2, 5, 12, 14, 17 and 20 in Figure 3) out of 23 with accurate rotational corrections have more than 70% of their observed rotational corrections within the system thresholds (Figure 3), meaning that the system can correct rotations for only 8% of the entire population of our patients. For 26 out of 84 fractions (31%), the 5th to 95th percentile of corrections span within 3°, 3° and 6° in roll, pitch, and yaw, respectively, of their mean values (Figure 3). This means that if these systematic rotational corrections were avoided by setting up patients such that their rotational corrections averaged to zero across the respiratory cycle, then these rotations could be corrected by the system at least 90% of the time for these 26 fractions.

The changes to D95 and D99 as a fraction of the prescribed dose (R_x) are shown in Figure 3(d) for the 23 patients (31 targets) with accurate rotations. Rotations of any magnitude are assumed to be not corrected by the system and equal to the average rotation per X-ray image pair across the entire treatment course. Some targets were intentionally underdosed to spare a nearby OAR. We define compromised treatments as those with more than 10% difference between the D99 and D95 in the planned target DVH. The arrows indicate three targets that were treated with compromised plans (3 out of 31). The percentage D95/R_x and D99/R_x decrease from 105.1% ± 13.2% to 100.8% ± 17.6% and from 101.1% ± 14.5% to 96.7% ± 19.0%, respectively, for all 31 targets. For uncompromised targets (28 out of 31), the average change to the percentage D99/R_x is −2.7% ± 5.8%. Excluding targets from patient 4, 18, and 21 with rotations exceeded ± 5° in at least one direction, the average change to D99/R_x is −1.1% ± 2.3%. A 3D gamma analysis is used to assess changes to the planned dose distribution due to patient orientation using average observed rotations for three patients (patients 1, 4 and 18 in Figure 3). The minimum and average 2%/2mm pass rate is 91% and 95.2% respectively, for all voxels greater than 50% of the maximum planned dose. This suggests that the approximation of rotating dose and neglecting attenuation changes are reasonable even for large angles of rotations.

The Spearman correlation coefficient for change in D99/R_x and the distance between imaging isocenter to the fiducial center is −0.4. This suggests that a larger distance between imaging isocenter and the fiducials might lead to a larger rotational error if rotations are not corrected. Table 1 illustrates the sensitivity of change in percentage D99/R_x to rotations for 72 patients (98 GTVs). We found that this change is strongly correlated with the magnitude of the rotation (Spearman r = −0.87).

Table 1. Percentage change in D99/Rx after rotations applied for 72 patients (98 GTVs).

rotation direction	angle (º)	mean (%)	SD (%)
roll	−3	−1.5	3.7
	+3	−0.8	2.9
	−5	−3.8	6.2
	+5	−2.7	5.8
pitch	−3	−0.5	2.4
	+3	−0.9	2.4
	−5	−1.8	4.4
	+5	−2.5	4.2
yaw	−3	−0.4	2.8
	+3	−1.3	3.6
	−5	−2.3	6.2
	+5	−3.5	6.9

Rigid body errors

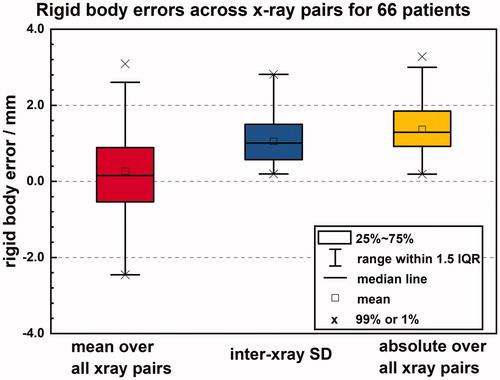
We found that 20.4% of the 89 GTVs for the 66 patients with rigid body reported had at least one fiducial implanted in the GTV and the distance between the center of the GTV and the fiducial center is 41 ± 24 mm for them. Figure 4 shows the inter-patient and intra-patient (inter-x-ray) signed rigid body error as well as the inter-patient absolute value of the rigid body error. The absolute value of the rigid body error is a quantity that can trigger treatment interrupts. It very frequently exceeds the default limit (2 mm) for our patients. Rigid body errors grouped by fractions for 66 patients are drawn (Supplementary Figure 3). The absolute values of rigid body errors are found to be uncorrelated with Synchrony errors (Spearman r < 0.2) so the proposed PTV margins are based on adding these two types of errors quadratically. They resulted in 3.7, 3.3 and 3.4 mm in SUP-INF, LT-RT and ANT-POST directions, respectively. However, considering the precision of the CT resolution errors are rounded to the next integer, 4 mm isotropic margins are sufficient to compensate for Synchrony and rigid body errors for 95% of the patient population, if the target or if rotations have a negligible impact on target coverage (e.g., spherical targets centered about the imaging isocenter). Rotational angles and rigid body errors are found to be uncorrelated (Spearman r < .2 for roll, pitch, and yaw rotational directions), which may imply that the large rotations observed for some patients are not associated with fiducial migration.

Figure 4. Rigid body errors across X-ray pairs for 66 patients. The mean, inter-x-ray SD, and absolute values of signed rigid body errors across all X-rays for each patient.

Model linearity and motion amplitude

A relatively strong linear correlation (Pearson r = 0.67) is found between peak-to-peak amplitudes of target SUP-INF motions (17.4 ± 7.4 mm) and marker radial motions (10.0 ± 4.7 mm) for the 624 models but a negligible multiple correlation coefficient (r = 0.10) [42] is found among internal and external motion amplitudes and radial Synchrony errors over all models (2.0 ± 0.6 mm). The R² value per model (representing model linearities or conversely the lack of hysteresis) are shown as a function of SUP-INF correlation errors in Supplementary Figure 4. The dashed lines show the 95th percentile of SUP-INF correlation errors (2.2 mm) and 80th percentile of R² values (0.80).

The mean peak-to-peak amplitudes of target motions in SUP-INF, LT-RT, ANT-POST directions across models for all patients are 17.5 ± 5.3, 4.0 ± 1.9 and 7.5 ± 3.3 mm, respectively, and the corresponding inter-model standard deviations are 4.0 ± 2.5, 1.3 ± 0.9 and 2.0 ± 1.4 mm, respectively. The mean peak-to-peak marker radial motion across models for 72 patients is 10.8 ± 3.7 mm. The corresponding inter-model standard deviation for all patients is 2.7 ± 1.5 mm.

Hypothesis testing

Following the organ contouring consensus guidelines [47], a radiation oncologist has identified the liver segment in which each patient has their fiducials implanted. Sixty-one patients were identified as having fiducials exclusively in either the left or right side of the liver. No significant difference in radial Synchrony errors are found for either gender (95% CI –0.1 to +0.3 mm, p =.26) or left/right lesion location (95% CI −0.4 to +0.1 mm, p = .20). Similarly, no significant difference is found between peak-to-peak SUP-INF target motion amplitudes (95% CI −0.7 to +4.7 mm, p =.14) or rigid body errors (95% CI −0.3 to +0.5 mm, p =.71) for left/right lesion location. The dome-to-target distance is 63.1 ± 30.9 mm for 72 patients (98 GTVs). No correlation is found between the radial Synchrony errors and dome-to-target distance (Spearman r = −0.1) or between rigid body errors and dome-to-target distance (Spearman r = −0.1). The correlation between age and radial errors is negligible (Spearman r = 0.3). We also found that the number of fiducials used for tracking does not make a significant difference in the amplitude of rigid body errors (95% CI −0.5 to +0.5 mm, p > 0.3).

Limitations of this study

Due to the partial volume effect we propose 4 mm isotropic margins even though our data support the use of non-isotropic margins. We acknowledge that the proposal of the PTV margins based on root-mean-square averaged tracking errors that cover the 95th percentile of our patient population may be overly conservative as some geometric errors may cancel out when they are in opposite directions [27].

This study does not investigate uncertainties in rotational corrections associated with using less than four fiducials [46], different motion in different liver segments [48], larger spacing between fiducials and targets [49] or changes in liver rotational orientation across the respiratory cycle [27]. Due to the small number of patients (N = 23) with implanted fiducials that meet the criteria for accurate calculation of rotation corrections, the results may be biased in some way (e.g., patients who have fiducials implanted that meet these criteria may have other common characteristics such as lesion location, number, size of lesions and health status). Our method to estimate the dose change to targets due to uncorrected rotations treats the patients as rigid bodies and neglects the change in beam attenuation. The effect of changing beam attenuation is only investigated for three cases. In addition, the PTV expansion used to assess uncorrected rotations was typically a 5 mm isotropic margin, slightly larger than the 4 mm margin what we propose here.

Rigid body errors may also be an overly simplified way to characterize the margin required for organ deformation especially for complicated target volumes and when there are larger distances between the lesion and the fiducials. The dose increases to OARs (stomach, duodenum, the rest of the small bowel, and heart) are not discussed which might be another important concern when there are uncorrected rotations or organ deformation.

Discussion

For 95% of patients, margins of 3, 2 and 2 mm (errors are rounded to the next integer) in SUP-INF, LT-RT and ANT-POST directions, respectively, are sufficient to account for Synchrony errors (Figure 1). Winter et al. [26] gave quantitative estimates of total Synchrony error averaged per fraction for liver SBRT treatments (N = 27). The correlation and predictor errors were selected for data immediately before the beam delivery, and within a 20 s-window before the corresponding X-ray image pair, respectively. They reported the 95th percentile of absolute correlation errors in each direction as 3.3, 2.1 and 1.8 mm for the SUP-INF, LT-RT and ANT-POST directions, respectively, and an overall radial PTV margin of 4 mm. Although our work considers the RMS error per model, instead of considering mean errors per fraction, our results agree well with Winter et al.’s data [26].

Pepin et al. [24] extracted different percentiles of residual errors from 100 Synchrony models for 23 lung patients. The correlation, predictor, and targeting errors were added linearly to estimate non-isotropic margins of 6.9 mm in the SI direction, 4.6 mm in the AP direction, and 3.5 mm in the lateral direction. However, they used a more stringent requirement on 95% of model points, rather than our 95th percentile of patients, and they included all data during the entire treatment. Inter-model variations of radial Synchrony errors for individuals are relatively small (mostly <1 mm) as shown in Figure 1(b). Supplementary Figure 1 illustrates that distributions of correlation and predictor errors for each patient are similar from fraction to fraction, indicating that the system tracks the target motion for an individual. Our observations (Figure 1 and Supplementary Figure 1) indicate that patients tend to have higher or lower Synchrony errors consistently throughout the treatment course. Hence, patient-specific margins are a possibility for these treatments, perhaps based on data from the first treatment fraction or a dry-run session prior to treatment planning, similar to that proposed by Pepin et al. [24] for lung patients.

For the phase dependence of the correlation and predictor errors, the systematic effects cancel out throughout the respiratory cycle for most patients in any direction, as shown in Figure 2. However, the SD across the respiration phases for individuals is not negligible. The blurring effects of dose distribution can get worse when the motion is out of phase, and it leads to less sharp penumbra [50]. This finding confirms our relatively conservative approach of using unsigned errors to estimate PTV margins that take the dose blurring effects into consideration. Chan et al. [27] using ten phases over the respiratory cycle, pointed out that the correlation errors were not statistically phase-dependent (p > .05) which is consistent with our work.

Only 6 out of 23 patients could be treated with most of their rotations corrected because of the limitation in magnitudes of corrections the system can apply. The dose to targets is sensitive to rotations as shown in Table 1. Ideally, fiducial placements should be improved so that rotations can be tracked more frequently. This could be done using a kV X-ray c-arm imaging system, which would allow the fiducial positions to be validated in vivo during the implant procedure using oblique planar images. The Synchrony tracking system should be allowed to correct for larger rotations. For example, the system can correct for up to ± 5° for prostate treatments [51], which is beneficial for the patients. Errors could still be reduced if the patients were set up such that rotational corrections average to zero across the respiratory cycle. User’s confidence in these rotations could be increased with on-board volumetric imaging planned to be included in a future release of the CyberKnife system. The rotational corrections in all directions are non-negligible and may contribute to systematic beam delivery errors if their effects are not minimized. The relatively large inter-patient variations (Supplementary Figure 2) indicate that those patients set up with rotational errors systematically different from each other. The intra-fractional variations (Figure 3) indicate that non-negligible rotations also occur from X-ray to X-ray, over timescales comparable to the respiratory cycle. This can be even more problematic for the remaining 49 patients whose rotational corrections are unknown. The dosimetric change due to systematic rotations has been assessed for this small group of patients with accurate corrections (N = 23). More than 4% reduction in D95 and D99 as a fraction of the prescribed dose has been observed for their treatments. In any case, the imaging isocenter should be placed as close as possible to the center of fiducials to minimize dose change introduced by rotations.

Chan et al. [27] approximated the cumulative dosimetric effects due to residual correlation, predictor and rotational errors using data binned into ten breathing phases for 24 liver patients treated with CyberKnife. They reported relatively small systematic rotational corrections of −0.26° ± 0.51°, 0.14° ± 0.71°, 0.65° ± 0.61° in roll, pitch and yaw directions, respectively. The rotations observed for our patient population (N = 23) deviate more from zero and have a larger SD than those reported by Chan et al. [27]. However, some of the aggregate errors presented in that work were averaged over each bin of the respiratory cycle and over the total number of fractions so our results cannot be compared directly. We present intra- and inter-fraction rotation corrections for each X-ray pair acquisition, so it is perhaps not surprising that we have larger SDs across the patient population. Chan et al. [27], appeared to have had more success aligning patients with rotational corrections close to zero than in our experience. However, there are some similarities between our observations. Chan et al. also observed larger rotations for a subset of their patients, remarking that 23% (6 of 24 total patients) have rotations >2°. Their fiducial implants also do not always meet the criteria for accurate rotation corrections, with only 24 of 46 patients meeting their criteria.

Chan et al. [27] estimated the dosimetric effect of correlation, predictor errors and uncorrected rotation errors using a ‘pseudo-4D’ dose calculation method. They considered changes to CTV and PTV coverage and investigated if a 3 mm isotropic treatment margin PTV was sufficient to cover all residual tracking errors. They rotated and translated the contours for the CTV and PTV based on the aggregate translational and rotational errors for several bins of the respiratory cycle, each equally weighted in the final dose accumulation. They found a median dose reduction of 1.1% and 0.0% for PTV and CTV, respectively, for their patients. Based on these results and on other concerns, including the increased dose to OARs for patients with small residual errors, they argued against larger and non-isotropic margins. However, changes to coverage based on rotating contours, both in Chan’s work and in ours, may neglect the dose broadening effects and associated increase in penumbra due to tracking errors [16,50]. These errors may affect different parts of the target differently due to the large numbers of small fields used by the CyberKnife system and when errors with opposite signs occur at different extremes of the respiratory cycle. Further study is warranted to assess more accurately the dosimetric changes due to Synchrony and rigid body errors as well as uncorrected rotations for these treatments.

Xu et al. [28] calculated translational and rotational corrections for 23 liver patients by comparing live X-ray images, and deformations relative to one reference X-ray image pair near the beginning of the treatment. They found absolute rotational angles of roll, pitch and yaw were 1.2° ± 1.8°, 1.8° ± 2.4° and 1.7° ± 2.1°, respectively, the SD of which are more consistent with our findings.

The intra-patient (inter-x-ray) variations in rigid body errors, presumably associated with the respiratory cycle is relatively small (0.6 ± 0.4 mm) as shown in Figure 4, suggesting that rigid body errors for most individuals are relatively constant over their treatment courses. This could be applied to adaptive liver treatments. If a patient had positive errors during the first treatment fraction, a margin expansion could be considered for future treatments. Xu et al. [28] concluded that intra-fractional fiducial migration was unlikely based on small 3D fiducial displacements (0.2 ± 0.2 mm) when the fiducials were aligned rigidly. Furthermore, only small systematic volumetric increases (1–2%) were observed in that study in subsequent fractions relative to the first fraction which they thought may be related to radiation-induced edema. We did not find a strong correlation between rigid body errors and rotational corrections. This suggests that these large magnitude rotational corrections are not due to fiducial migration. However, organ deformation may contribute to biases in the rotational corrections included in our analysis, since changes in fiducials’ spacing may lead to the exclusion of certain data if the criteria for accurate rotation corrections are not met.

Target motion amplitudes were found to be strongly correlated with predictor errors but were weakly correlated with correlation errors [26]. In our study, using the peak-to-peak amplitudes of SUP-INF target motion and radial marker motion cannot predict the size of Synchrony errors according to the negligible correlation (multiple correlation r = 0.10). However, most models correlating internal and external marker motions are nearly linear which can be applied to other types of treatment modalities for liver treatments. The results and methodology concerning target motion amplitudes for liver lesions vary among research groups (see review by Langen et al. [5]). Gierga et al. [52] found that the internal liver tumor motion and external marker motions are well correlated with the maximum peak-to-peak SUP-INF motion of 25 mm. This result is consistent with our data but only four liver patients were assessed in their work. Liang et al.[53]’s log file study on SBRT liver patients (N = 14) found the range of liver motions (5% cut off of the inspiration and expiration positions) for their patient population was 5.1–17.3 mm, 0.4–4 mm and 0.9–7.7 mm in the SUP-INF, LT-RT and ANT-POST directions, respectively, which are similar to our findings of 17.5 ± 5.3, 4.0 ± 1.9 and 7.5 ± 3.3 mm in the SUP-INF, LT-RT and ANT-POST directions (peak-to-peak amplitudes), respectively. The large amplitudes of target motion suggest that motion management, such as abdominal compression, gating or active breathing control should be used if these treatments are delivered using conventional LINAC systems.

Conclusions

Our study proposes 4 mm isotropic PTV margins that encompass Synchrony errors and rigid body errors for liver SBRT treatments on CyberKnife. The small intra-patient variations in both Synchrony errors and rigid body errors suggest that customized margins for individuals may be a possibility perhaps based on a dry-run session prior to planning. More patient data (with accurate system calculated rotational corrections) are required to better estimate of the impact of uncorrected rotations. However, this error can be minimized with improved fiducial placement and by taking more care during CT simulation to ensure that the imaging isocenter can be placed as close as possible to the center of fiducials. Linear models correlating internal and external marker motions might be applied to other treatment modalities for liver treatments.

Acknowledgments

The authors kindly thank Lisa Goggin and Fabienne Hirigoyenberry from Accuray Inc. for helpful discussions. Dr. Graham Cook and the clinical CyberKnife team at the Ottawa Hospital Cancer Centre are also acknowledged for support and technical help in this project.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Ontario Consortium for Adaptive Interventions Radiation Oncology [number ORF-RE File #: RE-04-026]; and by a research grant from Accuray Inc., CA.