Impact of NaOH based perfusion-decellularization protocol on mechanical resistance of structural bone allografts

ABSTRACT

Introduction

To mitigate the post-operative complication rates associated with massive bone allografts, tissue engineering techniques have been employed to decellularize entire bones through perfusion with a sequence of solvents. Mechanical assessment was performed in order to compare conventional massive bone allografts and perfusion/decellularized massive bone allografts.

Material and methods

Ten porcine femurs were included. Five were decellularized by perfusion. The remaining 5 were left untreated as the “control” group. Biomechanical testing was conducted on each bone, encompassing five different assessments: screw pull-out, 3-points bending, torsion, compression and Vickers indentation.

Results

Under the experimental conditions of this study, all five destructive tested variables (maximum force until screw pull-out, maximum elongation until screw pull-out, energy to pull out the screw, fracture resistance in flexion and maximum constrain of compression) were statistically significantly superior in the control group. All seven nondestructive variables (Young’s modulus in flexion, Young’s modulus in shear stress, Young’s modulus in compression, Elastic conventional limit in compression, lengthening to rupture in compression, resilience in compression and Vickers Hardness) showed no significant difference.

Discussion

Descriptive statistical results suggest a tendency for the biomechanical characteristics of decellularized bone to decrease compared with the control group. However, statistical inferences demonstrated a slight significant superiority of the control group with destructive mechanical stresses. Nondestructive mechanical tests (within the elastic phase of Young’s modulus) were not significantly different.

KEYWORDS:

• Massive bone allograft
• perfusion-decellularization
• biomechanics
• mechanical assessment

Introduction

In limb salvage surgery, massive bone allografts remain remarkable tools for biological reconstruction across various conditions like oncology, infections, trauma, or malformations. These allografts, sourced from tissue banks, offer readily available untreated grafts^1–3 without requiring immunosuppressive therapy for patients. However, post-operative complications, including non-unions, infections, fractures, or resorptions, are commonly reported in the literature^4–7 possibly attributed to immune response to these untreated grafts.

Our team has developed a comprehensive perfusion protocol for decellularizing porcine massive bone allografts^8,9. Following precise perfusion and immersion sequences, acetone, sodium hydroxide and hydrogen peroxide are used in turn to, respectively, precipitate fats, dehydrate and initiate degradation of cell membranes; destroy cell membranes in depth with a basic solution; complete decellularization and ensure prion elimination through the action of free radicals. Inspired by clinical protocols for bone material filling, our aim is to create better biologically integrated massive bone allografts with reduced post-operative complications.

Indeed, while the solvents utilized in our protocol facilitate effective decellularization and diminish the immunogenicity of future bone grafts, they also pose certain drawbacks. Their aggressive chemical composition can lead to degradation of the extracellular matrix. Acetone, for instance, acts as a potent dehydrating agent and may exhibit relative corrosiveness when applied to soft tissues. Furthermore, protein denaturation, akin to that induced by sodium hydroxide, is a known consequence¹⁰. Additionally, hydrogen peroxide, while effective, may have a mild demineralizing effect on the bone surface, potentially impacting its mechanical properties¹¹. Although the adverse biological effects of these solvents have been documented⁹, a biomechanical perspective is presently lacking—an essential consideration in the pursuit of a novel generation of massive bone allografts.

Biomechanical studies have extensively explored the properties of healthy, pathological, and animal bones^12–17, including investigations into decellularized bone filling materials^11,18,19. Presently, only two preliminary studies from our team focused on the mechanical properties of perfusion-decellularized porcine forearms with only one examining the NaOH-based perfusion-decellularization process^8,20.

Perfusion-decellularization has been extensively studied in various organ systems, but its application to bone remains relatively unexplored. Despite the crucial role of bone’s mechanical properties in developing structural grafts capable of withstanding stress, literature in this area is limited. The utilization of a NaOH protocol for perfusion-decellularization of porcine femurs represents a novel approach, with no prior mechanical testing conducted on such massive bone allografts.

Given the lack of established quality standards or comparative studies, our objective is to quantify the extent of mechanical property degradation in decellularized porcine bone compared to untreated native porcine bone. Previous researches studying mechanical capacities of human cancellous bone decellularized (called “defatting”) by detergents baths showed no statistically significant difference when compared to fresh frozen cancellous bone^19,21,22. However, due to differences in methodologies and materials, caution must be exercised when comparing these findings.

Since massive bone allografts are commonly implanted without prior treatment, direct comparison of our decellularized porcine femurs with untreated porcine femurs is appropriate. Additionally, we will establish an acceptable degradation threshold based on physiological loading conditions, specifically the elastic phase of the Young’s modulus, experienced by bones of the corresponding animal weight. If a treated bone fractures within the expected physiological range for its weight (500–700 N), it suggests that the decellularization protocol may be excessively aggressive, rendering it unsuitable for clinical use.

This study aims to assess the mechanical characteristics of massive bone allografts decellularized by perfusion using the same protocol as in our previous study⁹. We chose the femur model due to its ease of perfusion control^9,20 and its relevance for future in vivo assessments. Our primary goal was to assess the potential impact of our NaOH-based perfusion-decellularization protocol on the bone extracellular matrix, comparing treated and untreated porcine femurs¹¹. Ultimately, we aim to determine the mechanical capacities of perfusion-decellularized porcine femurs compared to native untreated porcine femurs, within the physiological range or maximum weight load of their mechanical constraints, to inform potential human applications.

Material and methods

Ten porcine femurs from 5 Belgian Landrace pigs were utilized in this study. All the pigs were adult females weighing between 50 and 70 kg (500 – 700N). The experimental protocol received approval from the local ethics committee (number 2020/UCL/MD/027 and A1/UCL/2021-A1, Comité d’Ethique de Bruxelles, Belgium).

Unfortunately, the existing literature did not provide the basis for conducting a power calculation to determine a sample size sufficient for achieving statistical significance. Given the novelty of this method, no prior scientific studies had investigated this procedure on pig femurs. Consequently, we empirically determined the sample size, selecting 5 animals, resulting in a total of 10 femurs tested, based on the availability of animals.

All animals were sedated with an intramuscular injection of Rompun-Zoletil (2 mg/kg and 6 mg/kg) and anesthesia was maintained with isoflurane gas. Euthanasia was performed with an intravenous injection of T61 (1 ml/5 kg).

The femurs were carefully harvested and dissected, preserving their nutrient arteries. The bones were then perfused with warm (37°C) heparinized physiological fluid (25.000 I.U.) to thoroughly cleanse the bone vascular network of all blood material⁹.

Conditioning

Half of the harvested femurs (N = 5), forming the “decellularized” group, underwent a NaOH-based decellularization protocol detailed in a previous study Figure 1(a)⁹. To achieve effective decellularization, mimicking the physiological flow of bone perfusion was not deemed a crucial requirement. Moreover, mammalian bone perfusion typically involves terminal perfusion, resulting in minimal variation in perfusion flow. In our protocol, consistent parameters were maintained across experiments: the perfusion rate, total perfusion time, and solvent concentrations remained constant from one experiment to the next. During the decellularization steps (pure acetone, pure sodium hydroxide, and 7,5% hydrogen peroxide solution), the average perfusion rate was 7 ml/min, while during rinsing phases, it was 5 ml/min. Due to the microscopic, branched, and random organization of the bone venous return to the metaphysis, no backflow was monitored. The entire decellularization protocol spanned a duration of 7 days.

Figure 1. Cutting steps. A: Decellularized and control pair. Dots on bones show section planes. Decellularized samples are shown with an asterisk. B: Band saw cutting. C: Polishing phase. D: Final samples for each test, S + I = Screw pull-out + Indent; B = 3-points bending; T= torsion; C= Compression.

The other half of the harvested femurs was allocated as the “control” group. Femurs (left and right) from the same animal were randomly allocated, each to a different group. Both control and decellularized bones were all preserved at −80 °C before mechanical testing. The entire protocol was carried out under the same temperature (room temperature, 20°C), humidity (40%) and pressure conditions (atmospheric pressure).

Each bone underwent a rigorous cutting protocol. To ensure comparable experimental conditions between each sample, each bone was cut and refrozen within one hour. The bones were cut using a diamond band saw (Exakt Technologies®, Exakt 310CP, Oklahoma City, USA) following a template designed for conducting all mechanical tests on the same bone Figure 1(b–d). A polishing phase ensured that the dimensions between each sample of every bone were as similar as possible Figure 1(c). They were furthermore sized using CT acquisitions (Siemens Definition AS, 128 detectors) while being maintained at a temperature of −80 °C. These measurements facilitated data normalization. As the mechanical tests were carried out on diaphyseal bone segments, mimicking massive intercalary bone allograft, no extrapolation on cancellous or metaphyseal bone tissue is possible.

Screw pull-out

The screw pull-out test was conducted twice on each bone (S1 and S2). Those two measurements were averaged to enhance precision. We drilled a 2.5 mm hole into the cortex to accommodate a standard stainless steel 3.5 mm cortical screw (Depuy-Synthes®, Figure 2(b). A drilling guide was 3D-printed to ensure a perpendicular axis and comparable position for each screw pull-out test Figure 2(a).

Figure 2. Screw pull-out test. A: Sample drilling with a 3D-printed guide. The asterisk shows the tested bone sample. B: Image of a 3.5 mm cortical screw inserted in the sample. C: Installation. The arrow shows the head of the screw sliding into the dedicated clamp. D: During the test, the bone is fixed by nuts. The arrow shows the rupture of the bone.

All screws were allowed to protruded through the cortex. A custom-made connection clamp was created to attach the screw head to the traction-compression machine (Zwick Roell, type BZ2-MM480×x.EC01, Germany) Figure 2(c). The bone was clamped flat by metal rods fastened by nuts Figure 2(d). Raw measurements were obtained in simple vertical traction and three variables were recorded: maximum force until pull-out (N), maximum lengthening until pull-out (mm) and extraction energy required for complete pull-out (J). This last variable is represented by the area under the curve (AUC) of the force-displacement curve. It is calculated through numerical integration using the trapezoidal method (Supplementary data, Figure S1).

Three-points bending test

The three-points bending test (B), also known as the flexion test, was carried out on a rectangular cortical strip. We extrapolated the geometric shape for our mathematical calculations, introducing a method that, while diminishing the precision of our conclusions, ensured maximum comparability between samples Figure 3(c). This test was executed using the same machine employed for the screw pull-out test. The sample was placed on two metal rods and a third sharper rod applied pressure to the center of the sample until fracture occurred Figures 3(a,b). Raw measurements were analyzed under simple vertical compression and two variables were documented: Young’s modulus in flexion (MPa) and resistance in flexion (MPa). The equations utilized for the first variable, following ISO 178, are as follows: F represents force (N), L denotes the distance between the two support rods (mm), b signifies the section base (mm), h indicates the height of the section (mm), and s represents deflection (mm). The resistance in flexion corresponds to the highest point on the curve, which is the point of maximum constraint.

${\sigma }_{\mathit{flexion}}=\frac{3\ast \mathit{F}\ast \mathit{L}}{2\ast b\ast h^2}$

${\epsilon }_{\mathit{flexion}}=\frac{600\ast \mathit{s}\ast \mathit{h}}{\mathit{L}}$

Figure 3. Three points bending test. A: Pre-loading image of the sample marked by an asterisk. B: Loading of the sample before fracture. C: Extrapolation of the model for the mathematical results. 1 = actual dimension of the sample, 2 = the rectangular volume chosen for the mathematical operation.

Torsion

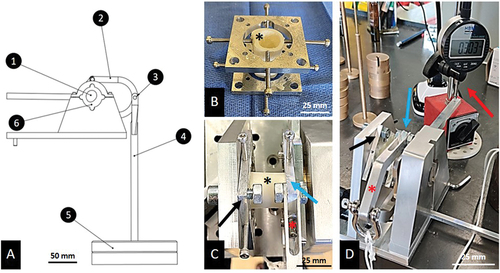
A custom-made torsiometer was specially designed and machined for the experiment Figure 4(a). This provides control over the ideal dimensions of this torsiometer for our samples. The torsiometer was employed primarily for comparing different groups, ensuring consistency by utilizing the same machine. The tool’s measurement reproducibility was validated using 3D printed samples. Each sample was placed in the rotating part. It was centered and locked by 8 clamping screws (four above and four below) Figure 4(b). Each clamping screw was tightened with a torque screwdriver to 0.3 Nm. Subsequently, the sample was placed in the torsiometer Figure 4(c). 100 g loads were progressively added to the end of the rotating part. Through the distributor, the displacement of the end of the rod measured by an infra-millimetric digital gauge Figure 4(d) allows to acquire the shear’s modulus according to the next formula where G is the shear’s modulus (MPa), dl is the length of the lever (mm), [p*g*cos$(\mathit{\phi }$)] is the perpendicular force to the earth surface (N) (considering the angle of torsion $\mathit{\phi }$, the weight p and the gravitational force g), L is the length of the measurement arm (mm), x is the vertical displacement (mm), l is the sample length (mm), D is the average outside diameter of the sample and d is the average inside diameter of the sample.

$\mathit{G}=\frac{\mathit{dl}\times \mathit{p}\times \mathit{g}\times \cos \left(\phi \right)}{\frac{arctan\left(\frac{x}{L}\right)}{\mathit{l}}\times \frac{\pi }{32}\times \left(D^4-d^4\right)}$

Figure 4. Torsion test. A: Designing and prototyping of the custom-made torsiometer. 1=sample; 2=distributor; 3= point of transformation from a rotative movement to a linear movement; 4= weights holder; 5 = 100 g load; 6= screws area. B: Centering and fixation of the sample. The black asterisks show the bone samples. C: inside the torsiometer, black arrows show the fixed side of the element, blue arrows show the rotating side of the element. D: Complete set-up during experiment. Red asterisks show the distributor and red arrow shows the infra-millimetric gauge measuring displacement at the very end of the lever arm.

This mathematical formula considers the concepts of the polar inertia of a hollow cylinder²³ and Hooke’s law of torsional momentum²⁴. The general uncertainty can be expressed using the following formula.

$\frac{\mathrm{\Delta }G}{G}=\left(\frac{\mathrm{\Delta }M}{M}+\frac{\mathrm{\Delta }\theta }{\theta }+\frac{\mathrm{\Delta }{\mathit{I}}_{0,\mathit{rot}}}{I_{0,\mathit{rot}}}\right)\approx 4\mathrm{\%}$

It is crucial to consider the uncertainty associated with sample centering, a factor addressed by the König-Huygens theorem²⁵ (Illustrated in the Supplementary data, figure A3). This acknowledgment of sample centering uncertainty, guided by the König-Huygens theorem, adds a layer of precision to our experimental considerations. In addition, for a comprehensive understanding of the mechanical principles underlying torsion deformation, the reader is referred to the mechanical physics formulas provided in Supplementary data (refer to Figure A2).

Compression

The samples (cortical rings) were carefully sanded to ensure parallel and flat surfaces in order to distribute the compression loads as evenly as possible over the sample Figure 5(a). The mobile plate of the compression machine was fitted with a free ball joint to adapt the position of the plate Figure 5(b). Raw measurements were recorded in simple vertical compression and five variables were documented: Young’s modulus (MPa), calculated following the formula (ASTM E111):

$\mathit{E}=\frac{{\mathit{\sigma }}_{\mathit{II}}-{\sigma }_I}{{\epsilon }_{\mathit{II}}-{\epsilon }_I}$

Figure 5. Compression test. A: Pre-loading sample. B: Loaded sample after fracture occurrence. Subtle fracture lines are pointed out by white arrows. C: Transversal CT-scan acquisition of post-compression test showing fracture lines (white arrows). D: Axial CT-scan acquisition of post-compression test showing fracture lines (white arrows).

With $\left({\epsilon }_I;{\sigma }_I\right)$ and $\left({\epsilon }_{\mathit{II}};{\sigma }_{\mathit{II}}\right)$ as points in the elastic phase. (see Supplementary data for basic theory).

Elastic conventional limit (MPa) is defined as the mathematical limit between the elastic phase and the plastic phase of Young’s stress-strain curve. Its value can be obtained by the next formula (ASTM E9):

${\sigma }_{\mathit{e},0.2\mathrm{\%}}={\sigma }_0+\mathit{E}\times \left(\mathit{\epsilon }-0,002\right)$

Maximum constrains (MPa), signified as the pressure where the sample breaks; lengthening to rupture (mm); as the lengthening of the bone sample before breaking and resilience (J); as the amount of total energy needed to break the sample, calculated following the numerical integration (see Supplementary data).

Unlike the torsion test, compression test is a destructive test. In doing so, it was interesting to scan the samples after compression in order to compare the fracture pattern of control bones with decellularized bones Figures 5(c,d).

Vickers hardness

Vickers hardness measurement is a reliable index for the comprehensive study of materials. To ensure robust results, we conducted 10 acquisitions per sample, subsequently averaging them for greater precision. The examination took place within the cortical thickness of the samples at a consistent cortical height Figure 6(a). To do this, each hemi-cortex that had undergone screw pull-out test was embedded in epoxy resin in a precise position Figure 6(b). This position exposes the surface to be tested to the indentation Vickers hardness machine (Emco-test®, DuraJet G5, Salzburg, Austria). Vickers hardness or Hardness value (HV) correlates to the depth to which a punch penetrates a material with a given force Figure 6(c). The determination of the Vickers unit involves a straightforward geometric relationship between diagonals on an indentation image, as illustrated in the following formula (ISO 6507):

$\mathit{HV}=\frac{2\times \mathit{F}\times \sin \left(\frac{{136}^{\circ }}{2}\right)}{9.80665\times d^2}$

Figure 6. Vickers hardness test. A: Medullary view of a sample after screw pull-out. Red rectangles show the cut plane where the indent will be performed. White asterisk shows the screw mark. B: Embedded samples exposing the cut plane. C: microscopic view of a punch on a bone surface.

Where F is the force applied by the machine (N) and d is the mean of the indentation’s diagonals (mm).

Statistical analysis

Descriptive statistics for each test were performed. Considering bone laterality, femurs obtained from the same animal were randomly distributed into distinct groups (control or decellularized). Despite originating from the same animal, paired samples inference tests were not conducted due to the nature of our experimental design. While efforts were made to select bones that were as similar as possible, variations in skeletal morphology within each individual could not be controlled. Plus, it’s important to note that paired samples inferences are applicable when the same sample is tested both before and after the event under evaluation, which does not align with our experimental setup. To assess the normality of our sample distribution, Shapiro-Wilk tests were performed, which are suitable for small sample sizes (N = 5)^26,27. In cases where normality was rejected, statistical inferences were derived using the non-parametric Mann-Whitney test. Conversely, when normality was confirmed, statistical analyses were conducted using independent T-tests. Levene’s test was consistently employed to verify the equality of variances for independent T-tests. In our next experiments, t-tests were performed for 11 of the 12 items for which a normality distribution was confirmed and a Mann-Whitney test was performed only for the one item “energy required for screw extraction” determined to be non-normal. All statistical manipulations were performed using IBM SPSS software (V.27, SPSS, Inc., Chicago, IL, USA). As we expected to observe a decrease in the mechanical properties of the decellularized bones, our statistical inferences were interpreted as a single-tail trial and the statistical significance threshold was set for p-values less than 0.05.

Results

Screw pull-out

Descriptive statistics are listed in Table 1. Notably, the central values exhibit clear distinctions, while the distribution values appear relatively similar. Figure 7 provides box plots for each variable.

Figure 7. Boxplots of the 12 measured variables during the 5 mechanical tests. S: boxplots from the screw pull-out test. B: boxplots from the 3-points bending test. T: boxplot from the torsion test. C: boxplots from the compression test. I: boxplot from the indentation/Vickers test. * = Lightly significant; ns = not significant.

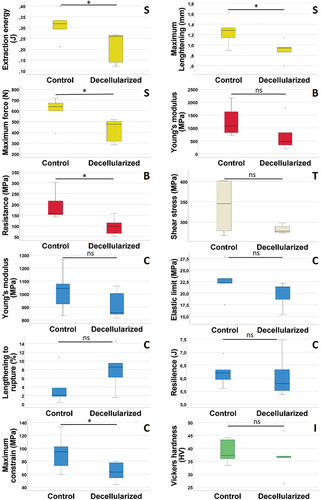
Table 1. Descriptive statistics of the variables from the screw pull-out test.

Variable	Treatment	Mean	Standard deviation	95% IC	Variance	Range
Maximum force (N)	Control	602.31	128.21	443.11–761.50	16437.72	330.06
	Decellularized	419.76	110.23	282.90–556.63	12150.09	235.64
Maximum Lengthening (mm)	Control	1.25	0.27	0.92–1.59	0.07	0.73
	Decellularized	0.90	0.20	0.65–1.15	0.04	0.55
Extraction energy (J)	Control	0.31	0.07	0.23–0.39	0.01	0.19
	Decellularized	0.21	0.07	0.12–0.30	0.01	0.14

For the maximum force to pull out a screw test (Shapiro p-values = 0.20 and 0.15 for control and decellularized groups respectively), t-test was slightly, yet significantly, higher in the control group compared to the decellularized group (p-value = 0.021). For the maximum elongation for screw removal (Shapiro p-values = 0.96 and 0.71 for control and decellularized groups respectively), t-test was slightly significantly higher in the control group compared with the decellularized group (p-value = 0.022). For the energy required to extract the screws (Shapiro p-values = 0.90 and 0.03 for control and decellularized groups respectively), Mann-Whitney statistical inference was slightly but significantly higher in the control group compared to the decellularized group (p-value = 0.028).

Three-points bending

Table 2 provides descriptive statistics for the two variables. While the values of dispersion for both variables appear relatively similar but the disparity in central tendencies may impact the overall interpretation of the dataset. As before, a box-plot per variable was carried out and can be seen in Figure 7.

Table 2. Descriptive statistics of the variables from the 3-points bending test.

Variable	Treatment	Mean	Standard deviation	95% IC	Variance	Range
Young’s modulus (MPa)	Control	1281.57	603.07	532.76–2030.39	363697.40	1435.90
	Decellularized	724.96	632.08	−59.86–1509.79	399520.45	1575.61
Resistance (MPa)	Control	194.52	67.08	111.22–277.82	4500.46	160.11
	Decellularized	98.11	42.37	45.5–150.72	1795.25	107.29

For the Young’s modulus for the flexion (Shapiro p-values = 0.45 and 0.18 for control and decellularized groups respectively), t-test was not significantly higher in the control group compared with the decellularized group (p-value = 0.081). However, for the resistance before fracture (Shapiro p-values = 0.13 and 0.83 for control and decellularized groups respectively), t-test was slightly, yet significantly, higher in the control group compared with the decellularized group (p-value = 0.013).

Torsion

Unfortunately, during our first torsion test, the two first bones were damaged before the torsion was applied and had to be removed from the series. Descriptive statistics of this variable are listed in Table 3. Central values seem quite similar in both groups but the dispersion values are very broad. Interestingly, it is the control group that shows broader dispersion. Figure 7 shows the torsion box-plot.

Table 3. Descriptive statistics of the Shear’s modulus from the torsion test.

Variable	Treatment	Mean	Standard deviation	95% IC	Variance	Range
Shear’s modulus (MPa)	Control	339.56	71.58	225.67–453.46	5123.21	135.24
	Decellularized	280.95	11.46	262.71–299.19	131.40	25.30

The shear’s modulus from rotational constrains (Shapiro p-values = 0.11 and 0.15 for control and decellularized groups respectively) showed a t-test that was not significantly higher in the control group compared with the decellularized group (p-value = 0.100).

Compression

Descriptive statistics of the variables are listed in Table 4. All central tendencies and dispersion values seem well comparable to one another. These descriptive statistics are represented by five box-plots in Figure 7.

Table 4. Descriptive statistics of the variables from the compression test.

Variable	Treatment	Mean	Standard deviation	95% IC	Variance	Range
Young’s modulus (MPa)	Control	1028.46	163.55	825.39–1231.54	26746.19	429.80
	Decellularized	916.40	109.25	780.74–1052.05	11936.50	245.94
Elastic limit (MPa)	Control	22.60	3.67	18.04–27.16	13.49	10.32
	Decellularized	19.79	2.81	16.30–23.28	7.92	6.81
Maximum constrain (MPa)	Control	92.60	28.53	57.18–128.03	813.95	74.13
	Decellularized	63.87	15.31	44.85–82.88	234.42	35.98
Maximum lengthening (mm)	Control	3.75	4.11	−1.35–8.85	16.86	10.39
	Decellularized	8.06	4.72	2.20–13.92	22.29	12.92
Resilience (J)	Control	6.21	0.50	5.59–6.82	0.25	1.34
	Decellularized	6.10	0.85	5.04–7.16	0.73	2.11

For the Young’s modulus (Shapiro p-values = 0.91 and 0.21 for control and decellularized groups respectively), t-test was not significantly higher in the control group compared with the decellularized group (p-value = 0.119). For the elastic limit (Shapiro p-values = 0.64 and 0.19 for control and decellularized groups respectively), t-test was not significantly higher in the control group compared with the decellularized group (p-value = 0.106). For the maximum constrain of compression (Shapiro p-values = 0.91 and 0.61 for control and decellularized groups respectively), t-test was slightly significantly higher in the control group compared with the decellularized group (p-value = 0.041). For the maximum lengthening before a fracture occurs (Shapiro p-values = 0.09 and 0.96 for control and decellularized groups respectively), t-test was not significantly higher in the control group compared with the decellularized group (p-value = 0.081). Finally, for the resilience, or the needed energy to break a bone through compression (Shapiro p-values = 0.89 and 0.28 for control and decellularized groups respectively) t-test was not significantly higher in the control group compared with the decellularized group (p-value = 0.407).

Vickers hardness

Descriptive statistics of this variable are listed in Table 5. This test shows very good stability of the values. One box-plot from the Figure 7 shows this dispersion and central tendency with the conclusion of the statistical inference.

Table 5. Descriptive statistics of the Hardness Value from the Indentation/Vickers test.

Variable	Treatment	Mean	Standard deviation	95% IC	Variance	Range
Hardness Value (HV)	Control	38.82	4.72	32.96–44.68	22.27	10.81
	Decellularized	36.68	7.24	27.68–45.67	52.48	20.48

The Vickers index from microscopic indentations (Shapiro p-values = 0.41 and 0.41 for control and decellularized groups respectively) showed a t-test that was not significantly higher in the control group compared with the decellularized group (p-value = 0.297).

Discussion

In these experiments, we undertook a comparison between untreated and decellularized porcine bones to assess their mechanical properties. The treated bones were decellularized by perfusion using a previously described method⁹. Twelve variables were measured through five mechanical tests. Due to the aggressive nature of the solvents utilized in the decellularization protocol, our initial expectation was a notable reduction in the mechanical properties of the bones¹¹. We therefore decided to carry out our statistical inferences in a single-tail trial. Under the experimental conditions of this study, all destructive test items were statistically significantly superior in the non-treated group, but no significant differences were demonstrated for the nondestructive test items.

Our descriptive statistical studies of the central tendency seem to support our initial hypotheses. In fact, we can see a clear difference in the central tendencies when evaluating loading up to fracture (e.g., maximum lengthening, maximum constrain, maximum force, resistance). However, for tests that were less destructive and assessed bone mechanical behavior within an elastic deformation zone (physiologically relevant working zone), central tendency measures appeared more comparable between the control and decellularized groups.

Interpretation of variability measurements poses challenges, likely attributable to the limited number of samples per group. It should also be noted that the central tendency of a single variable seemed to show a superiority of decellularized bone. Indeed, the maximum compression lengthening (or lengthening to rupture) was on average much higher in the decellularized group.

Our statistical inferences demonstrated a significant mechanical superiority of untreated control bone in only 5 of the 12 variables. This was minimal in each case.

An important aspect of this research is that the variables showing a significant superiority of control bones compared to decellularized ones are all fracture parameters (extreme loading) as described for descriptive statistics discussion. Notably, these differences become apparent when the stress on the material reaches its maximum, occurring before the material failure. In our experimental setup, these peak stresses far exceeded the physiological bone load/stress range, or elastic phase corresponding to the maximum weight loading onto the bone (500 to 700 Newtons considering our pig models). It is essential to emphasize that these maximum rupture constraints, such as those observed in screw pull-out tests or bending fracture resistance, surpass both the elastic and plastic phases of the materials. An important consideration for the long-term functionality of bones is their ability to operate within the elastic phase^28,29.

According to our inferential tests, the variables showing no significant superiority of the control group were mainly nondestructive variables such as the Vickers test, the torsion test and the limit of elasticity in compression. This observation also supports the hypothesis that the mechanical properties of decellularized bone are preserved while supporting maximal physiological weight (corresponding to the nondestructive area of the Young’s modulus curve, the elastic phase).

It should be added that the resilience test is a surface calculation rather than a linear measurement, contributing to its enhanced accuracy. The conclusion of this last test is probably also one of the most important conclusions of this work: even up to fracture, the total energy required to break a decellularized bone during compression shows no statistical difference compared to the total energy required to break a control bone. This variable analyses the boundary between the elastic and the plastic phase. It is a measure taken at the upper limit of the physiological range in which a bone typically operates³⁰. This elastic limit variable shows a p-value of 0.106. This supports the hypothesis that non-treated bone exhibits no statistically significant superiority of their elastic phase from their Young’s modulus. As a matter of fact, since the resilience and the elastic limit showed no difference between the two groups, we may extrapolate that the major modifications in the bone tissue after decellularization impact intrinsically the plastic phase rather than the elastic phase. This nuanced understanding underscores the specific conditions under which differences in mechanical properties are evident and emphasizes the robustness of decellularized bone within the physiologically weight-relevant stress range.

Numerous studies in the literature have delved into the mechanical properties of bone tissue^19,31–38. Studies have also been carried out on porcine bone tissue^14,39. Interestingly, there are several bone treatment techniques with current clinical application that are known to have a detrimental effect on the mechanical properties of bone allografts. For instance, irradiating freeze-dried allograft has a negative synergistic effect on the graft resistance¹⁹. While this topic is still debated, the effect of irradiation alone on massive bone allografts remains controversial⁴⁰ but seems to be dose dependent⁴¹. This technique is nevertheless in clinical application using irradiation under cold temperatures which seems to offer some protection to the graft structural resistance⁴². This recent literature confirms the detrimental effect of a sterilization treatment but nonetheless supports its application on bone allografts. Indeed, the mechanical resistance loss is an accepted side effect of the treatment. Surgeons routinely consider this known factor in their reconstruction plans, emphasizing the delicate balance between achieving sterility and preserving the mechanical integrity of bone allografts. As a small mechanical strength loss is acceptable (e.g., after irradiation) and massive bone allografts are being harvested and implanted without any irradiation or freeze-dry process, the smallest substantial mechanical loss caused by decellularization—and described in this paper—can also be acceptable.

Furthermore, our NaOH-based perfusion-decellularization protocol is an original procedure using the intrinsic vascular network of bone. Very few articles have been published on this subject. Our team has recently published two studies regarding these decellularization techniques in which several different protocols were compared on porcine forearm bone models^8,20. DePaula et al. are one of the few teams to have tested the unique effect of hydrogen peroxide on the mechanical capacity of bone grafts¹¹. According to them, a slight demineralization of the surface can be observed when the bone is in contact with this solvent. This may lead to a possible loss of overall mechanical strength of the graft. In the future, our teams will be carrying out biochemical studies to assess collagen cross-linking in the extra-cellular matrix following decellularization.

This study stands out for its originality, particularly in its exclusive focus on a specific decellularization protocol selected for the assessment of decellularized allografts. Additionally, the development of a femoral bone model was undertaken, chosen for its adaptability to our diverse array of tests. A notable addition to our test repertoire is the inclusion of a torsion test, further enhancing the scope of our investigations. This unique approach allows us to provide novel insights into the mechanical properties of decellularized allografts.

The first identified limitation is the number of samples tested with 5 samples per group. However, we have tried to minimize this bias in several ways. Firstly, by performing duplicates of certain tests, such as the screw pull-off and indentation tests; this allows us to refine the precision of our results by averaging these acquisitions. Secondly, to further increase the reliability of our results, these statistical tests were carried out in “single tail.” Given the limited cohort size of 5 samples per group, there exists a potential risk of observing differences not solely attributable to the perfusion-decellularization process but rather to inherent inter-sample variability. To mitigate this risk, we employed several strategies. Firstly, we sourced femurs from female Landrace pigs of identical age and weight, ensuring uniformity within the study population. Secondly, we implemented a meticulous protocol for sample preparation, including precise cutting using diamond saw and polishing techniques, which were strictly adhered to. Additionally, we standardized the morphology of the samples using medical imaging, thereby minimizing the likelihood of inter-sample variability. Despite the originality of this research and the interesting results, a larger cohort would increase the certainty of our conclusions.

The second limitation is the absence of a cyclic fatigue test. Our discussion is based on the fact that the mechanical characteristics of the two groups may not differ as long as the mechanical stress remains within a physiological range, i.e., within the range of the elastic phase of the bone. The test best suited to verify this last assertion would be a fatigue test, which mimics walking cycles with physiological loads. Unfortunately, logistical constraints prevented the implementation of this test in our laboratory.

Lastly, all our tests were carried out under non-physiological conditions of temperature and humidity. Bone is like all human biological tissues at 37 °C and 99% humidity in normal physiological conditions. For less mineralized tissues such as blood vessels or tendons, this condition is crucial for any test because inter-sample variability can be greatly modified by experimental conditions^43,44. For bone tissue however, it is implicitly accepted, as literature shows, that it can be tested outside physiological conditions because of its high mineral composition and very low elasticity and viscosity^12,17,39,45. Furthermore, all samples were tested and compared in the same experimental conditions.

Based on those results, a preclinical feasibility study on human bone allograft was approved by our ethical comity. The same perfusion-decellularization protocol will be submitted to human bones and the same biological and mechanical in vitro assessments will be carried out in order to confirm our results in the pig’s model and be able to clinically implement this type of allografts to humans. In that aspect, we would like to include a cyclic fatigue test to be as exhaustive as possible.

This study aimed to characterize the impact of our decellularization by perfusion protocol on the mechanical properties of massive bone allografts. Our results compellingly demonstrate that our decellularization protocol does not compromise the mechanical qualities of the bone as long as the stress respect the maximum physiologic weight the studied bones should support. This, in conjunction with the biological characterization of massive bone allografts decellularized by perfusion, not only supports the initiation of preclinical in vivo testing but also lays the groundwork for subsequent preclinical in vitro studies on human bone allografts. These steps represent significant progress toward clinical translation, with the ultimate goal of enhancing the outcomes of limb salvage surgery through the improvement of massive bone allografts.

Authors contribution statement

Robin Evrard, Maxendre Feyens and Julie Manon contributed to research design, acquisition, analysis and interpretation of data. Robin Evrard contributed to drafting the paper. Benoit Lengelé, Olivier Cartiaux and Thomas Schubert equally contributed to revising the paper critically, to approving the submitted and final versions.

All authors have read and approved the final submitted manuscript

Acknowledgment

Two authors are Research Aspirants (PhD students) of the FNRS (Fonds de la Recherche Scientifique, Applications ID 40010491 and ID 40004991 respectively, Belgium). The work was performed in the Université Catholique de Louvain (UCL), Brussels, Belgium.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/03008207.2024.2356586

Additional information

Funding

Two authors are Research Aspirants (PhD students) of the FNRS (Fonds de la Recherche Scientifique, Applications ID 40010491 and ID 40004991 respectively, Belgium). The authors did not receive any money from any specific funds.