?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.ABSTRACT
This paper derives predictive reduced-order models for rocket engine combustion dynamics via Operator Inference, a scientific machine learning approach that blends data-driven learning with physics-based modelling. The non-intrusive nature of the approach enables variable transformations that expose system structure. The specific contribution of this paper is to advance the formulation robustness and algorithmic scalability of the Operator Inference approach. Regularisation is introduced to the formulation to avoid over-fitting. The task of determining an optimal regularisation is posed as an optimisation problem that balances training error and stability of long-time integration dynamics. A scalable algorithm and open-source implementation are presented, then demonstrated for a single-injector rocket combustion example. This example exhibits rich dynamics that are difficult to capture with state-of-the-art reduced models. With appropriate regularisation and an informed selection of learning variables, the reduced-order models exhibit high accuracy in re-predicting the training regime and acceptable accuracy in predicting future dynamics, while achieving close to a million times speedup in computational cost. When compared to a state-of-the-art model reduction method, the Operator Inference models provide the same or better accuracy at approximately one thousandth of the computational cost.
Introduction
The emerging field of scientific machine learning brings together the perspectives of physics-based modelling and data-driven learning. In the field of fluid dynamics, physics-based modelling and simulation have played a critical role in advancing scientific discovery and driving engineering innovation in domains as diverse as biomedical engineering (Yin et al. Citation2010; Nordsletten et al. Citation2011), geothermal modelling (O'Sullivan et al. Citation2001; Cui et al. Citation2011), and aerospace (Spalart and Venkatakrishnan Citation2016). These advances are based on decades of mathematical and algorithmic developments in computational fluid dynamics (CFD). Scientific machine learning builds upon these rigorous physics-based foundations while seeking to exploit the flexibility and expressive modelling capabilities of machine learning (Baker et al. Citation2019). This paper presents a scientific machine learning approach that blends data-driven learning with the theoretical foundations of physics-based model reduction. This creates the capability to learn predictive reduced-order models (ROMs) that provide approximate predictions of complex physical phenomena while exhibiting several orders of magnitude computational speedup over CFD.
Projection-based model reduction considers the class of problems for which the governing equations are known and for which we have a high-fidelity (e.g. CFD) model (Antoulas Citation2005; Benner et al. Citation2015). The goal is to derive a ROM that has lower complexity and yields accurate solutions with reduced computation time. Projection-based approaches define a low-dimensional manifold on which the dominant dynamics evolve. This manifold may be defined as a function of the operators of the high-fidelity model, as in interpolatory methods that employ a Krylov subspace (Bai Citation2002; Freund Citation2003), or it may be determined empirically from representative high-fidelity simulation data, as in the proper orthogonal decomposition (POD) (Lumley Citation1967; Sirovich Citation1987; Berkooz et al. Citation1993). The POD has been particularly successful in fluid dynamics, dating back to the early applications in unsteady flows and turbulence modelling (Sirovich Citation1987; Deane et al. Citation1991; Gatski and Glauser Citation1992), and in unsteady fluid-structure interaction (Dowell and Hall Citation2001).
Model reduction methods have advanced to include error estimation (Veroy et al. Citation2003; Grepl and Patera Citation2005; Veroy and Patera Citation2005; Rozza et al. Citation2008) and to address parametric and nonlinear problems (Barrault et al. Citation2004; Astrid et al. Citation2008; Chaturantabut and Sorensen Citation2010; Carlberg et al. Citation2013), yet the intrusive nature of the methods has limited their impact in practical applications. When legacy or commercial codes are used, as is often the case for CFD applications, it can be difficult or impossible to implement classical projection-based model reduction. Black-box surrogate modelling instead derives the ROM by fitting to simulation data; such methods include response surfaces and Gaussian process models, long used in engineering, as well as machine learning surrogate models. These methods are powerful and often yield good results, but since the approximations are based on generic data-fit representations, they are not equipped with the guarantees (e.g. stability guarantees, error estimators) that accompany projection-based ROMs. Nonlinear system identification techniques seek to illuminate the black box by discovering the underlying physics of a system from data (Brunton et al. Citation2016). However, when the governing dynamics are known and simulation data are available, reduced models may be directly tailored to the specific dynamics without access to the details of the large-scale CFD code.
This paper presents a non-intrusive alternative to black-box surrogate modelling. We use the Operator Inference method of Peherstorfer and Willcox (Citation2016) to learn a ROM from simulation data; the structure of the ROM is defined by known governing equations combined with the theory of projection-based model reduction. Our approach may be termed ‘glass-box modelling’, which we define as the situation where the form of the targeted dynamics is known (here via the partial differential equations that define the problem of interest), but we do not have internal access to the CFD code that produces the simulation data. That is, we know what dynamics to expect, but we may only calibrate our models using outputs of the full-order CFD model. This glass-box setting is in contrast to black-box modelling approaches which do not exploit knowledge of the governing equations. We build on our prior work in Swischuk et al. (Citation2020) by formally introducing regularisation to the Operator Inference approach. Regularisation is critical to avoid overfitting for problems with complex dynamics, as is the case for the combustion example considered here. A second contribution of this paper is a scalable implementation of the approach, which is available via an open-source implementation.
Methodology
This section begins with an overview of the Operator Inference approach. We then augment Operator Inference with a new regularisation formulation, posed as an optimisation problem, and present a complete algorithm for regularisation selection and model learning. The section concludes with a scalable implementation of the algorithm, which can then be applied to CFD problems of high dimension.
Operator Inference
We target problems governed by systems of nonlinear partial differential equations. Consider the governing equations of the system of interest written, after spatial discretisation, in semi-discrete form
(1)
(1) where
is the state vector discretised over n spatial points at time t,
denotes the m inputs at time t, typically related to boundary conditions or forcing terms,
and
are respectively the initial and final time, and
is the given initial condition. We refer to Equation (Equation1
(1)
(1) ) as the full-order model (FOM) and note that it has been written to have a polynomial structure:
are constant terms;
are the terms that are linear in the state
, with the discretised operator
;
are the terms that are quadratic in
, with
; and
are the terms that are linear in the input
, with
. This polynomial structure arises in three ways: (1) it may be an attribute of the governing equations; (2) it may be exposed via variable transformations; or (3) it may be derived by introducing auxiliary variables through the process of lifting. As examples of each: (1) the incompressible Navier-Stokes equations have a quadratic form; (2) the Euler equations can be transformed to quadratic form by using pressure, velocity, and specific volume as state variables; (3) a nonlinear tubular reactor model with Arrhenius reaction terms can be written in quadratic form via the lifting transformation shown in Kramer and Willcox (Citation2019) that introduces six auxiliary variables. Higher-order terms may be included in the formulation as well, but in this work we focus on a quadratic model due to the nature of the driving application.
A projection-based reduced-order model (ROM) of Equation (Equation1(1)
(1) ) preserves the polynomial structure (Benner et al. Citation2015). Approximating the high-dimensional state
in a low-dimensional basis
, with
, we write
, where
is the reduced state. Using a Galerkin projection, this yields the intrusive ROM of Equation (Equation1
(1)
(1) ):
where
,
,
, and
are the ROM operators corresponding to the FOM operators
,
,
, and
, respectively. The ROM is intrusive because computing these ROM operators requires access to the discretised FOM operators, which typically entails intrusive queries and/or access to source code.
The non-intrusive Operator Inference (OpInf) approach proposed by Peherstorfer and Willcox (Citation2016) parallels the intrusive projection-based ROM setting, but learns ROMs from simulation data without direct access to the FOM operators. Recognising that the intrusive ROM has the same polynomial form as Equation (Equation1(1)
(1) ), OpInf uses a data-driven regression approach to derive a ROM of Equation (Equation1
(1)
(1) ) as
(2)
(2) where
,
,
, and
are determined by solving a data-driven regression problem, and
is the state of the OpInf ROM.Footnote1
OpInf solves a regression problem to find reduced operators that yield the ROM that best matches projected snapshot data in a minimum-residual sense. Mathematically, OpInf solves the least-squares problem
(3)
(3) where
is the dataset used to drive the learning with
denoting a reduced-state snapshot at timestep j,
are the associated time derivatives, and
is the collection of inputs corresponding to the data with
. To generate the dataset, we employ the following steps: (1) Collect a set of k high-fidelity state snapshots
by solving the original high-fidelity model at times
with inputs
. (2) Apply a variable transformation
to obtain snapshots of the transformed variables. Here
is the map representing a reversible transformation (e.g. from density to specific volume) or a lifting transformation (Qian et al. Citation2020). (3) Compute the proper orthogonal decomposition (POD) basis
of the transformed snapshots.Footnote2 (4) Project the transformed snapshots onto the POD subspace as
. (5) Estimate projected time derivative information
. The training period
for which we have data is a subset of the full time domain of interest
; results from the ROM over
will be entirely predictive.
Equation (Equation3(3)
(3) ) can also be written in matrix form as
(4)
(4) where
and where
and
is the length-k column vector with all entries set to unity. The OpInf least-squares problem Equation (Equation3
(3)
(3) ) is therefore linear in the coefficients of the unknown ROM operators
,
,
, and
.
The OpInf approach permits us to compute the ROM operators ,
,
, and
without explicit access to the original high-dimensional operators
,
,
, and
. This point is key since we apply variable transformations only to the snapshot data, not to the operators or the underlying model. Thus, even in a setting where deriving a classical intrusive ROM might be possible, the OpInf approach enables us to work with variables other than those used for the original high-fidelity discretisation. We will see the importance of this later for a reacting flow application. We also note that under some conditions, OpInf recovers the intrusive POD ROM (Peherstorfer and Willcox Citation2016; Peherstorfer Citation2020).
Regularisation
The problem in Equation (Equation4(4)
(4) ) is generally overdetermined (i.e.
), but is also noisy due to errors in the numerically estimated time derivatives
, model mis-specification (e.g. if the system is not truly quadratic), and truncated POD modes that leave some system dynamics unresolved. The ROMs resulting from Equation (Equation4
(4)
(4) ) can thus suffer from overfitting the operators to the data and therefore exhibit poor predictive performance over the time domain of interest
.
To avoid overfitting, we introduce a Tikhonov regularisation (Tikhonov and Arsenin Citation1977) to Equation (Equation4(4)
(4) ), which then becomes
(5)
(5) where
is a full-rank regulariser. The minimiser of Equation (Equation5
(5)
(5) ) satisfies the modified normal equations
(6)
(6) which admit a unique solution since
is symmetric positive definite.
An regulariser
,
and
the identity matrix, penalises each entry of the inferred ROM operators
,
,
, and
, thereby driving the ROM toward the globally stable system
. Since the entries of the quadratic operator
have a different scaling than entries of the other operators, we construct a diagonal regulariser
, with
, such that the operator entries are penalised by
, except for the entries of
, which are penalised by
. That is, with
, Equation (Equation5
(5)
(5) ) can be expressed as
The scalar hyperparameters
and
, which balance the minimisation between the data fit and the regularisation, must be chosen with care. The ideal regulariser produces a ROM that minimises some error metric over the full time domain
; however, since data are only available for the smaller training domain
, we choose
and
so that the resulting ROM minimises error over
while maintaining a bound on the integrated POD coefficients over
. That is, we require the state
produced by integrating Equation (Equation2
(2)
(2) ) to satisfy
,
and
, for some B>0. This in turn ensures a bound on the magnitude of the entries of the high-dimensional state
:
(7)
(7) where
is the ith element of the jth POD basis vector. Note that the bound B may be chosen with the intent of imposing a particular bound on the
since the sums
can be precomputed. For example, our regularisation strategy provides a computationally efficient way to impose the temperature limiters proposed by Huang et al. (Citation2019).
Algorithm 1 details our regularised OpInf procedure, in which we choose B as a multiple of the maximum absolute entry of the projected training data . This particular strategy for selecting
and
could be replaced with a cross-validation or resampling grid search technique, but our experiments in this vein did not produce robust results. The training error
in step 13 may compare
and
directly in the reduced space (e.g. with a matrix norm or an
norm), or it may be replaced with a more targeted comparison of some quantity of interest.
Table
The regularisation approach of Algorithm 1 may be viewed as a stabilisation method since it selects a ROM with reasonable behaviour over a given time domain. It should be noted, however, that this method does not modify an existing ROM to achieve stability, different from other stabilisation methods such as eigenvalue reassignment (Kalashnikova et al. Citation2014; Rezaian and Wei Citation2020). The optimisation is driven by a penalisation but has no built-in constraints, which is a major advantage in terms of the computational cost, but the resulting ROMs are not guaranteed to preserve properties such as energy conservation. Adding constraints to Operator Inference to target conservation, similar to the work in Carlberg et al. (Citation2018), is a subject for possible future work.
Scalable implementation
The steps of Algorithm 1 are highly modular and amenable to large-scale problems. The variable transformation of step 2 consists of
elementary computations on the original snapshot matrix
. To compute the rank-r POD basis
in step 3, we use a randomised singular-value decomposition algorithm requiring
operations (Halko et al. Citation2011); since
, the leading order behaviour is
. The projection
in step 4 costs about 2nk operations. Note that
is small compared to
, as typically
–
and
–
. The time derivatives
in step 5 may be provided by the full-order solver or estimated, e.g. with finite differences of the columns of
. In the latter case, the cost is
. Step 6 is a simple
selection. The computational cost of steps 2–6 is therefore
.
The subroutine TrainError comprising steps 7–13 must be evaluated for several choices of
and
. In step 8, we solve the minimisation problem Equation (Equation5
(5)
(5) ) via the linear system Equation (Equation6
(6)
(6) ). Forming
and
costs
operations, but these can be precomputed once and reused in each subroutine evaluation; for specific
and
, we form
and compute
with only
additional operations since
is diagonal. Solving Equation (Equation6
(6)
(6) ) via the Cholesky decomposition has a leading order cost of
operations (Demmel Citation1997), but this estimate can be improved upon with iterative methods for larger r if desired. The ROM integration in step 9 can be carried out with any time-stepping scheme; for explicit methods, evaluating the ROM at a single point, i.e. computing the right-hand side of Equation (Equation2
(2)
(2) ), costs
operations. The total cost each evaluation of TrainError
is therefore dominated by the cost of solving Equation (Equation6
(6)
(6) ), which is independent of n and k.
Finally, the minimisation in step 14 is carried out with a derivative-free search method, which enables fewer total evaluations of the subroutine than a fine grid search. However, a coarse grid search is useful for identifying appropriate initial guesses for and
.
Results
This section applies regularised OpInf to a single-injector combustion problem, studied previously by Swischuk et al. (Citation2020), on the two-dimensional computational domain shown in Figure . We first describe the governing dynamics, a set of high-fidelity data obtained from a CFD code, and the variable transformations used to produce training data for learning reduced models with Algorithm 1. The resulting OpInf ROM performance is then analysed and compared to a state-of-the-art intrusive model reduction method.
Figure 1. The computational domain for the single-injector combustion problem. On the left, monitor locations for numerical results. On the right, a typical temperature field demonstrating the complexity and nonlinear nature of the problem.
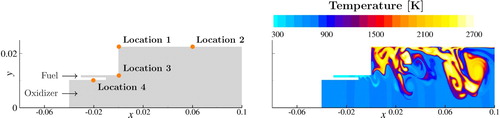
Problem setup
The combustion dynamics for this problem are governed by conservation laws
(8)
(8) where
are the conservative variables,
are the inviscid flux terms,
are the viscous flux terms, and
are the source terms. Here ρ is the density
,
and
are the x and y velocity
, e is the total energy
, and
is the ℓth species mass fraction with
. The chemical species are CH
, O
, H
O, and CO
, which follow a global one-step chemical reaction
(Westbrook and Dryer Citation1981). See Harvazinski et al. (Citation2015) for more details on the governing equations.
At the downstream end of the combustor, we impose a non-reflecting boundary condition while maintaining the chamber pressure via
(9)
(9) where
and
. The top and bottom wall boundary conditions are no-slip conditions, and for the upstream boundary we impose a constant mass flow at the inlets. Swischuk et al. (Citation2020) show that if the governing equations (Equation8
(8)
(8) ) are transformed to be written in the specific volume variables, many of the terms take a quadratic form. Following that idea, we choose as learning variables the transformed and augmented state
where p is the pressure
, T is the temperature
,
is the specific volume
, and
are the species molar concentrations
given by
with
the molar mass of the ℓth species
. As shown in Swischuk et al. (Citation2020), the equations for
,
, and ξ are exactly quadratic in
, while the remaining equations are quadratic with some non-polynomial terms in
. Note that, differently from Swischuk et al. (Citation2020),
here is chosen to contain specific volume, pressure, and temperature, even though only two of the three quantities are needed to fully define the high-fidelity model (and the equation of state then defines the third). We augment the learning variables in this way because doing so exposes the quadratic form while also directly targeting the variables that are of primary interest for assessing ROM performance. In particular, the resulting ROMs provide more accurate predictions of temperature when temperature is included explicitly as a learning variable. We can do this since the transformations are applied only to the snapshot data, not to the CFD model itself. Indeed, constructing the full-order spatial operators in these transformed coordinates would be both impractical and inexact. This flexibility to learn from transformed snapshots instead of transformed full-order operators is a major advantage of the non-intrusive OpInf approach in comparison to traditional intrusive projection-based model reduction methods.
To generate high-fidelity training data, we use the finite-volume based General Equation and Mesh Solver (GEMS) (Harvazinski et al. Citation2015) to solve for the variables over
cells, resulting in snapshots with
entries each. The snapshots are computed for 60,000 time steps beyond the initial condition with a temporal discretisation of
, from
to
. The computational cost of computing this dataset is approximately 1200 CPU hours on two computing nodes, each of which contains two Haswell CPUs at 2.60 GHz and 20 cores per node.
Scaling is an essential aspect of successful model reduction and is particularly critical for this problem due to the wide range of scales across variables. After transforming the GEMS snapshot data to the learning variables , the species molar concentrations are scaled to
, and all other variables are scaled to
. This scaling ensures that null velocities and null molar concentrations are preserved. For example, some upstream regions of the injector have zero methane concentration at all times. By construction, the POD basis vectors and thus the ROM predictions will preserve those zero concentration values.
We implement Algorithm 1 via the rom_operator_inference Python package,Footnote3 which is built on NumPy, SciPy, and scikit-learn (Walt et al. Citation2011; Pedregosa et al. Citation2011; Virtanen et al. Citation2020). The time derivatives in step 5 of Algorithm 1 are estimated with fourth-order finite differences, and the least-squares problem in step 8 are solved by applying the LAPACK routine POSV to Equation (Equation6(6)
(6) ). The learned ROMs are integrated in step 9 with the explicit, adaptive, fourth-order Runge-Kutta scheme RK45, and the error evaluation of step 13 uses the
norm in the reduced space. To minimise the function TrainError
in step 14, we find an initial estimate of the minimiser via a coarse grid search, then refine the result with a Nelder-Mead search method (Nelder and Mead Citation1965). The code and details are publicly available at https://github.com/Willcox-Research-Group/ROM-OpInf-Combustion-2D.
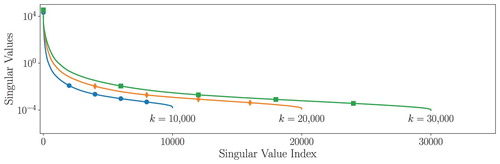
Sensitivity to training data
We study the sensitivity of our approach to the training data by varying the number of snapshots used to compute the POD basis and learn the OpInf ROM. Specifically, we consider the three cases where we use the first ,
, and
snapshots from GEMS as training data sets. In each case we compute the POD basis and, to select an appropriate reduced dimension r, the cumulative energy based on the POD singular values:
, where
are the singular values of the learning variable snapshot matrix
(see Figure ). Specifically, we choose the minimal integer r such that
is greater than a fixed energy threshold. Table shows that r is increasing linearly with the number of snapshots, indicating that the basis is not being saturated as additional information is incorporated. This is an indication of the challenging nature of this application, due to the rich and complex dynamics. Table also shows the column dimension
of the data matrix
in the Operator Inference problem, which grows quadratically with r; choosing r so that
helps ensure that
has full rank.
Table 1. The basis size r required to exceed a given cumulative energy level increases linearly with the number of snapshots k in the training set; the dimension
increases quadratically with r.
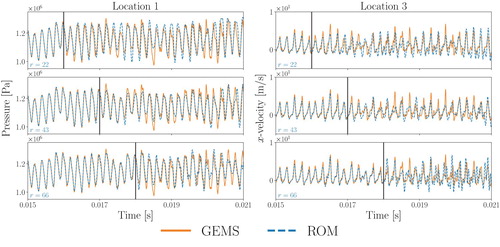
Figure plots the GEMS and OpInf ROM results for pressure and x-velocity predictions over time at two of the monitor locations in Figure .Footnote4 While it can be misleading to assess accuracy based on predictions at a single spatial point, these plots reveal several representative insights. First, each OpInf ROM faithfully reconstructs the training data but has some discrepancies in the prediction regime. Second, the pressure and x-velocity frequencies are well captured throughout the time domain, but the amplitudes are sometimes less accurate in the prediction regime. The effects of the 5000 Hz downstream pressure forcing are clearly visible in the pressure. Third, we see the importance of the training data–as the amount of training data increases, the ROM predictions change significantly and generally (but not always) improve. This is yet another indication of the complexity of the dynamics we are aiming to approximate.
Figure 3. Traces of pressure and x-velocity through time at monitor locations 1 and 3 of Figure , respectively, for (top row),
(middle row), and
(bottom row) training snapshots. The vertical black lines separate the training and prediction periods. For each choice of k, the error over the training domain is low, but increasing k has a significant impact on the behaviour in the testing domain. Here r is chosen in each case so that
.
The effectiveness of the low-dimensional basis differs among the state variables. Let denote the GEMS simulation data at time t with components
corresponding to a single state variable (e.g. pressure or temperature), and let
be the preprocessing variable transformation and scaling with reverse operator
(i.e.
for all t). Given the basis
for the scaled learning variables, the projection of the GEMS data onto the basis is
Let
denote the components of the projection corresponding to the state variable of interest. Next, letting
denote the ROM state (the result of integrating Equation (Equation2
(2)
(2) )), the reconstructed ROM prediction in the original state variables is
Let
be the components of this reconstruction corresponding to the state variable of interest. We define the spatially averaged relative errors for the projection and the ROM predictions as
respectively. Figure plots these errors against time for pressure and temperature using a POD basis with r = 43 vectors computed from the first
training snapshots. While both error measures for pressure remain low throughout the full time interval, both the projection errors and the ROM prediction errors for temperature increase significantly at the end of the training regime. The temperature profile is influenced by both the advective flow dynamics and the local chemical reactions, which in combination lead to a highly nonlinear and multiscale behaviour that is difficult to represent with the POD basis after the training period. However, while the ROM struggles to accurately predict the detailed temperature variations pointwise, it does adequately predict the general trends of temperature evolution beyond the training horizon. Figure shows the time-averaged temperature profiles for the GEMS data and for an OpInf ROM, suggesting that the ROM captures the time-averaged behaviour of the temperature dynamics.
Figure 4. Spatially averaged relative errors in time for pressure and temperature (left) and temperature profiles for the GEMS dataset and an OpInf ROM averaged over time steps (right). The basis comprises the r = 43 dominant singular vectors of
training snapshots.
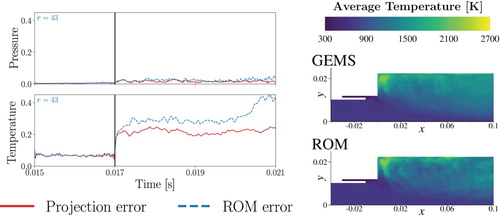
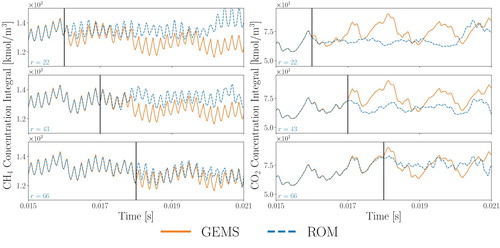
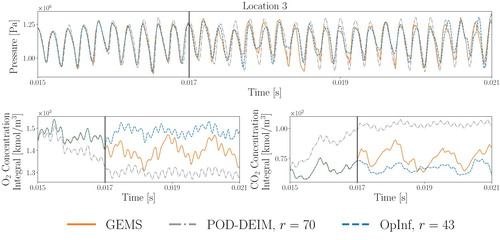
Figure plots CH and CO
concentrations integrated over the spatial domain. These measures give a more global sense of the ROM predictive accuracy and the predicted chemical reaction rate. In each case, the ROMs are able to accurately re-predict the training data and capture much of the overall system behaviour in the prediction phase, with slightly more training error as the number of snapshots increases.
Comparison to POD-DEIM
We now compare regularised OpInf to a state-of-the-art nonlinear model reduction method that uses a least-squares Petrov-Galerkin POD projection coupled with the discrete empirical interpolation method (DEIM) (Chaturantabut and Sorensen Citation2010), as implemented for the same combustion problem in Huang et al. (Citation2019) and Huang et al. (Citation2018). This POD-DEIM method is intrusive–it requires nonlinear residual evaluations of the GEMS code at sparse discrete interpolation points. This also increases the computational cost of solving the POD-DEIM ROM in comparison to the OpInf ROM: integrating a POD-DEIM ROM with r = 70 for 6000 time steps of size takes approximately 30 min on two nodes, each with two Haswell CPUs processors at
and 20 cores per node; for OpInf, using Python 3.6.9 and a single CPU on an AMD EPYC 7702 64-core processor at
with
RAM, we solve Equation (Equation5
(5)
(5) ) with
training snapshots and r = 43 POD modes in approximately
and integrate the resulting OpInf ROM for 60,000 time steps of size
in approximately
. While these measurements are made on different hardware, and though the execution time for POD-DEIM can be improved with optimal load balancing, the difference in execution times (30 min versus 1 s) is representative and illustrates one of the advantages over POD-DEIM of the polynomial form employed in the OpInf approach.
Figure compares select GEMS outputs to POD-DEIM and OpInf ROM outputs, with each ROM trained on training snapshots. As before, the OpInf ROM dimension
is chosen such that
; the POD-DEIM ROM, which uses an entirely different basis than the OpInf approach, requires r = 70 vectors to achieve the same level of cumulative energy. Both approaches maintain appropriate pressure oscillation frequencies, and while neither model accurately predicts the global species concentration dynamics after the training period, the OpInf ROM reconstructs the training data more faithfully than the POD-DEIM ROM. Huang et al. (Citation2019) show similar results for the same POD-DEIM model with 1 ms of training and 1 ms of prediction; here we are using 2 ms of training and 4 ms of prediction. Note from Figures and that the OpInf ROMs achieve excellent prediction results for the 1 ms period following the training.
Figure 6. Pressure trace at monitor location 3 of Figure (top) and spatially integrated O and CO
molar concentrations (bottom), computed by GEMS, a POD-DEIM ROM, and an OpInf ROM. Both ROMs use
training snapshots with r chosen so that
.
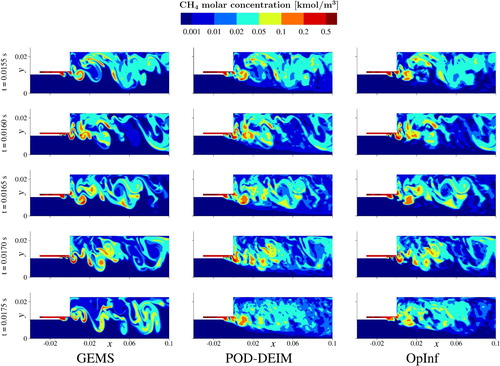
Figures and show, respectively, full-domain results for the temperature and molar concentration of CH. The figures show the solution at time instants within the training regime, at the end of the training regime, and into the prediction regime. As with the point traces shown earlier, we see that the ROMs have impressive accuracy over the training region, but lose accuracy as they attempt to predict dynamics beyond the training horizon. However, many of the coherent features are reasonably predicted, especially the recirculation zone dynamics near the dump plane (
in Figure ) shown in the temperature fields. Significantly, both ROMs maintain appropriate temperature ranges throughout the prediction phase. The POD-DEIM ROM explicitly enforces such limits by reconstructing the full solution at each time step, constraining the temperature to a desired range, and projecting the result back to the reduced space (see Section IV.G of Huang et al. Citation2019); in contrast, the OpInf ROM selects a regularisation that results in bounded behaviour due to the criteria
(see Equation (Equation7
(7)
(7) )). In other words, POD-DEIM limits the temperature in the online phase, while OpInf builds a similar constraint into the offline phase.
Figure 7. Temperature fields produced by GEMS (left column), POD-DEIM (middle column), and OpInf (right column), where each ROMs uses training snapshots, with r chosen so that
. Each row shows results for a given time, with an increment of
between rows. The training period ends at
(fourth row);
(last row) is well into the prediction regime.
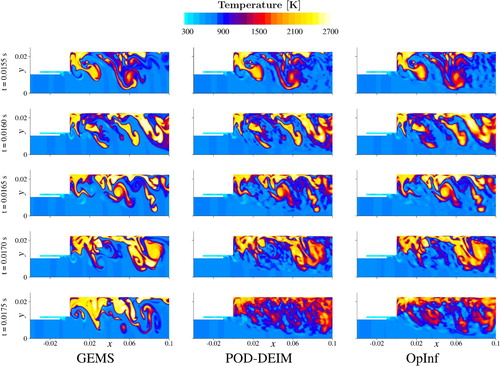
Figure 8. Molar concentrations of CH produced by GEMS (left column), POD-DEIM (middle column), and OpInf (right column), where each ROMs uses
training snapshots, with r chosen so that
. Each row shows results for a given time, with an increment of
between rows. The training period ends at
(fourth row);
(last row) is well into the prediction regime.
Conclusions
The presented scientific machine learning approach is broadly applicable to problems where the governing equations are known but access to the high-fidelity simulation code is limited. The approach is computationally as accessible as black-box surrogate modelling while achieving the accuracy of intrusive projection-based model reduction. While the conclusions drawn from the numerical studies apply to the single-injector combustion example, they are relevant and likely apply to other problems. First, the quality and quantity of the training data are critical to the success of the method. Second, regularisation is essential to avoid overfitting. Third, achieving a low error over the training regime is not necessarily indicative of a reduced model with good predictive capability. This emphasises the importance of the training data. Fourth, physical quantities that exhibit large-scale coherent structures (e.g. pressure) are more accurately predicted by a reduced-order model than quantities that exhibit multiscale behaviour (e.g. temperature, species concentrations). Fifth, a significant advantage of the data-driven learning aspects of the approach is that the reduced model may be derived in any variables. This includes the possibility to include redundancy in the learning variables (e.g. to include both pressure and temperature). Overall, this paper illustrates the power and effectiveness of learning from data through the lens of physics-based models as a physics-grounded alternative to black-box machine learning.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Correction Statement
This article has been corrected with minor changes. These changes do not impact the academic content of the article.
Additional information
Funding
Notes
1 From here on we use to indicate a compact Kronecker product with only the
unique quadratic terms (
,
,
, …); for matrices, the product is applied column-wise.
2 Or any other low-dimensional basis as desired.
4 See https://github.com/Willcox-Research-Group/ROM-OpInf-Combustion-2D for additional results.
References
- Antoulas AC. 2005. Approximation of large-scale dynamical systems. Philadelphia (PA): SIAM.
- Astrid P, Weiland S, Willcox K, Backx T. 2008. Missing point estimation in models described by proper orthogonal decomposition. IEEE Transactions on Automatic Control. 53(10):2237–2251.
- Bai Z. 2002. Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems. Applied Numerical Mathematics. 43(1–2):9–44.
- Baker N, Alexander F, Bremer T, Hagberg A, Kevrekidis Y, Najm H, Parashar M, Patra A, Sethian J, Wild S, et al. 2019. Workshop report on basic research needs for scientific machine learning: core technologies for artificial intelligence. Washington (DC): USDOE Office of Science (SC). Report No. https://www.osti.gov/servlets/purl/1478744.
- Barrault M, Maday Y, Nguyen NC, Patera AT. 2004. An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique. 339(9):667–672.
- Benner P, Gugercin S, Willcox K. 2015. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Review. 57(4):483–531.
- Berkooz G, Holmes P, Lumley J. 1993. The proper orthogonal decomposition in the analysis of turbulent flows. Annual Review of Fluid Mechanics. 25:539–575.
- Brunton SL, Proctor JL, Kutz JN. 2016. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences. 113(15):3932–3937.
- Carlberg K, Choi Y, Sargsyan S. 2018. Conservative model reduction for finite-volume models. Journal of Computational Physics. 371:280–314.
- Carlberg K, Farhat C, Cortial J, Amsallem D. 2013. The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. Journal of Computational Physics. 242:623–647.
- Chaturantabut S, Sorensen DC. 2010. Nonlinear model reduction via discrete empirical interpolation. SIAM Journal on Scientific Computing. 32(5):2737–2764.
- Cui T, Fox C, O'Sullivan MJ. 2011. Bayesian calibration of a large-scale geothermal reservoir model by a new adaptive delayed acceptance metropolis hastings algorithm. Water Resources Research. 47(10).
- Deane A, Kevrekidis I, Karniadakis GE, Orszag S. 1991. Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders. Physics of Fluids A: Fluid Dynamics. 3(10):2337–2354.
- Demmel JW. 1997. Applied numerical linear algebra. Philadelphia (PA): SIAM.
- Dowell EH, Hall KC. 2001. Modeling of fluid-structure interaction. Annual Review of Fluid Mechanics. 33(1):445–490.
- Freund R. 2003. Model reduction methods based on Krylov subspaces. Acta Numerica. 12:267–319.
- Gatski T, Glauser M. 1992. Proper orthogonal decomposition based turbulence modeling. In: Instability, transition, and turbulence. New York (NY): Springer; p. 498–510.
- Grepl M, Patera A. 2005. A posteriori error bounds for reduced-basis approximations of parametrized parabolic partial differential equations. ESAIM-Mathematical Modelling and Numerical Analysis (M2AN). 39(1):157–181.
- Halko N, Martinsson PG, Tropp JA. 2011. Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Review. 53(2):217–288.
- Harvazinski ME, Huang C, Sankaran V, Feldman TW, Anderson WE, Merkle CL, Talley DG. 2015. Coupling between hydrodynamics, acoustics, and heat release in a self-excited unstable combustor. Physics of Fluids. 27(4):045102.
- Huang C, Duraisamy K, Merkle CL. 2019. Investigations and improvement of robustness of reduced-order models of reacting flow. AIAA Journal. 57(12):5377–5389.
- Huang C, Xu J, Duraisamy K, Merkle C. 2018. Exploration of reduced-order models for rocket combustion applications. In: 2018 AIAA Aerospace Sciences Meeting; Orlando, FL. Paper AIAA-2018-1183.
- Kalashnikova I, van Bloemen Waanders B, Arunajatesan S, Barone M. 2014. Stabilization of projection-based reduced order models for linear time-invariant systems via optimization-based eigenvalue reassignment. Computer Methods in Applied Mechanics and Engineering. 272:251–270.
- Kramer B, Willcox K. 2019. Nonlinear model order reduction via lifting transformations and proper orthogonal decomposition. AIAA Journal. 57(6):2297–2307.
- Lumley J. 1967. The structures of inhomogeneous turbulent flows. Atmospheric turbulence and radio wave propagation. p. 166–178.
- Nelder JA, Mead R. 1965. A simplex method for function minimization. The Computer Journal. 7(4):308–313.
- Nordsletten D, McCormick M, Kilner P, Hunter P, Kay D, Smith N. 2011. Fluid–solid coupling for the investigation of diastolic and systolic human left ventricular function. International Journal for Numerical Methods in Biomedical Engineering. 27(7):1017–1039.
- O'Sullivan M, Pruess K, Lippmann M. 2001. State of the art of geothermal reservoir simulation. Geothermics. 30:395–429.
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al 2011. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research. 12:2825–2830.
- Peherstorfer B. 2020. Sampling low-dimensional Markovian dynamics for pre-asymptotically recovering reduced models from data with operator inference. SIAM Journal on Scientific Computing. 42(5):A3489–A3515.
- Peherstorfer B, Willcox K. 2016. Data-driven operator inference for nonintrusive projection-based model reduction. Computer Methods in Applied Mechanics and Engineering. 306:196–215.
- Qian E, Kramer B, Peherstorfer B, Willcox K. 2020. Lift & Learn: physics-informed machine learning for large-scale nonlinear dynamical systems. Physica D: Nonlinear Phenomena. 406:132401.
- Rezaian E, Wei M. 2020. A hybrid stabilization approach for reduced-order models of compressible flows with shock-vortex interaction. International Journal for Numerical Methods in Engineering. 121(8):1629–1646.
- Rozza G, Huynh D, Patera A. 2008. Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations: application to transport and continuum mechanics. Archives of Computational Methods in Engineering. 15(3):229–275. http://dx.doi.org/10.1007/s11831-008-9019-9.
- Sirovich L. 1987. Turbulence and the dynamics of coherent structures. I. Coherent structures. Quarterly of Applied Mathematics. 45(3):561–571.
- Spalart P, Venkatakrishnan V. 2016. On the role and challenges of CFD in the aerospace industry. The Aeronautical Journal. 120(1223):209.
- Swischuk R, Kramer B, Huang C, Willcox K. 2020. Learning physics-based reduced-order models for a single-injector combustion process. AIAA Journal. 58(6):2658–2672.
- Tikhonov AN, Arsenin VY. 1977. Solutions of ill-posed inverse problems. New York (NY): Wiley.
- Veroy K, Patera A. 2005. Certified real-time solution of the parametrized steady incompressible Navier-Stokes equations: rigorous reduced-basis a posteriori error bounds. International Journal for Numerical Methods in Fluids. 47:773–788.
- Veroy K, Prud'homme C, Rovas D, Patera A. 2003. A posteriori error bounds for reduced-basis approximation of parametrized noncoercive and nonlinear elliptic partial differential equations. In: Proceedings of the 16th AIAA Computational Fluid Dynamics Conference; Orlando, FL. Paper AIAA-2003-3847.
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. 2020. SciPy 1.0: fundamental algorithms for scientific computing in python. Nature Methods. 17:261–272.
- Walt Svd, Colbert SC, Varoquaux G. 2011. The NumPy array: a structure for efficient numerical computation. Computing in Science & Engineering. 13(2):22–30.
- Westbrook CK, Dryer FL. 1981. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combustion Science and Technology. 27(1–2):31–43.
- Yin Y, Choi J, Hoffman EA, Tawhai MH, Lin CL. 2010. Simulation of pulmonary air flow with a subject-specific boundary condition. Journal of Biomechanics. 43(11):2159–2163.