A survey of inconsistency indices for pairwise comparisons

ABSTRACT

Pairwise comparisons are a well-established tool to compare weights of criteria and alternatives or, more in general, any entities. Their ultimate goal is to facilitate the search for a suitable weight vector. In this context, the concepts of inconsistency and inconsistency index have emerged. This manuscript has two goals. Firstly, it surveys the most relevant inconsistency indices by means of a self-contained exposition. Secondly, by analyzing recent trends and milestones it presents some conclusions and a discussion on possible directions of future research.

KEYWORDS:

• Pairwise comparison matrix
• preference relation
• consistency
• inconsistency index
• multi-criteria decision-making

Man is a rational animal: so at least I have been told. Throughout a long life, I have looked diligently for evidence in favour of this statement, but so far I have not had the good fortune to come across it. (Bertrand Russell)

1. Introduction

Very often, in operations research, economics, engineering, and other fields of science, it is necessary to estimate a positive normalized vector, i.e. a “weight” vector $w=(w_1,\dots ,w_n)$ such that $w_i>0$ and $w_1+\cdots +w_n=1$. Simple examples of weight vectors could be $w=(0.4,0.2,0.3,0.1)\mathrm{and}w=\left(\frac{1}{3},\frac{1}{6},\frac{1}{10},\frac{1}{4},\frac{3}{20}\right).$ Components of w are often called weights or priorities and, among other uses, they have been employed (i) as coefficients of convex linear combinations of n vectors, (ii) weights of the n arguments of linear functions, (iii) relative weights of criteria in multi-criteria decision making problems, (iv) subjective probabilities, and (v) proportions in which to split a given quantity.

Problems arise when weights need to be determined subjectively by an expert or a decision maker. Namely, when each weight $w_i$ is estimated by asking its value directly to an expert, the cognitive burden could be excessive and, especially when n is large, the likelihood of incurring in cognitive biases could be a risk.¹ A common strategy to avoid these pitfalls is to divide the problem into subproblems and then tackle these latter ones. In this context, a pairwise comparison $a_{ij}$ is a value, usually provided by an expert, expressing his estimation of the ratio between weights $w_i$ and $w_j$, i.e. $a_{ij}\approx w_i/w_j$. For sake of example, the possible value $a_{24}=3$ indicates that the expert considers $w_2$ three times greater than $w_4$. Of course, since all the weights are positive, we also know that, in general, $a_{ij}>0$.

Besides splitting the problem into smaller and more tractable subproblems, pairwise comparisons give the analyst the possibility of estimating how irrational the judgments of a given experts are. We can consider the example in Figure 1(a), with $a_{12}=2$, $a_{23}=3$, and $a_{13}=6$, which is a set of non-contradictory pairwise comparisons. A set of non-contradictory pairwise comparisons is called consistent. If $a_{13}$ is replaced by ${\dot{a}}_{13}=4$, the set of comparisons, now depicted in Figure 1(b), becomes inconsistent. If, instead, $a_{13}=4$ is replaced by ${\ddot{a}}_{13}=1/5$, as shown in Figure 1(c), it is sensible to say that the new set of comparisons is even more inconsistent than the one in Figure 1(b).

Figure 1. Example of sets of pairwise comparisons and their consistency. (a) A set of consistent pairwise comparisons, (b) a set of inconsistent pairwise comparisons and (c) another set of inconsistent pairwise comparisons.

Figure 2. Visual interpretation of an inconsistency index. Each index represents a mapping of PCMs to the real line.

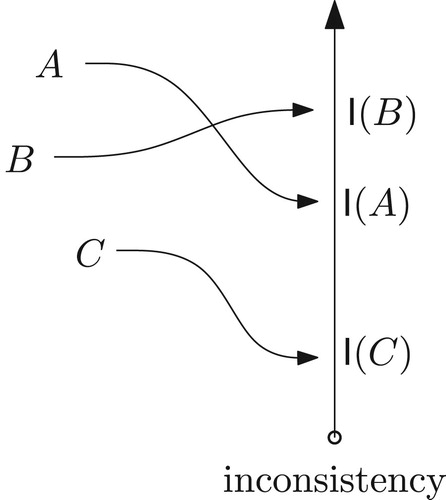
Figure 1 evidences how sets of pairwise comparisons can either be consistent or inconsistent but also that the condition of consistency can be violated to different extents, and therefore the concept of inconsistency should be a matter of degree.

Although a subset of $(n-1)$ pairwise comparisons $a_{ij}$, chosen so that they induce a spanning tree on the set of weights, would be sufficient to determine the weight vector w, for sake of robustness, in Multi Attribute Value Theory (MAVT) Keeney and Raiffa (1976, 123) stated that “it may be desirable to ask additional questions thereby getting an over-determined system of equations, fully expecting that the set of responses would be inconsistent in practice”. Even more so, in the Analytic Hierarchy Process (AHP), Saaty (1977) required that all the $n(n-1)/2$ pairwise comparisons be elicited. Of course, as reminded by Keeney and Raiffa, redundancy of information may lead to inconsistencies, since it is hardly ever possible to be consistent. Even in this case, both proponents of MAVT and AHP agree: Saaty (1977) stated that pairwise comparisons should be “close” to consistency and Keeney and Raiffa (1976, 205) recommended that inconsistencies be kept at a “nominal level”. The role of inconsistency indices is precisely that of quantifying the deviation of a set of pairwise comparisons from being consistent. The goal of this paper is to offer an overview of inconsistency indices and their ramifications.

This manuscript is organized as follows. The next section introduces the concepts of pairwise comparison matrix and inconsistency index. Section 3 is a self-contained presentation of some notable inconsistency indices. Section 4 completes the presentation of the inconsistency indices with a summary of recent comparative studies. Section 5 elaborates on other uses and ramifications of the concept of inconsistency index. Section 6 draws some conclusions.

2. Pairwise comparison matrices and inconsistency

A pairwise comparison matrix is a mathematical structure collecting pairwise comparisons. More formally, a pairwise comparison matrix (PCM) is a positive square matrix $A=(a_{ij}{)}_{n\times n}$ where $a_{ij}>0$ is the subjective estimation of the ratio between $w_i$ and $w_j$. Note that, it is reasonably assumed that $a_{ii}=1\mathrm{\forall }i$ and $a_{ij}=1/a_{ji}\mathrm{\forall }i,j$. Hence, a PCM has the following structure: $A=\begin{array}{ccccc}& w_1& w_2& \cdots & w_n\\ w_1& a_{11}& a_{12}& \cdots & a_{1n}\\ w_2& a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ w_n& a_{n1}& a_{n2}& \dots & a_{nn}\end{array}=\begin{array}{ccccc}& w_1& w_2& \cdots & w_n\\ w_1& 1& a_{12}& \cdots & a_{1n}\\ w_2& 1/a_{12}& 1& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ w_n& 1/a_{1n}& 1/a_{2n}& \dots & 1\end{array}.$ Among the many methods to estimate a suitable weight vector w from a PCM A, two gained a special importance. The first is the eigenvector method, for which the weight vector is the normalized solution of the system $Aw={\lambda }_{max}w$ where ${\lambda }_{max}$ is the Perron-Frobenius eigenvalue of A (Saaty 1977) and where w is considered a column vector. The second is the geometric mean method, according to which each weight $w_i$ is the geometric mean of the elements on the ith row of A (Crawford and Williams 1985). Also in this case, the vector w is further processed so that its components sum up to 1.

A pairwise comparison matrix is consistent, if and only if, (1) $a_{ik}=a_{ij}{a}_{jk}\mathrm{\forall }i,j,k.$(1) Condition (1(1) $a_{ik}=a_{ij}{a}_{jk}\mathrm{\forall }i,j,k.$(1) ) is a formalization and generalization of the idea of consistency exemplified in Figure 1(a). Its interpretation is that each pairwise comparison $a_{ik}$ is indirectly supported by all comparisons between $w_i$ and $w_k$ passing through $w_j\mathrm{\forall }j$.

An inconsistency index associates pairwise comparison matrices to real numbers. That is, if $\mathcal{A}$ is the set of all the pairwise comparison matrices, an inconsistency index ² is a function $\mathsf{I}:\mathcal{A}\to \mathbb{R}$. The usual semantic of an inconsistent index is that the greater $\mathsf{I}\left(A\right)\in \mathbb{R}$, the greater is the inconsistency of A.

It was shown that the consistency condition (1(1) $a_{ik}=a_{ij}{a}_{jk}\mathrm{\forall }i,j,k.$(1) ) is equivalent to any of the following:

• There exists a positive vector $w=(w_1,\dots ,w_n)$ such that $a_{ij}=w_i/w_j\mathrm{\forall }i,j$

• The Perron-Frobenius eigenvalue of A is equal to n

• The matrix A has rank 1.

It is easy to envision that such a variety of conditions has been a fertile ground for the development of different inconsistency indices.

3. Inconsistency indices

The first and by far the most popular inconsistency index was introduced by Saaty (1977) in his theory of the Analytic Hierarchy Process (AHP) and is an affine transformation of the Perron-Frobenius eigenvalue of A, here denoted as ${\lambda }_{max}$: $\mathsf{C}\mathsf{I}\left(A\right)=\frac{{\lambda }_{max}-n}{n-1}.$ To make this quantification of the inconsistency more intelligible, Saaty (1977) showed that it can alternatively be expressed as $\mathsf{C}\mathsf{I}\left(A\right)=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j=1}^n\left(a_{ij}\frac{w_j}{w_i}-1\right),$ where w is the Perron-Frobenius eigenvector of A. Moreover, Saaty (1977) proposed to divide $\mathsf{C}\mathsf{I}$ by the so-called Random Index $R{I}_n$, the average $\mathsf{C}\mathsf{I}$ calculated on a large number of PCMs of order n with entries sampled from the scale $\{1/9,1/8,\dots ,8,9\}$, thus obtaining the Consistency Ratio $\mathsf{C}\mathsf{R}=\mathsf{C}\mathsf{I}/R{I}_n$. Moreover, still Saaty proposed the threshold 0.1 for $\mathsf{C}\mathsf{R}$ so that only matrices with $\mathsf{C}\mathsf{R}\left(A\right)\le 0.1$ should be classified as sufficiently consistent. Alonso and Lamata (2006) computed the values of $R{I}_n$ of large datasets of random PCMs and Aupetit and Genest (1993) provided a tight upper bound for the value of $\mathsf{C}\mathsf{I}$ in the cases when entries of A are expressed on a bounded scale.

Essentially for historical reasons, $\mathsf{C}\mathsf{R}$ has been the dominating inconsistency index for the last 40 years. Nevertheless, other inconsistency indices have gained prominence since the inception of $\mathsf{C}\mathsf{I}$ and $\mathsf{C}\mathsf{R}$. Crawford and Williams (1985) proposed to use the geometric mean method to estimate the weight vector $w=(w_1,\dots ,w_n)$ and formulated the Geometric Consistency Index, $\mathsf{G}\mathsf{C}\mathsf{I}\left(A\right)=\frac{2}{(n-1)(n-2)}\sum _{i=1}^{n-1}\sum _{j=i+1}^n{\ln }^2\left(a_{ij}\frac{w_j}{w_i}\right).$ Thresholds and formal properties of $\mathsf{G}\mathsf{C}\mathsf{I}$ were studied by Crawford (1987) and Aguarón and Moreno-Jiménez (2003). Brunelli, Critch, and Fedrizzi (2013, Proposition 2) showed an equivalent formulation of $\mathsf{G}\mathsf{C}\mathsf{I}$ and proved that it is proportional to another inconsistency index (Fedrizzi and Giove 2007, formula (10)).

Koczkodaj (1993) proposed a measure of inconsistency for a PCM of order three. Duszak and Koczkodaj (1994) generalized the original proposal to $n\ge 3$, and presented the inconsistency index, $\mathsf{K}\left(A\right)=\underset{i<j<k}{max}min\left\{\left|1-\frac{a_{ik}}{a_{ij}{a}_{jk}}\right|,\left|1-\frac{a_{ij}{a}_{jk}}{a_{ik}}\right|\right\}.$ Csató (2018b) provided a full characterization of index $\mathsf{K}$ by means of six axioms.

Grzybowski (2016) considered the index $\mathsf{K}$ and replaced the $max$ operator with the arithmetic mean. The validity of the obtained inconsistency index, i.e. $\mathsf{A}\mathsf{T}\mathsf{I}\left(A\right)=\frac{1}{\left(\genfrac{}{}{0em}{}{n}{3}\right)}\sum _{i=1}^{n-2}\sum _{j=i+1}^{n-1}\sum _{k=j+1}^{n}min\left\{\left|1-\frac{a_{ik}}{a_{ij}{a}_{jk}}\right|,\left|1-\frac{a_{ij}{a}_{jk}}{a_{ik}}\right|\right\}$ was related by Grzybowski (2016) to the reliability of the priority vector.

Golden and Wang (1989) studied an inconsistency index based on the dissimilarity between the columns of A and the priority vector w. First they transformed the original PCM A in $\overline{A}=({\overline{a}}_{ij}{)}_{n\times n}$ whose entries are normalized so that each column add up to one. At this point, their index is $\mathsf{G}\mathsf{W}\left(A\right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\left|{\overline{a}}_{ij}-w_i\right|.$ Shiraishi, Obata, and Daigo (1998) proposed to take the coefficient $c_3$ of the characteristic polynomial of A as a measure of inconsistency. They found an analytic formula for $c_3$ which can be used as an inconsistency index ${\mathsf{c}}_{\mathsf{3}}\left(A\right)=\frac{1}{\left(\genfrac{}{}{0em}{}{n}{3}\right)}\sum _{i=1}^{n-2}\sum _{j=i+1}^{n-1}\sum _{k=j+1}^n\left(2-\frac{a_{ik}}{a_{ij}{a}_{jk}}-\frac{a_{ij}{a}_{jk}}{a_{ik}}\right).$ It is worth noting that the interpretation of ${\mathsf{c}}_{\mathsf{3}}$ is reversed. Namely ${\mathsf{c}}_{\mathsf{3}}\le 0$ and equal to 0 if and only if A is consistent. Brunelli, Critch, and Fedrizzi (2013) proved that ${\mathsf{c}}_{\mathsf{3}}$ is proportional to another index proposed by Peláez and Lamata (2003).

Stein and Mizzi (2007) considered $s_j$ to be the sum of the entries on the jth column of A and defined $h\left(A\right)=\left(n/\sum _{i=1}^n{s}_j^{-1}\right)$ to be their harmonic mean. They proved that $h\left(A\right)\ge n$ and equal to n if and only if A is consistent, and defined the Harmonic Consistency Index: $\mathsf{H}\mathsf{C}\mathsf{I}\left(A\right)=\frac{\left(h\right(A)-n)(n+1)}{n(n-1)}.$ Cavallo and D'Apuzzo (2009, 2010, 2012) generalized the idea of PCM from the algebraic point of view using commutative linearly ordered groups and proposed and justified a new inconsistency index, ${\mathsf{I}}_{\mathsf{C}\mathsf{D}}\left(A\right)=\prod _{i=1}^{n-2}\prod _{j=i+1}^{n-1}\prod _{k=j+1}^n{\left(max\left\{\frac{a_{ik}}{a_{ij}{a}_{jk}},\frac{a_{ij}{a}_{jk}}{a_{ik}}\right\}\right)}^{1/\left(\genfrac{}{}{0em}{}{n}{3}\right)}.$ The index ${\mathsf{I}}_{\mathsf{C}\mathsf{D}}$ is equal to 1 in the case of consistent matrices and strictly greater than 1, otherwise. In addition, Brunelli (2016b, Proposition 1) showed that ${\mathsf{I}}_{\mathsf{C}\mathsf{D}}$ is functionally related to another inconsistency index (Brunelli 2016b, formula (2)).

While attempting to formulate a method for increasing the rationality of preferences, Takeda (1993) proposed the following inconsistency index $\mathsf{M}\mathsf{C}\left(A\right)=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^n{\left(\prod _{k=1}^n{a}_{ij}{a}_{jk}{a}_{ki}\right)}^{1/n}.$ It is straightforward to show that $\mathsf{M}\mathsf{C}\ge 1$ and that it is related to another index proposed, later on, by Wu and Xu (2012).

Salo and Hämäläinen (1995) considered the sets $R_{ij}=\{a_{ik}{a}_{kj}|k=1,\dots ,n\}$. Each set contains all the theoretical values of $a_{ij}$ obtained indirectly through alternative k. Clearly, if A is consistent, each set $R_{ij}$ is a singleton. At this point, Salo and Hämäläinen (1995) proposed the following inconsistency index $\mathsf{A}\mathsf{I}\left(A\right)=\frac{2}{n(n-1)}\sum _{i=1}^{n-1}\sum _{j=i+1}^n\frac{max{R}_{ij}-min{R}_{ij}}{(1+max{R}_{ij})(1+min{R}_{ij})},$ which can be interpreted as a normalized sum of the lengths of the intervals induced by the sets $R_{ij}$'s. Index $\mathsf{A}\mathsf{I}$, which is the acronym of Ambiguity Index, was used to evaluate the inconsistency of pairwise comparisons in decision processes related to energy production (Salo and Hämäläinen 1995) and traffic planning (Hämäläinen and Pöyhönen 1996).

Fedrizzi and Ferrari (2018) based their inconsistency index on an interpretation of a PCM as a contingency table. First they defined a chi-square-based consistent approximation of the matrix A and called it $E=(e_{ij}{)}_{n\times n}$ and then they defined their inconsistency index as ${\chi }^2\left(A\right)=\sum _{i=1}^n\sum _{j=1}^n\frac{(a_{ij}-e_{ij}{)}^2}{e_{ij}}.$ If A is consistent, its rank is equal to 1 and its columns are collinear vectors. Employing the concept of cosine of angles between vectors, Kou and Lin (2014) proposed an inconsistency index related to a quantification of the lack of collinearity between the columns of A. The analytic formula of the Cosine Consistency Index is $\mathsf{C}\mathsf{C}\mathsf{I}\left(A\right)=\sqrt{\sum _{i=1}^n{\left(\sum _{j=1}^n{b}_{ij}\right)}^2},$ with $b_{ij}=a_{ij}/\sqrt{\sum _{k=1}^n{a}_{kj}^2}$.

Gass and Rapcsák (2004) used the Singular Value Decomposition to decompose A in the form $A=UD{V}^{\mathrm{T}}$ where D is a diagonal matrix with diagonal entries ${\alpha }_1,\dots ,{\alpha }_n$. Then, they find the rank one approximation $A_{\left[1\right]}=u{\alpha }_1{v}^{\mathrm{T}}$ where u and v are the first columns of U and V, respectively. Finally, their inconsistency index is $\mathsf{S}\mathsf{V}\mathsf{D}\left(A\right)=\parallel A-A_{\left[1\right]}\parallel ,$ where $\parallel \cdot \parallel$ denotes the Frobenius norm.

Kułakowski (2015) considered the condition of order preservation (COP) proposed by Bana e Costa and Vansnick (2008) and suggested the following inconsistency index $\mathsf{E}\left(A\right)=\underset{i,j}{max}\left\{a_{ij}\frac{w_j}{w_i}-1\right\}.$ Small values of $\mathsf{E}$ guarantee that COP is preserved. Although it was presented for the case of w estimated as the maximum eigenvector of A, this index can be extended to the case of w estimated by means of other methods.

Barzilai (1998) used the logarithm as group isomorphism to pass from the multiplicative to the additive approach and proposed the following as a measure of inconsistency $\mathsf{R}\mathsf{E}\left(A\right)=\frac{\sum _{i=1}^n\sum _{j=1}^n{\left(\log a_{ij}-\log \frac{w_i}{w_j}\right)}^2}{\sum _{i=1}^n\sum _{j=1}^n(\log a_{ij}{)}^2},$ where w is estimated using the geometric mean method. $\mathsf{R}\mathsf{E}$ is normalized since its values always range in the interval $[0,1]$.

Dixit (2018) drew a parallel between pairwise comparison matrices and time-irreversible Markov chains and introduced $\mathsf{S}\left(A\right)=\frac{1}{{\lambda }_{max}}\sum _{i=1}^n\sum _{j=1}^n{u}_i{w}_j{a}_{ij}\log a_{ij},$ where w and u are the principal right and left eigenvectors of A, respectively. Besides acting as an inconsistency index, $\mathsf{S}$ has an interpretation in statistical physics and it can be adapted to work with matrices with missing entries. This issue will be discussed more in detail later in the paper.

From the presentation of the inconsistency indices proposed so far, it is possible to informally study some of their basic properties. Table 1 summarizes some of them. The table should be taken as a rough analysis since these properties have not been thoroughly formalized in the literature.

Table 1. Some characteristics of inconsistency indices.

	Index
Property	$\mathsf{C}\mathsf{I}$	$\mathsf{G}\mathsf{C}\mathsf{I}$	$\mathsf{K}$	$\mathsf{A}\mathsf{T}\mathsf{I}$	$\mathsf{G}\mathsf{W}$	${\mathsf{c}}_{\mathsf{3}}$	$\mathsf{H}\mathsf{C}\mathsf{I}$	${\mathsf{I}}_{\mathsf{C}\mathsf{D}}$	$\mathsf{M}\mathsf{C}$	$\mathsf{A}\mathsf{I}$	${\chi }^2$	$\mathsf{C}\mathsf{C}\mathsf{I}$	$\mathsf{S}\mathsf{V}\mathsf{D}$	$\mathsf{E}$	$\mathsf{R}\mathsf{E}$	$\mathsf{S}$
Weight vector${}^{\mathrm{a}}$	Y	Y	N	N	Y	N	N	N	N	N	Y	Y	N	Y	Y	Y
Maxitive${}^{\mathrm{b}}$	N	N	Y	N	N	N	N	N	N	N	N	N	N	Y	N	N
Closed form${}^{\mathrm{c}}$	N	Y	Y	Y	N	Y	Y	Y	Y	Y	Y	Y	N	N	Y	N

Note: $\mathrm{Y}=\mathrm{yes}$, $\mathrm{N}=\mathrm{no}$.

${}^{\mathrm{a}}$The formulation of the inconsistency index makes explicit reference to the weight vector w or it has been shown that it can be rewritten as a function of the components of w.

${}^{\mathrm{b}}$The inconsistency index focuses on the most inconsistent triad or element of the matrix.

${}^{\mathrm{c}}$The inconsistency index can be formulated in a closed form or has an analytic solution. For some indices, e.g. $\mathsf{G}\mathsf{W}$ and $\mathsf{E}$, this depends on the method used to estimate the weight vector.

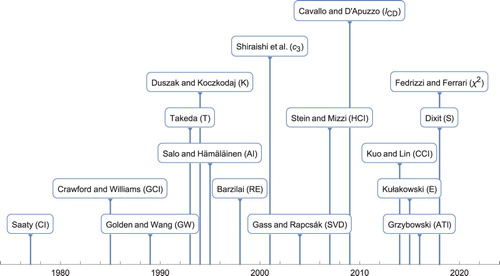
Figure 3 presents the timeline of inconsistency indices whose definitions have been recalled in this section. Other notable approaches, often variants or generalizations, have been proposed, among others, by Siraj, Mikhailov, and Keane (2015), Kułakowski and Szybowski (2014), Szybowski (2016), Osei-Bryson (2006), Wan, Chen, and Zhang (2013), Peláez, Martínez, and Vargas (2018), Brunelli and Fedrizzi (2018), and Mizuno (2019).

Figure 3. Timeline of the main developments of inconsistency indices.

4. Comparative studies

Two main streams of comparative studies stand out from the literature. The first, mostly based on numerical simulations, has investigated whether different inconsistency indices are similar or dissimilar. The second stream, based on formal studies, has aimed at understanding the meaning of different indices.

4.1. Similarities between indices

The first comparative studies appeared already in some of the papers introducing specific indices. For instance, Obata et al. (1999) compared their index ${\mathsf{c}}_{\mathsf{3}}$ with the better known $\mathsf{C}\mathsf{I}$. Comparisons of $\mathsf{C}\mathsf{I}$ with single indices were made, among other, by Stein and Mizzi (2007) for $\mathsf{H}\mathsf{C}\mathsf{I}$ and Fedrizzi and Ferrari (2018) for ${\chi }^2$. More comprehensive numerical studies were proposed by Brunelli, Canal, and Fedrizzi (2013), Kazibudzki (2016) and Cavallo (2018).

Formal studies have also been proposed to study relations between indices. Bozóki and Rapcsák (2008) compared $\mathsf{C}\mathsf{I}$ and $\mathsf{K}$ and derived formal results for the case of PCMs of orders 3 and 4. In particular, $\mathsf{C}\mathsf{I}$ and $\mathsf{K}$ are equivalent in the case of order 3. Brunelli, Critch, and Fedrizzi (2013) and Brunelli (2016b) proved that some indices which were independently introduced are, instead, functionally related, and therefore equivalent. Cavallo (2018) showed that, in fact, there are many indices which are functionally related in the case of PCMs of order 3.

As a corollary to the numerical studies, we present a summary study based on a dataset of perturbed PCM of order 6. A perturbed PCM is obtained by perturbing the entries of a consistent PCM with independent random noises ${ϵ}_{ij}$'s. More formally, given a consistent PCM $A^C=(a_{ij}^c{)}_{n\times n}$ a perturbed PCM $A^P=(a_{ij}^p{)}_{n\times n}$ is a PCM with entries $a_{ij}^p=a_{ij}^c{ϵ}_{ij}i<j,$ where ${ϵ}_{ij}\sim \mathrm{Lognormal}(0,{\sigma }^2)$ and the lower triangular entries are obtained by reciprocity. Figure 4 shows that there is a kernel of similar indices, but also some outliers.

Figure 4. Degrees of similarity between inconsistency indices, tested on perturbed PCMs of order n=6 obtained with $\sigma =0.43$. Thick solid lines denote a value of the Spearman index greater than 0.95. Thin dashed lines denote a value of the Spearman index greater than 0.9. Double circled inconsistency indices have been found functionally related to some others proposed in the literature.

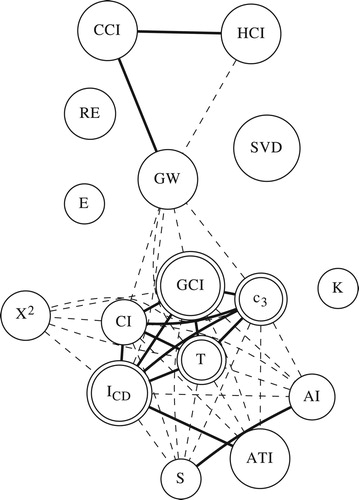
Furthermore, since some of them are functionally related they also have a double interpretation. On one hand, an analyst might be tempted to rely on indices from this kernel. On the other hand, when evaluating inconsistency, it might be prudent to use two dissimilar indices in order to consider separate evidence. It must be noted that the fact that an index is dissimilar to the others is not per se a negative feature.

4.2. Soundness of indices

The second stream of comparative studies has focused on formal properties of inconsistency indices. That is, the goal of these studies has been the definition of some basic reasonable properties which should be satisfied by any theoretically sound estimation of inconsistency. Some early attempts of formalization were proposed already by proponents of single inconsistency indices. For example, Barzilai (1998) claimed that his index $\mathsf{R}\mathsf{E}$ satisfies a number of good properties. Only recently full-fledged formal studies have appeared in the literature. Brunelli and Fedrizzi (2015a) proposed five properties and tested them on various inconsistency indices, showing that they are quite restrictive. A sixth property was added later on by Brunelli (2017) and two more by Csató (2018a). Koczkodaj and Szwarc (2014) independently proposed another set of axioms and showed that index $\mathsf{K}$ satisfies these properties. Koczkodaj et al. (2017) claimed the necessity of normalization of any inconsistency index. Koczkodaj and Urban (2018) proposed a new set of axioms to improve those proposed by Koczkodaj and Szwarc. At present, it seems that the major divergence between different axiomatization attempts is on whether to consider the inconsistency level of the most inconsistent triad of comparisons as representative of the inconsistency of the entire pairwise comparison matrix (as done by index $\mathsf{K}$) or to allow indices to average local inconsistencies (as done by the vast majority of indices). Commentaries on different attempts of studying formal properties of inconsistency indices were written by Koczkodaj et al. (2016) and Brunelli (2016a).

5. Other uses of inconsistency indices

The use of inconsistency indices is not limited to the mere quantification of inconsistency. In the years, they have proven useful for other tasks. Among the most notable uses, one might recall those presented in this section.

5.1. Inconsistency reduction

As also recalled by Keeney and Raiffa (1976, 123), “[inconsistencies] can be used by the analyst to ‘force’ the decision maker to rethink through his preferences”, which means that when a decision maker expresses pairwise comparisons which are too inconsistent he is invited to revise them. One of the first attempts to support analysts and decision makers was presented by Harker (1987a), where he analyzed the sensitivity of the index $\mathsf{C}\mathsf{I}$ to the entries of the matrix A and suggested to rethink the entries to which the value of $\mathsf{C}\mathsf{I}$ is the most sensitive. Similar approaches, which consider a measure of global consistency and indicate the contribution of each entry to suggest which ones ought to be revised, were adopted by Ishizaka and Lusti (2004), Ergu et al. (2011), Siraj, Mikhailov, and Keane (2012), and Kou, Ergu, and Shang (2014). Pragmatically, Bozóki, Fülöp, and Poesz (2011) proposed to define a maximal tolerable level of inconsistency, say δ, and then find the “closest” matrix to the original A such that its inconsistency, measured by different indices, is smaller or equal to δ. A similar approach was used by Xu and Cuiping (1999) to find an approximation of the original matrix by another matrix with $\mathsf{C}\mathsf{R}$ lower than 0.1. Bozóki, Fülöp, and Poesz (2015) presented some optimization problems to find the minimum number of entries to be changed to transform a generic PCM in a consistent one. Li and Ma (2007) exploited the idea proposed by Genest and Zhang (1996) and employed Gower plots for the visual analysis of inconsistency and its determinants. Temesi (2018) presented an analysis of different techniques for inconsistency reduction with a special attention on the connection between entries of the PCM and verbal statements.

There is not an agreement on whether automated procedures for inconsistency reduction have a positive effective on the reliability of the final result. Benítez et al. (2012) and Finan and Hurley (1997) claimed that there is a positive effect. Conversely, Gaul and Gastes (2012) and Gastes and Gaul (2012) questioned the validity of automated approaches for the improvement of inconsistency. This said, an involvement of the decision maker in the revision process is always deemed auspicable.

5.2. Incomplete pairwise comparison matrices

The use of inconsistency indices has gone beyond the mere quantification of inconsistency. One of the most important uses has been that of dealing with PCMs with missing comparisons. An incomplete pairwise comparison matrix is a PCM with some entries missing. The following is an example of incomplete PCM with entries $a_{13}$ and $a_{14}$ missing: (2) $A=\left(\begin{array}{cccc}1& 2& x& y\\ 1/2& 1& 1/3& 1\\ 1/x& 3& 1& 2\\ 1/y& 1& 1/2& 1\end{array}\right).$(2) Given an incomplete PCM one can follow two approaches: estimate the weight vector $w=(w_1,\dots ,w_n)$ only from the information coming from the given entries (Harker 1987b) or try to estimate the given entries. If one follows the second strategy, a widely accepted approach is to seek for the values of the missing entries which seem the most coherent with the known entries of the matrix. Considering the previous example, values of the missing entries are the solutions of the optimization problem ${\arg \min }_{x,y>0}\mathsf{I}\left(A\right),$ Various inconsistency indices have been used as objective functions. Shiraishi and Obata (2002) proposed to maximize the index ${\mathsf{c}}_{\mathsf{3}}$, bearing in mind that the interpretation of this index is reversed: the greater its value, the smaller the inconsistency. Peláez and Lamata (2003) proposed something similar with their index. However, since their index is proportional to ${\mathsf{c}}_{\mathsf{3}}$, this approach is equivalent to the one proposed by Shiraishi and Obata (2002). Koczkodaj, Herman, and Orlowski (1999) and Bozóki, Fülöp, and Koczkodaj (2011) followed the same approach for index $\mathsf{K}$. Similar techniques were implemented by Bozóki, Fülöp, and Rónyai (2010) for $\mathsf{C}\mathsf{I}$ and Khatwani and Kar (2016) for $\mathsf{C}\mathsf{C}\mathsf{I}$. The proposal by Bozóki, Fülöp, and Rónyai (2010) is particularly interesting because it regards the most popular inconsistency index, $\mathsf{C}\mathsf{I}$, and optimizes a non-trivial objective function by means of an algorithm based on cyclic coordinates.

Another research direction regarded the extensions of inconsistency indices to the calculation of inconsistency of incomplete PCMs and possibly the real-time prediction, while filling the entries, of the inconsistency of the complete PCM (Wedley 1993). For example, ${\lambda }_{max}$ always exists for a PCM, but deeper results were necessary to extend it to incomplete PCMs (Oliva, Setola, and Scala 2017). The capacity of an inconsistency index to be extensible to incomplete PCMs should be considered a good property. Recently, Ureña et al. (2015) offered a comprehensive survey on incomplete preferences and related topics.

5.3. Extensions to other representations of pairwise comparisons

It is safe to say that the theory of pairwise comparison matrices — and the development of inconsistency indices with it — has been extended in two distinct directions. Although a full exposition of this topic is well beyond the scope of this manuscript (see instead Xu 2007), it is important to underline the fundamental concepts.

1. The first type of extensions regards pairwise comparisons expressed on different representation domains. For example, additive preferences are expressed on the entire real line and reciprocal preference relations, also called fuzzy preference relations, are expressed on the unit interval $]0,1[$ (sometimes $[0,1]$). Consistency indices for reciprocal preference relations have been introduced, among others, by Fedrizzi and Giove (2007) and Herrera-Viedma et al. (2007). Nonetheless, the number of inconsistency indices proposed for these approaches is small when compared to those proposed for PCMs. In fact, other representations of pairwise comparisons can be transformed into PCMs by means of suitable morphisms resulting in different approaches being de facto isomorphic (Cavallo and D'Apuzzo 2009). Oftentimes such isomorphisms have revealed that inconsistency indices proposed separately for different approaches were instead equivalent. The existence of transformations between different representation domains implies that inconsistency indices normally used for PCMs can straightforwardly be extended to many other representations of preferences.

2. The second direction includes approaches which generalize the concept of pairwise comparison matrix to introduce uncertainty in the judgments by employing probability theory, fuzzy sets theory, interval arithmetics and so forth. When the judgments are expressed as fuzzy numbers one could use, for instance, the inconsistency index proposed by Ramík and Korviny (2010), Ramík and Perzina (2010) and commented by Brunelli (2011), or the indices proposed by Fedrizzi and Marques Pereira (1995), Ohnishi et al. (2008), Kubler et al. (2017). In the case of preferences expressed as real intervals, one could, instead, refer to the indices proposed by Li, Wang, and Tong (2016), Cavallo and Brunelli (2018), Zhang (2017), and Liu et al. (2018). Other representations, like those based on hesitant fuzzy sets, have been objects of proposals (Zhang and Wu 2014; Zhu and Xu 2014; Liu, Xu, and Liao 2016). A monograph on non-conventional representations of preferences and the measurement of their inconsistency with a special emphasis on fuzzy sets was recently written by Krejčí (2018). By observing the indices proposed in these extended frameworks, one can however note that they are generalizations of well-known indices used for PCMs, or at the very least they have a very clear interpretation in the real valued case. Hence, when the general representations collapse into real numbers, then also the proposed inconsistency indices collapse in well-known ones.

Although both types of generalizations have been a fertile ground for the introduction of inconsistency indices, one can argue that their originality is limited, since they often descend from indices already proposed for PCMs. For this reason, the analysis of indices proposed for PCMs does not seem limiting and results on these indices can be extended to their generalizations.

5.4. Group decision-making

Since most of real-world decisions are not made by individuals, but by groups and committees, the relation between inconsistency and group decision-making has attracted a great deal of attention. The fundamental premise is that, given m individual PCMs $A_1,\dots ,A_m$, a group PCM $A^{\ast }$ can be obtained as the entry-wise weighted geometric mean of the individual PCMs, (3) $A^{\ast }={\left(a_{ij}^{\ast }\right)}_{n\times n}={\left(\prod _{k=1}^m{\left(a_{ij}^{\left(k\right)}\right)}^{{\omega }_k}\right)}_{n\times n},$(3) where ${\omega }_1,\dots ,{\omega }_m$ with ${\omega }_k\ge 0$ and ${\omega }_1+\cdots +{\omega }_m=1$ are the degrees of importance (or voting powers) of different decision makers in the preference aggregation process. It has been proven that this aggregation method (3(3) $A^{\ast }={\left(a_{ij}^{\ast }\right)}_{n\times n}={\left(\prod _{k=1}^m{\left(a_{ij}^{\left(k\right)}\right)}^{{\omega }_k}\right)}_{n\times n},$(3) ) is the only one which satisfies a number of reasonable properties (Aczél and Saaty 1983).

A research question regarded possible implications between the inconsistency of individual PCMs $A_1,\dots ,A_m$ and the inconsistency of the group PCM $A^{\ast }$. Initially, Xu (2000) claimed the proof that the $\mathsf{C}\mathsf{I}$ of the group preferences cannot be greater than the $\mathsf{C}\mathsf{I}$ of the most inconsistent individual PCM, i.e. $\mathsf{C}\mathsf{I}\left(A^{\ast }\right)\le max\left\{\mathsf{C}\mathsf{I}\right(A_1),\dots ,\mathsf{C}\mathsf{I}(A_m\left)\right\}$. Lin et al. (2008) found a fallacy in Xu's proof, thus leaving it as a conjecture. Liu, Zhang, and Wang (2012) finally proved Xu's conjecture and Grošelj and Stirn (2012) showed that it comes from more general results by Elsner, Johnson, and Dias da Silva (1988). Escobar, Aguarón, and Moreno-Jiménez (2004) provided similar results for the case of index $\mathsf{G}\mathsf{C}\mathsf{I}$. Brunelli and Fedrizzi (2015b) used a more general approach and related the property of being below a given threshold with some general properties of a given inconsistency index.

A second research direction has tried to formulate algorithms able to account for consensus and consistency within the same mathematical model. There is a vast literature on this subject, but a common goal seems to be that of reaching a sufficiently consensual solution keeping the inconsistency of preferences under a given threshold (Chiclana et al. 2008; Wu and Xu 2012; Escobar, Aguarón, and Moreno-Jiménez 2015).

In spite of the relevance of these results, the inconsistency of the group pairwise comparisons has to be interpreted with some caution. In fact, a low level of inconsistency of the group preferences should not be taken as a guarantee of their reliability, since the group preferences could have been obtained by fusing extremely inconsistent individual pairwise comparisons. Seemingly, some deeper reflection on the interpretation of the (in)consistency of a group PCM and its implications is due.

5.5. Weaker rationality conditions

It is nowadays accepted that consistency, albeit desirable, is an utopic condition which can hardly ever be reached in practice. Out of the many possible conditions of rationality, consistency is the most restrictive. Then, some authors (Basile and D'Apuzzo 2002, 2006) preferred to investigate conditions weaker than consistency as, for instance, transitivity, $a_{ij}\ge 1\mathrm{and}{a}_{jk}\ge 1\Rightarrow a_{ik}\ge 1\mathrm{\forall }i,j,k,$ restricted $max$ –$max$ transitivity $a_{ij}\ge 1\mathrm{and}{a}_{jk}\ge 1\Rightarrow a_{ik}\ge max\{a_{ij},a_{jk}\}\mathrm{\forall }i,j,k,$ rank-order consistency (Finan and Hurley 1996), weak consistency (Cavallo, D'Apuzzo, and Basile 2016), and pairwise dominance (Saaty and Vargas 2012). Unlike inconsistency indices, which are based on a concept of “cardinal” distance, so far indices used to capture the violation of these weaker conditions have been proposed as simple counts of how many times the condition is violated in a given PCM (Kułakowski 2018). Further research could help bridge this gap.

6. Discussion

In a recent a bibliographical study on the publications about pairwise comparisons in multi-criteria decision-making in the years 2010–2015, Kou et al. (2016) stated that “The most popular research topic is the inconsistency issue”. The scope of this survey is precisely that of offering an overview on inconsistency indices and their connections with related topics.

Oppositely to some studies questioning the connection between rationality of pairwise comparisons and reliability of decision (Linares 2009; Temesi 2011), the vast majority of the literature seems to agree on the fact that a high degree of inconsistency of pairwise comparisons could be symptomatic of a lack of quality of these latter. This, in final analysis, could negatively affect the quality of the weight vector $w=(w_1,\dots ,w_n)$ obtained from the pairwise comparisons. Remarkably, this point of view, albeit more studied in the AHP, is relevant for other methodologies, such as MAVT.

In spite of a well-established definition of consistency, there is not a meeting of mind on a unique definition of inconsistency. In fact, each inconsistency index can be seen as an implicit definition of inconsistency. In this paper, we explicitly considered 16 inconsistency indices – each reflecting a different perspective on the quantification of inconsistency – and reviewed their developments also in connection with other aspects of pairwise comparisons. It is also interesting to reckon that most of the methods for deriving a weight vector w from A also implicitly define an inconsistency metric. In fact, the derived w can be associated to a consistent matrix $(w_i/w_j{)}_{n\times n}$ and so what the method for deriving the vector really does is finding the “closest” (with respect to an implicit metric) matrix $(w_i/w_j{)}_{n\times n}$ to A. Of course, the metric quantification of “closest” can be interpreted as the level of inconsistency of A.

Within the study of inconsistency indices some promising research niches have manifested themselves and are worth few additional remarks.

• Studying formal properties of inconsistency indices has made some formal order and improved our understanding of what the indices really do. It has also shifted the discussion on the general idea of inconsistency index and on what we really mean with this definition. Although there is not (and there might never be) a complete agreement on what basic properties ought to be satisfied by an inconsistency index, it is safe to say that analyzing formal properties of inconsistency indices is a necessary step in order to make them intelligible and communicable.

• Algebraic studies have appeared in the recent literature (Cavallo and D'Apuzzo 2009; Koczkodaj, Szybowski, and Wajch 2016; Cavallo and Brunelli 2018). These studies employ concepts from abstract algebra and they have helped clarify some controversial aspects of the pairwise comparisons technique. Similarly, they helped define and study mathematically sound inconsistency indices. Hence, they should be welcome in the literature, as long as they are not an end unto themselves.

• Most of the studies on inconsistency indices have been based on formal methods or on Monte Carlo simulations. Needless to say, real-world pairwise comparisons presents regularities and patterns and are far from being random. Results on inconsistency indices, and on preference relations in general, are as realistic as they are based on real data. This was recently acknowledged, among others, by Bozóki et al. (2013) and Cavallo et al. (2018) in some studies on pairwise comparisons and by Regenwetter et al. (2006) in a critique of the random culture in computational social choice. Due to these reasons, and considering the scarcity of empirical studies in the literature, it is foreseeable that new studies of this type could be valuable contributions.

• A concrete problem, with practical implications, is the determination of the so-called thresholds. Inconsistency is a matter of degree but it is very often used together with some sharp thresholds, as the widely accepted rule that matrices with $\mathsf{C}\mathsf{R}\le 0.1$ are not too inconsistent and thus acceptable. That is, a crisp decision rule must be stipulated on the fuzzy concept of “too inconsistent”. In spite of this impasse, it is still safe so say that deeper statistical studies (Lin, Kou, and Ergu 2013, 2014) on threshold values, also in relation to the index on which they are used, could improve the decision analysis process. Another viable solution would be that of favoring indices whose values have a clear interpretation.

• Many inconsistency indices have been proposed thus far. This does not mean that there is not space to introduce new ones. Rather, this should entail that, to make a valuable contribution, when introducing a new index scholars need to account for the existing indices, pointing out the novelties in the newly introduced one and clearly show its properties and discuss its advantages.

All in all, the study of the inconsistency of pairwise comparisons has attracted the attention of scholars from the most disparate fields of science, such as mathematics, behavioral sciences, and economics, just to name a few, and the use of different tools of scientific inquiry, like formal methods and behavioral studies. It is the author's opinion that this ought to be regarded as a paragon of how different fields can build on each other.

Acknowledgments

I am indebted to Michele Fedrizzi, my mentor, who introduced me to this research topic 15 years ago. My conversations with Michele have nurtured many of the ideas and visions presented in this manuscript. I also wish to express my gratitude to the Editor and the reviewers for their comments.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Notes on contributors

Matteo Brunelli

Matteo Brunelli obtained his Bachelor and Master degrees from the University of Trento, Italy, and his PhD from Åbo Akademi University, Finland. He spent five years as a Postdoctoral researcher at Aalto University, Finland, and he is presently an Assistant Professor at the Department of Industrial Engineering of the University of Trento. His research interests include decision analysis, preference modeling, mathematical representations of uncertainty and fuzzy sets.

Notes

1. Consider, for example, the “subadditivity effect” bias (Hilbert 2012).

2. Inconsistency indices have often been equivalently called consistency indices in the literature.