Estimation of variance components, heritability and the ridge penalty in high-dimensional generalized linear models

Abstract

For high-dimensional linear regression models, we review and compare several estimators of variances ${\tau }^2$ and ${\sigma }^2$ of the random slopes and errors, respectively. These variances relate directly to ridge regression penalty λ and heritability index h², often used in genetics. Several estimators of these, either based on cross-validation (CV) or maximum marginal likelihood (MML), are also discussed. The comparisons include several cases of the high-dimensional covariate matrix such as multi-collinear covariates and data-derived ones. Moreover, we study robustness against model misspecifications such as sparse instead of dense effects and non-Gaussian errors. An example on weight gain data with genomic covariates confirms the good performance of MML compared to CV. Several extensions are presented. First, to the high-dimensional linear mixed effects model, with REML as an alternative to MML. Second, to the conjugate Bayesian setting, shown to be a good alternative. Third, and most prominently, to generalized linear models for which we derive a computationally efficient MML estimator by re-writing the marginal likelihood as an n-dimensional integral. For Poisson and Binomial ridge regression, we demonstrate the superior accuracy of the resulting MML estimator of λ as compared to CV. Software is provided to enable reproduction of all results.

KEYWORDS:

• Random effects
• Ridge regression
• Empirical Bayes
• Marginal likelihood
• Cross-validation

1. Introduction

Estimation of hyper-parameters is an essential part of fitting high-dimensional Gaussian random effect regression models, also known as ridge regression. These models are widely applied in genomics and genetics applications, where often the number of variables p is much larger than the number of samples n, i.e. $p\gg n$.

We initially focus on the linear model. The goal is to estimate error variance ${\sigma }^2$ and random effects variance ${\tau }^2$ or functions thereof, in particular the ridge penalty parameter, $\lambda =\frac{{\sigma }^2}{{\tau }^2}$, or heritability index, $h^2=\frac{p{\tau }^2}{p{\tau }^2+{\sigma }^2}$. Here, the ridge penalty is used in classical ridge regression to shrink the regression coefficients towards zero (Hoerl and Kennard 1970), whereas heritability measures the fraction of variation between individuals within a population that is due to their genotypes (Visscher, Hill, and Wray 2008). The estimators of ${\sigma }^2$ and ${\tau }^2$ can be used to estimate λ or h², or for statistical testing (Kang et al. 2008). We review several estimators, based on maximum marginal likelihood (MML), moment equations, (generalized) cross-validation, dimension reduction, and for degrees-of-freedom adjustment. Some of these estimators are classical, while others have recently been introduced.

We systematically review and compare the estimators in a broad variety of high-dimensional settings. For estimation of λ in low-dimensional settings, we refer to Muniz and Kibria (2009); Månsson and Shukur (2011); Kibria and Banik (2016). We address the effect of multi-collinearity and robustness against model misspecifications, such as sparsity and non-Gaussian errors. The comparisons are extended to the linear mixed effects model, with $q\ll n$ fixed effects added to the model and to Bayesian linear regression. The linear model part is concluded by a genomics data application to weight gain prediction after kidney transplantation.

The observed good performance of MML-estimation in the linear model setting was a stimulus to consider MML for high-dimensional generalized linear models (GLM). MML is more involved here than in the linear model, because of the non-conjugacy of the likelihood and prior. Therefore, approximations are required, such as Laplace ones. While these have been addressed by others (Heisterkam, van Houwelingen, and Downs 1999; Wood 2011), we derive an estimator which is computationally efficient for $p\gg n$ settings. For Poisson and Binomial ridge regression, we demonstrate the superior accuracy of MML estimation of λ as compared to cross-validation.

Our software enables reproduction of all results. In addition, it allows comparisons for one’s own high-dimensional data matrix by simulating the response conditional on this matrix, as we do for two cancer genomics examples. Computational shortcuts and considerations are discussed throughout the paper, and detailed at the end, including computing times.

1.1. The model

We initially focus on high-dimensional linear regression with random effects. Variables are denoted by $j=1,\dots ,p$ and samples by $i=1,\dots ,n$. Then:(1) $$\begin{array}{l}{y}_{n\times 1}=X_{n\times p}{\beta }_{p\times 1}+{ϵ}_{n\times 1}\\ {\beta }_{p\times 1}\sim \mathcal{N}(0,{\tau }^2{\mathrm{I}}_p)\\ {ϵ}_{n\times 1}\sim \mathcal{N}(0,{\sigma }^2{\mathrm{I}}_n).\end{array}$$(1)

Here, $y=(y_1,\dots ,y_n)$ is the vector of responses, $\beta ={({\beta }_1,\dots ,{\beta }_p)}^T$ corresponds to the random effects and $ϵ={({ϵ}_1,\dots ,{ϵ}_n)}^T$ is a vector of Gaussian errors. Furthermore, X is a fixed n × p matrix: ${(X_1\cdots X_n)}^T,$ with $X_i={(x_{i1},\dots ,x_{\mathit{ip}})}^T$.

1.2. Estimation methods

We distinguish three categories of estimation methods:

1. Estimation of functions of $({\sigma }^2,{\tau }^2)$, in particular: i) $\lambda =\frac{{\sigma }^2}{{\tau }^2}$ (Golub, Heath, and Wahba 1979), used in ridge regression to minimize $\left|\right|y-X\beta |{|}_2^2+\lambda |\left|\beta \right|{|}_2^2$ ; and ii) heritability $h^2=\frac{p{\tau }^2}{p{\tau }^2+{\sigma }^2}$ (Bonnet, Gassiat, and Lévy-Leduc 2015).

2. Separate estimation of ${\sigma }^2$ (Cule, Vineis, and De Iorio 2011; Cule and De Iorio 2012), possibly followed by plug-in estimation of ${\tau }^2$.

3. Joint estimation of ${\sigma }^2$ and ${\tau }^2$.

Below, we discuss several methods for each of these categories. They have several matrices and matrix computations in common, which we therefore introduce first.

1.3. Notation and matrix computations

Throughout the paper, we will use the following notation:(2) $$\begin{array}{l}\widehat{\beta }={\widehat{\beta }}_{\lambda }={\mathrm{C}}_{\lambda }y={(X^{T}X+\lambda I_{p\times p})}^{-1}{X}^{T}y \mathrm{i}.\mathrm{e}.\text{the}\text{linear}\text{ridge}\text{estimator}\hfill \\ H=H_{\lambda }=X{\mathrm{C}}_{\lambda }=X{(X^{T}X+\lambda I_{p\times p})}^{-1}{X}^T\mathrm{i}.\mathrm{e}.\text{the}\text{hat}\text{matrix}.\hfill \end{array}$$(2)

Many of the estimators below require calculations on potentially very large matrices. The following two well-known equalities can highly alleviate the computational burden.

First, $\mathrm{C}=C_{\lambda }$, and hence also $\widehat{\beta }$ and H, can be efficiently computed by using singular value decomposition (SVD). Decompose $X=U_{n\times n}{D}_{n\times n}{(V_{p\times n})}^T$ by SVD, and denote ${\mathbf{\Lambda }}_q=\lambda {\mathrm{I}}_q$. Then,(3) $$C={(X^{T}X+{\mathbf{\Lambda }}_p)}^{-1}{X}^T=V{(D^2+{\mathbf{\Lambda }}_n)}^{-1}D{U}^T.$$(3)

The latter requires inversion of an n × n matrix only. Second, the following efficient trace computation for matrix products applies to $\text{tr}(H)=\text{tr}(X{C}_{\lambda }):$ (4) $$\text{tr}\left(A_{p\times n}{B}_{n\times p}\right)=\sum _{i=1}^n\sum _{j=1}^p[A°B^T{]}_{\mathit{ij}}.$$(4)

2. Methods

2.1. Estimating functions of ${\sigma }^2$ and ${\tau }^2$

2.1.1. Estimating λ by K-fold CV

A benchmark method that is used extensively to estimate $\lambda ={\sigma }^2/{\tau }^2$ is cross-validation. Here, we use K-fold CV, as implemented in the popular R-package glmnet (Friedman, Hastie, and Tibshirani 2010). Let f(i) denote the set of samples left out for testing at the same fold as sample i. Then, CV-based estimation of λ pertains to minimizing the cross-validated prediction error:(5) $${\lambda }_{\mathit{cv}}=\underset{\lambda }{\text{arg} \text{min}}\left\{\sum _{i=1}^n{(y_i-X_i{\widehat{\beta }}_{\lambda }^{-f\left(i\right)})}^2\right\},$$(5) where ${\widehat{\beta }}_{\lambda }^{-f(i)}$ denotes the estimate of $\beta$ based on training samples $\{1,\dots ,n\}\setminus f(i)$ and penalty λ. Note that for leave-one-out-cross-validation (n-fold CV) the analytical solution of (5) is the PRESS statistic (Allen 1974).

2.1.2. Estimating λ by generalized cross validation

Generalized Cross Validation (GCV) is a rotation-invariant form of the PRESS statistic. It is more robust than the latter to (near-diagonal) hat matrices $H_{\lambda }$ (Golub, Heath, and Wahba 1979). For the linear model, the criterion is (Hastie, Tibshirani, and Friedman 2008):(6) $$\text{GCV}\left(\lambda \right)=\sum _{i=1}^n(\frac{y_i-X_i^T{\widehat{\beta }}_{\lambda }}{n-\text{tr}\left(H_{\lambda }\right)}{)}^2$$(6) where the trace of $H_{\lambda }$ can be computed efficiently by (4). Then, ${\lambda }_{\text{gcv}}=\text{arg} {\text{min}}_{\lambda }\text{GCV}(\lambda )$.

2.1.3. Estimating heritability by HiLMM

Heritability is defined by $h^2=\frac{p{\tau }^2}{p{\tau }^2+{\sigma }^2}$. A recent method which estimates heritability directly using maximum likelihood is proposed by Bonnet, Gassiat, and Lévy-Leduc (2015). Analogously to Eq. (12)(12) $$P\left(y\right)=\mathcal{N}(y;\mu =0,\mathbf{\Sigma }=X{X}^T{\tau }^2+{\sigma }^2{I}_n).$$(12) , it is based on writing:(7) $$y\sim \mathcal{N}(0,h^2{\sigma }^{*2}\mathrm{R}+(1-h^2\left){\sigma }^{*2}{\mathrm{I}}_n\right),$$(7) where ${\sigma }^{*2}=p{\tau }^2+{\sigma }^2$ and $R=X{X}^T/p$. Now, apply an eigen-decomposition to R: $R=\text{QL}{Q}^T$. Then, heritability is estimated by Bonnet, Gassiat, and Lévy-Leduc (2015):(8) $$h^2=\underset{h^2}{\text{arg} \text{max}}(-\hspace{0.17em}\text{log}\hspace{0.17em}(\frac{1}{n}\sum _{i=1}^n\frac{{\tilde{y}}_i^2}{h^2({\ell }_i-1)+1})-\frac{1}{n}\sum _{i=1}^n(\hspace{0.17em}\text{log}\hspace{0.17em}(h^2({\ell }_i-1)+1)),$$(8) with ${\ell }_i$ and ${\tilde{y}}_i$ the ith element of L and $\tilde{y}=Q^{T}y$, respectively. The authors provide rigorous consistency results for their estimator, as well as theoretical confidence bounds, also for mixed models and sparse settings.

2.2. Estimation of ${\sigma }^2$

The two methods below rely on an estimate $\widehat{\beta }={\widehat{\beta }}_{\lambda }$, where $\lambda ={\sigma }^2/{\tau }^2$ is estimated by (G)CV. Then ${\sigma }^2$ is estimated conditional on $\widehat{\beta }.$ If desired, ${\tau }^2$ may then be estimated by ${\widehat{\tau }}^2={\widehat{\sigma }}^2/\widehat{\lambda }.$

2.2.1. Basic estimate

A basic estimate of ${\sigma }^2$, and often used in practice, is given by (Hastie and Tibshirani 1990):(9) $${\widehat{\sigma }}^2=\frac{{(y-X\widehat{\beta })}^T(y-X\widehat{\beta })}{\nu }$$(9) which is the residual mean square error. Here, the residual effective degrees of freedom (Hastie and Tibshirani 1990) equals $\nu =n-\text{tr}(2H-H{H}^T)$, with H as in (2). We also considered (9) with $\nu =n-\text{tr}(H)$, as in Hellton and Hjort (2018), which rendered similar, slightly inferior results.

2.2.2. PCR-based estimate

The estimator for ${\sigma }^2$ may also be based on Principal Component Regression (PCR). PCR is based on the eigen-decomposition $X^{T}X=\tilde{\mathrm{Q}}{\mathrm{D}}^2{\tilde{\mathrm{Q}}}^T$. Denoting $\mathrm{Z}=X\tilde{\mathrm{Q}}$ and $\alpha ={\tilde{\mathrm{Q}}}^T\beta$, we have $y=\mathrm{Z}\alpha +ϵ$. Then, Z is reduced from p columns to $r\le \text{min}(n,p)$ principal components, a crucial step (Cule and De Iorio 2012). Using the reduced model, ${\sigma }^2$ is estimated by the residual mean square error (Cule and De Iorio 2012):(10) $${\widehat{\sigma }}_r^2=\frac{{(y-Z_r{\widehat{\alpha }}_r)}^T(y-Z_r{\widehat{\alpha }}_r)}{n-r}.$$(10)

2.3. Joint estimation of ${\sigma }^2$ and ${\tau }^2$

2.3.1. MML

An Empirical Bayes estimate of ${\sigma }^2$ and ${\tau }^2$ is obtained by maximizing the marginal likelihood (MML), also referred to as model evidence in machine learning (Murphy 2012). This corresponds to:(11) $$\underset{{\sigma }^2,{\tau }^2}{\text{arg} \text{max}}P\left(y\right)=\underset{{\sigma }^2,{\tau }^2}{\text{arg} \text{max}}{\int }_{\beta }\ell (y;\beta ,{\sigma }^2)\pi (\beta ;{\tau }^2)d\beta .$$(11)

Since $y=X\beta +ϵ,P(y)$ is simply derived from the convolution of Gaussian random variables, implying $E[y]=E[X\beta ]+E[ϵ]=0$, and $V[y]=V[X\beta ]+V[ϵ]=X{X}^T{\tau }^2+{\sigma }^2{I}_n$, so(12) $$P\left(y\right)=\mathcal{N}(y;\mu =0,\mathbf{\Sigma }=X{X}^T{\tau }^2+{\sigma }^2{I}_n).$$(12)

This is easily maximized over ${\sigma }^2$ and ${\tau }^2$. Note that after computing $X{X}^T$ (12) requires operations on n × n matrices only.

2.3.2. Method of moments (MoM)

An alternative to MML is to match the empirical second moments of y to their theoretical counterparts. From (12) we observe that the covariances depend on ${\tau }^2$ only. Hence, we obtain an estimator of ${\tau }^2$ by equating the sum of $y_i{y}_k$ to that of the theoretical covariances, ${\mathbf{\Sigma }}_{\mathit{ik}}=\mathbb{E}[y_i{y}_k]$, with $\mathbf{\Sigma }$ as in (12). Then, with ${\mathbf{\Sigma }}^X=X{X}^T$, an estimator for ${\sigma }^2$ is obtained by substituting ${\widehat{\tau }}^2$ and equating the sum of $y_i^2$ to the sum of theoretical variances, ${\mathbf{\Sigma }}_{\mathit{ii}}=\mathbb{E}[y_i^2]$ :(13) $$\begin{array}{l}{\widehat{\tau }}^2=\frac{{\sum }_{i\ne k}^{n,n}{y}_i{y}_k}{{\sum }_{i\ne k}^{n,n}{\mathbf{\Sigma }}_{\mathit{ik}}^X}\hfill \\ {\widehat{\sigma }}^2=n^{-1}\sum _{i=1}^n(y_i^2-{\widehat{\tau }}^2{\mathbf{\Sigma }}_{\mathit{ii}}^X).\hfill \end{array}$$(13)

These equations also hold for non-Gaussian error terms, which could be an advantage over MML. Moreover, no optimization over ${\sigma }^2$ and ${\tau }^2$ is required, so MoM is computationally very attractive.

3. Comparisons

For the linear random effects model (ridge regression) we study the following settings:

• $\beta$ and $ϵ$ generated from model (1), independent X

• $\beta$ or $ϵ$ generated from non-Gaussian distributions, independent X

• $\beta$ and $ϵ$ from model (1), multicollinear X

• $\beta$ and $ϵ$ from model (1), data-based X.

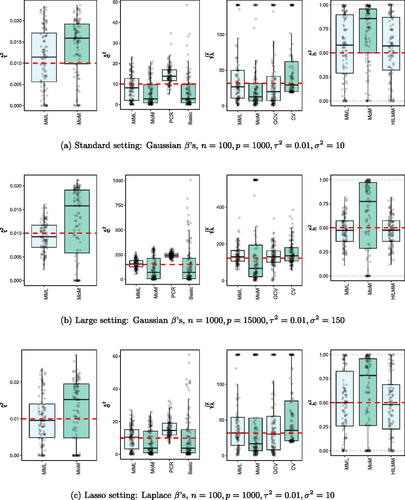
As is common for real data, the variables, i.e. the rows of X, were always standardized for the L₂-penalty to have the same effect on all variables. All the results are based on 100 simulated data sets. Cross-validation is applied on 10 folds. Results from n-fold CV (leave-one-out) were generally fairly similar. We focus on the high-dimensional setting with $n=100,p=1000$, with excursions to larger data sets and dimensions of real data. In all visualizations below the red dotted lines indicate true values. Moreover, values larger than 20 times the true value were truncated and slightly jittered. Discussion of all results is postponed to Sec. 3.4.

3.1. Independent X

In correspondence to model (1) we sample:(14) $$\begin{array}{ll}{y}_{n\times 1}=X_{n\times p}{\beta }_{p\times 1}+{ϵ}_{n\times 1}\hfill & \hspace{1em}{ϵ}_i\stackrel{\text{iid}}{\sim }\mathcal{N}(0,{\sigma }^2)\hfill \\ x_{\mathit{ij}}\stackrel{\text{iid}}{\sim }\mathcal{N}(0,1)\hfill & \hspace{1em}{\beta }_j\stackrel{\text{iid}}{\sim }\mathcal{N}(0,{\tau }^2).\hfill \end{array}$$(14)

Figure 1a and b display the results for $n=100,p=1000,{\tau }^2=0.01,{\sigma }^2=10$ and for a large data setting $n=1000,p=15000,{\tau }^2=0.01,{\sigma }^2=150$ (which both imply $h^2=0.5$).

Figure 1. Results for independent.

3.2. Departures from a normal effect size distribution

We study the robustness of the methods against (sparse) non-Gaussian effect size distribution or error distribution. In sparse settings, many variables do not have an effect. To mimic this, we simulated the β’s from a mixture distribution with a ‘spike’ and a Gaussian ‘slab’:(15) $${\beta }_j\stackrel{\text{iid}}{\sim }{p}_0{\delta }_0+(1-p_0)\mathcal{N}(0,{\tau }_0^2).$$(15)

Here, we set $p_0=0.9,{\tau }_0^2=0.1,$ which implies ${\tau }^2=\mathbb{V}({\beta }_j)=\mathbb{E}({\beta }_j^2)-\mathbb{E}{({\beta }_j)}^2=(1-p_0){\tau }_0^2=0.01$, as in the Gaussian β_j setting. Moreover, we also considered:$${\beta }_j\stackrel{\text{iid}}{\sim } \text{Laplace}(\mu =0,b=0.0707)\hspace{1em}\text{and}\hspace{1em}{\beta }_j\stackrel{\text{iid}}{\sim } \text{Uniform}(a=-0.17,b=0.17)$$where again the parameters are chosen such that $E({\beta }_j)=0$ and ${\tau }^2=\mathbb{V}({\beta }_j)=0.01.$ Apart from $\beta$ all other quantities are simulated as in (14). Results are displayed for ${\sigma }^2=10,{\tau }^2=0.01,n=100,p=1000$ in Figure 1c for the Laplace (= lasso) effect size distribution and in Supplementary Figure 3 for the spike-and-slab and uniform effect size distribution.

Moreover, we considered heavy-tailed errors by sampling$$ϵ{\prime }_i\stackrel{\text{iid}}{\sim }{ \mathrm{t}}_4\hspace{1em}{ϵ}_i={(10/2)}^{1/2}ϵ{\prime }_i$$where the scalar is chosen such that ${\sigma }^2=\mathbb{V}({ϵ}_i)=10$, as in the Gaussian error setting. Apart from $ϵ$, all other quantities are simulated as in (14). Results are displayed in Supplementary Figure 3c.

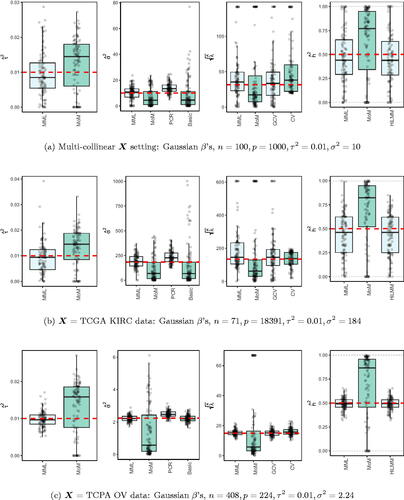
3.3. Multicollinear X

3.3.1. Simulated X

Next, the design matrix X is sampled using block-wise correlation. We replace the sampling of X in simulation model (14) by:(16) $$\begin{array}{l}{X}_{n\times p}\sim \mathcal{N}(0,\mathbf{\Xi }),\hfill \end{array}$$(16) where $\mathbf{\Xi }$ is a unit variance covariance matrix with blocks of size $p^{*}\ll p$ with correlations ρ on the off-diagonal. Figure 2a shows the results for $\rho =0.5,p^{*}=10,n=100,p=1000$.

Figure 2. Results for multi-collinear and real.

3.3.2. Real data X

Finally, we consider the estimation of ${\tau }^2$ and ${\sigma }^2$ in a high- and medium-dimensional setting where X are real data, with likely collinear columns. The first data set (TCGA KIRC) concerns gene expression data of p = 18, 391 genes for n = 71 kidney tumors. The second data set (TCPA OV) holds expression data of p = 224 proteins for n = 408 ovarian tumor samples. Details on both data sets are supplied in the Supplementary Information. To generate response y we use model (14) with X given by the data. Here, ${\tau }^2=0.01$ and ${\sigma }^2$ is set such that $h^2=0.5.$ Figure 2b and c show the results.

3.4. Discussion of results

3.4.1. MML vs MoM, basic and PCR

Figures 1 and 2 and Supplementary Figure 3 clearly show superior performance of MML compared to MoM: both the bias and variability are much smaller for MML. Generally, MML also outperforms the Basic and PCR estimators of ${\sigma }^2$. The PCR estimator approaches the performance of MML for the KIRC and TCPA data (Figure 2b and c), and the Basic estimator performs reasonably well for the latter (p < n) data set. For other settings, the Basic estimator performs equally inferior as MoM. The results highlight the importance of joint estimation of ${\sigma }^2$ and ${\tau }^2$ in high-dimensional settings, because of their delicate interplay.

3.4.2. MML vs GCV and CV

For the estimation of λ MML seems slightly superior to GCV and CV. GCV shows more estimates that deviate towards too small values of λ (e.g. Figures 1b and 2b, i.e. the large p settings), whereas CV tends to render somewhat more skewed results, either to the right (Figures 1a and c, 2a), or to the left (Figure 2b). For the spike-and-slab and uniform effects sizes and the t₄ errors the right-skewness of the CV-results is more pronounced (Supplementary Figure 3), indicating that minimization of the cross-validated prediction error (5) is more vulnerable to non-Gaussian y than MML and GCV. Note that the Laplace setting (Figure 1c) relates directly to the lasso prior with scale parameter $1/{\lambda }_1$ (Tibshirani 1996). The results indicate that MML with Gaussian prior could be useful to find the lasso penalty, or serve as a fast initial estimate by simply setting the lasso penalty ${\lambda }_1=\sqrt{2}/\widehat{\tau }$, which follows from the variance of the lasso prior.

3.4.3. MML vs HiLMM

For the estimation of heritability h² Figures 1 and 2 and Supplementary Figure 3 show very comparable performance of MML and HiLMM. This similar performance is not surprising given that both methods are likelihood-based. Hence, while reparametrizing the likelihood (7) is certainly useful to study it as function of h² (Bonnet, Gassiat, and Lévy-Leduc 2015), the reparametrization seems not beneficial for the purpose of estimating h². In addition, unlike HiLMM, MML also returns estimates of ${\tau }^2$ and ${\sigma }^2$. Finally, comparing Figure 1a and b we observe that both MML and HiLMM clearly benefit from the larger n and p.

4. Data example

We re-analyse the weight gain data, recently discussed in Hellton and Hjort (2018). Details on the data are presented there, we provide a summary. The data consists of expression profiles of n = 26 individuals with kidney transplants, where profiles consists of 28,869 genes as measured by Affymetrix Human Gene 1.0 ST arrays. The data is available in the EMBL-EBI ArrayExpress database (www.ebi.ac.uk/arrayexpress) under accession number E-GEOD-33070. It is known that kidney transplantation may lead to weight gain, and the study by Cashion et al. (2013) investigates whether gene expression can be used to predict this. Such a prediction can be used to decide upon additional measures to prevent excessive weight gains. We reproduced the analysis by Hellton and Hjort (2018) as much as possible, including their prior selection of 1000 genes. Details on minor discrepancies, and an alternative analysis that accounts for the gene selection are discussed in the Supplementary Material. These did not affect the comparison qualitatively.

In Hellton and Hjort (2018), the authors illustrate their focused ridge (fridge) method and compare it with conventional ridge. In short, fridge estimates sample-specific ridge penalties, based on minimizing a per sample mean squared error (MSE) criterion on the level of the linear predictor $X_i\beta$. Since $\beta$ is not known, it is replaced by an initial ridge estimate, ${\widehat{\beta }}_{\lambda }.$ Their sample specific penalty then depends on $X_i$, and also on both $\widehat{\lambda }$ and ${\widehat{\sigma }}^2$. The authors use GCV (6) to obtain λ, and a slight variation of (9) to estimate ${\sigma }^2$. They show that fridge improves upon GCV-based ridge estimation. We wish to investigate whether i) MML estimation of $\lambda ={\sigma }^2/{\tau }^2$ also improves the performance of GCV-based ridge regression; and ii) whether MML estimation further boosts the performance of the fridge estimator. Here, predictive performance is measured by the mean squared prediction error (MSPE) using leave-one-out cross-validation (loocv).

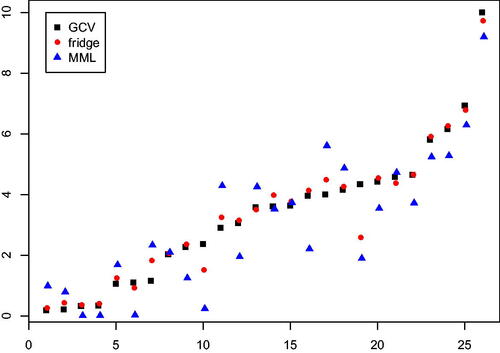
The estimates of MML differ markedly from those of GCV: $({\widehat{\lambda }}_{\text{MML}},{\widehat{\sigma }}_{\text{MML}}^2)=(0.77,0.59)$, while $({\widehat{\lambda }}_{\text{GCV}},{\widehat{\sigma }}_{\text{GCV}}^2)=(20.92,8.08)$. Using ${\widehat{\lambda }}_{\text{MML}}$ instead of ${\widehat{\lambda }}_{\text{GCV}}$ for the estimation of $\beta$ substantially reduced the mean squared prediction error: ${\text{MSPE}}_{\text{MML}}=14.40,$ while ${\text{MSPE}}_{\text{GCV}}=16.38$, a relative decrease of 12.1%. Using ${\widehat{\lambda }}_{\text{GCV}}$, as in Hellton and Hjort (2018), fridge also reduced the MSPE, but to a lesser extent: ${\text{MSPE}}_{\text{fridge}}=15.80,$ a relative decrease of 3.5% with respect to ${\text{MSPE}}_{\text{GCV}}.$ Application of fridge using ${\widehat{\lambda }}_{\text{MML}}$ did not further decrease ${\text{MSPE}}_{\text{MML}}$, nor did it increase it. Possibly, the already fairly small value of ${\widehat{\lambda }}_{\text{MML}}$ left little room for improvement. Figure 3 displays absolute prediction errors per sample and illustrates the improved prediction by ridge using ${\lambda }_{\text{MML}}$ (and to a lesser extent by fridge) with respect to ridge using ${\lambda }_{\text{GCV}}$.

Figure 3. Absolute prediction errors (obtained by loocv; y-axis) for ridge using ${\lambda }_{\text{GCV}}$, for fridge and for ridge using ${\lambda }_{\text{MML}}$. Sample indices (x-axis) are sorted by GCV results.

5. Extensions

5.1. Extension 1: mixed effects model

A natural extension of the high-dimensional random effects model (1) is the mixed effects model:(17) $$y=X_{\mathrm{f}}\alpha +X_{\mathrm{r}}\beta +ϵ,$$(17) where we assume that the n × m design matrix for the fixed effects, $X_{\mathrm{f}}$, is of low-rank, so $m\ll n$, as opposed to the random effects design matrix $X_{\mathrm{r}}$. Restricted maximum likelihood (REML) deals with the fixed effects by contrasting them out. For the error contrast vector $y-X_{\mathrm{f}}{\widehat{\alpha }}^{\text{OLS}}={\mathrm{A}}^{T}y,$ with $\mathrm{A}={\mathrm{I}}_n-X_{\mathrm{f}}{(X_{\mathrm{f}}^T{X}_{\mathrm{f}})}^{-1}{X}_{\mathrm{f}}^T$, the marginal likelihood for the variance components equals (see e.g. Zhang 2015):(18) $$P\left({\mathrm{A}}^{T}y\right)=\mathcal{N}(y;\mu =0,\mathbf{\Sigma }={\mathrm{A}}^T{\mathbf{\Sigma }}_r\mathrm{A})$$(18) with ${\mathbf{\Sigma }}_r=X_r{X}_r^T{\tau }^2+{\sigma }^2{\mathrm{I}}_n.$ In addition to maximizing (18) as a function of $({\sigma }^2,{\tau }^2)$, we attempted solving the set of two estimation equations suggested by Jiang (2007), but this rendered instable results inferior to maximizing (18) directly.

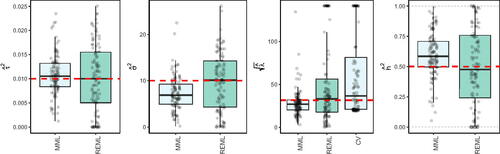
Alternatively, MML may be used, but it has to be adjusted to also estimate the fixed effects in the model. This implies replacing 0 in Gaussian likelihood (11) by $X_{\mathrm{f}}\alpha$, and optimizing (11) with respect to $2+m$ parameters, where m is the number of fixed parameters. The mixed model simulation setting is as follows:(19) $$\begin{array}{ll}{y}_{n\times 1}=X_{\mathrm{f},n\times m}{\alpha }_{m\times 1}+X_{\mathrm{r},n\times p}{\beta }_{p\times 1}+{ϵ}_{n\times 1}\hfill & {ϵ}_i\stackrel{\text{iid}}{\sim }\mathcal{N}(0,{\sigma }^2)\hfill \\ x_{f,\mathit{ik}}\stackrel{\text{iid}}{\sim }\mathcal{N}(0,1)\hfill & x_{r,\mathit{ij}}\stackrel{\text{iid}}{\sim }\mathcal{N}(0,1)\hfill \\ {\alpha }_k\stackrel{\text{iid}}{\sim }{p}_{0,f}{\delta }_0+(1-p_{0,f})\mathcal{N}(0,{\tau }_{0,f}^2)\hfill & {\beta }_j\stackrel{\text{iid}}{\sim }{p}_0{\delta }_0+(1-p_0)\mathcal{N}(0,{\tau }_0^2),\hfill \end{array}$$(19) where $n=100,p=1000,m=10,p_0=0.9,{\tau }_0^2=0.1$ (implying variance ${\tau }^2=(1-p_0){\tau }_0^2=0.01$ for generating random effects) and $p_{0,f}=0.5,{\tau }_{0,f}^2=0.20$ (implying variance ${\tau }_f^2=0.1$ for generating fixed effects). Note that we focused on a fairly sparse setting for the random effects and larger prior variance of fixed effects than of random effects, which enables a stronger impact of the small number of fixed effects. Figure 4 shows the results of REML, MML and CV (by glmnet, using penalty factor 0 for the fixed effects) for the estimation of ${\tau }^2,{\sigma }^2,\lambda$ and h².

Figure 4. Estimates for mixed effects model, ${\tau }^2=0.01,{\sigma }^2=10,n=100,m=10,p=1000$.

From Figure 4 we observe that REML indeed improves MML in terms of bias, however at the cost of increased variability. For the estimation of λ, CV is fairly competitive to REML and MML, although it renders markedly more over-penalization.

5.2. Extension 2: Bayesian linear regression

So far, we focused on classical methods. Bayesian methods may be a good alternative. We applied the standard Bayesian linear regression model, i.e. the conjugate model with i.i.d. priors $\pi ({\beta }_j)=N(0,{\sigma }^2{\tau }^2)$, with ${\tau }^2$ fixed and ${\sigma }^2$ endowed with a vague inverse-gamma prior (see Supplementary Material for details). For this model the maximum marginal likelihood estimator for ${\tau }^2$ is still analytical (Karabatsos 2018), and so is the posterior mode estimate of ${\sigma }^2$. 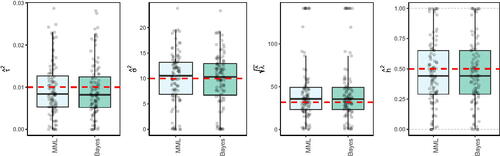Figure 5 shows the results in comparison to MML, i.e. maximization of (12), for the random effects case with multi-collinear X, as in Sec. 3.3.1. Results for other settings were in essence very similar.

Figure 5. Bayes and MML (12) estimates for multi-collinear X, with ${\tau }^2=0.01,{\sigma }^2=10,n=100,p=1000$.

From the results we conclude that the conjugate Bayes estimates are very close to those of MML. This is in line with the fact that both estimators maximize a marginal likelihood and the conjugate model with prior variance ${\tau }^2={\sigma }^2/\lambda$ is known to render posterior mean estimates of $\beta$ that equal the λ-penalized ridge regression estimates.

The conjugate Bayesian model is scale-invariant, because the β prior contains the error variance ${\sigma }^2$. Recently, it was criticized for its non-robustness against misspecification of the fixed ${\tau }^2$ when estimating ${\sigma }^2$ (Moran, Rockova, and George 2018). However, in practice one needs to estimate ${\tau }^2$ by either empirical Bayes (e.g. maximum marginal likelihood) or full Bayes. We repeated the simulation by Moran, Rockova, and George (2018) (see Supplementary Material). The results show that the estimates of ${\sigma }^2$ are much better when estimating ${\tau }^2$ by empirical Bayes instead of fixing it, and in fact very competitive to alternatives proposed by Moran, Rockova, and George (2018).

5.3. Extension 3: generalized linear models

5.3.1. Setting

Motivated by the good results for MML in the linear setting, we wish to extend MML estimation to the high-dimensional generalized linear model (GLM) setting, where the likelihood depends on the regression parameter $\beta$ only via the linear predictor, $X\beta$. Hence, likelihood $\mathcal{L}(\mathrm{Y};\beta ,X)$ is defined by a density $f_{\mu }(\mathrm{Y})$ (e.g. Poisson), where $X\beta$ is mapped to μ by a link function (e.g. $\text{log}\hspace{0.17em}$). As before, we a priori assume i.i.d. ${\beta }_j\sim N(0,{\tau }^2)$, here equivalent to an L₂ penalty $\lambda =1/{\tau }^2$ when estimating $\beta$ by penalized likelihood. In Heisterkam, van Houwelingen, and Downs (1999) an iterative algorithm to estimate λ is derived which alternates estimation of $\beta$ by maximization w.r.t. λ, requiring the computation of the trace of a Hessian of a $p\times p$ matrix. Here, the estimation of $\beta$ itself is much slower than in the linear case, because it is not analytic and requires iterative weighted least squares approximation. Below we show how to substantially alleviate the computational burden in the $p\gg n$ setting by re-parameterizing the marginal likelihood implying computations in ${\mathbb{R}}^n$ instead of ${\mathbb{R}}^p$.

5.3.2. Method

We have for the marginal likelihood:(20) $$\text{ML}\left(\lambda \right)={\int }_{\beta \in {\mathbb{R}}^p}\mathcal{L}(\mathrm{Y};\beta ,X){\pi }_{\lambda }\left(\beta \right)d\beta ={\int }_{\beta \in {\mathbb{R}}^p}\mathcal{L}(\mathrm{Y};\beta ,X)\varphi ({\beta }_1;0,1/\lambda )\cdots \varphi ({\beta }_p;0,1/\lambda )d\beta$$(20) where $\varphi (\beta ,\mu ,{\tau }^2)$ denotes the normal density with mean μ and variance ${\tau }^2$. Now a crucial observation is that for GLM:(21) $$\text{ML}\left(\lambda \right)=E_{{\pi }_{\lambda }\left(\beta \right)}\left[\mathcal{L}\right(\mathrm{Y};\beta ,X\left)\right]=E_{{\pi }_{\lambda }\left(\beta \right)}\left[\mathcal{L}\right(\mathrm{Y};X\beta \left)\right]=E_{\pi {\prime }_{\lambda }\left(X\beta \right)}\left[\mathcal{L}\right(\mathrm{Y};X\beta \left)\right]$$(21) because the likelihood depends on $\beta$ only via the linear predictor $X\beta$. Here, $\pi {\prime }_{\lambda }(X\beta )$ is the implied n-dimensional prior distribution of $X\beta$. This is a multivariate normal: $\varphi ({\beta }^X;\mu =0,{\Sigma }_{\lambda }=X{X}^T/\lambda )$. Therefore, we have:(22) $$\begin{array}{l}\text{ML}\left(\lambda \right)={\int }_{\beta \in {\mathbb{R}}^p}{g}_{\mathrm{Y},\lambda }\left(\beta \right)d\beta ={\int }_{\beta \in {\mathbb{R}}^p}\mathcal{L}(\mathrm{Y};\beta ,X)\varphi ({\beta }_1;0,1/\lambda )\cdots \varphi ({\beta }_p;0,1/\lambda )d\beta \hfill \\ ={\int }_{{\beta }^X\in {\mathbb{R}}^n}{h}_{\mathrm{Y},\lambda }\left({\beta }^X\right)d{\beta }^X={\int }_{{\beta }^X\in {\mathbb{R}}^n}\mathcal{L}(\mathrm{Y};{\beta }^X,{\mathbf{I}}_n)\varphi ({\beta }^X;0,{\Sigma }_{\lambda })d{\beta }^X.\hfill \end{array}$$(22)

Hence, the p-dimensional integral may be replaced by an n-dimensional one, with obvious computational advantages when $p\gg n$. Moreover, the use of (22) allows applying implemented Laplace approximations, which tend to be more accurate in lower dimensions. The Laplace approximation requires ${\widehat{\beta }}^X=\text{arg} {\text{max}}_{{\beta }^X}\{h_{\mathrm{Y},\lambda }({\beta }^X)\}$. We emphasize that this does generally not equal $X\widehat{\beta },$ where $\widehat{\beta }=\text{arg} {\text{max}}_{\beta }\{g_{\mathrm{Y},\lambda }(\beta )\}$ : the maximum of the commonly used L₂ penalized (log)-likelihood. However, ${\widehat{\beta }}^X$ can be computed by noting that(23) $$\text{log}\hspace{0.17em}{h}_{\mathrm{Y},\lambda }\left({\beta }^X\right)\propto \ell (\mathrm{Y};{\beta }^X,{\mathbf{I}}_n)-{\left({\beta }^X\right)}^T{\Sigma }_{\lambda }^{-1}{\beta }^X.$$(23)

In other words, this is the penalized log-likelihood when regressing Y on the identity design matrix ${\mathbf{I}}_n$ using an L₂ smoothing penalty matrix ${({\beta }^X)}^T{\Sigma }_{\lambda }^{-1}{\beta }^X=\lambda {({\beta }^X)}^T{(X{X}^T)}^{-1}{\beta }^X$. The latter fits conveniently into the set-up of Wood (2011), as implemented in the R-package mgcv. This also facilitates MML estimation of λ by maximizing $\text{ML}(\lambda )$, with $h_{\mathrm{Y},\lambda }({\beta }^X)$ as in (23). If the columns of X are standardized (common in high-dimensional studies), $X{X}^T$ has rank n – 1 instead of n, implying that ${(X{X}^T)}^{-1}$ does not exist and should be replaced by a pseudo-inverse ${(X{X}^T)}^{+}$, such as the Moore-Penrose inverse.

In a full Bayesian linear model setting, dimension reduction is also discussed by Bernardo et al. (2003), where $X\beta$ is substituted by a n-dimensional factor analytic representation, which requires an SVD of X. In addition, there it is not used for hyper-parameter estimation by marginal likelihood, but instead for specifying (hierarchical) priors for the factors.

5.3.3. Results

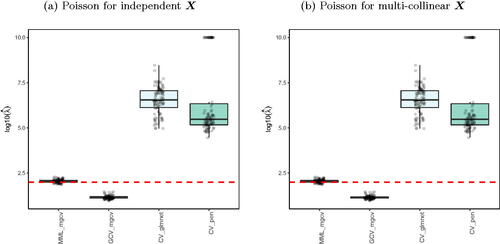
R packages like glmnet (Friedman, Hastie, and Tibshirani 2010) and penalized (Goeman 2010) estimate λ by cross-validation, and also mgcv allows, next to the MML estimation, (generalized) CV estimation (Wood 2011). Figure 6a and b show the results for Poisson ridge regression, with ${\mathrm{Y}}_i\sim \text{Pois}({\lambda }_i),{\lambda }_i=\hspace{0.17em}\text{exp}\hspace{0.17em}(X_i\beta ),\beta$ generated as in (14), and X generated as in (14) and (16), which denote the independent X and multi-collinear X setting, respectively.

Figure 6. λ estimates for Poisson ridge regression, $\lambda =1/{\tau }^2=100,n=100,p=1000$.

Figure 6 clearly shows the superior performance of MML based on (22) over CV. In particular, glmnet and penalized render strongly upward biased values. The mgcv GCV values are still inferior to MML based ones, but much better than the latter two, which may be due to the different regression estimators used (Laplace approximation versus iterative weighted least squares). We should stress that CV does not target for the estimation of λ as such, but merely for minimizing prediction error. Nevertheless, the difference is remarkably larger than in the corresponding linear case (see Figures 1 and 2).

The Supplementary Material shows the results for Binomial ridge regression. While the differences in performance are less dramatic than for the Poisson setting, MML still renders much better estimates of λ than CV-based approaches.

6. Computational aspects and software

All methods and simulations presented here are implemented in a few wrapper R scripts: one for the linear random effects model (which includes the conjugate Bayes estimator), one for the linear mixed effects model, and one for Poisson and Binomial ridge regression. Parallel computations are supported. The scripts allow exact reproduction of the results in this manuscript as well as comparisons for other simulation or user-specific real data X cases. In addition, a script is supplied to produce the box-plots as in this manuscript.

HiLMM, PCR and CV implementations are provided by the R-packages HiLMM, v1.1 (Bonnet, Gassiat, and Lévy-Leduc 2015), ridge, v1.8-16 (Cule and De Iorio 2012) (code slightly adapted for computational efficiency) and glmnet, v2.0-16 (Friedman, Hastie, and Tibshirani 2010). The methods MML, REML, Bayes, MoM, Basic and GCV were implemented by us for the linear random and mixed effects models. For Poisson and Binomial ridge regression we applied mgcv, v1.8-16 (Wood 2011) after our re-parametrization (22) to obtain MML and GCV results, while for CV glmnet and penalized, v0.9-50 (Goeman 2010) were applied. For all methods that required optimization the R routine optim was used, with default settings. CV was based on 10 folds.

Computing times of the various methods largely depend on n and p, much less so on the exact simulation setting. These are displayed for n = 100, 500 and $p={10}^3,{10}^4,{10}^5$ in Table 1, based on computations with one CPU of an Intel®Xeon^®CPUE5 - 2660v3@2.60 GHz server. For Poisson ridge regression, we only report the computing times of MML and GCV, because, as reported in Figure 6, the performance of CV-based methods was very inferior.

Table 1. Computing times for hyper-parameter estimation for linear and Poisson ridge regression.

	n = 100			n = 500
	$p={10}^3$	$p={10}^4$	$p={10}^5$	$p={10}^3$	$p={10}^4$	$p={10}^5$
Linear
MML	0.06	0.15	1.12	2.18	6.07	26.64
Bayes	0.04	0.31	4.38	1.10	7.78	93.25
MoM	0.01	0.08	1.03	0.17	2.32	23.70
PCR	0.05	0.39	5.36	1.39	10.31	116.80
Basic	0.05	0.46	6.56	1.44	12.40	145.18
GCV	0.20	0.46	4.56	12.26	26.41	111.38
CV	0.81	6.57	39.95	2.62	21.69	183.50
HiLMM	0.03	0.17	2.01	0.66	3.14	27.99
Poisson
MML_mgcv	0.32	0.33	0.31	26.21	40.19	48.17
GCV_mgcv	0.39	0.33	0.62	33.48	41.44	54.01

From Table 1 we conclude that MML is also computationally very attractive. Its efficiency is explained by the fact that, unlike many of other methods, it does not require an SVD or other matrix decomposition of X. Moreover, the only computation that involves dimension p is the product $X{X}^T$.

7. Discussion

We compared several estimators in a large variety of high-dimensional settings. The results showed that plain maximum marginal likelihood works well in many settings. MML is generally superior to methods that aim to separately estimate ${\sigma }^2$ (9, 10). Apparently, the estimates of ${\sigma }^2$ and ${\tau }^2$ are so intrinsically linked in the high-dimensional setting that separate estimation is sub-optimal. The moment estimator (MoM) is generally not competitive to MML. It may, however, be useful in large systems with multiple hyper-parameters to estimate relative penalties, which are less sensitive to scaling issues than the global penalty parameter (Van de Wiel et al. 2016). MoM may also be a useful initial estimator for more complex estimators that are based on optimization, such as MML.

Possibly somewhat surprising is the good performance of MML for estimating λ and h², as these are functions of ${\sigma }^2$ and ${\tau }^2$. For the estimation of λ it is generally better than or competitive to (generalized) CV, an observation also made for the low-dimensional setting (Wood 2011). The inferior performance of the basic estimator of ${\sigma }^2$ (9) implies that alternative estimators of λ that use ${\widehat{\sigma }}^2$ as a plug-in are unlikely to perform well in high-dimensional settings. Such estimators, including the original one by Hoerl and Kennard (1970), are compared by Muniz and Kibria (2009); Kibria and Banik (2016), who show that some do perform well in the low-dimensional setting. For Poisson ridge regression, similar estimators of λ are available (Månsson and Shukur 2011), but these rely on an initial maximum likelihood estimator of $\beta$, and hence do not apply to the high-dimensional setting. For estimating h² it should be noticed that HiLMM (Bonnet, Gassiat, and Lévy-Leduc 2015) aims to compute a confidence interval for h² as well. For that purpose their direct estimator (8) is likely more useful than MML on the pair $({\tau }^2,{\sigma }^2)$. We also used Esther (Bonnet et al. 2018), which precedes HiLMM by sure independence screening. It did not improve HiLMM in our (semi-)sparse settings, and requires manual steps. However, it likely improves HiLMM results in very sparse settings (Bonnet et al. 2018).

For mixed effect models with a small number of fixed effects, MML compares fairly well to REML, with a larger bias, but smaller variance. Probably the potential advantage of contrasting out the fixed effects is small when the number of random effects is large. REML may have a larger advantage in very sparse settings (Jiang et al. 2016) or when the number of fixed effects is large with respect to n. Estimates from the conjugate Bayes model are very similar to those by MML. We show that estimating ${\tau }^2$ along with ${\sigma }^2$ highly improves the ${\sigma }^2$ estimates presented by Moran, Rockova, and George (2018), where a fixed value of ${\tau }^2$ is used. In the case of many variance components or multiple similar regression equations, Bayesian extensions that shrink the estimates by a common prior are appealing, in particular in combination with efficient posterior approximations such as variational Bayes (Leday et al. 2017).

Our model (1) implies a dense setting, but we have demonstrated that the MML and REML estimators of ${\tau }^2$ and ${\sigma }^2$ are fairly robust against moderate sparsity, which corroborates the results by Jiang et al. (2016). Nevertheless, true sparse models may be preferable when variable selection is desired, which depends on accurate estimation of $\beta$. On the other hand, post-hoc selection procedures can be rather competitive (Bondell and Reich 2012). Moreover, the sparsity assumption is questionable for several applications. For example in genetics, it was suggested that many complex traits (such as height or cholesterol levels) are not even polygenic, but instead ‘omnigenic’ (Boyle, Li, and Pritchard 2017).

The extension of MML to high-dimensional GLM settings (22) is promising given its computational efficiency and performance for Poisson and Binomial regression. A special case of the latter, logistic regression, requires further research, because the Laplace approximations of the marginal likelihood are less accurate here (Wood 2011). Extension to survival is a promising avenue, because Cox regression is directly linked to Poisson regression (Cai and Betensky 2003). Alternatively, parametric survival models may be pursued. To what extent the estimates of hyper-parameters impact predictions depends on the sensitivity of the likelihood to these parameters. For the linear setting, a re-analysis of the weight-gain data showed that predictions based on ${\widehat{\lambda }}_{\text{MML}}$ improved those based on ${\widehat{\lambda }}_{\text{CV}}$. Karabatsos (2018) shows that MML estimation also performs well compared to GCV for linear power ridge regression, which extends ridge regression by multiplying λ by ${(X^{T}X)}^{\delta }$.

The MML estimator can be extended to estimation of multiple variance components or penalty parameters, which was addressed by iterative likelihood minorization (Zhou et al. 2015) and by parameter-based moment estimation (Van de Wiel et al. 2016). The latter extends to non-Gaussian response such as survival or binary. Further comparison of these methods with multi-parameter MML, both in terms of performance and computational efficiency, is left for future research. Finally, in particular in genetics applications, extensions of estimation of variance components by MML to non-independent individuals can be implemented by use of a well-structured between-individual covariance matrix $\mathbf{\Sigma }$ (Kang et al. 2008).

Although our simulations cover a fairly broad spectrum of settings, many other variations could be of interest. We therefore supply fully annotated R scripts https://github.com/markvdwiel/Hyperpar that allow i) comparison of all algorithms discussed here, also for one’s ‘own’ real covariate set X; and ii) reproduction of all results presented here.

Acknowledgment

Gwenaël Leday was supported by the Medical Research Council, grant number MR/M004421. We thank Jiming Jiang and Can Yang for their correspondence, input and software for the MM algorithm. In addition, we thank Kristoffer Hellton for providing the fridge software and data. Finally, Iuliana Ciocǎnea-Teodorescu is acknowledged for preparing the TCGA KIRC data.

Disclosure statement

No potential conflict of interest was reported by the authors.