Goodness-of-fit testing based on Gini Index of spacings for progressively Type-II censored data

Abstract

In this article, we propose two new scale invariant test statistics when the available data are subject to progressively Type-II censoring. The proposed tests are based on Gini index of spacings. It is observed thorough extensive Monte Carlo simulations that the proposed tests are quite powerful in compare to similar existing goodness-of-fit tests studied by Balakrishnan et al. and Wang. We also illustrate the method proposed here using a real data from reliability literature.

Keywords:

• Exponential distribution
• Gini index
• Goodness-of-fit testing
• Monte Carlo simulation
• Order statistics
• Progressive Type-II censoring
• Spacings

1. Introduction

In parametric procedures, we assume a specific distribution for a given dataset, on the contrary to the nonparametric methods that are distribution free and no particular probability model is considered. The goodness-of-fit technique first introduced by Karl Pearson (1900) is a statistical procedure for testing whether or not a probability distribution may be considered for modeling a given set of data. Many authors have been considered this problem and presented several methods for complete and censored data. See, e.g., D’Agostino and Stephens (1986), Huber-Carol et al. (2002) and Nikulin and Chimitova (2017) among others.

Censoring is a sampling method that allows the researcher to control the experimental time and costs by censoring a proportion of the sample while using the information of all the experimental units. Progressive Type-II censoring introduced first by Herd (1956) and Cohen (1963) is very common in reliability and life testing methods. In this type of censoring, n units are placed on a test according to the following plan. Remove R₁ units when the first failure occurs. Remove R₂ units when the second failure occurs. Finally, remove R_m units when the mth failure occurs. So, $R_1+R_2+\cdots +R_m=n-m$ units will be censored and m failure will be observed. The vector $\mathbf{R}=(R_1,\dots ,R_m)$ is called the progressive censoring scheme which is fixed prior to the study. See Balakrishnan and Aggrawala (2000), Balakrishnan (2007) and Balakrishnan and Cramer (2014) for an excellent overview on progressive Type-II censoring and related developments.

Several authors have been considered the goodness-of-fit testing problem based on progressively Type-II censored data. Pakyari and Balakrishnan (2012) presented a modification to the empirical distribution function (EDF)-based statistics. Balakrishnan, Habibi Rad, and Arghami (2007), Rad, Yousefzadeh, and Balakrishnan (2011), Park and Pakyari (2015), Baratpour and Habibi Rad (2016) and Noughabi (2017b) proposed statistics based on Kullback–Leibler information. Balakrishnan et al. (2002), Balakrishnan, Ng, and Kannan (2004) and Pakyari and Balakrishnan (2013) adopted spacings-based tests. Interested readers may also refer to Balakrishnan and Lin (2003), Balakrishnan, Habibi Rad, and Arghami (2007), Wang (2008), Kohansal and Rezakhah (2013) and Doring and Cramer (2019) among others.

There are some discussions in the literature that tests based on empirical distribution function (EDF-based), such as Kolmogorov-Smirnov, Cramér-von Mises and Anderson-Darling perform well in determining differences between distribution functions, whilst tests based on spasings are usuful for detecting the differences between densities (see e.g., Pyke 1965).

In this article, we present a test statistic based on Gini index of spacings. Gini index is a measure of dispersion based on the sum of pairwise distances between spacings. Several authors have employed Gini index for the problem of goodness-of-fit in the case of complete samples. See e.g., Jammalamadaka and Goria (2004), Noughabi, Arghami, and Mohtashami Borzadaran (2014), Noughabi (2017a). However, little works have been done when the available data are subject to censoring.

The rest of this article is organized as follows. In Sec. 2, the proposed test statistics are studied. The new tests are based on the weighted mean of the differences of overlapping spacings. The weights are designed in such a way that earlier differences assign more weights than the later differences. The power of these tests is studied by Monte Carlo simulations in Sec. 3. We will see that the new tests exhibit more power in comparison to competing spacing-based methods for most cases. We have considered the testing for the exponential and the normal models with different choice of alternative distributions. Finally, in Sec. 4, we present a real dataset and explain the proposed method.

2. Proposed tests

Let $X_{1:m:n},X_{2:m:n},\dots ,X_{m:m:n}$ be the progressively Type-II right censored sample with progressive censoring scheme $R=(R_1,R_2,\dots ,R_m)$ from a distribution with CDF, F(x).

We are interested to test that the censored data come from a population with a specific distribution function $F_0(x).$ That is, the null and alternative hypothesis are of the form: $$H_0:F(x)=F_0(x),\text{versus}{H}_a:F(x)\ne F_0(x)$$

Without loss of generality, one may use the probability integral transformation to reduce the above hypothesis to the hypothesis of uniformity by the transformation $U=F(X).$ That is, the problem reduces to testing the hypothesis of the form: (1) $$H_0:F(u)=u ,0<u<1\text{versus}{H}_a:F(u)\ne u ,0<u<1$$(1)

The overlapping spacings are defined by (2) $$S_i={\gamma }_i(U_{i:m:n}-U_{i-1:m:n}),\text{for}i=1,\dots ,m\text{and}{U}_{0:m:n}=0,$$(2) where $${\gamma }_j=\sum _{l=j}^m(R_l+1),1\le j\le m$$

Note that γ_j is the number of items under risk before the jth failure has occurred. The $\left\{S_i\right\}$ defined above is called one-step spacings and is the differences between consecutive observations. If the null hypothesis (1)(1) $$H_0:F(u)=u ,0<u<1\text{versus}{H}_a:F(u)\ne u ,0<u<1$$(1) is in fact false, then the spacings in (2)(2) $$S_i={\gamma }_i(U_{i:m:n}-U_{i-1:m:n}),\text{for}i=1,\dots ,m\text{and}{U}_{0:m:n}=0,$$(2) gives values more irregular than those from a uniform spacings. Hence, very small or very large values of (2)(2) $$S_i={\gamma }_i(U_{i:m:n}-U_{i-1:m:n}),\text{for}i=1,\dots ,m\text{and}{U}_{0:m:n}=0,$$(2) will indicate highly irregular spacings and will tend to reject the null hypothesis of uniformity. Statistics of the form (2)(3) $$G_k=\underset{1\le i<j\le m}{\sum _{i=1}^m\sum _{j=1}^m}{W}_l^{(k)} |S_i-S_j|,\text{for}k=1,2\text{and}l=1,2,\dots ,q,$$(3) are of great interest in contexts like goodness-of-fit testing (see, e.g., Pyke 1965 and Kale 1969 for a somewhat back dated but an excellent review). The idea of spacings can be generalized to say h-step (or higher-order) spacings for $1\le k<m$ defined by $$S_i^{(h)}={\gamma }_i (U_{i+h-1:m:n}-U_{i-1:m:n}),i=1,\dots ,m,U_{0:m:n}=0.$$

Note that $S_i^{(h)}$ are the spacings between h observations (see, e.g., Hartley and Pfaffenberger 1972).

Jammalamadaka and Goria (2004) introduced the Gini index of spacings for complete data defined by $\sum _i\sum _j|S_i-S_j|.$ This measure of dispersion provides sum of pairwise distances between the spacings. In this paper, we introduce the Gini mean difference of spacings for progressively Type-II censored data and propose two test statistics based on that, say (3) $$G_k=\underset{1\le i<j\le m}{\sum _{i=1}^m\sum _{j=1}^m}{W}_l^{(k)} |S_i-S_j|,\text{for}k=1,2\text{and}l=1,2,\dots ,q,$$(3) where $q=\frac{m(m-1)}{2}$ is the number of double sigma terms and $W_l^{(1)}$ and $W_l^{(2)},$ are decreasing weights defined respectively by: $$W_l^{(1)}=\frac{2(q+1-l)}{q(q+1)},l=1,2,\dots ,q,$$

and $$W_l^{(2)}=\frac{6{(q+1-l)}^2}{q(q+1)(2q+1)},l=1,2,\dots ,q.$$

Note that ${\sum }_{l=1}^q{W}_l^{(k)}=1$ for k = 1, 2. The two weights $W_l^{(1)}$ and $W_l^{(2)}$ are defined to be decreasing so that more weights are assigned to adjacent spacings. Also, $W_l^{(1)}$ employ linear weights whilst $W_l^{(2)}$ assigns quadratic weights. The exact distribution of G₁ and G₂ is not specified and in Sec. 3 we will use Monte Carlo simulations to find the emprical critical points. We will show that these tests exhibit more power in compare to existing tests based on spacings. The test statistics G₁ and G₂ are clearly location-scale invariant, with large and small values tend to rejection the null hypothesis.

Note that one may consider the generalized Gini mean difference of spacings defined by $$G_k^{(r)}=\underset{1\le i<j\le m}{\sum _{i=1}^m\sum _{j=1}^m}{W}_l^{(k)} |S_i-S_j{|}^r,\text{for}k=1,2\text{and}l=1,2,\dots ,q .$$

We have not considered this statistic here, however the special case of r = 2 corresponds to the Greenwood statistic (Greenwood 1946).

3. Simulation study

In this section, we will study the power of the proposed test statistics G₁ and G₂ thorough extensive Monte Carlo simulations using statistical software R. We generated 100, 000 random samples for different combinations of sample size n, number of failures m and censoring schemes R. The tests are evaluated at the 5% and 10% significance levels. We used the 27 censoring schemes employed by Balakrishnan, Ng, and Kannan (2004) and these are listed in Table 1 for convenience.

Table 1. Progressive censoring schemes used in the Monte Carlo simulations.

Scheme no.	n	m	$R=(R_1,R_2,\dots ,R_m)$
[1]	20	8	$R_1=12,R_i=0,$ for $i\ne 1$
[2]	20	8	$R_8=12,R_i=0,$ for $i\ne 8$
[3]	20	8	$R_1=R_8=6,R_i=0,$ for $i\ne 1,8$
[4]	20	12	$R_1=8,R_i=0,$ for $i\ne 1$
[5]	20	12	$R_{12}=8,R_i=0,$ for $i\ne 12$
[6]	20	12	$R_3=R_5=R_7=R_9=2,R_i=0,$ for $i\ne 3,5,7,9$
[7]	20	16	$R_1=4,R_i=0,$ for $i\ne 1$
[8]	20	16	$R_{16}=4,R_i=0,$ for $i\ne 16$
[9]	20	16	$R_5=4,R_i=0,$ for $i\ne 5$
[10]	40	10	$R_1=30,R_i=0,$ for $i\ne 1$
[11]	40	10	$R_{10}=30,R_i=0,$ for $i\ne 10$
[12]	40	10	$R_1=R_5=R_{10}=10,R_i=0,$ for $i\ne 1,5,10$
[13]	40	20	$R_1=20,R_i=0,$ for $i\ne 1$
[14]	40	20	$R_{20}=20,R_i=0,$ for $i\ne 20$
[15]	40	20	Ri = 1, for $i=1,2,\dots ,20$
[16]	40	30	$R_1=10,R_i=0,$ for $i\ne 1$
[17]	40	30	$R_{30}=10,R_i=0,$ for $i\ne 30$
[18]	40	30	$R_1=R_{30}=5,R_i=0,$ for $i\ne 1,30$
[19]	60	20	$R_1=40,R_i=0,$ for $i\ne 1$
[20]	60	20	$R_{20}=40,R_i=0,$ for $i\ne 20$
[21]	60	20	$R_1=R_{20}=10,R_{10}=20,R_i=0,$ for $i\ne 1,10,20$
[22]	60	40	$R_1=20,R_i=0,$ for $i\ne 1$
[23]	60	40	$R_{40}=20,R_i=0,$ for $i\ne 40$
[24]	60	40	$R_{2i-1}=1,R_{2i}=0,$ for $i=1,2,\dots ,20$
[25]	60	50	$R_1=10,R_i=0,$ for $i\ne 1$
[26]	60	50	$R_{50}=10,R_i=0,$ for $i\ne 50$
[27]	60	50	$R_1=R_{50}=5,R_i=0,$ for $i\ne 1,50$

We studied testing for the exponential and normal models as the null hypothesis. For the exponential model we considered the log-normal (LN) and F distributions as alternatives. Specifically, the following alternatives were used:

1. The log-normal distribution with scale parameter 1.0 and shape parameters 0.5 and 1.0, denoted, respectively, by $LN(0,0.5)$ and LN(0, 1) with the following pdf: $$f(x)=\frac{1}{\sqrt{2\pi }\sigma x}\text{exp}\hspace{0.17em}-\frac{{(\hspace{0.17em}\text{log}\hspace{0.17em}x-\mu )}^2}{2{\sigma }^2},x>0$$ where μ and σ are the mean and standard deviation of the logarithm. Both alternative models have skewed to the right density functions; however, the $LN(0,0.5)$ model is almost symmetric and will be easily distinguishable from the exponential distribution.

2. The Fisher’s F distribution with (5, 2) degrees of freedom denoted by F(5, 2) with pdf given by $$h(x)=\frac{1}{B(\frac{{\nu }_1}{2},\frac{{\nu }_1}{2})}{\left(\frac{{\nu }_1}{{\nu }_2}\right)}^{\frac{{\nu }_1}{2}}{(1+\frac{{\nu }_1}{{\nu }_2} x)}^{-\frac{{\nu }_1+{\nu }_2}{2}}$$

This alternative model has positively skewed density function. All the pdfs and CDFs are depicted in Figure 1.

Figure 1. Plot of pdf and CDF of standard exponential (solid black line), $LN(0,0.5)$ (dashed blue line), LN(0, 1) (dotted green) and F(5, 2) (dotted dashed red line).

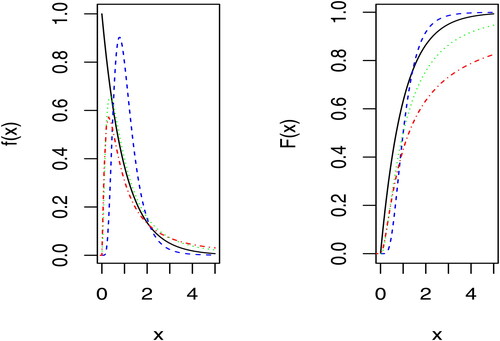
See Johnson, Kotz, and Balakrishnan (1994, 1995) for detailed discussion of the above mentioned distributions. We compare the empirical powers for the above mentioned alternatives to the Wang (2008) statistic: $$T_W=2 \sum _{i=1}^{m-1}\hspace{0.17em}\text{log}\hspace{0.17em}\frac{S_1^{\ast }+S_2^{\ast }+\cdots +S_m^{\ast }}{S_1^{\ast }+S_2^{\ast }+\cdots +S_i^{\ast }},$$ where $$S_i^{\ast }={\gamma }_i(X_{i:m:n}-X_{i-1:m:n}),i=1,2,\dots ,m-1,$$ are the spacings based on the censored data $X_{i:m:n}.$ Note that the Wang statistic T_W has chi-squared distribution with $2m-2$ degrees of freedom under the null hypothesis of exponentiality.

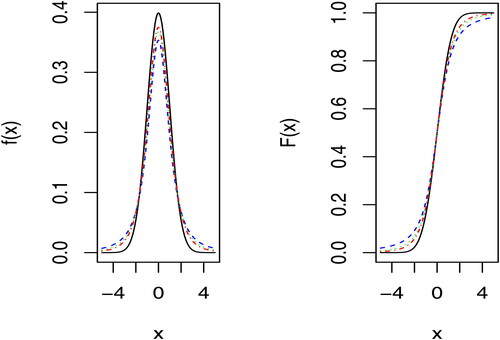
For testing the normal distribution we considered the student’s t distribution with 2, 3 and 4 degrees of freedom, denoted respectively by t(2), t(3), and t(4). In Figure 2, the pdfs and CDFs of the normal model and the alternative student’s t models are depicted. We compared the empirical power with the Balakrishnan, Ng, and Kannan (2004) statistic $$T_B=\frac{\sum _{i=2}^{m-1}(m-i)G_i}{(m-2)\sum _{i=2}^m{G}_i},$$ where $$G_i=\frac{X_{i:m:n}-X_{i-1:m:n}}{{\mu }_{i:m:n}-{\mu }_{i-1:m:n}},\text{for}i=2,3,\dots ,m,$$ and ${\mu }_{i:m:n}$ is the expected value of the ith progressively Type-II censored order statistic from the standard normal distribution. We used Royston (1982) approximation for ${\mu }_{i:m:n}$ as $${\mu }_{i:m:n}\approx {\Phi }^{-1}\left(\frac{i-0.375}{m+0.25}\right) ,$$ in our simulation study.

Figure 2. Plot of pdf and CDF of standard normal (solid black line), t(2) (dashed blue line), t(3) (dotted green) and t(4) (dotted dashed red line).

Table 2 shows the empirical power when testing for exponential model with alternative distributions $LN(0,0.5),$ LN(0, 1) and F(5, 2) for 5% and 10% significance levels. In most cases except the proposed tests G₁ and G₂ exhibit more power in compare to the Wang statistic. Indeed, for the log-normal alternative G₂ outperforms G₁ and both perform better than Wang statistic for most cases, specifically for LN(0, 1). In F(5, 2) alternative, for almost all schemes both tests G₁ and G₂ performs better than the Wang statistic T_W. Moreover, for scheme numbers 2, 5, 8, 14, 17 and 23 (all corresponding to the conventional Type-II right censoring), the G₂ statistic performs than G₁.

Table 2. Estimated power (%) for the log-normal and F distribution when testing for exponential model with $\alpha =0.10$ and $\alpha =0.05$ (in parenthesis).

	$LN(0,0.5)$			LN(0, 1)			F(5, 2)
Sch. No.	G 1	G2	TW	G1	G2	TW	G1	G2	TW
1	99.10	99.16	98.96	25.06	26.08	21.07	34.61	34.32	29.99
	(97.01)	(96.90)	(96.58)	(15.26)	(15.32)	(12.37)	(25.79)	(25.62)	(22.79)
2	91.17	93.19	96.15	25.36	28.14	28.01	16.80	18.38	14.32
	(81.82)	(84.17)	(88.35)	(15.32)	(16.81)	(16.22)	(09.22)	(09.99)	(07.53)
3	96.63	96.98	98.15	26.73	29.06	27.76	16.16	17.45	12.40
	(90.40)	(91.38)	(93.56)	(16.23)	(17.38)	(16.16)	(08.87)	(09.41)	(06.43)
4	99.73	99.80	99.67	22.49	24.07	18.51	46.37	43.94	41.38
	(98.91)	(99.09)	(98.74)	(13.46)	(14.27)	(10.66)	(38.14)	(36.23)	(33.98)
5	98.54	99.10	99.57	25.66	29.02	28.67	13.43	15.01	10.23
	(95.61)	(96.77)	(98.04)	(15.38)	(17.48)	(16.81)	(07.10)	(07.91)	(05.06)
6	99.17	99.42	99.72	22.77	25.51	22.82	37.83	36.00	30.86
	(97.21)	(97.78)	(98.73)	(13.65)	(15.18)	(13.42)	(30.41)	(28.71)	(24.06)
7	99.89	99.94	99.85	19.71	21.55	16.53	56.14	52.39	51.91
	(99.51)	(99.68)	(99.48)	(11.74)	(12.76)	(09.30)	(48.79)	(45.60)	(44.73)
8	99.76	99.88	99.91	22.37	26.01	23.57	17.17	17.47	13.20
	(99.06)	(99.41)	(99.56)	(13.37)	(15.64)	(13.75)	(09.60)	(09.92)	(07.41)
9	99.83	99.93	99.89	19.12	21.54	17.70	54.57	50.77	49.63
	(99.33)	(99.59)	(99.56)	(11.31)	(12.76)	(10.02)	(47.40)	(44.01)	(42.58)
10	100	100	99.99	41.47	44.29	35.03	38.35	37.33	33.36
	(99.96)	(99.96)	(99.93)	(28.66)	(30.23)	(23.65)	(29.71)	(28.67)	(25.88)
11	98.49	99.08	99.80	39.24	44.30	49.50	24.72	28.02	28.82
	(95.84)	(97.07)	(98.75)	(26.58)	(30.10)	(32.98)	(15.01)	(17.05)	(17.12)
12	99.67	99.82	99.98	42.92	47.79	51.68	24.02	27.21	26.02
	(98.82)	(99.10)	(99.82)	(29.78)	(33.07)	(35.33)	(14.79)	(16.60)	(15.66)
13	100	100	100	34.61	39.59	28.07	57.51	52.29	55.14
	(100.00)	(100.00)	(99.99)	(23.51)	(27.12)	(18.20)	(50.92)	(45.88)	(48.19)
14	99.99	100	100	47.43	54.72	57.92	19.82	23.81	21.18
	(99.97)	(99.99)	(99.99)	(34.01)	(39.92)	(41.65)	(11.56)	(14.14)	(12.09)
15	100	100	100	43.36	50.75	49.10	22.65	23.15	18.39
	(99.99)	(99.99)	(100.00)	(30.57)	(36.46)	(34.63)	(14.94)	(15.05)	(11.58)
16	100	100	100	27.26	33.63	22.94	74.00	67.07	72.77
	(100.00)	(100.00)	(100.00)	(17.86)	(22.41)	(14.18)	(68.66)	(61.52)	(66.83)
17	100	100	100	41.58	50.35	47.00	13.86	14.29	10.65
	(100.00)	(100.00)	(100.00)	(29.29)	(36.21)	(32.35)	(07.67)	(07.72)	(05.51)
18	100	100	100	36.95	45.28	37.89	26.71	22.36	22.83
	(100.00)	(100.00)	(100.00)	(25.44)	(31.94)	(25.09)	(18.53)	(15.10)	(15.46)
19	100	100	100	49.84	55.72	39.66	53.48	48.55	51.80
	(100.00)	(100.00)	(100.00)	(37.79)	(42.59)	(28.17)	(46.74)	(41.83)	(44.82)
20	100	100	100	62.21	69.89	76.60	33.44	39.61	42.54
	(99.99)	(100.00)	(100.00)	(48.95)	(55.99)	(61.70)	(22.42)	(26.76)	(28.21)
21	100	100	100	63.01	70.27	73.09	26.46	32.04	28.71
	(100.00)	(100.00)	(100.00)	(49.67)	(56.59)	(58.45)	(16.96)	(20.89)	(18.22)
22	100	100	100	36.48	46.14	29.23	80.39	72.79	81.22
	(100.00)	(100.00)	(100.00)	(25.86)	(33.77)	(19.21)	(75.86)	(67.88)	(76.44)
23	100	100	100	62.91	72.73	71.07	14.58	18.73	12.59
	(100.00)	(100.00)	(100.00)	(49.56)	(59.89)	(56.34)	(08.01)	(10.96)	(06.62)
24	100	100	100	49.22	60.94	50.89	48.45	40.50	45.73
	(100.00)	(100.00)	(100.00)	(36.73)	(47.52)	(37.47)	(41.43)	(33.89)	(38.71)
25	100	100	100	31.09	41.88	25.87	88.26	81.87	88.96
	(100.00)	(100.00)	(100.00)	(20.81)	(29.56)	(16.67)	(84.94)	(77.62)	(85.41)
26	100	100	100	50.91	63.54	54.33	25.53	19.34	23.81
	(100.00)	(100.00)	(100.00)	(37.44)	(49.45)	(39.67)	(17.49)	(12.34)	(15.99)
27	100	100	100	43.59	56.46	43.00	50.44	38.33	50.00
	(100.00)	(100.00)	(100.00)	(31.05)	(42.45)	(29.95)	(41.28)	(30.09)	(40.67)

Note: Maximum value for each scheme is emboldened.

Table 3 shows empirical power for the student’s t distribution with 2, 3, and 4 degrees of freedom when testing for the normal model at the 5% and 10% significance levels. Note that as one would expect, the power will decreases as the degrees of freedom increases. This is due to the fact that the t distribution will tend to the normal distribution with increase of the degrees of freedom and therefore any test will encounter difficulties to distinguish between the two distributions. It is observed from the table that the Balakrishnan, Ng, and Kannan (2004) statistic, T_B works better for smaller sample size, however for larger sample sizes ($m\ge 10$) starting from scheme 10, the proposed tests outperform the T_B statistic, except for the schemes corresponding to the conventional Type-II censoring. Moreover, the test statistic G₂ shows better power than G₁ for most cases.

Table 3. Estimated power (%) for the t distribution with 2, 3 and 4 degrees of freedom when testing for normal model with $\alpha =0.10$ and $\alpha =0.05$ (in parenthesis).

	t(2)			t(3)			t(4)
Sch. No.	G 1	G2	TB	G1	G2	TB	G1	G2	TB
1	32.25	32.19	36.18	22.16	21.99	25.67	17.82	17.63	20.56
	(24.31)	(24.20)	(27.54)	(15.06)	(14.92)	(17.31)	(11.17)	(11.01)	(12.76)
2	30.07	29.98	35.11	21.43	21.67	24.61	17.52	17.78	19.65
	(22.27)	(22.11)	(24.94)	(14.35)	(14.48)	(15.88)	(11.04)	(11.15)	(11.96)
3	32.63	32.47	37.05	22.78	22.79	25.43	18.35	18.52	20.18
	(24.57)	(24.32)	(27.27)	(15.43)	(15.49)	(16.87)	(11.58)	(11.65)	(12.42)
4	38.53	40.37	42.24	26.06	27.40	30.71	20.55	21.29	24.90
	(30.50)	(32.24)	(33.58)	(18.63)	(19.66)	(21.66)	(13.59)	(14.21)	(16.05)
5	37.70	37.57	45.39	26.25	26.44	31.90	20.75	21.12	24.84
	(29.63)	(29.29)	(34.24)	(18.54)	(18.68)	(21.51)	(13.61)	(13.88)	(15.51)
6	39.25	39.81	45.72	27.11	27.52	33.86	21.37	21.74	27.27
	(31.07)	(31.41)	(34.96)	(19.41)	(19.70)	(22.65)	(14.22)	(14.42)	(16.71)
7	42.57	46.13	46.50	28.46	30.83	34.08	21.99	23.60	27.55
	(34.77)	(37.88)	(36.96)	(21.01)	(22.86)	(24.01)	(14.88)	(16.10)	(17.70)
8	41.67	41.69	46.32	28.91	29.13	33.09	22.65	23.03	26.07
	(34.02)	(33.60)	(36.76)	(21.43)	(21.38)	(23.09)	(15.57)	(15.62)	(16.65)
9	43.40	46.16	47.11	29.20	31.14	34.79	22.63	28.35	28.10
	(35.51)	(37.92)	(37.60)	(21.65)	(23.06)	(24.58)	(15.47)	(16.30)	(18.08)
10	45.23	45.24	44.46	30.00	30.01	30.98	22.92	22.80	24.32
	(37.18)	(36.68)	(37.77)	(22.30)	(21.78)	(23.41)	(15.59)	(15.23)	(16.59)
11	35.96	35.90	45.14	25.09	25.35	31.70	19.99	20.26	26.46
	(27.91)	(27.72)	(32.16)	(17.68)	(17.96)	(20.58)	(13.09)	(13.35)	(15.08)
12	42.85	41.69	53.59	29.07	28.59	37.03	22.46	22.28	28.19
	(34.13)	(33.09)	(40.42)	(20.99)	(20.81)	(25.29)	(15.05)	(15.11)	(17.78)
13	57.93	60.59	52.11	38.80	40.92	37.97	28.90	30.38	30.18
	(50.48)	(53.06)	(44.18)	(30.65)	(32.68)	(28.77)	(21.04)	(22.47)	(20.87)
14	53.63	52.99	67.39	36.15	36.20	48.20	27.24	27.56	37.29
	(45.71)	(44.83)	(55.23)	(27.91)	(27.84)	(35.24)	(19.45)	(19.71)	(24.61)
15	56.69	55.13	65.80	38.73	37.73	48.22	29.18	28.68	37.97
	(49.03)	(47.04)	(54.87)	(30.35)	(29.33)	(35.30)	(21.25)	(20.62)	(24.74)
16	65.27	69.73	56.19	43.38	47.71	41.52	31.75	34.94	32.81
	(58.01)	(62.53)	(46.86)	(35.01)	(38.83)	(31.03)	(23.76)	(26.49)	(22.62)
17	62.11	61.65	68.86	42.41	42.61	49.98	31.58	32.14	38.94
	(54.88)	(54.33)	(61.38)	(34.03)	(34.04)	(39.51)	(23.55)	(23.93)	(27.47)
18	61.59	61.78	61.55	42.52	42.86	44.39	31.86	32.35	34.61
	(54.60)	(54.65)	(55.68)	(34.13)	(34.44)	(35.66)	(23.73)	(24.32)	(24.79)
19	65.79	67.75	54.30	44.71	46.57	39.04	33.15	34.39	30.73
	(58.56)	(60.52)	(48.61)	(36.47)	(37.99)	(31.57)	(24.95)	(26.03)	(22.48)
20	54.89	54.47	71.54	36.92	37.21	52.08	27.69	28.17	40.21
	(47.05)	(46.27)	(57.79)	(28.76)	(28.81)	(37.61)	(19.97)	(20.27)	(26.41)
21	63.48	61.13	78.25	43.14	41.63	58.26	32.07	31.17	44.96
	(55.85)	(52.83)	(67.90)	(34.55)	(32.91)	(44.92)	(23.76)	(22.76)	(31.25)
22	77.20	81.34	59.79	53.75	58.67	44.46	39.04	43.50	35.27
	(71.64)	(75.95)	(51.16)	(45.61)	(50.42)	(34.16)	(30.64)	(34.44)	(24.86)
23	73.11	72.35	83.14	50.86	50.79	63.51	37.42	36.80	49.29
	(67.10)	(66.37)	(76.75)	(42.81)	(43.00)	(52.79)	(29.14)	(29.73)	(37.14)
24	74.78	75.39	68.98	52.40	53.31	52.63	38.67	39.58	41.67
	(69.11)	(69.54)	(59.83)	(44.50)	(45.18)	(40.54)	(30.39)	(31.14)	(29.06)
25	80.80	85.24	61.64	56.53	62.58	46.43	41.05	46.28	36.39
	(75.62)	(80.58)	(52.39)	(48.54)	(54.55)	(35.04)	(32.53)	(37.50)	(25.49)
26	75.38	75.58	76.20	53.62	54.23	57.54	39.90	40.57	44.47
	(69.51)	(69.81)	(72.79)	(45.53)	(46.14)	(49.31)	(31.26)	(32.28)	(34.43)
27	74.21	75.64	67.29	52.80	54.37	49.98	39.40	40.82	38.71
	(68.42)	(69.99)	(63.98)	(44.80)	(46.37)	(42.48)	(30.89)	(32.45)	(29.56)

Note: Maximum value for each scheme is emboldened.

In summary, our proposed test statistics G₁ and G₂ perform well in compare to the existing test statistics and among them G₂ is the one that we recommend.

4. Illustrative data analyses

In this section, we illustrate the proposed goodness-of-fit procedure discussed earlier with a real dataset. The data is concerning times to breakdown of an insulating fluid tested at 34 kilovolts (see Nelson 1982, Table 6.1, 228). Wang (2008) randomly generated a progressively Type-II censored sample of size m = 8 from n = 19 observations. The log-data, the progressive censoring scheme employed and the spacings are given in Table 4. We are interested to test the suitability of the exponential model to the log-data. Note that $q=\frac{m(m-1)}{2}=28$ and the test statistic G₁ and G₂ are given, respectively, by $$G_1=\underset{i<j}{\sum _{i=1}^8\sum _{j=1}^8}{W}_l^{(1)} |S_i-S_j|=0.5192,$$

Table 4. Insulating fluid log-data.

i	1	2	3	4	5	6	7	8
$x_{i:m:n}$	0.18999	0.77997	0.95993	1.30996	2.77986	4.84962	6.49999	7.35000
Ri	0	0	3	0	3	0	0	5
Si	0.3951	1.1134	0.3073	0.4439	1.5577	1.0136	0.8494	0.2623
$S_i^{\ast }$	3.6098	10.6196	3.0593	4.5504	17.6388	13.6781	14.0726	5.1001

and $$G_2=\underset{i<j}{\sum _{i=1}^8\sum _{j=1}^8}{W}_l^{(2)} |S_i-S_j|=0.5045.$$

We used the Monte Carlo simulation to estimate the p-values; $p-{\text{value}}_{G_1}=P(G_1>0.5192)=0.8263$ and $p-{\text{value}}_{G_2}=P(G_2>0.5045)=0.8282.$

The values of the test statistics and the corresponding p-values are presented in Table 5. The p-values in Table 5 strongly suggest the exponential model for the log-data by all the test statistics. This result is consistent with the conclusion of Nelson (1982), Viveros and Balakrishnan (1994), Balakrishnan et al. (2002) and Wang (2008).

Table 5. Test statistics and the corresponding p-values for the data in Table 4 when testing for the exponential distribution.

Criterion	G1	G2	TW
Test statistic	0.5192	0.5045	16.4775
p-value	0.8263	0.8282	0.2859

Acknowledgments

We thank Open Access funding provided by the Qatar National Library.

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.