Fair water resources allocation with application to the south saskatchewan river basin

Abstract

A formal decision making methodology is presented for equitably allocating water among competing users in a river basin when taking into account both the societal and physical systems aspects of the allocation problem. More specifically, within the societal component of the decision problem, multiple participants, their multiple objectives, equity principles, and economic factors are taken into account, while the physical systems part reflects relevant hydrologic and environmental factors. The Cooperative Water Allocation Model (CWAM) incorporates these societal and physical systems concerns within the framework of a large-scale optimization program which is divided into two main steps. Firstly, water is allocated among users based on existing legal water rights regimes or agreements. In the second step, water and associated benefits are reallocated among stakeholders to maximize basin-wide welfare. The CWAM methodology is used to study the South Saskatchewan River Basin located in Alberta, Canada, to demonstrate how it can be conveniently applied to a complex water allocation problem.

Une méthodologie de prise de décision formelle est présentée pour répartir équitablement l'eau parmi les utilisateurs concurrents dans un bassin de rivière, en tenant en compte les aspects sociaux et physiques des systèmes du problème de la répartition. Plus précisément, plusieurs participants, leurs objectifs multiples, ainsi que les principes d'équité et les facteurs économiques au sein de la société composants le problème de la décision sont pris en compte; tandis que, la partie de systèmes physiques reflète les facteurs hydrologiques et environnementaux pertinents. La coopérative d’Allocation de l'eau Modèle (CWAM) intègre ces préoccupations sociétales et physiques des systèmes dans le cadre d'un programme d'optimisation à grande échelle qui est divisé en deux étapes principales. Tout d'abord, l'eau est répartie entre utilisateurs basés sur des droits légaux ou accordés sur le partage de l'eau. Dans la deuxième étape, l'eau et les bénéfices associés sont réaffectés entre les intervenants afin de maximiser le bien-être de l'ensemble du bassin. La méthodologie CWAM est utilisée pour étudier le bassin de la rivière Saskatchewan Sud (situé en Alberta, Canada), et de démontrer comment cette méthodologie peut être aisément appliquée à un problème complexe de répartition de l'eau.

Introduction

As a result of climatic change, burgeoning population, dramatically expanding industrialization of developing countries such as China and India, and widespread water pollution, fresh water is becoming an increasingly scarce natural resource. Accordingly, the importance of equitably allocating water among competing demands in a highly interconnected world is one of the great challenges facing humanity. Certainly, a systems approach is required to provide sound decision methodologies and insightful policies for managing water at the local, basin, regional, national, and international levels in order to reflect the value systems and concerns of all stakeholders.

The Aral Sea tragedy constitutes a well-known illustration of the devastating consequences that can be wreaked upon society by inappropriate water allocation within a relatively dry area of the world. Beginning more than eight decades ago during the Soviet era, massive quantities of water were diverted from rivers flowing into the Aral Sea for inefficient irrigation purposes such as growing cotton for export. This sequence of political decisions caused the Aral Sea to shrink drastically in size, ruined the Aral Sea fishing industry, created a toxic mix of highly concentrated pollutants in the sea, and, overall, gave the Aral Sea the infamous distinction of being one of the worst ecological disasters in history (refer to Wang et al. 2007a and Nandalal and Hipel 2007 along with references cited therein). The rapid shrinking of glaciers in the Rocky Mountains of Western Canada as a consequence of climate change (Martz et al. 2007) is causing the summer flows of the Saskatchewan River and its tributaries to decrease during the summer season (Schindler and Donahue 2006; Pomeroy et al. 2009). Because the rivers flowing from west to east across the provinces of Alberta and Saskatchewan eventually reach Lake Winnipeg in the province of Manitoba, changes in water balance could cause Lake Winnipeg and other nearby lakes to greatly decrease in size. Thus, Lake Winnipeg has the potential to become the “Aral Sea” of North America. Moreover, the relatively dry conditions and intermittent droughts in the Prairie provinces along with increased demand for water via intensifying activities such as irrigation, extraction of bitumen from the oil sands, industrialization, and population growth, suggest that conflict over water will intensify and the requirement of fairly allocating this scare resource among competing uses is urgently needed. As mentioned by many researchers and organizations (see, for instance, de Loë 2009; Hipel et al. 2008c; National Round Table on the Environment and the Economy 2009, and references contained therein), Canada faces a wide range of tough water management problems for which good systems thinking is required for effectively resolving them.

Systems thinking has a key role to play in virtually all areas of water resources and environmental management in Canada and elsewhere. In order to carry out a proper and realistic systems study one must consider all interconnected aspects of a given systems problem using a rich range of societal and physical systems models. Therefore, in this paper, the Cooperative Water Allocation Model (CWAM) used at the basin level, combines multiple stakeholders, their multi-dimensional objectives, and economic factors from the realm of societal systems, along with hydrologic and environmental factors from the physical systems domain, under the overall umbrella of a large-scale optimization formulation. The operational capability of CWAM for computing fair water allocation in a river basin is illustrated by applying CWAM to a complex water allocation problem in the South Saskatchewan River Basin located east of the Rocky Mountains in Southern Alberta, Canada.

Systems thinking

Systems thinking techniques for formally modelling and analyzing decision making processes have been developed within a range of systems-related disciplines including operations research (Blackett 1962; Waddington 1973; Hipel et al. 2008b), systems engineering (Sage 1992; Sage and Rouse 2009), decision analysis (Edwards et al. 2007), industrial engineering, project management (Johnson 1997), and systems science (Lawson 2010). Although there are many differences among these and other related systems-based disciplines, they do possess many common features and any differences that do exist are usually complementary (see, for instance, Johnson 1997; Emes et al. 2005; and Hipel et al. 2008c). These various disciplines are converging in their focus and objectives by readily developing and adopting new systems thinking approaches for addressing complex systems, or system of systems problems, and expanding their application domains to encompass important challenges now confronting society, such as security, global warming, sustainable development, infrastructure renewal, and logistics. Additionally, the systems-based disciplines recognize the need to be able to handle unforeseen problems, which may suddenly emerge in the future; decision-making in real time, such as internet-based commerce (Hipel et al. 2007); and the need to entertain the concept of a system of systems structure (see Hipel et al. 2009a) for references regarding a system of systems and its employment in sustainable development).

Systems methodologies can be utilized in the optimal management of complex water resources “systems of systems”. As argued by Hipel et al. (2008c), these systems methodologies and techniques can be employed within an adaptive (Holling 1978; Walters 1986; Gunderson 1999) and integrative (Mitchell 1990; International Conference on Water and Environment 1992) management approach to sustainable development, often in real time. Recently, Jain and Singh (2003), Loucks and van Beek (2005), and Nandalal and Simonovic (2003) have written books that present systems approaches to addressing complex problems in water resources planning and management. From a Systems Engineering standpoint which explicitly considers hierarchical multiple objectives, Haimes (2009) provides a comprehensive methodology for realistically addressing complex risk assessment and management decision problems in water resources and many other fields. Of particular concern is how to handle the multiple participant-multiple objective decision making aspects occurring in water resources and environmental management (Hipel and McLeod 1994; Hipel and Fang 2005; Hipel et al. 2008a).

Conflict, or differences of opinion, inevitably arises whenever people interact with one another. For example, because Canada has a reputation of possessing vast amounts of fresh water, private companies would like to consider Canada's water to be the same as any other commodity and export it in bulk quantities to other countries. Accordingly, environmentalists are in direct conflict with these companies at various locations in Canada, as exemplified by conflict studies carried out by Hipel and Fang (2005), Hipel et al. (2008c), and Hipel and Obeidi (2005) using the methodology of the Graph Model for Conflict Resolution (Fang et al. 1993). In other conflict situations, there may be a relatively large degree of agreement and cooperation among disputants. For instance, agricultural, industrial, commercial, residential, and other competing users in a river basin may adopt a “fair system” for equitably sharing water to mutually benefit all competing parties, as is explained later in this paper. Clearly, this interactive phenomenon called conflict arises in virtually every domain of human activity. Moreover, the types of conflict that can occur can range from being completely competitive, wherein decision makers behave in noncooperative ways, to highly cooperative, in which decision makers can form coalitions in order to reach win/win resolutions. An important type of conflict problem in water governance, especially in the face of water scarcity, is how to allocate water fairly among competing water users within a river basin.

Fairness in water allocation

Resource allocation problems are concerned with how limited resources should be distributed fairly among competing activities in the achievement of optimal performance of a complex system or system of systems. Essentially, fairness is an abstract socio-political idea that implies impartiality, justice and equity (Young 1994). The efficient and fair allocation of water has become a controversial issue within and among many countries (United Nations, World Water Assessment Programme (UNWWAP) 2003; Wang 2005). Conflicts often arise among irrigation, urban, industrial, recreational, environmental and other uses since water is often argued to be a public good and should be equitably used. In many negotiations, stakeholders or users base their initial positions in terms of rights (Giordano and Wolf 2001), which provokes the most fundamental of problems – how to allocate water rights in a fair way.

For water rights allocation inside a country, water rights systems form the legal basis for water management, each of which may be founded upon one of three basic doctrines: riparian rights, prior rights, and public allocation (Savenije and Van der Zaag 2000). Many recent studies promote water transfers and market mechanisms to improve economic efficiency and effectiveness of water resources utilization (McKinney et al. 1999; Mahan et al. 2002). This necessitates the fair allocation of water as property rights, which is the foundation for a water market.

For international river basins among nations, water sharing is generally dictated according to international water agreements defining ownership of the water resources. An agreement may be based upon one of the following principles: absolute sovereignty, absolute riverine integrity, limited territorial sovereignty, and economic criteria (Wolf 1999; Giordano and Wolf 2001). Although international water laws assert that the water should be equitably allocated, they provide no well-defined, transferable, and measurable criteria for water rights allocation, and few models concerning fair water rights for transboundary basins exist in the literature (United Nations 1997; Seyam et al. 2000).

Principles and methodologies for fair resource allocation

Fairness ideas include Pareto optimality, monotonicity, consistency, impartiality, priority, and envy-free (Young 1994). By adopting some of these principles, various mathematical models can be formulated for application to different equitable allocation problems, including integer allocation, divisible good allocation, cooperative games, and bargaining. It should be pointed out that depending on the nature of the resources, not all of the above principles may be achievable. The choice depends on one’s value system.

Consider a complex large-scale system, such as a water allocation system, consisting of competing uses which require the resources to fulfill their various activities. Let x = (x₁ , x₂ , …, x_h ) be the vector of decision variables representing the allocations to be determined and Ω denote the feasible set of x defined by the constraints. Without loss of generality, resource allocation can be viewed as a generic multiple objective optimization problem:

(1)

where , f_j (x) is the jth objective function, j = 1, 2,…, m. To trade off the multiple objectives, the concept of fairness must be accounted for by defining some type of aggregation function, , to optimize based upon the individual objective functions. Once a social aggregation objective function is defined, the generic multiple objective resource allocation problem can be restated as

(2)

Ogryczak et al. (2003) extend monotonicity, impartiality, and equitability principles, summarized in Table 1, to generic multiple objective resources allocation problems, and propose the lexicographic optimization approach for fair resource allocation. The priority principle is utilized by Wang (2005) in terms of a utility function aggregating the multiple objectives. When a utility function satisfies the monotonicity, impartiality, and equitability principles, it is called a perfectly equitable utility function for the generic resource allocation problem. The solution of the maximization of a perfectly equitable utility function will produce a perfectly equitable resource allocation scheme. If a utility function satisfies the monotonicity and priority principles, it is called a priority equitable utility function for the generic resource allocation problem. The solution of the maximization of a priority equitable utility function will produce a priority equitable resource allocation scheme. It has been shown (Yager 1988, 1997; Ogryczak et al. 2003) that the lexicographic maximin (or equivalent lexicographic minimax) problem is a specific formulation of the generic resource allocation problem, whose solution is a perfectly equitable allocation scheme. For priority equitable resource allocation problems, the priority-based sequential solution method can be utilized to find the allocation schemes.

Table 1. Fairness principles for multiple objective fair resource allocation.

Principle	Interpretative description
Monotonicity	Each user’s allotment becomes no worse when the amount of resources increases.
Impartiality	Allocations are made based on the availability of resources and the nature of demands, rather than the identities of the users.
Equitability	Resource is allocated to satisfy rational transfers such that a transfer of any small amount from an outcome to any other relatively worse-off outcome results in a more preferred overall outcome.
Priority	Resource is allocated according to the priority ranks of the individual demands, such as the realization of water rights allocation under a prior allocation regime.

Fairness principles in the generalized water allocation problem

The described fairness principles and solution concepts may be applied to water allocation at both the operational and local levels although the following discussion focuses on the former. The water allocation problem is formulated based on a generalized node-link river basin network system model (Wang 2005). For a typical water allocation problem, there are several thousand physical, policy, and systems control constraints. Typical physical constraints include mass balances and capacity limits. The system control constraints are used to compensate for the simplified abstraction of the river network, hydrological processes, or socioeconomic factors. For example, the total inflow to any non-storage node subtracting the return flows to it should exceed the total diversions from it because in reality those return flows are not available for diversion at that node.

A river basin network is a multiperiod configuration connected by the reservoir carry-over storage links. Thus, water allocation at the basin level is mathematically expressed as a generalized multiple objective multiperiod network flow programming problem: max or min f(Q,S,C,X_s ), where f(Q,S,C,X_s ) is a vector of multiple objectives, ; Q, S and C are, respectively, the vectors of network variables representing water flows, aquifer and reservoir storages, and pollution concentrations in link flows, aquifers or reservoirs; and X_s is the vector of non-network type decision variables (side variables), which may be water prices, water transport costs, pollution control costs, crop types, irrigation areas, and/or product prices. Some common types of objectives include: satisfying existing or projected water demands, minimizing the difference in water deficits among all demand sites, maximizing the flow to downstream nodes, maximizing economic production, minimizing the concentration of salts in the system, and minimizing water diverted from other basins. Accordingly, various fair water allocation problems are possible when the fairness principles are applied.

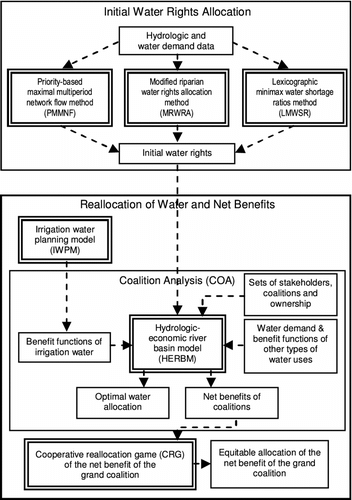
The Cooperative Water Allocation Model (CWAM)

Overall systems model

Integrated water resources management is a multiple dimensional process centered around the demands for water, the policy to meet these needs and a management strategy to implement the policy, which requires the integration of various components including physical, biological, chemical, ecological, environmental, health, social, and economic aspects (Singh 1995). After discussing water allocation issues at the basin level, fairness principles listed in Table 1 are embedded into the design of the Cooperative Water Allocation Model in this section.

Water allocation issues can be addressed at national, provincial, basin, and local levels. At the provincial or national level, a water allocation policy deals with the interacting obligations of water users and the regulatory authorities. In many countries, the state is the owner of all or nearly all water and allocates water permits or user rights (water rights) according to specific water rights systems (Savenije and Van der Zaag 2000). For international river basins between countries, generally there are no formal inter-country water rights systems but there do exist international water agreements defining ownership of the water resources (Wolf 1999). At the basin or operational level, a water allocation plan is concerned with shorter-term, usually annual, management of reservoir storage, river flows, and diversions. At the local level, the distribution rules and priorities are specified for water uses to share the diversions determined at the operational level (United Nations, Economic and Social Commission for Asia and the Pacific (UNESCAP) 2000).

As water scarcity is becoming a common occurrence in many countries (UNWWAP 2003), discussions have naturally begun to arise addressing institutions and polices for water allocation, and associated equity, efficiency and sustainability principles (UNESCAP 2000). Although many simulation and optimization models for water quantity, quality and economic management have been developed for operational use under various water rights systems (McKinney et al. 1999), most models and applications do not address the fairness issue, except for prior water allocation models developed using different modelling techniques including conventional simulation (Wurbs 2001), minimum-cost pure (Fredericks et al. 1998), or generalized (Hsu and Cheng 2002) network flow programming, and mixed integer linear programming models (Tu et al. 2003). The deficiencies of these formulations are discussed in detail by Wang et al. (2007b). There are only a few studies that jointly consider both efficiency and equity (Cai et al. 2002; Mahan et al. 2002); however, these models are formulated for specific case study areas rather than as generalized modelling systems.

Due to differences of capability in generating economic benefits, water allocations merely based on a water rights approach usually do not make efficient use of water for the whole river basin. Meanwhile, an economically efficient water allocation plan is generally not an equitable one for all water users or stakeholders. To overcome this dilemma, a modelling framework named the Cooperative Water Allocation Model (CWAM) has been developed by Wang et al. (2003, 2007a,b, 2008a,b) which can be used to promote cooperation of stakeholders in a river basin to obtain equitable, efficient, and sustainable water allocations. This methodology carries out water allocation in two steps: (1) initial allocation of water rights to water uses founded on legal water rights systems or agreements; and (2) reallocation of water to achieve efficient use of water and equitable redistribution of net benefits to promote cooperation of all stakeholders in a river basin. CWAM is applied to a complex water allocation problem in the South Saskatchewan River Basin in western Canada in the next main section, based on earlier work by Wang et al. (2008a) and Wang (2005). This model has also been applied to the Aral Sea Basin (Wang et al. 2007a; Wang 2005) to investigate allocation of water rights.

As shown in Figure 1, CWAM distributes water resources in two steps: initial water rights are firstly allocated to water uses, or users, based on rights systems or agreements, and then water is reallocated to achieve efficient use of water through water transfers. Correspondingly, sub-models are constructed to incorporate considerations for allocating resources in a fair and efficient manner in two aspects: (1) fair water rights allocation from a social-political viewpoint; (2) fair reallocation of benefits through side payments.

Figure 1 Components and data flows of the Cooperative Water Allocation Model (CWAM).

Priority and lexicographic approaches for water rights allocation

Three methods are developed for deriving initial water rights allocation among competing water uses: the priority-based multiperiod maximal network flow (PMMNF) programming, modified riparian water rights allocation (MRWRA) and lexicographic minimax water shortage ratios (LMWSR) methods. PMMNF is a very flexible approach and is applicable under prior, riparian and public water rights systems. MRWRA is essentially a special form of PMMNF adapted for fair allocation under the riparian regime. LMWSR is designed for application under a public water rights system, which adopts the lexicographic minimax fairness concept. Note that, for a non-storage demand site, the water rights are defined as a set of volume and pollutant concentration limits for all inflows and outflows. For a storage reservoir, the water rights are defined as a set of reservoir storage and pollutant concentration limits. Each of these three methods is designed for distinctive applications depending on existing or proposed water rights systems.

Priority formulation

The PMMNF method is designed for water allocation under various water rights allocation regimes. This method allocates water to meet inflow and storage demands strictly according to priorities. Junior uses are allocated after senior uses have been satisfied, as fully as possible, subject to hydrologic constraints. Priority is normally assigned to uses according to “first in time, first in right” under a prior water rights system, or following the relative locations of water uses under a riparian system, or according to the functional importance of water uses in a public water rights regime (Savenije and Van der Zaag 2000).

In the PMMNF formulation, each inflow link to a demand node is viewed as consisting of one or more dummy sublinks and each sublink has a withdrawal demand and corresponding priority. The storage of every reservoir is divided into several subzones according to reservoir operating rules. Each sub-zone has a storage and corresponding priority. If a vector x is used to represent all of the control or decision variables (Q, S, C and X_s) and Ω is utilized to denote the feasible set defined by the constraints in the PMMNF formulation, the problem can be expressed in a more compact form as:

(3)

where, , r_i is the priority assigned to a reservoir subzone or inflow sublink, from highest to lowest priority, and is the sum of the storage and inflows to demands owning the same priority r_i during all of the time periods.

Lexicographic formulation

Under a public water rights system, one approach for allocating equitable water rights is to have water shared among all demands such that shortage ratios of water uses and differences among them are reduced as much as possible while taking account of their relative importance (weights). This equitable water sharing can be formulated as a lexicographic minimax water shortage ratios program (Wang 2005).

(4)

where μ is the number of uses; is the number of planning periods, usually the number of months; is the vector of μτ elements , where these elements are sorted in a nonincreasing order; and is the water shortage ratio of demand node j during period t, in which is the weight for the corresponding water shortage ratio R(j,t). For a nonstorage demand node, the water shortage ratio during a time period is defined as the quotient obtained by dividing the difference between the corresponding inflow demand and total effective inflow by that demand. For a reservoir node, the water shortage ratio is defined by dividing the difference between the corresponding storage demand and actual storage by the storage demand.

Cooperative game theoretic approaches for water and net benefits reallocation

The second step of CWAM comprises three sub-models: the irrigation water planning model (IWPM), the hydrologic-economic river basin model (HERBM), and the cooperative reallocation game (CRG) of the net benefit of a given coalition. IWPM is a model for deriving benefit functions of irrigation water for all time periods. This model maximizes the total profit of irrigated crop productions within an irrigation demand node by adopting quadratic empirical crop yield-water and salinity functions. HERBM is the core component of the coalition analysis. It is a tool for finding optimal water allocation schemes and net benefits of various coalitions of stakeholders. The inputs include hydrologic and water demand data, initial water rights, water demand curves and benefit functions, stakeholders, coalitions, and owner-use relationships. CRG adopts cooperative game theoretic approaches to perform equitable allocation of the net benefits of a given coalition. The economically efficient use of water under a given coalition is achieved through water transfers (water reallocation) based on initial water rights.

In CWAM, constant price-elasticity water demand functions are adopted to derive the monthly net benefit functions of municipal and industrial demand sites and hydropower stations, while quadratic gross benefit functions are used to find the monthly net benefit functions of agriculture water uses, stream flow demands, and reservoir storage (Wang et al. 2008a).

Given a set of stakeholders or players under consideration for reallocation, a subgroup of stakeholders entering into a cooperative agreement and working together forms a coalition. Reallocation of water and net benefits through cooperation of stakeholders can be viewed as an n-person cooperative game. Simplifications are made to reduce the problem size in order to keep the computational load within a reasonable limit. The value of a coalition is defined as the maximum total net benefit that the coalition can gain based on the coalition members’ water rights over the entire planning period, subject to not decreasing the water flows and not increasing the pollutant concentrations in the flows to other stakeholders not taking part in that coalition. For details of the formulation, refer to Wang (2005). Solution concepts, including nucleolus, weak nucleolus, proportional nucleolus, normalized nucleolus and Shapley value, are adopted to solve the reallocation game. The nucleolus constitutes the reward vector for which excesses for all coalitions are as small as possible. An excess is the amount by which the worth of a coalition exceeds the aggregate payoff to its members in isolation (Schmeidler 1969). By changing the definition of the excess function, with the optimization algorithm remaining the same, variations of the nucleolus are defined. The weak nucleolus concept (Young et al. 1982) substitutes the excess with the average excess; proportional nucleolus (Young et al. 1982) replaces the excess with the ratio of excess to net benefit of a coalition; normalized nucleolus (Lejano and Davos 1995) substitutes the excess with the ratio of excess to the summation of all individual payoffs of the members in a coalition. The Shapley Value reflects a fair payoff distribution based on marginal contributions of players averaged over joining orders of the coalition (Shapley 1953). The various nucleolus solution concepts are perfectly equitable, because they lexicographically minimize the maximum coalition excess (Owen 1995).

To make fair net benefits reallocation and achieve basin scale economic efficiency, the second step of CWAM employs cooperative game theoretic solution concepts having side payments. In fact, the purpose of the model is to simulate fair water trades among stakeholders. One could argue that water transfers without side payments could be an alternative more likely to be accepted for encouraging cooperation to achieve Pareto improvements in economical efficiency of water allocation (Parrachino et al. 2006). However, the dilemma is that water transfers from one use to another imply that one loses money while the other gains more revenue. Because the revenue transfers are associated with water transfers between uses, a Pareto improvement cannot be achieved if initially assigned water rights are transferred unidirectionally between two stakeholders. Bidirectional water transfers between stakeholders are a necessary condition for achieving cooperation between stakeholders without side payments. Unfortunately, stakeholders, like agricultural and industrial users, often have gaps in marginal net benefits of water utilization, which lead to unidirectional water transfers and thus no economic incentive to cooperate if a strategy without side payments is taken in these situations. Cooperative game theory without side payments adopts the Nash-Harsanyi approach (Harsanyi 1959) which generally produces economic efficiency which is inferior to basin-wide economic optimization. The effectiveness of a solution without side payments highly depends on the composition of coalition stakeholders in which bilateral water transfers can take place between stakeholders. Even if stakeholders are grouped to consist of members whose water uses have variable marginal values, for example, upstream and downstream municipalities, in order to make Pareto improvements possible for stakeholders through water transfers only, Pareto improvements cannot be achieved among different types of uses for a stakeholder if no side payment is allowed. Due to these considerations, a strategy having side payments is adopted to solve the water allocation game in CWAM.

The allocation approaches of CWAM have sustainability implications embedded in their formulations. They introduce environmental sustainability considerations by treating environmental requirements as demands and allowing the inclusion of water quality constraints. The lexicographic method enforces the water sharing among users during shortage times and attempts to secure a sustainable economy and society.

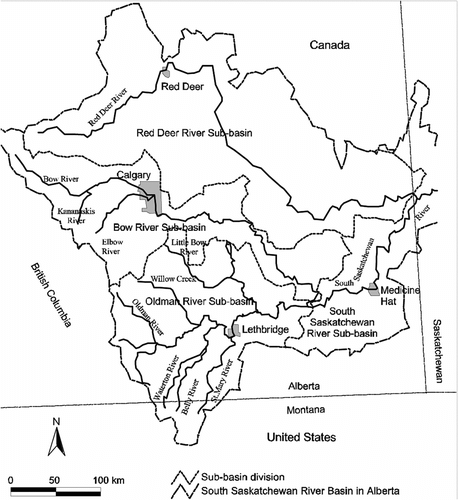
South Saskatchewan River Basin case study

The South Saskatchewan River Basin (SSRB) located in southern Alberta, Canada, is comprised of the Red Deer, Bow and Oldman River sub-basins and the portion of the South Saskatchewan River sub-basin located within Alberta (Figure 2). The SSRB drains about 120,000 square kilometers and possesses a primarily semi-arid climate (Dyson et al. 2004). The South Saskatchewan River originates in the Rocky Mountains of Canada and summer flows are highly dependent upon snowmelt from the mountains. More than 1.5 million people lived in the SSRB in 2004, about 81% residing in urban centers including Calgary (about one million residents), Lethbridge, Red Deer, and Medicine Hat.

Figure 2 The South Saskatchewan River Basin within the Canadian Province of Alberta.

Under the Water Act, the Government of Alberta owns the rights to all waters within its borders. Licenses for water uses assign the maximum amounts of withdrawals and priorities on a first-in-time, first-in-right basis (Alberta Environment 2003). According to the SSRB Water Management Plan approved in August 2006, Environment Alberta will no longer accept new water license applications for the Bow, Oldman, and South Saskatchewan sub-basin systems. New water allocations have to be obtained through water allocation transfers (Alberta Environment 2006).

Modelling scenarios

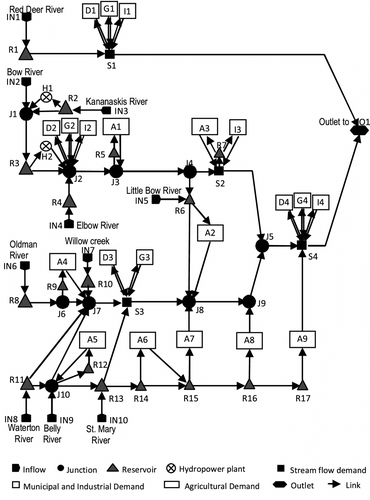
The SSRB model network is shown in Figure 3. It has 55 nodes in total, including 10 inflow (IN1 to IN10), 1 outlet (O1), 17 reservoirs (R1 to R17), 9 irrigation (A1 to A9), 4 domestic (D1 to D4), 4 general (G1 to G4), 4 industrial (I1 to I4), 2 hydropower plants (H1, H2), and 4 instream flow requirement (S1 to S4) demand nodes. In this case study, the general demand refers to municipal, excluding domestic, demand. The directed links to offstream irrigation, domestic, general, and industrial demand nodes are diversion canals, while the reversely directed links from them to nodes on streams represent the return flow routes. Thirteen irrigation districts and smaller privately-owned irrigation systems in the SSRB are aggregated into 9 irrigation nodes according to surface water sources and agroclimate zones. Groundwater supplies are not considered.

Figure 3 Network of the South Saskatchewan River Basin in southern Alberta.

The time horizon of the modelling in this study is one year having 12 monthly time periods. Details regarding sources of input data, water demand estimation and assumptions made in defining scenarios are described by Wang (2005). Water demands of irrigation regions are assumed to occur during the growing season. Monthly irrigation demands are determined by the irrigation water planning model (IWPM), a sub-model of CWAM, as the difference between crop potential evapotranspiration and effective precipitation when growing soft wheat, hard spring wheat, barley, canola, potatoes and alfalfa, as representative crops for the six crop categories. Salinity is considered in this study in order to explore the effects of water allocation on the salt concentrations in the river system and on the benefits of crop production.

Six case scenarios are investigated according to the combinations of water demands, hydrologic conditions, and methods for initial water rights allocation. In Cases A, B and C, initial water rights are allocated by the PMMNF method, reflecting Alberta’s existing prior water rights system. In Cases D, E and F, initial water rights are assigned by the LMWSR method, which reflects allocations under an assumed public regime. Case A (1995 wet & PMMNF) and Case D (1995 wet & LMWSR) represent the actual situations of water demands, tributary inflows and node adjustments in 1995. Case B (2021 normal & PMMNF) and Case E (2021 normal & LMWSR) consider the forecasted water demands in 2021, and the long term mean (1912-2001) tributary inflows and node adjustments. Case C (2021 drought & PMMNF) and Case F (2021 drought & LMWSR) explore water allocations under the forecasted water demands in 2021 and the hydrologic conditions of an assumed drought year. Since Case A represents the actual situation as of 1995, it is also used for calibrating model parameters such as water loss coefficients and node adjustments.

In the PMMNF method, ten priority ranks are assigned to all the demands in the SSRB: all domestic water demands have the highest priority rank; licensed withdrawals for satisfying irrigation, municipal, industrial and hydropower generation water demands and stream flow requirements are assigned priority ranks according to the “First in time, first in right” rule and their license application dates. In the LMWSR method, weights of water uses are set based on the “equivalent weighted shortages” rule, whereby water shortages are shared subject to equivalent weighted water shortage ratios. The higher the social utility, or the lower the water-shortage endurance that the use has, the larger is the weight.

The modelling results show that in the wet and normal hydrologic years, all offstream and hydropower generation water demands are satisfied if PMMNF is used, and are nearly satisfied when LMWSR is utilized. The total net benefits obtained from allocated initial water rights, in millions of dollars, are 871.735 (Case A), 1615.148 (Case B), 1517.558 (Case C), 870.3 (Case D), 1609.021 (Case E) and 1675.373 (Case F). Since water demands are satisfied or nearly satisfied under Cases A, B, D, and E, there is little need or incentive for water reallocation. Therefore, in this study reallocation is investigated for Cases C and F only. The upcoming discussion concentrates on the results of these two drought cases.

Initial water rights allocation in the South Saskatchewan River Basin

In Case C, water shortages appear at various locations, with the annual satisfaction ratios ranging from 0.966 (96.6%) to 0.475 (47.5%) as shown in Figure 4. Because the PMMNF method allocates water rights by sequentially maximizing the total effective inflows for all demands having the same priority rank from the highest priority to the lowest one, the demands having higher priorities have privileges to receive water, and an upstream demand has more advantage to take water than a downstream demand having the same priority rank. For example, the irrigation regions consisting of the St. Mary River Irrigation Region-West (A7), Taber Irrigation Region (A8), and St. Mary River Irrigation Region-East (A9), cannot be satisfied as fully as the Raymond and Magrath Irrigation Region (A6), although they divert water from the same water headworks system. The reason is that A6’s monthly demands can be fully satisfied by utilizing its licensed withdrawal at the priority rank 2, while the other three districts have to resort to their withdrawal licenses with lower priority ranks of 4 and 8. Another example showing the effects of priority setting is the water allocation among the domestic, general and industrial demands of the large municipality of Calgary under the drought Case C. All monthly domestic demands are satisfied even if there is severe drought, because under Alberta’s existing prior water rights system they are always assigned to the highest priority no matter when an application for withdrawals is submitted. The monthly satisfaction ratios of Calgary’s general (G2) and industrial (I2) water demands are found to be constant, at 0.695 and 0.475, respectively, because the demands required by future development are licensed with lower priority ranks. Calgary would have to yield the rights to utilize these withdrawal licenses with lower priority in the drought scenario.

Figure 4 Distributions of annual satisfaction ratios under Cases C and F.

Compared to the PMMNF method, the allocation by the LMWSR method under the drought Case F leads to more evenly distributed satisfaction ratios for offstream and hydropower generation water demands varying from 0.802 to 1, as shown in Figure 4. As the LMWSR method for water rights allocation searches for the vector of lexicographic minimax fair distribution of weighted shortage ratios by iteratively finding the minimax water shortage ratios and then fixing their upper bounds, the demands possessing higher weights have the privilege to receive water, and all demands of the same weight are equitably treated no matter if they are located upstream or downstream. For example, the monthly demands of the Raymond and Magrath Irrigation Region (A6) from May to August cannot be fully satisfied. However, A6 is fully satisfied by the PMMNF method in Case C. The domestic use (D2) of Calgary usually has higher monthly satisfaction ratios than general (G2) and industrial (I2) uses under the drought year scenario, since its demands are assigned larger weights.

Water and net benefits reallocation in the South Saskatchewan River Basin

Water uses in the SSRB are grouped under the ownership of nine stakeholders: City of Red Deer (RD) - domestic, general and industrial; Bow River hydropower stations and associated reservoirs (BH); City of Calgary (CA) - domestic, general and industrial; Eastern Industrial Region (EIN); irrigation regions and associated offstream irrigation reservoirs in the Bow River Sub-basin (BIR); City of Lethbridge (LB) - domestic and general; irrigation regions and associated offstream reservoirs in the Oldman River Sub-basin (OIR); City of Medicine Hat (MH) - domestic, general and industrial; and Alberta Environment (AE) - stream flow demand sites and onstream reservoirs. Due to data limitations, the values of stream flows and reservoir storages are not explicitly included in the objective functions of the hydrologic-economic river basin modelling and coalition analysis. Instead, their water rights are preserved through hydrologic constraints.

Net benefits of initial water rights

Annual net benefits based on initial rights allocated under the entirety of scenarios for Cases C and F are 1517.558 and 1675.373 million dollars, respectively. Irrigation, the dominant consumptive water use in the SSRB, receives large amounts of water, but produces low net benefits. Hydropower generation is the second largest water use, and also has a low water value. Although hydropower stations are non-consumptive users, they do compete for river flows with upstream uses and reservoir carry-over storages for future uses. The economic analysis of the allocated initial rights demonstrates that the differences of water values for different water uses can be shown by the different monthly marginal net benefits of raw water based on withdrawal rights to non-storage demand sites. For example, in drought Case C, the marginal values of raw water withdrawn from the junction node J2 to the general (G2) and industrial (I2) demands of Calgary are more than $1.8 per cubic meter during all months, and are significantly higher than other uses. The marginal values of irrigation withdrawals are between $0.015 and $0.051 per cubic meter.

For the drought Case F, the marginal values of raw water withdrawals based on the initial water rights allocated by the lexicographic minimax water shortage ratios (LMWSR) method are similar to those allocated by the PMMNF method, except that those of the domestic, general and industrial uses of Calgary are more evenly distributed among months from $0.745 to $1.312 per cubic meter. The total annual inflow of non-storage demand sites in the SSRB based on the initial rights allocations by the LMWSR method is a little smaller than those allocated by the PMMNF method, and more water is left in the river system for satisfying stream flow requirements and is passed onto the downstream Province of Saskatchewan. However, the total net benefit based on the results of LMWSR is even greater than that obtained by PMMNF. This means that the LMWSR method can produce water allocations that are not only equitable but also as economically efficient as PMMNF.

Basin-wide optimal water allocation

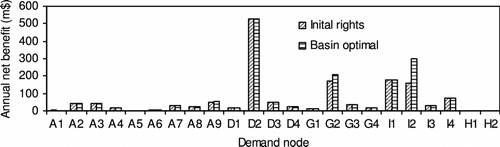
Annual net benefits of stakeholders under the initial and basin-wide optimal scenarios in Case C are summarized in Figure 5, which shows water trade (including both intra- and inter-stakeholder trade) will lead to an increase in the total net benefit of the SSRB in the amount of $170.5 million. Marginal net benefits of raw water withdrawals under the basin-wide optimal allocation scenario in Case C are evenly distributed among months due to the economic optimization covering all time periods. However, the marginal net benefits of raw water withdrawals at different locations and for different types of water uses may not be equal due to differences in their water demand or benefit functions, hydrologic constraints, and the upper bounds set on monthly water demands.

Figure 5 Annual net benefits of inflows allocated to demand sites (Case C).

Under the basin-wide optimal allocation scenario in Case F, large amounts of water are exchanged among irrigation regions, rather than being assigned to a more valuable user, the City of Calgary, and the gain of water trade is only $15.53 million. This is caused by the more evenly-spread water satisfaction ratios of initial water rights obtained by the LMWSR method.

Reallocation of net benefits among stakeholders

Excluding Alberta Environment, eight stakeholders are considered in the hydrologic-economic river basin modelling and coalition analysis. However, the comparative analysis of the initial rights and basin-wide optimal scenarios under both Cases C and F demonstrates that only four stakeholders (BH, CA, BIR and OIR) have significant changes of inflows and net benefits, while others are either nil or very small. Thus, the coalition analysis just needs to consider these four players. The reduction of stakeholders drastically decreases the coalition number to only 15. For every coalition, the multistart global optimization algorithm for coalition analysis utilizes the OQNLP solver (GAMS Development Corporation 2005) to generate hundreds of scatter trial points, select good starting points, and use the gradient-based nonlinear solver MINOS (Murtagh et al. 2002) for further optimization and final solution determination.

Stakeholders may have different capacities of water withdrawal and different gains of water uses when participating in different coalitions. For example, under Case C, if BH and CA pursue the intra-optimal allocation, they may only get nil and $28.110 million more than those obtained by their initial rights, respectively. But they can gain an increase of $38.642 million if they work cooperatively. The different capability of gains for a stakeholder involved in different coalitions makes it necessary to analyze all the possible coalitions of stakeholders in order to promote the grand coalition and equitably allocate the net benefits (side payments). The cores of the cooperative net benefit reallocation games under both Cases C and F are nonempty, which means there are infinite possible allocations satisfying the equity rationalities as long as they are located in the cores. The allocations by the four nucleolus and Shapley value solution concepts mentioned in the subsection entitled “Cooperative Game Theoretic Approaches for Water and Net Benefits Reallocation” can be used for comparison purposes.

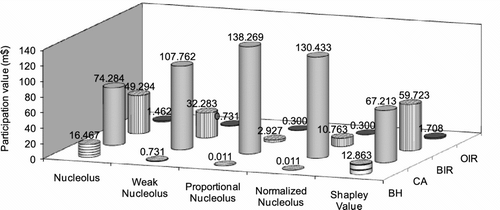
Value of participation in the grand coalition for each stakeholder is represented as the additional gain over the independent optimal (intra-stakeholder optimal) net benefit that can be produced based on his or her initial water rights. The additional gains under Case C after reallocation of water and net benefits with different cooperative game solution concepts are summarized in Figure 6. Under Case C, Calgary is normally allocated most of the additional gain over the intra-optimal scenario benefit, ranging from 67 to 138 million dollars, since it is the major contributor to the grand coalition. The Bow River Irrigation Regions (BIR) make additional gains from about 3 to 60 million dollars, by receiving a side payment from Calgary for the water trade among them. For participation in the grand coalition under Case F, the total additional gain over the intra-optimal allocation is only $13.815 million. Most of the gain is allocated to Calgary due to its significant contribution to the grand coalition. BIR’s gains range from $0.553 to $2.421 million, since it withdraws more water under the grand coalition scenario than its initial water rights. Bow River hydropower stations (BH) make additional gains of about 2 to 3 million dollars, by receiving side payments from Calgary and the Bow River Irrigation Regions (BIR) for water rights transferred to them.

Figure 6 Values of participation in the grand coalition for stakeholders under Case C reallocated with different cooperative game solution concepts.

Conclusions

The cooperative water allocation model (CWAM) is designed for pursuing fair and efficient water allocation among competing users at the basin scale level, based on systems thinking and the integration of hydrologic, environmental, societal, and economic considerations. As exemplified by the SSRB application in the previous section, CWAM constitutes a comprehensive systems methodology which is fully operational for tackling complex issues in water allocation. In particular, for two drought scenarios in SSRB, CWAM furnishes specific initial water rights allocation and subsequent reallocation of water as well as associated benefits for stakeholders to achieve basin-wide economic efficiency and fairness.

As is emphasized by Hipel and Fang (2005) and Hipel et al. (2007), a rich range of systems thinking approaches needs to be developed for addressing many types of complex water resources and environmental problems facing humankind at the present time and into the foreseeable future. For instance, how can the world community develop fair policies to allocate costs in reducing greenhouse gas emissions as well as adapting to the impacts of climate change? Perhaps some of the key ideas embedded within CWAM can be appropriately revised and extended for resolving this kind of problem. Another connected challenge is to design systems thinking methods for handling issues related to providing reliable fresh water supplies and other types of infrastructure security. Because negative and unforeseen emergent properties can arise from a given complex system of systems, real time adaptive and integrative decision making may be required in certain situations based upon vast amounts of data being continuously measured over time (Hipel et al. 2007). For instance, unsuspected health effects caused by synthetic pharmaceutical chemicals present in our water supply may require immediate action to rectify the situation.

Acknowledgements

The authors are grateful to anonymous referees who carefully reviewed their paper and provided constructive suggestions for improving it. They would also like to thank the Natural Sciences and Engineering Research Council (NSERC) of Canada for providing financial resources via Discovery Grants held separately by the first two authors as well as the Strategic Grant entitled Systems Engineering Approaches for Brownfield Redevelopment. Supporting facilities were furnished by the University of Waterloo, Ryerson University, and Centre for International Governance Innovation. An earlier version of this research was presented at a conference (Hipel et al. 2009b) and also discussed as part of the opening keynote address entitled “Water Resources in Canada: A Strategic Viewpoint” by K.W. Hipel at Water 2010 in Quebec City.