Establishment of channel networks in a digital elevation model of the prairie region through hydrological correction and geomorphological assessment

Abstract

Building channel networks in flat regions of digital elevation models (DEMs) is important for watershed delineation and hydrological modeling, particularly for areas with gently-sloped terrain, such as the Canadian Prairies. Existing drainage analysis methods cannot effectively address the spatial correlations of elevation across the flat regions, and the quality of the DEM-derived channel network is mainly evaluated through visual inspection. In this study a hydrological correction method is developed that integrates elevation information from both the existing digital channel network and the original DEM. A set of geomorphological indices is then introduced for quantitative evaluation of DEM-derived channel networks from the perspectives of flow direction and drainage pattern. Both the DEM correction and network assessment methods are implemented in a GIS environment. Their performance is demonstrated through a case study in southern Saskatchewan, Canada. The generated channel network is consistent with the known hydrological information and contains fewer parallel channels compared with existing methods. The developed methods could be valuable for a wide range of applications using the Canadian Digital Elevation Data (CDED) within the context of the Canadian Prairie region.

La construction des réseaux de canaux dans les régions plates des modèles numériques d’élévation (MNEs) est importante par rapport à la délimitation des bassins versants et la modélisation hydrologique, en particulier pour les zones terrestres qui ont majoritairement une pente douce, comme les Prairies canadiennes. Les méthodes d’analyse de drainage existantes ne peuvent pas traiter efficacement les corrélations spatiales d’altitude dans les régions plates, et la qualité du MNE dérivé d’un réseau de canaux est principalement évaluée par des inspections visuelles. Cette étude a développé une méthode de correction hydrologique qui a intégré l’information d’altitude du réseau de canaux numériques existants et l’original MNE. Un ensemble d’indices géomorphologiques ont ensuite été introduits pour l’évaluation quantitative des réseaux de canaux dérivés des MNEs du point de vue du sens d’écoulement et des réseaux de drainage. Les deux, la correction à l’aide du DEM et les méthodes d’évaluation du réseau, ont été mises en œuvre dans un environnement de SIG. Leur performance a été démontrée par une étude de cas au sud de la Saskatchewan, Canada. Le réseau de canaux générés par la méthode proposée a été compatible avec les informations hydrologiques connues et contenait moins de canaux parallèles comparés à d’autres méthodes utilisées présentement. Les méthodes développées pourraient être utiles pour améliorer une large gamme d’utilisations des données numériques d’élévation canadiennes (DNEC) dans le contexte de la région des Prairies canadiennes.

Introduction

Digital elevation models (DEMs) provide fundamental information for understanding the topographic control on the movements of water, sediments and contaminants over a watershed (Garbrecht and Martz 1997; Huang and Liu 2010; Liu and Tong 2011; Luo et al. 2006; Peng et al. 2011; Wu et al. 2007). They are among the most important inputs required by distributed rainfall-runoff and water quality models (Colombo et al. 2007; Jing and Chen 2011; Qin et al. 2009; Zhang et al. 2011). Numerous studies have been undertaken to explore automated watershed delineation using DEMs (Hutchinson 1989; Jenson and Domingue 1988; O’Callaghan and Mark 1984; Soille et al. 2003; Tarboton 1997). One difficulty that challenges all automated delineation methods is the establishment of channel networks in flat regions of DEMs. Although perfectly flat regions are rare in nature, they may exist in DEMs due to low quality input data, interpolation errors, or pit-removing procedures. Flow directions and aspects on a perfectly flat surface cannot be determined because the lowest elevation in a cell’s neighbourhood is unavailable. This problem is particularly important to watershed studies involving areas of gently-sloped landscape, such as the Canadian Prairies where the average slope is frequently less than 5% and the terrain is full of small depressions occupied by ponds or lakes. Because the vertical resolution of the Canadian Digital Elevation Data (CDED) is only one metre for the Prairie Provinces (with the exception of Alberta), it is often impossible to fully illustrate the subtle topographic features of lowlands. As the availability of high-resolution (at a scale of 10,000 or less) topographic data is still very limited for the majority of the prairie regions, CDED DEMs serve as key primary topographic data in a range of applications including flood protection, environmental impact assessment, water resources management, forest planning, and wildlife habitat protection. Thus, the limitation of CDED DEMs, with regard to the lowland representation, causes it to be problematic for various fine-scale watershed studies in the prairie region.

In general, existing methods for drainage analysis of DEM flat regions can be divided into two categories. The first category comprises methods that solely depend on information of the original DEM using various elevation gradients, as demonstrated by Jenson and Domingue (1988), Martz and Garbrecht (1998), Tribe (1992), Jana et al. (2007), and Jones (2002). The elevation gradient for a flat region cell is determined by considering the distance to the outlet cell, its distance to the nearest boundary cell, and a user-defined elevation increment of unit distance. The second category includes methods that incorporate the digital channel network (DCN) to enhance the flow direction identification, such as drainage enforcement and surface conditioning (Hutchinson 1989; Saunders 1999; Turcotte et al. 2001). However, the DCN is only helpful for identifying the positions of major channels, but not for estimating their elevation profiles. Overall, existing methods tend to treat flat regions as isolated patches. Strong spatial correlations in elevation are often observed in lowland regions, given the absence of interruption features such as waterfalls and cliffs. The elevation of a DEM cell is thus related to the elevation of its neighbouring cells with different correlation levels that vary with direction and distance (Zhang and Huang 2009). Existing methods are unable to effectively address such relationships, resulting in information loss or distortion in DEM-based drainage analysis.

On the other hand, the evaluation of DEM-derived channel networks has received less attention than building these networks. In fact, the nature of extracted channel networks strongly depends upon pre-selected threshold values within the geographic information system (GIS) framework, which in turn determines the geomorphological resolution of the drainage pattern (Kalin et al. 2003). The most common approach is to specify a Critical Source Area (CSA), which is defined as the minimum area required to drain to a point forming a channel (Garbrecht and Martz 1997; Kalin et al. 2003; Moussa and Bocquillon 1996). To date, there are no well-accepted guidelines for determining the CSA, making the extraction of channel networks a subjective process. In most studies, the CSA is assumed to be constant over a catchment and the value is assigned based on arbitrary judgment (Giannoni et al. 2005; Moussa and Bocquillon 1996). The CSA represents the scale of observation and affects the initiation positions of source channels. It has a profound impact on drainage density and structure and, consequently, on source-catchment delimitations. Once the channel initiations are defined, the essential topological and morphometric characteristics of the corresponding downstream channel network would be implicitly pre-defined because of their close dependence on channel initiation definition (Lin et al. 2006). With a coarse CSA, channels could be simplified and shortened, and many details of the drainage structure could not be recognized; in comparison, a small CSA may lead to an over-detailed network and high computational demands.

Furthermore, the validation of DEM-derived channel networks and their inter-comparisons have been mainly accomplished through visual inspection. Conclusions are often made based on qualitative criteria such as whether the calculated channel network looks convergent or whether parallel channels appear to be reduced. Results from field surveys are often regarded as the most reliable reference, but time limitation as well as human resources and financial constraints greatly affect the applicability of this kind of approach (Giannoni et al. 2005). When blue lines from large-scale topographic maps or high-resolution satellite images are available, the modeled network can be assessed based on its discrepancy with respect to these reference networks. However, the reliability of this kind of approach is limited to a fixed spatial scale. In general, either field surveys or blue lines could only help partially verify the channel networks.

Therefore, this study aims to improve the drainage analysis of DEM flat regions in the context of the Canadian Prairies through: (a) developing a spatial interpolation-based hydrological correction method to build channel networks; (b) introducing a set of geomorphological indices to quantitatively evaluate DEM-derived channel networks; and (c) demonstrating these methods via a case study in southern Saskatchewan.

Study area and data collection

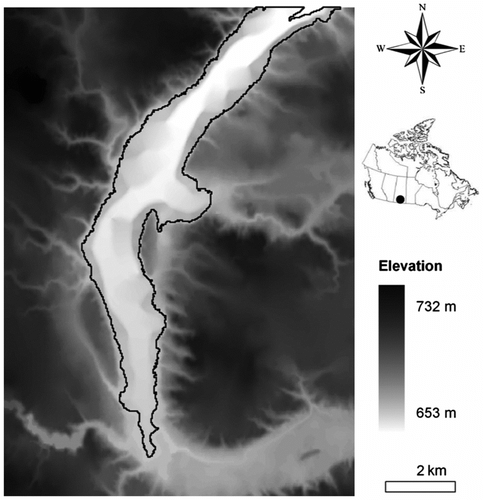
The study area covers the upper portion of the Big Muddy Creek Watershed (49°30’ – 49°45’ N, 105°30’ – 106°15’ W). The Big Muddy Creek is a tributary of the Missouri River and is approximately 307 km long. It rises on the plains north of the international border and flows southwest through the Big Muddy Badlands and the Big Muddy Lake before entering the United States. Elevation ranges from 654 m to 829 m with an average slope of 3.2%. Soils are dominated by brown Chernozems, formed from clayey lacustrine materials and clay loam glacial till. Agriculture is the dominant land use.

The original DEM was extracted from the CDED at the scale of 1:50,000. A number of flat regions were identified within the study area, and most of them are located in the long, shallow valleys of the Big Muddy Creek as well as its major tributaries. The largest flat region, with an area of 19.82 km² (Figure 1), was selected to demonstrate the proposed methods for hydrological correction and geomorphological assessment. The vector-DCN data were obtained from the National Hydro Network at the scale of 1:50,000 and was corrected using satellite imagery.

Figure 1 Original DEM of the selected flat region.

Methodology

Hydrological correction of a DEM flat region

The proposed hydrological correction method aims to replace the flat region with an interpolation surface generated from an integrated elevation dataset. This dataset includes a DCN assigned with elevation values and an adjacent zone from the original DEM. It is assumed that channels within the flat region are either identical to or flowing towards the DCN. The elevation profile is established according to estimated channel slopes. The adjacent zone is extracted from the original DEM to represent topographic features surrounding the flat region. The DCN and adjacent zone are integrated into one dataset by adjusting their elevation ranges. A spatial interpolator approach is then applied to build a smooth surface across the defined elevation points. The method is an extension to the approach proposed by Zhang and Huang (2009) and includes the following steps:

i.	Estimation of the DCN slope. A vector-DCN of the target area is extracted from the national dataset and classified using the Strahler order. Channels with the same order are assumed to have the same slope. Slopes of major channels are estimated based on field surveys or consultations with local experts. Slopes of other channels are then calculated based on Horton’s Slope Law.
ii.	Establishment of the DCN elevation profile. The vector-DCN is converted into a raster format with the same resolution as the DEM. Channel segments are represented by single lines, and water impoundments are simplified as their central lines. Elevation of the outlet cell is assumed to be zero. Elevations of other DCN cells are then calculated based on their distance to the outlet and channel slopes.
iii.	Exaction of the adjacent zone. Along the boundary of the flat region, the width of adjacent zone varies with (a) the shape of flat region boundary, (b) the distance of the DCN to the boundary, (c) the positions of topographic peaks and divides, and (d) the search radius of the interpolator. In the case of a complex topologic boundary, an iterative procedure can be enabled to reduce the number of DEM cells involved in order to improve the efficiency of interpolation.
iv.	Integration of elevation data. Elevations of adjacent zone cells that are higher than the flat region are increased so that these cells are above the entire DCN. The elevation range of these cells is linearly adjusted using a correction coefficient α. For α > 1, the relief of the adjacent zone is exaggerated to have an elevation range wider than that of DCN, and vice versa. Adjacent zone cells that are lower than the flat region remain intact.
v.	Spatial Interpolation. The Radial Basis Functions (RBFs) method is employed to estimate cell elevation over the flat region based on the integrated elevation dataset. The predictor is a linear combination of inverse multiquadric functions, and the coefficients are determined by minimizing the root mean square errors using cross validation. The interpolation procedure can be implemented through the Geostatistical Analyst in ArcGIS.
vi.	Post-interpolation treatment. A breaching method (Garbrecht and Martz 1997) is used to remove small sinks that may be generated during interpolation. An adaptive drainage enforcement (Soille et al. 2003) is also applied to correct the discrepancies with the DCN. At the end, the interpolation surface is then rescaled and fitted into the original DEM to replace the flat region.

Geomorphological assessment of a DEM-derived channel network

The formation of catchment drainage structure involves a number of factors such as soil, tectonics, vegetation, and climate that interact across multiple spatio-temporal scales. This complicated process cannot be fully reflected in a single DEM, even though some geological and hydrological features may be known in advance. A DEM-extracted channel network may approximate the actual drainage system in terms of holistic features, but it cannot completely represent all details of the natural system. This is especially true for the flat regions where the vertical resolution of the DEM is unable to fully characterize real topography.

Two types of drainage structures are common in nature. Dendritic networks often form in homogeneous, gently-sloped geologic beds and create heart-shaped or pear-shaped catchments. In contrast, parallel or trellis networks are often associated with matching fractures and create narrow, rectangular catchments. According to Benda et al. (2004), gently-sloped terrains generally favor dendritic channel networks, and the quantity of parallel channels is very limited. Based on these assumptions, the channel networks of flat regions are evaluated using a set of geomorphological indices from two perspectives − the flow direction and the drainage pattern.

Assessment of flow direction

The extraction of channel networks from a DEM is based on the determination of flow direction at every DEM cell. Although different CSAs result in channel networks with different scales, each network is indeed a cumulative version of the flow direction raster (FDR). A direct examination of the FDR can lead to the identification of undesirable drainage features in the modeled network at the finest scale.

First, the heterogeneity of the FDR is evaluated. Parallel channels are composed of DEM cells that have the same flow directions. The more heterogeneous the FDR is, the less likely parallel channels exist. A homogenous patch in the FDR indicates the presence of crowded parallel channels, and a stripped area suggests the existence of dispersed parallel channels. While some homogenous and stripped areas may be visually recognizable from the FDR, it is difficult to quantitatively characterize these patterns. In this study, the heterogeneity of the FDR is assessed using two indices of neighbourhood statistics in a moving rectangular window (5 cells × 5 cells): (i) N_d , the number of flow directions in the neighbourhood, ranging from 1 to 8, and (ii) N_c , the number of cells with same flow direction as the central cell, ranging from 1 to 25. With regard to a FDR cell, a low value of N_d and a high value of N_c suggest that the flow direction pattern around this cell is not heterogeneous. Such a cell likely contributes to the formation of parallel channels. Specifically, a cell with N_d ⩽ 2 and/or N_c ⩾ 23 is defined as a parallel channel cell, because at least two parallel channels run through its 5 × 5 neighbourhood.

Second, the FDR-based hydrological distance is assessed. The hydrological distance (HD) is the length of the path that a raindrop would follow on the surface of the terrain to reach the catchment outlet (Nardi et al. 2008). HD is calculated for each FDR cell by counting its downstream cells to the outlet cell at the catchment boundary. The resulting HD surface describes the efficiency of hydrological response at different locations. Isolines are generated from the HD surface to illustrate its spatial variation. Because parallel channels are relatively straight, the length of flow path from a parallel channel cell to its corresponding confluence node on the major channel often approximates the minimum spatial distance between these two points. As a result, HD isolines are parallel to each other in areas where parallel channels exist.

Assessment of drainage pattern

While the evaluation of the FDR focuses on fundamental features at the cell scale, the analysis of drainage pattern examines channels and catchment boundaries. One common difficulty in assessing drainage patterns of flat regions is that the reference data, such as large-scale topographic maps or high-resolution satellite imagery, are not readily available. This problem can be partially solved using information from adjacent regions as the reference. Catchments in the same basin share common features since they are within a similar geographical context. This similarity tends to become stronger when the catchments are closer. In this study, it is assumed that the actual channel network in a flat region somewhat resembles those in adjacent non-flat regions. Two drainage pattern indices are developed to facilitate the comparison.

The drainage pattern of a channel network is reflected by the shapes of catchments that are delineated using this network. If the network contains parallel channels, stripe-shaped catchments are formed correspondingly. In a raster format, these undesired catchments could be merely one-cell wide and have no sinuosity over a long distance. Catchment shape can be expressed through a compactness index (C_s ):

(1)

where P is the length of the catchment boundary, and A is the area of a circle that has the same size as that of the catchment (Bardossy and Schmidt 2002). The index approaches unity when the catchment approaches a circular shape, and vice verse. Therefore, a catchment with a bigger C_s is more likely to have a stripe shape. Bardossy and Schmidt also (2002) studied a number of catchments with various sizes in different geographical regions, and the value of C_s was found to vary from 1.48 to 2.63. If a catchment delineated from the DEM-derived channel network has a compactness index value beyond the normal range, it is suggested that the drainage structure of this catchment is not correctly identified. As for a specific channel network, C_s can be calculated for all small catchments derived from this network, and the histogram of C_s can then be used for a quantitative evaluation.

The drainage pattern of a channel network can also be evaluated from the perspective of drainage density. It defines the extent to which streams dissect a landscape as the total length of channels in a catchment divided by the area of the catchment, and it is a useful measure to describe morphological valley development (Vogt et al. 2003). The drainage density for channels of order w, D_w , is defined as:

(2)

where n_w and l_w are the number and mean length of channels of order w, respectively, and A_D is the total drainage area.

The total drainage density varies linearly with CSA on a log-log plot, which suggests a common power law relationship between them (Moussa and Bocquillon 1996; Yang et al. 2001). A similar relationship can be established between any specific D_w and CSA. However, it is not clear, considering different channel orders, whether D_w varies consistently as CSA varies. In other words, are the proportions of channel orders stable in terms of drainage density? In particular, the first-order channels (or source channels) are of unique importance, because they represent the initiation positions of the entire channel network and are sensitive to CSA changes. When CSA varies, all structural changes of the channel network begin with the disappearance or generation of first-order channels. Thus, the proportion of first-order channels can be regarded as a fundamental characteristic of channel network.

Horton’s Laws of stream number and length are widely used to characterize the hierarchical structure of a drainage network. The laws state that the bifurcation ratio (R_b ) and the stream length ratio (R_l ) are constant within a catchment (Roth et al. 1996):

(3)

(4)

Similarly, a drainage density ratio can be defined as:

(5)

which is also constant within a catchment because:

(6)

For a specific channel order, the ratio of D_w to the total drainage density (D) is a function of R_D and the order of the channel system (Ω). In particular, for the first-order channels, this ratio can be written as:

(7)

Equation (7) indicates that D₁/D decreases as either R_D or Ω increases. When the CSA gradually increases, declines discretely because the drainage network is shrinking, but R_D responds differently. According to previous studies (Beer and Borgas 1993; Helmlinger et al. 1993; Ichoku et al. 1996; Puente and Castillo 1996), R_b and R_l are fairly constant over different values of CSA, and the value of R_D is roughly stable at around 1.6 to 2.1. Yang et al. 2001 found R_b and R_l vary synchronously with a stable ratio. Veltri, M., P. Veltri, and M. Maiolo 1996 also indicated R_b and R_l are quite stable at different scales and reported a relationship, R_b = 0.56R_l .

Applying the reported range of R_D and a common range of w to Equation (7), the value of D₁/D lies between 0.45 and 0.6. We assume such a range is stable against the change of CSA. This is consistent with results from Moussa and Bocquillon (1996), in which the total length of the source channels was roughly 43% of the total for all the channels in three French watersheds despite the change of CSA. We further assume that this stability of D₁/D applies to channel networks of flat regions. A quantitative evaluation of the channel network can be conducted by examining the variability of D₁/D against the change of CSA.

Results and discussion

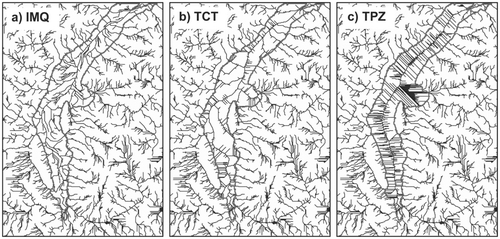
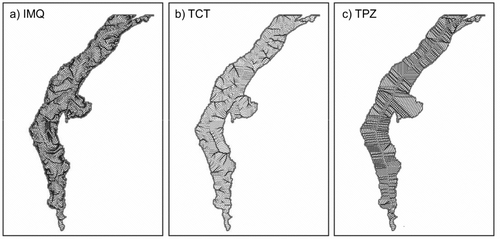
The DEM derived from the hydrological correction method (hereafter referred to as IMQ) is shown in Figure 2. Although the elevation range of this interpolation surface is very limited, this surface has a heterogeneous elevation variation with a clear trend declining from highland to lowland. The related channel network is presented in Figure 3a. Results from two existing methods are also presented. The method developed by Turcotte (2001) (Figure 3b) is regarded as representative of methods that use DCN data (hereafter referred to as TCT), and the method developed by Garbrecht and Martz (1997) (Figure 3c) is considered representative of methods that rely solely on original DEM data (hereafter referred as TPZ). Overall, all three methods produce convergent channel networks in the selected flat region and capture similar outlet positions on the boundary. The major channels in the IMQ and TCT networks are consistent with the vector-DCN, while those of the TPZ network are analogous to the geometric axis of the flat region. In the IMQ network, the tributary channels join the major channels with a desired dendritic pattern and the confluence nodes are distributed dispersedly within the flat region. TCT produces fewer tributary channels, and some of them are extremely short. The density of tributary channels in the TPZ network is relatively high. With the same CSA, channel density varies significantly among the three networks. Parallel channels are observed in both TCT and TPZ networks.

Figure 2 Corrected DEM by the IMQ method.

Figure 3 Channel networks derived from a) the IMQ method, b) the TCT method, and c) the TPZ method.

Figure 4 shows the distributions of N_d and N_c . Peaks at the left side of the graph for N_d and on the right side for N_c indicate a high proportion of parallel channel cells in the FDRs from TCT and TPZ. Cells with N_d ⩽ 2 account for 32% and 59% in the results of TCT and TPZ, respectively, but only 21% for IMQ; a similar pattern can be identified in terms of N_c . HD isolines derived from IMQ, TCT and TPZ networks are shown in Figure 5. Parallel isolines are observed over the entire HD surface from TPZ, indicating a simplified drainage system with numerous parallel channels. The patterns of HD isolines in IMQ and TCT networks are generally similar, but some parallel isolines are identifiable near the outlet and the central part of the main channel for the TCT network. The results of flow direction analysis indicate that IMQ is able to generate a more heterogeneous FDR and fewer parallel channels than TCT and TPZ.

Figure 4 Heterogeneity analyses of flow direction rasters using (a) N_c and (b) N_d .

Figure 5 Contours of hydrological distance derived from a) the IMQ method, b) the TCT method an c) the TPZ method.

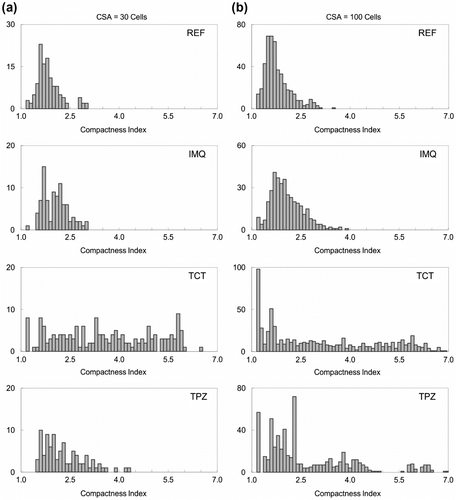
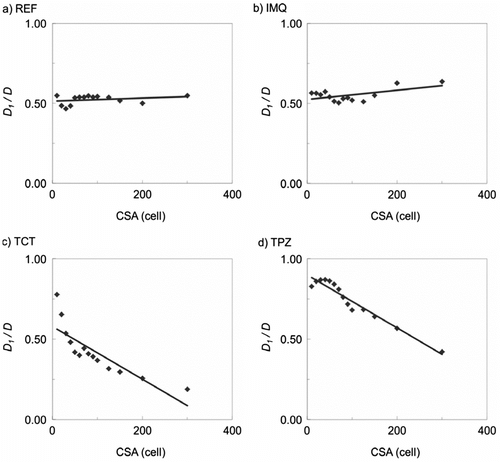
As shown in Figure 6, C_s varies between 1.3 and 3.5 for reference regions in the study area. The histogram exhibits a peak of 1.55 with a slight positive skewness, and the spread of histogram does not change significantly when CSA decreases from 100 to 30 cells. In this study, any catchment with a compactness index beyond the range of 1.3 to 3.5 is assumed to be a catchment with an undesired shape. If C_s > 3.5, the catchment is considered stripe-shaped and contains a parallel channel; if C_s < 1.3, the catchment has a shape close to a square and possibly stands between two stripe-shaped catchments. When CSA = 100 cells (Figure 6a), only the IMQ result is similar to the reference histogram. In contrast, unreasonable catchments accounted for 48% of the TPZ result. Reducing CSA from 100 to 30 cells (Figure 6b), IMQ still outperforms the other two methods, with a peak around 1.6 and a small positive skewness.

Figure 6 Histograms of Compactness Index for a) CSA = 100 cells and b) CSA = 30 cells.

Figure 7 indicates that the average value of D₁/D in the reference regions remains approximately 0.53 when CSA increases from 10 to 300 cells. The changes of D₁/D in different interpolation surfaces are presented in Figure 7. The closest agreement is produced by IMQ, varying between 0.50 and 0.57. This suggests that IMQ is able to develop a well-balanced dendritic channel network. In such a network, the emergence (or vanishing) of source channels, under a decrease (or increase) of CSA, is homogeneous across the entire network; thus, proportions of channels of different orders are relatively stable under varying CSA. In contrast, networks by TCT and TPZ include a large number of parallel channels. Because parallel channels tend to update their channel orders more slowly than the non-parallel channels due to a reduced number of confluence nodes, proportions of channels of different orders are varying in response to CSA changes.

Figure 7 Drainage density of first-order channels derived from a) the reference regions, b) the IMQ method, c) the TCT method, and d) the TPZ method.

The results indicate that TCT is able to assign accurate flow directions to cells overlapping the DCN, but it is not reliable for those outside of the DCN. Cell elevations are modified based on a perturbation coefficient using an inverse power-law function. In order to balance modification effects, the maximum radial influence of this coefficient must be equal to the maximum gap between the DCN and the modeled network provided by the D8 approach (Turcotte et al. 2001). However, problems could rise during the determination of the maximum gap. Although it is easy to identify the gap between two channels, it is difficult to determine the maximum gap between two channel networks. The majority of the cells are not processed and have to be left to the D8 approach, which inevitably results in numerous parallel channels. TPZ modifies the entire flat surface by imposing two gradients from opposite directions. Nevertheless, the main channel is always located at the axis of the flat surface since both gradients are isotropic. Such a scenario would be true only if the real terrain within the flat region is absolutely symmetrical along the axis. In addition, the two gradients could have similar patterns and create contours parallel along the short side of an elongated flat region with an outlet on the short side. Consequently, the tributaries would connect to the mainstream with a parallel pattern.

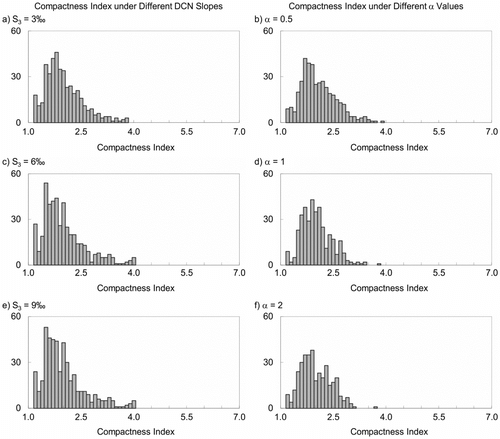
The sensitivity of the hydrological correction method to the DCN slope and coefficient α were examined. In this study, slopes of the three-order DCN were determined as 6‰ (S₁ ), 3‰ (S₂ ) and 1.5‰ (S₃ ), respectively. Both S₂ and S₃ were estimated through consultations with local experts or field surveys; S₁ was then calculated based on Horton’s Slope Law. Assuming a stable slope ratio, three scenarios were designed by setting S₃ as 3‰, 6‰ and 9‰ respectively, and S₃ = 1.5‰ was considered as the baseline. Overall, results suggest impaired heterogeneity of FDR with increased channel slope, as both the number of parallel channel cells (Figure 8a) and the number of ill-shaped catchments (Figure 9a) slightly increase. The trend of D₁/D in Scenario 1 is similar to the baseline, while a declining trend is observed in Scenarios 2 and 3 (Figure 10a). It was concluded that the hydrological correction method performed well with a low DCN slope. In fact, a steep elevation profile of the DCN is expected to help generate a surface with strong elevation variations, especially in areas where channels of different order are close to each other. However, if neighbouring cell elevations change similarly, the direction of the steepest slope may remain the same. On the other hand, if the elevation range of the DCN is overestimated, the declining trend from the source channels to the outlet may be offset by local changes (particularly in areas with high drainage density) and the desired dendritic pattern may thus be altered.

Figure 8 Heterogeneity analysis of flow direction rasters for different a) DCN slopes and b) α values.

Figure 9 Histograms of Compactness Index for different DCN slopes and different α values.

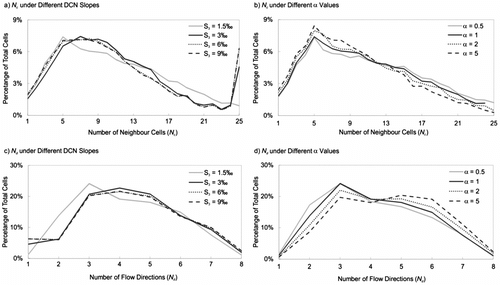
Figure 10 Drainage density of first-order channels associated with different DCN slopes and different α values.

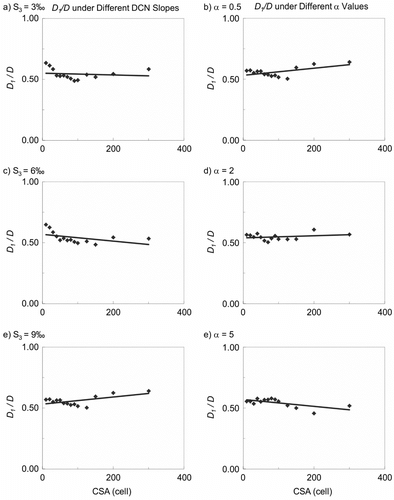
The coefficient α controls the extent to which the adjacent zone expands vertically or is compressed against the DCN. Given the same grid resolution, cells of the adjacent zone not only outnumber the DCN cells, but also distribute more densely, even if the zone width is limited to only several cells. Thus, the adjacent zone is more influential than the DCN in the interpolation process if it has the same elevation range (i.e., α = 1). This is desired because the estimated elevation profile of the DCN is relatively less reliable. However, the question is whether the influence of the adjacent zone needs to be further emphasized. Hence, two scenarios were set for α = 2 and α = 5, respectively. The third scenario, α = 0.5, was set to examine whether the influence on the DCN is strengthened. The condition of α = 1 is regarded as the baseline. Results of these scenarios are presented in Figures 8b, 9b and 10b. The heterogeneity of FDR in Scenario 3 is similar to the baseline, while a slight improvement is identified in other scenarios. In terms of catchment compactness, Scenarios 1 and 2 yield unexpected multiple peaks; again, Scenario 3 is similar to the baseline. The values of D₁/D are generally stable in all scenarios. The results indicate that the performance of hydrological correction is not very sensitive to the coefficient α. A slight improvement could be achieved by exaggerating the adjacent zone to enhance the projection of the surrounding relief into the flat region. However, the inverse multiquadric interpolation is implemented with equal consideration given to the four directions. The majority of the cells in the flat region is affected by the adjacent zone in two directions only, and this effect becomes weaker when cells of the flat region are closer to the DCN. Furthermore, the relief of the adjacent zone may be consistent with the elevation profile of the DCN if its data points are close to each other. Consequently, their combined effect on the interpolation process may not be significantly different from their individual effects.

Conclusions

Building accurate channel networks in flat regions is an important issue in watershed delineation and hydrological modeling, particularly for areas with gentle terrain. This study developed a hydrological correction method to modify flat regions of a DEM and introduced a set of geomorphological indices that could be used to assess the DEM-derived channel networks. The methods were applied to a DEM of southern Saskatchewan. Results showed that the channel network modeled by the proposed method was consistent with the known hydrological information and contained fewer parallel channels compared to networks modeled using two existing methods. Overall, the proposed methods have the following advantages: (a) the employment of a reliable spatial interpolation approach to reflect the spatial correlation of elevation; (b) the combination of elevation information from different sources; (c) the effective generation of convergent channel networks; (d) the quantitative evaluation of channel networks from geomorphological perspectives; and (e) the easy implementation in a GIS environment. The developed method could be valuable for improving a wide range of CDED applications within the context of the Canadian Prairie region.

Acknowledgements

This research was supported by the Major Science and Technology Program for Water Pollution Control and Treatment, the Canadian Water Network (CWN) of the Networks of Centers of Excellence, and the Natural Science and Engineering Research Council of Canada.