Challenging the standard dike freeboard: Methods to quantify statistical uncertainties in river flood protection

Abstract

In most developed and developing nations, a freeboard is being applied to flood defense structures as a margin of uncertainty in the estimated flood stage. In some jurisdictions, practice is shifting towards the use of confidence intervals based on the fitted flood probability distribution, albeit often relying on only one statistical distribution and on only annual maximum flows. In this paper, we argue that, independent of geotechnical, geomorphological or hydrological uncertainties pertaining to the estimation of flood stage, the application of standard freeboards ignores stochastic uncertainty, the inclusion of which would provide a more scientifically defensible measure for allowable freeboard. The river stage estimate is subject to multiple sources of uncertainty, including but not limited to model and parameter uncertainty. Consequently, freeboards should be determined via a frequency analysis that explicitly takes into consideration, as well as minimizes, the uncertainty of the estimate due to known factors. Confidence intervals are a common way to represent uncertainty of a statistical estimate such as for the river stage. The choice of the confidence level will be critical, and in many cases will be associated with significant cost implications for the construction or upgrade of flood defense structures. Quantitative flood risk assessments, which are emerging as a standard in developed nations, are well suited to address this issue by allowing loss and mitigation cost comparisons for different flood scenarios. Our paper provides guidance for confidence interval calculations of river stage using an extension of the classical peaks-over-threshold method for daily river levels.

Dans la plupart des pays développés et en développement, un freeboard est appliquée à inonder les structures de défense que d’une marge d’incertitude dans l’estimation du niveau d’inondation. Dans certains pays, la pratique évolue vers l’utilisation des intervalles de confiance sur la base de la distribution de probabilité des inondations équipée, toutefois en s’appuyant souvent sur ​​une seule distribution statistique et seulement débits maximums annuels. Dans cet article, nous soutenons que, indépendamment de la géotechnique, incertitude-certitudes géomorphologiques ou hydrologiques relatives à l’estimation des niveaux d’inondation, l’application des freeboards standards ignore incertitude stochastique, dont l’inclusion de fournir une mesure plus scientifiquement défendable pour le franc-bord admissible. L’estimation de la scène de la rivièreest soumis à de multiples sources d’incertitude, y compris mais sans s’y limiter, le modèle et l’incertitude des paramètres. Par conséquent, le freeboard doit être déterminées par une analyse de fréquence qui prend explicitement en considération, ainsi que minimise, l’incertitude de l’estimation en raison de facteurs connus. Les intervalles de confiance sont un moyen courant de représenter l’incertitude d’une estimation statistique, comme pour la scène de la rivière. Le choix du niveau de confiance sera essentiel, et dans de nombreux cas être associée à des incidences financières importantes pour la construction ou la mise à niveau des structures de protection contre les inondations. Évaluations des risques d’inondation quantitatives, qui apparaissent comme une norme dans les pays développés, sont bien adaptés pour traiter de cette question en permettant de comparer la perte et l’atténuation coûts pour différents scénarios d’inondation. Notre document donne des orientations pour le calcul de l’intervalle de confiance de l’étape de la rivière à l’aide d’une extension de la méthode des pics-plus-seuil classique pour les niveaux quotidiens de la rivière.

Introduction

In Canada and many other countries, freeboard is a frequently applied concept for the design of flood protection structures. For example, the US Federal Emergency Management Agency (FEMA 2006) focuses on protecting against the 100-year flood and (for certification purposes) requires that 0.915 m (3 feet) of freeboard be added to the estimated stage (height) of the 100-year flood. This is done to increase the level of confidence that the dikes will convey the associated flow. In the absence of comprehensive risk analyses, the use of a standard freeboard appeared sensible since dikes built only to the elevation of the 100-year flood would not necessarily survive it (because of waves, wind, dike subsidence and other uncertainties such as that of the 100-year flood stage estimate). Ignoring these types of uncertainty, adding 0.915 m of freeboard reduces the likelihood of flooding to some nominal return period in excess of 100 years which depends on each river’s hydraulics and cross-section. The principal problem of a fixed 0.915-m freeboard is that it results in very different levels of residual risk in different locations and, by extension, relates strongly to costs of flood mitigation. In response to this issue, the US Army Corps of Engineers (hereafter, the Corps) issued guidance to incorporate flood uncertainty to determine levee height for certification in lieu of FEMA’s fixed 0.915-m of freeboard (United States Association of Civil Engineers 1996). This document uses the 90–95% confidence interval of the estimated base flood elevation but maintains the concept of a minimum of 0.61 m (2 feet) freeboard above the mean value of the base flood elevation. The Corps will use the higher of these two values to determine dike height.

Similarly, in the UK, a study published by the Environment Agency (2000) recommends that practitioners and agencies move away from the application of fixed freeboards and allow for site-specific allowances, including the sampling uncertainty of the stage or discharge estimate. To the present authors’ knowledge, this has not been instituted to date.

In British Columbia, the standard for river dike crest elevations for a 1:200 year flood is typically 0.3 m above the instantaneous design flood level or 0.6 m above the maximum daily flow level, whichever results in the higher flood construction level. For agricultural lands, the higher of the 50-year return period instantaneous flow plus 0.3 m freeboard or the 50-year maximum daily flow plus 0.6 m freeboard is the recommended minimum level (e.g. British Columbia Ministry of Water, Land and Air Protection 2003). However, for some Canadian rivers, freeboard has been set higher to account for sediment deposition, debris jams and long-term dike settlement. For example, in Saskatchewan, the current practice is to add 0.5 m freeboard to the 500-year return period flood elevation. In Alberta as in Manitoba, the 100-year flood or the flood of record is used as the maximum return period to outline flood hazard areas, with the exception of Winnipeg where the 700-year flood level is used for design of flood mitigation. In the latter case, this is based on the stage of the 1997 flood plus 0.6 m of freeboard. In neither province is freeboard specified. A summary for other provinces can be found in the recently published National floodplain mapping assessment (MMM Group Ltd. 2014).

The decision as to the height of the freeboard most frequently is made by recommendation of the consulting firm executing the flood hazard assessment, and thus hinges on the experience and expertise of the study team. Quantitative flood risk assessments are the exception rather than the rule in Canada, even though they now have a strong foothold in European nations and, increasingly, in the US. Changes in flood risk due to development densification or non-stationarity of the flood records are not considered in assigning freeboard.

A globally accepted definition of freeboard is absent, but we will define it here as the vertical difference between the computed flood stage and the crest of the flood defense. The accuracy and precision of the flood stage estimate chosen for design of mitigation works plays a paramount role in ensuring safety from rare floods. Numerous reasons exist why calculations of the design flood stage may be imprecise at best, and unrealistic at worst. Freeboard is an expression of uncertainty in the flood stage estimate and includes waves (wind or boat traffic), or non-hydraulic factors like dike subsidence. The precise estimation of stage or return periods of rare floods poses several challenges. First, the long return period of, say, 200 years, often required in the dike design, extends beyond typically available data records. This is the case especially in countries with evolving risk tolerance where systematic urban development and associated infrastructure planning including flood hazard and risk management are largely a twentieth-century phenomenon. As a result, any estimate relies upon data extrapolation. A generally accepted procedure is a model-based extrapolation, in which a probability distribution is fitted to the available data, and the appropriate quantile of the fitted distribution is used as the return level estimate. For the return period of 200 years, this corresponds to the 0.995 quantile of the fitted distribution. The second difficulty is the model choice. Due to scarcity of the data in the far tail of the underlying distribution, which is the target for prediction of very rare floods, assessment of the tail fit is difficult, whereas extrapolation is unwarranted without a further model justification. Diagnostic plots and tests can assess that goodness-of-fit, but fail to clarify if the distribution will provide an accurate estimate of extreme events, particularly those that may not have been observed in the record on which the flood frequency calculations are based.

Several distributions are traditionally applied to annual peak flows and discharges to estimate flood frequencies; among them are the Log Pearson Type 3 distribution, the three-parameter log-normal (LN) distribution and the generalized extreme value (GEV) distribution. The first one has been recommended by the US Water Resources Council (1967). The LP3 distribution is unlikely to provide the best fit to the data in all cases, but its ubiquitous application guarantees a national standard. Both the LP3 distribution and the LN distribution are advised on the basis of having a flexible shape, determined by three parameters, and often providing an adequate fit to the data. The GEV distribution is also governed by three parameters, and is reported to provide the best fit among many other distributions (see Önöz and Bayazit 1995). An additional support for the GEV distribution comes from extreme value theory in which the GEV distribution is shown to arise as an asymptotic model for sample maxima, and hence can be viewed as a natural model for the annual peak flows and discharges that are typically used to fit these distributions. The GEV distribution describes the stochastic behaviour of maximum values of a process, much like the normal distribution describes the fluctuation of averages (due to the Central Limit Theorem), for a broad class of possible underlying distributions.

A drawback of modelling annual maximum series is that annual maxima ignore other high flows during a given year that contain important information on flood frequency. In addition, during dry years, very low maxima get entered into the analysis, perhaps unduly biasing the record that is slated to isolate extreme events (see e.g. Madsen et al. 1997). An alternative, which overcomes these issues, is to model excesses of measurements on a more refined time scale (such as daily observations) over some specified high threshold. Asymptotic arguments of extreme value theory suggest the generalized Pareto (GP) distribution as an approximate model for high threshold excesses. This approach is commonly referred to as the peaks-over-threshold (POT) method. We would like to emphasize that although empirical evidence usually cannot be called for to warrant model extrapolation to obtain flood stage estimates, models motivated by extreme value theory at least provide a theoretically justified basis for such extrapolations. For illustrative purposes but also in view of the above arguments, our analysis uses the POT method.

Methodology review

Climate change is increasingly introducing an element of uncertainty into statistical treatment of hydrological time series. Increases in atmospheric moisture content will, in many locations, seasonally increase precipitation volumes and intensities. Non-stationarity has been identified as a major hindrance to reasonable determination of flood discharge and stage (Milly et al. 2008).

A further source of error is introduced by the design of the defense structures and their foundations. Settlement of dike foundations and consolidation of dike materials themselves over time also need to be accounted for in the design. Geomorphic changes in the streambed such as river bed aggradation or scour can change the water surface profile and thus river conveyance, which ultimately affects freeboard. To decipher such changes, a study of the rates of sediment movement and channel bed changes is required. Freeboard may also be jeopardized by flow through natural or man-made obstructions, superelevation in channel bends and supercritical flow characterized by standing waves (hydraulic jumps) or cross waves during floods. Ice jams, temporary river blockages through landslide dams or debris flows may create flow stages far exceeding those computed from purely hydrological processes, and each of the above processes will need to be analyzed with a different set of tools not discussed in this paper. River stage and discharge finally hinge strongly on any artificial blockages on rivers that need to be treated separately.

The objective of this paper is to critique the notion of standard design freeboard on the basis of statistical uncertainty, and to motivate a shift towards a rational stochastic approach to compute estimation uncertainty. In particular, we identify several sources of uncertainty which arise due to the use of a statistical procedure, review available methods that can be applied to determine associated error bounds and use a case study to illustrate how the length of the data record influences the precision of the stage estimates. Geotechnical, geomorphological or hydrological variables, some of which may have been captured by the stage record but which would need to be analyzed separately to understand their individual contribution to calculate freeboard, are not addressed in the present paper.

For many rivers, stage or discharge data are available as daily measurements. For this reason, we adopt the POT method, which in a more simplistic earlier form has been widely used in hydrology (see e.g. Natural Environment Research Council NERC 1975). Extreme values are defined as those observations that exceed a specified high threshold. This approach allows for greater utilization of extremal data points in comparison to a frequently used block maxima method based on block (usually annual) maxima only. On the other hand, there is a need for a reasonable choice of a threshold that balances the model validity with estimation efficiency, as well as dealing with potentially more complex forms of non-stationarity.

The model and inference in the classic setup

In statistical applications involving modelling of extreme values, it is a common practice to approximate the distribution of sample extremes by a suitable limit distribution, without much regard to the underlying population distribution. Extreme value theory motivates the GP distribution as an approximate model for the sample excesses over a threshold when the threshold is sufficiently high and the data can be represented by a sequence of independent and identically distributed random variables (Balkema and de Haan 1974; Pickands III 1975). The GP distribution is governed by two parameters: scale and shape , the latter determining the tail behaviour of the underlying distribution and, as a result, having a larger influence on return level estimation.

A variety of statistical methods have been proposed to estimate parameters of the GP distribution. Among them are the method of moments, the method of probability weighted moments and the maximum likelihood estimation (see Beirlant et al. 2004 and references therein). In our data analysis, we use the maximum likelihood (ML) method due to its modelling flexibility and good asymptotic properties of the estimators. A basic reference in this context is Coles (2001). Provided shape parameter −0.5 (a condition often satisfied in practice), the ML estimators are consistent, asymptotically efficient and normally distributed: (1)

where n_u is the number of exceedances over given threshold u, is the inverse Fisher information matrix, stands for the bivariate normal distribution with mean vector zero and covariance matrix V and denotes convergence in distribution.

The choice of the threshold plays an important role. The threshold needs to be high for the approximation by the GP distribution to be acceptable, while leaving enough exceedances over the threshold for statistical inference. Several graphical tools are available to assist with the threshold selection, including the mean excess plot and parameter stability plots (see Coles 2001, section 4.3.1). The interpretation of these plots is, however, not always straightforward.

Return level estimation

In practice, it is often necessary to estimate the N-year return level, i.e. the level at which a given discharge or stage is exceeded on average once every N years. Typically, the return period N is required to be large. In the case of a dike design, we are using a return level of 200 years which is customary in BC, although in Alberta the 100-year return level flood has been used as the design basis for flood protection. If n_y denotes the number of observations available per year, then the N-year return level corresponds to -observation return level, which is the 1 − 1/(n_yN) quantile of the distribution of threshold excesses and hence can be estimated by inverting 1 – = 1/(n_yN), where denotes the estimated distribution of threshold excesses.

Under the GP model assumption and using the empirical estimate of the threshold exceedance probability, the N-year return level estimator is given by(2)

where are parameter estimators, is a specified threshold and is the number of exceedances over u in the sample of size . Confidence intervals for the return level q_N can be obtained from the delta method, which says that (3)

where evaluated at the ML estimates , matrix V is as defined in Equation (1(1) ), and N(0, ) stands for the normal distribution with mean zero and variance (e.g. Coles 2001, theorem 2.4). Hence, the (approximate) delta method-based 100(1 − α)% confidence interval for the return level is given by(4)

where ϕ(·) is the distribution function of the standard normal random variable, and denotes an estimate of . We note that for simplicity of presentation, we ignored uncertainty in the threshold exceedance probability, which typically is small compared to uncertainty in parameters σ and ξ (Coles 2001).

When the sample size of threshold excesses is not sufficiently large relative to the desired return period, the true sampling distribution for the return level estimator tends to be skewed, in which case the symmetric confidence intervals in Equation (4(3) ) would provide a poor approximation.

In order to overcome this deficiency, a generally more accurate approach is to use the profile likelihood function (Davison and Smith 1990). The profile likelihood function for a parameter of interest is defined as the maximum of the joint likelihood over the other parameter(s) of the model. Under suitable regularity condition, we have (Coles 2001, theorem 2.6):(5)

where is the profile log-likelihood for N-year return level and denotes the chi-square distribution with one degree of freedom. Hence, the (approximate) profile likelihood-based 100(1 − α)% confidence interval for the return level q_N is defined implicitly by (6)

where (1 − α) is the (1 − α)-quantile of the chi-square distribution with one degree of freedom.

In addition, we supplement the above two methods for confidence interval calculation with a parametric bootstrap. In particular, using the approximate normality of ML estimators in Equation (1(1) ), we generate (a large number of) bootstrap samples of model parameters. For each simulated pair of parameters, we compute  and then use the empirical α/2 and (1 − α/2) quantiles to give, respectively, the lower and upper bounds of a 100(1 − α)% bootstrap-based confidence interval for the return level q_N.

In conclusion, we would like to emphasize that confidence intervals serve to quantify the estimation uncertainty under the strong assumption that the model is correct. As such, they provide only a lower bound on the true uncertainty surrounding the parameter values. The model risk remains unaccounted for.

Extension to stationary time series

In reality, the assumption of independence between consecutive observations may not stand up to statistical or physical scrutiny. In this section, we briefly explain how the statistical procedure outlined above can be modified to address temporal dependence in a stationary hydrological time series.

One implication of temporal dependence in hydrological or climatic time series is the phenomenon of extremes clustering. Statistically, this means that exceedances over a high threshold will tend to occur close in time and are thus dependent within each cluster. This is illustrated by the persistence of high water levels over several days or weeks during snowmelt or during multi-day rainfall associated with a particular synoptic condition. Obviously, the discharge on day 3 of a flood is dependent on the previous days’ discharge if caused by the same hydroclimatic event, which is very likely. This can be addressed through de-clustering of the time series by identifying independent clusters of threshold exceedances, and then fitting the GP distribution to excesses of cluster maxima over the threshold. This model is justified by the point process representation result which states that, assuming long-range asymptotic independence (i.e. extreme observations sufficiently separated in time are independent), the excesses of cluster maxima form a non-homogeneous Poisson process with excess sizes following a GP distribution (see e.g. Beirlant et al. 2004, theorem 10.17). Due to independence of clusters, the methods using ML theory can then produce standard errors and confidence intervals.

A typical method for de-clustering is the runs method (Smith 1989). It requires fixing a high threshold u and the run length r, which determines the number of consecutive observations below u as separating two clusters. Threshold exceedances separated by less than r non-exceedances are deemed to belong to the same cluster. The run length is to be chosen to make observations in different clusters approximately independent. Ferro and Segers (2003) proposed an intervals de-clustering scheme, which is similar to the runs method but with the run length being estimated from the data. We use the latter method for numerical illustrations.

Illustrative data analysis

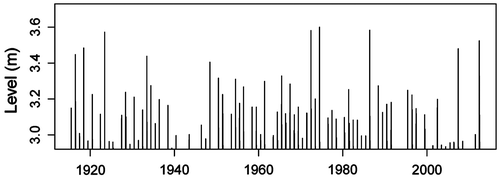
Our analysis uses daily water levels of Bow River at Banff, Alberta, with a record spanning the period 1915–2012. Banff is not protected by dikes, and thus the analysis is purely illustrative (Figure 1). However, it may be useful for future engineering projects for dikes of Banff, or downstream communities such as Canmore and, ultimately, Calgary. We apply the methodology outlined in the previous section. Our computations are performed using the open source statistical software R (R Core Team 2013), with the help of extreme value analysis libraries ismev and extRemes. We do not account for any river bed elevation changes at the stage site, which may bias the stage data. If applied to actual flood hazard or risk assessment, data on river bed elevation changes at the stage site, if available, should be used to correct the reported stage data. The stage data were purchased from Environment Canada. Data from 1998 were available in digital format; data from 1909 to 1998 had to be painstakingly digitized from hand-written copies.

Figure 1. Study area showing the upper Bow River watershed, and the rain gauge location on which the analysis in this paper is based.

The data are subject to strong seasonal variation and hence are highly non-stationary, i.e. the (joint) distribution of daily river stage levels changes over time, in particular, here, with the season. As from the risk assessment perspective only high levels of river stage are of concern, we chose to overcome the issue of non-stationarity by restricting our attention to the freshet (cf. Davison and Smith 1990). Under this approach, the results are directly interpretable and address the purpose of the dike in mitigating against overtopping of an extreme flood. While it is possible to model non-stationarity directly either via model parameters (see e.g. Coles 2001, chap. 6) or by pre-processing the data prior to the application of standard extreme value techniques as recommended by Eastoe and Tawn (2009), the result in this case is a collection of return level estimates associated with different time points within a year. Only the largest of them would be of interest for dike elevation design. Note also that such methods implicitly assume the same extreme hydroclimatic event type throughout the year. As river levels and discharge are controlled by different factors during the year (e.g. snowmelt and rainfall), such an assumption is not warranted.

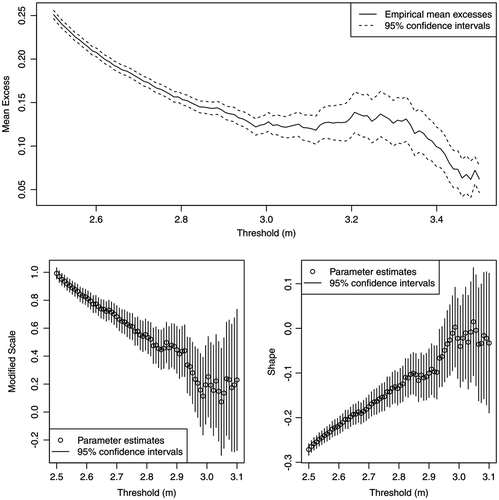
A preliminary analysis of water level against the day of the year for exceedances over the threshold of 2.95 m (roughly the 90th quantile of the entire dataset) suggests restricting the series to the interval between the 140th and 211th day of the year, which roughly corresponds to the period from May to August. We henceforth treat the restricted dataset as stationary. Subsequent analysis requires selection of a threshold above which the GP approximation is reasonable. Figure 2 displays the mean excess plot and the parameter stability plots to guide threshold selection. The aim is to identify the lowest threshold past which the empirical mean excess function is linear, while model parameter estimates are stable, subject to sampling variability. Based on these plots, we judge the gauge height threshold of 2.95 m as a reasonable choice. Given a threshold level, it is now possible to address the clustering effect at high river levels arising due to strong temporal dependence between observations, at least within short periods of time. Following the methodology outlined in the previous section, we use interval de-clustering to identify independent clusters of high river levels, and for each cluster compute the corresponding maximum. The estimated run length is four non-exceedances. Blocking over years is imposed to ensure that clusters do not span multiple years. The identified cluster maxima (plotted in Figure 3) are treated as a sample of independent observations to which the classical POT method can be directly applied to estimate return levels and quantify the associated estimation uncertainty.

Figure 2. Plots for selection of thresholds above which the approximation by a generalized Pareto distribution is reasonable. Top panel shows the mean excess plot; bottom panel displays the parameter stability plots. The plots are computed for data restricted to the high-level period from May to August.

Figure 3. Cluster maxima in excess of 2.95-m threshold based on the interval de-clustering method and blocking by years.

Record length and estimation uncertainty

In statistical modeling, data quantity is crucial, as the more data are available the more accurate is the estimation. Estimation with short data records is subject to a great degree of uncertainty about the true value of the quantity of interest. Naturally, the dike freeboard used with the stage estimate should reflect this uncertainty. To illustrate the influence of the record length on the stage estimate and, more importantly, on the associated estimation uncertainty, we have repeatedly re-estimated the 200-year return level within an expanding window, starting from the period 1915–1934 (20 years) and increasing it to 2012 in steps of 2 years. Figure 4 summarizes the results of this analysis. The bottom curve shows estimates of the 200-year return level (₂₀₀) computed using Equation (2(2) ) with parameters estimated using the maximum likelihood method. The three bands in different shades of grey show the magnitude of the upper bound of the 95% confidence interval for ₂₀₀ using the delta method approximation in Equation (4(3) ), the profile likelihood approximation in Equation (6(6) ) and the (parametric) bootstrap based on Equation (1(1) ) with bootstrap samples of size 100,000. It seems reasonable to interpret the difference between the upper bound of a 100(1 − α)% confidence interval for some small α ∈ (0,1) and ₂₀₀ as the amount of freeboard necessary to account for sampling variability in the 200-year return level estimate. For comparison, we also include the stage computed by adding the fixed margin of 0.6 m (the standard freeboard) to the 200-year return level estimate (dashed line). Recall that, unlike the delta method approximation, the profile likelihood and bootstrap methods account for skewness in the sampling distribution of the return level estimator and hence provide more accurate confidence bounds. As can be seen from figure 4, both the method based on the profile likelihood and the bootstrap method yield a freeboard well above the currently recommended freeboard of 0.6 m for records under 35 years. It should be emphasized that confidence intervals quantify estimation uncertainty only due to sampling variability. However, one expects the freeboard to account for all major sources associated with stage estimation. Hence, the freeboard of 0.6 m may not be sufficient even if a moderately sized record of 50–70 years is available.

Figure 4. Sensitivity of the 200-year return level estimate 200 and upper bounds of 95% confidence intervals computed using the delta method (DM), parametric bootstrap and profile likelihood (PL) to the length of data record. Estimation is repeated for expanding record length starting in year 1915 until 2012; the threshold is set to 2.95 m.

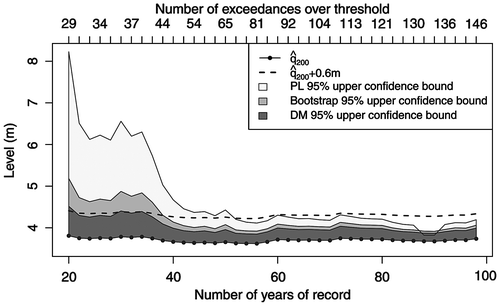
While in this particular analysis, return level estimates are fairly stable over the expanding estimation window, ranging between 3.62 m and 3.81 m, in general, when the record length is relatively short and different estimation windows are used, one can expect a much greater discrepancy in return level estimates. For example, the period 1952–1971 gives ₂₀₀ = 3.35 m versus ₂₀₀ = 3.58 m over the period 1930–1949, and ₂₀₀ = 3.81 m over the period 1915–1934. Neill and Watt (2001) further illustrate this point by reviewing inconsistencies in flood frequency analyses of six case studies.

Other sources of statistical uncertainty

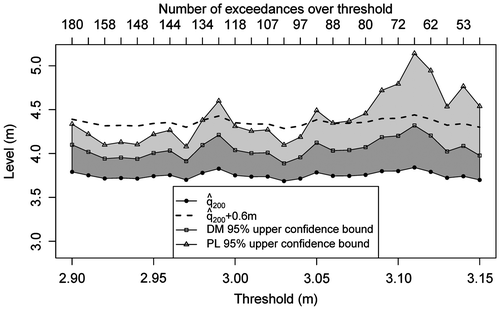
In addition to the uncertainty about parameters of the GP distribution used to model threshold excesses, several choices were made in the course of the analysis which potentially affect the results. In particular, these include the threshold choice and de-clustering scheme. Figure 5 illustrates the sensitivity of the 200-year return period estimate to changes in threshold level used in de-clustering and subsequent model fitting. As can be seen from the figure, return period estimation is fairly stable under variations in the threshold, ranging between 3.69 m and 3.84 m. Naturally, higher threshold values lead to larger variability, as indicated by wider confidence bands. The upper horizontal axis shows the number of exceedances of identified cluster maxima over a given threshold. We conclude that in this particular case study, the exact threshold choice plays only a minor role as long as it is chosen to balance the bias-variance trade-off. A more quantitative approach could be adopted in the case of a greater sensitivity of results to the threshold selection. In particular, it is possible to treat the threshold as a model parameter itself and estimate it from the data. This is typically done by considering a mixture model with the GP distribution above the threshold and making use of Bayesian inference (see Behrens et al. 2004; Tancredi et al. 2006; MacDonald et al. 2011). Wadsworth and Tawn (2012) propose the use of the penultimate approximation to guide threshold selection. Note that such methods automatically quantify the effect of threshold uncertainty in estimation, albeit introducing a much greater complexity to inference.

Figure 5. Sensitivity of the 200-year return level estimate 200 and upper bounds of 95% confidence intervals computed using the delta method (DM) and profile likelihood (PL) to threshold used for declustering and model estimation. The complete data record from 1915 to 2012 is used in estimation.

The sample size is predetermined; however, choices can be made with regard to the estimation method. In addition to the maximum likelihood method we use here, other popular frequentist methods include the method of moments and the method of probability weighted moments. Madsen et al. (1997) conduct a comparative analysis of these estimation methods in terms of their mean squared errors, and provide recommendations on which method should be used in terms of true model parameters and available sample size. In general, moments-based methods tend to have better small sample properties as they implicitly place restrictions on the existence of moments and hence parameter ranges, in particular the shape parameter. However, this same aspect can lead to an undesired negative bias (i.e. underestimation of return levels) when the underlying distribution has a fairly heavy upper tail (Nolde and Joe 2013). Another alternative is to use Bayesian inference methods. A Bayesian analysis produces a more complete output in terms of the entire posterior or even predictive distribution, although usually more care needs to be taken when doing Bayesian computations. In addition, a Bayesian analysis requires specification of the prior distribution for model parameters, whose choice may not be straightforward. When uninformative priors are used, the Bayesian and maximum likelihood inferences tend to be self-consistent (see e.g. Coles 2001, chap. 9.1).

Last but not least, the model choice plays a crucial role in any statistical analysis. Neill and Watt (2001) again provide good examples of how the use of different models leads to sometimes-remarkable inconsistencies in return period estimation. While standard goodness-of-fit tests can be employed in classical problems dealing with the central part of the data, the lack of data in the tails and the need for extrapolation beyond the data range make such techniques non-applicable in the context of extreme value estimation.

Conclusion

Flood mitigation structures are subjected to the risk of failure by breach or overtopping, and the cost of construction and maintenance. For most rivers, the design standard, namely the 200-year flood plus freeboard, has not changed despite increases in floodplain development. Jakob and Church (2011), amongst many others, have pointed out that densification of urban development and infrastructure construction must lead to an increase in flood risk even for a stationary flood hazard. Accordingly, they advocate that rigorous quantitative risk assessments be applied and motivate mitigation that is upgraded commensurate with the changes in flood risk. Quantitative flood risk assessments include consideration of a spectrum of flood return periods, but should also include the confidence bounds in the flood stage calculations of those return periods considered. For now, and prior to any institutionalization of quantitative flood risk assessments in Canada, regulations for most rivers presume that flood mitigation against the 200-year return period event including freeboard is a reasonable compromise between the flood risk and the cost. This paradigm, although tested very few times by extreme floods, would only be valid if indeed the 200-year stage estimate is presumed to be correct and the specified freeboard provides adequate insurance against the uncertainty in the statistical estimate and physical processes that may affect a river’s cross-section shape.

We have described a basic methodology for the analysis of extreme values with a model motivated by extreme value theory. The salient point of our contribution is that the freeboard should be determined statistically and should not be based on a largely arbitrary standard that neither accounts for record length nor reconciles often-huge differences in potential flood risk. Uniform applicability of an arbitrary value is statistically unfounded. In particular, the record length has a profound effect on the precision of statistical estimation. Reliance on short stage records will usually require much higher freeboard because the statistically derived confidence intervals span a much larger range in stage, thus exemplifying big error ranges. The paper has also demonstrated the inadequacy of stage records for Bow River of less than 35 years in length being used to determine a practical freeboard. This critical record length is likely different for other rivers depending on the statistical properties of their respective data sets. The choice of the coverage probability for the confidence interval guiding the freeboard should hinge on the flood risks, not the flood hazard. For floodplains with high and very high economic or life loss potential, a high (95 or 99%) confidence interval may be appropriate; for low-risk floodplains, a lower confidence interval may be a reasonable compromise unless future floodplain development is proposed. In some cases, particularly for long time series, this may result in freeboards less than the standards. In other cases, particularly for shorter time series, freeboards may be significantly higher than the locally applied standard. Therefore, we recommend that professional practice abandon the notion of an arbitrary freeboard and encourage the use of statistically defined error margins to define appropriate dike elevations. These should be supplemented with quantitative flood risk assessments to optimize benefits to society.

A time series with a very short record relative to the desired return period alone can hardly be expected to provide sufficient information for the accurate statistical estimation of the associated return period. The resulting wide confidence interval duly reflects estimation uncertainty. When the freeboard based on this confidence interval is beyond practically implementable size, alternative techniques ought to be considered. One possibility to improve precision of the statistical procedure is to bring in additional information such as expert judgement (Coles and Tawn 1996; Nolde and Joe 2013), regional information (Coles and Powell 1996) or paleohydrologic bound data (O’Connell et al. 2002; Baker 2008).

The statistical analysis presented in this paper only examines one aspect of uncertainty in flood safety. Application of this method does not absolve the practitioner or approving agency from examining other sources of uncertainty that have been outlined in the introduction of this contribution. For example, Brandimarte and Di Baldassarre (2012) describe a simulation-based methodology which considers data uncertainty in addition to parameter uncertainty. To incorporate several factors affecting the dike into the dike design and to devise associated freeboard computation procedure, a multivariate extreme value analysis can be used, which will be the subject of a future publication.

Acknowledgements

Mike Church, Roy Mayfield and two anonymous reviewers provided helpful comments on earlier versions of this paper. The first author would like to acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada.