Groundwater contribution to winter streamflow in the Canadian Rockies

Abstract

Alpine watersheds represent an important source of fresh water in western Canada. Understanding of hydrological processes in headwater environments is crucial to effectively manage and allocate alpine water resources. Since rainfall, snowmelt and glacier melt make minimal contributions to streamflow during winter months, essentially all winter flow in unregulated streams is provided by groundwater discharge. Therefore, the analysis of winter flow provides critical information regarding the magnitude of groundwater discharge and its relation with the physiographical characteristics of watersheds such as climate, geology and topography. Streamflow records of 18 watersheds (21–3900 km²) in the Canadian Rocky and Columbia mountain ranges were analyzed. Winter flows were in a narrow range (0.2–0.6 mm d^–1) throughout the study area, and had a relatively small inter-annual variability, while the flows during spring, summer and fall had a large inter-annual variability. This suggests that the groundwater storage is filled up to the maximum capacity every year, and the groundwater discharge in winter is mostly controlled by the stationary factors such as the spatial variability of geology, topography and climatic variables. Precipitation inputs, reflected in the long-term mean annual flow, had a strong correlation with the long-term mean winter flow, indicating the dominant effect of the climatic gradient. Bedrock geology influenced winter flows, where the watersheds underlain by younger rocks having generally higher permeability and porosity had higher winter flow, while the topographic effects were not discernible. These suggest that the local effect of topography on the hydraulic gradient is averaged out, but the geological influence on the aquifer hydraulic property operates at a scale comparable to the size of the study watersheds.

Les bassins hydrographiques alpins sont une source importante d’eau douce dans l’ouest du Canada. La compréhension de la dynamique hydrologique de ces réservoirs est essentielle à la gestion et l’allocation de ressources hydriques alpines. Puisque la pluie, la fonte de la neige et des glaciers apportent des contributions minimales à l’écoulement fluvial pendant la saison hivernale, l’eau dans les ruisseaux non contrôlés par des barrages provient de l’eau souterraine. Par conséquent, l’analyse des débits d’hiver fournit de l’information essentielle en ce qui concerne l’ampleur de la décharge d’eau souterraine et sa relation avec les caractéristiques physiographiques des bassins hydrographiques tels que le climat, la géologie et la topographie. Les données de débits dans 18 bassins (21–3900 km²) dans les montagnes des Rocheuses Canadiennes et la chaîne Columbia ont été analysées. Les débits hivernaux varient peu (0.2–0.6mm d^–1) en fonction de l’emplacement du cours d’eau et d’une année à l’autre. Par contre, les débits de printemps, d’été et d’automne montrent une grande variabilité interannuelle. Ceci suggère que l’eau souterraine atteint une capacité maximale à chaque année, et que l’évacuation de celle-ci est contrôlée par des facteurs fixes tels que la géologie, la topographie et le climat. Les précipitations, représentées par le débit moyen annuel à long terme, sont fortement corrélées aux débit moyen hivernal, ce qui indique l’importance du régime climatique. Les bassins versants situés sur des formations géologiques perméables ont un débit hivernal plus élevé, ce qui suggère que la géologie influence les propriétés hydrogéologiques à une échelle comparable à celle des bassins versants étudiés. Les résultants ne montrent aucun effet de la topographie sur les débits hivernaux.

Introduction

Urbanization is increasingly advancing towards alpine environments in western Canada. Hence, our understanding of headwater processes in alpine environments is crucial to better manage or allocate water supply in alpine and downstream environments (Burn et al. 2008; Welch and Allen 2012). Climate change, which is projected to be more severe in mountainous and high-latitude environments, will also influence future water resources, including groundwater (Taylor et al. 2013). Thus, water managers must consider multiple stressors to future water supply. Currently, there is an emphasis on the impact of climate change on low flows, particularly summer flows, which is often when water demand is highest (Cooper et al. 1995; Smakhtin 2001; Barnett et al. 2005; Price 2011). However, winter flows are equally important, especially in cold regions, as they provide water supply for up to 6 months of the year. Low flows are not only important for water balance considerations, but also for terrestrial wildlife, aquatic ecosystems, municipal and industrial regulations, effluent concentrations and water withdrawals (Bradford and Heinonen 2008; Burn et al. 2008; Rood et al. 2008).

Southwestern Canada has experienced an average 0.9°C increase in temperatures over the last century, and daily minimum temperatures show stronger increasing trends than daily maximum temperatures (Zhang et al. 2000). The increasing minimum temperatures are likely driving increased mean annual temperatures. Furthermore, Zhang et al. (2000) found total annual precipitation increases of 5–35% over southern Canada during the last century, although precipitation anomalies within southern Canada result in some areas exhibiting decreasing trends in winter precipitation. Thus, the impacts of changing climatic conditions have high spatial variability, leading to varying impacts on hydrologic trends (Burn and Hag Elnur 2002; Jyrkama and Sykes 2007).

Changes in air temperature and precipitation can greatly influence the hydrological regime, especially for cold regions where snowmelt provides a large fraction of the water input (e.g. Barnett et al. 2005). Increasing temperatures may be influencing the hydrologic regime by causing increased summer evaporation and decreased runoff, and increased snowmelt and winter rainfall which increases winter flow (Rivard et al. 2009). The spatial distribution of streamflow trends in Canada was mapped by Zhang et al. (2001) using 30-, 40- and 50-year study periods. They showed that watersheds in southern Canada generally had decreasing mean annual flow (Zhang et al. 2001). Similarly, Rivard et al. (2009) examined baseflow and groundwater levels across Canada, and found decreasing mean annual baseflow trends in southern Canada.

Several studies conducted in the Rocky Mountains have shown evidence of earlier or decreased peak flows and decreasing mean annual flow, with an emphasis on decreasing summer flows (Zhang et al. 2001; Barnett et al. 2005; Rood et al. 2005, 2008). A distinctive shift in the annual hydrograph has pushed the peak flow earlier in the year and thus reduced river flows in the late summer season (Burn and Hag Elnur 2002; Rood et al. 2008). Detailed studies of streamflow variability were conducted in the central Rocky Mountains using 31 gauging stations (Rood et al. 2005). Over the past century, 21 river reaches showed a pattern of decreasing mean annual flow, of which 11 had statistically significant decreases at p < 0.05, where p is the measure of confidence for the Pearson trend (Rood et al. 2005). Although mean annual flow in the Bow River at Banff has been decreasing, the data show statistically significant increases (p < 0.05) in baseflow for January and March (Rood et al. 2008).

Baseflow is the portion of streamflow that comes from groundwater and other delayed sources (Tallaksen 1995). Winter flow occurs in the period when there is little direct input of rain or snowmelt to streams. Therefore, winter flow represents the baseflow that is almost entirely supplied by groundwater discharge and lake storage. In mountainous environments around the world, baseflow is sourced from release from lakes (Burn et al. 2008), fractured bedrock aquifers (Tromp-van Meerveld et al. 2007; Andermann et al. 2012; Welch and Allen 2012), talus and moraine aquifers (Caballero et al. 2002; Clow et al. 2003; Langston et al. 2011; Muir et al. 2011) and shallow unsaturated storage (Price 2011).

Talus and moraine deposits can store large amounts of groundwater and greatly influence the baseflow within a watershed. The coarse materials transmit water quickly, while underlying finer materials will allow for slow release of groundwater (Clow et al. 2003). In addition to these surficial aquifers, deep bedrock aquifers can provide a substantial part of baseflow. In the Himalayas, groundwater storage in fractured bedrock was found to be a significant contributor to baseflow and vital for water balance considerations (Andermann et al. 2012). Within the Panola Mountain Research Watershed, Georgia, USA, 14–21% of streamflows were attributed to bedrock fractures (Tromp-van Meerveld et al. 2007).

The Canadian Rocky Mountains and Columbia Mountains (Figure 1) host the headwaters of numerous large rivers, supplying water to millions of North Americans. The hydrographs of mountainous rivers in this region are dominated by snowmelt inputs and exhibit strong inter-annual variability depending on the condition of snowmelt and the magnitude and timing of summer rain. The amount of snowmelt and rainfall inputs is expected to be much greater than the groundwater storage deficit. As a result, groundwater storage attains maximum capacity every summer. This results in a consistent winter stream flow every year, as seen in the annual hydrographs (Figure 2). In January and February, daily average air temperature remains well below 0°C and the majority of precipitation falls as snow. As such, the streamflow during January–February is essentially determined by groundwater inputs. Therefore, the analysis of winter flow in alpine streams in January–February will reveal useful information on the hydrogeological characteristics of mountain watersheds, even though winter flow data have uncertainties associated with ice cover and other sources of errors (see Methods).

Figure 1. (a) Index map showing the location of the study area; (b) location of the watersheds and gauging stations (refer to Table 1 for gauging station abbreviations and other information); (c) distribution of the 1971–2000 normal annual precipitation (after Natural Resources Canada 2010).

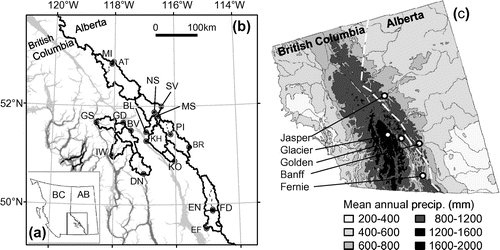
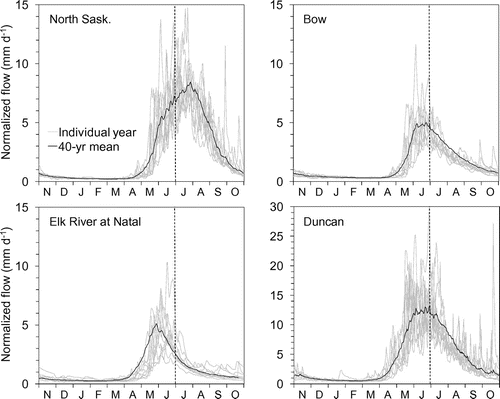
Figure 2. Daily discharge hydrographs of normalized flow showing 10 individual years (2001–2010) and the long-term mean (1971–2010) for the North Saskatchewan River at Saskatchewan Crossing, Bow River at Banff, Elk River at Natal, and Duncan River. Vertical dashed lines indicate 1 July.

The objective of this study is to investigate the physiographical factors that control the hydrogeological behaviour of mid- to high-latitude mountain river basins, by analyzing winter flows. Several main factors that influence baseflow include topography, geology and climate. While the spatial distribution of climatic variables, precipitation in particular, has a strong influence on baseflow, in a given climatic region catchment geology is considered by most to be the primary control on baseflow, as it determines the potential storage within the system (Farvolden 1963; Smakhtin 2001; Tague and Grant 2004; Price 2011). Topography also plays a crucial role in baseflow generation, where topographic gradients control the transmission of groundwater (Forster and Smith 1988; Price 2011; Welch and Allen 2012). Lastly, as the timing, amount and form of precipitation have a major influence on the hydrologic budget, changing climatic conditions may further alter streamflow regimes (Smakhtin 2001; Tague et al. 2008; Price 2011). To better understand the hydrogeological characteristics of the headwater regions, the following questions will be addressed: (1) has there been consistent increase or decrease in winter flow? (2) Is there spatial variability in winter flow within the study region? (3) If so, what controls this spatial variability?

Study area

The study area comprises the Rocky and Columbia Mountain Ranges (Figure 1). The watersheds in the area are sorted into three groups based on their location: northern Rockies, southern Rockies and Columbia Mountains (Figure 1; Table 1). The majority of watersheds are located in national parks (NP), where land-use impacts from mining and logging are limited. Small- to medium-scale watersheds (21 to 3900 km²) were selected to compare the influence of dominant watershed attributes and climate conditions on winter baseflow among the watersheds.

Table 1. List of watersheds (WS) and their attributes including the name and Water Survey of Canada ID of the watershed (location shown in Figure 1), abbreviated symbol of the watershed, region (Col = Columbia Mountains; NR = northern Rockies; SR = southern Rockies), duration of discharge data (including period length), gauge elevation (G. elev), median elevation (M. elev) of watershed, vegetation cover (Veg), glacier cover, hypsometric intregral (HI), average slope (Av. slp), fraction of the watershed underlain by the bedrock youger than Cambrian (Young BR) and drainage density (DD).

Watershed name	Watershed ID	WS abbr.	Region	Duration of record (period)	Area (km^2)	G. elev (m)	M. elev (m)	Veg (%)	Glacier (%)	HI	Av. slp (deg)	Young BR (%)	DD (km^–1)
Gold	08NB014	GD	Col	1974–2011 (38)	429	815	2100	40.0	18.94	0.46	26.9	0	0.65
Goldstream	08ND012	GS	Col	1964–2010 (47)	934	610	1700	66.2	8.94	0.45	28.3	35	0.62
Beaver	08NB019	BV	Col	1986–2011 (26)	1150	829	1900	54.8	9.38	0.42	26.7	6	0.62
Illecillewaet	08ND013	IW	Col	1965–2011 (47)	1150	510	1775	57.1	2.3	0.43	29.4	50	0.62
Duncan	08NH119	DN	Col	1963–2011 (49)	1310	597	1950	33.6	12.39	0.46	29.9	31	0.65
Silverhorn	05DA010	SV	NR	1972–2010 (39)	21	1707	2450	12.4	10.45	0.52	25.7	0	0.63
Mistaya	05DA007	MS	NR	1967–2010 (44)	248	1634	2200	30.5	5.97	0.34	23.0	0	0.65
Pipestone	05BA002	PI	NR	1985–2010 (26)	306	1560	2300	42.3	3.34	0.41	19.9	29	0.63
Miette	07AA001	MI	NR	1973–2011 (39)	629	1045	1975	58.2	0.51	0.42	17.2	0	0.70
North Sask.	05DA009	NS	NR	1971–2012 (42)	1923	1354	2250	34.2	17.6	0.38	21.9	15	0.68
Bow	05BB001	BR	NR	1912–2012 (101)	2210	1384	2150	54.5	4.13	0.36	19.8	34	0.65
Athabasca	07AA002	AT	NR	1972–2010 (39)	3873	1019	2075	43.6	11.76	0.37	17.0	2	0.67
Kootenay	08NF001	KO	NR	1946–2011 (66)	416	1176	1650	82.6	0.11	0.28	20.8	12	0.83
Blaeberry	08NB012	BL	NR	1971–2011 (41)	587	875	2000	46.5	19.55	0.44	27.7	38	0.68
Kicking Horse	08NA006	KH	NR	1974–2010 (37)	1850	788	1950	56.5	5.38	0.41	25.7	6	0.68
Fording	08NK018	FD	SR	1971–2011 (41)	621	1230	1975	48.5	0	0.41	23.5	100	0.70
Elk at Natal	08NK016	EN	SR	1960–2011 (52)	1840	1200	1975	52.7	0.64	0.34	23.2	100	0.71
Elk at Fernie	08NK002	EF	SR	1971–2011 (41)	3090	1000	1875	59.0	0.39	0.35	22.5	100	0.72

Mean annual precipitation varies between 450 and 1500 mm in the study area (Figure 1) (Natural Resources Canada [NRC] 2010). Large differences occur in part due to orographic effects, which result in significant precipitation falling on the western side of the mountain ranges. The large elevation range (600 m to over 3000 m) within the mountainous watersheds leads to large gradients in air temperature, and also variability in rain and snow, as more precipitation occurs as snow at higher elevations where temperature is lower. Large accumulation of snow during the winter months, and its rapid melting in spring and early summer, dominates the flow regime of rivers in the area.

The complex tectonic development and subsequent glacial reworking has resulted in highly variable bedrock geology and geomorphology in the area. The geomorphology is a result of glacial erosion during the Pleistocene, leading to various glacial, fluvioglacial and glaciolacustrine deposits (Burn et al. 2008). The northern Rockies and Columbia Mountains are dominated by Proterozoic and lower Paleozoic sediments, while the southern Rockies also have significant younger Mesozoic to Quaternary sediments. The dominant bedrock lithology consists of layered limestone, shale and sandstone, with older Cambrian bedrock having significant quartzite.

Methods

Stream discharge and climate data

Daily stream discharge data (Water Survey of Canada [WSC] 2014) were analyzed for 18 watersheds within the Canadian Rocky and Columbia Mountains (Figure 1). These watersheds had unregulated flow and continuous data including winter months for a minimum of 25 years. Most watersheds had more than 35 years of records (Table 1). Daily average flow data (m³ s^–1) were divided by the watershed area to compute area-normalized discharge, which is referred to as runoff (mm d^–1) in this paper. The hydrological year (HY) in this study starts on 1 November and ends on 31 October. For example, HY 2011 starts in November 2010. The beginning of the HY corresponds with the start of the winter season, where there is minimal input to streamflows from rainfall.

Winter baseflow is used in this study to represent groundwater discharge from the aquifer storage months after the seasonal inputs have stopped. In order to minimize the effects of storm flow generated by winter rainfall, the winter flow is defined as the average runoff for January–February of each HY. Effects of occasional rainfall during this period are discussed in the results. The data were analyzed for temporal trends using all available data, and for spatial variability among watersheds using 41-year averages (1971–2011) for 12 out of 18 watersheds, and 26–39 year averages overlapping in the 1971–2011 period for the remaining six watersheds (Table 1). The period 1971–2011 was selected as it is the most consistent long-term data throughout the watersheds.

Analyzing winter flow data is challenging due to the uncertainty of low-flow measurements. Numerous factors affect the quality of these measurements such as the presence of river ice, inability to accurately measure low flows with current instrumentation and poor weather conditions leading to rushed and potentially inaccurate measurements (Hamilton 2008). Of all the daily discharge data used to compute winter (January–February) flow statistics in this study, 86% had a grade of “B” indicating the presence of ice cover. To account for the effects of ice, the Water Survey of Canada (WSC) adjusts rating curves by adding a shift to match the discharge predicted by the rating curve with observed discharge (Hamilton and Moore 2012). While this procedure ensures that discharge values are accurate within the uncertainty of manual discharge measurements on the days of measurement, it makes it difficult to quantify the uncertainty in continuous daily discharge data using statistically rigorous methods (Hamilton and Moore 2012).

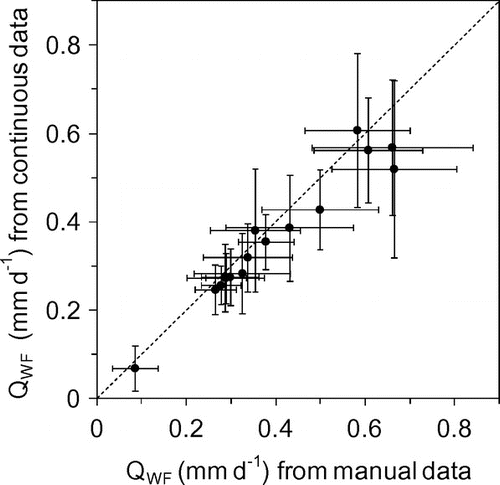
Here, an attempt is made to assess a rough order of magnitude of uncertainty in winter flow data by comparing the values of mean winter flow computed from continuous daily flow data with those from manual discharge measurements retrieved from station visit summary records provided by David Hutchinson and Dennis Lazowski at the WSC (personal communication). The results are summarized in Figure 3, which compares the computed mean winter (January–February) flow and its standard deviation for the entire period of available matching data (6 to 16 years depending on locations). The data from January to February 2005 are excluded for the five gauging stations in the Columbia Mountains as they are affected by an unusually large rain event (see the Results section). Long-term mean winter flow (Q_WF) values are similar between the two data sets, even though the continuous daily data tend to yield slightly lower values. While this is not a direct measure of uncertainty, it does indicate how well the Q_WF computed from continuous daily data are constrained by manual measurements. Based on the data shown in Figure 3, the uncertainty in Q_WF is expected to be on the order of ± 20–40%.

Figure 3. Comparison of mean winter flow (Q_WF) computed from manually measured discharge and from continuous daily data for 16 watersheds. Error bars indicate one standard deviation on either side of the mean value. Dashed line indicates the 1:1 match.

The homogenized monthly average air temperature data (Vincent et al. 2012) and the adjusted monthly total precipitation and rainfall data (Mekis and Vincent 2011) were obtained for five weather stations within the study area (Figure 1) to examine the temporal variability of temperature and precipitation in the proximity of watersheds. These are the only stations in the study area with consistent, long-term data sets for the study period. The homogenized temperature data were unavailable for Fernie weather station; therefore, raw temperature data (Environment Canada 2014) were used to calculate monthly average temperatures from daily temperatures. Several years were excluded where monthly average temperatures could not be computed based on a lack of daily average temperature data. If more than 5 consecutive days or 8 days of the month were missing, the monthly average temperature was not computed for Fernie weather station.

Statistical analysis

Statistical trend analyses were conducted for annual mean temperature, winter (January–February) mean temperature, annual total precipitation, annual mean streamflow and winter flow using both parametric and non-parametric methods based on previous studies (Zhang et al. 2001; Yue and Wang 2002; Rood et al. 2008). The objective of the analysis was to establish the presence or absence of long-term climatic trends and, if present, their correlation with streamflow. Pearson's product moment correlation coefficient, r (Helsel and Hirsh 2002, 218) was used to test whether the data had a linear increase or decrease at a significant level of p < 0.05 for those data series that had approximately normal distribution based on the normality test (Helsel and Hirsh 2002, 113). The non-parametric Mann–Kendall test was used to compute the rank correlation coefficient, τ, for all data series, as it does not require the normal data set (Cunderlik and Burn 2004). Some authors suggest pre-whitening the data series to remove serial correlation (e.g. von Storch 1995; Helsel and Hirsh 2002), but Yue and Wang (2002) found that serial correlation does not affect the Mann–Kendall statistics and the whitening can obscure real trends. A lag-one serial correlation coefficient greater than 0.1 was found for the mean annual flow of 10 out of 18 streams, and for the winter flow of five streams. To investigate the potential effects of serial correlation, the trend-free pre-whitening (TFPW) procedure (Yue et al. 2002) was applied to remove serial correlation from the data. However, the TFPW procedure did not change the significance of the trends in mean annual flow or winter flow for any streams. Therefore, the raw data sets were used for the Mann–Kendall test without pre-whitening in this study.

Watershed attributes

The information on bedrock geology was compiled from the geological maps of Alberta (Alberta Geological Survey [AGS] 2004) and British Columbia (British Columbia Ministry of Energy and Mines [BCEM] 2005). An attempt was made to represent geological attributes using lithology (e.g. sandstone, shale, limestone). However, the lithological heterogeneity within each geological unit made it difficult to calculate meaningful numbers using this approach. Therefore, for each watershed the fraction of areas underlain by rocks having different ages was calculated, and sorted into the Cambrian and older periods, Ordovician to Permian, and Triassic to Quaternary. The older Cambrian units are dominated by quartzite and other weathering-resistant rocks, whereas younger Triassic to Quaternary units are dominated by sandstones, siltstones and carbonate rocks.

The effect of topography was examined using a digital elevation map (DEM) (NRC 2013) having a grid cell size of 20 m. The slope angle was calculated for each grid cell and sorted into 5° bins to calculate the frequency distribution of slopes within a watershed. The watershed hypsometric curve was calculated by sorting the cell elevation into 100 equal intervals and developing the cumulative frequency curve. Hypsometry refers to the cumulative frequency distribution plots of elevation with respect to area, and is commonly used to examine the geomorphic stage of development of a basin (e.g. Hurtrez and Lucazeau 1999). The hypsometric integral (HI) is defined by:(1)

where z_mean, z_min and z_max are mean, minimum and maximum elevation within the watershed.

Drainage density (km^–1) has an influence on the hydrologic response of watersheds to precipitation and snowmelt, where high drainage density tends to cause rapid responses. Drainage density is defined by:(2)

The stream length was calculated from stream channels delineated on the DEM using the flow accumulation method by the spatial analyst tool of ArcGIS10.1 (Environmental Systems Research Institute [ESRI] 2013). This was necessary as the available river network data only included major river channels, and did not include low-order streams. Grid cells with flow contributions from a minimum of 1 km² were classified as streams.

The information on vegetation cover was obtained from CanVec data derived from satellite imageries ranging in resolution from 15 to 30 m (NRC 2007). The data set classifies vegetation into several types, but for the purpose of this study, only the presence and absence of vegetation are used to calculate the fraction of vegetated area in each watershed. Uncertainty in vegetation cover estimates arises from unclassified areas caused by shadows and cloud cover, resulting in up to 35% of the watershed area being unclassified. The fraction of glacier cover was estimated from the Landsat-based glacial cover data from 2005, which covers all of western Canada at a 25-m grid resolution (Bolch et al. 2010). By analyzing the correlation between these watershed attributes and flow data, their effects on the spatial variability of winter flow can be observed.

Results

Regional climatic trend

Five weather stations throughout the study area were used to analyze temporal trends of temperature and precipitation. However, it should be noted that the five weather stations are located at relatively low elevations (Table 2), which may not represent the climatic trend over the entire watershed. Mean annual temperatures and mean winter (January–February) temperatures had a statistically significant (p < 0.05) increase at all weather stations over the past 80–124 years (Table 2). Total annual precipitation trends were not as prominent as temperature, with only Jasper showing a statistically significant (p < 0.05) increase over the past 80 years, at an average rate of 0.19 mm y^–1. Furthermore, winter precipitation (November–February) did not have any significant trends.

Table 2. Statistics of air temperature and precipitation recorded at the key meteorological stations in the region (see Figure 1 for locations). Bolded terms are statistically significant at p < 0.05.

Weather station	Region	Station elev (m)	Series length	Annual Temperature			Rate(deg y^–1)	Jan–Feb temp			Rate(deg y^–1)	Annual Precip.			Rate(mm y^–1)
				n	r	τ		n	r	τ		n	r	τ
Banff	NR	1384	1888–2011	115	0.42	0.30	0.022	123	0.34	0.24	0.028	108	0.008	0.017	–
Jasper	NR	1062	1930–2011	73	0.46	0.34	0.011	77	0.29	0.21	0.044	81	0.45	0.33	0.194
Golden	NR	785	1902–2011	91	0.53	0.36	0.020	105	0.40	0.28	0.045	92	0.192	0.114	–
Fernie	SR	1001	1914–2011	81	0.37	0.24	0.012	81	0.39	0.25	0.040	66	0.047	0.020	–
Glacier	Col	1248	1908–2011	90	0.54	0.40	0.018	101	0.46	0.32	0.039	91	–0.007	–0.024	–

Note:

Col, Columbia Mountains; NR, northern Rockies; SR, southern Rockies. Parameters: n, number of years; r, Pearson’s r; and τ, Kendall τ.

Regional hydrograph characteristics

Figure 2 shows the hydrographs for four watersheds, which best represent the streamflow characteristics in the respective regions (see Figure 1 for locations). The overall shape of the hydrographs is similar, with the baseflow periods beginning in November and the spring freshet starting in April. The summer high-flow period is followed by a gradual recession in September and October. Summer flow has a large inter-annual variability reflecting the high variability of snow accumulation, melt and summer precipitation. In contrast, winter flow has relatively low inter-annual variability, except for some years with unusual winter rain storms (discussed below in the section on winter flow variability).

The timing of peak flows is earlier and the snowmelt-driven high-flow period is shorter in the southern Rockies region (see Elk River in Figure 2), which has a warmer climate than the northern regions. The warmer climate of the southern Rockies region is reflected in the lack of glacial coverage (< 1%; see Table 1). Moving farther north, the Bow River and the Duncan River have similar peak flows, occurring between late May and early July. Compared to the southern Rockies watersheds, the summer high-flow period is longer in the northern Rockies and Columbia due to longer snowmelt periods. The North Saskatchewan River, the northernmost watershed shown in Figure 2, has later peak flows occurring in mid to late July, and longer high-flow periods, compared to the Bow River, presumably due to the colder climate and higher snow accumulation. This is reflected in the higher glacier coverage (18%; Table 1) of this watershed compared to the others shown in Figure 2.

Of the 18 watersheds, only the Bow River and the Elk River at Natal had statistically significant (p < 0.05) declines in mean annual flow over the duration of records (101 years for the Bow and 58 years for the Elk at Natal; Table 3). Other watersheds did not have significant declines in mean annual flow, but the record lengths are shorter (Table 1).

Table 3. Pearson’s r and Kendall’s τ coefficients for the temporal trend of winter flow (Q_WF) and mean annual flow (Q_mean) over the entire duration of record, and the correlations between Q_WF and January–February mean air temperature (T_winter), and between Q_WF and Q_mean. Bolded terms are statistically significant at p < 0.05. Pearson’s r is shown only for those data sets that passed the normality test (see text). Mean annual flow during 1971–2011 (or shorter time period, see text; Q_mean), mean winter baseflow during 1971–2011 (Q_WF) and winter flow index (WFI = Q_WF/Q_mean).

Watershed name	WS abbr.	Region	Duration of record	Qmeam (mm d^–1)	QWF(mm d^–1)	WFI	QWF		Qmean		QWF vs Twinter		QWF vs Qmean
							r	τ	r	τ	r	τ	r	τ
Gold	GD	Col	1974–2011	3.67	0.40	0.11	–	0.336	–	0.007	0.180	0.105	0.348	0.287
Goldstream	GS	Col	1964–2010	3.55	0.65	0.18	–	0.096	–0.259	–0.159	0.088	0.175	0.021	0.090
Beaver	BV	Col	1986–2011	3.09	0.55	0.18	–	0.142	–0.077	–0.012	0.036	0.074	0.068	0.013
Illecillewaet	IW	Col	1965–2011	3.93	0.64	0.16	–0.022	–0.166	–0.177	–0.120	0.083	0.177	–0.083	–0.086
Duncan	DN	Col	1963–2011	4.07	0.56	0.14	–	0.068	–0.108	–0.081	0.273	0.252	–0.154	–0.096
Silverhorn	SV	NR	1972–2010	1.76	0.20	0.11	–0.134	–0.098	–	–0.144	0.066	0.053	0.187	0.098
Mistaya	MS	NR	1967–2010	2.20	0.24	0.11	0.053	0.351	–0.207	–0.121	0.198	0.205	0.215	0.148
Pipestone	PI	NR	1985–2010	1.62	0.28	0.17	–0.020	0.015	–0.233	–0.132	0.064	–0.111	0.318	0.201
Miette	MI	NR	1973–2011	1.42	0.14	0.10	0.210	0.151	–0.115	–0.102	0.379	0.228	0.219	0.112
North Sask	NS	NR	1971–2012	2.36	0.24	0.10	0.360	0.249	–0.075	–0.094	0.425	0.269	0.200	0.151
Bow	BR	NR	1912–2012	1.47	0.34	0.24	0.241	0.153	–0.238	–0.168	0.145	0.081	0.140	0.147
Athabasca	AT	NR	1972–2010	1.90	0.27	0.14	–	–0.136	–	–0.155	0.145	0.063	0.217	0.089
Kootenay	KO	NR	1946–2011	1.00	0.07	0.07	–	0.072	–0.133	–0.098	0.134	0.123	0.235	0.243
Blaeberry	BL	NR	1971–2011	2.45	0.35	0.14	–	0.061	–0.126	–0.004	0.052	0.116	0.175	0.160
Kicking Horse	KH	NR	1974–2010	1.87	0.27	0.15	0.016	0.024	–0.136	–0.044	0.142	0.142	0.045	0.014
Fording	FD	SR	1971–2011	1.11	0.28	0.25	0.397	0.267	–0.162	–0.068	0.370	0.217	0.397	0.342
Elk at Natal	EN	SR	1960–2011	1.18	0.27	0.23	0.187	0.060	–0.357	–0.212	0.249	0.148	0.138	0.112
Elk at Fernie	EF	SR	1971–2011	1.31	0.37	0.28	–	0.030	–0.224	–0.101	0.358	0.274	0.225	0.235

Note:

Col, Columbia Mountains; NR, northern Rockies; SR, southern Rockies; WS, watershed.

Temporal variability of winter flow

Winter flow in this paper is defined by the mean flow in January and February, which is not directly affected by summer and fall precipitation or spring snowmelt (Figure 2). As it is sustained almost entirely by the discharge of groundwater from the storage, winter flow generally has a small inter-annual variability (Figure 4). However, a significant increase in winter flow occurs in some years (see Duncan River in Figure 4). The factors that can potentially influence winter flow include winter rainfall, high air temperature causing snowmelt, and the water inputs in the previous hydrological year. Only a small fraction of winter precipitation normally falls as rain in the mountains. In four of the five weather stations, approximately 15% of precipitation was rainfall;,the exception was Fernie, which had up to 40% of winter precipitation in rainfall. At the weather stations in Banff, Golden, Jasper and Glacier NP, less than 100 mm of rainfall occurred during December–February of most years, except for 1981 and 2005 at Glacier NP. These small winter rainfall events do not affect flow (Figure 5), but large events appear to generate runoff and increase flow. For example, the 1981 event in Glacier NP recorded 45 mm of rainfall over 3 days, and the 2005 event had 127 mm over 8 days, which resulted in increased winter flow in the Duncan River and other Columbia Mountain watersheds. These large rainfall events are rare and their occurrence did not have a statistically significant increase over the duration of the study period.

Figure 4. January–February mean flow for Duncan River, Bow River at Banff, Elk River at Natal, and North Saskatchewan River at Saskatchewan Crossing.

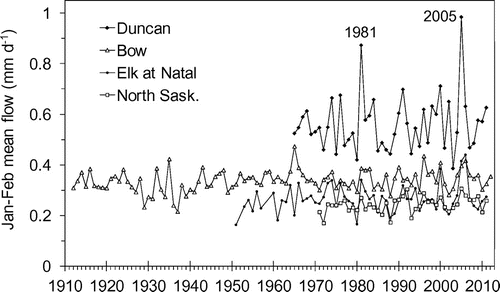
Figure 5. Relation between total January–February runoff in the four watersheds and total December–February rainfall at corresponding weather stations: Bow River – Banff, Kicking Horse River – Golden, Goldstream River – Glacier, Elk River (Natal) – Fernie, and Athabasca River – Jasper. (a) All available data; (b) years with rainfall < 80 mm.

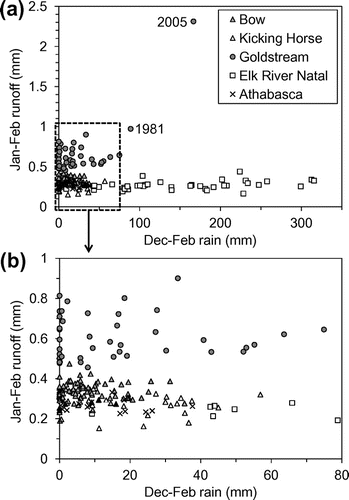
Due to the warmer climate of the southern Rockies region, the Fernie weather station frequently recorded December–February rainfalls in excess of 100 mm, causing higher flow as seen in the Elk River at Natal (Figure 5). There was a significant correlation between winter rainfall at Fernie and winter flow in the Elk River at Natal (Pearson’s p = 0.033); flow increased by roughly 0.05 mm d^–1 from the years with low (< 100 mm) to high (> 300 mm) winter rainfall (Figure 5). It should be noted the Fernie weather station is located in the southernmost part of the region (Figure 1) and at a much lower elevation (1001 m) compared to the mean elevation of the watersheds (Table 1). Therefore, winter air temperature and rainfall in Fernie are expected to overestimate those in the watersheds.

Air temperature is expected to have little effect on winter flow because average air temperatures in January–February are well below 0°C. Only four out of 18 watersheds had statistically significant correlation (p < 0.05) between January–February air temperature and winter flow (Table 3). The watersheds with statistically significant correlation were not all from the same region, with two from the northern Rockies and two from the Columbia Mountains.

Winter flow is sustained by the groundwater recharged prior to the winter. The amount of pre-winter recharge is expected to be related to the amount of snowmelt and rainfall in summer and fall, which in turn should be reflected in the mean annual flow during the preceding year. In order to investigate the effect of the previous year’s input on winter flow, the mean annual flow of the previous HY was compared to the winter flow of the following year (see Figure 6 for examples). There was no correlation between winter flow (Q_WF) and mean annual flows (Q_mean) from the previous year for 16 out of 18 watersheds. In addition, seasonal average flows for summer (June–August) and fall (September–October) did not have any significant correlation to winter flows, implying that winter flow is insensitive to the previous year’s water input.

Figure 6. Relationship between winter flow (Q_WF) and mean annual flow (Q_mean) from the previous year (for example, Q_WF 2010 vs. Q_mean 2009).

Finally, the long-term trend of winter flow was examined for the entire duration of records for each watershed. Only four out of the 18 watersheds had a significant increase in winter flow over the period of record (Table 3). The Bow River had a statistically significant increase over 1912–2012 due to a few low-flow years in the 1930s, but the change was insignificant (p = 0.84) over the past 70 years (1943–2012).

Spatial variability in winter flow

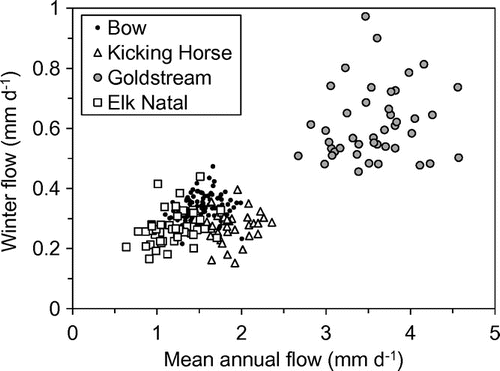
Since stream flow is driven by hydrological inputs (precipitation minus evaporation), a strong correlation is expected between the spatial distribution of precipitation (Figure 1) and flow. Hydrological inputs are difficult to quantify in mountainous watersheds, but long-term mean annual flow gives an integrated measure of the average hydrological input over the watershed. As expected, average values of Q_WF over the analysis period of 1971–2011 (or shorter periods for the watersheds with shorter records) had a strong correlation with the average values of Q_mean over the same period (Figure 7), clearly showing the dominant effect of climate. In particular, average values of Q_WF and Q_mean were higher in the Columbia Mountains watersheds, which are located in the high precipitation zone (Figure 1), compared to other regions.

Figure 7. Relation between the long-term average values of mean annual flow (Q_mean) and winter flow (Q_WF). The lines indicate the winter flow index (WFI = Q_WF / Q_mean). See Table 3 for the abbreviation of gauging stations.

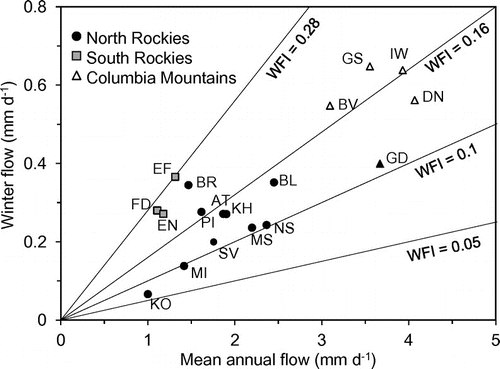
Since Q_mean represents the effects of climate, taking the ratio of Q_WF to Q_mean gives a useful index to examine the effects of the factors other than climate. This ratio is referred to as the winter flow index (WFI):(3)

The WFI is similar to the low-flow index (LFI) proposed by Burn et al. (2008) to represent the watershed characteristics of different regions in Canada. The LFI has a tendency to produce large variability in smaller watersheds, as landscape heterogeneity greatly influences LFI (Burn et al. 2008). Numerous physiographical factors have the potential to affect winter flow, namely topography, elevation, geology and soil cover. These factors are examined below in an attempt to identify the significant factors influencing the groundwater storage and flow processes that sustain winter flow.

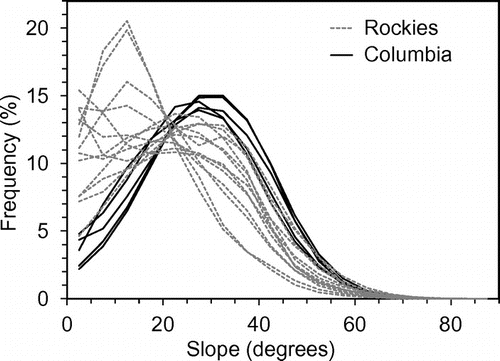
The frequency distribution of slope within each watershed was used to investigate the influence of topography on winter flow. Large variation occurred between 0–40° slopes throughout the study regions (Figure 8). The Columbia Mountains watersheds had a low frequency of 0–20° slopes and high frequency of 20–40° slopes compared to the Rockies watersheds (Figure 8) and higher values of average slope (Table 1), suggesting more rugged, steep topography.

Figure 8. Frequency distribution of grid-cell slope in the watersheds.

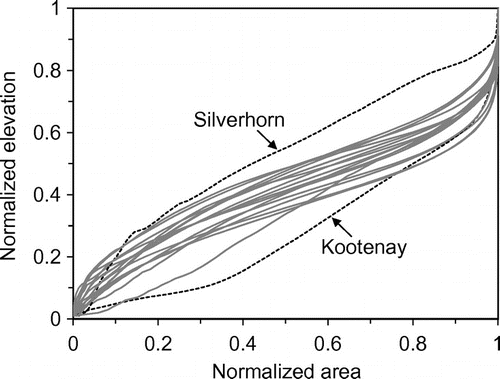
The normalized hypsometric curves allow for comparisons of geomorphic development stages to be made among watersheds having different sizes and elevation ranges (Figure 9). The majority of watersheds had similar S-shaped hypsometric curves, indicating the mature development stage (Willgoose and Hancock 1998). The HI fell within a relatively narrow range of 0.34–0.46 except for the Silverhorn River and the Kootenay River watersheds (Figure 9). The high HI value and concave shape of Silverhorn River suggest a relatively young development stage, whereas the low HI value and concave shape of Kootenay River suggest a relatively old development stage characterized by a large portion of valley floor.

Figure 9. Hypsometric curves of the watersheds. Silverhorn River watershed has a high HI (= 0.52) and Kootenay River watershed has a low hypsometric integral (HI) (= 0.28).

Drainage density ranges between 0.62 and 0.83 km^–1 (Table 1) with an average of 0.67 km^–1. The southern Rockies watersheds had relatively high drainage density, averaging 0.71 km^–1, and the Columbia Mountains watersheds had relatively low drainage density, averaging 0.63 km^–1. The northern Rockies watersheds had drainage densities spanning the entire range.

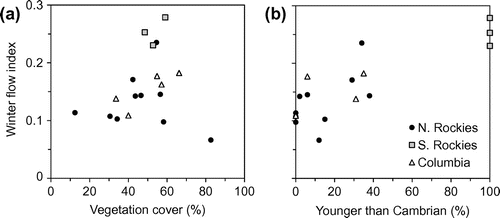
The mean winter flow showed a significant correlation with the average slope of the watershed when the overall correlation was examined for all watersheds (Figure 10a; Table 4). However, there appears to be no correlation among the watersheds within each region. The strong overall correlation is driven by the cluster of high-slope watersheds in the Columbia Mountains, which happen to have high winter flow due to the wetter climate (see Figure 7). Therefore, the apparent correlation in Figure 10a reflects the regional difference in climate. This is demonstrated clearly by comparing the winter flow index (WFI) to average slope (Figure 10d), which had no significant correlation (p = 0.92). The HI showed no correlation with the mean winter flow (Figure 10b) and the WFI (Figure 10e).

Figure 10. Relation between topographic parameters and the long-term average winter flow (a–c), and the winter flow index (d–f).

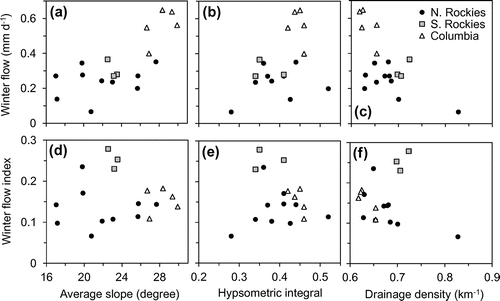
Table 4. Pearson’s r and Kendall’s τ correlation coefficients between the watershed attributes and winter flow (Q_WF), and winter flow index (WFI). Bolded terms are statistically significant at p < 0.05.

Basin attribute	QWF		WFI
	r	τ	r	τ
Average elevation	–0.37	–0.34	–0.140	–0.192
Station elevation	–0.71	–0.53	–0.060	–0.085
Vegetation cover	0.06	0.16	0.183	0.242
Glacial cover	0.23	0.12	–0.410	–0.268
Geology (younger than Cambrian)	0.13	0.37	0.836	0.581
Hypsometric integral	0.44	0.35	–0.120	–0.106
Average slope	0.72	0.49	0.024	0.098
Drainage density	–0.63	–0.33	–0.120	–0.072

Drainage density had a negative overall correlation with the mean winter flow (Figure 10c; Table 4). However, similarly to average slope and HI, the drainage density did not appear to correlate with WFI, as indicated by randomly scattered points in Figure 10f and a significance level of p = 0.62 (not shown). This suggests that the apparent overall correlation in Figure 10c reflects the regional difference in climate rather than the effects of drainage density itself.

As the local climate has the potential to influence streamflows, mean elevation and glacial coverage were also examined. The WFI did not have a significant correlation with mean elevation or glacier cover (Table 4).

Soil cover is expected to influence groundwater flow, as the soil layer can provide storage capacity. The information on soil cover was not available; therefore, vegetation cover was used as a surrogate as trees generally grow in areas with thick enough (> 0.5–1 m) soil covers. Vegetation covers had a large variation ranging from 12 to 83% of the watershed area, with the majority of watersheds falling within 40–60% (Table 1). Contrary to the expectation, vegetation cover did not have a significant correlation with WFI (Figure 11a; Table 4).

Figure 11. Effects of (a) vegetation cover and (b) the age of bedrock on the winter flow index.

The type of bedrock controls the permeability and porosity of potential aquifers and, hence, is expected to influence groundwater inputs to winter streamflow. In general, the older Precambrian and Cambrian rocks are expected to have lower permeability and porosity than the younger Mesozoic rocks. The age of bedrock is expressed by the percentage of rocks that are younger than Cambrian in the watershed (Table 1). The age of the bedrock has a significant correlation (p = 0.00003) with the WFI (Figure 11b). Generally, the northern Rockies watersheds have the oldest bedrock and lowest WFI, whereas the southern Rockies watersheds, having the youngest bedrock, have the highest WFI.

Discussion

Effects of topography and geology on winter flow

Winter flow was uncorrelated with the mean flow in the previous year (Figure 6), as well as with precipitation in previous summer and fall seasons (data not shown), indicating that groundwater discharge during winter months in each watershed is largely controlled by the stationary factors, such as topography and geology, and the inter-annual variability in rain and snowmelt input has minor effects. The influence of topography on mountain streams has been demonstrated in previous studies. For example, in steep terrain, the depth to water table can be a subdued replica of the surface topography, thereby affecting the runoff response (Vivoni et al. 2007; Welch and Allen 2012). Payn et al. (2012) found that during the snowmelt period, more shallow flow paths are hydrologically connected to streams, therefore increasing the influence of topography on baseflows. Furthermore, Welch and Allen (2014) suggest topographic controls, such as the location of ridges and valleys, influence the position of bedrock groundwater flow divides and contributing areas.

The effects of topographic factors (i.e. slope, hypsometry and drainage density) appear to be discernible when they are compared with winter flow values (Figures 10a–c), but are not discernible when they are compared with WFI. The correlations in Figures 10a–c are entirely dependent on the cluster of watersheds in Columbia Mountains, which receive much higher precipitation inputs than other regions (Figures 1 and 7). Therefore, it is likely that the regional climatic variability has an overwhelming influence on winter flow, and the apparent correlations in these figures do not represent a cause–effect relation.

Among the three topographic parameters examined in this study, statistically significant (p < 0.05) correlations were found between HI and drainage density, and between HI and average slope. In general, the watersheds in the Columbian Mountains had relatively high HI and slope, and low drainage density. Conversely, those in the southern Rockies had low HI and slope, and high drainage density (Table 1). These regional differences likely reflect the differences in the interactions among various geomorphological processes reflecting the tectonic and climatic setting of each region. However, the discussion of geomorphological processes is beyond the scope of this study.

The age of bedrock appears to have some influence on the groundwater hydraulics in the study region, as the WFI has a significant correlation with the age of bedrock (Figure 11b). The older Cambrian rocks are dominated by quartzite, and other weathering-resistant rocks, and are expected to have lower porosity and permeability compared to the younger rocks. This may be influencing the higher WFI of the watersheds with younger rocks, particularly in the southern Rockies watersheds which are dominated by Triassic and younger sedimentary rocks. The high winter flow of the southern Rockies watersheds may be influenced by winter rain (Figure 5), but the effect is expected to be relatively minor (< 0.05 mm d^–1).

Scale of measurements

Geology affects the hydraulic properties (e.g. conductivity) of aquifers, and topography affects the hydraulic gradient. Therefore, both geology and topography were expected to influence the winter flow fed by groundwater discharge. However, only geology appeared to have a discernible effect on the WFI (Figure 11b). The apparent lack of topographic effects may be related to the scale of measurements, or the size of watersheds examined in this study. The effect of local slopes may be significant in first-order watersheds (< 10 km²), but it may not be observable in larger watersheds (10²–10³ km), where the contributions from individual slopes are averaged out and buffered by the complex interaction between slopes and stream channels. In contrast, the bedrock geology affects a large region at a scale comparable to the area of higher order watersheds.

Another explanation is related to the focus of this study on the winter period. It is possible that the hydraulic gradient (i.e. slope) has a strong control on the drainage of groundwater recharged by snowmelt and rain during the summer and fall, but its effect decreases as the groundwater storage reservoir becomes depleted in the winter. In contrast, geology has a strong influence on the storage capacity of aquifers through porosity. Therefore, the watersheds with younger bedrocks and higher porosity may have higher storage capacity, which sustains relatively high winter flow, resulting in the high WFI. Surficial sediments commonly found in alpine environments include talus, moraine and alpine meadows, which can have the potential to store significant amounts of groundwater (e.g. Clow et al. 2003; Hood and Hayashi 2015). Unfortunately, however, limited data were available for the distribution of surficial sediments within the study area, and thus their influence on winter flows could not be directly analyzed. It is expected that bedrock geology (e.g. hard quartzite in older formations vs. soft shale in younger formations) has an indirect influence on surficial geology.

Spatial consistency of baseflow

The mean annual flow of rivers examined in this study had a large variability ranging from 1 mm d^–1 to over 4 mm d^–1, equivalent to annual discharge of 400 mm to 1500 mm, and reflecting the large variability in precipitation inputs (Figure 1). Despite the large variability in mean annual flow, winter flows in the majority of watersheds are confined to a narrow range between 0.2 and 0.6 mm d^–1 (Figure 7). Winter flow in mountainous environments is provided by groundwater stored in aquifers including bedrock fractures, talus/moraine units and soils. With this in mind, winter flow is likely controlled by the aquifer hydraulic properties and the gradient that drives groundwater flow. This study attempted to determine the key factors controlling the groundwater flow, but the effects of these factors were not clear. The interplay between material property (i.e. geology) and gradient (i.e. topography) likely has a strong influence on groundwater discharge. In addition, the spatial integration of heterogeneous processes, such as infiltration, storage and groundwater flow, likely plays an important role in the consistency of baseflow at a large watershed scale. Insights into such processes may be gained from numerical experiments using two- or three-dimensional groundwater flow models (e.g. Haberlandt et al. 2001; Tague and Grant 2009; Welch and Allen 2012) and their comparison with field-based hydrological observations in first-order watersheds.

Possible effects of climate warming

This study investigates the sensitivity of groundwater discharge to topography, geology and other physiographical factors by examining winter (January–February) flow, which is least affected by the variability in air temperature and precipitation. There was no temporal trend in winter flow in most of the watersheds over the duration of records (25–100 years; Table 3). Throughout the entire study area, annual mean temperatures as well as average January–February temperatures all had significant increases during the period of record (Table 2). Although winter temperatures are still well below 0°C, a shift in snow/rain ratio, as a result of increasing temperatures, may cause winter rainfalls to increase above 80 mm, which has been shown to increase winter baseflow (Figure 5). Currently, the southern Rockies have the highest winter rainfall amounts and, as such, the watersheds within this region may provide early indication of climate change effects on winter baseflow. Although the influence of winter rainfall is relatively small (< 0.05 mm d^–1), as estimated from Figure 5, this may continue to increase in the southern Rockies and also extend to the Columbia Mountains and northern Rockies. Therefore, similar to the findings of previous studies (Zhang et al. 2001; Rivard et al. 2009), we find that future winter flows may increase as a result of increased winter rainfall. This may be accompanied by decreased snowpack development and reduction in summer baseflow.

Conclusions

Stream flows within the Canadian Rocky and Columbia Mountains are almost entirely sustained by the groundwater released from storage during the winter months of January and February, when there is no input of atmospheric water except for rare mid-winter rain storm events. Therefore, analyzing the spatiotemporal variability of winter flow in the mountainous watersheds is expected to reveal valuable information about groundwater in alpine and subalpine environments. This study attempted to explore the variability of groundwater flow and storage characteristics in 18 watersheds using the winter-flow analysis. Winter flows were confined within a narrow range of 0.2 to 0.6 mm d^–1 for all the watersheds, and had a relatively small inter-annual variability in contrast to a large inter-annual variability of spring and summer peak flows. Most of the watersheds did not show significant correlations between winter flow and the previous year's mean flow, which reflected the rain and snowmelt input during the spring and summer. This suggests that the groundwater storage is filled up to the maximum capacity every year, and the groundwater discharge in winter is mostly controlled by the stationary factors such as the spatial variability of climate, geology, and topography. This follows the “fill and spill” conceptual model, in which subsurface flow occurs when bedrock depression storage is filled and overflows (Tromp-van Meerveld and McDonnell 2006). Therefore, ample spring snowmelt and summer precipitation annually fill bedrock depression storage and provides consistent winter baseflow.

Long-term mean winter flows were strongly correlated with long-term mean annual flows, where the latter represents an integrated measure of the average hydrological input to the watersheds. Winter flows and mean annual flow were both greater in the watersheds within the Columbia Mountains, where long-term mean annual precipitation were two to three times higher than in the Rockies. These indicate the dominant control of the climatic gradient on winter flow and hence, groundwater discharge. For the analysis of non-climatic factors, the dominant influence of climate is removed by using the ratio of winter flow to annual flow (i.e. winter flow index, WFI). Topographic factors, such as slope and hypsometry, did not have a significant correlation with the WFI, indicating that local effects of topography influencing hydraulic gradient may be averaged out at the scale of watersheds examined in this study (21–3900 km²). The type of bedrock had a significant correlation with the WFI, whereby the watersheds underlain by younger bedrocks having generally higher permeability and porosity had higher values of the WFI. Indicating, as expected, that bedrock geology influences the hydraulic properties of aquifers, at the scale comparable to the size of watersheds.

This study was not able to offer a clear understanding of the hydrogeological processes controlling the consistent groundwater fluxes in the alpine and subalpine regions. However, it pointed out the need for future studies to elucidate the interplay between geological and topographical factors and the effects of integration of small-scale heterogeneity.

Acknowledgements

We thank David Hutchinson and Dennis Lazowski (WSC) for providing the gauging station information, Evan Mutual and Igor Pavlovskii for GIS assistance, and Brian Menounos and Roger Wheate for glacier cover data. Constructive comments by the editor and two anonymous reviewers improved the quality of the paper. This study was funded by the Natural Sciences and Engineering Research Council of Canada through the Discovery Grant and Climate Change and Atmospheric Research Grant (Changing Cold Regions Network).