Dynamics of groundwater floodwaves and groundwater flood events in an alluvial aquifer

Abstract

In gravelly floodplains, streamflood events induce groundwater floodwaves that propagate through the alluvial aquifer. Understanding groundwater floodwave dynamics can contribute to groundwater flood risk management. This study documents groundwater floodwaves on a flood event basis to fully assess environmental factors that control their propagation velocity, their amplitude and their extension in the floodplain, and examines the expression of groundwater flooding in the Matane River floodplain (Québec, Canada). An array of 15 piezometers equipped with automated level sensors and a river stage gauge monitoring at 15-minute intervals from September 2011 to September 2014 were installed within a 0.04-km² area of the floodplain. Cross-correlation analyses were performed between piezometric and river-level time series for 54 flood events. The results reveal that groundwater floodwave propagation occurs at all flood magnitudes. The smaller floods produced a clear groundwater floodwave through the floodplain, while the largest floods affected local groundwater flow orientation by generating an inversion of the hydraulic gradient. Propagation velocities ranging from 8 to 13 m/h, which are two to three orders of magnitude higher than groundwater velocity, were documented while the induced pulse propagated across the floodplain to more than 230 m from the channel. Propagation velocity and amplitude attenuation of the groundwater floodwaves depend both on flood event characteristics and the aquifer characteristics. Groundwater flooding events are documented at discharge below bankfull (< 0.5 Qbf). This study highlights the role of flood event hydrographs and environmental variables on groundwater floodwave properties and the complex relationship between flood event discharge and groundwater flooding. The role that groundwater floodwaves play in flood mapping and the ability of analytical solutions to reproduce them are also discussed.

Les crues provoquent la propagation d’ondes phréatiques dans les aquifères alluviaux. Comprendre la dynamique des ondes phréatiques peut contribuer à la gestion des risques d’inondation par rehaussement de la nappe. Cette étude documente des ondes phréatiques à l’échelle événementielle pour évaluer les facteurs environnementaux contrôlant leur vitesse de propagation, leur amplitude et leur extension dans la plaine alluviale, et examine des inondations par rehaussement de la nappe dans la plaine alluviale de la rivière Matane (Québec, Canada). Quinze piézomètres équipés de capteurs de pression hydrostatique et une station de jaugeage ont été installés dans une portion de la plaine alluviale et la rivière Matane. Les mesures ont été prises toutes les 15 minutes de Septembre 2011 à Septembre 2014. Les corrélations-croisées entre les niveaux piézométriques et de la rivière de 54 événements de crues révèlent la propagation d’une onde phréatique à toutes les crues. L’étude du gradient hydraulique révèle que les plus grandes crues engendrent également une inversion de l’écoulement souterrain dans la plaine. Des vitesses de propagation de 8 à 13 m/h, soit de deux à trois ordres de grandeur plus élevés que l’écoulement de l’eau souterraine, sont observées et se propagent à travers la plaine à plus de 230 m de la rivière. Des événements d’inondation par rehaussement de la nappe sont documentés à des événements de crues bien en dessous du niveau plein bord. Cette étude met en évidence le rôle de la forme des hydrogrammes et des variables environnementales sur les ondes phréatiques et révèle la relation complexe entre l’amplitude des crues et les inondations par rehaussement de la nappe phréatique. Le rôle des ondes phréatiques pour la cartographie des inondations par rehaussement de la nappe et la capacité des solutions analytiques pour les reproduire sont également discutés.

Introduction

Hydrostatic and hydrodynamic processes govern a wide range of interactions between surface water and groundwater in gravelly floodplains. Among the interactions that occur between the groundwater and surface water is the groundwater floodwave that propagates through floodplains following rapid changes in river stage. The mechanisms of hydraulic pressure head propagations through floodplain environments have been discussed by previous studies (Sophocleous 1991; Vekerdy and Meijerink 1998; Jung et al. 2004; Lewandowski et al. 2009; Vidon 2012; Cloutier et al. 2014). The pressure wave effect was revealed by observations of rapid changes in groundwater levels due to flood events at distances from the river that cannot be explained by Darcian velocities. Several authors have observed propagation velocities that are two to three orders or magnitude higher than groundwater velocities (Jung et al. 2004; Lewandowski et al. 2009; Vidon 2012; Cloutier et al. 2014). Groundwater floodwaves can be interpreted either as kinematic waves (i.e. Jung et al. 2004) or as dynamic waves (Vekerdy and Meijerink 1998; Cloutier et al. 2014), depending on the dispersive and diffusive behaviour of the floodwave propagation.

Groundwater floodwaves are part of the hydrological response of a river corridor. They can indicate the degree of wetland-to-river connectivity where the floodplain material is highly permeable (Larocque et al. 2015, this issue), they are critical in revealing the occurrence and duration of intense biogeochemical transformations (Vidon 2012), and they are a key element in the delineation of groundwater flooding (Cloutier et al. 2014). Groundwater flooding has no substantial effect on river or floodplain morphology, but it is typically of a longer duration than overbank flooding and can find its way into basements as well as block roads and railways. Groundwater flooding is largely recognized as a flooding process that can cause severe consequences to man-made infrastructures in chalk systems (e.g. Finch et al. 2004; Cobby et al. 2009), and groundwater hazard and risk maps are available for such consolidated aquifers (Hughes et al. 2011). However, groundwater flooding from an alluvial aquifer connected to high river levels is still a poorly understood flooding process (Macdonald et al. 2012) in comparison with processes such as overbank flooding and ice- or log-jam flooding, which perform geomorphic work on floodplains that provides evidence for assessing the extent of flooded areas (Demers et al. 2014). Furthermore, groundwater flooding may occur far beyond the hyporheic zone, where there is no direct groundwater–surface water connection (Mertes 1997). Groundwater flooding can be due to the propagation of groundwater floodwave when the water table rise is greater than the thickness of the unsaturated zone. Groundwater flooding is controlled by factors that include floodplain morphology, the initial thickness of the unsaturated zone, hydraulic properties of the floodplain geology, and groundwater inflow from a regional aquifer (Macdonald et al. 2012). Morphological units such as abandoned channels, overflow channels or swales represent floodplain features susceptible to groundwater flooding. These units are generally below bankfull levels and can be considered negative reliefs (Lewin and Ashworth 2014); they may be saturated prior to the streamflood crest. A better understanding of groundwater floodwave propagation is needed to determine the extent and frequency of groundwater flooding in alluvial aquifers.

Groundwater floodwaves have been documented using both field studies (Lewandowski et al. 2009; Vidon 2012; Cloutier et al. 2014) and analytical solutions (Ha et al. 2008; Dong et al. 2013). Using arrays of piezometers, Vidon (2012) and Cloutier et al. (2014) studied the groundwater level fluctuations in response to a series of flood events in the sandy floodplain of Fishback Creek (Indiana, USA) and in the gravelly floodplain of the Matane River (Québec, Canada), respectively. In these unconfined aquifers, they showed that groundwater level rises occurred at a time lag that was proportional to the distance between a piezometer and the river. This finding was explained by the presence of a groundwater floodwave controlled by river stage rather than by precipitation. Cross-correlation analysis between precipitation and groundwater levels showed significantly lower correlation values (R = 0.2–0.3) than those from cross-correlation analysis between river stage and groundwater levels (R > 0.9; Cloutier et al. 2014). Both studies also revealed that groundwater floodwave amplitudes decrease with distance from the river bank, but that the ratio of river stage amplitude to groundwater amplitude was independent of the flood event magnitude and that a hydraulic gradient inversion occurs at the highest flood events. In confined aquifers, pressure transfer is almost instantaneous compared to in unconfined aquifers where lags can be much higher (Lewandowski et al. 2009) and propagation slower (Vekerdy and Mejerink 1998). In the unconfined Matane River aquifer, the propagation velocity remains relatively constant but is affected by conditions of the unsaturated zone before a flood event (Cloutier et al. 2014).

Using analytical solutions, Ha et al. (2008) showed that the shape of flood hydrographs plays an important role in bank storage and discharge. The shape of flood hydrographs is strongly related to environmental factors, ranging from drainage basin areas to rainfall structures. They suggest that river water infiltration into the aquifer and bank storage increase with river stage and flood duration. Similarly, Dong et al. (2013) suggested that the difference in response time might result from different hydrographic geometries such that rapid river stage variations will promote quicker groundwater responses. The shape of hydrographs generated by analytical solutions are generally asymmetrical but they rarely consider the full complexity of natural and successive flood events. However, propagation velocity is not only related to the geometry of the flood hydrograph. Using analytical solutions, Dong et al. (2013) showed that the propagation velocity of groundwater floodwave is proportional to the aquifer diffusivity as well as the distance at which the wave propagates in the floodplain. They calculated propagation velocities from 0.5 to 8 m/h for aquifer diffusivities from 0.4 to 50 m²/h, respectively.

Field studies and analytical solutions highlight the need to fully assess the role of environmental factors through the use of field data on propagation velocity, amplitude and the lateral extent of the groundwater floodwave (Ghasemizade and Shirmer 2013). The aim of this study is to document the key properties of groundwater floodwaves in a gravelly alluvial aquifer. While Vidon (2012) and Cloutier et al. (2014) focused on seven flood events, this study analyses a 3-year data set that includes 54 flood events. The study relies on time series analysis of hydraulic heads measured at 15 locations in the floodplain. The large number of flood events provides a wide array of conditions from which to identify the key factors influencing groundwater floodwaves. The role that groundwater floodwaves play in flood mapping and the ability of analytical solutions to reproduce them are discussed.

Materials and methods

Study site

The Matane River valley is located on the northwest portion of the Gaspé Peninsula, in eastern Québec, Canada (Figure 1a). The Matane River system is a 1678-km² basin flowing from the Notre-Dame mountain range to the south shore of the St. Lawrence Estuary. The flow regime of the Matane River is nivo-pluvial, with two periods of high discharges, the first occurring at snowmelt in May and the second occurring in the fall when rain events are more frequent and vegetation less active. Bankfull discharge (Q_bf) is estimated at 350 m³/s, the mean annual river discharge is 39 m³/s (1929–2009) and the minimum discharge (considered as baseflow) is on the order of 5 m³/s. Discharge values are available from the Matane gauging station operated by the Centre d’expertise hydrique du Québec (CEHQ 2014; station 021601). The climate normal for the 1981–2010 period indicates an average daily temperature of 2°C and total annual precipitation of 1032 mm (Environment Canada 2014; Amqui station). For the 3-year study period (2011–2014), the average daily temperature was 3°C while the average annual total precipitation was 1052 mm (Ministère du Développement durable, de l’Environnement et de la Lutte contre les changements climatiques 2014; station 7057692).

Figure 1. Location maps for (a) the Matane River basin, Québec, Canada; (b) the study site within the coarse sand/gravelly floodplain; and (c) the piezometers within the study site. The names of the piezometers reflect the perpendicular distance (in m) from the Matane River. The river stage sensor and the automatic camera are indicated. asl: above sea level.

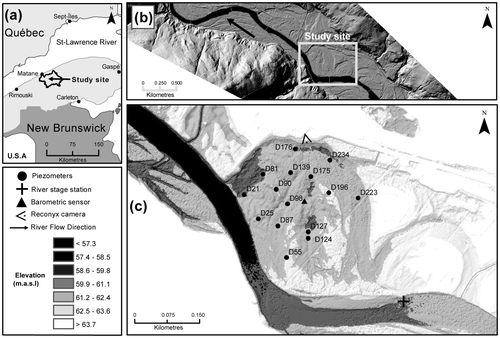
The lithology of the Matane valley is deformed sedimentary rock associated with the Appalachian orogenesis from the Cambro–Ordovician period. The irregular meandering planform flows into a wide semi-alluvial valley cut into recent fluvial deposits (Figure 1b; Lebuis 1973; Marchand et al. 2014). The entire floodplain of the Matane River consists of gravel deposits from lateral migration of the meandering river on top of which thin layers of overbank deposits are found. The mean channel and valley widths are 55 m and 475 m, respectively, and the average river gradient is 0.2 (m/100 m). According to borehole data from the valley floor, the average unconsolidated sediment thickness is 49 m. The entire alluvial aquifer of the Matane valley is an unconfined coarse sand/gravel and pebble aquifer with a mean saturated thickness of 46 m, except near the city of Matane, where the alluvial aquifer is overlaid by a 30-m-thick silty/clay marine deposit.

The study site, located 28 km upstream from the estuary (48°40'5.678"N, 67°21'12.34"W), is characterized by an elongated depression that corresponds to the abandoned channel and a few overflow channels (Figure 1c). These morphologic features are part of the wetland, and its characteristics are fully described in Larocque et al. (2015, this issue). The floodplain is very low, with the deepest parts of the depression being lower than the river water level at discharges well below bankfull. The mean groundwater level at the study site is 58.8 m above mean sea level, whereas the average surface elevation of the floodplain is 60.4 m above sea level, i.e. the average unsaturated zone is 1.6 m. A borehole next to the study site revealed that the unconfined alluvial aquifer thickness is 47.4 m overlying a 7 m till deposit over the bedrock. The aquifer consists of coarse sands and gravels covered by overbank sand deposit layers of variable thickness, from 0.30 m at the top of high ground to 0.75 m within abandoned channels. At the regional scale, equipotential lines follow those of the topography; thus, the Matane River is draining the regional aquifer. At the study site, the Matane River is a gaining stream, i.e. the groundwater flow gradient is towards the river. However, hydraulic gradients can change drastically, whilst the gradient can temporarily be from the river towards the valley wall at high flows (Cloutier et al. 2014).

Data collection

An array of 15 piezometers equipped with pressure sensors were installed in a 0.04-km² area on the study site (Figure 1c). The piezometers were made from 38 mm polymerized vinyl chloride (PVC) pipes sealed at the base and equipped with a 0.3-m screen at the bottom end. At every location, piezometers reached 3 m below the surface, but because of the surface microtopography, the piezometer bottoms reached various depths within the alluvial aquifer (Table 1). However, the bottom end would always be at or below the elevation of the river bed (58.4 m). Piezometer locations and altitudes were determined using a Magellan ProMark III differential global positioning system (GPS). At each location, hydraulic conductivities (K) were derived from slug tests using the Hvorslev (1951) method. Hydraulic diffusivity (D) was estimated from the ratio of transitivity (T = Kb, where b = saturated thickness) to the storage coefficient (S). Automated level loggers (Hobo U20-001) recorded groundwater levels every 15 minutes from 1 September 2011 to 10 September 2014 (3 hydrological years) and from 6 July 2012 to 10 September 2014 (2 hydrological years) for 10 and five piezometers, respectively. Table 1 shows the period of operation of each pressure sensor, and the proportion of valid data. A river stage gauge was installed in the upstream section of the study site where river banks and bed are stable (Figure 1c), and recorded water levels every 15 minutes from September 2011 to September 2014. The upstream location of the river gauge implies that the water level in the river will always be at a higher elevation than the water table elevation that is measured within the study site. Time series were corrected for barometric pressure from a barologger located at the study site (Figure 1c). Finally, an automatic camera (Reconix Hyperfire PC800) was installed in January 2013 to monitor the presence of water on the floodplain surface (Bertoldi et al. 2012). The camera was installed to focus on the depression in the eastern section of the study site (Figure 1c). Pictures were taken every hour during the sampling period.

Table 1. Sampling and physical properties for the 15 piezometers installed at the study site. The names of the piezometers refer to the perpendicular distance of the sensors to the river bank (in m).

Piezometer	Sampling dates		Sampling period	Valid data	Surface elevation	Sensor depth	Hydraulic conductivity	Hydraulic diffusivity
	From	To	(y)	(%)	(m asl)	(m)	(m/s)	(m^2/h)
D21	01 09 2011	10 09 2014	3.0	99.9	59.65	2.93	0.0002	170
D25	07 09 2011	10 09 2014	3.0	99.9	60.55	2.85	0.0002	166
D55	01 09 2011	10 09 2014	3.0	97.2	61.18	2.95	0.0003	237
D81	01 09 2011	10 09 2014	3.0	99.9	59.62	2.80	0.0007	564
D87	12 12 2011	10 09 2014	2.8	82.4	60.97	2.92	0.0009	758
D90	06 07 2012	10 09 2014	2.2	99.9	60.96	2.89	0.0032	2713
D98	06 07 2012	10 09 2014	2.2	99.9	59.88	3.00	0.0008	695
D124	06 07 2012	10 09 2014	2.2	99.9	59.90	1.45	0.0024	2005
D127	01 09 2011	10 09 2014	3.0	99.9	59.99	1.80	0.0013	1084
D139	07 09 2011	10 09 2014	3.0	99.9	60.83	2.75	0.0008	724
D175	01 09 2011	10 09 2014	3.0	99.9	60.03	2.98	0.0006	527
D176	01 09 2011	10 09 2014	3.0	98.0	59.51	2.80	0.0002	179
D196	06 07 2012	10 09 2014	2.2	99.9	61.04	2.70	0.0001	124
D223	01 09 2011	10 09 2014	3.0	99.9	60.31	2.75	0.0002	177
D234	06 07 2012	10 09 2014	2.2	99.9	59.95	2.88	0.0003	294
						Median	0.0006	527
					Interquartile range		0.0007	563

asl: above sea level.

Data analysis

Figure 2a shows the river stage time series and selected groundwater level time series from three piezometers located at various distances from the river for the 3-year sampling period. River stages values are higher than the water table values because of the upstream location of the river gauge. A strong correlation can be observed between groundwater levels and river stage at a wide range of flood magnitudes. Figure 2b shows for a shorter time period that there is an increasing time lag with distance from the river between the maximum groundwater level and the maximum river stage. Surface water–groundwater interactions and floodwave propagation in floodplain environments have been studied using analytical solutions (Cooper and Rorabaugh 1963; Vekerdy and Meijerink 1998; Ha et al. 2008; Dong et al. 2013), principal component analysis (Lewandowski et al. 2009), cross-correlation analysis (Cloutier et al. 2014; Larocque et al. 2015, this issue) and numerical modelling (Sophocleous 1991; Bates et al. 2000). Cross-correlations are widely used to quantify (1) the intensity of the relationship between river stage and groundwater levels and (2) the time lag between the maximum groundwater levels and the maximum river stage (Larocque et al. 1998; Vidon 2012; Cloutier et al. 2014). A cross-correlation can be computed for the entire time series (Larocque et al. 2015, this issue) or for an individual flood event (Cloutier et al. 2014), thus providing information on different scales of interactions between groundwater and surface water.

Figure 2. Time series for (a) river stage and groundwater levels at three locations in the floodplain for the entire sampling period; (b) river stage and groundwater levels at three locations in the floodplain for a 2-month period – three selected flood events are indicated using black triangles. Selected flood events for the cross-correlation analysis are indicated using a black triangle at the time of the peak flow. The water level in the river is at a higher elevation than the water table elevation measured within the study site because the river gauge is located slightly upstream from the site. masl: metres above sea level.

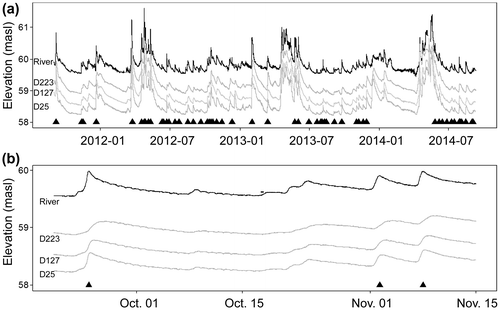
Here, cross-correlation analyses between the river stage and groundwater levels at every location were undertaken for individual flood events. Flood events were selected based on a significant change of river stage (> 4 cm), a minimum duration (> 60 h) and a minimum rising limb duration (> 10 h). The end point of a flood event was determined from either the beginning of a new event or the return of the flow stage to pre-event values. Care was also taken to avoid complex responses due to multiple rain events occurring over short time intervals. As an example, Figure 2b illustrates three flood events selected and the other three flood events rejected between 20 September and 15 November 2013. In this example, flood events before and after 15 October were not selected because of small changes in river stage or because of a complex river stage response. Using these criteria, 54 flood events were selected for the cross-correlation analysis (Figure 2a). Median flood event duration, median rising limb duration and median river stage amplitude for the 54 flood events were 200 h, 27 h and 0.34 m, respectively.

For each selected flood event, the time lag at which the maximum correlation (r_{xy_max}) occurred between groundwater level and river stage was extracted for each piezometer. The relationship between the time lag at r_{xy_max} and the perpendicular distance from the piezometer to the river allows computation of the velocity at which the crest of the floodwave propagates through the aquifer (Cloutier et al. 2014). Because of the large number of flood events considered in this study, velocity propagation was examined in relation to characteristics of the flood events, including initial river and groundwater levels, length of the rising limb, maximum river stage reached during the flood, flood duration, time since the previous flood event and amplitude, i.e. the maximum river stage minus the initial river stage.

Hydraulic heads were used to compute hydraulic gradients in the floodplain. Vidon (2012) and Cloutier et al. (2014) illustrated the inversions of hydraulic gradient in the floodplain at high river stages using piezometric maps at specific time steps during a flood event. Here, linear regressions between groundwater levels recorded at all piezometers and the perpendicular distance to the river were calculated at every time step to produce continuous time series of hydraulic gradients. Positive gradients indicate that groundwater levels increase towards the valley side and thus that the floodplain is discharging in the river (gaining stream); negative gradients indicate that bank storage is in process (losing stream). The use of all groundwater levels represents a way to integrate the water-level fluctuations within the entire floodplain.

The occurrence of groundwater flooding was evaluated using the difference between the water level recorded by the automated level loggers in the piezometers and the topography at each piezometer location. A positive value suggests that there is water above the ground. When this occurs, it is assumed that the water on the surface is the expression of high water table since the floodplain is fully saturated at the piezometer location. The automatic camera was used to confirm the presence of water at one location on the study site. Groundwater levels are mapped for the flood event, allowing visualization of the spatial extent and depth of groundwater flooding. Similar methods using topographic depression and water levels were used by Macdonald et al. (2012) to map the extent and location of groundwater flooding.

Results

Propagation velocities from cross-correlation analysis

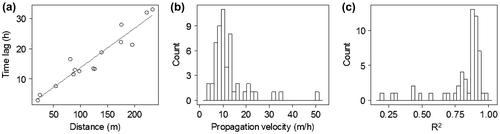
Propagation velocity was computed for all 54 flood events. Figure 3a shows a typical relationship between the time lag of r_{xy_max} and the perpendicular distance to the river for a flood event. The linear relationship is highly significant (R² = 0.91, p < 0.01) and has a slope of 0.13 h/m. The propagation velocity is given by the inverse of the slope, which for this event becomes 7.7 m/h. Seventy-five percent of all flood events have an R² higher than 0.80 while the median value for all flood events is 0.88 (Figure 3b). The strong linear relationship between time lag and distance supports the use of the slope as an estimation of propagation velocity for most flood events. The median propagation velocity is 10.4 m/h, while 50% of the propagation velocities lie between 8.2 and 13.5 m/h (Figure 3c).

Figure 3. (a) Time lags at which the maximum correlation occurred for a single flood event between the river stage and the groundwater level time series, in relation to the distance from the river bank where the groundwater was measured for all piezometers (n = 15) of the study site. The inverse of the slope represents the propagation velocity. (b) Distribution of propagation velocities for the 54 flood events as computed from the relationship between the time lag of r_{xy_max} and distance from the river bank. (c) Distribution of the coefficients of determination (R²) from the linear relationship between the time lag of r_{xy_max} and the distance from the river bank for the 54 flood events.

Propagation velocity can also be computed by averaging the time lags for all flood events at each piezometer (Figure 4a). There is a strong linear relationship between the averaged time lags and distance from the river (R² = 0.93, p < 0.01). The propagation velocity computed from the slope of the relationship is 9.7 m/h, and the strong linear relationship suggests that the propagation velocity is relatively constant throughout the floodplain.

Figure 4. Mean (of the 54 flow events) time lags at which the maximum correlation was measured from cross-correlation analysis between river stages and groundwater levels for all 15 piezometers: (a) using the perpendicular distance between the piezometers and the river bank; (b) using the upstream distance between the piezometer and the river bank. The error bars represent the 95% confidence interval.

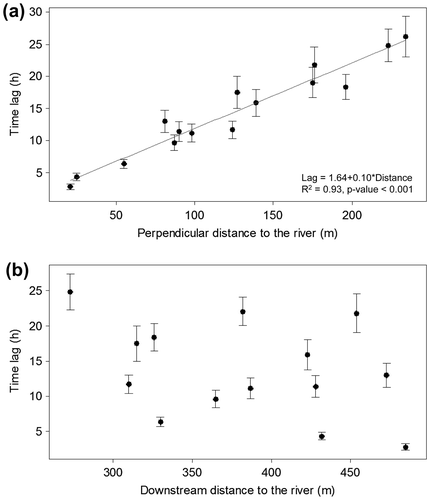
The meander configuration at the study site (Figure 1c) suggests that the floodwave could also be travelling from upstream to downstream within the floodplain. To investigate this displacement, Figure 4b presents the distribution of averaged time lags when plotted against the downstream distance between the river bank and the piezometers on the floodplain. No pattern emerges from the scatter of points, and it seems clear that the main advection pattern during flood events is perpendicular to the river towards the valley side.

Groundwater floodwave amplitude attenuation

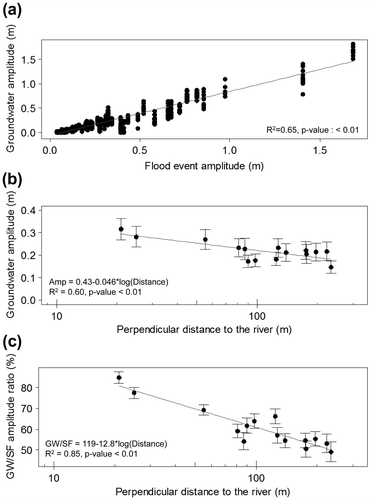
Figure 5 illustrates ways to look at amplitude attenuation as the floodwave propagates thorough the floodplain. A strong relationship exists between the groundwater amplitude and the flood event amplitude for all flood events and all piezometers (R² = 0.65, p < 0.01; Figure 5a). There is significant attenuation of the groundwater amplitude recorded within the floodplain with distance from the river bank (R² = 0.60, p < 0.01; Figure 5b). The groundwater amplitude decreases logarithmically from 0.30 m at 25 m to 0.20 m at nearly 200 m from the bank. To examine the river stage amplitude for each flood event, Figure 5c plots the ratio of groundwater to river stage amplitude in relation to the piezometer’s distance from the bank. The logarithmic relationship is significant (R² = 0.85, p < 0.01), and suggests that the groundwater amplitude tends towards 50% of the flood event amplitude at the outer piezometers of the study site.

Figure 5. (a) Groundwater amplitude fluctuations in relation to the river stage amplitude for the 54 selected flood events. For each river stage amplitude, groundwater amplitudes for the 15 piezometers are shown. (b) Mean groundwater amplitudes (of the 54 flow events) recorded by the piezometers as a function of the perpendicular distance of the piezometers from the river banks for all 15 piezometers. (c) Mean ratio of groundwater amplitude (GW) to the river stage amplitude (SF) for the 54 selected flood events as a function of the perpendicular distance from the river banks for all 15 piezometers.

Flood event characteristics and floodwave propagation velocities

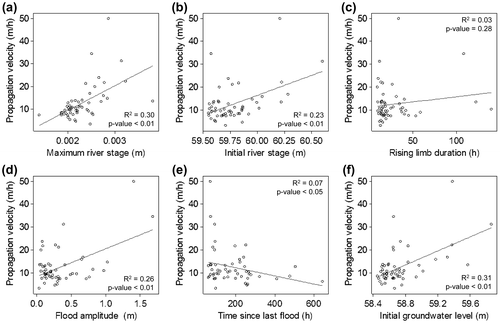
Figure 6 shows the groundwater floodwave propagation velocities in relation to flood event characteristics. For illustration purposes, linear models are drawn on the scatter plots. Propagation velocity appears to be positively related to maximum (R² = 0.30, p < 0.01) and initial (R² = 0.23, p < 0.01) river stage, with flood amplitude (R² = 0.26, p < 0.01) and with initial groundwater level (R² = 0.31, p < 0.01). However, propagation velocity is inversely related to the time since last flood (R² = 0.07, p < 0.05) and has no significant relationship with the rising limb.

Figure 6. Dispersion diagrams showing propagation velocity with flood event characteristics for the 54 flood events: (a) maximum river stage, (b) initial river stage, (c) rising limb, (d) flood amplitude, (e) time since last flood, and (f) initial groundwater level.

Relationships between propagation velocity and flood event characteristics are relatively weak and are mainly influenced by the extreme values of the scatter plot. Furthermore, flood event characteristics are strongly related to each other (for example, flood amplitude is strongly linked to maximum river stage). It is thus difficult to consider them separately. To consider the role of a combination of flood event characteristics, flood events for the entire study period were classified by season of occurrence. Classifying the flood event by season represents the integration into one variable of several factors affecting the groundwater floodwave propagation.

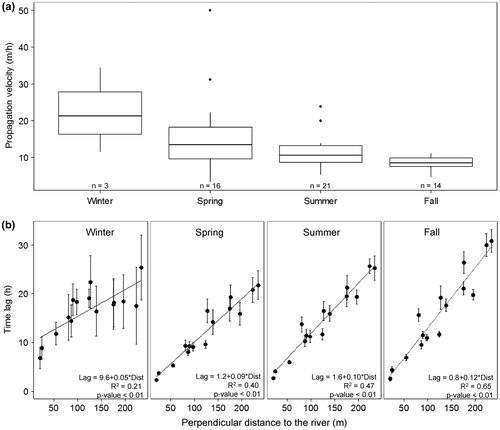
When considering the distribution of propagation velocities according to the seasons for all flood events (Figure 7a), winter must be interpreted carefully because only three selected flood events occurred during that season (because of the presence of an ice cover and accumulated snow generally between December and March/April) while 16, 21 and 14 selected flood events occurred during spring, summer and fall, respectively. The median propagation velocities and their seasonal variability (interquartile range) decrease from spring to fall by 37 and 80%, respectively. The groundwater floodwave velocities are larger (median = 13.4 m/h) and highly variable (interquartile range = 11.5 m/h) during spring, while being smaller (median = 8.4 m/h) and less variable (interquartile range = 2.33 m/h) during fall. Linear relationships between the time lag and the distance from the river for each piezometer and for the four seasons are shown in Figure 7b. For all seasons except winter, linear relationships are relatively strong and significant. Propagation velocities derived from the slopes are 11.1, 10.0 and 8.3 m/h for spring, summer and fall, respectively. These values are similar to those that would result from averaging the slopes from all events (Figure 7a). The decreasing trend in propagation velocity from spring to fall is particularly intriguing in light of the variability of flood event characteristics. The propagation velocities are smaller for the fall period even though maximum and initial river stages, flood amplitude and initial groundwater level are not minimal during that season.

Figure 7. (a) Propagation velocity measured for the 54 selected flood events according to their season of occurrence. (b) Mean time lag for the 54 flood events at which the maximum correlation occurs between river stage and groundwater levels, in relation to the perpendicular distance from the river banks to where the groundwater was measured according to the season of occurrence.

Hydraulic gradients

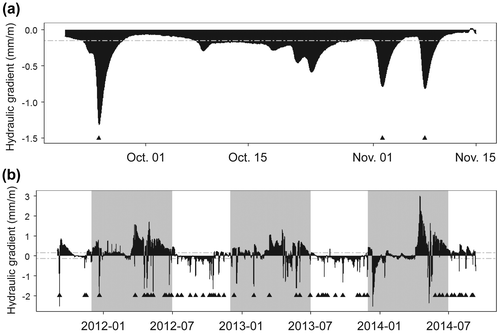
Hydraulic gradients were computed from the linear relationship between groundwater levels and distances from the river to produce a continuous time series (Figure 8). Flood events are indicated by the black triangle while the region where the hydraulic gradient is not significantly different than 0 (1 – α = 0.95) is located between the dashed lines. Figure 8a illustrates the hydraulic gradient time series for a 2-month period (the same period as shown in Figure 2b). For that period, the hydraulic gradient was mainly from the river towards the floodplain, suggesting that bank storage was occurring. The higher negative gradient during the flood event reveals the strong hydraulic gradient from the river towards the aquifer. Figure 8b shows the changing nature of exchanges between the river and the groundwater throughout the year. Considering only the hydraulic gradients that are significant (60% of the sampling period), the floodplain discharges to the river more than 69% of time while bank storage occurs 31% of the time. Bank storage, or negative gradient, occurs for a short period of time and is highly related to flood events as 41 of the 54 flood events are linked to bank storage processes. Season-wise, the floodplain is discharging to the river from December to July while bank storage is most important for flood events occurring between July and November.

Figure 8. Time series of hydraulic gradients from the linear regression for the 15 piezometers between groundwater levels and perpendicular distances from the banks for (a) a 2-month period (same period as shown in Figure 2b) and (b) the 3-year period. Negative values suggest that the hydraulic gradient is from the river towards the floodplain. The black triangles indicate flood events. The dashed lines indicate regions where hydraulic gradients are not significantly different from zero. December to July are indicated with gray areas.

Groundwater flooding

Groundwater flooding was determined to occur when the piezometers measured hydraulic head above the floodplain surface. This suggests that the unsaturated zone is reduced to zero and that water can accumulate on the top of the saturated zone, above the floodplain surface. Although the measured water levels in the piezometers represent groundwater pressure, they are assumed to also reflect groundwater flooding because of the high hydraulic conductivity of the floodplain deposits. To support this assumption, the automatic camera confirmed the presence of water above the floodplain surface for events where hydraulic head is measured as being above the floodplain surface. Figure 9a shows a picture of groundwater flooding taken during the 254-m³/s flood event that occurred from 22 April to 8 May 2014. As Matane River bankfull discharge is estimated as 350 m³/s, no overflow occurred at the study site. Water can accumulate from overland flow and precipitation, but the strong coherent patterns revealed by the floodwave propagation analysis suggest that the surface ponding is linked to the water table rising above ground level. Figure 10b illustrates the river stages at which groundwater flooding occurred on the floodplain during the study period. Eight flood events produced groundwater depth above the floodplain surface at various locations at discharges well below bankfull (Figure 9c–j), and only one flood event larger than bankfull occurred at the study site (Figure 9k). Groundwater flooding always occurred in the lowest parts of the floodplain, which includes the abandoned meander loop and the overflow channel features. The elevations of these features (Figure 1c) are below the bankfull level elevation of 60.6 m. The largest flood event (374 m³/s; Figure 9k) produced the highest expression of the water table, but no clear relationship exists between peak discharges and groundwater flow in the floodplain, likely due to the initial condition of hydraulic heads within the floodplain. For example, the 146-m³/s flood event (Figure 9e) produced groundwater flooding of a larger magnitude than that of the 182-m³/s flood event (Figure 9g).

Figure 9. (a) Groundwater flooding events revealed by a picture taken from the reconyx camera at a flood event of 254 m³/s. (b) Time series of river stages with indication of a period of groundwater flooding from hydraulic head measurements above the floodplain surface. The dashed line represents the bankfull discharge level. (c–k) Water pressure expression maps for nine flood events. The water pressure is expressed as a measure of hydraulic head measure above or below the floodplain surface. The dark gray to black shade indicates increasing increasing hydraulic head above the floodplain surface, while the light gray to white shade colours indicate the depth below the surface at which the groundwater levels are found. The bottom parts of e and j are empty due to missing data for the flow events.

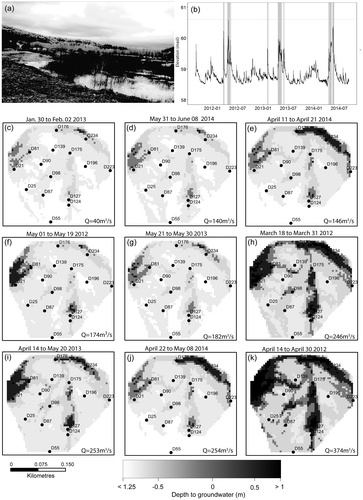
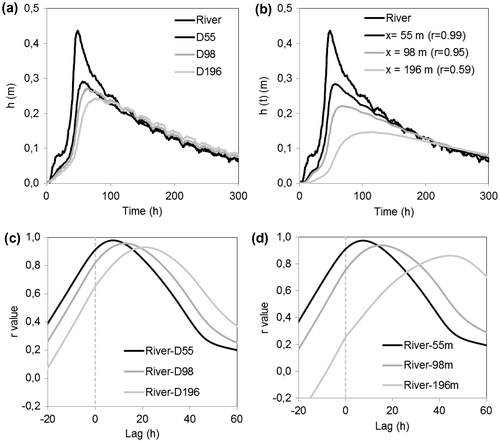
Figure 10. Water table responses to a flood event at different distances from the river: (a) measured in this study and (b) simulated using Dong et al. (2013). Cross-correlation functions between the river stage and (c) measured water table levels and (d) simulated water table levels.

Discussion

At the flood event scale, the cross-correlation analysis between the piezometric and river level time series revealed the strong interaction between groundwater and surface water in the gravelly floodplain study site of the Matane River. The analysis shows both the increasing time lag at which maximum correlation occurs and the amplitude attenuation with increasing distance from the river bank. These results indicate that the groundwater floodwave is a dynamic wave that occurs over a wide range of flood event magnitudes. From the relationship between the time lag and the location of the piezometer in the floodplain, propagation velocities ranging between 8 and 13 m/h were documented, and the induced pulse could propagate to more than 230 m from the channel across the floodplain (four times the mean channel width). Similar velocities were observed by Vekerdy and Meijerink (1998) over a floodplain of more than 8 km in width. In the phreatic aquifer of the Danube, Vekerdy and Meijerink (1998) documented propagation velocities ranging from 6 to 9 m/h, with the larger velocities being closer to the river banks. In the Matane River floodplain, the floodwave propagation velocity appears constant throughout the floodplain, but this could be due to the smaller width of the floodplain (300 m). For a smaller number of flood events (N = 7), Cloutier et al. (2014) reported propagation velocities between 7 and 12 m/h for flood events occurring in summer and fall in the Matane River floodplain. The slightly larger propagation velocities reported here could be due to the presence of several flood events occurring in spring, when the largest values are observed.

By documenting a large number of flood events, this study sheds light on two dynamics of groundwater floodwaves that are relevant for watershed management. The first dynamic is how the flood event hydrographs affect groundwater wave properties. Flood event characteristics impact the propagation velocity of groundwater floodwaves. When considered individually, maximum river level and initial groundwater level are positively related to propagation velocity. This suggests that a larger flood event will produce faster floodwave propagation, and that the higher the groundwater level in the floodplain, the faster the floodwave will propagate. It is worth noting that the rising limb does not seem to determine a significant impact on floodwave propagation velocity. Chen and Chen (2003) ran simulations of the effect of hydrograph shapes on infiltration rates and bank storage. They suggested that hydrographs with a sharp rise, a high stage and a long duration led to larger infiltration rates and larger bank storage. Thus, hydrograph properties can play an important role in the rate and volume of stream infiltration and return flow. The present study supports these simulations by highlighting the effect of flood event stages on floodwave velocity propagation. Higher velocities are likely to produce a floodwave that propagates through the entire floodplain and thus increases the bank storage zone.

Although significant variability was observed for groundwater floodwave properties (e.g. propagation velocities, groundwater amplitude), this study also revealed seasonal patterns. It was found that much of the variability in groundwater floodwave propagation velocity can be explained by a seasonal component. Grouping the events by season allows the integration of both flood hydrograph geometries and environmental characteristics. Propagation velocities were then explained by a seasonal component. Also, bank storage processes that were quantified by changes in hydraulic gradient within the floodplain appear to be of larger amplitude for flood events occurring between July and November. The results also show that amplitude attenuation followed a similar logarithmic decrease at all flood event amplitudes. This supports Vidon’s observation that groundwater levels with amplitudes high enough to affect soil biogeochemistry occurred at all flood event magnitudes (Vidon 2012).

The second dynamic relates to the complex relationship between flood event discharge and groundwater flooding in a floodplain. In the current study, groundwater flooding occurred to various extents for a total of nine flood events. This study attempted to link flood event discharges to groundwater flooding properties such as spatial distribution and depth. However, the relationship between flood discharge and groundwater flooding is complex, since groundwater flooding occurs at a variety of discharge rates below and above bankfull. Most discharges producing groundwater flooding are below the levels proposed by Cloutier et al. (2014) from linear relationships between groundwater levels and flood event discharges for the 2011 summer and fall period. The combination of initial groundwater levels and flood event amplitudes may provide an explanation of this complex relationship. Most flood event amplitudes were below 0.5 m, but many ranged between 0.5 and 1.5 m (Figure 6d), while the initial groundwater levels showed that the average unsaturated zone was 1.6 m. Since groundwater flooding occurs when the water table rise is greater than the thickness of the unsaturated zone, it is important to characterize the pre-flood unsaturated zone thickness. For instance, this emphasizes the fact that even the smallest flood event (40 m³/s [0.1 Q_bf]) caused the water table to rise above the floodplain at piezometer D176 (Figure 9). The occurrence of groundwater flooding and discharge below or above bankfull highlights the degree of connectivity between the stream and its alluvial aquifer. Most importantly, these results provide insight into the dominant factors for groundwater flooding processes in the Matane River floodplain: (1) the topography, i.e. floodplain morphological features such as abandoned meander loops or overflow channels below bankfull levels; and (2) the initial thickness of the unsaturated zone before a flood event.

Analytical solutions represent an avenue to examine the dynamics and extent of groundwater floodwave and to propose adequate strategies for groundwater flooding attenuation. As an illustration, the analytical solution proposed by Dong et al. (2013) was implemented and used with one of the flood events documented in this study. Hydraulic diffusivity (D) needs to be determined before applying the analytical solution. The median hydraulic diffusivity at the study site is 527 m²/h, while 50% of the values range between 177 and 738 m²/h (Table 1). The median hydraulic diffusivity was used in the analytical solution.

Figure 10a and b shows the selected flood event with the measured and simulated responses of the water table at 55, 98 and 196 m from the river bank (i.e. at specific piezometer locations). The simulated responses of the water table reflect the expected decreasing amplitude of the water table fluctuation and the increasing time lag with increasing distances from the river. However, it seems clear that the correspondence between the simulated and the measured water table changes decreases with distance from the river. Correlation coefficients calculated between the measured and the simulated water levels are 0.99, 0.98 and 0.86 at distances of 55, 98 and 196 m, respectively. The decreasing correspondence with distance is also revealed by the comparison of measured and simulated cross-correlation functions between river levels and piezometer levels (Figures 10c–d). Similar responses are observed at x = 55 m (max r_xy(k) of 0.978 and 0.972 for observed and simulated time series respectively, and similar delays of 7 hours for both time series), but adequacy decreases with distance from the river. Adequacy is still good at x = 96 m, although the max r_xy(k) is slightly lower and the delay is longer. At x = 196 m, the adequacy between the measured and simulated cross-correlations is significantly worse, with slightly more attenuation and a delay that is twice too long with the simulated data. As a result, the propagation velocity for the measured floodwave (10.4 m/s) is twice that for the simulated floodwave (4.1 m/s). This discrepancy suggests that the use of D = 500 m²/h is adequate for distances of up to 100 m, but that D changes beyond this distance. To obtain adequacy at the level of 55 m using the analytical solution of Dong et al. (2013), the diffusivity has to be adjusted to 1100 m²/h and 2800 m²/h for the 98 m and 196 m distances, respectively. Several factors could explain the need to adjust the diffusivity with distance from the river bank. The heterogeneity of hydraulic conductivity and diffusivity at the site (Table 1) and the orientation of the floodwave within the floodplain are two of them (Ha et al. 2007). Overall, however, the analytical solution with proper characteristics appears to be an efficient tool to document how the floodwave propagates through the floodplain, if sufficient data on the floodplain hydraulic properties are available. This suggests that the propagation and the attenuation of a groundwater floodwave, and eventually the groundwater flooding extension, could be calculated from anticipated events and hence produce groundwater flooding maps. Only one event was used here for the discussion, but the available data set would allow fully testing analytical solutions such as the one proposed by Dong et al. (2013).

Groundwater flood risk assessment in fluvial environments remains a challenge. More data and a larger array of flood events are required to fully assess the mechanisms and drivers involved in groundwater flooding, as well as to develop adequate analytical solutions. The assessment of groundwater flooding in an alluvial aquifer connected to high river levels also remains an important challenge because this flooding process can cause damage to man-made infrastructures. The high hydraulic connection between the alluvial aquifer and the river suggests dynamics from both ways, i.e. streamfloods can induce groundwater flooding, but the aquifer can drain easily at streamflood recession. A better understanding of groundwater–surface water interactions may promote the development of new management practices. For example, lateral connectivity between groundwater and surface water tends to be recognized as a groundwater–river continuum in the freedom space river management approach (Biron et al. 2014; Larocque et al. 2015, this issue). This approach applies hydrogeomorphic principles to delineate zones that are either frequently flooded or actively eroding, or that include riparian wetlands and within which rivers are left free to evolve rather than being forced to flow in a corridor shaped by human interventions.

Conclusions

The objective of this research was to the document key properties of groundwater floodwaves in a gravelly floodplain using a 3-year data set that includes 54 flood events. It was thought that analysis of a large number of flood events would reveal key factors influencing groundwater and surface water interactions in a gravelly floodplain. Cross-correlation analyses were used to document the propagation velocity of groundwater floodwaves.

The strong linear relationship between time lag and distance from the river bank during selected flood events suggests a median propagation velocity of 10.4 m/h, while 50% of the propagation velocities were between 8 and 13 m/h. Floodwave velocities were larger and highly variable during spring, while being smaller and less variable during fall. The main advection pattern during flood events is perpendicular to the river toward the valley side, and the propagation velocity is relatively constant throughout the floodplain. The logarithmic relationship of the ratio of groundwater to river stage amplitude suggests a damping effect through the floodplain by the decreased groundwater amplitude as distance from the river bank increases. Analyses of groundwater flooding reveal no clear relationship between peak discharges and groundwater flooding magnitude, but do show that low morphological features in the floodplain are vulnerable to flooding at river discharges well below bankfull.

By documenting a large number of flood events, this study sheds light on the mechanisms related to groundwater floodwaves that must be considered for watershed management: (1) the role of flood event hydrographs and environmental variables on groundwater floodwave properties; and (2) the complex relationship between flood event discharge and groundwater flooding. Using these data, analyses such as bank storage estimation, bank storage zone delineation, and further exploration using analytical solutions to document both propagation and attenuation of groundwater floodwaves would be the next step. These could bring further insight to groundwater and surface water interactions in a gravelly floodplain and would provide a framework for forecasting groundwater flooding.

Acknowledgements

This project was funded by the Ministère du Développement durable, de l’Environnement et de la Lutte contre les changements climatiques of the Quebec government, as part of the Programme d’acquisition des connaissances sur les eaux souterraines (PACES) 2012–2015, and by the Ouranos consortium, as part of the "Fonds vert" for the implementation of the Quebec Government Action Plan 2006–2012 on climate change. The authors acknowledge the support of numerous field assistants, and thank Laure Devine for the English revision. The authors thank Jörg Lewandowski, two anonymous reviewers and the Editor and Associate Editor for constructive comments that helped improve significantly the overall quality of the paper.