Sediment modelling and design optimization for stormwater ponds

Abstract

Stormwater ponds, including dry ponds, wet ponds and constructed wetlands, have been widely used for sediment removal from stormwater runoff. In this paper, sediment removal mechanisms, modelling approaches and optimization of design for stormwater ponds are reviewed and discussed. The settling velocity for discrete particles is introduced and compared. Settling velocity distribution should be characterized for individual sites for the most cost-effective design of new stormwater ponds. Different methods for estimating trap efficiency of stormwater ponds are then summarized, including empirical models and theoretical models. The sediment transport modelling method is also discussed. Optimization of pond design for improved sediment removal is described, with many key factors taken into account such as residence time, vegetation, wind, turbulence, stratification, inflow and outflow. A high system hydraulic efficiency can be achieved through proper design of the shape of the pond, length-to-width ratio, baffling, depth, and the location of inlets, outlets and vegetation. Finally, various issues associated with typical numerical models for sediment transport in stormwater ponds are discussed. This review paper intends to provide a state-of-the-art of sediment modelling in stormwater ponds and to point the direction for design optimizations.

Les bassins de retenue des eaux pluviales, y compris les étangs asséchés et humides et les marais artificiels, sont couramment utilisés pour l’élimination des sédiments se trouvant dans le ruissellement des eaux pluviales. Dans le présent document, sont réexaminés et discutés des systèmes d’élimination des sédiments, des approches de modélisation et l’optimisation de la conception des bassins d’eaux pluviales. La vitesse de sédimentation de particule discrète est présentée et comparée. La distribution de la vitesse de sédimentation devrait être personnalisée pour des sites individuels pour la conception la plus rentable. Puis, les méthodes différentes pour l’estimation de l’efficacité de capture sont résumées, en ce compris les modèles théoriques et empiriques; également discuté est le procédé de modélisation du transport des sédiments. Se décrit est l’optimisation de conception des étangs pour améliorer l’élimination des sédiments, en tenant compte des facteurs-clés tels que le temps de séjour, la végétation, la vente, la turbulence, la stratification, l’entrée et sortie. Par les conceptions appropriées de la forme d’étang, le rapport longueur/largeur, la déflexion, la profondeur et l’emplacement des entrées, sorties et la végétation, l’efficacité hydraulique de système élevée est réalisable. Enfin, quelques problèmes associés à les modèles numériques courants pour le transport des sédiments dans les bassins de retenue des eaux pluviales sont discutés. Ce document de synthèse-ci entend fournir un état d’art de modélisation de sédiment dans les bassins de retenue et montrer le chemin pour l’optimisation de conception.

Keywords:

• Design
• hydraulic efficiency
• modelling
• runoff
• sediment
• settling velocity
• stormwater
• transport
• trap efficiency
• vegetation

Introduction

Nonpoint source pollution from urban runoff has been established as a major cause of receiving water degradation. In 2005, for instance, a water quality study found that 90% of sediment that had entered the Bow River from Calgary, Alberta, was from the stormwater system (City of Calgary 2005). Studies have also noted that excessive sediment can adversely impact aquatic life and fisheries, source waters for drinking water supplies, and recreational uses (USEPA 1999). Fine particulates are also known to carry heavy metals (e.g. lead, copper, zinc), polychlorinated biphenyls (PCBs), polycyclic aromatic hydrocarbons (PAHs) and other pollutants (GCI and WWEI 2011). Ellis and Revitt (1982) found in an experimental study that particles smaller than 100 μm (accounting for 15% of the total sampled mass) carried 70% of the existing metal pollutants.

In an effort to reduce the sediment and pollutant loadings in receiving waters, a number of structural and nonstructural best management practices (BMPs) have been developed over the years. One of the structural BMPs being used extensively for stormwater management is stormwater ponds, consisting of dry ponds, wet ponds, wetlands and any hybrid ponds (City of Calgary 2011). Dry ponds hold stormwater runoff in the wet season, and are completely dry for the rest of the year (Shammaa and Zhu 2001). By comparison, wet ponds and constructed wetlands maintain a permanent pool volume (OMOE 2003). Each of these types of stormwater ponds provides detention volume for stormwater runoff, thus reducing the peak runoff in order to control flooding. Meanwhile, these structures are now also widely used for water quality treatment. In this context, the proportion of the incoming sediment that is deposited or trapped (i.e. removal efficiency or trap efficiency) is one of the most important properties of stormwater ponds.

Governments in North America have in recent years proposed legislations or best practices for sediment removal criteria for stormwater ponds. The Alberta guideline (AENV 2001) calls for the removal of a minimum of 85% of sediment with a particle size of 75 μm or greater. In Ontario, the facilities are required to meet the water quality objectives of the long-term average removal of 80, 70 and 60% of suspended solids in the total runoff volume for “enhanced,” “normal” and “basic” protection levels, respectively (OMOE 2003). The City of Calgary has mandated the removal of a minimum of 85% total suspended solids (TSS) for particle sizes greater than or equal to 50 μm (City of Calgary 2011). Given these requirements, it is important to assess the performance of existing ponds and predict the trap efficiency of new ponds, making the introduction of a suitable modelling technique for sediment removal imperative.

According to the United States Environmental Protection Agency (USEPA 2002), detention dry ponds and retention wet ponds offer an average removal efficiency of 49% and 80%, respectively, for TSS. In a 2014 international stormwater BMP database pollutant category summary, the medians of inlet and outlet concentrations of TSS for different BMPs were summarized (GCI and WWEI 2014). The median calculated removal efficiencies of TSS for dry detention basin, wet retention pond and wetland basin were found to be 66, 76 and 62%, respectively.

Though these BMPs have a significant capacity to remove sediments, there exists a gap between the real-life effectiveness and the legislation and best practice standards for major ponds. Additionally, the total amount of suspended solids in stormwater entering the stormwater ponds is highly variable, resulting in large variations in removal efficiencies. Birch et al. (2006), for instance, found the range to vary from −12% to 93%. The significant fluctuation of removal efficiencies may be due to such influencing factors as physical particle characteristics (e.g. size, shape and density), residence time, vegetation, wind, stratification and turbulence level, among others. Thus, a comprehensive understanding of various key factors in trap efficiency is essential. Based on this knowledge, the design of stormwater ponds can be optimized to meet the specifications laid out in current legislations.

A large number of recent studies have focused on sediment in stormwater ponds. A state-of-the-art review is urgently needed to summarize the modelling techniques of sedimentation and provide a design guide to municipalities outlining strategies for improved sediment trap efficiency. Discrete particle settling is discussed in the following section since it is the dominant sedimentation mechanism for particles in stormwater runoff. The traditional models for estimating the trap efficiency of stormwater ponds and sediment transport modelling are also summarized in the next section. Optimization of pond design for improved sediment removal is described in the subsequent section. Then, typical numerical models used to simulate sediment transport in stormwater ponds are described in the next section. Finally, the concluding comments are presented. Note this paper does not address the flocculent settling of cohesive particles.

Sediment removal mechanisms and modelling approaches

The dominant removal mechanism for sediment in stormwater ponds is sedimentation. Sedimentation is the process in which particulates settle to the bottom of a water column. The complexity of the sedimentation process has led to the development of many approaches for determining the trap efficiency within a pond, the most common among which are the traditional empirical and theoretical methods, and sediment transport models.

Particle settling velocity

Stokes (1851) first derived an equation for spherical particles with a low Reynolds number to predict their settling velocity, w_s:(1)

where ρ_p = particle density; ρ_f = fluid density; d_p = particle diameter; g = gravitational acceleration; ν is kinematic viscosity. Equation (1(1) ) is only valid for small particles with Reynolds number less than 1 (R < 1), R = w_sd_p/ν.

Generally, settling velocity can be expressed as (Garcia 2008)(2)

where C_d is the drag coefficient; and .

Many efforts have been made to develop a method for extending the expression of drag coefficient to a much wider range of Reynolds numbers (Fair et al. 1954; Clift et al. 1978; Haider and Levenspiel 1989; Cheng 1997). For engineering practice (Huber and Dickinson 1988), the value of C_d is adopted as follows:(3) (4) (5)

In fact, Equation (2(2) ) is limited in its usefulness in that it is not explicit in terms of w_s, such that one must compute settling velocity by trial and error (Garcia 2008). Based on Equation (2(2) ), several quasi-theoretical formulas or empirical correlations for evaluating the settling velocity of individual particles have been developed by defining dimensionless particle diameter (Turton and Clark 1987; Cheng 1997; Brown and Lawler 2003; Jimenez and Madsen 2003; Camenen 2007; Song et al. 2008; Garcia 2008). A number of formulae for spherical particles and natural sand particles are described as follows.

For spherical particles, two empirical correlations were proposed by Brown and Lawler (2003). They first selected a raw data set of 480 points of high quality from past experiments conducted in square vessels and circular cylinders. The two empirical equations they presented were based on this corrected data set of 480 data points. The equation presented as Equation (6(6) ) below has been found to be valid at the moderate Reynolds number (R ≤ 4000) with an accuracy of approximately ± 2.5% of the experimental data, while Equation (7(7) ) works for the whole range of Reynolds number (R ≤ 2 × 10⁵) and has an accuracy of approximately ± 7.5% of the experimental data.(6) (7)

where w_s^* and d_p^* are the dimensionless settling velocity and particle diameter, which are expressed, respectively, as(8) (9)

For natural sand particles, Cheng (1997) developed a formula based on the experimental data of quartz sand,(10)

A new empirical formula with marginally greater accuracy than Equation (10(10) ) was proposed by Song et al. (2008).(11)

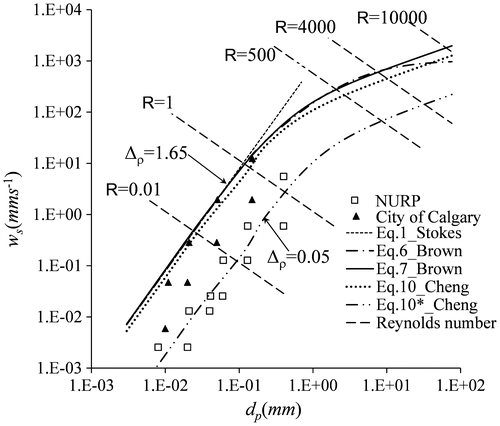
Equations (1(1) ), (6(6) ), (7(7) ) and (10(10) ) were chosen for further analysis. The settling velocity calculated by these equations is shown in Figure 1. In these calculations, the density of particles is kept at 2650 kg/m³, equivalent to the density of quartz. The temperature of the water is 15°C, and the density is 999.1 kg/m³. Equation (1(1) ) of Stokes is valid at low Reynolds number values (R ≤ 1), corresponding to a particle size less than 0.113 mm and w_s less than 10.1 mm/s in this case. An obvious difference between Equation (6(6) ) and Equation (7(7) ) is seen at large particle sizes. As for natural sand particles (Equation 10(10) ), the settling velocity is slightly smaller than spherical particles.

Figure 1. Settling velocity for different particle sizes.

Settling velocity as measured by the Nationwide Urban Runoff Program (NURP; USEPA 1983) is much smaller than the values yielded by Equations (1(1) ), (6(6) ), (7(7) ), and (10(10) ). The curve of Equation (10(10) )^*_Cheng is calculated by Equation (10(10) ) with particle density of 1050 kg/m³ and water temperature of 15 °C. The calculated value of this curve is close to the NURP settling velocity distribution.

The settling velocity, adopted by the City of Calgary for sediment removal, is indicated in their Stormwater management & design manual (City of Calgary 2011). In Table 1, the settling velocities of Calgary, NURP, Equation (1(1) ) and Equation (10(10) ) are compared.

Table 1. Particle size and settling velocities for sediment removal.

City of Calgary, 2011				Estimation by equations		NURP, USEPA (1983)
Size range (mm)	Density (kg/m^3)	Fraction (%)	Settling velocity (mm/s)	Velocity of Equation (1(1) ) (mm/s)	Velocity of Equation (10(10) ) (mm/s)	Size Range (mm)	Fraction (%)	Settling velocity (mm/s)
< 0.01	1500	23	0.00592	< 0.00238	< 0.00178	≤ 0.020	20	0.00254
0.01 - 0.02	2000	9	0.0473	0.0476–0.19	0.0356–0.142	0.02 - 0.04	10	0.013
0.02 - 0.05	2500	13	0.283	0.286–1.786	0.213–1.31	0.04 - 0.06	10	0.0254
0.05 - 0.15	2650	23	1.95	1.964–17.676	1.44–11.0	0.06 - 0.13	20	0.127
> 0.15	2650	32	12.4	> 17.676	> 11.0	0.13–0.4	20	0.593
-	-	-	-			0.4–4.0	20	5.503

Note:

The settling velocities of Equation (1(1) ) and Equation (10(10) ) are calculated based on the size range and density given by the City of Calgary.

The settling velocities of Equation (1(1) ) and Equation (10(10) ) are calculated based on the size range and density for the City of Calgary. For the particle size less than 10 μm, the velocity adopted by Calgary is 0.00592 mm/s, which is more than 2 times greater than those calculated by means of Equation (1(1) ), Equation (10(10) ) and NURP. For the particle size range between 0.01 mm and 0.15 mm, the velocity adopted by Calgary is near the value yielded by Equation (1(1) ), which is calculated on the lower end of the size range. For the particle size larger than 0.15 mm, the velocity adopted by Calgary is kept at 12.4 mm/s, and is smaller than the value of Equation (1(1) ).

By contrast, the settling velocity of NURP is found to be much smaller than the recommend values for Calgary, except in the size range of < 0.01 mm. In fact, the NURP values were recommended in the 1994 stormwater guidelines of the Ministry of Environment and Energy for Ontario (MOEE 1994) as well as in the 2000 Stormwater management & design manual of Calgary (City of Calgary 2000). However, as it was no longer felt to be appropriate, the data were removed in the 2003 stormwater guideline of Ontario Ministry of the Environment (OMOE 2003) and in the Stormwater management & design manual for the City of Calgary (2011). Although NURP settling velocity and particle size distribution may not accurately characterize the particles in some locations, they do provide a conservative estimate for stormwater treatment practice design (Gulliver et al. 2010).

From the above equations (1)–(11), Figure 1, and Table 1, it can be inferred that the settling velocity is predominantly determined by particle density and size distribution. Karamelegos et al. (2005) pointed out densities of particles in stormwater ranging from 1100 to 2860 kg/m³, with the most common values falling within the 1400 to 1800 kg/m³ range. Different particle size classes would be expected to have different densities due to variations in the percentage of organic matter, and changes in mineralogy. The particle densities were found to vary from event to event based on rainfall intensity, storm duration, season, and other environmental factors (GCI and WWEI 2011).

As for the particle size distribution, the majority of particles in stormwater are considered to be “fine” for the City of Calgary and NURP (Table 1). Ball and Abustan (1995) also reported from an urban catchment that 70–92% of particles were less than 100 μm. This finding is consistent with Randall (1982). However, other studies also indicated that coarse particles can be dominant as well (Sartor and Boyd 1972; Shaheen 1975; Sansalone et al. 1998). In fact, particle size distribution, as a major factor in settling velocity, varies based on land use, site location and storm intensity. Such changes in particle size distributions may help to explain some of the variations in TSS concentrations in BMP effluent. Accordingly, for the most cost-effective design of new stormwater treatment practices, particle size distribution or settling velocity distribution should be characterized for individual sites (Gulliver et al. 2010).

In addition, temperature can also influence settling velocities of stormwater particles through fluid viscosity. The settling velocities in Table 1 for the City of Calgary, Equation (1(1) ) and Equation (10(10) ) are all based on a temperature of 15°C. Guy (1969) noted that settling velocities decrease as temperature decreases and viscosity increases. In addition, salinity from winter road de-icing salt can also create vertical density stratification, and impact on particle settling. For individual particles, settling velocities decrease due to a rise in the water density with salinity. However, particles with high amounts of clay and organic matter might flocculate and settle faster with greater salinity (Portela et al. 2013).

Empirical models for sediment removal efficiency

Empirical models are one of the traditional methods available to predict sediment removal efficiency. Heinemann (1984) and Verstraeten and Poesen (2000) provided overviews of a number of empirical models that can be used for predicting trap efficiency, the most widely used of which are discussed here.

Brown (1943) was one of the first researchers to link empirical data on trap efficiency to reservoir characteristics. Based on the data from 15 reservoirs, Brown plotted trap efficiency against C_a/A_c, the ratio of the reservoir storage capacity C_a (which can be expressed in acres/ft) and the catchment area A_c. Two other popular empirical curves for trap efficiency were proposed by Churchill (1948) and Brune (1953). Churchill’s curve was based on a sedimentation index (SI, equal period of retention divided by mean velocity), while Brune correlated trap efficiency with the ratio of reservoir storage capacity (C_a) and annual inflow (I).

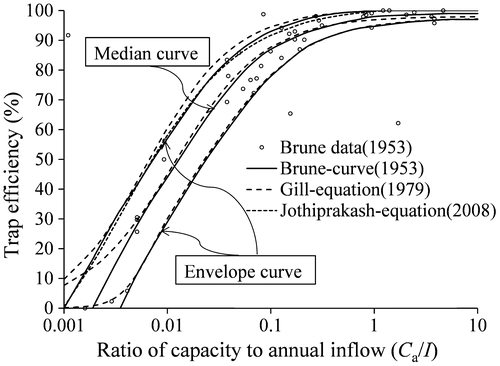
Among these curves, Brune’s method is one of the most widely used. Brune’s curves and data from 44 normal ponded reservoirs in the United States are shown in Figure 2. The envelope curves in Figure 2 were transformed by the United States Department of Agriculture-Soil Conservation Service (USDA-SCS, 1983) into curves for predominantly coarse-grained sediments (upper curve), for mixtures of grain sizes (median curve) and for primarily fine sediments (lower curve). However, no information is given as to whether this transformation was based on field observations (Verstraeten and Poesen 2000).

Figure 2. Trap efficient curves of Brune, Gill and Jothiprakash.

Several researchers developed algebraic best-fit equations to these curves, with the major equations listed in Table 2. The calculated values of the equations by Gill (1979) and Jothiprakash and Garg (2008) are shown in Figure 2. In general, the equations of Gill (1979) match Brune’s original curves, except at the range of low capacity/annual inflow ratio, while the equation for coarse sediment from Jothiprakash and Garg (2008) is well fitted for the entire range.

Table 2. Empirical equations for trap efficiency (TE).

Researchers	Empirical equations
Dendy (1974)
	Adding additional data of 17 small reservoirs (Ac ≤ 60 km^2) to Brune’s curve
Gill (1979)	For fine sediment:
	For medium sediment:
	For coarse sediment:
Ward (1980)
	Ca and I are in hectare-m and m^3 yr^−1
Heinemann (1981)
	Based on data of 20 ponded reservoirs, Ca and I are in m^3 and m^3 yr^−1
Jothiprakash and Garg (2008)	For medium sediment:
	For coarse sediment:

Theoretical models for sediment removal efficiencies

Theoretical models are the other traditional method used to predict sediment removal efficiency. Among the theoretical models, Camp’s model (Camp 1945), DEPOSITS (Ward et al. 1977), CSTRS (Wilson and Barfield 1984), BASIN (Wilson and Barfield 1985), SWMM (Huber and Dickinson 1988), and STEP (Verstraeten and Poesen 2001) are the models most often used to estimate trap efficiency. Camp (1945) investigated sedimentation in an ideal rectangular continuous flow tank. In Camp’s study, the tank was considered a completely mixed system with a quiescent and steady flow and no re-suspension of sedimentation. A critical velocity (w_c) was defined based on the water depth (h) and the time required for the inflow to flow through the tank (L/u_t):(12)

where L and b are the length and width, respectively, of the settling zone; u_t is the horizontal velocity of flow in the tank; A_t is the surface area of the tank; and Q is the water discharge. For particles with settling velocity w_s ≥ w_c, all the sediment will be able to settle and the trap efficiency will be 100%; for those with w_s < w_c, trap efficiency is the ratio of w_s to w_c. Camp’s ideal trapping efficiency (TE) in the rectangular pond is described below:(13)

Chen (1975) modified Camp’s (1945) model by taking turbulent flow into account:(14)

In the SWMM model (Huber and Dickinson 1988), a dimensionless turbulence factor α is defined:(15)

where u_* is shear velocity and n is Manning’s n. The parameter α may now be used as a weighting factor to obtain the overall trap efficiency from quiescent condition (α = 1) to turbulent condition (α = 0.01) by means of Equations (13(13) ) and (14(14) ).(16)

For different particle sizes, trap efficiency can be calculated using a discrete particle size distribution (Camp 1945; Verstraeten and Poesen 2000),(17) (18)

where X_c equals the fraction of particles having a settling velocity of less than the critical settling velocity, and ΔX_i equals the fraction of particles having a settling velocity of w_si.

The above models are based either on plug flow or on complete mixing, neither of which frequently occurs in reality, and only some aspects of sediment transport processes are considered in each model (Zhang 2009). Thus, recent models have been developed for stormwater ponds to deal with the complex hydraulic conditions, and to explain where and when sediments will settle (Torres et al. 2008).

Sediment transport models

Generally, sediment transport modelling has spatial formulations varying from one-dimensional (1D), to 2D depth-averaged, to fully 3D flow and sediment transport models. The governing equations in 1D sediment transport models are the 1D St. Venant equations coupled with the transport equation for the sediment. Widely used 1D models, such as CCHE1D, HEC-6 and EFDC-1D, have been used to study sediment transport, scour and deposition in rivers and channels (USACE 1993; Wu and Vieira 2002; Hamrick 2001). The concentration of a suspended load is described by the convection–diffusion equation in the MIKE 11 model (DHI 1995; Neary et al. 2001):(19)

where  = cross-sectional average sediment concentration; Q = water discharge; A = cross-sectional flow area; K = dispersion coefficient; S_e = erosion (resuspension) flux; and S_d = deposition flux.

Erosion flux and deposition flux are expressed as(20) (21)

where M^* = bed erodibility;  = cross-sectional average flow velocity; h = flow depth; and U_ce = cross-sectional critical erosion velocity; h^* = average depth through which particles settle; and U_cd = cross-sectional critical deposition velocity.

Equation (19(19) ) can be used to simulate the fine grain transport with diameters < 0.062 mm; for coarse sediments with grain sizes greater than or equal to 0.062 mm in diameter, the sediment continuity equation is as follows (DHI 1995; Neary et al. 2001):(22)

where z_b = bed level; Q_s = sediment discharge, including suspended and bed-load; p^′ = sediment porosity; and W = width of cross section at water surface. Equation (22(22) ) can simulate the total-load sediment transport and update the bed level.

Popular 2D models for sedimentation include MIKE-21, FLUENT, CCHE2D, RMA and Rubar20, among others (Wu 2001; DHI 2003; Gharabaghi et al. 2006; Torres et al. 2008). The 2D governing equation for suspended-sediment processes is described as follows (Garcia 2008):(23)

where C is depth-averaged suspended sediment concentration; U and V are the depth-averaged water velocity components; E_b is upward bed-sediment entrainment flux at near bed; D_b is downward suspended-sediment deposition flux at near bed; and is horizontal plane mass-diffusivity coefficient, usually only including the eddy diffusivity and neglecting the dispersion due to depth averaging.

In the CCHE2D model (Wu et al. 2000), the entrainment flux E_b and deposition flux D_b are formulated as(24)

where C_be = the depth-averaged suspended-load concentration at the equilibrium state, and β = non-equilibrium adaptation coefficient of suspended load. In order to allow the user to choose the most appropriate method for site-specific studies, four formulae for C_be were recommended in Wu and Wang (2003). The bed deformation, meanwhile, can be calculated by a bed-load-layer approach (van Rijn 1987; Brors 1999):(25)

where q_bx and q_by represent the bed-load flux in the x and y directions, respectively.

Besides the bed-load-layer approach (van Rijn 1987), another two dominant approaches for treatment of bed and near-bed processes are the total-load approach and the active-layer and active-stratum approach (Garcia 2008), which are not discussed further here.

When the governing equations (Equations 23(23) and 25(25) ) are adopted for sediment processes, the primary sediment unknowns are the suspended-sediment concentration and the bed-surface elevation z_b. All other sediment-related terms in Equations (23(23) ) and (25(25) ), such as sediment mass-diffusivity coefficient , bed-load flux q_bx and q_by, and fall velocity w_s, are functions of flow variables and primary sediment unknowns, and are treated as auxiliary – often empirical – relations. These auxiliary relations are described in detail in Garcia (2008).

For 3D models, MIKE-3, FLUENT, CCHE3D and EFDC-3D are some of the popular commercial computational fluid dynamics (CFD) codes capable of simulating flow and sediment transport in ponds, lakes, rivers and oceans (Jia et al. 2001; DHI 2003; Zhang 2009; Ji and Jin 2014). Most 3D models use the following equation as the governing equation for suspended sediment processes (Garcia 2008):(26)

where c = local suspended sediment concentration; u, v, and w are the flow velocities in the x, y, and z directions, respectively; ɛ_s = turbulent mass-diffusivity coefficient, which is related to the eddy viscosity and the turbulent Schmidt number for sediment.

When the bed-load-layer approach is used, Equation (25(25) ) can also be adopted to calculate the bed level and bed-load transport. The exchange of sediment between the suspended sediment layer and bed-load layer in the 3D transport model is also through downward deposition sediment flux D_b and upward entrainment flux E_b (Garcia 2008).

In the EFDC-3D model (Tetra Tech Inc. 2007), the net flux of entrainment flux E_b minus deposition flux D_b at the near-bed is given by evaluating Equation (27(27) ):(27)

where c_be is the near-bed equilibrium concentration; c_be in EFDC can be calculated by means of the empirical formulae given in Van Rijn (1984), Smith and McLean (1977), and Garcia and Parker (1991). c_b is the near-bed non-equilibrium concentration, and is the result of suspended-sediment computations at the near-bed.

In the MIKE-3 model (DHI 2003), the deposition is described as (Krone 1962)(28)

where p_D is an expression of the probability of deposition(29)

where τ_b is bed shear stress, and τ_cd is critical shear stress for deposition.

The erosion features follow two modes for hard bed (Partheniades 1965) and soft bed (Parchure and Mehta 1985):(30) (31)

where E is the erodibility, m is the power of erosion, τ_ce is the critical bed shear stress for erosion and γ is the erosion coefficient. With regard to the governing equations for 3D transport models, i.e. Equation (25(25) ) and Equation (26(26) ), almost all system-closure considerations are basically the equivalent of 2D models. These closure auxiliary relations are also described in detail in Garcia (2008).

The above governing equations are for single-phase flows. When the transport of sediment is considered as two phases (liquid phase and solid phase), Euler–Euler and Euler–Lagrange are two popular modelling approaches to simulate the transport of solid phases (Yan 2013). In the Euler–Euler approach, different phases are modelled on a continuum using the Navier–Stokes equations. In the Euler–Lagrange approach, the sediment phase is represented by tracking discrete particles, taking into account momentum and mass transfer between the two phases. The Lagrangian particle tracking approach assumes that the sediment particles are spherical and at low concentrations; thus, particle–particle interactions can be ignored.

The sediment distribution can be determined by these transport models, and thus the trap efficiency is calculated as concentration or total mass of inlet and outlet,(32)

where C_in and C_out are the sediment concentrations entering and leaving stormwater ponds, respectively, and M_in and M_out are, respectively, the sediment masses entering and leaving the stormwater ponds.

Optimizing pond design for improved sediment removal

In order to improve trap efficiency, more attention must be directed to the key considerations for BMP designs, including residence time, vegetation and physical particle characteristics, as well as other factors such as wind, stratification, turbulence level, inflow, effluent and sediment loading.

Pond design for residence time

The design criterion for the volume of dry pond, wet pond and constructed wetland is 1:100 year storage capacity, and the detention time is a minimum of 24 h (City of Calgary 2011). For stormwater ponds with a fixed volume, the removal efficiency of sediments is found to be positively related to the retention time. The nominal residence time (t_n) equals the ratio of the pond volume over the discharge (V_t/Q). Thus, the inflow into the pond must be well distributed throughout the pond by avoiding short-circuiting and poor utilization of the available detention storage such as dead zones (Persson et al. 1999). A high system hydraulic efficiency can be achieved through proper design of the shape of the pond, length-to-width ratio, baffling, depth, and the location of inlets and outlets.

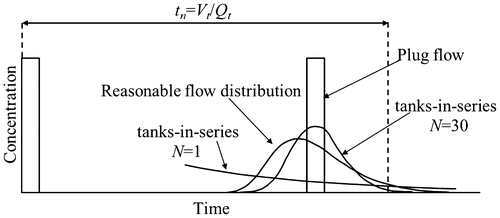
A hydraulic efficiency index has been proposed by Persson et al. (1999). If a pulse experiment is conducted at the inlet of a stormwater pond by adding a tracer such as Rhodamine, the retention time distribution (RTD) curve can be derived by measuring tracer concentration at the outlet. The flow condition within the pond is thus revealed by the position and distribution of the RTD curve (Su et al. 2009). A number of tracer responses in a detention system from the pulse experiment are presented in Figure 3. Under plug flow conditions, the concentration–time distribution results in a spike (Persson et al. 1999). If the behaviour of flow through the basin is described using a tanks-in-series model, the continuously stirred flow condition means the number of well-mixed tanks-in-series is N = 1, in which the concentration–time distribution takes the form of an exponential function, and the tracer concentration at the outflow reduces continuously due to the flow dilution (Figure 3). The larger the N, the closer the flow condition approaches plug flow. However, the natural concentration–time distribution lies somewhere between the distributions of plug flow and fully mixed conditions (Figure 3).

Figure 3. Tracer concentration time distribution under different conditions.

Based on the work of Thackston et al. (1987) and Kadlec and Knight (1996), the hydraulic efficiency index λ can be calculated (Persson et al. 1999):(33)

where e_v is the effective volume ratio utilization of detention systems, e_v = t_mean/t_n; N is the number of tanks-in-series N = t_mean/(t_mean − t_p); and t_mean and t_p are the mean detention time and the time of the peak outflow concentration, respectively.

Thus, the hydraulic efficiency index λ can be simplified as(34)

The hydrodynamic performance can be classified as: good hydraulic efficiency with 0.7 > λ, satisfactory hydraulic efficiency with 0.5 < λ < 0.7 and poor hydraulic efficiency with λ < 0.5. In addition to field tracer experiments, CFD modelling can be a powerful tool to determine the RTD. In pond design, it is now possible to improve hydraulic efficiency by optimizing pond layout to reduce short-circuiting and dead zones. Recently, the effect of pond shape, length-to-width ratio, baffling, construction, and layout of inlets and outlets on hydraulic efficiency was investigated by several 2D CFD models such as MIKE 21, TABS-2, FLUENT and PHOENICS (Persson et al. 1999; Shilton 2000; Adamsson et al. 2005; Su et al. 2009). Persson et al. (1999) studied the geometries of 13 hypothetical ponds using 2D MIKE 21 models and a Reynolds-averaged Navier–Stokes (RANS) CFD model with k-ε turbulence closure (Table 3). They found that elongated systems provide high hydraulic efficiency. The rectangular ponds with a length-to-width ratio less than 4:1, as well as L-shaped ponds with an effective length-to-width ratio of 3:1, were found to have a poor hydraulic efficiency with λ < 0.5. The current design criteria of the OMOE specify a pond-length-to-pond-width ratio of 4:1 to 5:1 (OMOE 2003). For the rectangular wetlands simulated by Su et al. (2009), λ reaches 0.9 or even higher when the aspect ratio is greater than 5. According to a recent study simulating 89 constructed wetlands (Zounemat-Kermani et al. 2015), the aspect ratio should be at least 9 in order to achieve an appropriate rate for hydraulic efficiency in rectangular constructed wetlands. Modified rounded rectangular constructed wetlands in their study showed improved λ by up to 23%.

Table 3. Modelling studies of pond hydraulic design.

Authors	Model	Notes
Persson et al. (1999)	2D MIKE 21	13 hypothetical ponds
Shilton (2000)	3D PHOENICS	Rectangular ponds with and without a baffle
Adamsson et al. (2005)	3D FLUENT and 2D MIKE21	A large rectangular physical model of a detention tank
Jansons and Law (2007)	2D MIKE 21	Nine stormwater ponds with more complex and realistic configurations
Su et al. (2009)	2D TABS-2	20 wetlands with different aspect ratios, configurations of inlet and outlet, and obstruction designations
Zounemat-Kermani et al. (2015)	2D depth-average model	89 artificial constructed wetlands

The significant effects of baffles, as well as of obstructions such as a subsurface berm or an island, were demonstrated by Persson et al. (1999) and Persson (2000), where hydraulic performance can be improved by decreasing instances of short-circuiting. In another study, the baffle was found to increase detention time and water mixing (Shilton 2000). Su et al. (2009), meanwhile, suggested that the obstruction-width-to-wetland-width ratio, rather than the amount of obstruction, is the most significant factor influencing hydraulic efficiency.

Different inlet and outlet configurations in a rectangular tank were considered by both Persson et al. (1999) and Su et al. (2009). The inlet and outlet were located at the midpoint or corner of the tank, and distributed inflow was also taken into account in one scenario. Compared with the inlet–outlet configuration of midpoint–midpoint and corner–corner, these studies found a distributed midpoint to be the best configuration to improve λ and to ensure that the fluid runs uniformly (Persson et al. 1999; Su et al. 2009).

In terms of pond shape, teardrop- and kidney-shaped ponds were found to have a higher hydraulic efficiency than most rectangular-shaped ponds with the same surface area (Jansons and Law 2007).

Vegetation

The influence of vegetation cannot be neglected, especially for constructed wetlands. An increased proportion of vegetation within the vicinity of a given facility is expected to provide higher treatment effects (Larm and Hallberg 2008). The vegetation reduces water velocity and traps particles, and thus increases the effect of the sedimentation process (Larm and Alm 2014). Tanner and Headley (2011) used experimental tanks (12 × 0.7 m³) with 0.36 m² floating wetlands, and found the addition of living plants provided a large submerged root surface area and removed approximately 34 to 42% of the turbidity associated with very fine suspended particulates within three days. The presence of vegetation was also reported to reduce resuspension of particles (Braskerud 2001).

Uniform vegetation can increase the residence time of a pond by reducing the pond’s mean velocity. However, the effects on the residence time of more complex vegetation patterns and varying densities, such as those created naturally by the vegetation’s variation throughout the seasonal growth cycle, are uncertain (Hart et al. 2014). By means of a tracer experiment in a natural pond in southern Sweden, vegetation patches were found to create preferential flow paths within the pond, leading to short-circuiting, which created a reduced effective volume of the pond, and thus a residence time lower than the nominal residence time (Hart et al. 2014). Some studies also reveal that the pickerelweed leaf debris sedimentation in autumn and algal suspended solids may increase TSS concentration (Song et al. 2015).

In general, the effect of vegetation on retention time can be studied by means of tracer experiments and numerical models. Tracer experiments are not often used due to the expensive associated costs. In numerical modelling, four approaches have mainly been adopted: (1) vegetation is considered only as a bed roughness effect and is modelled by assigning very high friction factors such as Manning’s n (Somes et al. 1999); (2) vegetation is treated as an obstacle and exerts a retarding drag force on flow (Kadlec 1990); (3) individual vegetation elements are directly replicated within the computational domain (Tsavdaris et al. 2013); and (4) vegetation is modelled as a different flow zone from open parts of the pond by using porous media (Fan et al. 2008; Mattis et al. 2012; Tsavdaris et al. 2015). Use of the porous media condition has become a popular method, where porous media have been modelled by the addition of a momentum source term to the 3D Navier–Stokes equations. Tsavdaris et al. (2015) simulated a vegetated pond using the Ansys Fluent code with porous media condition, with the results indicating that the vegetated pond system does not differ substantively in terms of velocity magnitude to the non-vegetated system, and that the horizontal recirculation is enabled especially at the interface of different vegetation covers.

According to Larm and Hallberg (2008), the removal performance of constructed stormwater wetlands is slightly higher than that of conventional pond systems. By analysis of data from 46 facilities, Larm and Alm (2014) found the correlation between the vegetation and trap efficiency to be 0.042, suggesting that there is only a minor increase in treatment efficiency with increasing percentage vegetation. Based on these results, Larm and Alm (2014) noted that the effects of vegetation should be investigated further because of the high degree of uncertainty. The weak effect of vegetation on the trap efficiency in these studies may be due to the fact that other influencing parameters also change between these ponds. Spatial distribution of vegetation in stormwater ponds, such as fully vegetated wetlands, or planted floating wetlands, influences the distribution of the hydraulic residence time in different ways. An elliptical pond with a central vegetated island was found to be effective in improving retention time and promoting mixing (Tsavdaris et al. 2015). To improve treatment performance of sediments, it was suggested that vegetation be located within the main flow path of stormwater ponds in order to serve as an obstacle.

Other factors

Wind – Analysis of the field data and computer simulations by Shaw et al. (1997) revealed that the shear velocities associated with wind-generated currents in stormwater ponds may be sufficiently large to prevent particle settling, and, in extreme cases, to cause re-suspension of deposited and contaminated sediment. Bentzen (2009) simulated the effect of wind in two real ponds during runoff events using MIKE 3. TSS removal efficiency was found to change from 98% (no wind) to 79% (10 m/s west wind) with no initial sediment on the bottom. Khezri et al. (2012) investigated the effect of wind on the TSS removal efficiency in a pilot-scale sedimentation tank with different directions and magnitudes. The experiment with the wind blowing in the same direction of water flow showed that removal efficiency decreased from 61% (no wind) to 45% (7 m/s wind speed), which might be due to short circuit formation. When the wind was in the opposite direction of water flow, TSS removal efficiency initially increased with the increase of wind velocity from 0 to 2.5 m/s. It then decreased with a velocity increase to 5 m/s, since small opposing wind speeds can increase particle retention time whereas higher wind velocities could cause particle re-suspension (Khezri et al. 2012). Gillis et al. (2015) have also investigated flow short-circuiting caused by wind influence in a stormwater retention pond in Saskatoon, Saskatchewan. Thus, proper inlet and outlet siting may be selected by considering prevailing wind direction for stormwater pond design. Also, densely emergent vegetation can provide shelter from wind and minimize wind-driven water flow (Kadlec and Wallace 2008).

Inflow – Higher flow rates at an inlet will cause particles to move a greater distance before settling. The re-suspension of deposited sediment, as well as the tendency toward short-circuiting, mainly occurs during larger influent flow rates. In a recent tank experimental study by He and Marsalek (2014), an increase of the flow rate from 4 to 6 L/s resulted in a reduction in TSS removal efficiency from 46 to 13%. Energy dissipation at the pond inlet is thus required, and the distance between the inlet and the outlet should be extended as far as possible. Furthermore, a dual inlet/outlet structure in the pond is not recommended. The inflow sediment concentration also affects the trap efficiency: Larm and Alm (2014) reported that trap efficiency is over 80% for all facilities where inlet concentrations were higher than 100 mg/L.

Effluent – Effluent flow rate is a key controlling factor for TSS reduction in stormwater ponds. In order to obtain sufficient detention time, the retrofitting of outlets is popular. The multi-level outlet may be the most promising design option, because it varies the outflow discharge in order to provide the required detention time. Real-time control of the outlet is another common technique. Gaborit et al. (2013) used the SWMM model to improve the performance of stormwater ponds through real-time control for outlet effluent using rainfall forecasts. In their study, TSS removal efficiency was found to increase from 46% to about 90% by adopting the real-time control strategies of the outflow. Similar studies were conducted by Muschalla et al. (2014) to model TSS transport by SWMM.

Sediment loading – In general, a stormwater pond can achieve a greater reduction in total sediment loading when runoff sediment loading is high. Higher loadings usually result in greater removal efficiencies. In the study of two ponds located within the Phantom Lake watershed in Bellevue, Washington, pond “A” proved to be less efficient, but it reduced much more pollutant loading than pond “C” due to the larger inflow volume with abundant sediment loading (Comings et al. 2000).

Stratification – It is found that stormwater ponds stratify frequently, if only for short periods of time (hours or days) during warm, sunny and calm periods (Xenopoulos and Schindler 2001; Abis and Mara 2006; Song et al. 2013). The internal hydrodynamic behavior of stratified water bodies significantly influences the movement of suspended particles in the water column (Condie and Webster 2001). For instance, research on 10 shallow urban stormwater ponds in southern Ontario revealed that many of the ponds were adequately thermally stratified during much of the summer, and persistent stratification for 10 to 30 consecutive days was observed in some ponds (He et al. 2015). Concentrations of suspended solids, as well as total phosphorus (TP), and particulate nutrients (carbon, nitrogen and phosphorus) were found to be higher in bottom waters compared to in surface waters, which suggested the predominant influence of stratification on re-suspension and internal nutrient loading (He et al. 2015). As noted by Condie and Webster (2001), stratification tends to be enhanced by strong solar radiation and high turbidity, while mixing is enhanced by strong winds through both mechanical stirring and evaporative cooling at the water surface. In addition, waste stabilization ponds and lagoons, which have depths in excess of 2 m, often exhibit marked stratification at most times of the year (Kadlec and Wallace 2008). As such, a shallower depth in stormwater ponds may be beneficial in reducing stratification.

Turbulence level – Turbulence is negatively related to TSS removal efficiency since it impedes the settling of suspended solids and may even cause resuspension of settled particles. In general, a larger flow velocity is associated with higher turbulence level. The wind, waves and vegetation also increase the turbulence level (Bentzen 2009; Tsavdaris et al. 2015). As noted by Papa et al. (1999), the removal rate of TSS is reduced by about 10% when the turbulence level increases. If the disturbance is strong enough, (e.g. by wind force or by high inflows), the suspended solid removal efficiency can be negative, and the pond can become a source of contamination to the downstream receiving waters (Su et al. 2010).

The presence of engineered structures in the flow path can also accelerate sedimentation due to long retention times. Meanwhile, shallow flow depths are beneficial for sedimentation due to shorter retention time. Recommendations in the literature regarding pond depth range between 1.0 m and 2.5 m, including allowance for sediment accumulation; furthermore, safety and aesthetic issues limit the depth (OMOE 2003). Estimates of performance are found to decline with pond age, perhaps due to a lack of proper maintenance of stormwater BMPs. In this regard, some researchers reported that even limited maintenance can prevent declines in stormwater pond performance (Erickson et al. 2010). However, few stormwater ponds receive regular maintenance; for example, Klein (2012) reported that most of the estimated 32,000 stormwater BMPs in Maryland are maintained less than once every three years.

Discussion on numerical models

Several vertical integrated 2D and 3D models have been used to analyze sediment transport in stormwater ponds. Though these models were developed to investigate settling processes and concentration distributions by considering the complex pond geometry, unsteady hydrodynamics, variable fluxes and particle characteristics, limitations of these numerical models still persist. Rarely, models have been used to optimize pond design to improve removal efficiency.

Gharabaghi et al. (2006) simulated two ponds with 2:1 and 8:1 length-to-width ratios in one storm event by employing a 2D RMA model, which was developed by the Coastal and Hydraulics Laboratory, US Army Corps of Engineers. The model included RMA2 for hydrodynamic modelling, and SED2D for sediment transport modelling (Table 4). In their study, sediment deposition and bed elevation change were calculated and the pond with the 8:1 ratio showed higher sediment removal efficiency (89%) than the pond with the 2:1 ratio (82%). As noted by King et al. (2003), the 2D RMA model is limited in that only a single sediment particle size can be modelled for each simulation. Due to this limitation, Gharabaghi et al. (2006) only simulated a 2-μm particle size, since over 50% of effluent suspended sediment sizes had a size of less than 3.73 μm.

Table 4. Brief description of sediment module inputs.

Researcher	Model	Main inputs for sediment simulation
Gharabaghi et al. (2006)	RMA2 for hydrodynamics; SED2D for sediment transport	Influent sediment concentration, sediment particle size, settling velocity, initial sediment concentration, deposition characteristics of the sediment, and sediment diffusion coefficients, water temperature, etc.
Torres et al. (2008)	Rubar20 2D CFD software	Median particle diameter, settling velocity, critical shear stress, calibration coefficient, density of particles, etc.
Bentzen (2009)	MIKE 3 for hydrodynamics; convection diffusion equation for sediment	Sediment particle size, settling velocity, critical shear stress for deposition, critical shear stress for erosion，erosion coefficients, power of erosion, suspended sediment, concentration at open boundaries, dispersion coefficients, consolidation transition coefficient, bed layer thickness, etc.
Zhang (2009)	FLUENT:3D time-averaged N-S equation for fluid phase，Lagrangian discrete phase model for sediment phase	Inlet distribution of particles, particle size d20, d50, d80, d90, particle density, bed shear stress, etc.

Torres et al. (2008) identified preferential sedimentation zones, and compared the effluent concentration of TSS between simulation and observation using the Rubar20 model. This model is based on convection–diffusion terms coupled with the Saint-Venant equation, where the median particle diameter is needed to calculate the critical shear stress. However, 2D modelling of the outlet TSS concentration necessitates further improvement by taking into account the variability and the heterogeneous characteristics of the particles.

Bentzen (2009) investigated the transport, deposition and resuspension of highway-deposited sediments in wet detention ponds by means of MIKE 3 software. The MIKE 21 (2D) and MIKE 3 (3D) software include three sediment modules: (1) a sand transport module for non-cohesive sediment transport; (2) a mud transport module for cohesive and cohesive/granular sediment mixtures; and (3) a particle tracking module. The input of the model comprises information about particle properties and bed-material, including consolidation transition coefficient, bed layer thickness and particle size distribution (Table 4).

Zhang (2009) used the Euler–Lagrange approach in Ansys FLUENT to simulate rectangular stormwater ponds with different inlet and outlet pipe arrangements and various flow rates. The Lagrangian particle tracking approach assumes that sediment particles are spherical and of low concentrations, and thereby no particle interactions. The estimation of trap efficiencies and spatial distribution in stormwater ponds was conducted, with the model deemed appropriate for low sediment-laden flows due to the assumption of the Lagrangian particle tracking approach.

The Discrete Particle Method (DPM) is not a new technique for modelling sedimentation phenomena in stormwater ponds. The main challenge with the DPM method, though, is a lack of satisfactory bed boundary conditions which can clearly represent complex sedimentation phenomena such as dynamic settling and erosion, especially for real ponds. Yan (2013) extended the DPM for full-scale stormwater ponds, and proposed a new relationship based on particle settling velocities for bed boundary conditions. Consequently, improvements were made in the modelling of the spatial and temporal distribution of sediment settling in stormwater ponds. Removal efficiencies and deposition zones were also predicted. A number of studies have also used DPM to investigate sediment transport in stormwater ponds (Chebbo et al. 1998; Dufresne et al. 2009; Vosswinkel et al. 2012). It is worth noting that the DPM method requires detailed information about particle characteristics such as particle size (d₂₀, d₅₀, d₈₀, d₉₀) and particle density (Table 4).

Due to the complexity of real ponds, and the absence of measured data such as particle size distribution of influent and effluent sediments, and bed-sediment characteristics, the accuracy of model-predicted sediment removal effectiveness is still in need of improvement. In particular, the volume of field monitoring data available in the literature must increase in order for numerical models to be sufficiently verified.

Concluding comments

Stormwater ponds are widely used in urban stormwater management to provide protection from flooding and improvement of downstream water quality. Sediment trap efficiency in the ponds usually varies greatly, and sometimes even shows negative efficiency. It is important to identify the key influencing factors for trap efficiency, and to improve the design of stormwater ponds to meet the specifications outlined in existing legislation. Thus, this paper has reviewed and discussed sediment removal mechanisms, modelling approaches and design optimization for stormwater ponds.

The predominant removal mechanism for sediment in stormwater ponds is settling. The settling velocity is primarily dependent upon particle size characteristics and the density differences between the fluid and the particle. Various formulae for predicting the settling velocity for discrete spherical particles and natural sand were reviewed. The settling velocity and particle size distribution by the Nationwide Urban Runoff Program (NURP) was found to be smaller than the value of these settling velocity formulae, which may be due to the fact that particles in NURP have a larger percentage of organic matter with smaller particle density.

Two traditional approaches for predicting sediment removal efficiencies have been summarized – empirical models and theoretical models. Sediment transport modellings from 1D to 2D depth-averaged, to fully 3D flow, as well as two phase-related models (Euler–Euler and Euler–Lagrange), have also been reviewed.

In order to optimize pond design for improved sediment removal, a number of key considerations were presented, including residence time and vegetation, as well as factors such as wind, thermal stratification, turbulence level, inflow, effluent and sediment loading.

Longer residence times correspond to greater trapping efficiency. Elongated systems and baffles have been noted to provide greater residence time. Distributed inflow has been identified as the optimal inlet configuration for uniform flows. In terms of pond shape, teardrop- and kidney-shaped ponds have been identified as having a higher hydraulic efficiency than most rectangular shaped ponds with the same surface area.

The influence of vegetation cannot be neglected. In numerical modelling for the effect of vegetation, four approaches are mainly adopted, with the porous media condition having emerged as a popular method. In order to improve retention efficiency of sediments, vegetation is suggested to be located at the main flow path of stormwater ponds.

The effect of wind has been found to vary with wind direction and magnitude. When the wind blows in the opposite direction to water flow, removal efficiency initially increases with low wind velocity, then decreases with higher velocities. The removal efficiency always decreases when flow direction is congruent with wind direction.

It is worth noting that temperature stratification of stormwater ponds retards re-suspension of sediment; however, very strong inlet flow rates may cause re-suspension of accumulated sediment. The turbulence is negatively related to TSS removal efficiency. In order to obtain sufficient detention time, multi-level outlets and employing a real-time control strategy for the outlet are the most promising design option. Larger sediment loading input necessitates frequent maintenance, and the sediment removal performance declines with stormwater BMP age if the basin lacks proper maintenance.

Several numerical models have been used to investigate the settling processes of stormwater ponds. However, due to the complexity of real ponds, and the absence of measured data, the accuracy of numerical models for predicting sediment trap efficiency is still in need of improvement. It is recommended that the volume of field monitoring data be increased, which could help to verify the numerical models.

This paper contributes to the body of knowledge on sediment modelling and design optimization for stormwater management, and presents research that is of high relevance to the environmental science, hydraulic engineering, and stormwater management fields.

Notations
	=	The following symbols are used in this paper:
A	=	=cross-sectional flow area;
Ac	=	=catchment area;
At	=	=the surface area of the tank;
b	=	=the width of the settling zone in the tank;
	=	=cross-sectional average suspended sediment;
C	=	=depth-averaged suspended sediment concentration;
c	=	=concentration of the suspended sediment;
Cin, Cout	=	=the sediment concentration entering and leaving stormwater ponds;
Ca	=	=reservoir storage capacity (can be expressed in acres/feet);
Cd	=	=the drag coefficient;
Cbe	=	=the depth-averaged suspended-load concentration at the equilibrium state;
cbe	=	=near-bed equilibrium concentration;
cb	=	=the near-bed non-equilibrium concentration;
dp	=	=particle diameter;
dp*	=	=dimensionless particle diameter;
Db	=	=downward suspended-sediment deposition flux at near bed;
Eb	=	=upward bed-sediment entrainment flux at near bed;
E	=	=the erodibility;
ev	=	=the effective volume ratio utilization of detention systems;
g	=	=gravitational acceleration;
h	=	=water depth;
h*	=	=average depth through which particles settle;
I	=	=annual inflow ratio;
K	=	=dispersion coefficient;
L	=	=the length of the settling zone in the tank;
Min, Mout	=	=the sediment mass entering and leaving stormwater ponds;
M*	=	=bed erodibility;
m	=	=the power of erosion;
n	=	=Manning’s roughness coefficient;
N	=	=the number of tanks-in-series;
	=	=sediment porosity;
pD	=	=an expression of the probability of deposition;
Q	=	=water discharge;
Qs	=	=sediment discharge, including suspended and bed-load;
qbx, qby	=	=bed-load flux in x, y direction;
R	=	=Reynolds number;
Sd	=	=deposition flux;
Se	=	=erosion (re-suspension) flux;
SI	=	=sedimentation index;
TE	=	=trap efficiency;
tn	=	=nominal residence time;
tmean	=	=the mean detention time;
tp	=	=the time of the peak outflow concentration;
	=	=cross-sectional average flow velocity;
Ucd	=	=cross-sectional critical deposition velocity;
Uce	=	=cross-sectional critical erosion velocity;
U, V	=	=the depth-averaged water velocity components;
u, v, w	=	=flow velocities in x, y, z directions;
ut	=	=horizontal velocity of flow in the tank;
u*	=	=shear velocity;
Vt	=	=pond volume;
wc	=	=critical velocity;
ws	=	=settling velocity;
ws*	=	=dimensionless settling velocity;
wsi	=	=settling velocity of the particle with the ith diameter;
W	=	=width of cross section at water surface;
Xc	=	=the fraction of particles having a settling velocity less than the critical settling velocity;
ΔXi	=	=the fraction of particles having a settling velocity of wsi;
zb	=	=bed level
	=	=turbulence factor;
	=	=non-equilibrium adaptation coefficient of suspended load;
ρp	=	=particle density;
ρf	=	=fluid density;
ν	=	=kinematic viscosity;
	=	=horizontal plane mass-diffusivity coefficient;
	=	=turbulent mass-diffusivity coefficient;
τb	=	=bed shear stress;
τcd	=	=critical shear stress for deposition;
τce	=	=critical bed shear stress for erosion;
γ	=	=erosion coefficients;
λ	=	=hydraulic efficiency index;
	=	=is ratio of density difference of particle and fluid to the fluid density.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China [grant numbers 51379058, 51379060 and 51479064], Qing Lan Project and PAPD Project, and the Fundamental Research Funds for the Central Universities [grant numbers 2016B06714 and 2014B07814]. Additional support from the City of Calgary is also gratefully acknowledged.