Trade-offs and the importance of separating science and values in environmental flow assessment

Abstract

Hatfield and Paul (2015) note the potential for hidden value trade-offs in desktop models used for establishing environmental flows, which highlights the need to separate the contributions of science vs. values when developing flow regulations. This is best achieved with regulatory frameworks that clarify underlying values and objectives, identify any trade-offs that may be entertained between instream and out-of-stream uses, and provide clear guidance on the ecological and socio-economic contexts where different trade-offs and corresponding regulations may be implemented. Accurate flow-ecological response relationships are key to credible assessment of trade-offs or protection of instream values; when quantitative relationships are unavailable, model predictions and performance are highly sensitive to the assumed shape of the flow-ecology relationship. For example, by assuming that habitat capacity asymptotes at 20% of mean annual discharge, Hatfield and Paul (2015) implicitly discount the ecological value of higher base flows. Although cross-calibration of desktop models has value, performance of models for predicting environmental flows is best evaluated against independent measures of biological response to varying discharge (e.g. observed flow effects on fish biomass, production or other ecological attributes).

Introduction

Hatfield and Paul (2015) present a novel comparison of four desktop methods for setting environmental flows. Although their focus is on evaluating the performance of different desktop models, their presentation highlights the importance of clearly defining the roles of science vs. values in the process framework for setting environmental flows, at both technical and policy levels. This is especially important in applications where potential trade-offs between instream uses (e.g. environmental values like fish production) and out-of-stream uses (e.g. irrigation, drinking water, hydroelectric power) are implicit. Clearly separating the objective science that informs the biological consequences of resource extraction from value-based trade-offs between environmental and economic benefits is critical in resource management; Hatfield and Paul (2015) provide a reminder of the challenges inherent in this. Although Hatfield and Paul (2015) emphasize the importance of maintaining transparency between values and science, their discussion introduces some ambiguities. These are explored below with the goal of bringing greater clarity to the separation of science and values in the process chain of instream flow management.

Hatfield and Paul astutely observe that “Desktop methods are born from the desire for quick, simple answers to the question ‘How much water does a river need?’ (sensu Richter et al. 1997)” (316). This succinctly encapsulates the desire of resource managers to apply robust but credible decision-making tools that require limited investment of time and resources. However, Hatfield and Paul also observe that “…there is no single answer to how much water a river needs…”; (317), and state that “The conclusion from the presented results is no single ‘right’ answer exists to this question because different evaluators, and therefore different desktop methods, emphasize different values when making trade-offs” (316). This statement highlights the implicit lack of separation of science and values that may be present in the decision-making framework leading to instream flow recommendations.

Whether there is a single “right” answer to “How much water does a river need?” depends on whether this is treated as an objective science question or a value-based one. From an objective science standpoint, how much water is needed to protect specific environmental or biological attributes like fish production or water quality clearly has a “right” answer (i.e. a specific flow or range of flows); this flow may be unknown, difficult to assess, or simply bounded by high uncertainty, but an objective answer nevertheless exists, even if the effort required to identify it (or reduce uncertainty to a reasonable level) is high. However, if the question “How much water does a river need?” is understood to include benefits from both instream and out-of-stream uses, then there clearly is no right or wrong answer, since the amount of water the river needs will vary with the values of the observer. This ambiguity in interpretation of “required flows” highlights the importance of separating science (i.e. the objective impact of flow on environmental attributes) from values (i.e. trade-offs between environmental and economic values that may also affect flow recommendations). The conclusion by Hatfield and Paul (2015) that different desktop methods emphasize different values indicates that objective science and values are regularly confounded in many desktop models. Although Hatfield and Paul emphasize the need for clarity in management objectives that may involve trade-offs, clarity is equally required in defining what constitutes objective science, and when and where trade-offs enter the process chain that leads to instream flow decisions. To this end, it is useful to recognize a hierarchy of elements that are necessary for ensuring that the roles of science and values are explicit in the instream flow decision-making process (Figure 1). These elements are briefly considered below.

Figure 1. Flow diagram illustrating the ideal separation of science and values in the steps leading to flow regulation (see text for detailed description).

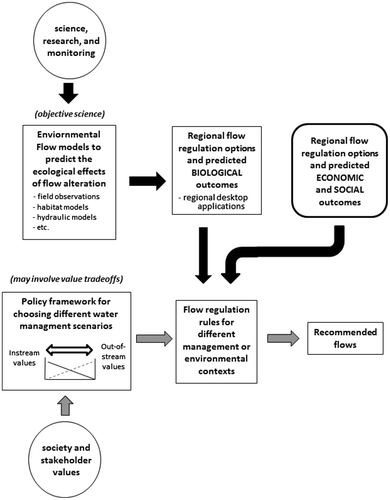
Element (1) Identification of higher level management objectives for flow regulation (policy guidance; explicitly value-based)

Higher level policy objectives are the first step where values may be identified and potentially traded off. For example, policy objectives may range from (a) manage flows so there is no negative impact on instream values like habitat, production or biodiversity; to (b) impacts may be acceptable if the economic benefits are high and harm is restricted within defined limits; or (c) a variable level of harm may be deemed acceptable depending on the specific ecological/economic context (cost/benefit) of the proposed water withdrawals.

Specific value trade-offs are implicit in all of the above policy options. For (a), environmental attributes are explicitly recognized as protected values (sensu Chan 2008) and given primacy over economic benefits (i.e. no trade-off is permitted). For (b), some specified level of harm is allowed, i.e. environmental values are protected beyond a specified level of impact; and in (c) neither environmental nor competing economic values are given primacy, and broad trade-offs among values are entertained. In this last case, detailed guidance on the context-specificity of value trade-offs is needed to ensure consistency in outcomes. These examples are not intended to be prescriptive or exhaustive, but rather to illustrate the range of embedded values and potential trade-offs in management objectives, and the importance of making them explicit. While detailed trade-off assessments are most common in rivers with significant ecological, economic and stakeholder interests (Poff et al. 2003, 2015), the trade-offs implicit in more generic flow management decisions – where desktop applications are commonly used – should also be clearly understood. Similarly, structural limitations built into desktop applications also need to be clearly understood; desktop methods that are explicitly designed to address low-flow concerns are less likely to protect instream values across the full hydrograph (e.g. flow needs for fish passage or spawning).

Element (2) Identifying how changes in flow alter environmental/ecological attributes (explicitly science-based)

Establishing relationships between flow and ecological values (e.g. fish production, biodiversity, stream health) is a purely science-based exercise (Arthington et al. 2006; Poff and Zimmerman 2010), and has been emphasized as the key information bottleneck in many instream flow methodologies (e.g. ELOHA, Poff et al. 2010). Desktop methods explicitly include some assumed relationship between flow and ecological condition. This step is essentially value-free, beyond the implicit recognition that ecological attributes have value and are therefore the focus of efforts to manage the environmental impacts of flow regulation. This step also generates the core information required to evaluate instream flow needs and trade-offs, along with relationships between flow and out-of-stream benefits, and often represents a major source of uncertainty, considered in more detail later.

Element (3) A transparent regulatory framework based on 1–2 above that separates science and values in the decision-making process (Figure 1)

Many frameworks have been developed and implemented for managing instream flows. The degree to which they clearly articulate values in higher level objectives and separate science and values in the decision-making process varies; a comprehensive review is beyond the scope of this discussion, and readers can refer to Richter et al. (2012) and Kendy, Apse, and Blann (2012) for examples of frameworks with clearly defined higher-level values that are supported by specific flow management rules with the underpinning science and criteria for trade-offs clearly articulated.

Element (4) Specific flow management rules that clearly define the nature of any trade-offs that may be entertained among instream and out-of-stream values (based on 1 above), including clear guidance on the contexts where different rules and trade-offs should be applied (incorporates value trade-offs)

If trade-offs are permitted between environmental and out-of-stream values, rules that provide context-specific guidance are essential to ensure some level of consistency in management. Regulations that allow different levels of impact to fishless vs. fish-bearing streams with respect to riparian management or instream flows (e.g. Hatfield et al. 2003) are one example. A lower level of protection is often given to fishless streams, commensurate with ensuring that there are minimal impacts to downstream fish-bearing reaches. It is implicit that reduced protection to fishless streams is based on society valuing the protection of fish (vertebrates) more than the protection of invertebrates, and society is therefore prepared to entertain a higher level of impact to fishless streams, although this rationale is rarely articulated. Alternatively, invertebrate populations and communities may be considered more generally resilient than fish or vertebrate populations, and consequently deemed to warrant a lower level of protection to achieve similar management outcomes; in this case no value trade-off underlies differences in fishless/fish-bearing stream regulations. Regardless, clear separation of science and values is best served when the rationale underling cryptic value trade-offs in management rules is made explicit.

The first potential entry point where cryptic values can manifest is in the choice of regulations that identify either a no-flow (hands-off) threshold below which water withdrawals are not permitted, vs. regulations that allow water withdrawals at all flows. Low-flow cut-offs may ensure greater protection of instream values, but at the cost of potential hardship to out-of-stream users. Second, if low-flow cut-offs are identified, the specific choice of flow threshold beyond which no withdrawals are permitted may also represent a value trade-off. For example, the Alberta desktop method recommends that an 80% flow exceedance value be adopted to protect values associated with low flows (i.e. water withdrawals would not be permitted 20% of the time, on average; Locke and Paul 2011). In contrast, a much lower 95% flow exceedance value is recognized by the Environmental Agency in England and Wales as the threshold for exercising caution in water abstraction (Armstrong and Nislow 2012), indicating a different trade-off between instream and out-of-stream values.

The choice of “performance measure” used by a flow management rule or desktop application may in itself have embedded values. For example, the Presumptive Standard approach (Richter et al. 2012) allows up to 10% of water extraction at all flows and is designed to be protective of the natural flow regime, and therefore protects higher channel-forming flows, but not necessarily low flows in the absence of a lower cut-off threshold, thereby implicitly giving greater protection to higher flows. In contrast, the common application of the Tennant method is to protect low-flow habitat for salmonids, either for summer rearing or overwintering, by identifying a threshold below which water should not be abstracted; while the Tennant application may be precautionary with respect to low flow fish habitat, it may not be protective of higher (i.e. channel-forming or fish passage) flows, implying that low-flow values (in this simplistic example) are valued more than high-flow ones which are better protected by the Presumptive Standard. Note, however, that this interpretation follows Hatfield and Paul’s comparatively narrow interpretation of the Presumptive Standard; Richter et al. (2012) are explicit that the Presumptive Standard approach is intended to protect the natural shape of the annual hydrograph, and may not be protective of ecological function at low flows. In fact, three of the four examples that Richter et al. cite in their seminal 2007 paper incorporate low-flow cut-offs, in recognition of the fact that even limited water withdrawals at very low flows may result in strong negative impacts to biological values. Finally, the Department of Fisheries and Oceans (DFO) Framework method discussed by Hatfield and Paul (2015) identifies a lower no-take threshold while also limiting abstraction at higher flows using the Presumptive Standard approach, weighting values similarly across all flows, which is typical of holistic approaches that try to manage for ecological attributes across the full hydrograph (i.e. Building Block approach; Gopal 2013; Linnansaari et al. 2012).

Potential consequences of embedded assumptions in biological performance measures

Accurate flow-ecological response relationships are essential for properly characterizing trade-offs between instream and out-of-stream uses. The importance of embedded assumptions in flow–ecological response relationships can be understood by examining the biological performance metric chosen by Hatfield and Paul (2015) to compare different desktop models. Hatfield and Paul (2015) created a simple discharge–ecological response function (their performance measure) by assigning flows in excess of 20% mean annual discharge (MAD) a score of 1 (maximum habitat suitability), and assigning a score of 0 (no suitable habitat) to zero discharge, with a linear response in between (Figure 2a). The logic behind their index was described as follows:

…PMs [performance measures] were developed as indicators of instream ecological values for fish, using a simple habitat-rating curve based on 20% MAD, which corresponds to the widely used Tennant value for “good” habitat (Tennant 1976). Support for a ~20% MAD threshold comes from Rosenfeld and Ptolemy (2012), who showed that food availability for rearing Coho juveniles declined substantially at flows below this level. Also, 20% MAD was a value that represented maximum or near-maximum weighted useable area for rearing juveniles of several species of salmonids in western North America streams (Hatfield and Bruce 2000). For the biology PMs, all flows ≥ 20% MAD were assigned a habitat score of 1 (i.e. maximum suitability), zero flow was assigned a score of 0 (i.e. no suitability). All flows < 20% MAD were assigned a habitat score based on a linear relation between 0 and 1…” (310).

Figure 2. Habitat quality score (rating curve for generating biological performance metrics) as a function of mean annual discharge (MAD) for (a) the relationship used by Hatfield and Paul (2015) assuming that habitat quality asymptotes at 20% MAD; (b) assuming habitat quality asymptotes at 30% MAD; (c) assuming a positive x-intercept, e.g. for species that require higher velocity habitats; and (d) assuming a non-linear biological response to flow.

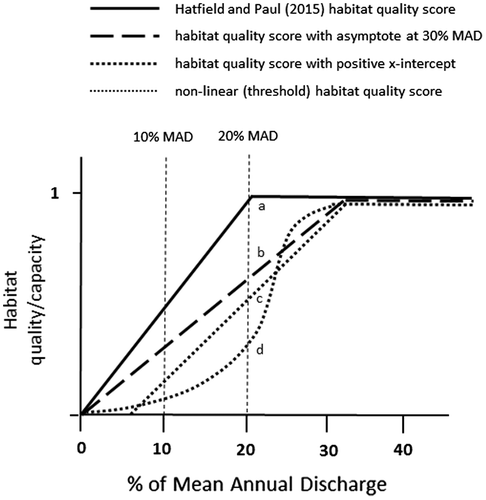
Generating a curve to represent the biological response to flow is a critical step in assessing the consequences of flow regulation (Arthington et al. 2006). Such curves have three main attributes that exert leverage on the predicted consequences of water withdrawals. The first is the threshold discharge where habitat quality begins to decline (or, conversely, the discharge where it is maximized; Figure 2), the second is the x-intercept (the discharge where habitat suitability is 0); and the third is the assumed shape of the curve (linear vs. non-linear). Hatfield and Paul identify 20% MAD as the threshold discharge below which habitat quality declines, and cap habitat quality at a value of 1 for flows in excess of 20% MAD, citing Tennant (1976). However, this is an inaccurate citation, as Tennant (1976) identifies 20% MAD as “fair or degrading” habitat from April to September, when “good to excellent” habitat is in the range of 40–50% MAD (Binns and Eiserman 1979; Tennant 1976). Although Tennant does identify winter flow as “good” at 20% MAD, “excellent to outstanding” winter flows remain in excess of 20% MAD according to Tennant. Capping habitat quality at a value of 1 for flows in excess of 20% MAD is thus inconsistent with Tennant (1976), and implicitly discounts the value of low flows above a 20% MAD threshold.

This is illustrated in Figure 2. If, for the sake of argument, 30% MAD is taken as the flow that maximizes habitat quality, habitat ratings at low flows are considerably reduced (Figure 2b; habitat quality at 10% MAD is 0.5 using the Hatfield and Paul flow–ecological response relationship, and 0.33 using 30% MAD as maximum habitat quality). Similarly, the assumed intercept also influences habitat quality. Species with a positive x-intercept (e.g. fish that require fast-water habitat that is absent at zero discharge) may experience even lower habitat quality at low flows (e.g. 0.2 at 10% MAD; Figure 2c). Note, however, that some species may have a negative x-intercept, e.g. suitable habitat may be present for still-water species even at zero discharge. Finally, non-linear threshold responses to flow are common (Arthington et al. 2006), and this may further reduce habitat quality at low flows (e.g. 0.1 at 10% MAD; Figure 2d). Collectively, the composite flow–ecological response relationship generated by Hatfield and Paul tends to minimize the impacts of predicted water withdrawals by selectively reducing habitat quality at higher flows and potentially inflating it at lower flows. This may be inconsequential when applying a composite discharge–ecological response relationship for the purpose of comparing different desktop models, as used by Hatfield and Paul (2015). However, consequences of applying this relationship to setting actual instream flows could be significant, as it appears biased towards minimizing the potential biological consequences of water withdrawals. This example highlights the sensitivity of flow-ecological response relationships to the choice of parameter values, and the importance of properly rationalizing them if their technical basis is poorly supported.

In this case, more credible alternatives exist to the Hatfield and Paul (2015) rating curve. For instance, Hatfield and Bruce (2000) derived relationships between optimal flow and MAD (used here as an index of stream size) based on meta-analysis of maximum weighted usable area from 127 PHABSIM (Physical Habitat Simulation) modelling studies from western North America. Their derived relationship for optimal juvenile rearing flows for generalized stream salmonids (Figure 3a, expressed as a percentage of MAD) shows that optimal flows are higher in small streams and decline with stream size. This trend has been noted elsewhere (e.g. Jowett 1997), and is driven by higher average water velocity in larger streams and rivers, which generally require lower relative discharge to achieve the intermediate velocities preferred by juvenile salmonids (Rosenfeld et al. 2007). This relationship provides a quantitative basis for adjusting the threshold discharge where habitat quality declines, as illustrated in Figure 3b. Although more realistic than fixing optimal discharge at 20% MAD regardless of context, such a rating curve approach should nevertheless be applied with great caution, because it is based on modelled trends in available habitat from PHABSIM studies which remain poorly validated. In addition, the relationship cannot reliably be extrapolated to infer optimal flows in smaller streams below ~3 m³·s⁻¹ MAD, as it greatly overestimates optimal flows below this stream size threshold (e.g. see Figure 7b in Rosenfeld et al. 2007). However, it provides some empirical basis for inferring optimal flows as a function of stream size, and predicts optimal flows for smaller streams (where desktop approaches are more likely to be applied) closer to the range of percentage of MAD identified as optimal in earlier studies (e.g. Tennant (1976; Binns and Eiserman 1979; but see also Newcombe and Ptolemy 1985).

Figure 3. (a) Optimal flow (expressed as a percent of mean annual discharge [MAD] in m³·s⁻¹) that maximizes modelled weighted useable area for juvenile salmonids in PHABSIM studies from western North America, plotted as a function of stream size indexed by mean annual discharge (MAD). Optimal flow = [2.71^{(−6.12+(0.679 ln(MAD*35.3))+(1.77 ln(49)))}] · 35.3⁻¹ · MAD⁻¹. (b) Variable rating curves (inferred flow-ecology relationships) that result from higher optimal flows in smaller streams illustrated in (a), resulting in displacement of the threshold for decline in habitat capacity to higher flows in smaller channels. The solid black line represents the performance curve used by Hatfield and Paul (2015). Note that lines are displaced slightly to minimize visual overlap.

Uncertainty and value trade-offs

The true ecological impacts of flow alteration are often highly uncertain (Castleberry et al. 1996; Williams 1996, 2010), even when considerable resources are available for detailed instream flow studies (e.g. Bradford et al. 2011; Patten et al. 2001; Poff et al. 2003). In principle, this uncertainty is usually lowest at the extremes of flow alteration (e.g. under very large or very small water withdrawals; Figure 4). Uncertainty in ecological effects at intermediate levels of flow alteration allows considerable scope for interpretation of acceptable impact levels depending on risk tolerance, and provides another entry point for values to influence environmental flow determinations. For example, in the absence of clear policy guidance, flow thresholds can be chosen that are either precautionary with respect to instream values, or precautionary with respect to out-of-stream uses (vertical lines in Figure 4), based on identical information. Probability-based approaches incorporating the likelihood of risk to ecological values have been proposed (e.g. Turner et al. 2016), but the perceived level of acceptable risk that harm will occur (tolerance for error) to either instream or out-of-stream values remains a value-based decision.

Figure 4. Hypothetical relationship between confidence in the degree of ecological impairment and flow alteration. In principle, the range of greatest uncertainty in the impacts of water withdrawal at low flows is at intermediate levels of water extraction (i.e. impacts of very small withdrawals are likely to be low with a high level of confidence; impacts of very large withdrawals at low flow are likely to be significant with a reasonable level of confidence).

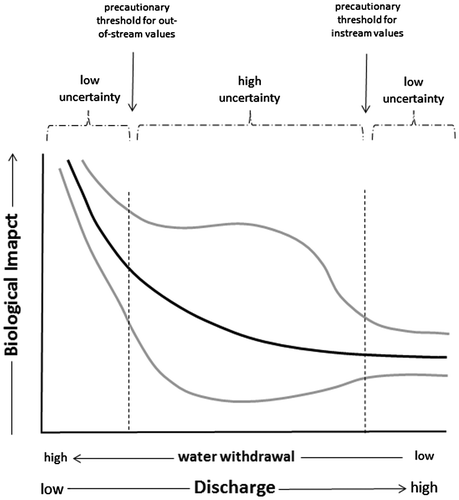
A primary goal of instream flow science is to reduce uncertainty around the biological response to flow alteration. The cost–benefit decision on how much to invest in reducing this uncertainty is itself a value judgement, and is reflected in the research investment that society makes in environmental flow science. Cost-effective approaches for reducing uncertainty in the consequences of flow regulation are essential, and centre on developing accurate regional flow-ecological response relationships (Arthington et al. 2006). This is best achieved through co-ordinated regional research programs, and may include flow manipulation and adaptive management experiments (Bradford et al. 2011; Poff et al. 2010; Souchon et al. 2008), as well as routine monitoring of regulated streams and rivers as part of water licensing agreements. While data from routine monitoring may contribute meaningfully to the development of regional flow-ecology relationships, they are generally not a substitute for a targeted research program and the statistical power associated with carefully designed regional studies. Jurisdictions that have invested in research (e.g. examples in Kendy, Apse, and Blann 2012) generally develop the strongest empirical basis for regulating flows.

The detection limits chosen to monitor ecological impacts of flow regulation may also involve non-transparent value trade-offs. Statistical power will establish the minimum detectable change in ecological attributes associated with flow alteration, which will, by default, effectively set the level of allowable harm; i.e. if change in ecological function is below the detection threshold, then it will be acceptable by virtue of the fact that it is undetectable. Since the minimum detectable effect size depends on the resources invested in monitoring and assessment, the choice of minimum detection threshold represents an additional opportunity for value trade-offs, e.g. between investment in assessment vs. the perceived value of detecting an impact. For example, Michigan state established a maximum allowable reduction in fish habitat capacity of 10% for coldwater streams (Zorn, Seelbach, and Rutherford 2012). However, other protocols may require considerably lower sampling power (e.g. sufficient to detect only a 50% or larger change in ecological attribute such as fish biomass; Hatfield, Lewis, and Babakaiff 2007; Lewis et al. 2012), which by default sets a much larger tolerance for ecological impact.

Desktop approaches and embedded values

Hatfield and Paul highlight the importance of making explicit the value trade-offs that may be embedded in desktop tools, and how these trade-offs align with policy guidance. However, not all approaches necessarily specify trade-offs. For example, Tennant does not specifically recommend a particular flow, but rather identifies how habitat quality changes with flow (e.g. Tennant presents a categorical flow-ecological response relationship). Generic desktop approaches that are based on a sliding scale of ecological quality as a function of discharge, like Tennant, allow the user to transparently and subjectively choose the level of habitat protection they desire, i.e. the user specifies the value trade-off.

The specific flow thresholds chosen by Hatfield and Paul (2015) for their application of the Tennant method (20% MAD in winter, 40% MAD in summer) is not a prescriptive recommendation of the Tennant approach but rather represents a specific value trade-off chosen by Hatfield and Paul for their modelling scenarios, i.e. it is a subjective choice of threshold on the Tennant habitat quality scale. On the other hand, regionally customized desktop tools like the BCIFM (Hatfield et al. 2003) and the DFO Framework for Ecological flow requirements (DFO 2013) are indeed prescriptive with specific built-in flow recommendations that allow no subjective choice of threshold by the user, so that the value trade-off is embedded in the assessment tool. For example, the DFO method allows a maximum water diversion of 10% of instantaneous flow with a low-flow cut-off at 30% MAD; in contrast, the BCIFM has no low-flow cut-off where withdrawals are prohibited, and allows anywhere from a minimum 10% diversion at low flows to 80% diversion at high flows, which would not necessarily be protective of high flow needs, e.g. for migratory fish passage at difficult barriers. In this case the DFO framework flows are more protective of environmental values, and therefore have a very different embedded value-trade-off than the BCIFM method.

Ideally, desktop or other flow decision tools should provide objective guidance on how ecological and environmental attributes change with flows (or advice on the likelihood of change). With this information, tolerance for different levels of impact to environmental attributes (the value-based trade-off) should follow as a management decision based on clearly defined policy and management objectives. Regional policy objectives and trade-offs can be directly built into a customized tool using context-specific flow regulations (e.g. the proportion of flow that can be diverted, or no-take cut-off thresholds; see examples in Richter et al. 2012 and Kendy, Apse, and Blann 2012). However, the science rationale for any trade-off and why specified rules or thresholds are deemed protective of environmental values needs to be clearly presented. If an “off-the-shelf” tool from the published literature is adopted, then the built-in value-trade-offs, if any, need to be consistent with policy guidance that specifies the context where trade-off are or are not considered appropriate (Element 1 above). Ideally, desktop tools should be customized to match clearly defined policy and management objectives, rather than the other way around.

Evaluating desktop models against a common set of standardized measures, as presented by Hatfield and Paul, may be a useful exercise for comparative purposes. However, desktop or other instream flow models are best validated against actual benchmark measurements of biological response to flow regulation, rather than indirect metrics that are thought to be correlated with ecological attributes. Evaluating model predictions against the observed biological response to altered flow (the flow–ecology relationships of Poff et al. 2010) needs to be the gold standard by which performance of difference models is judged. Directly measuring biological responses to flow is not a simple task, but is essential for model evaluation and generating credible regulatory frameworks for environmental flow needs.

Acknowledgements

We thank Scott Babakaiff and Jennifer Turner for helpful comments on this manuscript, but the authors bear sole responsibility for the final content.